Nb impurity-bound excitons as quantum emitters in monolayer WS₂

Abstract

Point defects in crystalline solids behave as optically addressable individual quantum systems when present in sufficiently low concentrations. In two-dimensional (2D) semiconductors, such quantum defects hold potential as versatile single photon sources. Here, we report the synthesis and optical properties of Nb-doped monolayer WS₂ in the dilute limit where the average spacing between individual dopants exceeds the optical diffraction limit, allowing the emission spectrum to be studied at the single-dopant level. We show that these individual dopants exhibit common features of quantum emitters, including narrow emission lines (with linewidths <1 meV), strong spatial confinement, and photon antibunching. These emitters consistently occur within a narrow spectral range across multiple samples, distinct from common quantum emitters in van der Waals (vdW) materials that show large ensemble broadening. Analysis of the Zeeman splitting reveals that they can be attributed to bound exciton complexes comprising dark excitons and negatively charged Nb.

Introduction

Defects in crystalline semiconductors are quantum systems that possess unique local electronic structures. When sufficiently isolated from one another, these defect-derived states can be individually addressed by optical means. The quantum nature of such isolated defects manifests in non-classical statistics of emitted photons, which is of fundamental importance to quantum technologies¹. Intentional incorporation of dilute impurities is a promising approach to achieving single photon emission as previously shown in various wide-bandgap materials^2,3 and conventional semiconductors^4,5.

Two-dimensional (2D) semiconductors, such as monolayer transition metal dichalcogenides (TMDs), are an attractive platform to realize single-photon sources by quantum defect engineering due to their versatility and ease of integration into on-chip photonics⁶. While single photon emission in monolayer semiconductors has been widely reported, these emitters typically depend on naturally occurring defects whose origins remain unclear⁷. The emitters therefore often lack spectrally deterministic character, displaying variability in their energy over tens of millielectronvolts (meV). This variability, sometimes referred to as ensemble broadening, describes the energy distribution of individually addressable emitters. It arises from non-uniform strain, dielectric environment, and electrical potential across the sample. Recently, defect engineering by ion beam irradiation has been shown to reduce the ensemble broadening of the emitters to some extent^8,9. Impurity doping is an alternative approach to achieving virtually identical emitters. However, maintaining precise control over impurity concentrations within the parts-per-million (ppm) range, where quantum emission characteristics are expected, remains a challenge^10,11.

Here, we demonstrate the synthesis of Nb-doped monolayer WS₂ in dilute dopant concentrations and investigate its optical response as it approaches the single impurity limit. We show that Nb dopants manifest as an intense, inhomogeneously broadened emission peak below the free exciton lines at high concentrations. In contrast, at concentrations approaching a few ppm, they manifest as a single, spectral-resolution-limited peak. In this dilute limit, the emitters exhibit photon antibunching and ensemble broadening below 5 meV, which is more than an order of magnitude smaller than that of strain-induced emitters. Further, we show that these quantum emitters can be best described as bound exciton complexes with partially free dark exciton character.

Results

Synthesis of WS₂ monolayers with tunable Nb doping

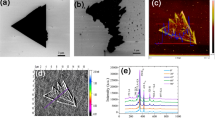
Nb is known to be an acceptor dopant in group six TMDs, characterized by its high solubility up to alloying limits^12,13. While Nb doping in monolayer TMDs has been demonstrated previously^13,14, dilute doping at levels below 10¹¹ cm⁻² remains largely unexplored^11,15. In this study, we prepare Nb-doped WS₂ by chemical vapor deposition (CVD) in vapour-liquid-solid mode using liquid-phase metal precursors as established in our previous works^12,16,17. To achieve controlled doping in the dilute limit, we apply serial dilutions of the Nb precursor solution across five orders of magnitude prior to its mixing with the W host precursor solution. The mixture is then drop-cast onto a SiO₂/Si substrate and reacted with S vapor at 850 ^oC to yield monolayer WS₂ crystals with Nb concentrations ranging from 10¹³ cm⁻² down to 10⁸ cm⁻² (see Supplementary Fig. 1 and Methods for detailed synthesis protocols). The synthesized monolayer crystals are lifted off from the growth substrate and encapsulated between hBN layers to minimize extrinsic disorder (Fig. 1a, see Supplementary Fig. 2 for fabrication details). To ensure the absence of local strain, which can yield unintentional localized emitters¹⁸, the encapsulated samples are flattened with an atomic force microscope (AFM) tip. The flattened regions of the sample show a smooth surface with sub-nanometer roughness over several micrometer lengths (Fig. 1b).

Fig. 1: Dilution of Nb dopants in WS₂ monolayers.

a Schematic illustration depicting the preparation of WS₂ monolayers with ultra-dilute Nb dopants. CVD denotes chemical vapour deposition and AFM represents atomic force microscopy. b AFM height image of the encapsulated sample after tip cleaning. Shown below the image is the height profile along a line crossing the sample, with its position indicated on the image. Scale bar is 1 µm. c Magnified high-angle annular dark field-scanning transmission electron microscopy (HAADF-STEM) image of Nb dopant in the WS₂, accompanied by the corresponding intensity profile integrated across the row of W atoms where the Nb is situated. d A series of HAADF-STEM images acquired on Nb-doped WS₂ samples at different doping concentrations. Scale bar is 1 nm.

Atomic-resolution Z-contrast imaging of monolayer samples using high-angle annular dark field-scanning transmission electron microscopy (HAADF-STEM) shows that all Nb atoms are substitutional at the W position (Fig. 1c). The Nb concentration, as determined from a series of scanning transmission electron microscopy (STEM) images (Fig. 1d), exhibits a linear relationship with the nominal Nb concentration in the precursor mixture (Supplementary Fig. 3).

Emitter distribution

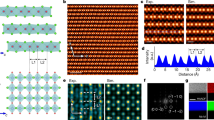
Representative photoluminescence (PL) spectra of the samples are shown in Fig. 2a. Nb-doped samples exhibit low energy emission features below 1.95 eV that are absent in undoped samples. The intensity of the broad low-energy emitter (${{\rm{NbX}}}_{{\rm{G}}}$) scales with the Nb concentrations, indicating that these emitters arise from transitions involving a large number of Nb centers (Supplementary Fig. 4). In the dilute doping regime of 5 ppm and below, the intensity of the sharp low-energy peaks (${{\rm{NbX}}}_{{\rm{L}}}$) remains largely constant but their occurrence decreases with dopant concentration (Fig. 2c). This observation suggests that each spatially isolated ${{\rm{NbX}}}_{{\rm{L}}}$ peak is associated with one or a few emissive dopants within the excitation spot.

Fig. 2: Evolution of emission features as a function of Nb-doping.

a Typical photoluminescence (PL) spectrum of WS₂ monolayers with varying Nb-doping levels, with sharp Nb peak (${{\rm{NbX}}}_{{\rm{L}}}$) and broad Nb peak (${{\rm{NbX}}}_{{\rm{G}}}$) identified. Peak positions related to neutral excitons (${{\rm{X}}}^{0}$), negative trions (${{\rm{X}}}^{-}$), dark trions (${{\rm{X}}}_{{\rm{D}}}^{-}$), and dark excitons either in phonon replica form or bound to native defects (${{\rm{X}}}_{{\rm{D}}}^{0}$/${{\rm{DX}}}_{{\rm{D}}}^{0}$) are shown for reference. b Two distinct Nb-induced emissions—a ${{\rm{NbX}}}_{{\rm{G}}}$ peak and a ${{\rm{NbX}}}_{{\rm{L}}}$ peak—each fitted with different functions. c PL intensity maps of ${{\rm{X}}}^{0}$, ${{\rm{NbX}}}_{{\rm{G}}}$ and ${{\rm{NbX}}}_{{\rm{L}}}$ peaks in samples doped at different concentrations. Each column shows PL maps for different peak energies for the same sample. The contours of the monolayers are shown by white dashed lines. Black and grey pixels denote areas where the respective peaks were not detected: black for areas within the sample region and grey for areas outside the sample. The detection thresholds for ${{\rm{X}}}^{0}$ and both Nb peaks (i.e., ${{\rm{NbX}}}_{{\rm{G}}}$ and ${{\rm{NbX}}}_{{\rm{L}}}$) are set to 5% and 20% of the highest intensity in the map, respectively. Scale bar is 5 µm. Spectra in (a and c) were obtained with a 473 nm continuous -wave (CW) laser with a power of 5 µW. Spectra in (b) were obtained with a 532 nm CW laser with a power of 0.5 µW. All measurements were conducted at a temperature of 4 K.

Samples with Nb concentrations equal to or exceeding 50 ppm predominantly display broad emission features with linewidths of approximately 20 meV at 4 K. The peaks can be fitted with a few Gaussian functions, indicating that inhomogeneous broadening defines their line shape (Fig. 2b). The appearance of multiple peaks may be attributed to various Nb defect configurations such as Nb-S-vacancy pairs (Supplementary Fig. 5) and Nb-dimers (Supplementary Fig. 6), which become appreciable at higher Nb concentrations. Consequently, the Nb-derived emission is more prone to disorder broadening with increasing Nb-doping (see Supplementary Note 1 for details). In contrast, samples with estimated Nb concentrations of 5 and 0.1 ppm exhibit sharp emission features with linewidths around 310 µeV. These peaks exhibit Lorentzian line shape with an asymmetric tail, indicating negligible inhomogeneous broadening contributions.

Confocal PL mapping shows that the ${{\rm{NbX}}}_{{\rm{G}}}$ peaks appear uniformly across the sample whereas the ${{\rm{NbX}}}_{{\rm{L}}}$ peaks are observed only at selected spots (Fig. 2c). This trend is generally consistent with the expected reduction in the number of Nb atoms within the laser spot with decreasing concentration, approaching the limit of single emitters.

Single photon characteristics

The narrow emission peak in the 0.1 ppm sample (${{\rm{NbX}}}_{{\rm{L}}}$) can be attributed to individual Nb, given that the expected average distance between the impurities exceeds the diffraction limit of the excitation laser. This peak displays blinking and spectral jittering (Fig. 3a), which are common features of quantum emitters located close to the material surface. Under non-resonant continuous-wave (CW) laser excitation, the emitter saturates quickly with increasing laser power (Fig. 3b, Supplementary Fig. 7), in line with the relation for excitons bound to a small number of defects that can be described as a two-level system¹⁹. This saturation behavior is well described by $I=2{I}_{{\rm{sat}}}/(1+{P}_{{\rm{sat}}}/P)$, where $I$ (${I}_{{\rm{sat}}}$) is the (saturated) PL intensity and $P$ $({P}_{{\rm{sat}}})$ is the (saturating) excitation power. The extracted ${P}_{{\rm{sat}}}$ is 0.5 µW, which is almost three times lower than the values reported for dilute chalcogen defects at a density of 10¹⁰ cm⁻² (i.e., 10 ppm) under similar excitation conditions^20,21.

Fig. 3: Optical characteristics of the Nb-induced single photon emitters.

a Time evolution of PL spectra highlighting the region of ${{\rm{NbX}}}_{{\rm{L}}}$ as well as free trions and neutral exciton peaks over 60 s. b Power dependence of the integrated PL signal. Error bars represent standard deviation of the fitted curves. ${P}_{{\rm{sat}}}$ denotes the saturating laser power of ${{\rm{NbX}}}_{{\rm{L}}}$. c Time-resolved PL data fitted to a triexponential function, revealing three distinct lifetime components: ${\tau }_{1}$, ${\tau }_{2}$, and ${\tau }_{3}$.The long component (light grey curve) corresponds to the broad background (BG) feature in the bottom panel of 2b (i.e., the grey area underneath the sharp Nb peak). The sharp Nb peak represents the single photon emitter (SPE). The instrumental response function (IRF) of ~0.2 ns is also shown. The time difference $\,{\tau }_{0}$ between the rise time of the IRF and the emitter is indicated. d Second-order photon correlation of the two faster-decaying components marked with light and dark orange lines in (c). Intensity correlation shows antibunching with 0.27 ± 0.22 at zero delay. Uncertainty is obtained from the standard deviation of 390 peaks for t ≠ 0. A 532 nm CW laser is used in (a, b), whilst a pulsed laser tuned to the A-exciton resonance is used in (c, d). All measurements were conducted at 4 K.

The PL decay transient of the emitter (Fig. 3c) can be described by a triexponential decay function comprising fast (0.6 ns), moderate (80 ns), and long (1600 ns) decay components. From the intensity ratios, we attribute the long decay component to the broad background emission and the shorter-lived components to the sharp Nb peak (see Supplementary Note 2 and Supplementary Fig. 8 for more details). A delay time of 0.5 ns in the intensity peak relative to the excitation pulse indicates the time between the exciton generation and its capture by the Nb centers.

We investigate the quantum nature of the emitter by collecting photons in the spectral window of 10 meV around the 1.92 eV peak and examining their second-order autocorrelation function (g⁽²⁾(t)) with a Hanbury Brown and Twist (HBT) interferometer. Due to the spectral overlap of the long-lived broad background emission (see Supplementary Note 3 for its origin), which is only weakly non-classical, and the sharp peak of interest, we differentiate their photon statistics by utilizing pulsed laser excitation and deconvoluting the g⁽²⁾(t) function according to the known lifetimes of the components. Specifically, we bin the coincidence counts in 32 ns intervals aligned with the excitation pulse to capture the photon statistics of the localized Nb-peak as shown in Fig. 3d (see Supplementary Note 4, Supplementary Fig. 9 and 10 for details). Comparison of the zero-delay dip with the integrated counts at delays up to 200 µs yields g⁽²⁾(0) = 0.27 ± 0.22, revealing the single-photon nature of the ${{\rm{NbX}}}_{{\rm{L}}}$ peak, with an estimated quantum yield of ~10⁻⁵ (see Supplementary Note 5 and Supplementary Fig. 11).

Origin of the Nb-induced single photon emitters

Substitutional Nb impurities are known to be p-type dopants in group 6 TMDs^10,12. Our gate-dependent PL measurements show that the dilute impurities are not sufficient to compensate for the natural n-doping of the host, suggesting that all Nb atoms are negatively charged (Supplementary Figs. 12, 13). Such negatively charged acceptors are predicted to trap free excitons with a large binding energy, resulting in the formation of bound exciton complexes²². We perform magneto-optical spectroscopy to verify the exciton character of the ${{\rm{NbX}}}_{{\rm{L}}}$ peak. Polarization-resolved PL spectra are obtained by exciting the sample with linearly polarized light in the presence of an out-of-plane magnetic field (B_⊥) up to 9 T (Faraday configuration). Figure 4a shows that the ${{\rm{NbX}}}_{{\rm{L}}}$ peak exhibits a clear Zeeman splitting, resembling that of spin-forbidden dark trion peak (X_D^-). The distinct splitting with the “cross” pattern (Fig. 4b) is consistent with the behavior of spin-forbidden dark excitons^23,24,25. The g-factor of the ${{\rm{NbX}}}_{{\rm{L}}}$ is determined to be ~ −10.4, comparable to that of ${{\rm{X}}}_{{\rm{D}}}^{-}$ (g ~ −12.3) (Fig. 4c, Supplementary Fig. 14). This g-factor is similar to that of common quantum emitters in W-based TMDs (g = −8 ~ −13)^26,27,28. Unlike the native and strain-induced quantum defects in W-based systems, ${{\rm{NbX}}}_{{\rm{L}}}$ exhibits negligible zero-field splitting, which is a defining feature of neutral excitons trapped in a symmetric confining potential²⁹. The negligible linear polarization anisotropy from these emitters (Supplementary Fig. 15) is consistent with the nonpolar nature of an isolated substitutional Nb defect.

Fig. 4: Origin of the localized Nb emitters.

a Colour plot of the polarization-resolved magneto-PL spectra of a dilute Nb-doped sample measured in the Faraday configuration. The spectrum in the upper panel shows the PL spectrum at 0 T. b PL spectra of ${{\rm{NbX}}}_{{\rm{L}}}$ at selected fields (B_⊥), with the splitting of ${{\rm{NbX}}}_{{\rm{L}}}$ tracked with dashed lines. c Zeeman splitting of ${{\rm{NbX}}}_{{\rm{L}}}$ as a function of B_⊥, where the g-factor is derived from the linear fit (red line). Magneto-PL measurements were conducted at a temperature of 1.6 K with a 532 nm CW laser. d Density functional theory (DFT) band structure with spin-orbit coupling (SOC) for a 10 × 10 supercell of WS₂ with one Nb⁻¹-substituted W atom, is shown on the left panel. The corresponding projected density of states (pDOS) of the total orbital and orbital contributions of Nb⁻¹ which are overlayed over the total density of states (DOS) in grey shade, is shown on the right panel. e Schematic of the band structure at K’ with the single-band g-factors. ${g}_{{CBM}}^{\uparrow (\downarrow )}$ represent the spin-up (spin-down) g-factor of conduction band minimum (CBM) bands, ${g}_{{VBM}}^{\uparrow (\downarrow )}$ represents the spin-up (spin-down) g-factor of valence band maximum (VBM) bands, and ${g}_{{Nb}}^{\uparrow (\downarrow )}$ represents the g-factor of spin-up (spin-down) Nb defect bands. The optical transition responsible for ${{\rm{NbX}}}_{{\rm{L}}}$ is also shown. f Schematic illustration of the excitons diffusing (denoted by the dashed arrows) and eventually binding to a mobile electron or a single Nb ion to emit at energies redshifted by the respective binding energies, indicated by the horizontal dashed lines.

To further verify the origin of the ${{\rm{NbX}}}_{{\rm{L}}}$ peak, we analyze various recombination pathways involving Nb acceptors by comparing the measured g-factors with those obtained by first principles calculations. Our density functional theory (DFT) band structure with spin−orbit coupling (SOC) for a 10 × 10 supercell with one Nb⁻¹ ion substituting a W atom indicates that Nb-induced bands lie just below the valence band maximum (VBM), hybridizing strongly with the valence band states (Fig. 4d). We compute the single-band g-factors for the VBM, conduction band minimum (CBM), and the Nb defect level (${g}_{{\rm{VBM}}}$, ${g}_{{\rm{CBM}}}$ and ${g}_{{\rm{Nb}}}$, respectively). The Nb state predominantly comprises ${d}_{{z}^{2}}$ orbitals and the corresponding g factor is small (${g}_{{\rm{Nb}}}\,$~ −1.0 for spin up and 1.0 for spin down Nb states, respectively). The total g-factor for the spin-allowed transition, involving an electron in the CBM recombining radiatively with a hole at the Nb site amounts to ~ 7.0 for spin-up and ~ 7.6 for spin-down states, respectively. On the contrary, the g-factor for the calculated spin-forbidden transition, which is  ~ −9.4, largely agrees with the experimental observation (Fig. 4e).

We thus conclude that neutral dark excitons bound to ionized Nb, which may be denoted as ${\rm{N}}{{\rm{b}}}^{-}{{\rm{X}}}_{{\rm{D}}}^{0}$, best describes the origin of the ${{\rm{NbX}}}_{{\rm{L}}}$ peak. The brightening of dark excitons bound to Nb centers can be ascribed to the hybridization of VBM with the Nb states, breaking the valley selectivity and leading to an enhanced radiative recombination efficiency of the dark excitons⁷. Additionally, phonon-emitter coupling can also facilitate the formation of an admixture of dark and bright excitons within the same valley³⁰. The energy separation between ${{\rm{X}}}_{{\rm{D}}}^{0}$ and ${\rm{NbX}}$, which is the binding energy of the complex, is ~100 meV. This large binding energy, distinctly greater than that of dark trions (~20 meV), agrees with the expectation that stationary charges are more effective in trapping excitons than free carriers^22,31 (Fig. 4f).

Ensemble broadening of single emitters

We evaluate the spectral reproducibility of the ${{\rm{NbX}}}_{{\rm{L}}}$ in 0.1 ppm samples in comparison with the state-of-the-art quantum emitters in related van der Waals (vdW) materials. In our study, ${{\rm{NbX}}}_{{\rm{L}}}$ peaks across multiple samples consistently fall within an energy range of 20 meV (Supplementary Fig. 16). Figure 5a shows the histogram describing the distribution of 83 ${{\rm{NbX}}}_{{\rm{L}}}$ energies surveyed across four different samples. Two distinct emitter clusters centred around 1.92 eV and 1.93 eV exhibit an ensemble broadening of 1.8 ± 0.7 meV and ~3.5 ± 1 meV, respectively. We speculate that these cluster originate from Nb in different chemical environment such as nearby surface functional groups and chalcogen-site defects.

Fig. 5: Ensemble broadening of 2D quantum emitters.

a Histogram showing the localized Nb emitter distribution (${{\rm{NbX}}}_{{\rm{L}}}$) surveyed across various positions in multiple samples nominally doped at 0.1 ppm. Fitted Gaussian curves for the two main emitter clusters, alongside their full-width-at-half-maximums (FWHM), are shown. Spectra surveyed were acquired with a 473 nm and 532 nm CW laser at 4 K. b Comparison of the ensemble broadening of the 0.1 ppm sample with that of various other two-dimensional (2D) materials, namely strained GaSe³⁵, strained monolayer MoTe₂³⁴, strained WS₂ and WSe₂^32,33, He-ion bombarded MoS₂⁹, beam-treated hBN grown under high-pressure high-temperature^36,37, and annealed C-implanted hBN³⁸. All the data correspond to measurements conducted at cryogenic temperatures. Note: Open symbols represent emitters of unknown structural origin, while solid symbols represent emitters whose structural origin has been identified. Red denotes single-layer chalcogenide semiconductors and blue represent ultrathin hBN (less than 100 nm thick).

Figure 5b presents a comparison of the spectral reproducibility of quantum emitters in various vdW materials, characterized by ensemble broadening at cryogenic temperatures (a more comprehensive survey is presented in Supplementary Table 1 and Supplementary Fig. 17). The comparison is made against different methods used to induce emitters, such as strain^32,33,34,35, beam irradiation^9,36,37 and ion implantation³⁸. Notably, the ensemble broadening of ${{\rm{NbX}}}_{{\rm{L}}}$ is at least one order of magnitude smaller than those of other emitters in 2D TMD systems^9,32,33,34 and is comparable to state-of-the-art emitters in hBN, including those derived from known defect structures^38,39 and produced under refined synthetic conditions^36,37. Moreover, our values are similar to those found in non-vdW systems with known impurity structures, such as Cl-doped ZnSe quantum wells⁴⁰, diamond hosting SiV centers⁴¹, and NV centers⁴². The overall trends suggest that dilute substitutional doping is a promising approach for generating energetically well-defined quantum emitters.

Discussion

We have demonstrated the bottom-up growth of monolayer WS₂ with ultra-dilute Nb dopants. In this concentration limit, individual Nb-derived states can be optically excited one at a time using a focused laser beam, resulting in single photon emission. Unlike point defects in insulators, the excited Nb states are more accurately described as a trion-like bound exciton complex with partial free-exciton character. The binding energy of these complexes are few times greater than that of trions, possibly due to their larger reduced mass.

Our study represents the initial steps towards realizing a broad palette of reliable and robust 2D quantum emitters. It is predicted that excitons form a variety of stable bound complexes with different emission characteristics depending on the defect species. While Nb-doped WS₂ is identified as an attractive system in this study, these emitters require significant enhancements in brightness, purity, and operational temperature to be viable for practical applications. Notably, classical background emission from common defects poses significant challenges. Exploring different impurities in high-quality host crystals may provide critical insights into the design principles necessary for optimizing the characteristics of these impurity-induced emitters.

Methods

Growth of dilute Nb-doped WS₂ monolayers

An initial solution was prepared by dissolving 1 mg niobium (V) oxalate (C₁₀H₅Nb₂₀.H₂O, Alfa Aesar) in 40 mL H₂O, which approximates to 1 at% Nb when mixed with 50 mg of W precursor. The initial solution was then subjected to a series of 10:1 dilution to achieve the desired dilute concentration, governed by the ${C}_{1}{V}_{1}={C}_{2}{V}_{2}$ relationship where C₁(V₁) represents the initial concentration (volume) and C₂V₂ represents the concentration (volume) of the Nb precursor. After a series of necessary dilutions, 50 mg sodium tungstate dihydrate (Na₂WO₄·2H₂O, Sigma–Aldrich) was added to the dilute Nb volume with addition of H₂O to bring to the total water volume to 40 mL, forming the dilute Nb in W precursor mixture. The metal precursor mixture was then drop-cast on SiO₂/Si substrate, followed by a blow-dry with a N₂ gun. A furnace with a 1 in. diameter horizontal fused quartz tube was used for the chemical vapour deposition (CVD) growth. Throughout the growth process, a mixture of 25 sccm of hydrogen/argon (5% H₂/95% Ar) and 25 sccm Ar gas was used as carrier gas; ∼10 mg of S powder was introduced in the upstream region, which reached ∼300 °C during the growth. Before reaching the growth temperature of 850 °C, the furnace was stabilized at 200 °C for 5 min and ramped up at a rate of 20 °C/min, followed by 10 min of annealing at 850 °C. After 10 min of annealing, the furnace was slid to the upstream region to vaporize the sulfur, and the reaction lasted for 5 min. After the reaction, the furnace lid was opened, and the gas flow was increased to 500 sccm to allow for rapid cooling.

STEM sample transfer, imaging and analyses

The STEM samples were prepared with the polycarbonate transfer method as in our previous work¹⁷. HAADF- and MAADF-STEM images were acquired with an aberration-corrected JEM-ARM200F (JEOL) instrument equipped with a cold-field emission gun and an ASCOR probe corrector, which was operated at 80 kV. HAADF- and MAADF-STEM images were collected at semi-angles ranging between 68–280 mrad and 30–120 mrad, respectively, with a convergence semi-angle of 31 mrad.

Peak detection and filtering in PL maps

For the emitter distribution analyses, the photoluminescence hyperspectral data, in the energy range of 1.90 eV to 2.07 eV with a resolution of 1014 steps per pixel, were imported into MATLAB R2023a (v9.14) for further data processing and analysis. Background pixels with low total intensity (i.e., below 0.02 of total normalized background) were removed from the dataset to enhance visualization and focus solely on relevant features. Subsequently, the data from all samples were concatenated to facilitate direct comparisons. A script was developed to remove cosmic signal interference within the photoluminescence spectra. This algorithm employed a peak search methodology to identify cosmic peaks characterized by their intensity (minimum peak prominence of 500) and narrowness (limited to a maximum of 5 data points). Once identified, these cosmic peaks were replaced by the average of the three data points located on both the left-hand side (LHS) and right-hand side (RHS) of the peak. The normalized combined dataset, ranging between 0 and 1 for peak detection, was subjected to further analysis.

A tailored MATLAB script was formulated to execute peak detection and filtering across all pixels in the photoluminescence hyperspectral data. For each pixel, the script applied peak detection algorithms using the ‘islocalmax’ and ‘islocalmin’ functions to identify local maxima and minima in the PL spectra within the specified energy range. Identified peaks were subjected to a set of criteria to confirm the validity of their selection. These criteria encompassed evaluating peak height to discard saturated signals, assessing the distance from neighbouring minima to filter out noise and alleviate broaden peaks, and checking the height difference from the closest minimum to eliminate low-intensity peaks. The script recorded the positions of peaks and intensities of peaks that satisfied all criteria for every pixel.

First, the lowest (${X}_{\min }$) and highest intensities (${X}_{\max }$) in each map were identified. The as-acquired intensity ($X$) of each feature was then normalized using Min-Max normalization, expressed as ${X}_{{norm}}=(X-{X}_{\min })/({X}_{\max }-{X}_{\min })$. This process rescales all data points in the photoluminescence map from 0 (representing the background) to 1 (representing the maximum signal). Specifically, for the ${{\rm{X}}}^{0}$ peak, peaks within the range of 2.05–2.07 eV with an intensity greater than 0.05 of the normalized background were selected. Further analysis was conducted for the Nb signal in the low energy range, specifically below 1.95 eV. Peaks with an intensity greater than 0.2 of the normalized background and a width exceeding 15 data points, classified as ${{\rm{NbX}}}_{{\rm{G}}}$ signals, were selected. Similarly, for ${{\rm{NbX}}}_{{\rm{L}}}$, peaks that showed an intensity above 0.2 of the normalized background but have a width smaller than 15 data points were selected.

Optical spectroscopy

Low temperature photoluminescence measurements and mapping (presented in Fig. 2) were performed using a home-built optical system on the cryostat (Quantum Design PPMS and attocube attoCFM). A 473 nm CW laser (spot diameter ~1 μm²) was used to generate the PL maps by raster scanning the xy piezo stage. The PL spectra were recorded on Andor Kymera 328i spectrometer equipped with Andor iDus CCD.

Time-resolved photoluminescence was acquired in a closed-cycle cryostat (attocube attoDRY1000) coupled with a home-built optical setup. For the lifetime measurement, a pulsed laser (NKT Photonics SuperK FIANIUM) with repetition rate tunable between 1.95 to 78.2 MHz, set to 600 nm was cleaned by a band-pass filter and shone onto the sample through a cold objective lens (f = 2.87 mm, 0.82 NA). The reflected PL signal was collected by the same lens, separated with a non-polarizing beam splitter (NPBS, Thorlabs BS013), filtered by a pair of tunable filters (Semrock Versachrome) and a long-pass filter (Thorlabs FELH0600), before detected by a single photon detector (SPD, Excelitas SPCM-AQRH-16) and a time-correlated single photon counting (TCSPC) module (PicoHarp 300). The integrating spectral window was verified with a spectrometer (Andor IsoPlane320, Kuro2048B, 1800 g/mm 500 nm) by diverting the signal with a removable mirror. For the g⁽²⁾(t) measurement, a NPBS (Thorlabs BS014) was used to split the signal and detect together with another SPD of the same model. A short-pass filter (Thorlabs FESH0700) was installed between the two SPDs to eliminate crosstalk. The TCSPC was operating in the time-tagged time-resolved (TTTR) mode and the data was post-processed to construct the g⁽²⁾(t) curve.

In polarization-resolved measurements, a 532 nm CW laser (Laser Quantum gem 532) was shone onto the sample with the same setup, with an additional polarizer and analyzer placed before and after the laser entering and exiting the NPBS. Their transmission axes are aligned parallel to each other for co-polarization. A half-waveplate (HWP, Thorlabs AHWP10M-580) mounted on a motorized rotational mount (Thorlabs PRM/M1Z8) was installed between the NPBS and the objective lens. The spectrum was collected as a function of the HWP angle.

Magneto-PL measurements were obtained with a 532 nm linearly polarized laser focused onto the sample positioned on a x-y-z-piezo stage in a cryostat (attocube attoDRY2100) filled with He exchange gas cooled to 1.6 K. The magnetic field was applied perpendicular to the sample plane (Faraday configuration) up to 9 T with superconducting coils. The σ⁺ and σ⁻ circular polarization components were resolved by reversing the polarity of the magnetic field whilst collecting the signal through a fixed configuration of a linear polarizer and a λ/4-waveplate.

Device fabrication and gate dependent PL spectroscopy

The sample was coated with LOR 3 A resist and baked for 5 min. Then, a second layer of S1805 photoresist was deposited and baked for 1 min. Laser lithography (Heidelberg Instruments μMLA) was used to deposit the electrodes. Cr and Au electrodes with thicknesses of 3 and 50 nm, respectively, were deposited on the FLG using a standard thermal evaporator. The sample was immersed in PG remover for 1 h and kept at 60 °C to remove the photoresist and lift off the metal. For the measurements, the sample was mounted on a chip carrier positioned on a set of x/y piezo positioners. The sample was excited with a pulsed laser set at 78.2 MHz repetition rate and wavelength of 600 nm. The gate voltage on the sample was regulated with a Keithley source meter.

First-principles calculations

The density functional theory calculations in this work were conducted within the VASP code⁴³ using the Perdew, Becke and Ernzerhof approximation for the exchange-correlation functional⁴⁴. The projected-augmented wave with an energy cut-off 450 eV were used. The Nb⁻¹-doped 10 × 10 supercell (1 at% Nb) was fully relaxed with a single Γ-point until the total energy changes less than 10⁻⁵eV between two consecutive iterations, and all forces are converged to less than 0.02 eV/Å. Spin-orbit coupling was included in the non-self-consistent calculation to obtain the band structure for the 10 × 10 supercell Nb⁻¹-WS₂. The g-factors of the WS₂ CBM and VBM were computed using the numerical approach in Quantum ESPRESSO package⁴⁵ described in ref. ⁴⁶ and ref. ⁴⁷ The g-factor for the flat defect band was estimated by assuming that the valley contribution is negligible. The orbital contribution of the defect band is also taken to be zero because the band arises from ${d}_{{z}^{2}}$ orbitals.