Introduction

Absolutely pure water without any ions is rarely found on our earth and other planets in the universe. The presence of ions affects the structure and dynamics of water in its vicinity differently1,2,3,4, which can influence the processes of ice nucleation5,6, charge transport7,8,9, energy storage10,11 and so on. Among them, understanding the impacts of ions on the icing process is of vital importance as it is related to the origin of life, and undesired ice accumulation often poses a threat to survival of living organisms12. Early studies reported that the size of ice grains can be simply tuned by changing the type and concentration of ions13. It can be attributed to the selective adsorption of ions at the ice/water interface. Besides, the ZnCl2 salt at a specific concentration has been proposed to achieve great modulation effect on the anti-freezing ability of aqueous electrolyte14. Our previous research found that chaotropic-type anions bestow upon water the higher tetrahedral entropy, leading to the lower freezing point of aqueous solutions15. However, the impact of ion concentration is hard to be predicted only through the tetrahedral entropy of water. Despite decades of extensive research14,16,17, a comprehensive understanding of the microscopic mechanisms underlying ionic specific effects (species and concentration) on ice formation and inhibition has remained elusive. This challenging topic is of utmost importance for both fundamental research and practical applications.

Water is widely recognized as an exceptionally poor glass-forming liquid18,19,20, as it readily crystallizes into ice below its homogeneous nucleation temperature21,22,23,24. This characteristic severely restricts its low-temperature applications such as organ cryopreservation, food preservation and energy storage. It is known that the glass-forming ability (GFA) of pure water are strongly influenced by pressure25,26, and adding salt has the similar effect (breaking local tetrahedral order) to applying pressure27. Tanaka pioneeringly proposed a “two-order parameter model” to regulate the GFA of water-salt mixture with varying concentration by balancing bond-order and density-order28,29,30. Therefore, introducing appropriate salts and optimizing the concentration to design a glass-forming liquid (GFL) with ultralow glass transition temperature (Tg), which is always much lower than the melting temperature (Tm), with the relation of Tg ≈ 2Tm/3, would be an attractive anti-freezing strategy31,32. The decrease of Tg enables the constructive solution to remain in a liquid state at lower temperatures over a broad range via bypassing crystallization state, which is closely related to the entropy of solution systems.

Here, we proposed an entropy-driven GFL (EDGFL) with ultralow Tg by modifying salt concentration using water–cesium acetate (CsAc) mixture as a model system. CsAc can be dissolved in water with exceptionally high salt concentrations (>50 mol kg−1), enabling us to explore a wide range of concentrations. The phase transition temperature and concentration of CsAc electrolyte follow a V-shape relationship and the lowest Tg of −128 °C is achieved at 10 m (mol kg−1). Through in-depth molecular dynamics (MD) simulation analysis, we found that the 10 m CsAc electrolyte lies in the most balanced position between tetrahedral entropy of water and two-body pair entropy related to the ions, further expanding the previous understanding of anti-freezing ability modulated only by the tetrahedral entropy of water15. Therefore, this optimized electrolyte can bypass the energy-driven ice crystallization, while effectively avoids too strong interaction between ions in those systems with higher concentrations, thus contributing to the lowest Tg. This optimized EDGFL (10 m CsAc) exhibits a high ionic conductivity of 0.8 mS cm−1 at −80 °C, enabling a PEDOT-based AC line filter to work at the ultralow temperature of −95 °C, and an activated carbon-based supercapacitor to work in an ultra-wide temperature range of −95 to +120 °C with considerable capacitance and excellent stability. Moreover, this optimized EDGFL can be added into the ZnAc2 electrolyte to realize stable Zn-ion batteries in a wide temperature range from −50 to +70 °C. Our proposed physical picture of EDGFL can provide directions for both theoretical advancement and practical applications under extreme climate over the whole universe.

Results

Designing anti-freezing EDGFL

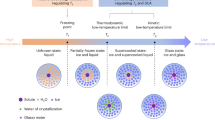
To rationally design anti-freezing EDGFL without a crystallization process, it is essential to study temperature-component binary phase diagrams of solid-liquid transitions. The well-known equilibrium phase diagram describes only stable components, while the non-equilibrium one takes the supercooled and vitrification regions into account33. Figure 1a depicts a typical binary non-equilibrium phase diagram of water–salt system, illustrating three distinct zones denoted as I, II and III. In zone I, aqueous solution undergoes a gradual process of ice precipitation below curve AE. The resulting concentrated solutions remain in a supercooled state below Te until reaching Tg. Two concentration regions (Xe to Xm and Xm to Xd) exist in zone II. The solution located at the region from Xe to Xm remains in a supercooled liquid state below curve GE, and suffers gradual icing process below curve EC before reaching Tg. Within the concentration between Xm and Xd, supercooled liquid state is retained below curve GE without icing process, and eventually turns into glassy state below curve MD. Notably, the solutions at the concentration of Xm deliver the lowest Tg, making them particularly suitable for designing EDGFL. In zone III, the solutions beneath curve BG progressively precipitate hydrated solutes, while the remaining solutions keep in a supercooled state below Tp until eventually transitioning into the glassy state.

Fig. 1: Designing an entropy-driven glass-forming liquid with Tg of −128 °C.
figure 1

a Non-equilibrium binary (water-salt system) phase diagram. Te is the eutectic temperature of solutions. Tp is the peritectic temperature of solutions. Tg is the glass transition temperature of solutions. b DSC test of CsAc aqueous solutions from −170 to +20 °C at the heating rate of 5 °C min–1. c The major phase transition temperature versus the concentration of CsAc. Blue balls, melting temperature Tm; gray balls, glass transition temperature Tg. d In situ optical microscopic observations of CsAc with different concentrations in a cooling process. e The concentration dependence of viscosity η at different temperatures. f Ionic conductivities of CsAc with different concentrations at the temperature range of −80 to + 25 °C. g Modified Walden plot for the 10 m CsAc electrolyte at the temperature range of −80 to 0 °C.

Full size image

To illustrate our design principle for EDGFL, we explore the phase transition behavior of CsAc electrolyte with varying concentrations using differential scanning calorimeter (DSC), which can precisely disclose the thermodynamic change associated with temperature34. Figure 1b displays the heat changes of CsAc electrolyte at different concentrations from 1 to 50 m. Typically, the ice melting process displays sharp endothermic peaks, while the glass-liquid transition exhibits a distinct step35. When the concentration is lower than 7.5 m, the CsAc electrolyte obeys the varying rule in equilibrium phase diagram due to the limited cooling rate33 and only experiences crystalline phase transition during cooling process. When the concentration equals to 7.5 m, in addition to the icing process, glass–liquid transition begins to occur (also found in the 8.5 m CsAc system). The corresponding icing process demonstrated a rather broad peak centered at around −82.4 °C. This should be correlated to the special concentration region in the non-equilibrium binary phase diagram of the water-salt solution system (Fig. 1a). Once the concentration surpasses 8.5 m, all the electrolyte systems turn into good glass-forming liquid, meaning that the icing process is impeded and glass–liquid transition happen instead. At the concentration of 10 m, it exhibits a lowest Tg, while the Tg increases at higher concentrations thereafter. By concluding the solid-liquid transition temperature of CsAc electrolytes with varying concentration according to DSC results, a V-shape phase diagram is presented (Fig. 1c). Two districts depicting freezing points and Tg were separated by different color pattern in this V-shape phase diagram. Obviously, the 10 m CsAc electrolyte is located at the turning point with a lowest Tg of −128 °C. This specific concentration is closed to Xm of zone II mentioned in Fig. 1a, in line with our expectation for EDGFL. The influence of cooling rate on the Tg was further studied. As shown in Supplementary Fig. 2, the faster cooling rates (10 and 20 K min−1) and a slower cooling rate (2 K min−1) can lead to higher and lower Tg values, respectively, indicating that Tg is the dynamics transition temperature rather than the thermodynamic transition temperature. However, the cooling rate presents no influence on the concentration-dependence transition behavior in various CsAc electrolytes with concentrations of 10, 20, and 30 m, confirming the overall transition and structure varying rules are determined mainly by the concentration. To visualize the phase transition process more intuitively, we employed an in-situ optical microscopy system combined with a cooling stage to detect the solid-liquid phase transition process of CsAc electrolytes with various concentrations (Supplementary Fig. 3 and Fig. 1d). As the temperature decreases at the rate of 1 °C min−1, a water drop (50 μL) of 5 m CsAc solution begins to freeze at −49 °C, consistent with the DSC results. For the EDGFL sample of 10 m, no ice precipitation is observed even at −128 °C, and it develops into a glassy state instead. Upon further cooling to −190 °C (close to temperature limit of the cooling stage), the glassy state is found with the formation of cracks. Similarly, the 20 m CsAc solution shows no sign of ice crystallization, and cracks appear at a higher temperature of −154 °C.

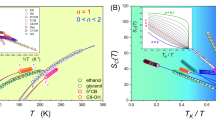
Next, the concentration dependence of shear viscosity and ionic conductivity for CsAc electrolytes at different temperatures was investigated (Fig. 1e, f and Supplementary Fig. 4). At the temperature above -20 °C, an increase in concentration leads to a corresponding elevation in viscosity (Fig. 1e). However, when the temperature drops below −60 °C, the viscosity is no longer monotonically changed along with the increased concentration, and a minimum viscosity was observed at 10 m. Obviously, the reversed order in viscosity of CsAc electrolytes with different concentration towards lower temperature implies a postponement of the Tg in 10 m. Therefore, the 10 m CsAc electrolyte is described as the optimized EDGFL in the following text. We also analyze the viscosity data by fitting them with temperature according to Vogel–Fulcher–Tammann relation to derive the Angell plot, which classifies the types of glass-forming liquids36. Upon cooling, strong liquids display Arrhenius-type slowing down dynamics, while fragile liquids exhibit a super-Arrhenius-type one. Apparently, the EDGFL appears to behave as a fragile liquid (Supplementary Fig. 5), which is totally different from the pure water exhibiting fragile-to-strong glass formation upon cooling. Besides, the increase in salt concentration (>10 m of the optimized EDGFL) results in the increase of the fragility (denoting the decrease in the glass-forming ability). This should be ascribed to the promotion of the salt precipitation process caused by the strong pair interactions related to ions. The optimized EDGFL also delivers the highest ionic conductivity (compared with other concentrations) at temperatures lower than −40 °C, with a high value of 0.8 mS cm-1 at −80 °C (Fig. 1f). To assess the ionization state in EDGFL, the modified Walden relation has been applied to better analyze the conductivity–viscosity dependence. This more realistic fractional Walden rule has been introduced with an exponent α as37,38:

$$\varLambda {\eta }^{\alpha }=C$$
(1)
$$\log \varLambda=\log C+\alpha \log {\eta }^{-1}$$
(2)

where \(C\) is a constant, \(\varLambda\) is the ionic conductivity and \(\eta\) is the viscosity. The α factor denotes the slope of the line and in a way gives the deviation factor from the ideal 1 M KCl solution (with a slope closing to 1). Different electrolytes are expected to form different lines on the plot with different slope α. The conductivity–viscosity dependence of the 10 m CsAc solution at different temperatures was exhibited in Fig. 1g. The α exponent (a constant between 0 and 1 according to the transition state theory) in the fractional Walden rule with a value smaller than 1 actually indicates a higher conductivity value than the ideal system at the same viscosity39. Thus, the 10 m CsAc system presenting an α value of 0.67 could be related to more completely dissociated cations and anions in water or the effect of concentration-induced structure inhomogeneities40. Moreover, the α values for other concentrations are all higher than that of the 10 m system (Supplementary Fig. 6), revealing its best ion transport performance under the same viscosity among various concentrations.

A series of variable temperature characterizations were conducted for CsAc electrolytes with different concentrations to solidate above results. In-situ Raman spectra were used to verify the phase transition under varying temperatures. As shown in Fig. 2a, an obvious ice peak at ~3100 cm−1 was observed in 5 m CsAc electrolyte at −80 °C, in accordance with that in pure water at −30 °C (Supplementary Fig. 7). However, for the EDGFL, no any ice peak exists at temperature ranging from +25 °C to −180 °C (Fig. 2b, Supplementary Fig. 8), which is consistent with previous DSC and in-situ microscopy measurements in Fig. 1b, c. Since the EDGFL keeps in liquid state prior to Tg, with no ice nucleation and crystalized salt, its solvation structure remains stable and undergoes no apparent change as lowering temperature till −180 °C (Supplementary Figs. 9a, b). Additionally, 2D correlation spectra (2DCOS) were further derived from the in situ Raman spectra, enabling the discrimination of sequential thermal response of distinct species41 (Fig. 2c). Based on Noda’s criterion, the thermal responsive order of different species to temperature decrease follows: strong HB > non-HB > weak HB (see determination details in Supplementary Table 1). As the temperature decreases, water molecules with strong HB exhibit the swiftest response, accompanied by an intensified HB strength. Conversely, the thermal sensitivity of water molecules involved in weak and non-HB is comparatively sluggish, culminating in an inadequate establishment of the tetrahedral water clusters. Consequently, this engenders the solution exhibiting more diversified conformation (metastable states), fostering a propensity towards vitrification. Moreover, in-situ XRD measurements reveal that in 5 m CsAc electrolyte, the diffraction peaks of ice appear as the temperature is decreased to −80 °C (Fig. 2d). When the temperature further decreases to -150 °C, more intensified peaks can be obviously found. In sharp contrast, none of diffraction peaks from ice are observed in EDGFL even at −150 °C (Fig. 2e).

Fig. 2: In situ variable-temperature characterization.
figure 2

In situ Raman spectra of a 5 m and b 10 m CsAc at different temperatures. c 2D synchronous and asynchronous spectra (2DCOS) generated from (b). The in situ XRD patterns of d 5 m CsAc and e 10 m CsAc at different temperatures. In situ LF-NMR T2 relaxation spectra of f 5, g 10, and h 20 m CsAc electrolyte at different temperatures.

Full size image

Furthermore, the relaxation kinetics change of water molecules in various electrolytes was analyzed using in-situ low-field nuclear magnetic resonance (LF-NMR) tests. The spin-spin relaxation time (T2) in LF-NMR unveils the degrees of freedom of water, with a smaller T2 implying a more restricted motion of water molecules42. As shown in Fig. 2f, the 5 m CsAc displays a single T2 peak (~1629 ms) at +25 °C, representing the water molecules with high fluidity. As the temperature is gradually lowered to −80 °C, the peak shifts leftward with a smaller T2 value (left unfrozen water), indicating a significantly lower degree of freedom of water molecules due to increased viscosity. The 20 m CsAc yields a much smaller T2 peak position (~613 ms) at +25 °C due to its higher viscosity, while the peak shifting trend (versus changing temperature) is similar to that of 5 m CsAc but at a lower T2 under −80 °C (Fig. 2h). The T2 peak of the optimized EDGFL (~1072 ms at +25 °C) is located between the peaks of the 5 m and 20 m CsAc (Fig. 2g). Nevertheless, it shifts leftward in a slow speed along with the decreasing temperature. This suggests that a considerable portion of water in the EDGFL still remains a certain fluidity, resulting in the lowest viscosity at −80 °C. The in-situ 1H NMR spectrum of the EDGFL and 20 m CsAc also exhibit similar results (Supplementary Fig. 10a, b). As the temperature is decreased to −80 °C, the 1H peak of water molecule in the above two electrolytes both shifts and broadens, indicating more hydrogen bonds (HBs) formation at lower temperature. However, the peak broadening is more pronounced in 20 m CsAc electrolyte compared to the optimized EDGFL, which is mainly ascribed to the insufficient relaxation time caused by the increased viscosity43,44. These results are in well line with the aforementioned rheometer measurements.

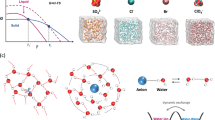
For better understanding the elaborate correlation between thermodynamic properties and anti-freezing ability, classical molecule dynamics (MD) simulations were performed to provide deeper insight into the structure and high-entropy microscopic origin of the EDGFL (Fig. 3). The water structure in the EDGFL was examined by radical distribution function (RDF). The water–water correlation in real space can be described by the oxygen–oxygen RDF (Fig. 3a). As the lift of the concentration, the second and third solvation shells undergoes gradually inward movements, resulting in a more compact and disorder liquid structure. The second solvation shell originally at a distance of ~4.5 Å is closely related to deformation extent of the tetrahedral structure in the first solvation shell45. Its collapse reveals a highly disrupted HB network under elevated salt concentration. Besides, the fraction of ice-like water molecules (tetrahedral order parameter Qtet above 0.8, serve as the initial nucleation sites for ice crystal) decreases with elevated salt concentrations, further confirming the break of HB network (Supplementary Fig. 11). However, the HB lifetime among water molecules prolongs as elevated concentration, enhancing the likelihood of freezing. According to the aforementioned DSC results, the solid-liquid transition point and salt concentration are not monotonically dependent. The opposite trends of Qtet and HB lifetime implies the possible existence of a critical concentration with a lowest solid–liquid transition temperature.

Fig. 3: Molecular dynamic simulations.
figure 3

a Calculated OW-OW radical-distribution function (RDF) of aqueous CsAc electrolytes at different concentrations. All RDFs are shifted vertically for visual clarity. The red dots represent the second and third peak positions; vertical dashed lines are marked for 1 m CsAc. b The interaction energy between Cs+ and H2O, H2O and H2O, Cs+ and Ac- at different concentrations. c The schematic of the competing and dynamics exchange of various structures (ionic solvation structure, ion pair and tetrahedral structure) in the CsAc electrolyte and their specific contributions to the Sex. d Tetrahedral entropy (OW-OW, dashed line with hollow balls) and two-body pair entropy (Cs+-OW, Ac−-HW, Cs+-Ac−, solid lines with solid balls) in CsAc electrolyte with different concentrations. e Relationship of \({S}_{2}^{{ions}}\) (\({S}_{2}^{{iw}}\) + \({S}_{2}^{{ip}}\)) and \({S}_{Q}\) of the CsAc electrolyte with different concentrations.

Full size image

Although the tetrahedral ordering plays a key role on liquid–solid transition process of the H2O solvent, it’s still hard to explain the turning point of Tg at a concentration of 10 m. Another important issue lies in the severe salt aggregation behavior caused by enough low temperature at too high concentrations, which is strongly related to the interaction among ions and water molecules in solution. Therefore, a more comprehensive consideration should be given to the microscopic structures and two-body correlations between ion–ion pairs/ion–water in this complex system. As demonstrated in Fig. 3b, the increased salt concentration weakens the interactions of adjacent water molecules, whereas enhances ion–water and ion–ion interactions. The former contributes favorably to the entropic increase of the system, while the latter two will reduce the entropy. Therefore, the Tg value of the CsAc electrolytes with various concentrations should be closely related to the competitive effect between tetrahedral order of water and pair order of ions.

These two competing interactions collectively affect the total entropy of the system (\(S\)), which can be expressed as46:

$$S={S}_{{id}}+{S}_{{ex}}$$
(3)

where \({S}_{{id}}\) represents the ideal gas entropy, \({S}_{{ex}}\) represents the excess entropy. The \({S}_{{ex}}\) is closely related to the structure of liquid, which is an ideal tool for analyzing our current liquid system. The translational section of the \({S}_{{ex}}\) is approximated to two-body excess entropy, \({S}_{2}\,({S}_{{ex}}^{{tr}}\approx {S}_{2})\), which can be expressed according to atom-atom RDF functions \({g}_{\alpha \beta }(r)\) as follow47:

$${S}_{2}/N{k}_{B}=-2\pi \rho {\sum}_{\alpha,\beta }{x}_{\alpha }{x}_{\beta }{\int }_{\!\!\!\!0}^{\infty }{dr}\left\{{g}_{\alpha \beta }\left(r\right){{\mathrm{ln}}}{g}_{\alpha \beta }\left(r\right)-[{g}_{\alpha \beta }\left(r\right)-1]\right\}{r}^{2}$$
(4)

where N is the number of particles, \({k}_{B}\) is the Boltzmann constant, \(\rho\) is number density of particles, and \({x}_{\alpha },\,{x}_{\beta }\) are the mole fraction of component \(\alpha,\,\beta\) in the system, respectively. We previously used tetrahedral entropy \({S}_{Q}\) to discuss orientational distribution of water, which mainly define the anti-freezing ability of the water solvent in different systems. Generally, ionic solvation shells, ion pairs and tetrahedral water clusters coexist in aqueous solution. The radical alignment of the water dipoles in ionic solvation shell contradicts the tetrahedrally directional HB network, while ion pairs simultaneously influence the strength of interactions of ion–water (Fig. 3c). Water molecules are confined by ionic field, developing the translational order (\({S}_{2}^{{iw}}\)) and forming a spherical shell (primary solvation structure), which characterizes the arrangement of water in the radical direction. Moreover, ion pairs also exhibit translational order (\({S}_{2}^{{ip}}\)) owing to strong electrostatic interactions. The \({S}_{2}^{{iw}}\) and \({S}_{2}^{{ip}}\) strongly correlate to the balance process of free and aggregated ions, which mainly influence the phase states especially at high salt concentrations. The tetrahedral structure of water molecules primarily captures their orientational order\(\,{S}_{Q}\), thus greatly disclose the difficulty of forming ice crystals. Therefore, these structure orders compete with each other (denoted as a dynamics exchange process), and indicate overall electrolyte structure include solvent distribution and component interactions. We count in \({S}_{2}^{{ions}}\) (\({S}_{2}^{{iw}}\) + \({S}_{2}^{{ip}}\)) and \({S}_{Q}\) as effective \({S}_{{ex}}\) to further unveil the phase transition properties. As shown in Fig. 3d, the \({S}_{Q}\) originated from interactions among water molecules progressively increases with the continuously rising salt concentration, which is consistent with the decrease in tetrahedral order and interaction strength between water molecules. Nevertheless, the \({S}_{2}\) of cation–anion pair (Cs+-Ac−) and ion–water (Cs+-OW, Ac−-HW) delivers a contrary trend with a stable changing speed, owing to the continuously strengthening interaction at higher concentrations. Considering the contribution of both water structure and ions function to the effective \({S}_{{ex}}\), the correlation between \({S}_{2}^{{ions}}\) and \({S}_{Q}\) at different concentrations can be depicted in Fig. 3e. It can be more clearly found that a perfectly linear relationship is achieved with the salt concentration below 10 m, indicating their synchronous varying behaviors. At this period, the liquid-solid transition of the aqueous solution is driven by energy and it mainly encounters the ice crystallization process of H2O molecules at a lower temperature. However, after the salt concentration is further increased, the linear relationship can no longer be retained since the breaking extent of tetrahedral water structure is close to saturation while interactions between ion pairs or ion–water continuously enhance. Now the aqueous system enters an entropy-driven state and it is hard to experience water freezing process. Therefore, a comprehensive consideration of both \({S}_{2}^{{ions}}\) and SQ can better unveil the dependence of concentration, effective \({S}_{{ex}}\) and phase transition behaviors in salt solutions. The results and variation trend of the solutions using another two water models (TIP4P/ICE and OCP3) are the same as that using the TIP4P-2005 model (Supplementary Fig. 12), indicating its availability in analyzing thermodynamic glass transition behaviors. Besides, the balancing relationship between SQ and \({S}_{2}^{{ions}}\) under different cooling rates were also exhibited in Supplementary Fig. 13. Although a little deviation occurred at various concentration condition, the transition point from crystallization region to the vitrification region still lied in the 10 m, further revealing the concentration-dependence transition behavior is not determined by the cooling rate, in well accordance to the results of DSC tests in Supplementary Fig. 2.

The special phase transition behavior of the EDGFL can be depicted in the scheme of Supplementary Fig. S14. In the typical cooling process, the liquid in a high-energy state thermodynamically gravitates towards a stable equilibrium state with lower energy. However, the liquid sometimes inevitably goes through a multitude of metastable states before reaching the final crystalline state. Interaction builds the order, while thermal motion leads to disorder. Thereafter, crystallization is energy-driven, while the vitrification process is governed by entropy. The phenomenon of liquid solidification can be perceived as a competition between energy and entropy. In our designed EDGFL system with a proper distribution in effective Sex, entropy takes on a favorable position in the competition against internal energy, thus promoting the vitrification transition. To deeply investigate the kinetics of structure transformation between liquid-like and ice-like water in EDGFL, the making rate constant (k) and breaking rate constant (k’) of ice-like water in both pure water and EDGFL at −80 °C were compared (Supplementary Fig. 15a and 15b). Notably, the k’ is always larger than k, since the neighboring water molecules need to adjust their positions and orientations to form an energy-favorable ice-like structure48. However, the k′ of EDGFL is larger than that in pure water, while the k is much smaller (Supplementary Fig. 15b). This result further confirms the much less possibility of liquid-solid transition in EDGFL, which inhibits the freezing process and promotes vitrification. To present the impact of EDGFL on ice crystal growth intuitively, we constructed an original ice slab in EDGFL for MD simulation at −80 °C (Supplementary Figs. 16 and 17). Following a sufficiently long period of equilibrium relaxation (100 ns), the initial ice slab completely melts and converts into liquid state, consistent with the aforementioned results.

All-temperature energy storage enabled by EDGFL

The EDGFL has superior anti-freezing capability, making it an excellent candidate for use in energy storage devices under extremely low temperature. To illustrate its practical availability, we applied the proposed EDGFL in supercapacitors (SCs). Symmetric active carbon (ATC)-based SCs delivered a specific capacitance of around 400 mF cm−2 under the room temperature. The capacitance exhibits hardly no decay at −40 °C (~98.7% retention), while can retain over 84% even at −70 °C and ~67 % at −80 °C, as presented in Fig. 4a, b and Supplementary Fig. 18. These performances indicate that the elimination of ice nucleation in EDGFL can ensure adequate ion conductivity for SCs even under ultralow temperature environments. It is no doubt that much higher performance can be obtained when the environmental temperature rises, with a significant increased (168.3% compared to +25 °C) capacitance of near 700 mF cm−2 at +80 °C (Fig. 4a, c). Even under an ultrahigh temperature of +120 °C, it can perform stable capacity of ~900 mF cm−2 at 10 mA cm−2. In addition, the fabricated SCs demonstrate great stability within a long-term high-temperature state, obtaining more than 84.4 % capacitance retention after 5000 cycles at +80 °C (Fig. 4d). This can be attributed to the high boiling point of the EDGFL electrolyte at ~+145 °C, as confirmed by the DSC result in Supplementary Fig. 19.

Fig. 4: Energy storage applications all over wide temperature window (supercapacitors: −95 to +120 °C; ZIBs: −50 to +70 °C).
figure 4

a Areal capacitance of symmetric active carbon (ATC)-based supercapacitors at different temperatures (−80 to +120 °C). The charge-discharge curves at the temperature range of b −80 to −40 °C and c +40 to +120 °C. The long-cycle stability at (d) +80 °C and (e) −95 °C. f Optical pictures, (g) and (h) rate performances at varied temperature of the PANI || Zn full cells using the pure ZnAc2 and ZnAc2 + EDGFL electrolytes. (i) Long-term stability of the ZIBs with ZnAc2 + EDGFL as the electrolyte.

Full size image

More strikingly, the EDGFL-SCs display considerable capacitance (200 mF cm−2 at 0.1 mA cm−2) and stable performance even operated under an ultralow temperature of -95 °C for 2000 cycles (shown in Fig. 4e). Above all elucidate the great potential utilization of our EDGFL in energy storage systems adapted to extreme environment broadening to both high and ultralow temperatures. Besides, the universality of the designed EDGFL on aqueous batteries was further studied. As exhibited in Fig. 4f, the 10 m CsAc was added to the pure zinc acetate (ZnAc2) electrolyte as a modifying component to improve the anti-freezing ability. Obviously, the pure ZnAc2 electrolyte had opaque ice when the temperature was decreased to −20 °C, while the composite electrolyte of CsAc and ZnAc2 can restrain the freezing behavior even at a much lower temperature of −80 °C (Fig. 4f), in accordance with the DSC result in Supplementary Fig. 20. When this modified electrolyte was used for constructing wide-temperature Zn-ion batteries (ZIBs), great rate performance towards varying temperature can be achieved (Fig. 4g, h), with a high capacity of around 160 mAh g−1 even at –50 °C, much better than that of pure ZnAc2 system (less than 4 mAh g−1 at –20 °C). Besides, the polyaniline (PANI) || Zn full cells can retain ~67% original capacity after 800 cycles at −40 °C (Fig. 4i) and stably work for hundreds of cycles under +70 °C, as presented in Supplementary Fig. 21. These results indicate the great function of the optimized EDGFL in broadening adaptable temperature ranges of various energy storage devices.

Ultralow-temperature AC line filter enabled by EDGFL

Low-temperature applicability of electronic components is one of the most important conditions for future electric machines in extremely cold scenarios, in addition to energy storage field. One of the most common units is aluminum electrolytic capacitors (AECs), which are widely used in various electric appliances. Special design of electrode structure coupled with proper materials can endow SCs with the similar AC line filtering property of AECs49,50. Therefore, to further confirm the great function of above EDGFL, we introduced it into micro SCs (MSCs) with PEDOT as active materials to study the low-temperature filter performance, as illustrated by the scheme and optical pictures in Fig. 5a. The designed MSCs with a small interdigitated space of 50 μm demonstrated great rate performance. Even under ultrahigh scan rates higher than 100 V s−1, quasi rectangle shape of cyclic voltammetry curve can be retained (Fig. 5b). Bode plots representing mutual dependence between frequency and phase angles of both AECs (220 μF, 6.3 V) and PEDOT MSCs are shown in Fig. 5c–e. Under room temperature (25 °C), PEDOT MSCs delivered a frequency of 259 Hz at −45° phase angle, comparable to the AECs’ response ability. At the representative frequency of 120 Hz, the corresponding phase angle of PEDOT MSCs reaches −51.1°, a little poorer than −83.9° from AECs. When the temperature was lowered to −70 °C (Fig. 5d), AECs lost the original advantage in filtering ability (only 2 Hz at the typical phase angle of −45° and −6° phase angle at frequency of 120 Hz). This can be ascribed to the steep decline in conductivity of the liquid electrode. It this case, the AECs function more like a resistor rather than capacitor. As for our PEDOT MSCs, fairly good performance can be retained, with a frequency of 159 Hz at −45° phase angle and −46° phase angle at frequency of 120 Hz, much better than AECs. More severe decay of filtering properties in AECs can be observed in Fig. 5e, with nearly no filtering behavior. As the temperature was further lowered to −95 °C both for two kinds of devices, the PEDOT MSCs using the EDGFL as electrolyte still preserved some filter performance. The areal capacitance (Ca) of above two kinds of devices under +25 °C and −95 °C were compared in Fig. 5f. Apparently the PEDOT MSCs presented higher Ca than AECs under all frequency range, especially in the high-frequency regions under an ultralow temperature condition. The practical filter function of above capacitors was conducted further under varied temperatures (Fig. 5g, h). At room temperature, both AECs and PEDOT MSCs exhibited great AC line-filtering performance at 120 Hz. However, under a low temperature of −70 °C, signals filtered by AECs demonstrate apparent fluctuation, while our PEDOT MSCs can still ensure the flat output. Above results reveal the great potential of the EDGFL utilized in filter electric units as candidates for commercial AECs under ultralow-temperature environments.

Fig. 5: AC line filter application at room temperature and low temperature.
figure 5

a Schematic of PEDOT-based AC line filter on Ti/Au interdigitated electrodes (PEDOT MSCs). b The optical photo of PEDOT MSC. c CV curves of PEDOT MSCs at different scan rates. Impedance phase angle on the frequency for PEDOT MSCs and commercial 220 μF aluminum electrolytic capacitors (AECs) at c +25 °C, d −70 °C, e −95 °C. f Areal capacitance versus frequency of PEDOT MSCs and commercial 220 μF AEC at +25 °C and −95 °C. AC line-filtering performance of g commercial 220 μF AEC and h PEDOT MSCs at +25 °C and −70 °C.

Full size image

Discussion

In summary, a concept of using entropy-driven glass-forming liquid (EDGFL) as a kind of anti-freezing electrolytes is proposed and verified. With the help of thermodynamic tools, we find that the competition of two kinds of excess entropy in salt solutions is the essential reason for avoiding ice nucleation process through the vitrification route. By modulating the proper concentration, the aqueous solution can avoid the energy-driven ice crystallization and achieve a lower Tg. The tetrahedral entropy of water solute and two-body pair entropy related to ions together determine the glass transition process. Thus, a critical concentration of 10 m for CsAc electrolyte is capable of realizing the lowest Tg in phase diagram. Guided by above understanding, we applied the optimized EDGFL and successfully developed an ATCB-based supercapacitor operated in an ultra-wide temperature range (−95 to +120 °C) and a PEDOT-based AC line-filter adapted for the ultralow temperature of −95 °C. When introduced into the Zn-based electrolyte, the optimized EDGFL can also help achieve high-performance Zn-ion batteries under a wide temperature range (−50 to +70 °C). We believe our finding will foster future theoretical and experimental developments aiming at revealing the mechanism of ice nucleation/glass transition in supercooled liquid and designing more anti-freezing electrolytes for all-temperature-adapted applications based on water and aqueous solutions.

Methods

Fabrication of active carbon-based symmetric supercapacitors

Active carbon (Kurary, YP-80F), PVDF binder and super P conductive agent with a ratio of 8:1:1 was fabricated as a paste for coating on carbon paper, with an average thickness of 1000 μm and mass loading of around 20 mg cm−2. Two active carbon electrodes were used as positive and negative electrodes for constructing the symmetric supercapacitors. 75 μL 10 m CsAc electrolyte were added into the coin cell separated by a piece of glass fiber (GE-Whatman, 125 mm).

Preparation of PEDOT micro-supercapacitor (MFC)

Ti/Au interdigitated electrodes were purchased from Huizhou Xinwenxiong Trading Co., Ltd (Ti: 30 nm, Au: 100 nm. line width: 50 μm, line spacing: 50 μm, line length: 2.1 mm). Anodic polymerization of aqueous electrolytic monomeric bath was conducted in electropolymerizing of PEDOT electrodes using standard three-electrode configuration51. Ti/Au interdigitated electrode was used as working electrode, platinum wire as a counter electrode, and Ag/AgCl as a reference electrode. PEDOT was electrochemically grown on the Au surface in a solution containing 1 M H2SO4 and 50 mM EDOT. Potentio-dynamic mode was used in which the potential was swept from 0 to 1.1 V at a scan rate of 100 mV s−1 (vs. Ag/AgCl) for 20 cycles.

Electrochemical measurements

The electrochemical performances of various devices were conducted by the Neware battery test system (CT-4008Tn-5V10mA-164, Shenzhen, China). The voltage range of SCs and PANI||Zn batteries were set to 0–1.2 V and 0.5–1.5 V, respectively. All the electrochemical performances collected under varied temperatures were conducted under various environments including ambient places, electric oven (LICHEN, 202-00T, 25 to + 300 °C) and refrigerators with different temperature ranges from +80 to −95 °C (KEEKEN K-20, −22 to +15 °C; DW-86W28, −86 to −40 °C; DW-60-L30, −135 to −86 °C).

Characterizations

Various instruments utilized to study the fundamental characteristics of electrolytes are similar to our previous work15. DSC measurements were conducted within the cooling stage of +25 to −170 °C and heating stage of −80 to +20 °C all with a varying rate of 5 °C min−1 (METTLER TOLEDD DSC3). Raman spectra were all obtained by the 532 nm excitation laser (Horiba LabRAM HR Evolution). The T2 relaxation was measured by a LF-NMR analyzer (VTMR20-010V-I, SUZHOU NIUMAG ANALYTICAL INSTRUMENT CORPORATION). A homemade in-situ observation platform consisting of a high-resolution digital camera (Mshot, MS60) and a cooling stage (Linkam THMS600) was utilize to record the freezing process of various electrolytes. The crystal structures of various CsAc solutions under different temperature were gathered by the XRD instrument (Rigaku, MiniFlex600, Cu Kα). Viscosity measurements were performed by using a rheometer (TA/DHR-2) with the cone plate geometry (diameter 25 mm and angle 4°). The conductivity of the CsAc solutions at varied temperatures was collected by a conductivity meter (INESA, DDBJ-350). The CsAc electrolytes with a volume of 5 mL was placed in a glass tube and the electrode of the conductivity meter was immersed into the electrolyte under various environments including ambient places and refrigerators mentioned above. The conductivity meter can provide instant readings after reaching thermal equilibrium and the respective values were noted down. At least 30 different measurements in 1 min were gather to obtain the average value of ionic conductivity for a given sample composition at a temperature point.