Introduction

Superconducting transition metal dichalcogenides (TMDs) combine intricate effects of thickness with the physics of superconductivity, owing to the ability to accurately control the sample thickness in a clean manner via exfoliation. NbSe2, TaS2, NbS2, and TaSe2 all share a similar band-structure and a 2H crystal structure in their bulk form, and exhibit hole pockets in their transition metal bands around the K and Γ points1,2. Among these, the most extensively studied materials are NbSe2 and TaS2, where strong spin-orbit coupling (SOC) gives rise to Ising protection at the ultrathin limit3,4 and to the possible development of a triplet order emerging at high in-plane magnetic fields5,6,7. The symmetries and layered structure also enable exotic inter-layer effects such as the orbital Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) state8,9,10.

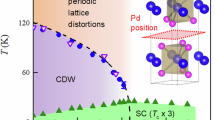
Significant attention was given to the effect of thickness on the superconducting properties of these materials3,4,11,12,13,14. Specifically, NbSe2 exhibits a reduction of the critical temperature Tc from 7.2 K at the bulk to 3 K at the monolayer limit3, accompanied by a suppression of the gap11,12. A similar suppression of Tc is seen in NbS213. Xi et al.3 suggested that this suppression is the result of fewer adjacent layers available to assist in Cooper pairing via interlayer interaction, an effect observed in high-Tc superconductors experimentally15 and also treated theoretically16. Remarkably, in TaS2 the inverse effect appears, with Tc increasing from 0.8 K in the bulk to 3 K in a single layer, as seen in transport experiments4,17,18. A similar enhancement is seen in TaSe214. Navarro-Moratalla et al.17 suggested that the strength of the effective coupling constant, accounting for electron-phonon coupling and Coulomb repulsion, could vary with thickness and possibly reverse the typical dependence of Tc on thickness. A different approach was taken by Yang et al.18, who focused on the role of the charge density wave (CDW) order that can suppress superconductivity by gapping segments of the Fermi surface. Altogether, the contrasting behavior between Nb- and Ta-based materials raises an important question: whether thickness-dependent superconductivity in these two groups is governed by the same mechanism.

In this work, we approach the question of thickness-dependent superconductivity in metallic 2H-TMDs by measuring the tunneling spectra of TaS2 devices of varying thickness, from bulk down to a monolayer. Spectra are measured using stacked all-TMD tunnel devices, where a MoS2 tunnel barrier is placed on top of the TaS2 layer. Measurements are taken at temperatures down to T = 20–30 mK, allowing us to resolve the smaller gaps of the bulk TaS2. We find that the TaS2 spectrum exhibits a well-behaved hard gap at all thicknesses, and that the order parameter Δ is related to Tc as expected for Bardeen-Cooper-Schrieffer (BCS) superconductivity. The thin samples exhibit a gap that survives well beyond our maximally attainable in-plane field of 8.5 T. The stability of this gap is a consequence of Ising spin-orbit protection6,11.

Our main result is found when tracking the thickness-dependence of the out-of-plane upper critical field Hc2, which sharply increases towards the thinner samples. We find that Hc2 depends quadratically on Tc and on Δ. Surprisingly, by compiling data of all other metallic TMD superconductors, we find that NbSe2, NbS2, and TaSe2 share the same quadratic dependence with the very same prefactor. This observation shows that the metallic TMD family shares a common mechanism driving superconductivity. This further suggests the existence of a single mechanism dictating the exact values of Hc2 and Tc across the entire family. We present a model where the strength of the CDW interaction drives this effective single-material behavior.

Results

Spectra at zero magnetic field and base temperature

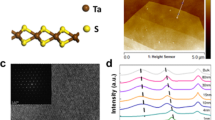
Our tunnel junctions were prepared in an Ar glove box by successive dry polydimethylsiloxane (PDMS) stamping of exfoliated flakes onto a SiO2 chip (see Methods for details). An optical microscope image of a representative tunneling device is shown in Fig. 1a, and a corresponding simplified schematic of a junction is presented in panel (b) for clarity, with the current path in white: electrons tunnel from the right Au electrode through the MoS2 barrier into the TaS2 flake.

Fig. 1: Tunnel junction architecture and tunneling spectra.
figure 1

a Optical microscope image of a typical tunneling device. The superconductor TaS2 is outlined in blue and the semiconductor MoS2 in red. Scale bar: 10 μm. b Simplified schematic of a tunnel junction. TaS2 is placed on a SiO2 substrate, and partly covered with a MoS2 barrier. Ti/Au electrodes are evaporated over the heterostructure (for tunneling contacts) and also on the bare TaS2 flake (for Ohmic drain contacts). The current path upon application of voltage using the electrodes is indicated by dashed arrows. c Cross-section of a 4-layer junction taken in a scanning transmission electron microscope (STEM). Ta atoms are easily distinguishable as bright dots. A 3-layer MoS2 barrier is visible on top. Scale bar: 2 nm. d Representative tunneling spectra at base temperature (≈25 mK) of TaS2 of different thicknesses. All devices show a hard gap, with diminishing gap width towards thicker samples. Curves are vertically offset for clarity.

Full size image

In order to verify the quality of the interface between materials and accurately determine the number of layers in each junction, we use a focused ion beam (FIB) and a scanning transmission electron microscope (STEM) to image the device cross-section. A representative STEM image taken on a 4-layer device with a 3-layer barrier, which we found to be the optimal barrier thickness, is shown in Fig. 1c. We observe clean, uniform atomic contact over several micrometers of cross-section for all of the junctions that displayed superconducting spectra.

The tunneling spectra, measured at base temperature (≈25 mK) on four tunnel junctions of different TaS2thicknesses with N = 1,4,11,20 (N being the number of layers) are displayed in Fig. 1d. Additional spectra, measured for all other thicknesses, are displayed in Fig. S1 of the Supplementary Information. The measurements were carried out using standard lock-in techniques, typically using a 10 μV AC voltage excitation. Junctions of all thicknesses exhibit a typical BCS-like tunnel spectrum with its two hallmark features: a strongly suppressed conductance inside the gap ("hard gap"), flanked by sharp quasiparticle peaks. We note that thin devices exhibit stronger peaks than thicker ones. We believe this trend to be coincidental, due to the longer time the thicker samples spent in the glove box before measurement.

Throughout this work, one should be careful to distinguish two similar, yet distinct, physical quantities: The first is the spectral gap Δspec, commonly defined as the distance in energy (or equivalently bias voltage) between the two quasiparticle peaks. The other is the BCS gap Δ, which is the parameter appearing explicitly in BCS theory and is uniquely related to the critical temperature Tc or the electron-phonon interaction strength. These gap parameters coincide at zero temperature and magnetic field. Below, while we directly measure Δspec, we convert it to Δ in order to highlight our results’ agreement with the BCS model (see Supplementary Information for details on the conversion).

We have measured a total of 22 junctions, ranging from a bulk N = 32 device down to a single layer thick TaS2 (note that “layer” refers to a single tri-atomic 1H layer). We observe an increase in Δ with decreasing N, in agreement with the behavior of Tc measured by others in electronic transport4,17. This trend is in stark contrast with NbSe2, in which the largest Δ and Tc are observed in bulk samples. The compiled Δ and Tc data measured on our TaS2 devices are shown in Fig. 2, with values of Δ vs. N in panel (b). As expected, we measured the largest gap in our monolayer sample, where Δ ≈ 460μeV, comparable to spectra taken by STM on detached flakes on top of a bulk sample19 and on 4Hb-TaS2 samples, where the 1H-TaS2 is interleaved with 1T-TaS220. Our results show that thin TaS2, including a monolayer, exhibits a finite-sized hard gap, contrary to the results presented in Ref. 21. The spectra can be fit to a generalized BCS model including anisotropy (see Supplementary Information). The singular monolayer device measured exhibits a second low energy gap, whose origin is not yet clear to us. This particular device is further discussed in the Supplementary Information in Section IB. Further investigation is required to resolve this issue, which is aside from the main focus of this work.

Fig. 2: Thickness dependence of critical temperature Tc and superconducting gap Δ.
figure 2

a Temperature evolution of the zero-bias tunneling conductance G0, normalized by its value in the normal state GN, of four representative junctions. Plotted in orange circles are the zero-bias points extracted from measured spectra. Plotted in blue dots are data measured while continuously cooling the samples from slightly above Tc down to base temperature. b BCS gap Δ vs. N. c Critical temperature Tc vs. N. Tc was taken to be the temperature at which the ratio G0/GN reaches 0.95. Overlaid in orange are data measured in transport devices by Refs. 4 and 17, exhibiting good agreement with our data. d Dependence of Δ/kB on Tc. The black line is a linear fit. In all panels, green plus-shaped markers indicate junctions whose thickness could not be directly observed in STEM and had to be estimated based on optical contrast. Error bars on N are  ± 1 to reflect extra or missing layers that were not seen in cross-section imaging. Determination of the error bars on Tc and Δ is detailed in the Supplementary Information.

Full size image

Thickness dependence of the critical temperature

Our tunneling measurements allow us to relate Tc to Δ and compare it with BCS theory. We measure the evolution of the zero-bias conductance G0 with temperature (see Fig. 2a) and define Tc as the temperature at which G0 reaches 95% of its saturation value GN, giving good agreement with values measured in transport4,17, see Fig. 2c. The dependence of Δ and Tc on N is shown in Fig. 2b, c. We clearly observe the trend of reduced gap and critical temperature in thicker samples, reaching saturation around N = 20. We then plot the measured Δ/kB (kB is Boltzmann’s constant) vs. Tc in panel (d). A linear fit to these data gives a slope of 1.73, in good agreement with the weak-coupling BCS model prediction of 1.76.

Tunneling spectra in applied magnetic field

We measure the spectra of all devices in the presence of a magnetic field, in the plane of the sample (parallel field, denoted H∣∣) or perpendicular to it (denoted H⊥). 2H-TMDs are all characterized by a strong Ising SOC3,4,22. Consequently, their electronic spins are locked in an out-of-plane orientation, making superconductivity robust against the applied in-plane field. Indeed, similar to thin NbSe2, spectra measured in our thinnest samples are only very slightly perturbed by H∣∣. As we show in Fig. S4, the hard gap and quasiparticle peaks persist up to fields exceeding 8.5 T. In thicker samples, the finite thickness allows the formation of circulating Meissner currents, whose effect induces pair-breaking11. Hc∣∣ is more easily accessible in thicker samples, and reaches a lower bound of  ≈ 1.8 T in samples with N ≥ 20.

We find more striking results when measuring the tunneling spectra in H⊥. Fig. 3a displays the spectra of three representative junctions. The bulk dataset, taken on a 20-layer sample, regains the flat metallic tunneling characteristic by H⊥= 80 mT. In tunneling measurements, where there is no sharp transition to the normal state, we define Hc2 as the magnetic field where the two linear regimes of the G0 vs. H⊥ curve intersect (see Fig. 3b). As we move to thinner samples, Hc2 extracted using this method grows to 0.37 T for the 4-layer sample and to 1.1 T for a bilayer, in agreement with the values reported in transport measurements4,17. We note that in some junctions, the high-field spectra retain a small zero-bias dip which remains stable far above saturation. The origin of this dip is not understood but does not affect our conclusions. The marked increase in Hc2 is seen in panel (c), where we track Hc2 vs. N. To glean information about the mechanism leading to such enhancement of Hc2, we plot its value vs. Δ2 in panel (d). Excluding two outlying points, the dependence appears linear, i.e., Hc2 ∝ Δ2. As we show below, this is a property expected for clean superconductors, yet it is far more general and can be followed throughout the entire metallic H-TMD material family – irrespective of whether the material is considered to be in the clean or dirty limit.

Fig. 3: Critical field Hc2 measurement.
figure 3

a Normalized tunneling conductance of three representative junctions, thickness indicated, in perpendicular magnetic field H⊥. The spectrum in the zero field is plotted in blue and the highest field data is in yellow. Curves are vertically offset for clarity, ΔH is the field step between curves. b G0/GN vs. H⊥for a bilayer and a 9-layer junction. Hc2 is defined as the intersection of the two linear regimes. The orange diamonds indicate the confidence bounds corresponding to the error bars used in the next panels. c Hc2 vs. N. d Hc2 vs. Δ2, with a linear least-squares fit to the data, excluding the two outlying points.

Full size image

Discussion

To understand the thickness dependence of Hc2, we compare TaS2 to other metallic H-TMD materials. We begin by plotting TaS2 Hc2 values vs. \({T}_{c}^{2}\) on a log-log plot in Fig. 4a, noting that Tc is proportional to Δ (Fig. 2d). To the TaS2 data points displayed in Fig. 3, plotted here in blue, we add the values for NbSe2, plotted in red, which we extract from the transport measurements taken by Xi et al.3. Surprisingly, both data collections appear to arrange on a single common trend-line, reflecting the same Hc2 vs. \({T}_{c}^{2}\) dependence, with the same pre-factors. We note, as seen previously, that whereas in the NbSe2 data sequence, the bulk samples have the higher Hc2 and Tc, in the TaS2 sequence the relation is reversed. Curiously, the two materials converge to the same values of Tc and Hc2 at the single-layer limit.

Fig. 4: Data compilation including additional materials and theoretical results.
figure 4

a Hc2 vs. \({T}_{c}^{2}\) for different TMD superconductors at different thicknesses. Experimental results in empty markers with least-squares linear fit, theoretical results in solid markers with a line of slope 1 superimposed as a guide to the eye. Inset: mean free path ℓ (circles, color) and coherence length ξ (triangles, black) for different materials. Blue: TaS2,4,17,31; red: NbSe2,3,4,30. (b-c) Hc2/Δ2 vs. Tc (b Experiment, c Theory, same legend as in a). All theoretical results were obtained based on the band structure of a monolayer, Tc is tuned only by the CDW strength b (for more detail, see Supplementary Information).

Full size image

To these two sequences, we also added two more data sets: (i) Three thicknesses of TaSe2, where Hc2 and Tc were measured by Yokota et al.23 using the self-inductance method for a bulk sample and by Wu et al.14 in transport. Remarkably, these data points reside on the very same trend spanned by the TaS2 and NbSe2 sequences. (ii) Bulk NbS2, with Hc2= 2.6 T and Tc = 5.7 K as reported in24. The solid line is a linear least-squares fit, yielding a slope of 1.06 ± 0.13. The surprising continuity between sequences belonging to different TMDs of varying thicknesses is the main result of this paper. Below, we coin this the “Metallic H-TMD Sequence”.

It is then instructive to compare the metallic H-TMD sequence, where we achieve tunability only by varying thickness, with other tuning methods. In Supplementary Fig. 5, we present two additional datasets taken on liquid-gate-controlled superconducting MoS2. One25 exhibits a slope corresponding to Hc2 ∝ Δ, agreeing with a dirty limit superconductor. The other dataset, from Costanzo et al.26 manifests a Δ2 dependence for the higher Tc range. We note that in both these MoS2 studies, the TMDs are electron-doped and are therefore not equivalent to the metallic TMDs, that are hole-doped.

In gated MoS2, modulation of superconductivity is achieved by control over carrier density as the main tuning parameter. Our work suggests that the metallic H-TMD sequence behaves analogously as a single continuous superconducting system, where the controlled parameters are the choice of material and the sample thickness, and these work together to determine a fundamental property that dictates the position of the sample along the Hc2 vs. \({T}_{c}^{2}\) line. We suggest that the property, that appears to affect superconductivity so strongly, is the CDW phase that is known to be present to various degrees in all of these materials.

We investigate this possibility by employing Gor’kov’s theory to compute Hc2 close to Tc, starting from a tight-binding model including SOC and the 3 × 3 CDW for both TaS2 and NbSe2 parameters. In this calculation, we assume the attractive phonon-mediated interaction is of equal strength on all three transition metal d-orbitals. We use the strength of the CDW order parameter, denoted by b, as the tuning parameter of Tc and Δ. However, it should be noted that the electron-phonon coupling is also expected to vary between different materials. We find that Tc depends strongly on b due to its effect on the DOS through the CDW27 (for details see Supplementary Information part III). More importantly, the calculated values of Hc2, shown in Fig. 4a, are proportional to \({T}_{c}^{2}\), and thus follow the same trend seen in the experimental data up to a significant numerical factor. This discrepancy is explored further below.

We further test the agreement between theory and experiment by plotting the ratio Hc2/Δ2. As seen in Fig. 4b, this ratio varies around a fixed value, a behavior that is also captured by our theoretical model. The deviations from the sequence imply variations in the band structure. Indeed, upon tuning the CDW strength b, the Fermi velocity vF varies as well, causing the deviation around the constant value shown in Fig. 4b. The accord between theory and experiment highlights the pivotal role of the interplay between CDW and superconductivity in TMD superconductors.

The comparison with theory also highlights a number of outstanding questions. The observed proportionality relation between Hc2 and Δ2 can be understood if we consider the Ginzburg-Landau (GL) critical field Hc2 = Φ0/2πξ2, where Φ0 is the flux quantum and ξ the GL coherence length. In a clean superconductor, one finds ξ ∝ ξBCS = ℏvF/πΔ, leading to Hc2 ∝ Δ2 as observed in our data, suggesting that our samples are in the clean limit. In this limit, we can obtain vF from the linear fit, and we find ℏvF ≈ 0.21 eVÅ (corresponding to vF ≈ 3.2 ⋅ 104 m/s), a value that is almost an order of magnitude lower than calculated in density functional theory (DFT) for monolayer TaS2 or measured in angle-resolved photoemission spectroscopy (ARPES)28,29. This also results in Hc2 that is about 80 times higher than expected when taking into account the vF obtained from the band-structure. This is the discrepancy clearly seen in Fig. 4. It is unclear why the disorder does not limit the vortex-core size, leading to a linear dependence of Hc2 on Tc.

As we show in the inset in Fig. 4, while the values of ξ extracted from the data and the value of the transport mean free path, ℓ, place bulk NbSe2 in the clean limit30, in TaS2 ℓ ≈ 20 nm (extracted using the data in Ref. 31), placing it between dirty and intermediate regimes. From the comparison between ℓ and ξ we conclude that this discrepancy is intrinsic and not driven by disorder. One possible origin is a velocity renormalization within Fermi liquid theory \({v}_{F}^{*}={v}_{F}/(1+{F}_{1}^{s}/2)\)32, where \({F}_{1}^{s}\) is the symmetric Landau parameter and \({H}_{c2}/{\Delta }^{2}\propto 1/{({v}_{F}^{*})}^{2}\). To the best of our knowledge, such a renormalization was never detected in ARPES measurements. Another option are strong correlation effects, as seen for example in heavy fermion materials33 or Coulomb repulsion effects34. Such an enhancement might reflect the breakdown of weak coupling theory in metallic H-TMDs, e.g., due to spin-fluctuations35, although H-TMDs exhibit phenomenological agreement with BCS theory seen in other quantities. The dramatic deviation of metallic H-TMDs from BCS theory therefore poses an outstanding question. Our results thus present the H-TMD sequence as a unified highly tunable superconducting system, allowing for testing the properties of superconductivity and its interplay with the CDW phase without any change to carrier density or pressure.

Methods

Device preparation

All tunnel junctions were assembled inside an Ar glove box with oxygen and water concentrations of  <10 ppm. Both TaS2 and MoS2 were bought from HQ Graphene, and both were exfoliated on Ultron Systems 1009R Silicone-Free Blue Adhesive Plastic Film. Materials were then mechanically transferred to 2 mm by 2 mm squares of Gel Pak Polydimethylsiloxane (PDMS) with retention level X4. The TaS2 was immediately stamped onto the surface of a Si chip with 285 nm oxide and was then placed under an optical microscope to look for flakes of appropriate lateral dimensions and thickness (determined by optical contrast). Then, similarly exfoliated MoS2 on PDMS was placed under the microscope to search for flakes to be used as tunnel barriers. When such a flake was found, it was mechanically stamped on top of the TaS2 flake at room temperature. The process required no heating or additional chemical manipulation. We found that the best results for tunneling were achieved when using tunnel barriers of 3-4 layers of MoS2. When the heterostructure was ready, it was patterned with electrodes in two successive processes of electron beam lithography and evaporation. We used Au electrodes, typically of 80 nm thickness with a 5 nm Ti adhesion layer. The first lithography and evaporation process was used for the tunnel electrodes. The second step, where Ohmic contacts were made, involved an additional short step of ion milling using Ar plasma while inside the evaporator, immediately prior to deposition. This additional step was found to improve the Ohmic contact resistance noticeably, as it removes the top layers of oxidation from the superconducting material.

Chemical degradation and its prevention

Due to the sensitivity of TaS2, we took great care to minimize the time when the sample is exposed to air, moving it as fast as possible from Ar to the vacuum of the electron beam and evaporator, and then into the cryostat. We found that when less than a day passes between first exposure and cooling, the quality of the data improves significantly. Conversely, when a complete heterostructure is left waiting for measurement for even a few weeks, the quality of the junctions degrades noticeably, even when left in the Ar glove box. This leads us to believe that TaS2 suffers from an additional type of degradation besides oxidation. Incidentally, the high N junctions presented in this paper were all on a chip that spent a while in the glove box before measurement, and indeed it has noticeably suppressed quasiparticle peaks.

Tunneling measurements

Typically, tunnel contacts that provided useful data were found to have a normal-state resistance in the range of 104 Ω to 105 Ω. Lower resistance junctions were too transparent and showed additional features in the conductance spectra related to Andreev reflections, and spectra measured on higher resistance junctions, on the order of a MΩ, were too noisy to extract helpful data from. Measurements were taken in a Bluefors LD250 dilution cryostat with a base temperature of 25 mK. Tunneling measurements were taken using standard lock-in techniques, typically with a voltage excitation of under 10 μV, allowing us to observe features with excellent resolution. The magnetic field was applied using a 2-axis vector magnet with maximum fields of 9T in-plane and 3T out-of-plane.