Introduction

The study of the complex dynamics of liquids and viscoelastic materials on various time scales down to picoseconds is of interest for fundamental research and of critical importance for a variety of industrial applications1,2,3,4. Because commercially available rheometers operate slowly, at frequencies below kHz, the principle of time-temperature superposition has traditionally been used to investigate the fast dynamics of liquids5,6,7,8. Although the assumption underlying this principle is useful in many cases, particularly in monitoring glass formers, it is not always valid, as evident in many soft materials6,9,10,11,12. Another approach is to obtain the macroscopic model of the liquid under study, based on molecular dynamics (MD) simulations13 on a time scale that is not accessible by experimental techniques, for example close to the picosecond range1,2,14. Recently, much attention has been paid to this approach, but it reaches computational limits as soon as it is necessary to observe macroscopic dynamics above the nanosecond range, and furthermore, despite the usefulness of MDs, experimental data for verification remain scarce8,9.

Therefore, to further investigate the fast dynamics of complex liquids and materials, techniques with higher operating frequencies are required. Brillouin scattering, which utilizes energy exchange between photons and thermally driven acoustic waves15,16,17,18, is conveniently employed at frequencies above 5 GHz, but less suited to the UHF range. The frequency shift of Brillouin-scattered photons depends on the acoustic properties of the medium, such as longitudinal modulus and density, but also on its local optical refractive index and thermal properties17,18. This leads to an indirect measurement of the local rheological properties. Brillouin scattering is also a weak process, which requires long integration time for analysis. In contrast, rheological measurements based on a solid mechanical body moving in liquid access directly the rheological information of the latter, and can operate with acquisition times well below the second. In consequence, most rheometers have in practice employed small-amplitude vibrating mechanical probes to interact with the liquid. Cantilevers19,20, micro-electromechanical techniques (MEMS)21,22,23, and quartz resonators, have indeed opened access to the rheology of liquid solutions up to a frequency of 100 MHz9. However, with these latter electromechanical techniques, it is not possible to further reduce the dimensions of the mechanical probe to achieve higher frequencies. Recently, time-resolved laser pump-probe experiments on vibrating nanoparticles enabled studying fluid-structure interactions between 7 GHz and 140 GHz24,25,26,27. However, to employ this approach at lower frequencies, the substrate noise must be overcome, which is a formidable task. As of today, a instrumental gap hence exists between 100 MHz and 7 GHz, covering all of the UHF range, where there is no method for analyzing the mechanical motion of a vibrating solid body in a liquid solution (Fig. 1a). However many liquids, such as alcohols with long molecular chains, are expected to display a complex dynamics in this frequency range28, and the associated timescales would additionally be accessible to MD simulations, offering a platform to compare experiments and numerical simulations. The UHF range covers numerous mechanical relaxation frequencies in polymer solutions, and has been little explored in biomechanics as well, essentially due to the absence of proper instruments. Measuring locally, and directly, the rheological properties of a liquid or a soft material over the largest possible frequency range, including the UHF, is also of great interest close to a phase transition, where the fluctuation spectrum broadens, and where microscopic spatial domains can form29. A method that would fill the present UHF gap in mechanical micro-rheology, and ideally offer fast acquisition, might hence have implications in the physics of glass formers, in the investigation of biological tissues, and in the science of polymers. We introduce and demonstrate such method here.

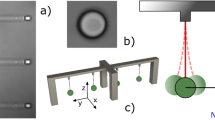
Fig. 1: Context positioning and technological concept of ultra-high frequency optomechanical micro-rheology.
figure 1

a Available small-amplitude high-frequency mechanical probes for liquid rheometry. *: ref. 26,27**: ref. 24, ***: ref. 25. b Electron micrograph of a suspended miniature silicon disk of radius a = 6 µm and thickness h = 220 nm, adjacent to a tapered optical waveguide. Release holes have been drilled though the disk to facilitate under-etching of the BOX layer, but play negligible role in relevant fluid-structure interactions. c Power spectral density (PSD) of a miniature disk radially vibrating on its fundamental RBM in air (black) and in liquid (red), with a line width of (γ/2π) and (γs/2π), respectively. d Distribution of radial displacement for the first RBM of a disk resonator.

Full size image

Results

We employ suspended disk resonators with a thickness of h = 220 nm and a radius a between 3 μm and 12 μm, and make use of multiple mechanical modes of these devices to develop a rheometry approach operating all over the UHF (see Supplements), focusing in the present report on frequencies between 100 MHz and 1 GHz. The mechanical motion of the disk is efficiently transduced thanks to a strong optomechanical coupling to its optical whispering gallery modes (WGM), allowing ultra-sensitive and fast optical measurements (see Supplementary Figs. S1 and S2). A measurement time as short as 70 μs is sufficient to obtain the desired rheological information in our experiments. The large signal-to-noise accessible with this optomechanical platform, combined with an analytical description of the hydrodynamics of fluids interacting with the moving disk, enable us extracting the mechanical properties of fluids with accuracy and precision. Experimental data and predictions of the model are first compared in the case of water, taken as a reference Newtonian liquid, in order to calibrate this new rheometry method and assess its level of validity and performance. After this calibration, the method is used on 1-decanol, a monohydric alcohol, in order to reveal its non-Newtonian behavior in the UHF range. The frequency response of optomechanical resonators immersed in the alcohol is measured, and the frequency dispersion of the liquid viscosity and elasticity is deduced from these measurements and from the model. The observed viscoelastic response is connected to the molecular dynamics of 1-decanol, illustrating that optomechanical rheometry can shed light on ultra-fast microscopic processes in the liquid.

Our optomechanical disk resonators, with radius a and thickness h, are fabricated from a silicon-on-insulator (SOI) wafer with a 220-nm thick (100) silicon layer over a 1-μm thick silicon oxide buried layer. They are placed in the vicinity of the optical waveguide (Fig. 1b). The optomechanical transduction method, which utilizes the mechanically-modulated optical WGMs evanescently coupled to the adjacent waveguide, enables access to the in-plane radial vibration mechanical modes of the disk in various environments, including in liquids30. The measured spectrum of the vibration mode of a disk is shown in Fig. 1c, revealing a large added dissipation and frequency downshift when the device is operated in water instead of air. Such frequency response can be described using a damped harmonic oscillator model including the fluidic force Ffluid exerted by the liquid onto the vibrating body:

$$\ddot{x}+{\gamma }_{s}\dot{x}+{\omega }_{s}^{2}x=\frac{1}{{m}_{s}}({F}_{{{{\rm{fluid}}}}}+\xi )$$
(1)

with γs and \({\omega }_{{{{\rm{s}}}}}^{2}\)=ks/mS the damping rate and resonant angular frequency of the bare disk in absence of liquid, ks the spring constant of the associated vibration, mS the associated mass, and ξ a random Langevin force. Upon immersion, the natural frequency of vibration becomes ω and the damping γ. The fluidic force can be modeled for radial vibrations of a disk, using a perturbative approach in which the pedestal is neglected and the device is considered as fully surrounded by the liquid. While this assumption may be employed for radial vibrations of high order and frequency covering all the UHF up to 3 GHz, such as those measured and presented in the Supplements (Supplementary Fig. S3), it is before all particularly well suited for the fundamental radial breathing mode of the disk, whose displacement amplitude is vanishing near the pedestal, as shown in Fig. 1d. In a recent work31, we analytically obtained the frequency downshift Δω = ωs-ω and quality factor Q≃ω/γ for this radial fundamental breathing mode, upon immersion in the liquid. To that purpose, we neglected the damping γs with respect to that exerted by the fluid, and expressed the susceptibility of the immersed resonator by writing Eq. (1), in absence of Langevin force, in the case of a harmonic oscillation x = Re(\(\widetilde{x}\,{{{{\rm{e}}}}}^{\,{{{\rm{j}}}}{{{\rm{\omega }}}}{{{\rm{t}}}}}\)):

$$-{\omega }^{2}+{\omega }_{s}^{2}+j\beta \omega=0$$
(2)

where the fluidic force exerted by a compressible viscous liquid can be expressed in complex notation \(\tilde{F}_{fluid}=m_{s}\beta j\omega\tilde{x}\), which is equivalent to the expressions of31 in the limit \(\omega\rightarrow\omega_{s}\):

$$\beta= {{{{\rm{p}}}}}_{1}\frac{(1+j)\sqrt{2\mu \rho {\omega }_{s}}}{{\rho }_{{{{\rm{s}}}}}h}+{{{{\rm{p}}}}}_{2}\frac{2\sqrt{2\mu \rho{\omega }_{s}}(1+j)+\frac{\rho h{\omega }_{s}}{2}({\int }_{0}^{2ka}{{{{\rm{J}}}}}_{0}({{{\rm{x}}}}){{{\rm{dx}}}}-j{\int }_{0}^{2ka}{{{{\rm{H}}}}}_{0}({{{\rm{x}}}}){{{\rm{dx}}}})}{a{{{\rho }}}_{{{{\rm{s}}}}}\left(1-\,\frac{{{{{\rm{J}}}}}_{0}({{{k}}}_{{{{\rm{s}}}}}{{a}}){{{{\rm{J}}}}}_{2}({{{k}}}_{{{{\rm{s}}}}}{{a}})}{{{{{\rm{J}}}}}_{1}^{2}({{{k}}}_{{{{\rm{s}}}}}{{a}})}\right)} \\ +{{{{\rm{p}}}}}_{3}\frac{\frac{j\rho h{\omega }_{s}}{{{{\rm{\pi }}}}}\,{{{\mathrm{ln}}}}\left(\frac{32a}{h}\right)}{a{{{\rho }}}_{{{{\rm{s}}}}}\left(1-\,\frac{{{{{\rm{J}}}}}_{0}({{{k}}}_{{{{\rm{s}}}}}{{a}}){{{{\rm{J}}}}}_{2}({{{k}}}_{{{{\rm{s}}}}}{{a}})}{{{{{\rm{J}}}}}_{1}^{2}({{{k}}}_{{{{\rm{s}}}}}{{a}})}\right)}$$
(3)

with μ the shear viscosity, ρ (ρs) the density of the liquid (solid), k = ωs/c (ks = ωs/cs) the acoustic wave number in the liquid (solid), with c (cs) the speed of sound in the liquid (solid). The longitudinal viscosity, or second viscosity coefficient, can be safely neglected in the UHF range considered here, for reasons discussed in ref. 31. \({{{{\rm{J}}}}}_{0}\left({{{\rm{x}}}}\right)\) and \({{{{\rm{H}}}}}_{0}\left({{{\rm{x}}}}\right)\) are Bessel and Struve functions:

$${{{{\rm{J}}}}}_{0}({{{\rm{x}}}})=\frac{1}{{{\rm{\pi }}}}{\int }_{ \! \! \! 0}^{{{\rm{\pi }}}}\cos ({{{\rm{xsin}}}}({{{\rm{\varphi }}}})){{{\rm{d}}}}{{{\rm{\phi }}}}$$
(4)
$${{{{\rm{H}}}}}_{0}({{{\rm{x}}}})=\frac{1}{{{\rm{\pi }}}}{\int }_{ \! \! \! 0}^{{{\rm{\pi }}}}\sin ({{{\rm{xsin}}}}(\varphi )){{{\rm{d}}}}{{{\rm{\phi }}}}$$
(5)

The closed-form expression Eq. (3) was derived under certain approximations, and it's individual terms correspond to three well-identified contributions in the fluid-structure interactions31. We added here an adjustable coefficient pi=1… 3 in front of each contribution, in order to precisely fit the experimental data acquired on liquid water, which we consider as a calibration compressible Newtonian liquid over the explored frequency range. The results of this fit are shown in Fig. 2, both for the quality factor and frequency shift, using reference values for water rheological properties (Table 1). A very good agreement is obtained for the calibrated model, which uses the coefficients listed in Table 1. The calibration also led consistent results on water-glycerol mixtures of varying glycerol concentration, hence does not seem to restrict to pure water. In water, if p1 = p2 = p3 = 1 (raw expression), the uncalibrated model captures the correct trend as function of frequency, but comes numerically off by up to 25%. Note that if compressibility effects in the liquid are neglected (k = 0), there is a strong deviation between model and measurements when increasing frequency. Indeed, while dissipation is mainly governed by shear friction for the largest disk radiuses (10 < a < 12 μm, lowest frequencies), compressibility and acoustic radiation are the dominant mechanisms for smaller radiuses (a < 10 μm, higher frequencies): they must absolutely be taken into account by the model.

Fig. 2: Ultra-high frequency optomechanical micro-rheology of liquid water.
figure 2

Mechanical quality factor and normalized frequency shift in water for the fundamental RBM of a silicon disk of thickness h = 220 nm and radius a varying between 3 and 12 µm, corresponding to RBM frequency between 200 and 850 MHz. Measurements in red are compared with predictions of our calibrated (uncalibrated) model in orange (green), and with predictions of an incompressible viscous model in dashed black. a Quality factor and b frequency shift (decrease) with respect to air. The error bars represent the 95% confidence interval, with the mean as the measure of center. Contributions to errors are discussed in the Supplements.

Full size image
Table 1 Optomechanical rheological measurements on liquid water
Full size table

The above frequency-dependent optomechanical (OM) measurements on water allow assessing the accuracy and precision of our method in the evaluation of physical properties of a liquid: density ρ, viscosity µ and sound velocity c. This is achieved by keeping the adjustable coefficients constant, and now minimizing an error function of (ρ,µ,c) when comparing our data with the predictions of the model. The properties of water obtained this way are listed with their uncertainties in Table 1. Uncertainties are calculated from the measurement errors for the quality factor and frequency shift shown in Fig. 2.

With the optomechanical micro-rheology technique now calibrated and characterized on a reference Newtonian liquid, we are prepared to investigate arbitrary liquids at ultra-high frequencies. Long-chain monohydric alcohols are expected to display relaxation dynamics in the UHF range, notably as a result of supramolecular re-organization governed by hydrogen bonds. Recent ultrasonic absorption experiments deduced relaxation frequencies close to the GHz in these alcohols, while the behavior at smaller frequency (up to tens of MHz) was obtained with a fast mechanical rheometer32. The frequency stitching of data obtained from the two methods led to partial agreement, with parameters estimated by the two methods varying by a factor up to 5. With our optomechanical rheological method now available, we can instead investigate the response all over the UHF range in a consistent manner. We chose 1-decanol (C10H22O) as a candidate for this study.

The measured mechanical response of the optomechanical devices immersed in 1-decanol is shown in Fig. 3. The results are compared with predictions of our analytical model, considering first 1-decanol as a compressible Newtonian fluid with frequency-independent mechanical properties (ρ = 827 kg/m3, µ = 11.8 mPa.s, c = 1380 m/s). Figure 3 clearly shows that such compressible Newtonian assumption fails at describing the measured trends in the UHF range. This is the signature of a viscoelastic response of the liquid, which invites us to explore frequency-dependent laws for the complex viscosity. Having checked that a simple Maxwell model, even involving multiple Maxwell bodies, was not sufficient to reproduce the observed trends, we improved the model complexity in steps, building on concepts of viscoelasticity established at lower frequency. Since the results of Fig. 3 involve at least two inflexion frequencies, a model with at least two characteristic frequencies is required. The simplest viscoelastic model capable to fit our data was found to be a summation of three terms: a first constant shear viscosity \({\mu }_{0}\) (Newtonian model), a second term corresponding to the Cole-Cole model33 with a (slow) relaxation time \(\tau\) and a third term associated to an extended Maxwell model1 of resonant frequency \({\omega }_{0}\) and (fast) relaxation rate \(\varGamma\):

$${{{\rm{\mu }}}}={{{\rm{\mu }}}}_{\infty }+\frac{{{{{\rm{\mu }}}}}_{0}-{{{{\rm{\mu }}}}}_{\infty }}{1+{\left({{{\rm{j}}}}\omega \tau \right)}^{{{{\rm{n}}}}}}+{{{{\rm{\mu }}}}}_{1}\frac{{{{\rm{j}}}}\omega \varGamma }{{{\omega }_{0}^{2}-\omega }^{2}+{{{\rm{j}}}}\omega \varGamma }$$
(6)
Fig. 3: Ultra-high frequency optomechanical micro-rheology of liquid 1-decanol.
figure 3

The mechanical response of miniature silicon disks of thickness h = 220 nm and radius varying between 3 µm and 12 µm, once immersed in liquid 1-Decanol. Quality factor (a) and normalized frequency shift (b) as function of frequency. Measured (red) and analytically calculated values, using a Newtonian model (green) and the non-Newtonian model discussed in the text (orange). The error bars represent the 95% confidence interval, with the mean as the measure of center. Contributions to errors are discussed in the Supplements.

Full size image

The Cole-Cole model has been successfully used in polymer science and in geophysics, with values of n between 0 and 234,35. It efficiently grasps physical situations where numerous internal degrees of freedom are involved34, as we anticipate being the case for the supramolecular dynamics in a long-chain liquid alcohol. As for the extended Maxwell model, it is obtained when taking into account the inertial response of the liquid, as required at the high frequencies considered here (see Supplements and Supplementary Figs. S3 and S4), and the associated relaxation rate seems to relate to intra-molecular dynamics (see below).

With Eq. (6) for the complex viscosity injected into Eq. (3), we obtain a very satisfactory agreement with measurements of the quality factor Q and frequency shift of resonators immersed in 1-decanol (Fig. 3). For that purpose, we inject the complex viscosity into our fluid structure model and minimize an error function with a sequential quadratic optimization algorithm, providing us with an evaluation of the parameters entering Eq. (6). Independent optimization runs provide consistent values for the parameters. The resulting parameters are listed in Table 2, together with parameter variance obtained over 200 optimization runs.

Table 2 Viscoelastic properties of 1-decanol at room T
Full size table

Discussion

As the here introduced optomechanical rheometry method ventures into the UHF range, literature data for comparison are scarce. In ref. 32, 1-decanol was studied by two different methods: shear wave impedance spectrometry between 6 MHz and 100 MHz, and acoustic absorption spectroscopy between 300 kHz and 3 GHz. The first method enabled access to the full complex shear viscosity in part of the very high frequency (VHF) range, when the second method attained the UHF range but only led the real part of the viscosity. While not providing the full rheological information in the UHF, the combination of these two methods enabled extracting two relaxation times in the measurement range, on the basis of a fit function with two Maxwell bodies (n = 1). By defining in our analysis a relaxation frequency \({({\tau }{*})}^{-1}\,=\Gamma /2\left[1+\sqrt{1+\frac{4{\omega }_{0}^{2}}{{\varGamma }^{2}}}\right]\), where the real viscosity is divided by two, we find τ*= 151 ± 11 ps, in the range expected for a molecular conformational isomerization (see Supplements). Meanwhile, our value of τ is consistent with the relaxation of hydrogen-bonded chain-like molecular clusters identified in ref. 32. This supports the interpretation of the visco-elastic terms of Eq. (6) as originating respectively from supramolecular (concerning molecule clusters) and intramolecular (within a single molecule) processes, a point that is yet reinforced by the analysis below.

Indeed, the introduced optomechanical rheology method enables now a measurement of the full complex viscosity in the UHF range, with its real (µ’) and imaginary (µ”) components, providing the complete rheological information. Since µ” is associated to the elastic response of the liquid, instead of the complex viscosity we rather consider the shear viscosity μ’ and shear elastic modulus jωµ”. In Fig. 4 we show the frequency dependence of these two quantities, as obtained from our fit of measurements. At low frequencies, the liquid exhibits a Newtonian behavior with a finite constant viscosity and no shear elastic modulus. At the highest frequencies beyond the GHz, the liquid displays a finite shear elastic modulus E that is plateauing close to 40 MPa. If the high-frequency behavior is governed by intramolecular conformational changes, this limit value of shear elasticity can be assimilated to the entropic elasticity of constituting molecules, which dictates the elongation of a single molecule in its equilibrium conformation36,37. Using such argument, the elastic modulus (E) at high frequency can be expressed as inversely proportional to the volume of a single molecule (V):

$$E=\frac{3{{{{\rm{k}}}}}_{{{{\rm{B}}}}}T}{V}$$
(7)
Fig. 4: The measured complex mechanical response of 1-decanol.
figure 4

The full rheological behavior of this long-chain alcohol, deduced from our UHF optomechanical measurements and models, is plotted as a function of frequency. a Shear viscosity. b Shear elastic modulus. The complex viscosity is given by Eq. (6) with parameters obtained from the measurements.

Full size image

From the inferred shear elastic modulus at high frequency (E = 40 ± 8 MPa), the volume of a single molecule of 1-decanol is estimated trough Eq. (7) to be V = 2.8 ± 0.7 × 10−22 cm3. Independently, using the molar mass and density of the liquid, one can determine the occupied volume per molecule. For 1-decanol (molar mass 158.28 g/mol and density 830 kg/m3) the occupied volume is 3.16 × 10−22 cm3, in good agreement with the former. This is evidence that the high-frequency shear elastic modulus of the liquid, and consequently the second relaxation time τ*, are indeed related to the conformational changes and stretching of molecules.

In conclusion, we have developed a new mechanical rheology method operating in the ultrahigh frequency range (UHF). The technique is based on nano-optomechanical resonators and supported by dedicated analytical models of fluid-structure interactions, allowing determination of the liquid properties with very good precision. The approach is used to measure the complex rheological response of a monohydric alcohol, 1-decanol, which shows a non-Newtonian behavior at ultra-high frequency. The exact form of this complex response sheds light on the molecular dynamics at nanosecond timescale in the liquid, accessing both supra- and intramolecular processes. With the UHF frequencies and quality factors reported in the present paper, the response time of our optomechanical rheometer could resolve sub-microsecond liquid evolutions in real-time. This includes conformational information, like the average volume occupied by a molecule. Because these information are obtained locally, within a micron-scale measurement volume, the method introduced here is a powerful tool to analyze fast processes in small quantities of viscoelastic materials. Optomechanical micro-rheology might for example track molecular dynamics within a micro-droplet during a rapid quench. This all paves the way for a rheological study of glass formers, but also for the mechanical investigation of microscale biological objects and membranes in physiological conditions, with unprecedented time-resolution.

Methods

We employ a tunable continuous-wave telecom laser to feed the whispering gallery modes (WGMs) of the disk, measuring the bus waveguide optical DC output as function of the laser wavelength. By fixing the laser wavelength in contrast, we look at the high-frequency (AC) modulation of the optical output, gaining access to the mechanical spectrum of the disk.

To ensure that the fluid is not affected by the heat generated by the laser, we keep the input laser power at the lowest level possible, and use of an erbium-doped optical amplifier and an electrical amplifier to amplify the output signal.

The optomechanical chip is fixed at the bottom of the liquid cell. The position of the two input and output fibers is controlled to maintain a constant optical transmission of the waveguide during measurement. The cell is filled with liquid using a syringe pump, while a top view camera helps determining the best coupling conditions for the fibers and monitoring the liquid level. The temperature of the liquid in the cell is monitored and controlled with a TEC controller connected to Peltier elements and a thermal resistor on the metallic parts of the liquid cell.

More details are given in the Supplements.