Introduction

For the majority of metallic systems, the electronic excitations therein can be described by the concept of quasiparticles in Landau’s Fermi liquid picture. At sufficiently low temperatures (T) where the life time of quasiparticles is predominantly limited by the elastic scattering on impurities or lattice defects, the Fermi liquid theory guarantees an elegant relationship between the thermal and electrical conductivities (κ and σ, respectively) contributed by quasiparticles: κ/σT = L. Here, the parameter L is the Lorenz number which is predicted to take the Sommerfeld value L0 = \(({\pi }^{2}/3){({k}_{B}/e)}^{2}\) = 2.44 × 10−8 W Ω K−2 (kB is the Boltzmann constant)1. This is the famous Wiedemann–Franz (WF) law established over one and a half centuries ago. The fact that the WF law prevails in almost all known metallic compounds is indeed not surprising: the elastic impurity scattering, always dominant at the zero-temperature limit, impedes the electrical (charge) and thermal (energy) transport in exactly the same momentum relaxing process. Very rare exceptions do exist with the value of L distinct from L0 down to the lowest T; such behavior is usually taken as evidence for the failure of quasiparticle description2, highlighting the non-Fermi-liquid physics introduced by critical fluctuations3,4 or one dimensionality5,6.

Despite the robustness of the WF law at T = 0 limit, a violation constantly occurs at intermediate T (ranging from a few kelvins to approximately the Debye temperature) when the inelastic scattering of quasiparticles sets in7. The inelastic electron–phonon (e–ph) and electron–electron (e–e) scattering processes relax the charge and energy flows in different rates, thus causing a T-dependent Lorenz number L(T) ≠ L08,9. As revealed by recent investigations, several scattering mechanisms can lead to severe finite-T deviation from the WF law, including small-angle (nearly momentum-conserving) e–ph and e–e scattering which may give rise to hydrodynamic transport9,10,11,12,13 and interband e–e scattering that can be important in semimetals14,15. In spite of the diversity of microscopic mechanisms, the above-mentioned inelastic scattering effects invariably cause a reduction of L in three-dimensional (3D) materials8,9,15, i.e., L < L0 for intermediate T.

In this paper, we report an unexpectedly enhanced L—contrary to the case in most metals and semimetals12,13,16,17—in a magnetic Weyl semimetal, NdAlSi. The topologically nontrivial band structure with multiple Weyl nodes in NdAlSi has been verified by both the density-functional theory calculations18,19,20 and the angle-resolved photoemission spectroscopy measurements21. The Weyl semimetal state hosting totally 40 Weyl nodes in paramagnetic NdAlSi is promised by the noncentrosymmetric space group I41md 21, whereas the magnetic-field(H)-induced spin-polarized state is also identified as a Weyl semimetal possessing a total of 56 Weyl nodes18; some of these Weyl nodes are close to the Fermi level (EF), as two of of the four Fermi surface pockets host Weyl fermions and are characterized by linear dispersions22. In NdAlSi, the Nd3+ (4f 3) local moments form a helical ferrimagnetic order below Tm = 7.3 K, which is proposed to emerge from the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction between 4f moments, mediated by the Weyl fermions (predominantly Nd 5d electrons)18. The helical ferrimagnetism, characterized by a unique up-down-down (u-d-d) spin configuration18, can be destructed by a magnetic field (H) along the crystallographic c ([001]) direction at a metamagnetic transition H = Hm and a fully-polarized state is stabilized above a crossover field Hp (Fig. 1b)19,20,23. The complex magnetic phases enriched by their interplays with low-energy quasiparticle excitations leave unique fingerprints in thermal transport. The behavior of longitudinal thermal conductivity κxx implies that the phonon heat conduction is strongly affected by scattering on local spins and magnetic excitations. More importantly, by scrutinizing the thermal Hall effect κxy, we revealed an enhancement of L exceeding L0 which develops at  ~30 K upon cooling, well above Tm; the enhanced L persists over a wide range of H and is only reduced in the polarized state. We proved that the unusually large L is not contributed by charge-neutral excitations, e.g., phonons and magnons. Instead, the finite-T deviation from WF law in NdAlSi can be interpreted by a model considering a Kondo-type scattering between localized and itinerant electrons. Such scattering mechanism, while being overlooked in most of the previous studies, may indeed play a role in a wide range of metallic compounds that possess local magnetic moments.

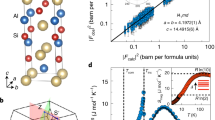
Fig. 1: Phase diagram and the longitudinal thermal conductivity κxx of NdAlSi.
figure 1

a Crystal structure of NdAlSi. b The magnetic phase diagram of NdAlSi, showing the paramagnetic (PM), up-down-down (u-d-d) helical ferrimagnetic and field-induced polarized (FIP) states19,20,23. Hm and Hp are the metamagnetic transition field and the crossover field for spin polarization, respectively. c A schematic of the experimental setup for thermal transport measurements with two differential thermocouples (left); a photograph showing the thermoelectric puck with sample mount (right). d Temperature (T)-dependent longitudinal thermal conductivities κxx (purple) and κzz (yellow) of NdAlSi, measured with thermal gradient ∇T parallel to the crystallographic a and c axes, respectively. Solid lines are estimated electronic thermal conductivities assuming the validity of the WF law in the whole range of T. e Zero-field κxx(T) measured in two NdAlSi samples (#1 and #6, purple and green circles, respectively) and a LaAlSi sample (black squares) from 2 to 300 K with JQ∥a. f The estimated non-electronic contribution of κxx in NdAlSi attained by subtracting the Wiedemann-Franz term \({\kappa }_{xx}^{{{{\rm{WF}}}}}={L}_{0}{\sigma }_{xx}T\) from the total κxx. The black curve is a fit of the phonon thermal conductivity κph to a modified Debye–Callaway model (Supplementary Note 2).

Full size image

Results

Longitudinal thermal conductivity

We first look into the coupling between the spin and lattice systems. Figure 1d shows the zero-field κxx(T) and κzz(T), measured with heat current JQ applied along crystallographic a ([100]) and c axes, respectively (see Methods for details; calibrations of the thermal-transport experimental setup are elaborated on in Supplementary Note 1). The electronic contribution κe, roughly estimated here by using the WF value \({\kappa }_{xx}^{{{{\rm{WF}}}}}={L}_{0}{\sigma }_{xx}T\) (solid lines in Fig. 1d), can account for less than one half of the total κ for both directions. The remaining part for T > 20 K (see below) can be taken as the phonon contribution κph(T); it exhibits a glasslike behavior characterized by the lack of a peak profile and the weak T dependence at high temperature7. The absence of phonon peak implies excessive scattering experienced by phonons at the temperature of several tens of kelvin—much above Tm. In contrast, a pronounced phonon peak on κxx occurs at  ~30 K in a nonmagnetic isostructural compound LaAlSi (Fig. 1e), highlighting the crucial role played by Nd 4f moments in the suppression of κph.

A likely cause of such suppression in the paramagnetic state of NdAlSi is the resonant phonon scattering off the crystal-electric-field (CEF) levels of the 4f multiplets24,25. In this scenario, the CEF multiplets absorb and emit phonons with the energy matching their level splitting, effectively impeding phonon heat conduction since the absorbed and emitted phonons have unrelated momenta. The CEF configuration for Nd3+ at zero field is composed of a ground state doublet and four degenerate excited doublets with an energy splitting  ~4.1 meV18,23. A fit of κph using modified Callaway model considering a simplified two-level system for resonant scattering (Supplementary Note 2) can reproduce the T dependence of experimental data (Fig. 1f); the effective energy splitting is determined to be  ~40 K (3.45 meV). According to the fit, an additional term in κxx besides κe and κph probably emerges below  ~20 K (Fig. 1f), consistent with a recent report26. We assign it to the contribution of magnetic excitations (i.e., magnons for T < Tm and paramagnons/fluctuations27 for T > Tm).

More information about the influence of magnetic excitations on heat conduction is revealed by a magnetothermal conductivity study. In Fig. 2a, we plotted κxx(H) (H∥c) at different T. From 4 K to 15 K, the isotherms are nonmonotonic with minima occurring at an intermediate H; for T ≳ 12 K, there is a single minimum located at Hmin in κxx(H) (hollow triangles), whereas at lower T two minima (\({H}_{min}^{1}\) and \({H}_{min}^{2}\), solid triangles) appear on each curve. We point out that the low-H decrease of κxx(H) can be mainly associated with κe (short-dashed line in Fig. 2a, see also Supplementary Fig. 1), whereas the high-H increase is most likely to be contributed by enhanced κph (the magnon thermal conductivity is supposed to decay with increasing H26). The T dependence of the characteristic fields determined from minima in κxx(H) is displayed in Fig. 2b, the implications of their possible origins are discussed in Supplementary Note 3. Note that Hmin roughly falls onto a line extrapolating to (H, T) = (0, 0) (magenta dashed line in Fig. 2b), pointing towards a putative H/T scaling behavior. Such a scaling is clearly verified in Fig. 2c, where Δκxx/κxx(0) = [κxx(H) − κxx(0)]/κxx(0) is plotted as a function of H/T. For T > 12 K, the minimum of κxx(H) occurs at a fixed H/T, a hallmark of the resonant phonon scattering25 that reflects the Zeeman effect of the 4f CEF levels. The H/T scaling is deviated at T < 12 K for both \({H}_{min}^{1}\) and \({H}_{min}^{2}\). Below  ~8 K, a hump-dip feature develops near \({H}_{min}^{2}\) with a local maximum showing up ahead of it (Fig. 2a), which probably manifests a sudden change in the scattering rate of heat carriers in the vicinity of Hp (Supplementary Note 3); above this feature, a remarkable increase of κxx occurs and becomes stronger upon cooling. We suggest that while the high-H upturn of κxx(H) can be naturally understood as a result of the weakened resonant scattering between phonons and 4f CFE levels, its strong enhancement at low T suggests that another phonon scattering mechanism, i.e, the scattering off magnetic excitations (magnons and/or paramagnons), comes into play; a severe suppression of the latter process at high H leads to an enhanced κph that can exceed 200% of the zero field κxx at 4 K (Supplementary Fig. 1a).

Fig. 2: Longitudinal thermal conductivity and magnetic excitation gap of NdAlSi.
figure 2

a κxx measured at various temperatures plotted as a function of H (applied along c). Curves are vertically shifted by 1 W m−1 K−1 for clarity. Short-dashed line denotes the electronic contribution estimated based on the WF law at T = 4 K. Characteristic fields Hmin (T ≥ 12 K) and \({H}_{min}^{1}\), \({H}_{min}^{2}\) (T < 12 K) are marked by hollow and solid triangles, respectively. Hm and Hp (see Fig. 1b) are indicated by black and gray bars, respectively. b T dependence of the characteristic fields defined in (a). Magenta thick line indicates a quasi-linear Hmin  − T relationship extrapolating to T = 0, H = 0 (dashed line). c Magnetothermal conductivity normalized to the zero-field value, \(\Delta {\kappa }_{xx}(H)/{\kappa }_{xx}(0)=[{\kappa }_{xx}(H)-{\kappa }_{xx}(0)]/{\kappa }_{xx}(0)\left.\right]\), plotted against H/T. Error bars in (b) are defined as the half widths of the field range wherein in the H derivative of Δκxx(H)/κxx(0) changes its value by 1. d Specific heat of NdAlSi measured under μ0H = 0 T (blue), 6 T (brown) and 14 T (yellow). The two vertical lines denote the magnetic transitions at Tm = 7.3 K and Tcom = 3.3 K; the latter marks an incommensurate-to-commensurate transition inside the ferrimagnetic state18. Inset: Best fits of magnetic heat capacity Cm at 14 T to a thermal activation model (see Methods). Fits were applied to a temperature range 2 K < T < 10 K. e The magnon excitation gap Δ (left axis) and corresponding temperature scale ℏΔ/kB (right axis) determined from fits of Cm(T) with the exponent n = 0 (green squares), n = −1 (purple circles), and analysis of the spin-lattice relaxation time T1 (red star). The evolution of Δ under magnetic field is approximately linear with an gap opening field 3.5–4 T. Inset: \({T}_{1}^{-1}\) plotted against T for μ0H = 12 T. The solid line is a fit to an exponential function yielding the magnon gap (“Methods”).

Full size image

The drastic depletion of scattering between phonons and (para)magnons strongly implies the development of a spectral gap for the latter. Similar to the case in quantum magnets α-RuCl327 and Na2Co2TeO628, it is likely that low-energy spin excitations are gapped out in the (H > Hp) spin-polarized state of NdAlSi. This conclusion is supported by specific heat (Fig. 2d) and 27Al nuclear magnetic resonance (NMR, inset of Fig. 2e) measurements (see Methods for details). A fit of the magnetic heat capacity Cm to a thermal activation model (Methods and Supplementary Fig. 2) for 2 K < T < 10 K yields a magnetic excitation gap Δ that opens roughly linearly with increasing H23 above 8 T (Fig. 2e). The gap opening field Hg (extrapolated to Δ = 0)  ~3.5–4.0 T appears to be lower than Hm at low T (Hm ≈ Hp ≈ 5.5 T for T = 2 K20). Fitting of the spin-lattice relaxation rate 1/T1 obtained from NMR experiment performed at μ0H = 12 T (Methods) also reveals a magnon gap consistent with the specific heat results (Fig. 2e). The increase of Δ from  ~10–15 K at 8 T to  ~25–35 K at 14 T can thus elucidate the reduction of phonon scattering off the magnetic excitations in this field range. In all, our results demonstrate that the phonon heat conduction in NdAlSi is appreciably hindered by spin-phonon coupling, predominantly scattering between phonon and magnetic excitations below  ~10 K and resonant phonon scattering on local moments for higher T.

Thermal Hall effect

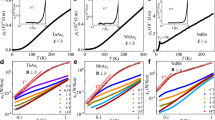
Now we turn to the electronic heat transport and examine the impact of scattering of local spins on the Lorenz number. Because phonons (and magnons at low T) contribute to a large portion of κxx and κzz (Fig. 1), determination of L from the longitudinal transport is difficult. Here, we use the Hall Lorenz number \({L}_{xy}\equiv \frac{{\kappa }_{xy}}{{\sigma }_{xy}T}\) (κxy and σxy are the thermal and electrical Hall conductivities, respectively) to test the validity of WF law in NdAlSi. Lxy also takes the value of L0 if the WF law is obeyed; otherwise, considering that the transverse transport coefficients κxy and σxy contain square term of the scattering rate, it is proposed that \({L}_{xy}/{L}_{0} \sim {({L}_{xx}/{L}_{0})}^{2}\) 16. In the upper panels of Fig. 3 we display the data of κxy measured at various temperatures on a NdAlSi single crystal (sample #1, see Methods and Supplementary Note 5 for experimental details), together with the hypothetic curves \({\kappa }_{xy}^{{{{\rm{WF}}}}}={L}_{0}{\sigma }_{xy}T\) simulated based on the measured σxy. The H-dependent Lxy determined from the ratio between κxy and \({\kappa }_{xy}^{{{{\rm{WF}}}}}\) are plotted in the bottom panels of Fig. 3. (More data taken on the same sample are shown in Supplementary Fig. 3) Surprisingly, at T = 4 K, κxy(H) appears to be larger than \({\kappa }_{xy}^{{{{\rm{WF}}}}}\) over a broad range of H (Fig. 3a): the value of Lxy exceeds 4 × 10−8 W Ω K−2 (i.e., Lxy > 1.6 L0) across the up-down-down ferrimagnetic phase regime below Hm and the field-induced paramagnetic regime between Hm and Hp20 (vertical bars in Fig. 3a); as the Nd 4f moments become fully polarized above Hp, Lxy(H) starts to decrease and the WF law is roughly recovered at μ0H = 14 T. For T > Tm = 7.3 K, the helical ferrimagnetic order is absent, yet the enhanced Hall Lorenz number Lxy(H) > L0 over the entire field range (0 ≤ μ0H ≤ 14 T) persists up to T ~30 K. The maximum Lxy reaches ≃2 L0 at 8 K and μ0H = 5.5 T (Fig. 3b). The κxy(H) measured at 40 K (Fig. 3f) and even higher temperatures (Fig. 3g, h and Supplementary Fig. 3) exhibits only marginal deviations, i.e., within the experimental error (Supplementary Note 1), compared with \({\kappa }_{xy}^{{{{\rm{WF}}}}}\).

Fig. 3: Magnetic field (H) dependence of the thermal Hall κxy and the Hall Lorenz number Lxy of NdAlSi.
figure 3

Data were measured in sample #1 with the temperature gradient ∇T and the H-field applied along the a and c axes, respectively. Top panels: Experimental κxy(H) (solid circles) compared with the electronic contribution \({\kappa }_{xy}^{{{{\rm{WF}}}}}={L}_{0}{\sigma }_{xy}T\) (solid lines) estimated based on a valid WF law. Vertical lines mark out the metamagnetic transition field Hm and the crossover field Hp for spin polarization20. Bottom panels: The Lxy corresponding to the data shown in (a–h), plotted against H. The horizontal lines are the Sommerfeld value L0. a T = 4  K, b T = 8 K, c T = 12 K, d T = 15 K, e T = 20 K, f T = 40 K, g T = 100 K, h T = 250 K.

Full size image

The thermal Hall study unveils an unusual enhancement of the Lorenz number in NdAlSi, suggesting a unique mechanism for the finite-T WF law violation in this compound; such enhancement survives much higher temperature and fields than the ferrimagnetic order, thus could not be straightforwardly linked to a special magnetic configuration. Nevertheless, the enhancement appears to be suppressed once the spin polarization is established at high H (Fig. 3a–c). The overall behaviors have been reproduced in three more samples (#2, #3, and #4), see Supplementary Fig. 4. In all samples, an Lxy considerably exceeding L0 is observed at low T, with a maximum value of  ~1.6–2.4 L0. Due to the uncertainties in the measurement of sample dimensions and lead distances, there may be an error of 10–15% in the absolute values of κxy and σxy, which precludes a detailed analysis of the potentially sample-dependent Lxy. Also, this error may contribute to the mismatches between the \({\kappa }_{xy}^{{{{\rm{WF}}}}}\) and measured κxy at T ≳ 100 K (Supplementary Figs. 3 and 4), making it difficult to comment on the exact validity of WF law for elevated temperatures (Supplementary Note 1). We note that the low-T enhancement of Lxy is absent in the isostructural compound SmAlSi, another Weyl semimetal with helical magnetic order29, in which the WF law is obeyed within the experimental error (see Supplementary Fig. 5). In the nonmagnetic counterpart LaAlSi, Lxy ≃ L0 is also verified (Supplementary Fig. 6).

We further measured the thermal Hall conductivity for an in-plane H, i.e., κxz. Owing to the difficulty of applying JQ along a and c in the same sample, we determined κxz by measuring transverse thermal gradient ∇Tz in the ac-plane (with JQ∥a) and longitudinal κzz in two different samples; H was applied along b in both cases (Supplementary Note 5). The results are summarized in Fig. 4. The most notable feature on κxz is a nonsaturating upward deviation from the WF value, L0σxzT, with increasing H; the Lorenz number Lxz (defined following the same way as Lxy) reaches  ~2.2 L0 at T = 20 K and μ0H =  14 T (Fig. 4b). Such enhanced Lxz is still evident at least up to 50 K (Fig. 4c), whereas for T ≳ 100 K the potential deviation from L0 is elusive due to experimental uncertainties (Fig. 4d–f). The nonmonotonic H-dependence manifested on the low-T Lxy (Fig. 3a–d) is absent on Lxz. We suggest that this phenomenon is probably linked to the high saturation field for magnetization with H applied in-plane (Supplementary Note 7 and Supplementary Fig. 9f; for H∥b, full spin polarization is unlikely to be achieved below 14 T), consistent with the easy-axis anisotropy of NdAlSi18,19. Hence, the comparison provides further evidence that the high-H drop of Lxy is associated with the spin-polarized state.

Fig. 4: The out-of-plane thermal Hall κxz(H) and Lxz(H) of NdAlSi.
figure 4

Data were measured with H∥[010](b) (see Supplementary Note 5 for details of the derivation of κxz.) Top panels: Experimental κxz(H) (solid diamonds) compared with the electronic contribution \({\kappa }_{xz}^{{{{\rm{WF}}}}}={L}_{0}{\sigma }_{xz}T\) (solid lines) estimated based on a valid WF law. Bottom panels: Lxz(H) determined from κxz(H). The horizontal lines denote the Sommerfeld value L0. a T = 10 K, b T = 20 K, c T = 50 K, d T = 100 K, e T = 150 K, f T = 200 K.

Full size image

Discussion

It has been verified that in various metals and semimetals12,13,16,17, abundance of inelastic e–e and e–ph scattering explicitly leads to a downward deviation from the WF law (i.e., L < L0) at intermediate temperatures. This is because the entropy flow is impeded by all types of inelastic scattering while the charge current is degraded only due to the momentum-relaxing (large-angle) scattering processes9,13. Our observation of Lxy > L0 in NdAlSi is, however, in contrary to such a universal picture elucidating a reduction of L, implying the presence of unique underlying physics that may have been overlooked previously. At first glance, the abnormally enhanced Lxy may reflect the inclusion of a nonelectronic contribution in κxy. Despite that charge-neutral excitations such as phonons25,30,31,32,33 and magnons34,35 can give rise to a thermal Hall signal as well, we have sufficient evidence to rule out them as the origin of the enhanced Lxy in NdAlSi. The T dependence of κxy shown in Fig. 5a indicates that the excess thermal Hall (exceeding the WF value given by the solid line) is most prominent between  ~5–25 K. The lack of corresponding feature in κxx (Fig. 1d) in this temperature range strongly disfavors the phonon Hall scenario31; the fact that the excess κxy persists up to at least 4 × Tm (≈30 K, Fig. 5b) also makes the magnon origin highly unlikely. Moreover, the amplitude of excess thermal Hall in NdAlSi invalidates the interpretations of phonon Hall and magnon Hall: it easily reaches (4–5) × 102 mW m−1 K−1 (Fig. 3, Supplementary Figs. 3 and 4), composing about one half of the total thermal Hall angle ∣κxy/κxx∣ ≃ 35% at 5.5 T and T ≃ 10–12 K (Fig. 5a). In contrast, a universal upper limit of ∣κxy/(μ0Hκxx)∣ < 2 × 10−3 T−1 has been revealed for the phonon Hall angle32,33,36 (see Supplementary Note 10 and Supplementary Table 1 for details); the magnon Hall is characterized by an even smaller Hall angle of 10−3 34.

Fig. 5: Finite T deviation from Wiedemann-Franz law and the Kondo-type scattering.
figure 5

a T-dependence of the in-plane thermal Hall κxy (blue circles), the thermal Hall angle κxy/κxx (green circles) and L0σxyT (black curve). Data were measured on NdAlSi sample #1 at μ0H = 5.5 T with ∇T∥a and H∥c. b Lxy measured under μ0H = 5.5 T at varying temperatures. Data were collected from four NdAlSi crystals (#1–#4). Measurement results of the isostructural compound SmAlSi are also shown. The red curve denotes Lxy(T) calculated based on our model of τ(ϵ) (Supplementary Note 9). The error bars were determined from the uncertainties (i.e., noise level) in the measurements of ΔTx and ΔTy (details in Supplementary Note 1). c The energy distribution of relaxation time τ (bottom) with a minimum that is symmetrical about the chemical potential; such feature of τ(ϵ) stems from the high-order (Kondo-type) scattering between 4f and 5d electrons (Supplementary Note 9). Integrands of the transport coefficients κxy (Q, top) and σxy (P, middle) derived for T = 3 K (Supplementary Note 8); red and blue colors stand for the cases with and without taking into account the Kondo-type scattering, respectively. d Schematic of the coexistence of the RKKY interaction (blue shaded region) and the Kondo interaction (red shared region) in NdAlSi; the two compete and the former dominates. The red and black arrows represent the spins of Nd3+ localized 4f and itinerant 5d electrons, respectively. Blue dashed lines denote the RKKY interaction between the local moments.

Full size image

Having established the electronic nature of Lxy enhancement, we can further narrow down the speculations on its cause. The anomalous transverse terms stemming from the Berry curvature of electron wavefunctions37 are irrelevant, because NdAlSi does not exhibit noticeable anomalous Hall effect (Supplementary Note 6 and Supplementary Fig. 10d)38. In doped SrTiO3, the electronic thermal Hall can be significantly boosted by a magneto-thermoelectric effect, which introduces an additional term Δκxy ~ −αxySdragT (αxy and Sdrag are the transverse thermoelectric conductivity and the phonon-drag term in thermopower, respectively)39. For NdAlSi, however, such a scenario is dismissed considering the vanishingly small Sdrag (Supplementary Fig. 7a). A drastically increased L up to  ~20 L0 has been reported in graphene near its charge-neutrality point40; the involved exotic heat carriers, i.e., the neutral Dirac fermion fluid, shall not leave any fingerprints in the Hall channel.

A model proposed by Goff over half a century ago, which was aimed at explaining the anomalous L > L0 in chromium41,42, may help us understand the enhanced ratio of heat to charge transport in NdAlSi. In Goff’s model, a minimum centered at ϵ = E − μ = 0 (μ is the chemical potential) characterizes the energy dependence of specific conductivity, σ(ϵ) ∝ N(ϵ)v2(ϵ)τ(ϵ), where N(ϵ) is the density of states (DOS), v is the carrier group velocity and τ is the relaxation time. Such a dip-like profile results in a weaker suppression of κ compared with σ at finite T, leading to an increase of L (see Supplementary Note 8 for details). For chromium, the dip feature is associated with the spin-density-wave gap that erases the electronic DOS on parts of its Fermi surfaces42. Later, the same model was invoked to interpret the enhanced L in high-temperature superconductors wherein the pseudogap (PG) physics is involved43,44,45 (the PG corresponds to a depletion of DOS centered at μ). For NdAlSi, there is no evidence for such PG-like DOS depletion. Instead, we attribute the large Lxy to a depression of τ(ϵ) that is symmetrical about ϵ = 0, as shown in Fig. 5c, which equally renders a dip in σ(ϵ). Taking such an attenuated relaxation time into account, the integrands of κxy (Q) and σxy (P) (Supplementary Note 8) show distinct energy profiles (Fig. 5c): at finite T, the former has more states contributing to the energy integral, giving rise to excess thermal Hall compared with electrical Hall, i.e., an enhanced Lxy.

In NdAlSi, the peculiar energy dependence of τ is most likely due to the elastic Kondo-type scattering between itinerant (Nd 5d) and localized (Nd 4f) electrons. It is known that Kondo scattering process can lead to such profile of τ(ϵ) and, subsequently, an increased L46,47,48. The most prominent interaction involving 5d and 4f electrons in this material is the RKKY interaction, as the itinerant Weyl fermions mediate the indirect exchange coupling between 4f moments18. Nonetheless, we point out that Kondo-type scattering is likely to coexist with the RKKY coupling: in Doniach’s phase diagram49, a system containing itinerant electrons and local moments in the weak-coupling and low-electron-DOS limits (which is the case of NdAlSi) is characterized by the coexistence of Kondo interaction and RKKY interaction, whilst the latter prevails (Fig. 5d). By considering higher-order scattering in an incoherent Weyl-Kondo scattering model (Supplementary Note 9), we can reproduce the energy-symmetric minimum of τ(ϵ) at ϵ = 0 (Fig. 5c); a numerical calculation based on the resulted integrand functions Q and P (Supplementary Note 9) yields a T-dependent Lxy that satisfyingly tracks the trend of the experimental data (red line in Fig. 5b). In this scenario, the high-H reduction of Lxy (Fig. 3a–c) can be naturally linked to weakened spin-flip scattering in the fully polarized state, wherein 4f moments are strongly pinned by the external field. The absence of notable excess thermal Hall in SmAlSi (Fig. 5b, Supplementary Fig. 5) probably reflects a much weaker Kondo scattering therein, whereas the validity of WF law in nonmagnetic LaAlSi (Supplementary Fig. 9) is fully consistent with our expectation.

The assignment of the underlying mechanism for the enhanced L to Kondo-type spin-flip scattering finds support from a recent experimental work, which reveals Kondo hybridization between local moments and Weyl fermions in another magnetic topological semimetal, CeAlGe50. Similar Kondo physics may come into play in a broad range of magnetic topological materials (note that the qualitative behavior of Kondo-scattering-enhanced Lxy(T) shown in Fig. 5b does not rely on the position of band crossing, nor does it change significantly when parabolic bands exist at μ, see Supplementary Note 9 and Supplementary Fig. 11); further explorations are required to elucidate its impact on various physical properties. We also note that an unconventional Nernst effect has recently been resolved in NdAlSi and is proposed to arise from a remarkable energy dependence of carrier relaxation time22; such energy dependence is predominantly linked to the abundance of scattering from magnetic fluctuations at the “hot spots” on specific Fermi surfaces, triggered by a Fermi surface nesting instability. The same mechanism can contribute to thermal transport as well and possibly adds to the enhancement of Lxy. Nevertheless, the impact of magnetic fluctuation scattering is rapidly suppressed in the magnetically ordered state22 and thus the large excess thermal Hall in the u-d-d state (Fig. 3a) cannot be attributed to this origin. At the present stage, the incoherent Kondo-type scattering model serves as the most applicable interpretation of experimental observations, though a more complete understanding may rely on future investigations invoking microscopic probes.

Our results unequivocally verify the intricate and enriched coupling between low-energy excitations and local magnetism in the magnetic Weyl semimetal NdAlSi. The phonon conduction is shown to be strongly affected by resonant scattering on CEF-split 4f multiplets and, at lower T, scattering off magnetic excitations. Moreover, apart from the Weyl-mediated RKKY interaction, we suggest that there is also a subtle Kondo-type interaction between the Weyl fermions and the local moments; such Kondo-like scattering endows the relaxation time with a unique energy dependence, which leads to an unusual deviation from the WF law with a remarkably enhanced Lorenz number. The relevance of Kondo physics in NdAlSi highlights the emergent correlation effects stemming from the interplay between local spins and relativistic quasiparticles in topological materials. On a final note, our work demonstrates that thermal Hall measurement, combining with the WF analysis, is a powerful probe for unveiling special energy dependence of transport coefficients within a narrow energy window (a few meV) around the Fermi energy. Further development of this technique may help clarify the novel physics in numerous correlated quantum materials.

Methods

Single crystal growth and characterizations

We synthesized high-quality single crystals of NdAlSi, LaAlSi and SmAlSi using the Al self-flux method20. The crystal orientation and stoichiometry were determined by the pattern of single-crystal X-ray diffraction and energy dispersive X-ray spectroscopy, respectively (Supplementary Fig. 8). Electrical transport measurements were performed using conventional Hall-bar configuration in a Quantum Design DynaCool-14 T Physical Property Measurement System (Supplementary Fig. 10, see Supplementary Note 6 for details). Magnetic properties were measured by a Quantum Design vibrating sample magnetometer up to 7 T (Supplementary Fig. 9, see Supplementary Note 7 for detailed discussions). In this work we studied six pieces of NdAlSi single crystals (samples #1, #2, #3, #4, #5, and #6); they were grown in the same batch and all cut and polished into a rectangular bar shape before measurement. The dimensions (length ×width × thickness) of the samples were 1.8 × 1.0 × 0.25 mm3 (#1), 2.0 × 0.9 × 0.19 mm3 (#2), 2.6 × 1.1 × 0.21 mm3 (#3), 2.6 × 0.9 × 0.19 mm3 (#4), 0.69 × 0.58 × 0.50 mm3 (#5) and 2.6 × 1.1 × 0.57 mm3 (#6). For samples #1–#4, measurements of κxx and κxy were performed with heat current JQ∥a and H∥c, whereas κxz was determined from the data measured in samples #5 and #6 (Supplementary Note 5). Here, the coordinates x, y, and z correspond to the crystallographic a([100]), b([010]) and c([001]) axes, respectively.

Thermal transport and thermoelectric measurements

In our thermal transport experiment, the sample was mounted on a home-built thermoelectric puck, which was loaded into a Quantum Design physical property measurement system (PPMS-9 T or 14 T). Measurements were taken under high vacuum conditions (pressure lower than 1 × 10−5 Torr). We used a one-heater-two-(differential-)thermocouple setup as shown in Fig. 1c, which allows the simultaneous measurement of the longitudinal and transverse temperature differences (ΔTx and ΔTy). A 1 kΩ chip resistor was attached to one end of the sample by VGE varnish serving as the heater; a low frequency AC current was applied to the heater by a Keithley 6221 current source. The quasi-AC method was adopted to reduce the DC background noise which appears to be inevitable in PPMS. The other end of the sample was fixed to a copper block with a piece of cigarette paper soaked by diluted VGE-varnish serving as the insulating layer. Two pairs of type-E thermocouple were attached to the sample by stycast 2850 FT (with carefully ensured electrical insulation between the thermocouple and sample) in a differential configuration depicted in Fig. 1c. The voltage signals on thermocouple were collected by Keithley 2182A nanovoltmeters. We monitored JQ to guarantee that ΔTx is smaller than 10% of the base temperature at T < 5 K and ΔTx < 0.5 K for T > 5 K. Using the same setup, the longitudinal (Seebeck) and transverse (Nernst) thermoelectric coefficients can be also measured by attaching two pairs of gold wires to the sample with silver paste. For the field-sweep measurements, the assembly was thermally stabilized for at least 15 min before field ramping at each temperature point. The sweeping rate of magnetic field was set as 2 mT/s. Additional thermal transport measurements utilizing steady-state methods and thermometers (instead of thermocouples) were also performed for a double check of the main results; for details of these examinations, see Supplementary Note 1.

Specific heat measurements and data analysis

Specific heat was measured by a long relaxation method in a Dynacool-14 T PPMS (Quantum Design). As shown in Fig. 2d and Supplementary Fig. 2a, at zero field, C(T) exhibits a sharp λ-type peak at Tm = 7.3 K (onset of ferrimagnetic order) and a weaker feature at Tcom ≃ 3.3 K (an incommensurate-to-commensurate magnetic transition), as well as a broad anomaly at around 16 K which is attributed to a CEF Schottky term CSch18,23. With increasing H, the two magnetic transitions are gradually smeared out and the Schottky hump moves to higher T. CSch can be well reproduced by assuming a ground state doublet separated from four degenerate excited doublets for the Kramers ion Nd3+ (the sketch depicted in the inset of Supplementary Fig. 2c), i.e., \({C}_{Sch}\propto {\Delta }_{s}^{2}/{[\cosh ({\Delta }_{s}/2{k}_{{{{\rm{B}}}}}T)]}^{2}\), where Δs is a CEF splitting energy of  ~4.1 meV23. Such picture is consistent with the suppressed phonon thermal conductivity in NdAlSi (Fig. 1e) stemming from the resonant scattering on the Nd3+ CEF levels.

The magnetic heat capacity Cm of NdAlSi can be obtained by a subtraction of (predominantly phonon) background estimated from the specific heat of nonmagnetic counterpart LaAlSi (Supplementary Fig. 2b). A more detailed analysis of the phonon contribution to specific heat is presented in Supplementary Note 4. Apart from the Schottky term CSch discussed above (red line in Supplementary Fig. 2b, inset), Cm contains the contribution from a system with independent magnetic excitations, which dominates at low T and can be described as51:

$${C}_{m}=\int_{\!0}^{\infty }Eg(E)\frac{df(E)}{dT}dE,$$
(1)

where g(E) is the density of states (DOS) and \(f(E)=1/[\exp (E/{k}_{B}T-1)]\) is the Bose factor for magnetic excitations. For an isotropic excitation spectrum taking the form E = Δε + αkβ, \(g(E)=({V}_{m}/2{\pi }^{2}\beta {\alpha }^{3/\beta }){(E-{\Delta }_{\varepsilon })}^{3/\beta -1}\). Thus, the acoustic branches as the leading term contributing to specific heat gives \({C}_{m}=A{T}^{{{{\rm{n}}}}}\exp (-\Delta /T)\) (here n = 3/β − 2 and Δ = Δε/kB), which is a thermally activated form controlled by a magnetic excitation gap Δ. For NdAlSi, the specific dispersion relation (i.e., β) of magnon band remains unknown, thus we applied this model to our data below 10 K with two fixed values of the exponent n: n = 0 (β = 3/2) and n = −1 (β = 3). The two choices yield slightly different Δ(H) (Fig. 2c). Nevertheless, the main conclusion that a magnon gap is opened linearly by a magnetic field μ0H(∥c) ≳ 3.5 T stays valid.

Nuclear magnetic resonance measurements

NMR measurements were performed using a commercial NMR spectrometer from Thamway Co.Ltd in an NMR-quality 12 T magnet (Oxford Instruments). Data were taken under an external magnetic field of 12 T along the c direction. The nuclear spin-lattice relaxation time T1 of 27Al nuclei was measured by the saturation-recovery method and the recovery of nuclear magnetization M(t) was fitted by a function \(1\,-\,M(t)\,/\,M(\infty )\,=\,{I}_{0}\{0.028\,\exp [-{(t/{T}_{1})}^{\beta }]\,+0.178 \exp [-{(6t/{T}_{1})}^{\beta }]\,+ 0.794 \exp [-{(15t/{T}_{1})}^{\beta }]\}\). For the long wave approximation in antiferromagnetic materials, 1/T1 is given by \(1/{T}_{1}\propto {T}^{3}\int_{{T}_{{{{\rm{AE}}}}}/T}^{\infty }xdx/({e}^{x}-1)\), where TAE represents the magnon excitation gap. For T ≪ TAE, \(1/{T}_{1}\propto \,{T}^{2}\,\exp (-{T}_{{{{\rm{AE}}}}}/T)\)52,53. As shown in the inset of Fig. 2e, 1/T1 is nearly T independent above  ~10 K as expected for a paramagnetic phase. Below 10 K, the rapid decrease of 1/T1 indicates a pronounced depletion of spectral weight and the opening of an energy gap in the magnon excitation spectrum; the gap size given by \(1/{T}_{1}\propto \,{T}^{2}\exp (-\Delta /T)\) is Δ ~29 K.