Introduction

Electromagnetic (EM) metamaterials consist of sub- wavelength elements arranged in 3D space periodically or quasi-periodically. They are artificial structures with EM properties not found in nature, such as negative dielectric constant, negative permeability and negative/zero refraction index. In order to realize more functions with such kind of materials, the concept of programmable metasurface (PMS), which is controlled electronically and arranged in 2D planar structures, is proposed. By tuning the phase, amplitude, polarization or even frequency of reflected impinging wavefronts in a programmable way with the aid of field-programmable gate arrays (FPGAs), the PMS has the capability to manipulate EM waves in real time, which makes the long-standing dream of improving propagation characteristics for transmission channels come true.

Due to its significant advantages, the deployment of the PMS has been investigated in various wireless communication scenarios1,2,3,4,5,6,7 to overcome negative effects of wireless channels. By turning the wireless environment into a programmable space, functionalities e.g., beam steering, beam splitting, wave absorption, wave polarization and phase control are achieved and incorporated as a parameter in the network design. Various benefits including signal coverage enhancement8, EM pollution reduction9, energy efficiency improvement10, signal focusing11 are brought to wireless communication systems.

In recent years, PMS is also combined with information science12 and digital signal processing13, to encode and transmit information without using conventional base-band modulating processes. Time-modulated metasurfaces have been proposed to control the spectral distributions of reflected EM waves14. By encoding the digital information in the time domain, wireless communication systems in new architectures are successfully constructed without using traditional radio-frequency components such as antennas or mixers. Prototypes based on binary frequency shift keying15, quadrature phase shift keying14,16, 8-phase shift keying17,18, quadrature amplitude modulation19 and even massive multiple input multiple output20 are demonstrated to verify the effectiveness. Space-domain modulation is also introduced to collaborate with time-domain coding PMSs, to achieve capabilities such as beam scanning21 or secure communication22.

Besides the wireless communication area, the PMS is also investigated for radio localization23,24, microwave imaging25 and reduction of radar cross section26. However, in the field of radar detection, which is one of the most important applications of EM waves, possible benefits that a PMS could bring to a radar system are not fully exploited. Investigations still focus on theoretical discussions of enhancing detection capabilities27,28 or achieving dual-functional radar- communication systems29,30. The difficulty of making the above theoretical discussion a reality in designing a practical radar system is the severe angle dispersion issue of existing PMSs. Due to multiple reflections between sub-wavelength elements and their corresponding ground31, the responses, in particular, the phase, of most published PMSs are sensitive to incident angles, with respect to both elevation- and azimuth-planes. The PMS angular sensitivity leads to nonreciprocity between incident and reflected EM waves, which results in a failure of accurate direction-of-arrival (DOA) estimation. Thus, while PMSs have been used to build wireless communication systems in new architectures, they have not yet been practically implemented in PMS-assisted radar systems.

Since it has been realized that the angle-sensitive issue is a sticking point for the implementation of PMSs to aid radar detection, some efforts have been reported to resolve the angle-sensitive issue of PMSs, for either magnitude32,33 or phase responses34. However, there is one key limitation of these reported works that they can only deal with responses for incident angles coming from one azimuth plane or two orthogonal azimuth planes, which are still a distance away from the capability of being applied in a practical radar system.

In this work, we report a digitally-controlled fully-resonant PMS whose reflected phase is stable for wide incidence angles from 0° to 50° in the elevation plane with respect to full 360° range in the azimuth plane, and a radar scheme which is integrated with such a PMS as a periscope for the detection of targets in urban environment. By manipulating reflected phases of impinging EM-waves, the PMS periscope generates multiple beams that scan in non-line-of-sight (N-LOS) areas with respect to the transmitting/receiving antenna, thus eliminates shadow areas of this radar caused by high buildings. To verify this PMS-aided radar scheme, we build a linear frequency-modulated continuous wave (LFMCW) radar system. In this system, the PMS periscope is assumed to be mounted on the facade of a building and controlled by FPGAs to cover those shadow areas. To validate its performance, we fly a drone into N-LOS areas of this radar in different elevation and azimuth cases, and draw its 3D flight paths by measuring the speed, distance and direction of it. Our approach offers a low-cost solution for the detection of N-LOS targets, which is critically important to track UAVs and guard skies in urban environment.

Results

Non-line-of-sight detection of radar based on programmable metasurface periscope with angular reciprocity

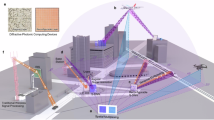
We first consider a representative urban environment that consists of several sub-regions, as illustrated in Fig. 1. In sub-region I, a direct path can be established between the radar and the prospective target, while the direct path is inhibited by buildings in sub-region II. Such an N-LOS situation is quite normal for radar operation in an urban environment. When an PMS is considered as a controllable periscope for the transmission channel, a new indirect propagation path can be established between the radar and the N-LOS target to aid the detection.

Fig. 1: Conceptual illustration of the N-LOS detection of radar based on PMS with angular reciprocity.
figure 1

By applying an isotropic angle-insensitive PMS, due to the angular reciprocity, beams from a radar can not only be scattered to targets in N-LOS regions, but also scattered back from those targets to the radar. In this case, such an PMS works as a periscope which establishes an indirect path for target detection in N-LOS regions.

Full size image

Since the phase response of each PMS element can be controlled independently, various reflection phase distributions are capable to be generated on the aperture of the entire PMS. In this case, dynamic beams are created when EM waves from a radar impinge onto it, which perform scanning within its area of competence. If the phase response of the implemented PMS is insensitive to the incident angle of impinging microwaves, the scattering from a target back to the PMS can achieve angular reciprocity to the radar, accordingly. Hence, a two-way double-hop channel is successfully established, which works just as a periscope and allows to accomplish the accurate detection task in N-LOS regions.

It can be seen from the above analysis that, the successful design of an isotropic angle-insensitive PMS is the key factor to realize the above radar scheme. Compared with a traditional scheme requiring multiple radar systems, the scheme in Fig. 1 with PMSs toward N-LOS regions is low cost, light in weight and offers an all-passive solution that avoids the strong interference between different radars in such a crowded area. Moreover, by including time-manipulation into the system, we can even combine target detection with information science to develop smart radar-networks.

Design of isotropic angle-insensitive programmable metasurface element

The first step is to improve the insensitivity performance in the elevation-plane. To this aim, we designed a reflection-type PMS element backed by a metallic cavity which constructs a fully resonant structure, instead of hybrid transmission-resonant structures in conventional PMSs. As plotted in Fig. 2a, although the sub-wavelength metallic pattern is a resonant structure, the space between the top metallic pattern and its corresponding metallic ground is still a transmission structure, whose response is relevant to elevations due to multiple reflections within this space. By introducing via fences to surround the metallic pattern as in Fig. 2b, the space between top metallic pattern and bottom metallic ground becomes a metallic cavity, in which multiple reflections can be eliminated. In this case, the overall PMS structure can be regarded as a whole resonator, whose reflections only take place on the top metallic pattern. In most cases, the response of a resonator is closely related to its resonant frequency while less relevant to other factors, enabling the response to be insensitive to incident angles in the elevation-plane.

Fig. 2: Operating mechanism and performance of the proposed angle-insensitive PMS element.
figure 2

a Multiple reflection model of a conventional PMS. b Single reflection model of the proposed IMS. c Geometry of the proposed PMS. d Equivalent circuit of the proposed PMS. e Reflection Phase of the proposed PMS versus different capacitance of the utilized varactor.

Full size image

The second step is to resolve the angle-sensitivity issue in the azimuth-plane. Since the element is now a fully resonant structure, we try to align those resonant frequencies corresponding to different azimuths by using several perturbation vias. With this measure, similar resonant frequencies for incidences coming from different azimuths can be achieved. In this case, insensitive responses with respect to different azimuths can be achieved.

The geometry of the isotropic angle-insensitive PMS element is illustrated in Fig. 2c. In the proposed geometry, the element is composed of two dielectric substrate layers which are isolated by a full metal ground plane. RF circuits are constructed on the upper dielectric substrate, while DC biasing circuits are on the lower one. This structure can be easily manufactured using a standard multilayer printed-circuit-board (PCB) fabrication process. F4B (εr = 3.5, tanδ = 0.0025) with a thickness of 3.3 mm and 0.7 mm are utilized for the upper and lower substrate, respectively.

The detailed layout of the element is also shown in Fig. 2c. Initially, the metallic pattern of a single element is constructed by 4 patches on the top surface of the upper dielectric. Those patches exhibit rotational symmetry and bridged by varactors through narrow metallic strips. Then, a square metallic fence achieved by metallic vias drilled into the upper dielectric is designed to surround the metallic pattern and form a resonant cavity. Finally, 4 perturbation vias are placed between adjacent patches. In the above structure, each patch is connected to its corresponding biasing circuit arranged on the bottom surface of the lower layer, by a metallic via through both dielectric layers. Parameters in Fig. 2c are: W = 22.7 mm, L = 27 mm, L1 = 6.7 mm, L2 = 6.9 mm.

It is seen in Fig. 2c that, this element is loaded with four varactors, so that the functionality of the PMS element can be dynamically reconfigured by changing the working state of varactors. According to the knowledge of digitally coded metasurface35 and its equivalent circuit in Fig. 2d, the phase of reflected waves can be manipulated in real time by applying different control voltages from the FPGA to the varactors. The control voltages applied to the four varactors in each element are identical to each other to achieve the same capacitance. MA46H120 varactor from MACOM with a low series resistance of 0.3 Ω36 and a tuning range from 0.149 pF to 1.304 pF37 is utilized in our design. To investigate EM characteristics of the element, a linearly polarized TM plane-wave along x-axis is excited with normal illumination in full-wave numerical simulations. The Floquet boundary is assigned to simulate the infinite periodic structure. For a normal incidence, the achieved phases with respect to different capacitances of the varactors are presented in Fig. 2e. A maximum 339° (−178° to +161°) phase-shift range can be tuned when the capacitance increases from 0.15 pF to 1.3 pF at the frequency of 3.35 GHz. To further illustrate its angular insensitivity performance, this isotropic element is compared with its counterparts without the metallic cavity or perturbation vias in Figs. 3 and 5, by spatial dispersion curves that illustrate the dependence of the reflection phase on the incident angle in both elevation- and azimuth-planes.

Fig. 3: Structure and performance of angle-sensitive PMS elements.
figure 3

a Structure of the Type A PMS element without the metallic cavity and perturbation vias. b Spatial dispersion curves under incidence with an azimuth of Ф = 0° for the Type A PMS element. c Spatial dispersion curves under incidence with an azimuth of Ф = 45°for the Type A PMS element. d Structure of the Type B PMS element without perturbation vias. a Structure. e Spatial dispersion curves under incidence with an azimuth of Ф = 0°for the Type B PMS element. f Spatial dispersion curves under incidence with an azimuth of Ф =45° for the Type C PMS element.

Full size image

Figure 3a shows the initial structure (Type A) from which the isotropic element is evolved from. The structure is designed to be symmetrical with respect to x- and y-axis, to achieve identical responses for incidence with the same elevation θ but different azimuths Ф, i.e., Ф = 0°, 90°, 180°, and 270°. For the same reason, this structure is also designed to be symmetrical with respect to Ф = ±45° planes. Figure 3b, c shows dispersion curves with respect to different incident elevations at 3.35 GHz when the azimuth of incidence is Ф = 0° and Ф = +45° planes, respectively. The varactor capacitance of an element is controlled to achieve phase-shift from −120° to +120° with an interval of 60° at the normal incidence (θ = 0°) coming from the Ф = 0° plane. Simulated results show that, the phase deviation issue is very serious in either Ф = 0° or Ф = +45° incident cases, especially when the shifted phase is between ±60°. It is also noticed that, the achieved phase-shift at the normal incidence (θ = 0°) in the Ф = +45o incident case does not correspond to the one (θ = 0°) achieved in the Ф = 0° incident case. The above results validate that, a PMS element designed in a conventional method suffers from spatial dispersion and behaves anisotropy for phase responses.

Figure 3d shows the improved structure (Type B) of a PMS element. Four rows of vias are drilled and metalized to form a cavity which surrounds the top metallic pattern. With this cavity, an additional EM boundary condition is introduced between its top metallic pattern and bottom metallic ground, which can eliminate those multiple reflections resulting in spatial dispersion for different elevations. Simulated results in Fig. 3e, f indicate that, the phase deviation is greatly suppressed, particularly for incident elevations below 50°. Since the PMS element is a full resonator structure, the reason can be explained by observing its resonant modes. In Fig. 4, electrical field distributions are plotted for the Ф = 0° incident case with different elevations, when the target phase shift is −60°. It is found that, when the incident angle is smaller than 50°, the excited modes inside the cavity are the quasi TE102-mode with similar electrical field distributions. However, the situation is quite different for those incidences with elevations larger than 60°. In these cases, excited modes are more like the diagonal quasi TE102-mode, whose electrical fields are no longer symmetrical with respect to the vertical plane.

Fig. 4: Electrical field distributions of the Type B PMS element under incidences with different elevations θ.
figure 4

a θ = 0°. b θ = 25°. c θ = 50°. d θ = 60°. e θ = 70°. f θ = 80°.

Full size image

Although the consistency of phase responses is greatly improved for Ф = 0° and +45° incident cases, respectively, the achieved phase-shift between these two incident cases still differs a lot from each other. It can be seen that, the maximum difference is about 27° which appears when the target phase-shift is 0° and −60°. The difference is still larger than 10° for 60° and −120° cases, while it is smaller than 10° only for the 120° case. As illustrated in Fig. 5a, b, an investigation is conducted by observing their electrical field distributions when the target phase-shift equals 0° (Cvar = 0.65 pF) for normal incidences (θ = 0°). It is found that, when the azimuth of the incidence is Ф = 0°, the excited resonant mode is a quasi TE102-mode. As a contrast, for the Ф = 45° incidence, the excited resonant mode is diagonal quasi TE102-mode. It is known that, the resonant frequency of the diagonal quasi TE102-mode is higher than that of the quasi TE102-mode, which also corresponds with the phenomenon that larger phase-shifts are achieved in Fig. 3f than those in Fig. 4e with the same capacitance of the varactor.

Fig. 5: Structure and performance of an angle-insensitive PMS element.
figure 5

a Electrical field distributions of the Type C PMS element under normal incidences with azimuths of Ф = 0°and Ф = 45°. b Structure and spatial dispersion curves of the Type C PMS element. c Spatial dispersion curves under incidence with an azimuth of Ф = 0°. d Spatial dispersion curves under incidence with an azimuth of Ф=45°.

Full size image

In order to align resonant frequencies between Ф = 0° and +45° incidences, four perturbation vias are introduced in the finalized structure (Type C) of the isotropic angle-insensitive PMS element as in Fig. 5b. It should be pointed out that, these four vias are symmetrically located with respect to the center of the cavity. As can be observed, the electric field is strong only around Vias 2&2’ for Ф = 0° in Fig. 5a, while it is strong around all the four perturbation vias for Ф = 45° in Fig. 5a. Therefore, when moving the above four vias symmetrically, it causes a strong change of the resonant frequency for the case of Ф = 45° but only a small change for the case of Ф = 0° in Fig. 5a, which helps to achieve the alignment of resonant frequencies, as well as the phase response between the two cases. The above investigations are verified in simulated results shown in Fig. 5c, d. Similar suppression of phase deviation as in Type B is achieved. Moreover, a good correspondence is also obtained between phase responses in Ф = 0° and + 45° incident cases. It should be pointed out that, there are two reasons that we use Ф = 0° and + 45° incident cases to evaluate the angle sensitivity issue in the azimuth plane. Firstly, the phase shift difference between the above two cases is larger than any other two cases that fulfill 0° < Ф < +45°. Secondly, the overall structure of the PMS is symmetrical with respect to Ф = 0°, 45°, 90°, and 135° planes.

For a better observation of the improvement, the mean square error of achieved reflection phase-shift (RPmse) and root mean square of reflection phase-shift error (RPErms) for Type A, B and C PMSs are quantitatively calculated and compared in Fig. 6a–d, respectively. It is noted that, the calculation is only carried out for incident elevations from 0° to 50° with an interval of 5°, due to the incident angle of impinging EM waves is ≤45° in most scenarios. It is observed that, both of the maximum RPmse and RPErms for Type C PMS are smaller than 3°, which are much better than those obtained from Type A&B PMSs and enough for most practical applications. As a conclusion of the above analysis, the proposed resonator-type PMS is capable to provide a stable phase-shift performance for the whole 360° in the azimuth-plane and ±50° in the elevation-plane, which indicates an isotropic angle-insensitive property in a full 100° cone-metric-space.

Fig. 6: Quantitative calculation of phase sensitivity for Type A, B and C PMS elements.
figure 6

a RPmse under incidence with an azimuth of Ф = 0°. b RPmse under incidence with an azimuth of Ф = 45°. c RPErms under incidence with an azimuth of Ф = 0°. d RPErms under incidence with an azimuth of Ф = 45°.

Full size image

Performance of an entire programmable metasurface periscope

To evaluate the performance of the proposed PMS periscope, a prototype including 10 × 10 elements is fabricated and measured. Photographs of the prototype, whose entire size is 289 × 294 mm2, are shown in Fig. 7a, b. Biasing voltages are provided and controlled by our developed FPGA module as in Fig. 7c, through biasing lines connected with 5 DC plugs located at the bottom of the PMS. It has been mentioned in the above section that, the period of a single element is set to be about λ/4. In order to reduce the complexity of biasing voltage control, a subarray composed of 2 × 2 elements shares the same biasing voltage in our proposed design, without the grating-lobe issue. Therefore, there are a total of 25 groups of biasing voltages utilized in the entire prototype.

Fig. 7: Structure and measured performance of the fabricated overall PMS.
figure 7

a Front view. b Back view. c FPGA board utilized for DC voltage controlling. d Measurement setup. e PMS arranged for different measurement cases. f Measured reflection phase under incidences with an azimuth of Ф = 0°. g Measured reflection phase under incidences with an azimuth of Ф = 45°. h Measured reflection amplitude under incidences with an azimuth of Ф = 0°.

Full size image

Measurements are conducted in an anechoic chamber. The configuration of the measurement system is illustrated in Fig. 7d, which is mainly composed of a signal generator, a transmitting horn antenna, a metasurface, an FPGA voltage controlling module, a receiving antenna, a multiple-channel receiver module, an A/D sampling module, a PC, two voltage sources, a coupler, a fixture and several sync cables. These sync cables are utilized to synchronize the signal generator, the receiver module and the A/D sampling module with the FPGA. In the measurement, a 3.35 GHz single-tone signal is generated by the Keysight N5172B signal generator, transmitted to the transmitting horn antenna through the directly-connected port of the coupler, radiated into the free-space and illuminated onto the metasurface in front of the transmitting horn antenna. The voltage on each biasing line of the metasurface is controlled by the coding sequence generated from the FPGA. After the manipulation, waves reflected by the metasurface are then reradiated to the free space and received by the receiving horn antenna. After that, signals are transmitted to the receiver module and down converted to the baseband. Through the A/D conversion, such baseband signals are compared with baseband signals that are down-converted from coupled port of the coupler to obtain phase and magnitude responses. It is noted that, the fixture enables the metasurface to rotate in both azimuth and elevation planes to meet different measurement scenarios as shown in Fig. 7e.

In the measurement of reflection phases under different biasing voltages, the transmitting and receiving antennas are placed 1.5 m away from the PMS to implement the plane wave excitation, following the far-field criteria d = 2D2/λ, where d is far-field distance and D is the dimension of the horns. Measured reflection phases at 3.35 GHz are plotted in Fig. 7f, g. In these figures, the achieved reflection phase that is equal to the measured value of a metallic plane with the same size of the overall PMS biasing voltage is defined as −180°, which also acts as the reference phase for other measurements. A measurement is conducted for biasing voltages increasing from 0 V to 18 V. Measured results for Ф = 0° (xoz-plane), θ = 0° (+z axis) incidence are plotted in Fig. 7f by the solid blue line with triangles, from which those specific voltage values corresponding to different reflection phases with an interval of

10o can be obtained. After that, reflection phases corresponding to the other three cases [(Ф = 0°, θ = 45°), (Ф = 45°, θ = 0°), (Ф = 45°, θ = 45°)] are also measured and plotted under the above specific voltage values. It is seen in Fig. 7f, g that, for both Ф = 0° and 45° planes, only a small deviation can be observed between different cases, indicating stable angular insensitivity are achieved at different incident angles with respect to both elevation and azimuth planes.

In order to have a more comprehensive cognition for the performance of the proposed PMS, reflection amplitudes are also measured at 3.35 GHz for the case of Ф = 0°, θ = 45°. A metallic plane with the same size of the overall PMS is used as a reference. As shown in Fig. 7h, a maximum loss of 1.63 dB occurs when the reflection phase equals 0o near the biasing voltage of 4 V. The amplitude variation within the entire tuning range is smaller than 1.34 dB, which is very beneficial for a stable beam scanning.

Furthermore, since the proposed PMS aims to act as a periscope for target detections, measured and simulated scattering patterns are also given in Fig. 8a–e for Ф = 0° and 45° planes, respectively. It should be pointed out that, a biasing strategy that is capable to achieve lower sidelobes is utilized based on the phase-amplitude graph as shown in Fig. 8f. In this strategy, the phase corresponding to smaller amplitude loss, e.g., −180° with 0.26 dB loss, is always assigned to the subarray located at the center of the PMS. In the meantime, this subarray (with −180o reflection phase) also acts the reference for other subarrays. Using this strategy, a tapered amplitude distribution from the center to the edge can be achieved across the entire aperture of the PMS, which corresponds to smaller sidelobe levels. It is seen in Fig. 8a–e that, sidelobes better than −10 dB can be achieved when the maximum scattering angle is smaller than 30° in the elevation plane. If a larger scattering range with −10 dB sidelobe levels is acquired, the PMS could be biased with each individual element instead of the subarray topology.

Fig. 8: Simulated and measured results of far-field scattering patterns with different biasing sequences.
figure 8

a Scattering pattern in Ф = 0o plane with a beam direction towards θ = 0o. b Scattering pattern in Ф = 0o plane with a beam direction towards θ = 15o. c Scattering pattern in Ф = 0o plane with a beam direction towards θ = 30o. d Scattering pattern in Ф = 45o plane with a beam direction towards θ = 15o. e Scattering pattern in Ф = 45o plane with a beam direction towards θ = 30o. f Reflection amplitude versus different reflection phases.

Full size image

Demonstration of a drone detection system

To demonstrate the capability of target detection in shadow areas caused by high buildings with the above PMS, a radar system is built to perform experiments of drone detection in an urban scenario. Figure 9a shows the constituent part of the PMS-based radar system, which is mainly composed of a signal generator, a T/R module, an A/D sampling module, a signal processing module, a voltage source, a monitor, transmitting & receiving horn antennas, an FPGA voltage-controlling module, a PMS and sync cables. These sync cables are utilized to synchronize the signal generator, the T/R module, the A/D module with the FPGA, which is mounted at the back of the PMS. Both transmitting and receiving horns are placed on the same height as the PMS in Fig. 9b. The distance between the PMS and horn is also 1.5 m, which is the same as the setup of the reflection performance measurement.

Fig. 9: Drone detection experiment based on the angle-insensitive PMS periscope.
figure 9

a Setup of the radar system. b Arrangement of the IMS and transmitting & receiving horns. c Experiment scenario with a drone flying in the shadow area of the horns. d Top view of the entire experiment scenario.

Full size image

During the experimental test, the radar system is mounted on the roof of the office building. As seen in Fig. 9c, d, A DJI Matrice 600 is sent into air and flies on the opposite side of the main beams of the two horn antennas. The 3.35 GHz carrier wave signal with a bandwidth of 30 MHz, emitted from the transmitting horn antenna with an average power of 5 watts, is modulated in frequency-modulated continuous waves and normally illuminated onto the PMS. 64 scattering beams with a direction interval of 7.5° and dwell time of 30 μs is generated by the PMS with pre-coded biasing sequences, to cover a 60° × 60° (−30° to 30° in both azimuth- and elevation-planes) tetragonal cone region. Reflected waves coming from the target are then radiated back to the PMS and received by the receiving horn antenna. Received signals are then demodulated into digital signals for further processing. The amplitude comparison algorithm is utilized in our system for the direction-of-arrival (DOA) estimation. The baseband sampling rate is 80 MHz with a delay of 4 μs. A two-dimensional FFT is utilized in the signal processing, in which a 2048-point FFT is conducted for the range estimation while a 512-point FFT is conducted for the speed estimation.

To demonstrate detection capability of the PMS-aided system, a flying trajectory, which starts at A1 located about 25 meters away from the PMS (Ф = −30°, θ = −15°) and ends at A2 which is over 80 meters away (Ф = 25°, θ = 25°), is carried out in the test as shown in Fig. 10a. In this trajectory, some estimated detection boundaries are included in the designated airspace, so as to have a comprehensive evaluation of the overall system. Two tests are carried out, in which the speed of drone is kept at 8 m/s and 12 m/s, respectively. Detected results corresponding to the above trajectory are also plotted in Fig. 10b, c, respectively. The range trajectory and azimuth are directly presented in the interface of the display console, while the radial velocity and elevation are marked beside the trajectory. It is interesting to note that the radar also picks up the wave of trees due to the blowing of the wind.

Fig. 10: Drone detection results.
figure 10

a Trajectory of drone flying when the transmitting and receiving horns are normal to the PMS in the azimuth plane. b Flight track of the drone at 8 m/s in the normal case. c Flight track of the drone at 12 m/s in the normal case. d Trajectory of drone flying when the transmitting and receiving horns are inclined at an angle of 45° to the PMS in the azimuth plane. e Flight track of the drone at 8 m/s in the 45° case. f Flight track of the drone at 12 m/s in the 45° case.

Full size image

In order to validate the effectiveness of the PMS under oblique incidence as conceptually illustrated in Fig. 1, another experiment [shown in Fig. 10d] is conducted, where the transmitting and receiving horns are inclined at an angle of 45° to the PMS in the azimuth plane. The flying trajectory starts at A1 located about 25 meters away from the PMS (Ф = 0°, θ = −15°) and ends at A2 which is over 80 meters away (Ф = 25°, θ = 25°). The speed of the drone is also maintained at 8 m/s in one test and 12 m/s in another, respectively. Corresponding experimental results for different velocities are presented in Fig. 10e, f, both of which demonstrate the effectiveness of target detection under oblique incidence from the radar.

It should be pointed out that, in our current demonstration prototype, we have included only a control channel to synchronize the signal generator, the T/R module, and the A/D module with the FPGA in a wired manner. However, in a real-world scenario illustrated in Fig. 1, a self-adaptive control channel should be incorporated into the radar. When the radar system operates in a wide-area surveillance mode, this control channel should be able to tell the radar when and where to illuminate a beam onto the metasurface for N-LoS detection. When a target is detected and the radar system switches from surveillance-mode to tracking-mode, this control channel should be able to inform the radar of the timing for switching tracking areas between LoS and N-LoS regions, based on the detected flight trajectory. It is also noted that, although the 30 MHz signal bandwidth (approximately 1%) used in our radar system is capable of providing a range resolution of 5 m, which is sufficient for our application to detect drones in urban environments, there are still certain deficiencies that may not meet the needs of other applications. Several measures, such as using a thicker substrate or etching a vacuum cavity beneath the top metallic patterns, can be implemented to further increase the relative spectrum bandwidth. Meanwhile, in order to extend the insensitive range beyond 50o, designing a compensation structure in the vertical dimension could be a possible approach.

The possible impact due to the weather conditions is also evaluated for the proposed radar system. It is observed in calculated results that38,39, even in the worst-case weather scenarios, e.g., heavey rain, heavy snow or dense fog, the attenuations at 3.35 GHz only range from several 10–4 dB to several 10–2 dB, since the detection distance in an urban environment is less than 1 km. Therefore, it is believed that such attenuations due to weather conditions will not significantly impact the radar’s operation.

Discussion

We have reported an angle-insensitive PMS periscope and a radar system for target detection in urban environment based on it. We have implemented our radar system to successfully demonstrate drone detection in shadow areas of a conventional radar. Our PMS periscope can be used to transmit and receive signals with the angular reciprocity, which is important for accurate detection in a radar scheme. The PMS-aided radar system for N-LOS detection is characterized by its low cost and easy deployment when compared with those multiple active-radar systems40,41,42, and it also offers better accuracy than the single active-radar system exploiting multipath returns43. With one distributed beam, the PMS can be simply treated as an optional module and work in a conventional radar system as a supplement. The proposed scheme could also be extended by using multiple PMSs in collaboration with the same active radar, or by having a single PMS in collaboration with multiple active radars, to cover larger regions. It should be pointed out that, the proposed PMS can contribute to wireless communications as well, where an accurate beam pointing is capable to greatly extend the link establishment range in N-LoS scenarios. The proposed approach is also capable to be extended to higher operational bands with proper reconfigurable components.

Methods

Evaluation of detection range

Let’s consider the target detection problem in our scenario and denote by Pt the horn transmit power, λ the carrier wavelength, R the distance between the PMS and horn, D the distance between the PMS and target, Ar the aperture of horn, σPMS RCS of the PMS, σt RCS of the target, GPMS the gain of the PMS. We also assume that the impinging wavefield can be approximated as a plane wave in the paths between horn and PMS, PMS and target. From the radar equation, we have that the power captured by the PMS from the transmitting horn is

$${P}_{1}=\frac{4{{{\rm{\pi }}}}{P}_{t}{A}_{r}{\sigma }_{PMS}}{4{{{\rm{\pi }}}}{R}^{2}{\lambda }^{2}}.$$
(1)

Then, the scattered power from the PMS is

$${P}_{2}={P}_{1}{G}_{PMS},$$
(2)

which can be recognized as the source and substituted into the radar equation for a second time. In this case, the power scattered from the target and recaptured by the PMS can be given as

$${P}_{3}=\frac{{P}_{2}{\sigma }_{t}{\sigma }_{PMS}}{{(4{{{\rm{\pi }}}}{D}^{2})}^{2}}.$$
(3)

Finally, the power received by the receiving horn from the PMS is

$${P}_{4}=\frac{{P}_{3}{G}_{PMS}{A}_{r}}{4{{{\rm{\pi }}}}{R}^{2}}=({\sigma }_{PMS}\times {G}_{PMS})\times \left({P}_{2}\times \frac{{A}_{r}}{4{{{\rm{\pi }}}}{R}^{2}}\right)\times \frac{{\sigma }_{t}}{{(4{{{\rm{\pi }}}}{D}^{2})}^{2}}.$$
(4)

In order to obtain detailed values of P4, we could recall the expression of received power in the measurement of reflection amplitudes which is written as

$${P}_{5}=\frac{{P}_{t}}{4{{{\rm{\pi }}}}{R}^{2}}\times \frac{4{{{\rm{\pi }}}}{A}_{r}}{{\lambda }^{2}}\times ({\sigma }_{PMS}\times {G}_{PMS})\times \frac{{A}_{r}}{4{{{\rm{\pi }}}}{R}^{2}}$$
(5)

In (5), P5 is obtained in the measurement while Pt, Ar, R and λ are known. Accordingly, the item of (σPMS×GPMS) can be easily calculated. It is derived from (1) and (2) that, Eq. (5) can be further simplified as

$${P}_{5}={P}_{2}\times \frac{{A}_{r}}{4{{{\rm{\pi }}}}{R}^{2}}$$
(6)

which is right the item in the second parentheses in (4). In this case, (4) can be rewritten as

$${P}_{4}=({\sigma }_{PMS}\times {G}_{PMS})\times {P}_{5}\times \frac{{\sigma }_{t}}{{(4{{{\rm{\pi }}}}{D}^{2})}^{2}}$$
(7)

Since P5 is about 13 dBm in the measurement and the minimum power level that can be detected by the receiver in our radar system is −120 dBm, while the typical RCS σt of DJI Matrice 600 is about 0.1 m2 in both our simulation and reported articles, the maximum detection range is estimated to be at least about 100 m.