Introduction

The transition from a metallic to an insulating state through the continuous variation of external parameters has captivated physicists for the past eight decades. A metal-insulator transition is characterized by the localization of conduction electrons preventing charge transport in the material. Depending on the system, three mechanisms have been proposed to explain this type of transition: the distortion of the crystal1, the disorder present in the system2 or the correlation between electrons3,4.

A lattice model with just one electron per site is expected to be metallic, but N.F. Mott argued that Coulomb repulsion could prevent electrons from jumping from a unit cell to a neighboring one, thus leading to electron localization4. The physics of the Mott insulator is well captured by the Hubbard model, which implies the formation of two sub-bands, one below the Fermi level, occupied by the localized electrons, and another one above the Fermi level, which remains empty. The resulting energy gap between the Hubbard sub-bands reflects the strength of the Coulomb repulsion5.

In systems with reduced dimensionality, electronic correlations become more relevant and many-body effects that do not exist or manifest in 3D may prevail. In particular, layered transition metal dichalcogenides (TMDs) represent a family of correlated quasi-2D materials that can exhibit intriguing phenomena such as Ising superconductivity, charge-density-waves, metal-insulator transitions or a quantum spin liquid phase6,7,8,9,10,11. Their van der Waals nature offers the possibility to combine different TMDs in a single compound imprinting new features through proximity interactions across interfaces, facilitating the design of artificial structures with unique properties12,13,14,15. For instance, a single layer of 1T-TaS2 or 1T-TaSe2 has a Mott insulating state related to a Star-of-David (SoD) charge density wave (CDW)6,7,16. Interleaving single layers of 1T-TaS2 with metallic single layers of 1H-TaS2 results in the unconventional superconductivity observed in 4Hb-TaS2 crystals17,18. Additionally, it has been suggested that the doping of a 2D Mott insulator, such as copper oxide layers in cuprates, underlies the high-temperature superconductivity observed in those systems19,20. In contrast, the effect of interlayer interactions on the correlated electronic properties in these van der Waals heterostructures remains largely unexplored.

In this work, we have considered a van der Waals heterostructure consisting of a single layer of 1T-TaS2 (a 2D Mott insulator) lying on a crystal of 2H-TaS2 (a metallic substrate). From quasi-particle interference (QPI) maps acquired through scanning tunneling microscopy/spectroscopy (STM/STS), we examine the evolution of the electronic properties of the system as a function of temperature. The QPI maps reveal the emergence of a Fermi contour in the 2D Mott insulator when the temperature drops below 11K, indicating the delocalization of the highly correlated Mott electrons. The new Fermi surface encompasses both the conduction electrons of the metallic substrate and the now-delocalized electrons of the 2D Mott insulator, thus showing the importance of interlayer interactions in defining the ground-state electronic properties of the system. With the help of Density Functional Theory (DFT) calculations, we describe the electronic bands of the hybridized 1T/2H system and identify the experimentally detected scattering vectors.

Results

Sample structure

Bulk 2H-TaS2 is metallic and below 78K presents a long-range order quasi-(3 × 3) incommensurate CDW21,22, associated with the appearance of a pseudo-gap at the Fermi level23. The 1T-TaS2 polymorph below 180K presents a commensurate CDW with an in-plane periodicity of \((\sqrt{13}\times \sqrt{13}){{{\rm{R}}}}13.{9}^{{{{\rm{o}}}}}\) dictated by the triangular arrangement of clusters consisting of 13 Ta atoms forming a Star of David6,24,25. The singly occupied 5d orbitals of the 12 outer Ta atoms of the SoD form the valence and conduction bands of the system. The 5d orbital from the remaining Ta atom at the center of the SoD forms a half-filled band. Contrary to the expected metallic behavior, the formation of the CDW is accompanied by a metal-insulator transition attributed to a Mott correlation mechanism6,7. The presence of the Hubbard gap at the Fermi level has been confirmed by several STM/STS and Angle Resolved Photoemission Spectroscopy measurements at low temperature26,27,28,29.

Figure 1 a shows an example of the polymorphic heterostructure comprising a 1T-TaS2 single layer on a 2H-TaS2 crystal. The V-shaped single-layer step edge at the center of the image separates the upper 1T terrace from the lower 2H terrace, where the T and H assignments are based on the CDW identification and STS measurements as explained in the following. The lower panel in Fig. 1b displays the line profile corresponding to the orange vertical line in Fig. 1a. The apparent step height corresponds to the expected value for a single layer step in a TaS2 crystal. The upper panel in Fig. 1b is a schematic model of the corresponding structure of the sample. Figure 1c shows an STS spectrum measured at 52K on the 1T terrace, where the Hubbard sub-bands above and below the Fermi level are resolved. The presence of a metallic substrate below the 1T-TaS2 single layer renormalized the energy position of the Hubbard sub-bands11,30,31,32 and contributes to the non-zero signal in the STS spectra at the Fermi level. Figure 1d displays a STS spectrum measured at 52K on the 2H terrace showing its metallic character and the reduction in LDOS at the Fermi level associated to the quasi-(3 × 3) CDW23.

Fig. 1: 1T/2H-TaS2 sample structure.
figure 1

a 1500 nm  × 700 nm section of a large area STM image showing a single layer step-edge. The upper and lower terraces correspond to the 1T and 2H polymorphic phases respectively. Image parameters: Vb = 300 mV, I = 100 pA b, Profile across the single layer step-edge shown in the STM image in (a) with an orange solid line. c STS spectrum measured on the 1T terrace showing the presence of the Lower and Upper Hubbard bands (LHB and UHB respectively). STS parameters: Vb = 400 mV, I = 500 pA, Vmod = 10 mV. d STS spectrum measured on the 2H terrace showing its metallic character. STS parameters: Vb = 400 mV, I = 500 pA, Vmod = 10 mV. All the measurements were performed at 52 K.

Full size image

Figure 2 a shows an atomically resolved STM image taken on the 2H terrace at 1.2K where both the atomic and the quasi-(3 × 3) CDW periodicities are apparent, the latter is highlighted with an orange rhombus. Figure 2b shows the Fast Fourier Transform (FFT) of the image shown in panel a. The spots corresponding to the atomic and CDW periodicities are marked with black and orange circles, respectively. In this case, the atomic and CDW lattices are aligned. An atomically resolved STM image acquired on the 1T terrace at 1.2K is shown in Fig. 2c. Both the atomic and the \((\sqrt{13}\times \sqrt{13}){{{\rm{R}}}}13.{9}^{{{{\rm{o}}}}}\) CDW periodicities are observed, the blue rhombus marks the unit cell of the CDW. Figure 2d shows the corresponding FFT, where the spots coming from the atomic and CDW periodicities are marked with black and blue circles, respectively.

Fig. 2: Charge density waves and atomic structure.
figure 2

a, b STM topographic image and corresponding FFT measured on the 2H-TaS2 terrace. Both the atomic and the quasi-(3 × 3) CDW periodicities are resolved and marked with black and orange circles, respectively, in the FFT panel. The CDW unit cell is also marked in orange in the STM panel. Image parameters: 20 nm  × 20 nm, Vb = 50 mV, I = 50 pA. c, d STM topographic image and corresponding FFT measured on the 1T-TaS2 terrace. Both the atomic periodicity and the \((\sqrt{13}\times \sqrt{13}){{{\rm{R}}}}13.{9}^{{{{\rm{o}}}}}\) CDW are resolved and marked with black and blue circles, respectively, in the FFT panel. The CDW unit cell is also marked in blue in the STM panel. Image parameters: 20 nm  × 20 nm, Vb = 500 mV, I = 300 pA.

Full size image

The electronic structure of this system, a single layer of 1T-TaS2 on a 2H-TaS2 crystal, shows the following evolution depending on the sample temperature22. Between 52 K and 27 K the STS data acquired on the 1T-TaS2 layer show the presence of the Hubbard sub-bands at both sides of the Fermi level, as expected for a Mott insulator22, see Fig. 1c. For sample temperatures between 27 K and 11 K the STS data still show the presence of the Hubbard sub-bands but a narrow zero-bias peak (ZBP), identified as a Kondo resonance33, appears between them. The intensity of this Kondo resonance is modulated following the periodicity of the \((\sqrt{13}\times \sqrt{13}){{{\rm{R}}}}13.{9}^{{{{\rm{o}}}}}\) CDW, see Supplementary Fig. 1. In this temperature range the system can be described as a lattice of Kondo impurities, spatially ordered by the CDW, but electronically decoupled from each other. Below 11K a coherent quantum superposition occurs between the Kondo clouds, making the Kondo impurities electronically periodic. The periodicity of the Kondo impurities, by virtue of Bloch’s theorem, ensures the appearance of a band at the Fermi level. This impurity band is quasi-flat with a characteristic width of the order of the Kondo resonance. The interaction between the impurity quasi-flat band and the metallic bands of the substrate results in hybridization that causes the opening of avoided band crossing and, most notably, a gap inside the Kondo resonance34,35. More importantly for the purpose of the present work, according to the Luttinger sum rule, the new Fermi surface of the system must contain both the conduction electrons from the 2H-TaS2 substrate and the (now de-localized) electrons from the Mott insulator34,35.

Several studies on van der Waals bilayers composed of 1T-TaS2 or 1T-TaSe2 layers lying on their corresponding 1H counterparts have been published recently11,32,36,37. The bilayers were grown on HOPG or graphene on silicon carbide and the STS data acquired on the 1T layer show a zero bias feature surrounded by two peaks at both sides of the Fermi level, attributed to an upper and a lower Hubbard sub-band11,32,36. The zero bias feature has been identified as a Kondo resonance11,32,36, which exhibits an additional internal structure when measured at a low enough temperature32,36. The main consensus is that the system consists of a triangular lattice of localized spins in the 1T layer, which are Kondo-screened by the conduction electrons of the metallic 1H layer11,32,36. Despite the coincidence in the experimental data, the origin of the internal structure in the Kondo peak is controversial. Based on the study of the internal structure of the zero bias feature, the ground state of the system has been attributed to either a non-magnetic heavy Fermi liquid state, also known as a coherent Kondo lattice36, or to a magnetically ordered phase32. These explanations are mutually exclusive. Furthermore, a theoretical study on a self-standing bilayer has proposed a completely different interpretation: the formation of a doped Mott system whose doping level depends on the distance between the layers37.

A specific characteristic of the formation of a coherent Kondo lattice, which distinguishes this ground state from the other proposals, is the de-localization of the Mott electrons, which should become part of the new Fermi surface of the crystal34,35. Although the gap opening within the Kondo resonance, due to this delocalization process has already been anticipated22 for 1T/2H-TaS2, as well as for 3D crystals of URu2Si2 and CeCoIn538,39, the actual delocalization process itself has not been directly probed so far. To do so, in this work we look for the appearance of a Fermi contour in the Mott insulating 1T layer of 1T/2H-TaS2 by measuring quasi-particle interference (QPI) maps around the Fermi level. It is well known that defects present on surfaces act as scattering centers for the conduction electrons thus leading to interferences (hence the term QPI) that result in the formation of standing waves in the surface LDOS40. Furthermore, the Fermi contour itself is encoded into the QPI pattern through the scattering selection rules, defect distribution and defect shape among other factors41,42,43. Above the Kondo lattice temperature, i.e. 11K, the 1T layer is a Mott insulator with the electrons localized at the center of every SoD cluster, see Supplementary Fig. 1 and ref. 22. Therefore we do not expect any signal on the QPIs due to the absence of conduction electrons. On the contrary, for sample temperatures below 11K, if the Kondo lattice is the ground state of the system, we do expect the appearance of a Fermi contour in the 1T-TaS2 layer due to the delocalization of the Mott electrons and their incorporation into the new Fermi surface of the sample.

Delocalization of highly correlated Mott electrons

To measure the QPI maps we acquired dI/dV curves in every pixel of several STM images measured on different regions of the 1T/2H-TaS2 heterostructure, sweeping the bias voltage across the Fermi level (see Supplementary Section 2 for details). The resulting dI/dV maps were averaged, Fourier transformed and symmetrized following the procedure described in Supplementary Section 3.

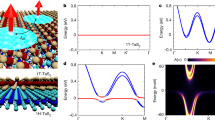
The upper panel in Fig. 3a shows an STS spectrum measured at the center of the SoD cluster on the 1T-TaS2 layer at 14 K, confirming the presence of a Kondo resonance with its width corresponding to the measurement temperature22. The lower panel shows the Fast Fourier Transform (FFT) of the corresponding QPI map measured in the energy range marked with the gray area in the upper panel. To improve the signal-to-noise ratio, the QPI maps are symmetrized and then the collected data are averaged in an energy window of 5 meV (see Supplementary Sections 3 and 4 for details). In the 14 K QPI we can identify the Bragg peaks corresponding to the periodicity of the \((\sqrt{13}\times \sqrt{13}){{{\rm{R}}}}13.{9}^{{{{\rm{o}}}}}\) CDW present in the 1T layer, marked with blue circles. The corresponding surface Brillouin zone (SBZ) is indicated by the black half hexagon. The yellow marks indicate the noise lines related to the scan direction, always kept around 8o with respect to a high symmetry direction of the CDW (see Supplementary Section 2). The noise lines are mirrored and propagated due to the symmetrization procedure followed to improve the signal-to-noise ratio, and the yellow dotted lines are the corresponding replicas emerging from the 1T CDW spots. Apart from the mentioned Bragg peaks and noise lines, we detect no QPI signal at the Fermi level at 14K. This is consistent with the existence of a Mott insulating state in the 1T layer. Thus, as expected, the 1T layer is a Mott insulator without conduction electrons to scatter.

Fig. 3: Tunneling spectroscopy and QPI maps.
figure 3

a Upper panel, STS spectrum recorded on 1T/2H-TaS2 at 14 K. Lower panel, QPI map measured in the energy range marked in gray in the upper panel. No signal is detected apart from the Bragg peaks corresponding to the \((\sqrt{13}\times \sqrt{13}){{{\rm{R}}}}13.{9}^{{{{\rm{o}}}}}\) CDW in the 1T layer, marked with blue hollow circles, and the noise lines attributed to the scan direction and propagated by the symmetrization procedure (see Supplementary Sections 2 and 3), indicated in yellow. The absence of a QPI here is expected because at 14K the 1T layer is a Mott insulator and therefore no free electrons are available for scattering. b Upper panel, STS spectrum recorded on 1T/2H-TaS2 at 1.2 K. The Kondo lattice gap appears at the Fermi level superimposed on the Kondo resonance (see region highlighted in gray). Lower panel, QPI map measured in the energy range marked in gray in the upper panel. Apart from the 1T CDW spots (blue hollow circles) and the noise lines (yellow lines) additional features are clearly resolved. This is expected because after the coherent Kondo lattice formation the Mott electrons are deconfined and form part of the the new Fermi surface of the system. The inset between both QPI maps gives a schematic representation of the atomic reciprocal lattice, where the atomic and 1T CDW spots are shown in black and blue hollow circles, respectively. The black halve hexagon represents the 1T CDW Surface Brillouin zone (SBZ) and the red-blue circle marks the region corresponding to the experimental QPI data shown in the QPI panels.

Full size image

The upper panel in Fig. 3b shows the spectrum measured at 1.2K on the same system. This temperature is well below that at which the Kondo lattice is formed. A narrow gap at the Fermi level can be seen within the Kondo resonance. Its appearance has been attributed to the coherent quantum superposition of the Kondo clouds screening the localized Mott electrons at the center of the SoD clusters22,34. A consequence of the coherent Kondo lattice formation is the de-localization of the Mott electrons, which now become part of the Fermi surface of the new periodic crystal34,35,38,39. The QPI map measured at 1.2 K (lower panel in Fig. 3b) shows a very rich structure in comparison with its 14 K counterpart (lower panel in Fig. 3a). At 1.2K, apart from the 1T CDW spots and the experimental noise (already described in the 14 K map and marked as in Fig. 3a), a number of new spots and structures can be clearly resolved. The existence of a QPI pattern at the Fermi level at 1.2K implies the existence of conduction electrons and, therefore, of a Fermi contour in the Mott insulator, i.e. the 1T-TaS2 layer. This is fully consistent with the formation of a coherent Kondo lattice below 11K, solving the controversy over the ground state of the system.

Kondo lattice Fermi contour

In the following we will trace back the origin of the most prominent signals in the experimental QPI maps. The 2H-TaS2 bulk electronic structure is obtained by means of DFT calculations. Details of these calculations and the resulting band structure can be found in the Methods section and Supplementary Section 5. The 2H-TaS2 crystals are metallic due to two doubly degenerate bands crossing the Fermi level whose origin are the Ta 5d half-filled orbitals. To simulate the CDW, we construct a (3 × 3) in-plane supercell. The dispersion of the metallic bands is slightly modified by the formation of this CDW6,22,44. The accuracy of our model for the CDW in bulk 2H-TaS2 is further corroborated by the comparison between the simulated STM images and the experimental ones measured around the Fermi level22. To calculate the modification in the band structure due to the formation of the coherent Kondo lattice, an impurity flat band with a width comparable to the one of the Kondo resonance is introduced at the Fermi level. The periodicity of the impurity band should be in principle that of the \((\sqrt{13}\times \sqrt{13}){{{\rm{R}}}}13.{9}^{{{{\rm{o}}}}}\) CDW. However, constructing a unit cell with the periodicities of both CDWs would lead to a very large unit cell, very demanding from the computational point of view. Since the impurity band is very narrow, we assume in the calculations that it has the periodicity of the (3 × 3) CDW of the 2H-TaS2 substrate. We have performed calculations with different widths for the impurity flat band to explore the influence of the chosen parameters in the results, see Supplementary Section 5 for details. Finally, the impurity band is coupled to all the conduction bands of the 2H crystal by means of an effective Hamiltonian described in the methods section and Supplementary Section 5. The hybridization between the impurity band from the 1T layer and the conduction bands from the 2H substrate results in the opening of avoided crossings at the Fermi level22,33,34. Consequently, the calculated LDOS presents a double peak structure at the Fermi level (see Supplementary Fig. 9), in good agreement with the experiments.

Figure 4a shows the resulting band structure around the Fermi level after the formation of the coherent Kondo lattice. These bands are mainly the doubly degenerate bands from the substrate mixed with the impurity flat band created by the formation of the coherent Kondo lattice. A number of avoided crossings can be seen. The band structure is discussed in detail in Supplementary Section 5. Figure 4b shows the corresponding constant energy contour (CEC) near the Fermi level, at -2 meV. The simplest way to connect the experimental QPI maps with the calculated CEC, is to calculate the autocorrelation of the CEC, the so-called Joint Density of States (JDOS), which provides the contribution of all the possible scattering events. This approach, which has been widely used in the past, gives very good results when the number of involved electronic bands is small. If, as in the present case, the number of bands is large, it is nearly impossible to determine which pairs of initial-final states are responsible for a given feature in the QPI map. To simplify the analysis and identify the most relevant scattering events, we performed band-selective JDOS calculations, in which only a few selected bands contributing to the CEC were considered. The details of these band-selective JDOS calculations are presented in Supplementary Section 6.

Fig. 4: Band-selective JDOS calculations.
figure 4

a DFT calculated energy bands around the Fermi level of the hybridized system. b Constant energy contour at -2 meV calculated from the DFT band structure shown in (a). The symmetry points of the 2H SBZ are indicated by the black letters, the coloured contours connected by double arrows are the ones considered for the partial JDOS calculations shown in (c, e). c Partial JDOS resulting from the scattering processes between the contours indicated by the double arrows in panel b, following the same color code and integrating over the 3meV energy window indicated by the pink shaded region in panel a. The 2H and 1T SBZs are indicated by the gray dashed and black solid lines, respectively. d Schematic representation of the 1T CDW in the reciprocal space, where the Bragg spots are represented as cyan filled circles and the black halve hexagon is the corresponding SBZ. The black dashed line marks the portion of the reciprocal space shown in (e). e Band-selective JDOS calculation overlaid on the experimental data recorded at 1.2 K. The panel is divided into three 120° sections. The upper right section shows the JDOS calculation presented in (c), the upper left section shows the experimental QPI map presented in Fig. 3b, and the lower section is the superposition of both.

Full size image

Figure 4c shows the results of the band-selective JDOS obtained by considering only three particular scattering scenarios and integrating over a 3 meV energy window based at the Fermi level, as indicated by the pink shaded area in panel a, in order to closely match to the experimental conditions. In red we represent the contribution from the intervalley scattering between the bands located at the K and K’ points, highlighted in purple and connected by the red double arrow in the CEC of (b). In orange and blue we represent the contributions from the scattering events between the purple band centered at K and either the green band centered at Γ (connected by the orange double arrow in panel b) or the brown band centered at K (connected by the blue double arrow). The gray dotted and black solid hexagons in panel c mark the SBZs corresponding to the (3 × 3) CDW periodicity employed in the calculation and the (\(\sqrt{13}\times \sqrt{13}\)) periodicity associated with the 1T CDW, respectively. The latter is the relevant one regarding the experiments, since our measurements are done on the 1T layer. We use the 1T-CDW as scaling reference. This is represented schematically in Fig. 4d, where the 1T SBZ is displayed again as a black hexagon and the 1T CDW Bragg spots are shown as cyan-filled circles. Finally, the band-selective JDOS calculation is compared with the experimental data in Fig. 4e, which is divided into three 120° sections. The upper left section displays the experimental QPI signal obtained at 1.2 K, already presented in Fig. 3b, the upper right section shows the band-selective JDOS calculations presented in (c), and the lower section is the superposition of both datasets. For reference, the portion of reciprocal space covered here is represented as a black dashed line in panel d.

Upon inspection of Fig. 4e, it is clear that some of the features present in the experimental QPI map can be explained as the scattering processes indicated in panel b, namely the strong and localized triangular features outside the 1T-SBZ (red signal in the partial JDOS calculation), the flower-like feature inside the 1T-SBZ (orange signal) and the hexagonal feature closer to the center of the map (blue signal). However, some features cannot be explained in this way, in particular the groups of spots located at and near the edges of the 1T-SBZ. Here it is worth noting that the DFT calculations are based on a perfect (3 × 3) periodicity to account for the 2H CDW, but they do not include the actual periodicity of the 1T CDW present in the overlayer. This was a compromise needed in order to keep the computational cost accessible (see Supplementary Section 5). Hence, although absent in the calculations, the periodicity of the moiré pattern arising from the superposition of both CDWs could be expected in the actual experimental data acquired in the 1T/2H system.

Figures 5a and b show two real-space representations of both the 2H and 1T CDWs, respectively, where the atomic positions of the Ta atoms are given by the gray filled circles. In the case of the 2H phase, the experimentally determined quasi-(3 × 3) CDW periodicity22,33 is indicated by the yellow filled circles, and its corresponding unit cell in the same color. In the case of the 1T phase, the \((\sqrt{13}\times \sqrt{13}){{{\rm{R}}}}13.{9}^{{{{\rm{o}}}}}\) CDW periodicity is highlighted in cyan, and the black lines connect the 12 outer Ta atom in every SoD cluster as a visual guide. The reciprocal space representation of both CDWs is displayed in Fig. 5c where, again, gray, yellow and cyan-filled circles correspond to the first-order Bragg peaks of the atomic lattice, 2H CDW and 1T CDW, respectively. The moiré pattern resulting from the superposition of both CDWs is, by definition, given by the difference vector between their respective Bragg peaks, which is indicated by a green solid line. Hence, the resulting moiré Bragg peaks are obtained by projecting this vector from the origin, giving as a result the green filled circles in Fig. 5c.

Fig. 5: Contribution of the 1T CDW periodicity.
figure 5

a Real-space lattice properties of the 2H-TaS2 phase, where the atomic and quasi-(3 × 3) CDW lattices are represented in gray and yellow, respectively. b Real-space lattice properties of the 1T phase, where the atomic and CDW lattices are represented in gray and cyan, respectively. c Reciprocal space representation of the combined 1T/2H system, following the same color code. The resulting CDW moire spots are represented in green. d Magnified reciprocal space representation following the same color code as in (c). The black half hexagon marks the 1T SBZ. The green dotted line corresponds to the lattice vector of the CDW moire and the green circles are the resulting moire spots after the symmetrization procedure. The red triangles mark the positions of the main K-K' intervalley features encoded in red in Fig. 4. The black dotted line corresponds to a lattice vector of the 1T CDW and also projects the red triangular features onto the edge of the SBZ, at the positions marked by the purple circles. e Superposition of the experimental QPI data and the band-selective JDOS calculations already presented in Fig. 4e with the additional marks of (d) overlaid on it.

Full size image

The above-mentioned procedure to determine the position of the expected CDW moiré spots is now reproduced in Fig. 5d at the same scale used previously in Fig. 4. Here, some of the 2H and 1T CDW spots are again represented as yellow and cyan-filled circles, respectively. Projecting from the origin, the difference vector between the 2H and 1T CDWs (green dotted line) results in the moiré spot marked as a green-filled circle inside the 1T SBZ. Due to the symmetrization procedure (see Supplementary Section 3), this spot is mirrored along the pink dashed line and replicated over the different high symmetry directions, producing the set of solid green hollow circles. Finally, all these spots should be mirrored also across the SBZ boundaries, leading to the dotted green circles. All these circles are also overlaid on the previously discussed experimental data in Fig. 5e, where they match perfectly the experimental spots located inside and outside the SBZ edges. The origin of all these spots can thus be attributed to the periodicity of the moiré pattern resulting from the superposition of both CDWs. The fact that these spots are present only in the 1.2K map and not in the 14K one (see Fig. 3) is yet another indication that at 1.2K we are sensitive to both the 1T and 2H periodicities, despite the fact that we are only tunneling into the 1T overlayer. This can be understood as a consequence of the mentioned hybridization between the 1T flat impurity band describing the periodic coherent Kondo lattice and the conduction bands of the 2H substrate, resulting in the de-localization of the 1T Mott electrons into the 2H band structure. Hence, the electronic structure of the combined system incorporates the symmetry of both the 1T and 2H CDWs. On the other hand, note that thermal smearing can be ruled out as a cause for the lack of signal in the 14K data, since the transition temperatures for both CDWs lie well above 14K (78K for the 2H phase and 183K for the 1T one6).

Regarding the spots located at the 1T SBZ border (purple circles in Fig. 5d and e), they can be explained as replica spots of the main intervalley scattering signal between the bands located at the K and K’ points, encoded in red in the previously discussed band-selective JDOS calculation (see Fig. 4) and highlighted here by the red triangles. This is explained in Fig. 5d, where the black dotted line corresponds to a lattice vector from the 1T CDW, as it connects two of its consecutive spots (cyan-filled circles). The projection of the same lattice vector from the position of one of the red triangles (the one filled in purple) ends up at the border of the 1T SBZ, precisely at the position of one of the features detected in the experiment, as indicated by the purple filled circle. Taking into account the already mentioned symmetrization procedure, this spot will be mirrored and propagated, resulting in the positions given by the purple hollow circles. The fact that we detect experimentally the K-K’ intervalley scattering replicas associated with the 1T CDW periodicity (purple circles in Fig. 5 d and e) confirms that we are tunneling into the 1T layer while having access to the electronic structure of the 2H substrate. Finally, note that neither the CDW moiré spots (green circles) nor the replica spots from the main K - K’ inter-valley process (purple circles) are present in the simulation shown in Fig. 5e. This was to be expected because the simulation does not include the 1T CDW periodicity, as previously explained.

In conclusion, a single layer of 1T-TaS2 goes through a metal-insulator transition at 180K. Here we have shown that it becomes metallic again below 11K when lying on 2H-TaS2. The transition back to a metallic state as temperature goes down is attributed to the formation of a coherent Kondo lattice, thus introducing a new periodicity, which, according to Bloch’s theorem, results in the appearance of a quasi-flat band at the Fermi level with a width comparable to the one of the Kondo resonance. This band ultimately hybridizes with the metallic bands of the 2H-TaS2 substrate, so that the new Fermi surface of the system incorporates both the conduction electrons from the latter and the now-delocalized electrons from the 1T-TaS2 Mott insulator, in accordance with Luttinger’s sum rule. By measuring QPI maps, we have observed the formation of a Fermi contour in the 1T-TaS2 layer below 11K and, with the help of DFT calculations, we have identified the origin of the most prominent features detected in them. In the end, we have shown how the interlayer interaction in a van der Waals heterostructure allows for the reversal of the metal-insulator transition while preserving the CDW of the system. As a side note, the appearance of a Fermi contour below 11K constitutes the first direct proof of the above-mentioned electron delocalization process and also solves the controversy on the nature of the ground state in similar van der Waals heterostructures, which has been attributed to a variety of possible reasons, such the formation of heavy-fermions, a magnetically ordered ground state or a doped Mott insulator32,36,37. Thus, our results provide additional and fundamental insight into the importance of interactions between layers in van der Waals heterostructures and pave the way to induce novel properties in highly correlated 2D systems.

Methods

Sample preparation

The 2H-TaS2 single crystal was exfoliated at room temperature in Ultra-High Vacuum (UHV) using a Nitto tape and then it was transferred to the Low Temperature STM without breaking the UHV conditions.

STM/STS measurements and tip preparation

The STM experiments were carried out in a low-temperature STM operating in Ultra-High Vacuum at a base pressure in the low 10−10 mbar. The UHV system is equipped with a preparation chamber and a load lock that allows sample exfoliation and transfer to the STM without breaking the UHV conditions at any point. Two different temperature regimes were employed during the measurements, one with the STM cooled with liquid nitrogen and pumped down with a scroll pump to lower the base temperature to 52K, and a second one with the STM cooled to a base temperature of 1.2 K. In this second regime two different stable temperatures were used in order to perform the (several days long) QPI maps, the already mentioned 1.2 K base temperature of the cryostat, and an intermediate temperature of 14 K. The latter was achieved by leaving open the two inner radiation shields of the cryostat (helium bath and Joule-Thomson (JT) pot) and, at the same time, applying heat with an internal resistive heater located at the JT pot and controlled by a PID circuit. This configuration allowed for a stable enough temperature in order to perform the QPI maps as described in section S2 of the SI.

The STS spectra have been measured using a lock-in amplifier, adding a modulation to the sample bias voltage signal between 4mV and 500 μV, depending on the particular experiment. In all cases the modulation frequency was 763 Hz.

The STM tips were home-made by electrochemical etching of a tungsten wire and cleaned in UHV by argon sputtering. Before the experiments the tips were checked against a Cu(111) sample to ensure that they presented a flat density of states at the Fermi level while resolving the well-known Cu(111) surface state without any additional features. An Au ball made from a 99.99% pure wire was adhered to the sample holder close to the TaS2 crystal so that the tip could be prepared in situ by performing indentations in the Au ball without opening the STM thermal shields and therefore keeping the sample thermalized and clean.

DFT modeling

DFT calculations for the 2H phase of the bulk TaS2 crystal have been carried out within the Projector Augmented Wave (PAW) method45 as implemented in the Vienna Ab Initio Simulation Package (VASP)46,47,48. We used a 350 eV plane wave cut off, the Perdew Burke Ernzerhof (PBE) functional49 and the Grimme D3 correction50, which proved to be adequate for 2H transition metal dichalcogenides51. We adopted a very strict 10−6 eV convergence criterion for the self-consistent electronic cycles and (18 × 18 × 4) and (6 × 6 × 4) unshifted Monkhorst-Pack grids for the Brillouin Zone (BZ) sampling of the (1 × 1) and (3 × 3) 2H-TaS2 reconstruction, respectively. All the geometry optimizations have been carried out optimizing the position of all the atoms until the maximum residual force was lower than 10−3 eV/Å.

The Kondo lattice formation was modeled using, as a conduction band, the DFT calculated kz = 0 portion of the band structure of the 2H-TaS2 system in the (3 × 3) CDW reconstruction in the [−0.5:1.5] eV energy range, including 22 substrate bands in total. The impurity band, on the other hand, had the typical dispersion for TaS2, that is a global maximum at the Γ point, local maxima at the K points of the BZ, saddle points at the M points and minima along the ΓM direction, and a small bandwidth of  ~ 15 meV. The conduction and impurity band have been coupled through the effective Hamiltonian34:

$$H={\sum}_{{{{\bf{k}}}}n}{\epsilon }_{{{{\bf{k}}}}n}{d}_{{{{\bf{k}}}}n}^{{{\dagger}} }{d}_{{{{\bf{k}}}}n}+{\sum}_{{{{\bf{k}}}}}{\varepsilon }_{{{{\bf{k}}}}}{c}_{{{{\bf{k}}}}}^{{{\dagger}} }{c}_{{{{\bf{k}}}}}+V\left({\sum}_{{{{\bf{k}}}}n}{c}_{{{{\bf{k}}}}}^{{{\dagger}} }{d}_{{{{\bf{k}}}}n}+h.c.\right)$$

where ϵkn is the one-electron energy of the conduction band (generated by the creation and annihilation operators \({d}_{{{{\bf{k}}}}n}^{{{\dagger}} },{d}_{{{{\bf{k}}}}n}\)), εk is the impurity band (generated by the creation and annihilation operators \({c}_{{{{\bf{k}}}}}^{{{\dagger}} },{c}_{{{{\bf{k}}}}}\)), n is the conduction band index, k is sorted within the 1stBZ, and the coupling potential V = 5 meV is assumed to be k- and band-independent22. More details about the DFT modeling of the Kondo Lattice formation are available in section 5 of the SI.