Introduction

In the research field of materials engineering, hydrogenating is one of the promising methods to manipulate the electrical and redox characteristics of metal oxides towards the favorable features for diverse applications1,2,3,4,5. The rearrangements of the crystal lattice with the deviation of metal atoms from their equivalent states have enormous impacts on the dielectric properties and energy states of electron of metal oxide during proton insertion, and therefore, a lot of effort has been devoted to tunable hydrogenation for these purposes. Moreover, inspired by proton migration into the oxides, there has been significant interest in oxide hydrogenation as a feasible strategy of hydrogen energy transportation for upcoming hydrogen economy6,7,8. Furthermore, recent studies have emphasized the vital role of H-binding energy of supporting oxides to enhance the catalytic activities of primary catalyst in electrolysis and photo-electrochemical systems9,10,11,12,13.

It has long been known that proton doping significantly impacts the inherent characteristics of metal oxide13,14. Therefore, the elucidation of the proton diffusion phenomenon from a hydrogen-rich atmosphere to the surface of hydrogen-poor metal oxides is important for further developments. To address this challenge, many efforts have been devoted to revealing this behavior. Experiments have verified that the sacrificial metals that have lower work functions accelerate the transfer of electron-proton pairs into the oxide lattice, motivating work on tunable oxide hydrogenation using sacrificial solid metal4,5,15,16. With respect to the hydrogenating phenomena itself, an exploration of proton movements using first-principles calculation revealed that the negatively charged oxide surface, driven by electron accumulation, contributes to lower energy barriers for proton migration15,16. Moreover, it has been confirmed that the proton capable metal oxide exhibits various phase conditions depending on a degree of the hydrogenation17,18, unlocking the great opportunity of tunable hydrogenated oxide and selectivity for favorable features.

However, it is worth mentioning that the question about natural forces governing the hydrogenation of the metal oxides has not been fully elucidated. Specifically, there are no significant clues or criteria to correlate hydrogenation origins with the degree of hydrogenation and the crystallographic order of lattice oxide. Undeniably, there have been many practical achievements, however, previous hydrogenation studies often neglect to consider the regularity of various crystal phases, obscuring the conception of oxide hydrogenation. That is, due to the lack of the cornerstone correlating the fundamental origins and material characteristics, consistent explanations of the natural force covering the proton movement are overlooked; and therefore, the sole descriptor for the impact of H-binding on physicochemical characteristics of metal oxide still remained elusive.

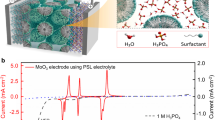
In this context, we present a detailed study of the oxide hydrogenation by devising a cation-solution treatment method for controllable hydrogenation in metal oxides. The basis of the original hypothesis was that the impetus of hydrogenation is likely to be associated with the equivalent electrochemical potentials difference between cation as a reducing agent and metal oxide. We attributed the proton migratory phenomena to the mixed potential-induced electrochemical galvanic reaction, which occurs at the interfaces of solid oxide and dissolved cations, accompanying with the proton migration from the acid reservoir, as depicted in Fig. 1a. Moreover, to reveal the sole impact of H-binding on inherent physicochemical properties of metal oxide, we have studied the electrochemistry of orthorhombic molybdenum trioxide (α-MoO3), one of the layered oxides having accommodatable sites for protons, and its hydrogenated state having identical orthorhombic crystal. In particular, the redox behavior was investigated in organic electrolyte based-lithium ion battery (LiB) system, which is a suitable platform for understanding the inserted proton effects while precluding proton intervention from the electrolyte. Remarkably, the redox characteristics of hydrogenated α-MoO3 (H-MoO3) in LiB systems were verified to be totally determined by means of the proton doping along with the enhancements of high rate performance and cyclic stability. Typically, it is found that there was no capacity limitation for partially reduced H-MoO3 in spite of the lower oxidation state of molybdenum at the expense of partial reduction with cation dopant. To elucidate this contradictory question, the completely distinguishable redox natures of H-MoO3 were demonstrated by computational density functional theory (DFT) and the nudged elastic band (NEB) approach. It is especially worthy noticing that proton adoption and its impacts on an intermolecular interaction contribute to the advent of the new sites and pathway for lithium-ion diffusion.

Fig. 1: Methodology of metal oxide hydrogenation.
figure 1

a Schematic illustration of metal oxide hydrogenation via galvanic redox reaction between metal oxide and metallic cation. b Linear sweep voltammetry (LSV) curves for proton intercalation at pristine α-MoO3 under 1 M H2SO4 solutions; two typical reduction reactions result in the orthorhombic H-doped MoO3 (HxMoO3), followed by the phase transition to the monoclinic HyMoO3. Cyclic voltammetry (CV) curves of Pt electrode under Mo(IV) cation solution, showing around 0.3 V vs. RHE of standard reduction potential. c Pourbaix diagram for molybdenum oxide, Cu metal, and redox couples for molybdenum and vanadium cations under acidic condition.

Full size image

Results

Methodology of galvanic redox reaction inducing metal oxide hydrogenation

Figure 1a illustrates a cation-solution treatment method that we designed for controllable hydrogenation in metal oxides. The linear sweep voltammetry (LSV) curves (Figs. 1b and S1a) indicate two distinct reductive potentials of 0.43 and 0.15 VRHE, respectively: first reduction peak corresponds to the proton and charge transport to α-MoO3 (HxMoO3, x < 0.4), and the second peak indicates an additional reduction reaction for proton storage with phase transition into monoclinic phase (HyMoO3, y > 0.4)17,18. The basic electrochemistry of the α-MoO3 capacitive nature provides notable feature of oxide hydrogenation; and we focused here on the possibility of tunable hydrogenation strategy via galvanic reaction using specific ionic reductants having proper standard potential.

To demonstrate that the mixed potential-induced galvanic reaction is the determinant of electron-proton pair migration, we studied the feasibility of Mo(IV) cation solution as hydrogenation trigger. The cyclic voltammetry (CV) analysis of Pt electrode under Mo(IV) solution, as shown in Figs. 1b and S1b, clearly shows that the oxidation current (for MoO2+(IV) + H2O → MoO2+ (V) + 2H+ + e−) occurs at around 0.30 VRHE, which is in agreement with the Pourbaix diagram for molybdenum19. As a proof of concept for electrochemical galvanic reaction, we organized the standard potentials of various molybdenum oxide phases corresponding to the degree of hydrogenation (MoO3/HxMoO3/HyMoO3), and that of cations (Mo(IV) and V(II)), and solid Cu metal as well to reconsider the conventional solid-metal treatments method in the electrochemical point of view as shown in Fig. 1c. Firstly, we used dark-brownish Mo(IV) cation solution as reductant (Fig. S2, the detailed explanation for MoO3 modification method is described in “Material preparation” section). The prepared hydrogenated α-MoO3 using specific Mo(IV) concentration shows the two distinct reflection (XRD) patterns corresponding to that of α-MoO3 (PDF#05-0508) and H0.34MoO3 (PDF#34-1230) as shown in Fig. 2a. Here, the major reflection peak corresponding to (020) plane of pristine α-MoO3 shift from 12.74 to 12.52o by means of hydrogenation, representing expanded d-spacing of (010) plane from 13.86 to 14.10 Å; and reciprocal space in selected area electron diffraction pattern (Fig. S3c, g) clearly shows the widened d-spacing of (020) plane from 0.692 to 0.704 nm by oxide hydrogenation. In Fig. S4, there was no significant variation in Raman spectra between pristine and hydrogenated α-MoO3, indicating that crystallographic characteristic is well-maintained during proton intercalation. Meanwhile, as shown in Fig. 2a, it was confirmed that H-MoO3 transforms back to prior α-MoO3 phase after heat treatments at 473 K, representing the reversible -/de-hydrogenation of the H-doped α-MoO3 (HxMoO3, x < 0.4). Additionally, the X-ray photoelectron spectroscopy (XPS) analysis confirmed that Mo5+ species in Mo 3d spectra (Fig. 2b) gradually and selectively increases with the occurrence of the surface adsorbed species corresponding to –OH in O 1s spectra (Fig. 2c) accompanying with chemical shifts of lattice oxygen to lower binding energy. With respect to the nature of H-binding, previous neutron diffraction studies of the hydrogen molybdenum bronze have demonstrated that proton is bonding with the oxygen atoms with a strong covalent O-H bond20,21. Similarly, the X-ray absorption near edge structure (XANES) spectra shifts to lower energy by means of proton doping, implying the lowered oxidation state of Mo atoms as shown in Fig. S5a. Typically, a stoichiometry of H-MoO3 is determined to be H0.342MoO3 by linear combination fitting as shown in Fig. S5b, which agreed with the electrochemical results for H-doped α-MoO3 (HxMoO3, x < 0.4) and XRD information of H0.34MoO3 (PDF#34-1230). Whereas, contrary to crystallographic analysis results, Fig. 2d shows the absence of stretching vibration frequency corresponding to the Mo-Oa (asymmetric oxygen) bonds represented at 865.03 and 820.67 cm−1, instead, a noticeable peak at 634.55 cm−1 by proton doping. It indicates that distribution of protons affects the Mo-O bond characteristics such as bond strength, distance, and dangling-OH angle. Overall, considering changes in lattice distance and interatomic Mo-O bond characteristic while maintaining the orthorhombic structure, it is reasonable to consider that the lattice structure of α-MoO3 is rearranged by the proton participation inside the oxide lattice.

Fig. 2: Material characterization of pristine and hydrogenated MoO3 (HxMoO3, x < 0.4).
figure 2

a X-ray diffraction (XRD) analysis of pristine, partially and fully hydrogenated MoO3 using Mo(IV) cation-reductant and that of after heat treatment at 473 K. The reduced MoO3 samples indicate that the strong diffraction patterns for the (020), (040), and (060) of MoO3 shift to lower angles, reflecting the widened d-spacing of (0k0) plane. X-ray photoelectron spectroscopy (XPS) analysis of pristine and reduced MoO3, showing the gradually increasing Mo5+ in (b) Mo 3d and adsorbed species (-OH) in (c) O 1s regions. d Fourier transform infrared spectroscopy (FTIR) analysis of pristine MoO3 and H-MoO3. e Structure configuration of pristine MoO3, H-MoO3 and Li-ion doped MoO3 calculated by DFT.

Full size image

Whereas, in case of cation-solution treatments using violet-colored V(II) solution as hydrogenation trigger, whose reduction potential value (V(III)/V(II), −0.255 VRHE22) is lower than that of HyMoO3/HxMoO3 (x < 0.4 < y, 0.15 VRHE), the V(II) cation treated α-MoO3 shows the monoclinic phase as shown in Fig. S6. In this case, XPS results show a varying oxidation state in Mo 3d spectra with increased surface absorbed species (Fig. S7), implying the presences of an additional redox reaction with proton insertion compared with the Mo(IV) treated case (HxMoO3, x = 0.342). We also examined the feasibility of cation-treatment methods using commercial WO3 (c-WO3, monoclinic), whose reduction potential for WO3/HxWO3 is lower than 0.3 VRHE23, and verify the identical trend of oxide hydrogenation (Figs. S8 and S9). In this regard, metal oxide hydrogenation strategy using solid state metal also could be accepted since the reduction potential of Cu metal (Cu/Cu2+, 0.34 VRHE, Fig. 1c) is lower than that of molybdenum oxide (MoO3/HxMoO3, 0.44 VRHE) even though this method requires for extra efforts to eliminate the solid metal residual. Hereby, these results provide the reasonable deduction to unveil the clues of the hydrogenation origins. Considering that crystal phase of proton capable oxides is restrictively determined by means of hydrogenation degree, and the hydrogenation degree is controlled by standard potential of metallic cation, it could be concluded that the nature force behind the oxide hydrogenation is the potential difference between proton capable oxide and metallic cation; namely, the proton and charge transfer could be driven spontaneously by the galvanic potential.

The next question in our study was oriented toward the physicochemical properties of H-MoO3 since there was no significant variation in morphology, crystallographic plane, and atomic vibrational Raman spectra. Thereby, it is the optimum conditions to investigate the sole impact of H-binding. We start by specifying the proton doping sites to understand the structural characteristic of H-MoO3 and the origins of lattice rearrangement. We conducted DFT calculation to estimate the stabilized H-sites of H-MoO3 (Fig. S10), through which it is found that intersectional asymmetric oxygen sites (intra-layer space) are the energetically favorable for proton dangling. Notably, as depict in Fig. 2e, it is extraordinary feature of proton doped α-MoO3 since it has been demonstrated that inter-layer space is the most stable site for other dopants using relatively large ionic radius, including Li+ (0.90 Å), Na+ (1.16 Å), and K+ (1.52 Å), or molecule such as H2O molecule24,25,26. Despite doping site is entirely distinguishable, most intriguingly, it is worthy of note that proton doping inside intra-layer space not only increases the d-spacing of (010) plane but also causes the widened inter-layer space (vdW gaps) from 0.764 to 0.854 Å. An ab initio molecular dynamic simulation (Supporting video) shows the Mo-O framework rearragements during the stabilizing process of protons inside octahedral MoO6. Intuitively, it can be seen that proton (0.87 × 10−5 Å) distribution affects the interatomic distance between molybdenum and oxygen atoms, which in turn causes widened vdW gaps and d-spacing of (010) plane. That is, the triggers for the noticeable lattice rearrangement are completely distinguishable between oxide hydrogenation and doping strategies using dopants with large ionic radius, raising a different perspective of varying characteristic of metal oxide by means of dopant types and sites.

Electrochemical properties of H-doped orthorhombic MoO3

To elucidate the effects of the H-binding on electrochemical characteristics of α-MoO3, electrochemical analyses in LiB systems for pristine MoO3 and H-MoO3 (HxMoO3, x = 0.342) were conducted as shown in Fig. 3. Specifically, the orthorhombic structure of α-MoO3 takes an accommodatable sites for Li-ion; inner-plane (intra-layer site) of MoO6 adjacent with Oa and Os (symmetric oxygen), and inter-plane (inter-layer site) of vdW gaps neighboring Ot (terminal oxygen) lattices of MoO3 (Fig. 2e)27. However, pristine MoO3 experiences an irreversible phase transition during the first lithiation process at 2.70 vs. Li/Li+ (Fig. S11a), which is a serious problem that limits the Li-ion accommodatable sites inside MoO3 structure26,27. In contrast, the initial CV curve for H-MoO3 indicates a suppressed current plateau around 2.70 V vs. Li/Li+ and an obvious reduction peak at 2.38 V vs. Li/Li+ as shown in Fig. S11b. For further clarification on this irreversibility, ex-situ XRD analysis of (de)lithiated electrodes were conducted. In Fig. S12a, ambiguous XRD patterns are observed for both lithiated MoO3 and H-MoO3, whereas, completely different results are seen following delithiation. As for delithated MoO3 (Fig. S12b), it shows the diffraction peaks at 11.29, 22.68 and 33.88° corresponding to (03k0) planes of LixMoO3 (x ~ 0.25) occurred by irreversible phase transformation26. Typically, pristine MoO3 exhibits the initial capacity loss of 47.7 mAh/g (LixMoO3, x ~ 0.29) (Fig. S13a) that is almost coincident with stoichiometry of irreversible phase. In contrast, XRD result of cycled H-MoO3 is exactly identical with that of H-MoO3 powder, and it could be demonstrated that there is no irreversible phase transformation as confirmed by the capacity fading of 24.8 mAh/g (H-Li0.15MoO3) (Fig. S13b). Accordingly, it is noteworthy that the low density of protons inside intra-layer site limits the Li-ion flooding into the inner-plane of MoO6, and ultimately inhibits the irreversible phase transition.

Fig. 3: Electrochemical properties of pristine MoO3 and H0.342MoO3 (H-MoO3).
figure 3

a Comparison of the third CV curves of pristine and H-MoO3, measured between 1.5 and 3.5 V vs. Li/Li+ at a scan rate of 0.1 mV s−1. b Voltammetric charge/discharge plateau of H-MoO3 measured at various potential sweep rates from 0.1 to 1.0 mV s−1. c The log (scan rate) versus log (peak specific current) plots for major cathodic peak with b-values as indicator to compare the pseudo-capacitive properties of pristine MoO3 and H-MoO3. d Rate capability at different current from 100 to 3000 mA g−1, followed by (e) cycling stability tests of MoO3 and H-MoO3 measured at a specific current of 1000 mA g−1.

Full size image

After the 2nd activation cycle, H-MoO3 achieves a reversible specific capacity of 1009.4 C g−1 (280.4 mAh g−1) at 0.1 mV s−1, which is higher than the capacity realized for pristine MoO3 (946.8 C g−1, 263 mAh g−1) and close to the theoretical capacity (1005 C g−1, 279 mAh g−1)27, as shown in Fig. 3a. Notably, it exhibits an additional pair of redox potential at 2.95 and 2.68 V vs. Li/Li+ for H-MoO3, and that is in stark contrast to the original redox characteristics in a whole range of high scan rates as shown in Fig. 3b. Besides, in quantitative capacitive analysis of the Li-ion intercalation behaviors, the b-value corresponding to major lithiation of pristine MoO3 was 0.71, whereas that of H-MoO3 was 0.88 as shown in Fig. 3c, representing the enhanced pseudo-capacitive like Li-ion diffusion features by the proton introduction28,29 (detailed instructions for correlation between sweep rate, redox peak current density, and b-value as the indicator of capacitive ion diffusion are described in Fig. S14). Similarly, log (ʋ) versus log (i) plot for anodic peak current (Fig. S14d) also indicates the enhanced capacitive Li-ion diffusion features of H-MoO3. This series of enhanced capacitive characteristics are also represented by enhanced rate capability shown in Fig. 3d. Typically, at the current of 1.0 A g−1, H-MoO3 achieved a stable specific capacity of 170.8 mAh g−1, while pristine MoO3 has 136.0 mAh g−1 with a small decline in capacity. Thereafter, as shown in Fig. 3e, pristine MoO3 shows the rapid capacity decaying early in the cycling process, capacity decrease to 84.1 mAh g−1 after 250 cycles, whereas, H-MoO3 shows the remarkably enhanced cycling stability, exhibiting 84.7% (144.3 mAh g−1) and 72.1% (122.9 mAh g−1) capacity retention at 1.0 A g−1 during 500 and 1000 cycles, respectively.

We further take interest in the existence of multiple redox peaks, and especially in an enhanced capability of H-MoO3. An intuitive advantage of the H-binding introduction has been known as band-gap tuning by advent of H-doping level30,31, which could be confirmed by our DOS calculations (Fig. S15). Then, to elucidate the redox characteristics, the formation energies for lithiated state of both pristine MoO3 and H-MoO3 were calculated. The pristine state retains the two accommodatable sites for Li-ion (inter/intra site) having formation energy of −2.026/−1.648 eV (Fig. 4a, Fig. S16); as discussed, however, due to the irreversible lithiation at the intra-layer site during initial discharge process, the redox peak of pristine state shows the one reversible major peak corresponding to the lithiation at the inter-layer sites. Whereas, since the H-MoO3 exhibits the asymmetrical distribution of proton insertion as a consequence of limited proton adoption (Fig. 2e), the formation energies for inter and intra-layer sites are divided into totally five cases as shown in Fig. 4b (Fig. S17, *, ** marks imply the lithiation sites derived from the lattice asymmetry); that is, the asymmetric lattice order induced by limited hydrogenation would result in differences of formation energy and distinctive redox potential (Fig. 3a). These structural characteristics give rise to the unique electrochemical properties of H-MoO3. Above all, first-principle calculation results in Fig. S17 indicate that the proton adoption sites are distinguished from the Li-ion accommodatable sites, through which it is confirmed that H-binding of H-MoO3 would have less influences on preservable Li-ion sites, facilitating a comparable capacity realization with pristine state. Thereby, even though it has long been accepted that there is a trade-off in relation to cation doping with entailed capacity limitation24,25,27, this assertion contains a principal exception in case of H-MoO3 since the Li-ion accommodatable sites are rearranged not by the cation interposition but by proton interference on Mo-Oa bonding. Moreover, as confirmed in ex-situ XRD analysis, H-MoO3 exhibits well-maintained orthorhombic structure on account of inhibited irreversible phase transition reaction during -/de-lithation, whereas, there is initial capacity loss corresponding to H-Li0.15MoO3. To examine the impacts of irreversible Li-ion (Liirrev) on H-MoO3, we compared the formation energy variation for both pristine MoO3 and H-MoO3 in accordance with single Liirrev remained inside intra-layer site. In Fig. S18, it can be seen that Liirrev-MoO3 exhibits nearly similar formation energies for each Li-ion accommodatable sites, whereas, H-Liirrev-MoO3 exhibits diverse formation energy gradient for each site; that is, formation energy of H-Liirrev-MoO3 differs through the Li-ion accommodatable sites. Accordingly, it is expected that Liirrev, which corresponds to the initial capacity loss, would heavily influence on physicochemical properties of H-MoO3, and as a result, contribute to changes in redox characteristic of H-MoO3 after 1st cycle as shown in Fig. S11b.

Fig. 4: DFT calculation results.
figure 4

Calculated formation energies corresponding to Li-ion interposition in (a) bulk α-MoO3 and (b) H-MoO3, * ** Marks represent the lithiation sites derived by proton interferences inducing lattice disorder. c Calculated energy barriers for Li-ion diffusion along the Li-ion accommodatable sites and (d) schematic illustration of feasible Li-ion diffusion pathways through the H-MoO3 lattice.

Full size image

We also investigated a role of H-binding in determining the diffusion rates by constructing the Li-ion diffusion paths and calculating the energy barriers using NEB simulation. According to the ARXPS results (Fig. S19), showing that the proton doping would occur throughout the surface and bulk regions of metal oxide, the energy barriers for available diffusion pathways of both pristine MoO3 and H-MoO3 (Figs. S20 and S21) were calculated on the basis of the most stable inter-layer site. The energy barrier for single Li-ion diffusion pathway along the inter-layer sites in pristine MoO3 is 0.5 eV, whereas, in case of H-MoO3 having various diffusion routes due to the asymmetrical lattice orders, the rate determining energy barrier for Li-ion moving along the inter-layer* to inter-layer sites is only 0.388 eV as shown in Fig. 4c and Fig. S21e. Moreover, the energy barriers of Li-ion moving from intra/intra*-layer to inter-layer are 0.238 and 0.121 eV, respectively, as shown in Fig. S22. That is, through the various diffusion pathways as a result of the asymmetrical lattice order by proton introduction, the bottleneck energy barrier for Li-ion diffusion through the bulk regions could be lowered by approximately 0.11 eV as represented in Fig. 4d. Therefore, we concluded that lattice rearrangement by proton adoption would modulate the electrical and redox characteristics, resulting in reversible cycling performance and faster kinetics of Li-ion along the intercalation sites of H-MoO3.

Discussion

In this work, we established the cornerstone of metal oxide hydrogenation by devising a cation-solution treatment strategy and demonstrated that the impetus of a proton diffusion through the oxide lattice is based on the galvanic redox reactions. Herein, we could verify through the experimental proof that the standard potentials of oxide and metallic cations are vital factors for the controllable proton doping. This methodology not only encompasses the implicit principle of conventional solid-metal treatment for oxide hydrogenation but also unveils the phase transition mechanism of metal oxide during electron-proton pair migration. Based on the thorough understanding of hydrogenation mechanisms, sole impact of H-binding with practical applicability of this method for intercalation-type energy storage materials in lithium-ion battery systems are demonstrated. In battery systems, there are significant differences in redox characteristics as protons participate in orthorhombic-MoO3. Typically, the proton doping with lattice rearrangement would cause the suppressed irreversible phase transition reaction and accelerated Li-ion diffusion with enhanced charge transfer reaction. Through the first principle DFT calculation, it is confirmed that the interposition of protons was entirely distinguished compared with other cation dopants, which results suggest the possibilities to overcome the trade-off in relation between cation doping and limited capacity for energy storage. Moreover, it could be demonstrated via NEB approach that asymmetric lattice order results in diffusion pathways of Li-ion having lower energy barriers along the intercalation sites, contributing to enhanced diffusion rates and pseudo-capacitive characteristics. We believed that this work would suggest insight of oxide reforming strategy via corrosion-based galvanic reaction and highlight the sole impact of H-binding on inherent properties of oxide for preferable materials engineering.

Methods

Material preparation

Orthorhombic structure MoO3 (α-MoO3) was synthesized through a one-step hydrothermal synthesis. Ammonium molybdate tetrahydrate (2 g, Sigma Aldrich) was added to 30 ml of deionized water and 10 ml of nitric acid (60%, Daejung) to form a solution. The prepared solution was transferred into a 100 ml Teflon-lined autoclave and heated in box furnace at 180 °C with the constant 5 °C min−1 of heating rate for 12 h. The obtained white powder was washed with distilled water several times using vacuum filtering, and dried under vacuum at 70 °C. As for monoclinic WO3, it is purchased from Sigma-Aldrich (CAS no: 1314-35-8) and used without any purifications. For metal oxide hydrogenation, specific amount of molybdenum chloride (MoCl5, Sigma Aldrich) is dissolved in acetonitrile (CARLO ERBA) to reduce the oxidation state of molybdenum cation: 2MoCl5 + 5 CH3CN → 2 MoCl4(CH3CN)2 + HCl + ClCH2CN. Afterward, 10 ml of deionized water was added to produce the acid condition by conjugate acid. To prepare the vanadium (II) solution, specific amount of ammonium metavanadate (NH4VO3) dissolved in 30 ml of deionized water and 10 ml of sulfuric acid (Daejung), during which VO3− species dissolve as the pervanadyl ion VO2+ (V): VO3− + 2 H+ → VO2+ + H2O. Then, excess amount of zinc metal powder was added to reduce the oxidation state of vanadium cation: 2VO2+ + 3 Zn + 8 H+ → 2 V2+ + 3 Zn2+ + 4H2O. The obtained solution was refined using vacuum filtering to remove the residual metal. Galvanic redox reaction induced metal oxide hydrogenation begins as the metallic cation solutions are added at the 0.2 g of metal oxide (MoO3, WO3) dispersed deionized water and stirred for 3 h at room temperature. The reduced metal oxide powder was washed with deionized water for several times to remove the residual metallic cation solutions and collected using vacuum filtering.

Material characterization

The structural properties of samples were analyzed by X-ray diffraction (XRD; Rigaku) using Cu Kα radiation (λ = 0.15406 nm). For Ex-situ XRD analysis of -/de-lithiated electrode, the electrode potential shift to 1.5 and 3.5 V vs Li/Li+, respectively, with the 0.1 mV s−1 of scan rate in Li-ion battery coin-cell systems, and the polarized electrodes were obtained after cell disassembling, followed by rinsing with dimethyl carbonate (DMC) solvent and dried naturally in argon purged glove box. Oxidation configurations of prepared samples are conducted using X-ray photoelectron spectroscopy (XPS, Thermo Fisher Scientific) using Al Kα (1486.6 eV) for excitation source at 100 W, and angle-resolved XPS (ARXPS) analysis for H-MoO3 was conducted by film mode with the photoelectron tilt angle from zero to 70o. To determine the stoichiometry of H-MoO3, the experimental Mo K-edge (19.999 keV) XANES spectra were obtained by Rigaku R-XAS Looper laboratory spectrometer in transmission mode with X-ray source (Mo, LaB6). The XAFS spectra were normalized by background subtraction and fitting linear polynomials to the pre-edge and post-edge regions of an absorption spectra, respectively. The surface morphologies of synthesized MoO3 were collected using high resolution transmission electron microscopy (TEM, Tecnain Fe F30 S-Win) and high-resolution scanning electron microscopy (SEM, S-4700 with EMAX system, Hitachi). Raman spectroscopy (Horiba) was measured with BX41 confocal microscope and the Fourier transform infrared spectrometer (FT-IR, Bruker) was measured by transmission mode.

Electrochemical measurements in acidic aqueous system

The redox features of pristine MoO3 under acidic condition were measured in three-electrode systems. It is equipped with rotating disk electrode (RDE, 0.196 cm2, glassy carbon) with a prepared MoO3 as working electrode, silver chloride (Ag/AgCl, \({a}_{{{Cl}}^{-}}=1\)) reference electrode, and Pt mesh counter electrode using three-electrode electrochemical cell kit filled with 1000 mL of a 1 mol/L sulfuric acid. The polarization curve of pristine MoO3 was measured by LSV with the 10 mV s−1 of scan rate from open circuit voltage (OCV, around 0.4 VAg/AgCl) to −0.8 VAg/AgCl under N2 purged sulfuric acid solution. The standard redox potential of molybdenum cation was measured using three-electrode electrochemical cell kit filled with 1000 mL of 0.1 mol/L Mo (IV) cation and 1 mol/L of sulfuric acid. It is equipped with Pt mesh working electrode, Ag/AgCl reference electrode and Pt rod counter electrode. The polarization curves were measured by CV between −0.3 and 0.8 VAg/AgCl with the 10 mV s−1 of scan rate. For the conversion of the applied potential vs. Ag/AgCl, the potentials of the obtained results are converted to the reversible hydrogen electrode (RHE) according to Nernst Equation: ERHE = EAg/AgCl + EoAg/AgCl + 0.059 pH. All expressions for voltammograms are reported without iR compensation.

Electrochemical measurements in lithium-ion battery system

The redox characterizations of prepared samples in Li-ion battery systems were investigated in two-electrode system using CR2032-type coin cell. The slurry, composed of the active materials (pristine MoO3, H-MoO3), supporting carbon (Super P), and binder (PAA) with a weight ratio of 7:2:1, was cast on Al foil, and the electrode was dried at 60 °C for 24 h in a vacuum oven. The coin cell was assembled with prepared electrode with a diameter of 10 mm (18 μm thickness with ~0.4–0.6 mg of active material, loading mass: 0.50–0.76 mg cm−2, areal capacity: 633.2 mC cm−2) as working electrode, Li metal (16 mm diameter, 160 μm thickness, 99.9% purity, Sigma-Aldrich) as counter/reference electrode, Celgard 2400 (18 mm diameter and 25 μm thickness) as separator, and 1 M of lithium hexafluorophosphate (LiPF6) dissolved in a mixture of ethylene carbonate and diethylene carbonate (EC/DEC, 1:1 by volume, battery-grade anhydrous: H2O < 10 ppm, purity > 99%, Sigma-Aldrich) as electrolyte in an argon gas-filled glove box (concentration of O2 and H2O < 0.1 ppm, ambient temperature of 25 °C). The Li metal and electrolyte were stored in the argon gas-filled glove box and used directly without any purification within 2 months of purchase. The electrochemical properties of assembled coin cell were investigated in the potential range between 1.5 and 3.5 V vs. Li/Li+ using potentiostat (Solatron Analytical, 1470E/1400 CellTest System) and battery cycler (WonATech, WBCS3000) in convection type environmental chamber (VisonScientific, VS-1203P1) with an ambient temperature of 25 °C. The cyclic performances were measured at various specific currents of 0.1, 0.2, 0.3, 0.4, 0.5, 1.0, 2.0, and 3.0 A g−1 to evaluate the rate capability. Long-term cycling tests were performed at specific current of 1000 mA g−1 for durability test in the potential range of 1.5–3.5 V vs. Li/Li+.

Computational details

To investigate the energetics of Li ion migration within pristine MoO3 and HnMoO3 with n = 0.33, we carried out first-principles electronic structure calculations within DFT scheme as is implemented with Vienna Ab initio Simulation Package 5.4.432,33,34,35,36. A plane-wave basis set with 500 eV energy cut-off is employed for the solution of the Kohn-Sham equation, and the exchange-correlation interactions among electrons are described within generalized gradient approximations37. Moreover, the DFT-D3 functional of Grimme et al.38 is chosen to properly treat the van der Waals interactions in MoO3 and H0.33MoO3 (Table S1). To optimize all geometric structures, the unit cells of pristine MoO3 and H0.33MoO3 which is three- and two-times larger in the x- and y-direction, due to the setting for n = 0.33, respectively, are fully relaxed until the energy and force differences between successive relaxation steps becomes less than 10-5 eV and 10-2 eV/Å, respectively. For H0.33MoO3, due to the randomness of H positions, we performed ab-initio molecular dynamics simulations to sample the geometry of H0.33MoO3 with timestep of 0.5 fs for 10 ps only at the Γ-point (Supporting video). All the ab-initio molecular dynamics are carried out under a canonical ensemble (NVT) controlled by Nosé-Hoover thermostat at 300 K, followed by static calculations to adopt the most stable configuration (Fig. S10). In all static calculations, \(3\times 2\times 1\) supercells are employed for both MoO3 and H0.33MoO3 together with Γ-centered \(3\times 5\times 3\) k-point grids for the Brillouin zone sampling.

To study Li diffusion, the energy barrier simulations are performed based on the climbing image nudged elastic band (CI-NEB) method with a force-based optimization scheme39,40. The forces convergence threshold orthogonal to the band is set to be less than 0.01 eV/Å in our CI-NEB calculations. For evaluating the structural stability of the initial and final states, formation energies (\({{{{\rm{H}}}}}_{{{{\rm{f}}}}}\)) are calculated (Table S2) by the following equations:

$${H}_{f}=E\left[{Li}+({H}_{0.33}){Mo}{O}_{3}\right]-E\left[\left({H}_{0.33}\right){Mo}{O}_{3}\right]-E\left[{Li}\right]$$
(1)

where the \(E[{Li}+({H}_{0.33}){Mo}{O}_{3}]\) and \(E[({H}_{0.33}){Mo}{O}_{3}]\) are the total energy of (H0.33)MoO3 system with and without one Li atom, respectively, and \({{{\rm{E}}}}\left[{{{\rm{Li}}}}\right]\) is the chemical potential which is the per atom energy from bcc Li metal.