Introduction

Recent years have witnessed significant advancements in acoustic functional materials, with the utilization of acoustic metamaterials and their programmable properties to craft functional hybrid structures. This category of structures encompasses various devices, including those showcasing acoustic negative modulus and refraction1,2,3, acoustic holograms4, acoustic cloaks5,6,7, mode transitions8, and acoustic lenses9,10,11. Yet, it’s worth noting that scatter-based metamaterials commonly work within a restricted frequency band due to their reliance on the cut-off frequency, which hinges on the irregular shapes of the scattering elements and their acoustic characteristics12,13. Furthermore, achieving goal-oriented design, such as enabling transmission through aberration layers, continues to pose challenges, particularly within conventional materials. Soft materials have gained popularity due to their flexibility and have found extensive applications in soft elastomeric devices14,15, soft robotics16,17, and flexible biomedical electronics18,19, areas where periodic structures of metamaterials have shown limited success. Recent strides in soft acoustic materials highlight that soft, porous silicone elastomer material can achieve highly controlled refractive indices20, ultra-low sound speeds21, and tunable Young’s modulus22 through changes in porosity of the materials. However, establishing the refractive index over a broadband range of ultrasound frequency bandwidths remains unresolved. Although some studies have proposed strategies for breaking this narrowband limitation by introducing tunable metagels in biomedical ultrasound or the use of bioinspired impedance transformers23,24,25, it’s important to note that metagels struggle to adequately address significant wave distortion in the research of medical ultrasound.

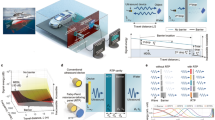
In medical ultrasound, underwater acoustic ranging, and urban pipeline inspection (Fig. 1A–C), it is desirable to transmit wave through an aberration layer with maximum transmission and minimum reflection. Impedance matching technology, exemplified in electrical, mechanical, acoustic, optical, and microwave engineering, has proven effective for energy transmission. However, acoustic impedance matching remains an unresolved issue in ultrasonic imaging due to the existence of aberration layers26,27. Only few studies have attempted to establish acoustic phase modulation through aberration layers, such as time-reversal mirrors28, spatio-temporal-interframe-correction29, and phase aberration correction algorithms30. Therefore, the development of precise controlled conduction and broadband phase modulation of ultrasonic waves in soft matter is of great significance for medical diagnosis and ultrasound-guided therapy.

Fig. 1: Schematic viewing of SML applications.
figure 1

A Medical ultrasound in brain tumor treatment, B underwater sonar ranging in AUV, C urban pipeline inspection. A generalized SML for all applications is established by universal full-wave equations in non-uniform layered medium to derive the phase accumulation of SML, and ensure the ultrasound wave for penetrating through AL.

Full size image

Transformation theory is a method proposed for wave control in electromagnetic waves and microwave engineering. Pendry et al.31 and Leonhardt32 designed cloaks that exclude electromagnetic fields outside of obstacles, a phenomenon later verified by experiments at microwave frequencies33. Milton et al. proposed a general elastodynamic equation of motion, shown to be form-invariant under coordinate transformations5. The effective properties of metamaterials in acoustics can also been extracted from reflection and transmission coefficients34. Other works have demonstrated that cloaks and illusion devices based on electromagnetic wave complementary metamaterials can create a virtual hole in a wall without distortion35,36. Building on the concept of coordinate transformation, a type of anisotropic acoustic complementary metamaterial has been proposed for canceling out aberration layers37. However, the limitation of acoustic transformation theory lies in its current focus on designing lens with curved shapes and extreme anisotropic acoustic property. An approach for utilizing impedance-matched two-dimensional gradient index functions to design soft metalens has not been proposed. Previous structure designs based on rigid metamaterials only support narrow working frequency, and no broadband experiments were given. Recently, phase-only acoustic holographic lens38 has been employed for transcranial ultrasound focusing even in vivo. However, the Fabry–Pérot resonance of unit cell in hologram lens restricts their broadband performance.

In this paper, we propose an acoustic soft metalens (SML) for canceling out strong impedance-mismatch and focusing sound energy suitable for transcranial ultrasound. We develop a composite soft metamaterial system by dispersing various percentages of micro-tungsten particles into a silicone elastomer substrate to achieve tunable acoustic properties. The broadband penetrating focusing capabilities of SML are then numerically and experimentally validated. The SML demonstrates a 14.19 dB improvement in transmission compared to the typical ultrasound transducer without the SML and achieves nearly ten times the spatial resolution over the frequency ranges from 50 kHz~0.4 MHz. Furthermore, ex vivo transcranial ultrasound applications have verified that the SML efficiently penetrates through aberration layers, such as human skull phantom. This advanced soft materials-metamaterials-gradient index fabrication scheme proposes the existence of fundamentally unique acoustic soft materials, bridging the gap of aberration layers over ultra-broadband ranges during ultrasound transmission.

Results

Schematic diagram and principle of the SML

Figure 1A illustrates brain tumor treatment as a key issue of medical ultrasound (Fig. 1A). The significant aberration of ultrasound in brain severely degrades the acoustic beam, which is expected to be resolved through the introduction of SML. In Fig. 1B we depict an autonomous underwater vehicle (AUV) sonar system to measure the target’s distance by transmitting acoustic waves through the AUV’s outer shell. An SML is mounted to sonar detection system for penetrating through the rigid outer shell of the AUV, which serves as an aberration layer in an underwater environment. Figure 1C represents a crucial issue in barriers detection, specifically urban pipeline inspection, which shares the same fundamental issue as medical ultrasound and underwater ranging. To enhance the reflected signal on the solid aberration layer from urban pipeline, we introduce the SML at the solid-water-interface (Fig. 1C). SML is used to cancel out aberration layers and allows the transmission of acoustic waves at higher energy, where the wave propagation direction is from the lower part of axis to higher part of axis inside of the medium. Our design begins with the quasi-2D complementary medium for canceling out ultrasound aberration, which is placed on the surface of aberration layers, as shown in center part of Fig. 1. Previous transformation theory has proven effective for manipulating the waves in diverse areas, including electromagnetic waves and microwaves. In addition, Shen et al.37 have demonstrated the ability to use negative anisotropic metamaterial to penetrate aberrating layers. However, there remains a significant challenge in designing an acoustic metamaterials with broadband penetrating performance.

The full wave equations in non-uniform layered medium with time-harmonic form \(\nabla [{\rho }^{-1}({{\boldsymbol{r}}})\nabla p({{\boldsymbol{r}}},t)]=\frac{1}{\kappa ({{\boldsymbol{r}}})}\frac{{\partial }^{2}p({{\boldsymbol{r}}},t)}{\partial {t}^{2}}\) has been used for both phase and amplitude information in aberration layered region. The acoustic phases accumulation from the monopole source, aberration layers, and hologram plane are defined as \(\varDelta {\varPhi }_{{MS}}({{\boldsymbol{r}}})\), \(\varDelta {\varPhi }_{{AL}}({{\boldsymbol{r}}})\), and \(\varDelta {\varPhi }_{{HP}}({{\boldsymbol{r}}})\), respectively. The pressure phase \(\varphi ({{\boldsymbol{r}}})\) in formal solution \(p({{\boldsymbol{r}}},t)=A({{\boldsymbol{r}}}){e}^{j(\omega t-{k}_{0}\varphi ({{\boldsymbol{r}}}))}\) could be replaced by the phase accumulation term with monopole source and aberration layers \(\varDelta {\varPhi }_{{MS}}({{\boldsymbol{r}}})+\varDelta {\varPhi }_{{AL}}({{\boldsymbol{r}}})\). The detailed descriptions of the phase accumulations are graphically shown in Fig. 2A. According to the phase accumulation process of wave propagation, the following relation should be demanded:

$$-(\varDelta {\varPhi }_{{MS}}({{\boldsymbol{r}}})+\varDelta {\varPhi }_{{AL}}({{\boldsymbol{r}}}))=\varDelta {\varPhi }_{{HP}}({{\boldsymbol{r}}})$$
(1)
Fig. 2: The arbitrary shape scattering elimination theory is based on the 2D hologram.
figure 2

A The schematic diagram of a 2D hologram by applying the acoustic time-reversal mirror techniques based on wave equation with reciprocity, one monopole source is placed at the right side of the aberration layers, the phase accumulation at the hologram plane can be calculated by phase change of the monopole source and aberration layers; B phase profile comparisons between SML and acoustic hologram; C phase change rate shows consistent tendency between SML and acoustic hologram while slightly shift happens in the reverse point of pressure phase.

Full size image

Firstly, without the existence of aberration layers, the sound pressure phase of monopole source can be expressed as \(\varDelta {\varPhi }_{{MS}}({{\boldsymbol{r}}})\). The free-space Green’s function in Eq. (2) has been used to describe the state of the acoustic field before it arrives at the aberration layered region. We emit a virtual monopole source at the image plane \({{{\boldsymbol{r}}}}_{0}({r}_{0},{z}_{0})\), which is backward propagated into the hologram plane \({{\boldsymbol{r}}}(r,z)\). The received sound pressure can be written as

$$p({{\boldsymbol{r}}}{|}{{{\boldsymbol{r}}}}_{0})=\frac{{jk}{\rho }_{0}{c}_{0}{a}^{2}}{{|}{{\boldsymbol{r}}}-{{{\boldsymbol{r}}}}_{0}{|}}{e}^{-{jk}|{{\boldsymbol{r}}}-{{{\boldsymbol{r}}}}_{0}|}$$
(2)

where \(k\) is the wavenumber in free space, \({\rho }_{0}{c}_{0}\) is the characteristic impedance in the background medium, and \(a < < \lambda\) is the radius of the monopole source, and we define the amplitude function \(A({{\boldsymbol{r}}}{|}{{{\boldsymbol{r}}}}_{0})=\frac{{jk}{\rho }_{0}{c}_{0}{a}^{2}}{|{{\boldsymbol{r}}}-{{{\boldsymbol{r}}}}_{0}|}\).

Secondly, for deriving the phase accumulation \(\varDelta {\varPhi }_{{AL}}({{\boldsymbol{r}}})+\varDelta {\varPhi }_{{MS}}({{\boldsymbol{r}}})\) with AL and monopole source, we utilize the principle of reciprocity in acoustic fields and the concept of time reversal mirror, the phase accumulation at the hologram plane has been used to reverse the wave into a single monopole source. The effective refractive index \({n}_{{eff}}({{\boldsymbol{r}}})\) is used to determine the transmission phase \({\psi }_{t}({{\boldsymbol{r}}},z)={k}_{0}{\int }_{0}^{z}{n}_{{eff}}({{\boldsymbol{r}}},z){dz}\) (see method section for details on arbitrary phase coding theory). The detailed derivation of the effective refractive index based on the phase modulation method is shown in the Materials and Method section. In our design, thickness z is fixed and the accumulation phase at the hologram plane along \({{\boldsymbol{r}}}\) direction can be determined by \({\varPhi }_{0}({{\boldsymbol{r}}})+\varDelta {\varPhi }_{{HP}}({{\boldsymbol{r}}})={k}_{0}{n}_{{eff}}({{\boldsymbol{r}}})z\). Here, \({k}_{0}\) is the wavenumber in free space, \({\varPhi }_{0}({{\boldsymbol{r}}})\) is the initial phase. Therefore, the effective refractive index in SML can be obtained by the accumulated holographic phase as follows:

$${n}_{{eff}}({{\boldsymbol{r}}})=\frac{{\varPhi }_{0}({{\boldsymbol{r}}})-(\varDelta {\varPhi }_{{MS}}({{\boldsymbol{r}}})+\varDelta {\varPhi }_{{AL}}({{\boldsymbol{r}}}))}{{k}_{0}z}$$
(3)

Here, \({{\boldsymbol{r}}}\) is a direction vector under the 2D asymmetric coordinate system. In our simulations, one aberration layers with inhomogeneous shape has been applied to calculate the acoustic accumulation path for recovering the phase information.

By introducing Eq. (1), the holographic phase \(\varDelta {\varPhi }_{{HP}}({{\boldsymbol{r}}})\) is determined by COMSOL Multiphysics that considering the phase accumulation \(-(\varDelta {\varPhi }_{{MS}}({{\boldsymbol{r}}})+\varDelta {\varPhi }_{{AL}}({{\boldsymbol{r}}}))=\varDelta {\varPhi }_{{HP}}({{\boldsymbol{r}}})\) from aberration layers and monopole source (Fig. 2A, B). In simulations (Fig. S1), the characteristic acoustic impedances of background medium (water or tissue) and aberration layers are \({Z}_{0}={\rho }_{0}{c}_{0}=1.48\times 1{0}^{6}\) Pa·s/m and \({Z}_{s}={\rho }_{s}{c}_{s}=3.5\times 1{0}^{6}\) Pa·s/m, respectively. Here, the densities for water and aberration layers are \({\rho }_{0}=1000\) kg/m3 and \({\rho }_{s}=2000\) kg/m3, and speeds of sound are \({c}_{0}=1480\) m/s and \({c}_{s}=2500\) m/s, respectively. In this case, the plane wave is expected to focus at the distance of \(d=50\) mm, and the maximum aperture of windowed plane wave is \({D}_{{in}}=120\) mm. Here, the aberration layer model by CT scanning has been introduced in our simulations to determine a specific hologram phase \(\varDelta {\varPhi }_{{HP}}({{\boldsymbol{r}}})\), which will be different when introducing different phantoms.

According to the above analysis, SML modulated the refractive index over a specific holographic plane, and the ideal holographic phase calculated by aberration layers compared with approximately designed SML phase profiles are shown in Fig. 2B. The designed quasi-2D acoustic hologram illustrated how the refractive index change will affect the intensity distribution through aberration layers. When we have \(d{\psi }_{t}({{\boldsymbol{r}}},z)/d{{\boldsymbol{r}}}\approx d{\varPhi }_{{HP}}({{\boldsymbol{r}}})/d{{\boldsymbol{r}}}\) as shown in Fig. 2C, the transmission phase change rate of SML (black solid line) approaches the ideal phase change rate calculated by aberration layers (red dash line). In this case, the sound waves are expected to penetrate through aberration layers. The detailed effective refractive index based on arbitrary phase coding theory is shown in the Materials and Method section.

We propose the following hypotheses for the design and operation of SML: (i) SML can be fabricated by silicone elastomer-micro tungsten composite due to the fact that tungsten with highest mass density in nature may contribute to largest range of tunable acoustic properties. (ii) A tunable acoustic refractive indices and densities can be achieved theoretically and experimentally by using different weight percentages of micro-tungsten particles. (iii) SML exhibits broadband focusing characteristics and effectively transmits the ultrasound wave through aberration layers.

Design and fabrication of SML

To validate the above hypotheses, we experimentally dispersed micro-tungsten particles with different concentration into the silicone elastomer substrate to obtain composite soft metamaterials with spatial variability, as shown in Fig. 3A (see method section for details on Material and Fabrication of SML). According to the effective medium theory (see method section for details on Determination of the Acoustic Impedance Function of SML), the micro tungsten-elastomer composite offers an efficient way to change the effective sound speed, density, and acoustic impedance of SML by tuning the weight percentage of micro tungsten particles (Fig. S2, see the Supplementary Materials). Based on the long-wavelength approximation, the effective parameters of the silicone elastomer-tungsten composite are described as

$${\rho }^{*}=\varphi {\rho }_{1}+(1-\varphi ){\rho }_{0}$$
(4)
$${{c}_{L}}^{*}=\sqrt{\frac{{\lambda }^{*}+2{G}^{*}}{{\rho }^{*}}}$$
(5)
$${{c}_{T}}^{*}=\sqrt{\frac{{G}^{*}}{{\rho }^{*}}}$$
(6)

where \({\rho }^{*}\), \({c}_{L}^{*}\) and \({c}_{T}^{*}\) represent the effective density, sound speeds of longitudinal and transverse waves, respectively. In general, the effective medium theory under the static limit can be obtained using the coherent potential approximation (CPA)39. The non-resonance-based design is key to achieving broadband material properties, which differs from the resonant-based effective medium theory such as homogenization scheme for acoustic metamaterials40.

Fig. 3: Design and fabrication of SML under cylindrical coordinate system.
figure 3

A Illustration of the designed SML applied in a human brain phantom by dispersing tungsten microparticles with silicone elastomer matrix and the SEM imaging at 100 μm and 300 μm scale, respectively. B Tested and theoretical acoustic refractive indices to weight percentage. Photograph in (B) represents sample preparation for SEM. C Schematic diagram of discrete layers distributions and the fabricated SML with seven descrete layers along radial direction. The image of the upper right region is the mixed SML under the weight percentage of 67.8%. D Measured sound speed and density distributions of SML compared with holographic phase by acoustic hologram based on the reciprocity principle.

Full size image

We measured the sound speed, density, acoustic impedance, and refractive index for micro-tungsten weight percentages of 0%, 10%, 20%, 25%, 30%, 35%, 40%, 45%, 55% and 60%, respectively (see Table S1 in Supplementary Materials). Each set of gel-tungsten composite sample is repeated three times at 5% intervals in the range of 20%-45% mass fraction. Scanning electron microscopy (SEM, FEI Quanta 650 FEG) images of the weight percentages of 25% and 60% micro tungsten powder dispersed in the silicone elastomer substrate were obtained. Thin slices of the sample were covered with a conductive layer of gold prior for observation, and the micrographs were obtained at a scale of \(100\,\mu m,300\,\mu m\) magnification, respectively (Fig. 3A). The SEM micrographs validate the uniform mixing of micro-tungsten particles in the elastomeric matrix.

Furthermore, we analytically derived the relationship between weight percentage and the refractive index (Fig. S2, see the Supporting Information) and experimentally validated (Fig. 3B). The measured refractive index distribution agrees well with the theoretical prediction of the effective medium theory under the long-wavelength approximation. The final fabrication of the SML includes curing the micro tungsten-elastomer composite in a 3D-printed acrylonitrile butadiene styrene (ABS) mold with dimensions of 120 mm × 25.5 mm (radius × thickness) to form seven discrete layers of different weight percentages of micro-tungsten arranged in an elastomeric ring along the \({{\boldsymbol{r}}}\) direction (Fig. 3C). The designed discrete refractive index and density of each layer are shown in Table S2. The sound speeds and densities along \({{\boldsymbol{r}}}\) direction are necessary for further calibration. As shown in Fig. 3D, sound speed and density distributions have been characterized to approach the holographic phase with red dash line obtained by aberration layers. This design aims for maximum energy transmission through aberration layers as the acoustic impedance of each SML layer is close to the background medium (Fig. S2, see the Supplementary Materials) when the micro-tungsten weight percentage is below 60%. The realized discrete speed of sound, refractive index, and weight percentages of micro-tungsten particles in different layers are shown in Table S3. When the sound speed of one layer is high, the corresponding density is low. The SML design provides a broadband strategy that allows for maximum transmissions of sound pressure without any bandwidth loss. The characterization experimental setup and broadband transmission performances of SML are shown in Fig. S3 to Fig. S4 and the experimental results agree well with simulations (Fig. S5). The further measured dispersion and attenuation effects on the refractive index of SML over frequencies from 0.5 MHz to 1.2 MHz are shown in Fig. S6, respectively.

CT-based transcranial ultrasound focusing setup and transient results

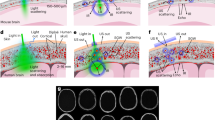
The bonding ability of silicone elastomer composites with metal particles provides excellent tunability and surface conformability, making them suitable for goal-oriented design. Leveraging this capability, we can easily and efficiently fabricate SML with superior broadband performance and design flexibility, which will be further applied in transcranial ultrasound focusing. Initially, a sine wave with five-cycle pulsed signal is generated for simulating the transient excitation process (Fig. 4A), which is then modulated through the SML to generate wavefront with corrected phase profile. The signal consists of 120 kHz or 0.5 MHz sinus pulse with five-cycles and a repetition of 165 ms. We acquire skull neuroanatomy data (CT data) from a 15-year-old volunteer participant to create the skull phantom for transcranial ultrasound focusing. Computed tomography imaging provides three scanning sections of human skull model (Fig. 4B–D), including coronal, axial, and sagittal cross sections, revealing parietal bone, temporal bone, mastoid cells, frontal sinus, occipital bone, and sphenoid bone, respectively. The transient signal generated by the transducer propagates through the SML and focuses on the intracranial region from the left side of the coronal section.

Fig. 4: Schematic of the CT-based transcranial ultrasound focusing setup and transient results.
figure 4

A CT illustration of the human skull model, with the sonication path (dotted blue lines), the ultrasound signal is pulsed sine wave at 120 kHz and 0.5 MHz with five-cycle with trigger interval of 165 ms. B–D Three scanning sections of the human skull by computed tomography imaging includes coronal cross-section, axial cross-section, and sagittal cross-section, respectively. E–G Transient propagation plots for a five-cycle pulse source at frequency of 120 kHz and 0.5 MHz (H–J). The bold ‘I’,’R’, ‘T’ represent incident wave, reflected wave, and transmitted wave, respectively, where E, F, and G correspond to the propagation time at \(80\mu s\), \(100\mu s\), and \(120\mu s\), respectively. Pr and Dis represent the normalized sound pressure and normalized displacement, respectively.

Full size image

As shown in Fig. 4E–G, the compression wave speed and the shear wave speed of a real human skull is 2500 m/s and 1400 m/s, respectively. The sound velocity of compressional wave and density of intracranial region are approximately 1500 m/s and 1000 kg/m3, respectively. The plane wave at a frequency of 120 kHz is modulated into focused wave at the propagation time of \(75\mu s\), focused to intracranial region at the propagation time of \(100\mu s\), and diverged outward from intracranial tissue at the propagation time of \(120\mu s\). At the propagation time of \(100\mu s\) and \(120\mu s\), it can be seen from the left side of the human skull phantom, some incident sound waves are reflected off the left outside of skull, but the majority of the energy remains focused inside the skull. Additional transient results at frequency of 0.5 MHz are shown in Fig. 4H–J, demonstrating that the SML effectively guides ultrasound waves through aberration layers, such as human skull.

It is important to mention that individual differences might lead to defocusing when employing the SML to penetrate aberration layers. Moving forward, the subsequent section will encompass a qualitative analysis and a comprehensive discussion of the experimental findings pertaining to transcranial ultrasound focusing through the utilization of the SML.

Experiments in ultrasound focusing through human skull phantom

We further investigate the experiments of SML for achieving broadband transmission through aberration layers made by biocompatible PLA-printed skull model. An ultrasound transducer from 50 kHz to 0.5 MHz (Fig. S7) is used for applications in transcranial ultrasound focusing in background medium as shown in Fig. 5A. The pulsed signal produced by function signal generator is processed by a power amplifier, impedance matching, and RF filter before being transmitted into the transducer to exit SML and generate ultrasonic waves. We employ a 3D-printed curved skull model as aberration layers, including parietal, occipital, temporal, sulcus for middle meningeal, frontal sinus, and sphenoid, respectively (Fig. 5B). The attenuation and heterogeneities in the human skull model have not been considered here but exist for real skulls in next part. The sound pressure levels in the human skull model with and without SML show significant differences. Without SML, the two-dimensional acoustic transmission intensity profiles exhibit unfocused ultrasound with sound pressure damping in the infratemporal region with a center position located 50 mm from the inner layer of the human skull model (Fig. 5C). However, with SML, a high intensity focused ultrasound (HIFU) spot appears, providing  accurate localization inside of the infratemporal region over a wide frequency range (Fig. 5D).

Fig. 5: Transcranial ultrasound focusing applications of SML.
figure 5

A Experimental photograph of ultrasound focusing through the human skull model. B 3D-printed human skull model including parietal, occipital, temporal, sulcus for middle meningeal, frontal sinus, and sphenoid, respectively. C Experimental broadband transcranial ultrasound focusing through human skull model from 50 kHz to 0.4 MHz without SML. D Experimental broadband transcranial ultrasound focusing through human skull model from 50 kHz to 0.4 MHz with SML. E Experimental statistical sound pressure level gain over 50 kHz to 0.4 MHz. F Line plot compares the relative pressure level through the human skull model along the transverse direction of \(r\) at frequency of 120 kHz and 0.4 MHz with and without SML.

Full size image

Furthermore, SML demonstrates its potential for enhancing both sound pressure level and spatial resolution across a wide frequency range suitable for ultrasound focusing. As shown in Fig. 5E, the error bar based on the box and whisker plot shows the statistical sound pressure level at the center focus region, which is used to indicate SPL median between the upper and lower quartiles. Compared to the transducers without SML, the measured sound pressure levels with SML increase by 13.4 dB, 13.2 dB, 13.8 dB, 11.7 dB, 14.6 dB, and 14.8 dB at frequencies of 50 kHz, 120 kHz, 200 kHz, 300 kHz, 400 kHz, and 0.5 MHz, respectively. The sound pressure level gain with SML is about 11.7 dB ~ 14.8 dB from 50 kHz to 0.5 MHz. The experimental line plot comparisons along the transverse focal plane X through the human skull model with and without SML at frequency of 120 kHz and 400 kHz are as shown in Fig. 5F. Although the focusing spot is not decreased with increasing frequency, SML still proves ability for improving spatial resolution and sound pressure levels over broad frequency band. We believe that better focusing performance could be achieved by increasing the numbers of discretization layers and reducing material attenuation. To further understand the broadband performance of the SML, broadband focusing results of SML are extended to a higher frequency range, which are shown in Fig. S8 in Supplementary Materials. This indicates that SML covers a wide frequency range of diverse applications from fish finder in ocean engineering to medical ultrasound focusing.

Ex vivo Applications in transcranial ultrasound focusing

Finally, we investigates the applications of SML for achieving broadband transmission through real human skull. The same broadband ultrasound transducer from 50 kHz to 0.4 MHz is used for applications in ultrasound transcranial focusing in background medium, as shown in Fig. 6A. Real skull bone consists of occipital bone, left parietal bone, sagittal structure, right parietal bone, frontal bone, and coronal structure, respectively, which are shown in Fig. 6B. In order to quantify the ultrasound signal properties, we extracted the signal waveforms from real skull (\(z=50{mm}\)) for both with and without SML. Skull point A is at the focal point when introducing SML, and points B, C, D, E are distributed around the focal point across parietal skull (Fig. 6A). With the existing of real human skull, ex vivo experiments show that human skull exhibits a transmission loss of 5.4 dB of sound pressure level defined by \({SPL}=20{lg}(\frac{{p}_{{Empty}}}{{p}_{{Skull}}})\), where \({p}_{{Empty}}\) and \({p}_{{skull}}\) represent the sound pressure in empty field and with human skull (Fig. 6C). To overcome this limitation of such a barrier in human skull, our introduced SML shows a 9.3 dB sound pressure enhancement through human skull (Fig. 6D) compared with non-focused field. It is worth noting that, by comparing with empty field, ex vivo experiments have shown that there is only enhancement at focal point A but no significant increasing in sound pressure level in the regions surrounding the focal points (B, C, D, E) of transcranial focused ultrasound (Fig. 6C, D). This remains consistent with the situation without the use of SML, which implies potential safety for non-focused intracranial region. The differences in sound pressure level gains between 9.3 dB and 11.7 ~ 14.8 dB arise from the acoustic impedance and geometric shape differences between real human skull and 3D printed materials; ex vivo experiments show that real human skull exhibits higher transmission loss. The relative sound pressure level in the real human skull with and without SML shows significant differences. Without SML, the two-dimensional acoustic transmission intensity profiles exhibit unfocused ultrasound with sound pressure damping across parietal region with a center position located 50 mm from the inner layer of the real human skull (Fig. 6E). However, with SML, a high-intensity focused ultrasound spot appears, providing accurate localization across the parietal region over a wide frequency range (Fig. 6F).

Fig. 6: Ex vivo transcranial ultrasound focusing applications of SML.
figure 6

A Experimental photograph of ultrasound focusing through real human skull in axial cross section, where A–E are different measured points across parietal bone. B Real human skull model including occipital bone, left parietal bone, sagittal structure, right parietal bone, frontal bone, and coronal structure, respectively. The curves indicate the signals travel through human skull without (C) and with (D) SML from the transducer to the hydrophone with the source frequency of 120 kHz. The \(t=0\) corresponded to the time at which the ultrasound reference signal was sent from the signal generator. Five different points A–E indicate the spatial variances without and with SML across human skull. Experimental broadband ex vivo transcranial ultrasound focusing through real human skull from 50 kHz to 0.4 MHz without (E) and with (F) SML.

Full size image

Discussion

We demonstrate that the advanced SML achieves tunable properties and enables broadband focusing for heterogeneous aberration layers. Theoretical analysis, material fabrication, and acoustic property characterization confirm that the micro-tungsten silicone elastomer composite system follows the model of effective medium theory under long-wavelength approximation41. Both simulations and experiments show that transmission through SML improves by 14.19 dB and achieves nearly ten times the spatial resolution through aberration layers compared to the ultrasound transducer without SML over the frequencies from 50 kHz~0.5 MHz. The ex vivo transcranial ultrasound focusing applications of SML demonstrate 9.3 dB energy enhancement and its potential in treatment and diagnosis. Therefore, SML integrates the features of soft materials14,16,20,21,22, metamaterials1,3,8,34,42,43, and gradient index theory5,6,7,36, making it soft, programmable, and tunable.

In conventional acoustic band gap materials, ultrasound waves are strongly scattered due to their wavelength being close to the size of scatters. Previous gradient index metamaterials applied periodic structures in phase control43,44,45, ultrasound focusing, and beam collimation8,9,10,11. However, these studies did not consider the high cut-off frequency, which may be limited by the lattice constant12,13,20,21,22. In this study, gradient tunable characteristics of micro-tungsten particles in soft materials allowed us to design SML for matching with aberration layers based on gradient refractive index theory. The size of micro-tungsten particles is 1000 times smaller than the minimum working frequency of 50 kHz ~ 0.4 MHz. Therefore, SML can be generally applicable as a deep-subwavelength device in geophysics, underwater ranging, and ultrasound medical imaging over the broadband range.

Our results demonstrate that silicone elastomer with micro-tungsten is a perfect candidate for broadband focusing and impedance matching. Although we explored the acoustic focusing effects on arbitrary aberration layers without multiple layers (such as skin, fat, skull, etc.), the extension of this work by using medical ultrasonic coupling gel or impedance-matching layer between SML and multi-layered aberration layers, which promises additional inspirations in imaging. Moreover, achieving precise controlled conduction and phase modulation of ultrasonic waves in soft matter is of great significance for medical diagnosis and induction therapy. SML can help surgeons accurately control the range of ultrasound beams in high-intensity focus ultrasounds. It may improve the spatial resolution of images for endoscopic ultrasonography and intraoperative ultrasound, especially in neurosurgery46. It may also open possibilities for opening the blood-brain barrier for drug delivery or sonodynamic therapy in humans using SML. In our present work, we only considered the axis-symmetrical cases; however, 3D design could be more complicated and may be fabricated by 3D acoustic hologram.

Additionally, by fast fabricating of large high-intensity focus ultrasound SML-based HIFU devices, ultrasound can be manipulated to accurately regulate neuro and tumor targeted ablation. While the current work presents an advanced soft metamaterial-gradient index method to overcome the barriers of ultrasound wave transmission through aberration layers, commercial ultrasound phased arrays can produce focused wave by multi-elements like the metalens with single aperture in this work. Effective refractive index along \({{\boldsymbol{r}}}\) direction based on eikonal equations can be achieved to eliminate reflection along axial direction of human skull (Fig. S9). When comparing curved focus lens and SML for the fair comparison, SML can accurately focus ultrasound at expected region and does not cause as much aberration as curved focus lens (Figs. S10–S11). We are also looking forward to the next step of applying our micro- and nanofabrication technology to clinical medical and phased array imaging quality enhancement. Overall, SML as an advanced soft materials-metamaterials-gradient index fabrication scheme may open a new door to medical ultrasound applications.

Methods

Arbitrary phase coding theory

In the complex medium, the acoustic wave equation in time-harmonic form can be written as

$$\nabla [{\rho }^{-1}({{\boldsymbol{r}}})\nabla p({{\boldsymbol{r}}},t)]=\frac{1}{\kappa ({{\boldsymbol{r}}})}\frac{{\partial }^{2}p({{\boldsymbol{r}}},t)}{\partial {t}^{2}}$$
(7)

where \(\kappa ({{\boldsymbol{r}}})\) is the bulk modulus, considering the form solution \(p({{\boldsymbol{r}}},t)=A({{\boldsymbol{r}}}){e}^{j(\omega t-k({{\boldsymbol{r}}})\psi ({{\boldsymbol{r}}}))}\), \(A({{\boldsymbol{r}}})\) is the space variance amplitude, \(k={k}_{0}n({{\boldsymbol{r}}})\) is the non-uniform wavenumber with the function of refractive index \(n({{\boldsymbol{r}}})\), \({k}_{0}\) is the wavenumber in free space, \(\omega\) is the angular frequency. By introducing the equation \(\varphi ({{\boldsymbol{r}}})=n({{\boldsymbol{r}}})\psi ({{\boldsymbol{r}}})\), the form solution \(p({{\boldsymbol{r}}},t)=A({{\boldsymbol{r}}}){e}^{j(\omega t-{k}_{0}\varphi ({{\boldsymbol{r}}}))}\) is introduced into the wave Eq. (7), the derivative equation should be

$$\frac{1}{\rho }{\nabla }^{2}(A{e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})})=\frac{1}{\kappa }(-{\omega }^{2})(A{e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})})$$
(8)

by expanding the first gradient operator on the left-hand side, the equation can be written as

$$\frac{1}{\rho }\nabla (\nabla A{e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})})+A(-j{k}_{0}){e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})}\nabla \varphi ({{\boldsymbol{r}}})=\frac{1}{\kappa }(-{\omega }^{2})(A{e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})})$$
(9)

Next, the second gradient operator can be expanded, and the equation can be further expressed as

$$\frac{1}{\rho }({\nabla }^{2}A{e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})}+\nabla A(-j{k}_{0}){e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})}\nabla \varphi ({{\boldsymbol{r}}})+\nabla A(-j{k}_{0}){e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})}\nabla \varphi ({{\boldsymbol{r}}}))+$$
$$A(-j{k}_{0})((-j{k}_{0}){e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})}\nabla \varphi ({{\boldsymbol{r}}})\nabla \varphi ({{\boldsymbol{r}}})+{e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})}{\nabla }^{2}\varphi ({{\boldsymbol{r}}}))=\frac{1}{\kappa }(-{\omega }^{2})(A{e}^{-j{k}_{0}\varphi ({{\boldsymbol{r}}})})$$
(10)

combining the real and imaginary parts of the above complex analytic equation, the imaginary part satisfies:

$$\frac{2\nabla A}{A}\cdot \nabla \varphi ({{\boldsymbol{r}}})+{\nabla }^{2}\varphi ({{\boldsymbol{r}}})=0$$
(11)

the real part satisfies:

$$\frac{{\nabla }^{2}A}{A}-{k}_{0}^{2}\nabla \varphi ({{\boldsymbol{r}}})\cdot \nabla \varphi ({{\boldsymbol{r}}})+{k}^{2}=0$$
(12)

under the high-frequency approximation\({\nabla }^{2}A/A < < {k}^{2}\), the following relation should be demanded:

$$\frac{d}{{ds}}\nabla \varphi=\nabla n({{\boldsymbol{r}}},z)$$
(13)

where \({ds}=\sqrt{d{{{\boldsymbol{r}}}}^{2}+d{z}^{2}}\), therefore the equation for achieving arbitrary phase modulation using refractive index can be expressed as

$${\psi }_{t}({{\boldsymbol{r}}},z)={k}_{0}{\int }_{0}^{z}n({{\boldsymbol{r}}},z){dz}$$
(14)

under the polar coordinate system, arbitrary phase modulation can be achieved using the effective refractive index and can be expressed as:

$${\psi }_{t}({{\boldsymbol{r}}},z)={k}_{0}{n}_{{eff}}({{\boldsymbol{r}}})z$$
(15)

Through a meticulous derivation process, it becomes evident that the phase of the sound pressure in the eikonal equation is solely contingent upon the refractive index \(\frac{d}{{ds}}\nabla \varphi=\nabla n({{\boldsymbol{r}}},z)\).

Skull bone modeling using computed tomography scanning

Computed tomography scanning of a skull model (15-years-old female) was performed at the Radiology Department of Affiliated Zhongshan Hospital of Xiamen University. The scan was conducted in helical mode with a slice width of 0.625 mm. All images were acquired using a power setting of 60 keV and a matrix size of 512 × 512. Subsequently, the skull model was 3D-printed and bisected along the sagittal suture. For imaging purposes, the temporal region of the skull was selected due to its relatively thin nature, rendering it an ideal candidate for generating a suitable acoustic aberration layer for ultrasound focusing. The ex vivo transcranial experiments in real human skulls have been reviewed and approved by the Ethical Committee of the Clinical Research Ethics Committee of the First Affiliated Hospital of Xiamen University.

Determination of the acoustic impedance function of SML

Tungsten microparticles with varying weight percentages \({\phi }_{m}\) were dispersed in the silicone elastomer substrate to achieve the refractive index function depicted in Fig. 1, where the weight percentages can be described as

$${\phi }_{m}=\frac{\varphi {\rho }_{2}}{{\rho }_{1}+\varphi {\rho }_{2}}$$
(16)

\(\varphi\) is the volume fraction of silicone elastomer-tungsten composite, \({\rho }_{1}\) and \({\rho }_{2}\) represents the density of silicone elastomer and tungsten microparticle, respectively. The minimum size of micro-tungsten powder is approximately 3000 times smaller than the smallest incident wavelength used in our experiments (3 mm at 0.5 MHz in water). The physical implications of the effective density and sound speed of SML could be understood from the point of view of the effective medium theory. The effective Lame coefficient and shear modulus are related as follows24:

$${\lambda }^{*}=\frac{(M-1){G}^{*}+(M+1){G}_{0}+{\lambda }_{0}}{1-M}$$
(17)
$${G}^{*}=\frac{{G}_{1}(1+\varphi )+{G}_{0}(1-\varphi )}{{G}_{1}(1-\varphi )+{G}_{0}(1+\varphi )}{G}_{0}$$
(18)
$$M=\frac{[{\lambda }_{1}+{G}_{1}-({\lambda }_{0}+{G}_{0})]\varphi }{{\lambda }_{1}+{G}_{1}+{G}_{0}}$$
(19)

The densities of silicone elastomer and tungsten used were \({\rho }_{0}={1013.7{\mbox{kg/m}}}^{3}\) and \({\rho }_{1}={19300{\mbox{kg}}/{\mbox{m}}}^{3}\), respectively. The Lame coefficient of silicone elastomer and tungsten used were \({\lambda }_{0}\) = 0.11 GPa and \({\lambda }_{1}\,\)= 20.19 GPa, respectively. The shear modulus of silicone elastomer and tungsten used were \({G}_{0}\) = 6.14 kPa and \({G}_{1}\) = 156 GPa, respectively. Fig. S2 demonstrates the effects of weight percentage \({\phi }_{m}\) on the effective longitudinal sound speed, effective transverse sound speed, effective density, acoustic refractive index, and acoustic impedance, respectively. The parameters are juxtaposed against the silicone elastomer and tungsten for comparison. With the increase of \({\phi }_{m}\), the effective density increased from \({1013{\mbox{kg}}/{\mbox{m}}}^{3}\) to \({19300{\mbox{kg}}/{\mbox{m}}}^{3}\), the acoustic refractive index increased from 1.4 to 3.2, and the acoustic impedance covered the range from \({10}^{6}{{\rm{Ns}}}/{m}^{3}\) to \({10}^{8}{{\rm{Ns}}}/{m}^{3}\), respectively. Based on \({\phi }_{m}=\frac{{m}_{2}}{{m}_{1}+{m}_{2}}\), the effect of weight percentage on the acoustic sound speed and density could be obtained. Consequently, the sound speed and density profile in SML in Fig. 2D could be obtained.

Acoustic field simulation of the SML model

Finite element simulation was employed to model the pressure acoustic scenario. The acoustic sound speed of SML is defined as \(c=\omega /k\), where \(\omega\) is the angular frequency. Within a water environment, we assume that only longitudinal waves propagate without attenuation (the attenuation coefficients of SML have been experimentally measured), which can be expressed by the equation

$$\frac{1}{{\rho }_{0}{c}_{s}^{2}}\frac{{\partial }^{2}p}{\partial {t}^{2}}+\nabla \cdot \left(-\frac{1}{\rho }\nabla p\right)=0$$
(20)

where \(p\) is the sound pressure, \({\rho }_{0}\) is the density, and \({c}_{s}\) is the sound speed. A variable density is included since the impedance matching conditions demand the varying density along the radius direction of SML. When it comes to skull structures, both shear and compressional waves should be considered, an can be expressed as

$$\rho \frac{{\partial }^{2}v}{\partial {t}^{2}}=(\lambda+\mu )\nabla (\nabla \cdot v)+\mu {\nabla }^{2}v$$
(21)

where v is the speed vector and λ and μ are the two Lamé constants, characterizing compression and shear moduli, respectively. Factoring in the effect of viscous thermal properties across various frequencies within the silicone-tungsten particles system, the measured sound attenuation coefficient is considered for each layer of the SML. This adjustment aids in simulating the authentic behavior of soft metamaterials. The specific sound attenuation coefficients are shown in Supplementary Material 7.

Mold design process for SML

To fabricate SML, molds were designed in Solidworks and 3D printed in PLA. To achieve seven discrete layers of different micro-tungsten weight percentage elastomers, we designed a 2-piece fit mold that consists of an outer ring (white) and an inner orbit (black). The 2-piece fit model allowed for the fabrication of a seven-layer SML after two different curing phases. The molds are separately printed and snapped together. The inner orbit is removed after the first 3 discrete layers of the mixture (red) are poured in and allowed to cure. The outer ring is then removed after the rest of the layers are poured in (blue).

Material and fabrication of SML

EcoflexTM 00-30 (Smooth-On) was used as the substrate for making SML with micron tungsten powder as scatterers. EcoflexTM 00-30 with one part A, one part B, silicone thinner and different mass fractions of tungsten powder were mixed in a container and fully stirred at room temperature. The mixture was placed into a vacuum chamber (DZF-6020, JINGHONG) to defoam. Then our prepared mixture was poured into the 3D-printed mold and put in oven at 60 °C for 45 minutes until it was solidified. After cooling for 20 minutes at room temperature, SML was removed from the mold. SML was sectioned into 7 discrete layers along the \({{\boldsymbol{r}}}\) direction, with each layer formed by mixing soft silica elastomer substrate and tungsten powder (99.8% metals basis, 1–5 \(\mu m\); Aladdin) at different weight percentages. The weight percentages of tungsten powder from the inner layer to the outer layer are 67.8%, 56%, 50%, 34.5%, 21.5%, and 6% respectively. According to gradient refractive index functions, the corresponding sound speed, density, and refractive index in different layers of the designed SML with weight percentage from 6% to 67.8% are shown in Table S3.

Determination of sound speed and acoustic Refractive Index of SML

The acoustic impedance is equal to the product of sound speed and density, which was obtained by ultrasound material experiments. To determine the refractive index \(n\) of the investigated micro-tungsten hybrid silicone layer, we measured the sound speed through insertion substitution method. The thickness of each sample is fixed to 5 mm, which is about 6 times smaller than the largest incident wavelength used in our experiments (30 mm at 50 kHz in water), and this process ensures the sample can be sub-wavelength thickness. Micro-tungsten particles distributed from 1-5 \(\mu m\) have been applied as sub-wavelength tunable powder to tune the effective sound speed and density of silicone elastomer. The minimum size of micro-tungsten powder is approximately 3000 times smaller than the smallest incident wavelength used in our experiments (3 mm at 0.5 MHz in water). Ultrasound pulses with frequency ranging from 0.5 MHz to 1 MHz were emitted and detected by using two pairs of broadband ultrasound transducers (transmitter and receiver) with a diameter of 30 mm. One pair of ultrasound transducers is under the center frequency of 0.75 MHz, another pair of ultrasound transducers is under the center frequency of 0.9 MHz. A signal generator (AFG 31000 SERIES; Tektronix) was used to generate the broadband pulse signal and the received signal data is then A/D converted by a digital oscilloscope (MDO32; Tektronix). When the propagation time difference of pulse waveform received by with and without SML, the transmitted signals shifted on the time-delay axis, allowing us to directly obtain the sound speed \(c\). Therefore, the sound speed of the SML sample can be calculated by

$$c=\frac{d{c}_{w}}{d+{c}_{w}\varDelta t}$$
(22)

and the acoustic refractive index

$$n=\frac{c}{{c}_{w}}$$
(23)

where \(d\) is the thickness of the sample, \(\varDelta t\) is the time difference of pulse waveform received by with and without SML, and \({c}_{w}\) is the sound speed of water. The measured sound velocities, densities and acoustic impedance are shown in Table S2. The attenuation coefficient can be calculated by

$$\alpha=\frac{1}{d}\left[20 \, {lg}\frac{{A}_{w}}{A}-20 \, {lg}\frac{{\left(Z+{Z}_{w}\right)}^{2}}{4Z{Z}_{w}}\right]+{\alpha }_{w}$$
(24)

where \({A}_{w}\) and \(A\) is the amplitude of water and soft metamaterial samples, \({Z}_{w}\) and \(Z\) is the characteristic impedance of water and soft metamaterial samples, respectively, and \({\alpha }_{w}\) is the attenuation coefficient of water.

Underwater acoustic focusing experiments of SML

High-frequency plane piston generator with the dimension of 12 cm and 125 kHz center frequency is customized from China Shipbuilding Heavy Industry Corporation (CSSIC), piezoelectric material particle splicing process with connected positive and negative terminals in parallel has been used. Send voltage response is characterized by BK8103 over distance of 1.50 m. Testing depth is 0.5 m, ambient water temperature is 10 degrees Celsius, and testing distance is 1.5 m, respectively. The calibrated frequency response, far-field directivity, sends voltage response, and received voltage response are shown in Fig. S7, respectively. The customized bracket for transducer and SML is made by metal modeling. The relative distance between the transducer and SML is strictly controlled, which is the same as that of numerical simulations. Since the phase shifting of sound waves in different regions of the skull model are very different, the temporal bone area of skull specimens was placed 1 mm away from the front surface end of SML, with only a thin dielectric layer in the middle. Ultrasound transmission experiments were performed in a water tank with dimensions of 2 m by 1.2 m by 0.8 m. The 3D mobile motor with a minimum accuracy of 1 micrometer has been used for sound field scanning experiments. Changing the input resistance value makes the input voltage of the transducer change from 5 V to 170 V. The five-cycle tone burst signal is generated using a waveform generator (AFG 31000 SERIES; Tektronix) with a frequency of 50 kHz and 0.5 MHz and with a trigger interval of 165 ms. A broadband needle hydrophone (NH1000; Precision Acoustics Ltd; Sensitivity 1330 mV/MPa at 0.5 MHz) with an acoustic center diameter of 1 mm is used to record acoustic signals in the scanning areas using motorized linear stages. The signals are acquired via a digital oscilloscope (MDO32; Tektronix) on a computer.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.