Introduction

Neural networks (NN) have shaped the landscape of machine intelligence by revolutionizing the way computers perform functions and make decisions1. Such advances are certainly underpinned by the performance improvements of silicon-based digital processors over the past few decades2. Nevertheless, a noticeable disparity has emerged between the capability to process larger volumes of data in a more efficient and faster manner and the limited scalability of digital circuits in the current era3,4. This unbalance has consequently echoed the interest of engineering analog optical computers under the umbrella of non-von Neumann architecture5,6,7,8. Through physically integrating data processing and storage, breaking down the barrier between hardware and software, and harnessing the high parallelism, energy efficiency and low latency enabled by optical waves, ubiquitous neuromorphic photonic frameworks are invented as special-purpose accelerators9,10,11. For instance, the large bandwidth of photonic along with maturing fabrication techniques is exploited to demonstrate an in-memory photonic tensor core capable of convolutionally processing images12,13,14,15, large-scale diffraction photonic neural networks to achieve multi-layer perceptrons16,17,18,19, and on-chip large coherent photonic networks to efficiently realize linear matrix-vector multiplication20,21. Beyond these linear operations, nonlinear activation functions are gaining efforts as well, hoping to implement deeper NN architectures in photonic22. Critically, though these findings suggest that discriminative optical NNs with classification capabilities are within reach, photonic generative NNs remain largely unexplored.

Generative models, such as ChatGPT, are designed to learn and replicate the abstract patterns or structures hidden in the data and are expected to produce novel and realistic outputs after optimization23,24. These models have supported diverse applications including image synthesis, text generation, data augmentation among many others25,26,27,28, and have become a milestone in the pursuit of artificial general intelligence. Unlike training discriminative networks, which comparably concentrate on learning boundaries between classes within a dataset, many generative models center on learning the distribution of the classes and usually require an additional data sampler. Sampling is crucial here because it determines the model’s ability to generate new data points aligning with the original data statistics29. The need for a data sampler, along with complicated training, results in the challenging photonic implementation of such generators. Notably, a pioneering design of a photonic generative network incorporates a physical random number generator as the data sampler and phase-change metasurfaces as computation weights. Though inspiring, the sampler is strictly required to convert random optical noises as digital voltages to realize randomness, while optoelectronic NN is heavily established on a 2 × 2 tensor core. The switch among domains of the sampler and the network greatly hinders an efficient and hardware-consistent implementation. The limited scale of computation weights constrains the generator’s expressivity, allowing it to generate only a single digit30. Another interesting approach suggests using a biased optical parametric oscillator as a noise sampler, although most computations are still carried out on digital platforms31.

In this work, we exploit the multiple light scattering as a natural noise source and present a scalable photonic diffractive generator (PDG) with 100 × 100 programmable weights capable of generating multiple digits’ images to achieve over 108 optical computing operations. By pursuing the spatial parallelism of light, we break the boundary between the optical noise sampler and the PDG thus demonstrate a more powerful generative network than achieved previously. Our PDG elaborately manipulates the spatial modes of light through diffractive phase layers coupled with free-space propagation. Regarding the noise source, we experimentally collect the scattering responses of a disordered medium at many spatial illuminating positions. Prior to this, we design two encoding strategies (random encoding and physics-aware encoding) that compress images to the illuminating position coordinates, which serves as the physical latent space of the noise sampler. The obtained speckle patterns and images are formed as pairs to optimize subsequent photonic generative NN, assisted by another digital discriminative network using generative adversarial network (GAN) framework. After training, through experiments and simulations, we validate PDG can produce clear and diverse images with different complexities thanks to the proposed encoding methods and scalable NN architectures. Last, we demonstrate that the generator can achieve image interpolation by simply varying illumination position of the incident light without any further training or processing.

Results

Overall framework

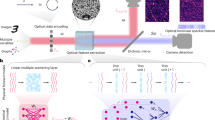
A schematic of our framework is illustrated in Fig. 1. In the proposed GAN, there are 3 essential blocks including a photonic noise sampler, a photonic diffractive generator G and a digital discriminator D (Fig. 1A). Generally, the generator takes a noise input to output a candidate ‘fake’ image o, and the discriminator endeavors to distinguish between ‘fake’ and ‘real’ data. During training, these two models engage in adversarial interactions and are believed to reach a Nash equilibrium state upon convergence. Subsequently, the generator is ready to produce new vivid data for inference. To achieve random noises in hardware, we exploit multiple light scattering in a disordered medium (ground glass) with inherent randomness (Fig. 1B). Such a complex process involves numerous interference events that give rise to a speckle pattern and can be described by a linear transmission matrix with Gaussian i.i.d elements.

Fig. 1: General workflow of Photonic Diffractive Generator (PDG).
figure 1

A An ordinary GAN architecture consists of three main components: a random vector sampling source, a generative network and a discriminative network. B Photonic random signal source. A CW laser illuminates the positions of optical disordered media for generating random input signals. C Internal working module of the PDG. The input optical signals pass through a well-engineered architecture with unified computing elements called the Diffraction Processing Unit (DPU). D Two specific encoding strategies for photonic random signal generation. Left subplot: images are arbitrarily mapped to different illumination positions without any prior knowledge. Right subplot: random images are preprocessed by a physics-aware encoder, and then mapped with certain illumination positions. E Detailed experiment configuration of the DPU. L1 and L2, relay lenses; SLM-A amplitude-only spatial light modulator; SLM-P phase-only spatial light modulator. The input laser is first optically encoded by SLM-A, and then undergoes photonic matrix computation, which is generated from phase modulation by SLM-P together with optical free space propagation. The detection process can then be considered as a quadratic non-linear activation function. The entire DPU configuration functions as a single layer perceptron in machine learning.

Full size image

Though this scattering effect is seemingly detrimental for applications like imaging, the intrinsic statistical properties can be tamed as an appropriate natural random noise generator, especially considering that GANs are probabilistic models that learn to generate samples by capturing the underlying probability distribution of the training data. But to use this noise as a meaningful input to the generator, pre-determined link between certain speckle patterns (noise input) and images (output) is required before training.

We therefore propose two encoding methods, i.e., random position encoding and physics-aware position encoding (Fig. 1C). For both of them, the lateral illuminating positions v = (x, y) of the scattering medium are essentially interpreted to the coordinates of latent parameter space of physical noise sampler. Given v, a deterministic noise vector z = S(v) reshaped from a two-dimensional speckle pattern can be acquired. The difference between them is that the former associates an image with a random position v while physics-aware encoding exploits a trained encoder to designate an image to the position coordinates (see Supplementary Text 4). To pursue the rich spatial modes of speckle patterns, we implement the generative part adopting diffractive deep neural networks for the end-to-end hardware consistency and for the sake of a potential all-optical implementation (Fig. 1D). The combination of multiple programmable optical layers used for light field modulation and fixed light propagation used for information mixing delivers rich computations and has empowered many applications. In experiments, we set up a reconfigurable optoelectronic block (known as diffractive processing unit) with off-the-shelf components, e.g., spatial light modulators (SLM) and cameras (Fig. 1E). For each unit, the incident beam first undergoes computational amplitude and phase modulations and then propagates in free space, after which the extracted feature is recorded by a camera, which can be considered as a quadratic nonlinear activation function on the complex optical field. By introducing more analog-digital and digital-analog conversions, such a programmable setup allows us to attain comparable or even better results with diffractive deep NNs. In a nutshell, the overall inference phase can be formalized as o = G(S(v)). We present an additional comparison between a digital GAN and PDG in Supplementary Fig. 6 to further elucidate the overall framework of our system.

Photonic noise sampler

To explain the random position encoding and physics-aware encoding in detail, we present comparison results in Fig. 2. Intuitively, a focused coherent laser illuminates a specific part of the scattering medium denoted by coordinates v = (x, y) and generates a speckle pattern as a result. To train the generator, an illuminating position, a resulting speckle pattern and a ground-truth image are bonded as pairs. To acquire adequate pairs, we scan across the medium by modulating incident light with various wavevectors (see “Methods”). Stated differently, the speckle patterns corresponding to these positions are fed as generator input and the paired images are considered as ground truths. For random encoding, we map images from a given dataset arbitrarily to these positions. Instead of random designation, physics-aware encoding aims to transform similar noise inputs to similar image outputs in a logical way. To this end, we utilize another digital variational autoencoder (VAE) to firstly compress an image to a latent space - a 2-dimensional vector representing a position coordinate - and map the image to the resultant speckle (see Fig. 2A and details in Supplementary Text 4). Thanks to memory effect32, when incident light is tilted or shifted a bit, the speckles tend to be correlated or slightly changed, which more or less corresponds to the smooth latent space of the trained encoder (thus ‘physics-aware’). An experimentally noise intensity pattern is shown in Fig. 2B. The fitted probability density function well approximates a Rayleigh distribution with experimental errors, as a result of Gaussian distribution of real and imaginary elements (see more theoretical discussions in Supplementary Text 1). The final mapping from the physics-aware encoder used in experiments is presented in Fig. 2C. As expected, the smooth trend of images are preserved by the encoder, manifested by the fact that neighboring images are changing gradually.

Fig. 2: Physics-aware encoding method.
figure 2

A Schematic graph of physics-aware encoding. A digital VAE is tuned in advance upon certain dataset. The encoder of the trained VAE first maps images to two-dimension latent space which corresponds to real-world illumination position (x, y). B Position-dependent speckles. Left: typical speckle intensity profile. Right: statistical histogram. The intensity of generated speckles follows Rayleigh distribution. C, D The encoding results for input images (C) and output speckle (D) are illustrated. E Training logs of PDG for two enconding strategies. Both of them are trained under the same environment and hyperparameters. Inset plot: one typical PDG output '0' and '9' for different methods.

Full size image

To compare them, we simulate two four-layer PDGs respectively. We use Pearson correlation coefficient (PCC)33,34 as image quality metric. The metric is a part of the overall training loss function, which evaluates the image quality of synthesized data to ground truths. As shown in Fig. 2E, the generator trained with physics-aware encoder exhibits higher baseline, i.e., higher quality images than that of random encoding (see inset Fig. 2E) with the improvement of average PCC as δPCC  = 0.151.

Photonic diffractive generator

To establish advanced generative network architectures in experiments, we implement cascaded and parallel diffractive layers built on diffractive processing unit respectively (Fig. 3). The cascaded architecture corresponds to the deep diffractive NN achieved previously17,18, in which the output from one layer is fed into the next layer. In comparison, inspired by the broad learning approach in machine learning, we propose a purely parallel architecture of photonic NN (Fig. 3B). It extracts different features individually by each layer and then synthesizes all features together by a weighted summation to formalize the network output. In this work, we exploit in-silico co-training methods for both photonic generator and digital discriminator and perform the experimental inference phase for the photonic generator. The experimentally-implemented phase plates are shown in Fig. 3C. With the deliberated architecture and physic-aware encoding method, the PDG is demonstrated to experimentally generate all categories of hand-written images from MNIST (see Supplementary Fig. 4 for sequence diagram of timing control). Due to the imperfections in experimental setup and absence of phase calibration, we applied precise experiment adjustment and adaptive fine-tuning training process to reproduce the simulation results experimentally (see details for experiment adjustment and adaptive training in Supplementary Text 3). Additionally, to enhance the image generation quality, we explore the use of a linear digital layer instead of optical readout from the camera. This linear layer is a trainable weight matrix implemented on digital platforms that projects features from the camera plane to the final desired output. A similar strategy has been widely explored to enhance the performance of optical computing hardware without imposing significant burdens on digital hardware35,36,37. As expected, this greatly increases the image quality thanks to the high precision operation of digital computers (Fig. 3D). We summarize the experimental results in a scatter plot in Fig. 3E. Besides the generated ‘0’ and ‘1’ images in Fig. 3D, we provide other 8 experimentally generated handwritten digits in Supplementary Fig. S9.

Fig. 3: PDG architecture and generation of handwritten numbers.
figure 3

A, B Cascaded (A) and parallel (B) architecture of PDG. C The designed phase plates for each DPU layer. Upper and lower rows correspond to cascaded and parallel architecture, respectively. D Two selected handwritten number ('0' and '1') generation results. Cas. + Opt., cascaded architecture with optical readout; Cas. + Dig., cascaded architecture with digital readout; Par. + Opt., parallel architecture with optical readout; Par. + Dig., parallel architecture with digital readout. E Quantitative evaluation of handwritten number generation on 200 chosen experiment results.

Full size image

Furthermore, to investigate the capability of producing images for the proposed PDG, we challenge it with more complex datasets including Fashion-MNIST38 and EMNIST39 in simulations. As illustrated in Fig. 4, a firm conclusion is that digital readout layer can improve the image quality while which architectures provide better results is more subtle and can depend on the target datasets. We therefore posit that sophisticated hybrid architectures including parallel and cascaded submodules could be optimized for a best task-specific performance, as recently demonstrated in photonic discriminative networks. By adding this shallow digital neural network, the performance of PDG model will be largely improved. Meanwhile, this hybrid architecture is also computational efficient. Our hybrid model can achieve performance comparable to that of a purely digital model while reducing the amount of digital computations by a factor of 10 (detailed demonstration is shown in Supplementary Text 2). Besides producing images, image interpolation is another fascinating generative task which has been used in data augmentation, artistic exploration, or semantic manipulation. Specifically, image interpolation realized by GAN is mentioned as image-to-image translation. GANs are learned to map an input image from one domain to a corresponding output image in another domain40. It aims to create new data points that lie between two or more existing samples smoothly and continuously, in other words, leading to the interpolation of latent sampling space. For example, if a generative model has been trained on two different face profiles, selecting an appropriate trajectory between these corresponding inputs allows the generation of an intermediate turning-face process. For the photonic implementation, thanks to the memory effect of scattering media and the proposed sampling method, we can realize image interpolation conveniently by just scanning from one input position v1 = (x1, y1) to another position v2  = (x2, y2). The typical interpolation results on the MNIST dataset41 are shown in Fig. 5B. In this demonstration we employ a linear scanning of the scattering media from v1 to v2, while in practice, one could determine an optimal path connecting the input instances in the representation space.

Fig. 4: Simulation results of PDG trained on Fashion MNIST and EMNIST-letter dataset.
figure 4

A, C Three selected simulation results of PDG on Fashion MNIST (A) corresponding to 'sneakers', 'shirts', 'trousers', and on EMNIST (C) corresponding to 'S', 'e', 'w'. B, D Statistics analysis of PDG performance over 4096 synthesized images on Fashion MNIST (B) and EMNIST (D). The height of bar represents the mean PCC, while the error bars denotes the standard deviation (STD) of PCC.

Full size image
Fig. 5: Image interpolation by scanning the illumination position of scattering media.
figure 5

A The schematic graph of image interpolation through scanning. B Typical results of image interpolation. The scan of illumination position from (x1, y1) to (x2, y2). The images gradually change from '9' to '0', from '9' to '7' and from '0' to '1'. Except for the first and last images, all intermediate images are new generated ones.

Full size image

Discussion

We have demonstrated that the photonic generator with proposed sampling methods can generate images in a variety of settings. In this work, we provide a compelling case for implementing photonic generative network by effectively communicating the SLM and the camera via a computer which allows for flexible layer scaling in a hardware-efficient manner, while the fully-optical approaches can be potentially implemented via diffractive deep neural network with improved energy efficiency and system latency in future work. Here in previous section, we take PCC as an image metric for evaluating the quality of generated images. However, PCC could only capture the linear relationship between generated images and ground truth. In order to further evaluate the quality and diversity of our generated data, we calculate the Frechet Inception Distance between two datasets, and the results are shown in Supplementary Fig. 8. For both the cascaded and parallel architectures, we perform ablation study on the layer number of the network (see Supplementary Fig. 3). As expected, more layers lead to performance improvement for both of them, which can attribute to the larger field of view (FOV) of the whole optical computing system42. Though cascaded architectures reach a higher baseline than parallel counterparts from this simulation study, in realistic experiments, the system errors aggregates more severely for cascaded networks, which can result in the model collapse. Indeed, each architecture has its own advantages and disadvantages. Beyond this performance differences, cascaded networks are more physically interpretable as the speckle images are processed and transformed gradually layer-by-layer, while for parallel architectures, intermediate feature maps are still speckle-like and are lack of intuitive physical meaning. But the parallel PDG could be suitable for parallel timing control to significantly improve the data throughput rate.

Inspired by the pipeline programming scheme widely used in field programmable gate arrays (FPGAs)43 and graphics processing units (GPUs)44, we can divide the total computing process into two modules: optoelectronic operation and host computer operation. Both of these modules are executed simultaneously and synchronized by system clock and mutual exclusion (Mutex) with the help of multi-thread programming scheme (see schematic details of parallel timing control in Supplementary Fig. 7). For example, for a four-layer parallel PDG with digital readout layer, time consumption of two modules including computation and device communication tends to be at the same scale with 97.9 ms and 85.4 ms respectively, indicating that the parallel accelerating programming scheme will positively double the output data rate for PDG.

Though the noise input can be straightforwardly obtained by illuminating the scattering media, the scanning range is constrained by the system aperture experimentally. Moreover, the scanning step cannot be too small, especially not smaller than the speckle size, otherwise two adjacent optical speckles might be too similar due to the memory effect to be distinguishable by the following generator. Consequently, there exists an upper bound for the number of independent physical noise sources that can be sampled, which is also limited by the diffraction limit (a detailed mathematical analysis is provided in Supplementary Text 5). This upper bound can affect the sampling process for PDG, especially when dealing with complex datasets such as ImageNet. A possible solution to enhance the sample capacity is to replace the phase gratings used for scanning with specially designed grayscale patterns. Unlike the previous binary-like scanning method, this grayscale wavefront shaping strategy offers additional channels for noise sampling. Additionally, it would be interesting to explore the potential advantages of using nonlinear speckles as noise37. Based on theoretical investigations into the random distributions of speckle patterns, while they are effective as noise inputs for formulating a photonic generative model, it is important to note that the speckle patterns still exhibit pseudo randomness due to the deterministic nature of the transmission matrix. Exploring truly random inputs, such as those generated by active random lasers45, could be an interesting direction for future research.

Our PDG is open to integrating other deterministic photonic neural networks to construct a full GAN structure in future studies46. Similarly, the physics-informed encoding model that facilitates training of the photonic generator could potentially be replaced by a photonic neural network in the near future, as it is a relatively shallow network. Based on the physics-informed encoding method, our PDG model is not just a photonic counterpart of a simple digital generator, but a part of a VAE-GAN combined model (see additional comparison between digital VAE-GAN and PDG in Supplementary Fig. 6). Such combined architecture is an important fraction in recent generative model researches47,48, whose main idea is to replace the conventional element-wise error loss by such competing training strategy. Meanwhile, the front-end VAE provides a relative smooth parameter space for back-end GAN.

For the whole generator, we use a rough-tuned VAE-encoder to generate two-dimensional coordinates, and then randomly project them to the high-dimension complex signals by the optical scattering media. These noisy speckle patterns are finally processed by photonic NN. In other words, PDG mathematically acts as a conventional complex GAN but harnesses a physics-informed encoding method based on prior knowledge from the dataset. However, we here just arbitrarily map images with certain spatial positions without considering any feedback knowledge of follow-up networks. This algorithm does not seem to reach a global optimum for the whole encoding task. To attain a global optimum, we need to incorporate the VAE into the training process collectively. Due to the non-differentiability and instability of scattering-media-based physical systems, it is hard to execute accurate backpropagation model for a sufficiently long time. Nevertheless, constructing a similar but more stable system can be achieved through more precise experimental controls and additional averaging of measurements in future studies37,49. In addition, recent studies have proposed several adaptive solutions to tackle physical systems with noise, such as forward-forward algorithm50, Bayes optimization51, dual adaptive training52, and physics aware training53. By utilizing above in-situ in-silico hybrid optimization algorithms, a joint training scheme could enhance the performance of PDG.

In summary, we have demonstrated a photonic noise sampler and a photonic diffractive generator to facilitate the implementation of generative networks in GANs. Through experiments and simulations, we substantiate that our system is suitable at producing meaningful images and seamlessly interpolating to novel data. Notably, we design two noise sampling methods to solve the generator training problem and to enhance the overall generation performance. Our current PDG platform suffers from system imperfections and low signal-to-noise ratio, limited resolution of modulation devices, and inability to generate complex real-world images as ImageNet. However, our proposed PDG exhibits the potential of scalability and flexibility among various datasets, in the future, by improving the precision and scale of photonics components, strengthening the signal-to-noise ratio, developing more sophisticated integration between digital and photonics parts, and refining the algorithms that allow for complex tasks execution in this architecture, optical or optical-electrical hybrid PDG platform could be capable of generating and processing complicated tasks like ImageNet in a fast and effective manner. Furthermore, it also stands as an effective example with other promising applications in image synthesis, anomaly detection and data augmentation in the realm of generative models.

Methods

Experimental setup

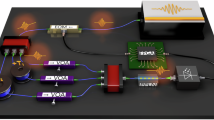
The detailed experimental setup to realize the PDG is illustrated in Supplementary Fig. 1 (a). We construct the noise sampler by employing a phase-only SLM (SLM-P1, 6μm pixel pitch), an objective lens (NA = 0.3), and a scattering medium (LBTEK, DW110-220). We form the DPU by utilizing an amplitude-only SLM (SLM-A, 8μm pixel pitch UPOLabs, HDSLM80RA), a phase-only SLM (SLM-P2, 8μm pixel pitch, UPOLabs, HDSLM80R), and a sCMOS camera (PCO panda 4.2). We configure L3, L4 and L3, L6 as two 4f systems with two different apertures (AP1 and AP2). These two apertures are used for optical path selection. To direct light through path1, we load a phase grating with grating period (Δ1,0). The modulated light is filtered by AP2 with only first-diffraction entering while being blocked by AP1. Equally, to direct light through path2 for speckle generation, we will load a new phase grating with (Δx,Δ2 + Δy), where Δx and Δy are scanning phase gratings and Δ1 ≈ Δ2 ≈ Δx ≈ Δy. This allows us to choose the desired optical paths by simply adding corresponding phase masks on SLM-P1. It’s worth noting that not using a galvanometer for scanning operation is because that a single galvanometer can hardly scan with such a small scanning step precisely. Though one could apply a telescope system at the output end of the galvanometer to enhance the angular resolution of scanning, it is challenging to incorporate a galvanometer system with the follow-up experiment devices. For cascaded PDG architecture, we first direct the light through path2 and enter DPU for front-end computing. Then, we change the phase mask of SLM-P1 to let the light pass through path1, leading to a basic DPU functionality for the remaining layers. For cascaded DPU workflow, the signal is captured with the camera in the previous layer and then reproduced with SLM-A in the later layer. Specifically, the feature map of the penultimate layer can be fed into a shallow digital layer rather than the direct camera readout to improve the model performance. As for parallel PDG architecture, with the input optical path fixed on path1, individual featured maps are all stored in the host computer and computed for a synthesized feature map by a weighted summation of existing feature maps, which could be post-processed either electronically or optically. The overall time synchronization of these devices is shown in Supplementary Fig. 4. We analyze the instability of the experiment setup in Supplementary Fig. 1(b). Notably, here the instability of this system is a significant issue and could be improved a lot by more careful engineering of the setup. Here, we analyze the instability just to make sure that our system is still reliable after the training process. Our system is estimated to be stable at around 8 × 103 seconds. This period is longer than the time for training process which contains two parts: data acquisition and in-silico training. For the former part, the fresh rate of our experiment setup is 11.26 fps, the whole data acquisition is around 364 seconds. For the latter part, every epoch for digital training averagely costs 13.45 seconds, and the training part consumes 5380 seconds. The entire time consumption is 5744 seconds. Phase gratings with grating period (Δx, Δy) on a phase-only spatial light modulator (SLM) focus the modulated light by an objective lens with numerical aperture (NA = 0.3) onto the scattering media. The position shifts for focus spots of different phase gratings are calculated as (Δx,Δy) = (λf/Δx, λf/Δy), where λ and f are the wavelength and focus length of objective lens respectively. By successively loading different phase gratings, we can scan the light across scattering media to generate optical random signals.

Data processing and figure evaluation metric

For DPU experimental setup, we employ an amplitude-only SLM with pixel size of 8μm to encode the input data with the range of [0, 1], where each input dimension is encoded by a macropixel with the size of 5 × 5. The overall encoded region occupies a region of 500 × 500 pixels at the central of the SLM plane and pixels in the rest of region are set to 0. We establish a 4f imaging system with two identical plano-convex lenses to map input encoding plane to phase modulation plane. We flip both sides of the phase plates due to the reverse replica of Fourier transform in 4f imaging system and then load them to a phase-only SLM with the same pixel size of 8μm for pixel-wised phase modulation. Notably, both SLMs process 10 bit-depth modulation ranging from 0 to 1023. In order to match the common HDMI communication protocol, we successively separate 10-bit number from higher to lower place into three parts with each bit-length as 3, 3, and 4, and send them to SLM controller via the red, green and blue channels in HDMI cable, respectively. We set a region of interest (615 × 615) of detection camera and then downsample the speckle images reducing the dimension to 100 × 100. For intermediate layer in cascaded architecture, the resultant feature maps need to be resized to a scale of 500 × 500 with nearest interpolation techniques. As for optical readout, we utilize a Gaussian filter with size of 12 × 12 in front of final output to alleviate the noise in photoelectric conversion. We use a figure evaluation metrics called Pearson Correlation Coefficient (PCC) as training loss function which is defined as:

$$PCC(F,R)=\frac{\sum (F-\bar{F})\cdot (R-\bar{R})}{\sqrt{\sum {(F-\bar{F})}^{2}\cdot \sum {(R-\bar{R})}^{2}}}$$
(1)

where F denotes the fake images generated by PDG and R denotes the real images in training dataset. \(\bar{F}\) and \(\bar{R}\) represent the mean value of fake and real images, respectively. When the fake images have the same distribution as that of real images, the PCC will become 1, otherwise the PCC will be less than 1.