Introduction

The burgeoning global population and urbanization are escalating CO2 emissions. The increase of atmospheric CO2 severely exacerbates global warming and the occurrence of extreme weather1, which places strain on sustainable development to achieve the net zero target by around 20502. Carbon capture and storage, therefore, emerges as an effective way to aid the scaling of carbon mitigation and removal efforts3, with projections indicating its full availability by 2030 and the potential to produce over 1 × 108 terajoules of energy per year by 20504. Among carbon capture and storage technologies, carbon mineralization stands out5. It typically employs natural ores and mimics their natural carbonation process involving the accelerated reaction between CO2 and alkaline minerals to permanently sequester CO2 as stable carbonates (i.e., CaCO3 and MgCO3)5,6. However, the inherently slow chemical kinetics of these reactions limit the carbonation rate, necessitating activation methods to create efficient reaction conditions7. Alternatively, industrial alkaline solid waste, notably more reactive than natural resources, offers a superior carbon sink8. To date, millions tons of alkaline solid wastes, including iron/steel slags9, construction and demolition wastes10, coal fly ash11, and waste gypsum12, are disposed of through industrial recycling. Notably, cement/concrete wastes, originating from cementitious construction materials whose manufacturing process contributes to over 8.0% of total global CO2 emission13, contain abundant chemically unstable components such as calcium hydroxide (Ca(OH)2, referred to as CH) that can be utilized for accelerated carbonation. These alkaline wastes exhibit enhanced carbonation reactivity in humid environments14, offering a promising avenue for accelerated carbon mineralization technology, and demonstrating a sustainable approach to harnessing industrial waste for climate change mitigation.

The feasibility of all CO2 mineralization schemes, whether employing natural rocks or alkaline solid wastes, critically depends on carbonation efficiency, which is largely influenced by the humidity within carbonation environments. The presence of moisture on mineral surfaces facilitates the release of cations such as Ca2+ through dissolution while simultaneously enabling CO2 speciation, both of which are essential processes for promoting carbonation reactions15. Therefore, achieving efficient mineral carbonation necessitates a specific relative humidity (RH). For instance, the reaction between CH and CO2 requires a minimum RH of approximately 8%16. Previous studies also illustrated that the thickness of water film on the CH surface determines the dissolution of CO2 and the formation of carbonates mediated by Ca2+, CO32−, and HCO3− species which controls the carbon mineralization efficiency17. In large-scale engineering constructions, carbonation is diffusion-controlled since the transport of CO2 into inner voids in between solid grains is essential for activating reactions18. The hydrophilicity of alkaline solid wastes leads to the RH-dependent water saturation states within the mesopores as described by the Kelvin equation19, which ultimately determines the overall carbonation rates of the materials. Specifically, optimal RH levels benefit the CO2 adsorption in mesopores while a higher RH causes full saturation and hinders the channel accessibility for CO2 transport. Experimental characterizations have been used to ascertain the water coverage in mesopores of forsterite and evaluate its effects on carbonation20. A series of experiments were also conducted to validate that a favorable RH range of 50 ~ 65% accelerates the carbonation of cement pastes21. However, previous experimental studies have overlooked the link between the thermodynamic state of confined water and the CO2 intake within multi-sized mesopores when seeking optimal carbonation RH. This oversight leaves the inconsistent optimal RH in different studies incomprehensible22. Atomistic simulations on calcium silicate hydrates and forsterite have demonstrated that the nanopore confinement significantly affects the domain (RH, temperature) of the stability of the adsorbed water film23. However, the optimal states of CO2 adsorption in confined mesopores still lack in-depth investigation.

In this study, we focus on CH, the most fundamental CO2-reactive mineral in alkaline solid wastes, and conduct comprehensive atomistic simulations to examine the CO2 adsorption properties in multi-sized CH slit pores with varying water coverage (indicating different RH levels). We find that the maximum CO2 intake occurs at the optimal RH corresponding to capillary condensation onset within the CH mesopores. This intriguing finding emphasizes the significance of transition states of confined water in activating reactions within the mesopores of hydrophilic materials. Furthermore, it enables us to establish a Kelvin-like model that accurately predicts the optimal RH for CO2 adsorption, providing insights and guidance for accelerated mineral carbonation in practical applications.

Results

Impact of water content and state

Multiple studies have revealed that carbonation of bulk alkaline solids primarily happens in the inner mesopores with the formation of calcium carbonate reducing the porosity24. Laboratory investigations further highlighted the facile mineralization reactivity occurring within a nanoconfined water film environment25, where nanometer-thick interfacial water film serves as a nano-reactor for carbonation20. Here, we investigate the CO2 adsorption and diffusion behavior in mesopores ranging from 2 to 10 nm under varying RH conditions using Grand Canonical Monte Carlo (GCMC). The slit pore models, which represent the packing voids between calcium hydroxide (CH) crystal grains at the mesoscale, are employed for this analysis. It is important to note that experimental studies maintain a constant environmental RH, allowing the water exchange inside the pores to achieve dynamic equilibrium during the entire carbonation process. In our simulations, we idealize this moisture equilibration by maintaining a constant water content and not allowing water exchange throughout the CO2 adsorption process. This approach barely impacted the final CO2 adsorption amount while significantly reducing computational costs.

Compared to a dry CH pore, the total CO2 adsorption amount increases with the initial water content in the pore due to the partial CO2 solvation in the water film (Fig. 1a–c). This observation is in line with recent experimental studies26. However, it is important to note that more water does not necessarily result in better CO2 adsorption (Fig. 1d, e). In the case of a 3 nm pore, the maximum CO2 adsorption is observed at a water coverage of ~4 water layers (one water monolayer has a water coverage density of ~8.6 nm−2). A higher water coverage (43.0 nm−2) dramatically decreases the amount and efficiency of CO2 adsorption due to the low diffusion coefficient of CO2 in liquid water. The optimal water coverage density of 34.4 nm−2 indicates a critical RH at which the capillary condensation begins (i.e., the well-defined adsorbed layered water and gaseous water suddenly fill up the entire pore as shown in Fig. 1e and Supplementary Fig. 1o). The water density distribution indicates the peculiar characteristics of water at this phase transition state (Fig. 1f). The water filling the pore during capillary condensation exhibits a significantly lower density compared to normal water in the layered state, indicating a metastable state (transition state) as theorized by Saam and Cole almost 50 years ago27. Based on the oscillatory mode of helium at low temperatures, they proposed a universal theory to describe the metastable state of liquids at capillary condensation within confined porous media, which later was successfully adopted by Keizer et al.28 to investigate the phase transition of sulfur hexafluoride in controlled-pre glass using molecular simulations and experiments. In our simulations, we observed the CH pore appears filled with liquid water at the onset of capillary condensation, yet the actual water content is slightly lower than the theoretical volume required for complete pore filling. This incomplete filling with barely discernible air voids results in a lower average water density within the pore compared to the fully saturated state (bulk water density). For more discussion on the low-density water at capillary condensation, please consult the Supplementary Note 1. Supplementary Discussion.

Fig. 1: CO2 adsorption in 3 nm CH slit pore with different water contents under 10 bars.
figure 1

a Total CO2 amount in the entire channel. b Dissolved CO2 amount in the interfacial water film. c Gaseous CO2 amount in the CH channel. The adsorption amount is taken from the average of the last 2 ns adsorption at the equilibrium stages. The value 8.6 nm−2 is the coverage density of one water monolayer on the CH surface. Error bars are from the standard deviation resulting from the last 1 ns simulation of CO2 adsorption. The unit is the number of molecules. d, e Molecular simulation snapshots showing CO2 adsorption into the CH channels with one and four water layers, respectively. f Water density distribution along the Z direction of the CH channel at different water coverage densities. g Diffusion coefficients of CO2 in the CH channel with different thicknesses of water coverage. Blue dashed lines stand for the diffusion coefficients of the surface-trapped CO2 and free CO2 in the dry CH nanopore. Red dashed lines designate the attractive potential between CO2 and CH surface (Eatt) and the adsorption energy of CO2 (Eads) as a function of the water coverage density. h The CO2 isosteric heat of adsorption (Qst) in 3 nm CH slit pores under varying water content. Source data are provided as a Source Data file.

Full size image

The capillary condensation at the critical water content is also characterized by a sudden drop of the CO2 diffusion coefficient within the CH channel (Fig. 1g). In the dry CH channel, the diffusion coefficients of surface-trapped CO2 (close to CH walls) and free CO2 (in the middle of the CH channel) are ~8.0 × 10−9 m2/s and 7.2 × 10−8 m2/s respectively, which set the lower and upper limits for CO2 diffusion in wet CH channels at any humidity. Gaseous CO2 in the CH channel can be considered as freely moving gas molecules in a closed environment, but their motions are constrained by interactions with water or the solid CH surface. The red dashed lines in Fig. 1g show the attractive potential between CO2 and CH surface (Eatt) and the adsorption energy of CO2 in the nanopore (Eads) as a function of the water coverage density. With a coverage density of one water monolayer, the strong attractive interactions among the CH surface, CO2, and H2O molecules result in the lowest CO2 diffusion coefficient. As the water film thickness increases, Eatt decays rapidly, causing CO2 molecules to desorb from the CH surface to the liquid/gas interface due to the hydrophobic nature of CO2. This desorption leads to an increase in CO2 diffusion coefficients. When the initial water coverage density reaches 34.4 nm−2, the layered water film suddenly fills the entire channel and engulfs all the CO2 in the channel (Fig. 1e). The consequent sudden drop of CO2 diffusion coefficient indicates that this water/CO2 mixed state exhibits much stronger interactions than CO2 in a layered water condition, where the high mobility of gaseous feature remains. To quantify these intensified CO2-water interactions with the increase in water content, we calculated the CO2 isosteric heat of adsorption (Qst) as shown in Fig. 1h. Qst is defined as the negative value of the differential enthalpy of adsorption, representing the heat released per molecule added to the adsorbed phase at constant temperature and very low loadings. Therefore, a higher Qst indicates greater thermodynamic stability for CO2 adsorption. As shown in Fig. 1h, the Qst of CO2 in CH slit pores gradually increases with water content, reaching the maximum value when water condensation occurs (water coverage density is 34.4 nm−2). This indicates that the CO2-water interactions, as the driving force for CO2 docking, are maximized at the water condensation condition, which thereby promotes CO2 adsorption amount.

Maximum CO2 intake

The analysis of CO2 adsorption in a 3 nm CH channel reveals that the maximum CO2 adsorption occurs at the RH just under which the capillary condensation jump occurs. This is further confirmed by the calculations of CO2 maximum intake in multi-sized CH mesopores ranging from 2.0 to 10.0 nm. The dynamic CO2 adsorption processes in different pores over time are presented in Supplementary Fig. 2 and Supplementary Fig. 3). The CO2 adsorption amount of the last 2 ns at equilibrium stages is analyzed and shown in Fig. 2a–f. The red boxes represent the CO2 concentration of CH mesopores in the equilibrium state, which shows that the maximum CO2 intake for different models all occurs at the onsite of capillary condensation. Under the maximum CO2 adsorption conditions, the majority CO2 molecules manifest as the dissolved state (Fig. 2g), which further confirms that the optimal CO2 adsorption state is the metastable water/CO2 mixed state (Fig. 1e). In addition, it is observed that the increasing pore size (2.0, 2.5, 3.0, 3.5, 4.0, 10.0 nm) requires an increasing optimal water coverage density (17.2, 25.8, 34.4, 34.4, 43.0, 111.8 nm−2) for maximum CO2 adsorption, which corresponds to an increased RH. This agrees with the dependence of condensation pressure on pore size: larger mesopores require larger water condensation pressure29. The maximum CO2 concentration in different CH mesopores exhibits a discernible threshold, which is approximately 0.28 g/cm3 and marginally varies with pore size. This critical value enlightens the maximum CO2 adsorption capacity in CH mesopores at the current pressure. The blue boxes demote the concentration of dissolved CO2 in water. Notably, an elevated concentration of CO2 is observed at lower water content (8.6 nm−2), which is attributed to the strong attraction exerted by the CH surface (Fig. 1g). This attractive potential decays dramatically with increasing water coverage, resulting in the decrease in CO2 concentration to a plateau.

Fig. 2: CO2 adsorption in multi-sized CH pores with different water contents under 10 bars.
figure 2

a–f Equilibrium CO2 concentrations in CH mesopores of 2.0, 2.5, 3.0, 3.5, 4.0, and 10 nm as a function of the water coverage density, respectively. The red dashed lines indicate the maximum CO2 intake in the entire pore. Error bars are from the maximum and minimum CO2 concentration in the last 1 ns simulation. g The specific values of the dissolved and total adsorbed CO2 amount in different CH mesopores. h Equilibrium CO2 density distributions perpendicular to the 10 nm pore under different water contents: CO2 density distributions in the channel with (I) low water contents and (II) all different water contents. i Schematic diagram showing hysteresis width changes of water adsorption/desorption isotherms in multi-sized mesopores. Source data are provided as a Source Data file.

Full size image

Before capillary condensation, CO2 molecules accumulate at the liquid/gas boundary between the layered water and the gas space (Fig. 2h), where the dissolved and gaseous CO2 molecules intensively exchange, reflecting the water layer instability as it is approaching the capillary phase transition. This water-layer/gas interface plays a crucial role in CO2 adsorption and shifts toward the middle region of the CH channel as the thickness of the water film increases until capillary condensation suddenly fills the entire channel with metastable low-density water (the water liquid right after the capillary jump gets denser as RH increases), which provides an ideal CO2 docking condition. It is important to note that the maximum CO2 intake occurring in a domain of RH that is within the adsorption/desorption hysteresis boundaries hence corresponds to metastable pore water with large density fluctuations as described by Saam and Cole27. Moreover, the hysteresis width of water adsorption/desorption isotherms increases with the mesopore size30, meaning the metastable states have a broader pressure range within larger pores (Fig. 2i). This is also reflected in the CO2 adsorption behaviors shown in Fig. 2a–f, where the 10 nm pore has a broader optimal water content range of 94.6 to 111.8 nm−2 compared to smaller pores.

Optimal humidity

The water contents for maximum CO2 adsorption in different pores suggest the optimal water layer thickness, which shows a significant linear relationship with the pore size with a slope of 0.31 (Fig. 3a). It should be noted that the critical film thickness at the point of capillary condensation (i.e., maximum water film thickness) for a slit pore is approximately 1/3 of the pore width31,32, which further confirms that the optimal condition for CO2 docking is the critical state of capillary condensation. The water content-dependent CO2 adsorption capacity in Fig. 2a–f can be converted to an RH-dependent CO2 adsorption capacity map for different pore sizes (Fig. 3b) through the Frenkel-Halsey-Hill equation33. The two constants of the Frenkel-Halsey-Hill equation were determined by fitting water adsorption isotherms from our simulations and previous experiments (Supplementary Fig. 4a). It should be noted that one of the parameters \(\alpha\) reflects the interactions between the material surface and adsorbates, which varies with respect to the material type and surface properties (details provided in the Supplementary Note 5; Supplementary Methods). Figure 3b holds engineering significance for efficient CO2 mineralization of alkaline materials with random pore size distribution. Previous experimental studies emphasized that large pore size benefited carbon capture capacity, as the expansion of pore size consistently leads to a higher quantity of stored CO234. However, these works tend to overlook the impact of RH and indiscriminately advocate for pore size expansion to facilitate carbon mineralization35. Figure 3b suggests that achieving a comparable carbonation efficiency in small-sized nanopores is feasible by meticulously controlling the optimal RH. The white dotted line denotes the optimal RH for CO2 adsorption (RHopt) in different CH mesopores. The regions below RHopt are the unsaturated states where the pore water remains layered on the surface. Above RHopt the pore is saturated with density-fluctuating metastable water, which approaches the normal-density water as RH increases. The mazarine edge line shows the upper limit of RH at which the pore is filled with normal-density water. Figure 3b shows that RHopt increases with pore size: a 4 nm pore only acquires ~60% RH for maximum CO2 adsorption, while a 10 nm pore necessitates an optimal RH of ~90%.

Fig. 3: Optimal RH for CO2 adsorption in multi-sized CH mesopores.
figure 3

a The calculated optimal water film thickness (converted from optimal water content) for CO2 adsorption as a linear function of pore size. Error bars are from the standard deviation resulting from the fitting process. b CO2 adsorption capacity as a function of RH and pore size. The amount of CO2 adsorption is normalized to the maximum adsorption capacity for each pore size. The white dotted line denotes the optimal RH for CO2 adsorption (RHopt), where the water capillary condensation occurs in CH mesopores. c Evaporation RH and capillary condensation RH as a function of pore size. The capillary condensation line accurately predicts the optimal RH for CO2 adsorption. \(x=\frac{d(1-2n)+2\delta }{{d}^{2}{(1-2n)}^{2}}\). Error bars are from the standard deviation resulting from the fitting process. d Comparison of the predicted optimal carbonation RH with experimental results. The dotted line of the RHopt tail indicates the pores smaller than 2 nm where the capillary condensation does not exist and the RHopt model thus is invalid. The pore size distributions (PSD) of CH and cement paste have main peaks at 25 nm and 4 nm49, respectively. The predicted RHsopt is ~94% and ~60% respectively, which are in line with the optimal carbonation RH observed in our and previous experiments21,37,50. e, f Water vapor sorption isotherms in cement paste and CH powder. The dashed lines outline the main RH (p/p0) ranges of capillary condensation. Source data are provided as a Source Data file.

Full size image

Since RHopt indicates the capillary condensation states in the pore, it is supposed to be predicted by the Kelvin-like pore size-dependent condensation pressure, which provides valuable guidance in selecting the RHopt in carbon mineralization engineering based on the pore size distribution of the materials. For hydrophilic slit pores, pore size-dependent equilibrium evaporation RH (RHeva) and condensation RH (RHcon) respectively write:

$${{\mathrm{ln}}({{\rm{RH}}}^{{{\rm{eva}}}})}=-\frac{2{\gamma }_{0}{V}_{m}}{{{\rm{R}}}T}\frac{d-2t+2\delta }{{(d-2t)}^{2}}$$
(1)
$${{\mathrm{ln}}({{\rm{RH}}}^{{{\rm{con}}}})}=-\frac{{\gamma }_{0}{V}_{m}}{{{\rm{R}}}T}\frac{d-2t+2\delta }{{(d-2t)}^{2}}$$
(2)

where \({\gamma }_{0}\), \({V}_{m}\), R, and T represent the planar surface tension of water, the molar volume of water, universal gas constant, and temperature, respectively. The Tolman length \(\delta\) is introduced here to correct the surface tension differences between planar surface and concave meniscus36. It is estimated by the water molecule size of 0.3 nm. d and t denote the pore size (diameter) and the maximum water film thickness at the capillary condensation state, respectively. The derivations of Eqs. 1 and 2 are provided in the Supplementary Note 4. Supplementary Method. Since t is proportional to d for slit pores32, letting t = nd, Eqs. 1 and 2 can be rewritten:

$${{\mathrm{ln}}({{\rm{RH}}}^{{{\rm{eva}}}})}=kx$$
(3)
$${{\mathrm{ln}}({{\rm{RH}}}^{{{\rm{con}}}})}=\frac{1}{2}{kx}$$
(4)

where \(k=-\frac{2{\gamma }_{0}{V}_{m}}{{{\rm{R}}}T}\) is a constant of ­ 1.05 nm at 300 K. \(x=\frac{d(1-2n)+2\delta }{{d}^{2}{(1-2n)}^{2}}\). n is approximately 1/3 yet should vary with the surface properties of the pore, which is found equal to 0.31 in our simulations (Fig. 3a). With n being determined, the theoretical RHcon model perfectly predicts the RHopt obtained from our GCMC simulation (Fig. 3c). The deviation for the 2 nm pore is because the surface/water interaction surpasses the capillary force in small pores, making the condensation equation less valid. It is worth noting that the simulated RHopt falls into the region between RHcon and RHeva when the Tolman correction for surface tension is not taken into account (Supplementary Fig. 5). This makes general sense because RHcon and RHeva for a finite size pore indicate the critical pressures of adsorption jump and desorption drop in Fig. 2i, respectively. The region between RHeva and RHcon suggests the metastable saturation states of the pore, which is favorable for CO2 intake. The incorporation of Tolman correction results in a more precise prediction of RHopt that is at the onsite of capillary condensation and follows the RHcon line. The RHcon model serves as a robust model for predicting optimal RH for CO2 sequestration with hydrophilic materials.

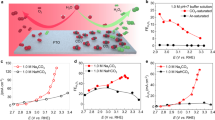
To validate this model, we compared the CH carbonation efficiency at different RH environments in experiments. The pore size distribution (PSD) of CH powder has a main peak at ~25 nm (Fig. 3d). Thus, the predicted RHopt is ~94%, which agrees with our experiments where the samples at 98% RH were carbonated much faster than those at RHs of 10%, 30%, 55%, and 75% (Supplementary Fig. 6). Similar to our results, Steiner et al.37 also found that the carbonation of CH was much faster at 91% RH than at 57%. In addition, we examined our prediction model with another data set of cement paste carbonation experiments. The cement paste has a smaller PSD with a main peak at ~4 nm due to the porous nature of the amorphous calcium silicate hydrates. The corresponding RHopt is predicted to be ~60%, which is also in line with the experimental results (Fig. 3d). Moreover, our experiments of water vapor sorption isotherms confirm that the main RH ranges of capillary condensation for cement paste and CH powder are 50–70% and >90% respectively (Fig. 3e, f), which are in line with their RHopt, validating our conclusion that optimal CO2 intake happens at the critical RH of capillary condensation. The validated model can be utilized to predict the optimal carbonation RH not only in laboratory studies but also in industrial applications. Currently, industrial activities related to carbon mineralization often rely on maintaining a constant RH, based largely on experience-based data. This approach overlooks the pore size distribution of different materials, which may deviate from the optimal conditions. Our proposed model serves as a guideline to enhance carbon capture and storage efficiency across various industrial processes, ultimately reducing labor and production costs and contributing to the achievement of net-zero emissions by 2050.

Discussion

The porous system develops in alkaline solids, wherein mesopores serve as efficient media for CO2 docking (Fig. 4a). Mineral carbonation within mineral pores can be broadly divided into five steps: CO2 diffusion into pores (physisorption), which reaches equilibrium rapidly; Dissolution of surface ions (release of metal and hydroxide ions); CO2 speciation (conversion to HCO3−/CO32− in pore solution); Reaction of HCO3−/CO32− with metal ions and precipitation; Nucleation and growth of carbonation products. While the first step (physisorption) reaches equilibrium quickly, the remaining steps are non-equilibrium processes that continue until carbonation reaches its limit. This is because CO2 chemisorption (speciation) requires overcoming a significant energy barrier (~113 kJ/mol in pure water38 and ~64 kJ/mol even in alkaline environments39). In contrast, CO2 diffusion encounters almost no energy barrier, resulting in a much faster rate for physisorption compared to speciation. Our study specifically investigates the impact of water content on the equilibrium CO2 adsorption capacity (CO2 reservoir size) within CH pores, which dictates the concentration of reactants (CO2) available for subsequent chemical reactions, ultimately controlling the overall carbonation efficiency. The conversion of CO2 to HCO3−/CO32− is a time-dependent, non-equilibrium process that affects the cumulative CO2 consumption rather than the equilibrium CO2 adsorption capacity within pores, which therefore is not our focus. Moreover, the carbonation efficiency in slit pores is influenced by numerous complex factors, which can be broadly categorized into three areas: material properties (including surface charges, surface texture, and pore size), carbonation environment (such as temperature, CO2 pressure, and RH), and structural dynamic variations (including changes in pore solution, pore structures, and surface properties). These factors dynamically affect both CO2 physisorption and chemisorption in porous minerals. Among these, surface properties and textures can be generally described through the interactions between the material surface and adsorbates (see Supplementary Note 4. Supplementary Methods for more details). The effects of temperature and pressure are widely recognized as having a unidirectional causal influence within suitable intervals. In contrast, significant discrepancies in optimal RH are observed across different porous systems, largely due to substantial variations in pore size distribution. Therefore, this work aims to elucidate the intricate dynamics of optimal RH for carbonation in various porous media.

Fig. 4: Schematic demonstration of pore size-dependent optimal RH for CO2 mineralization.
figure 4

a CO2 transport in humid mesopores. b The influence of RH on CO2 adsorption in mesopores. c Pore size dependent optimal RH for CO2 mineralization. When the pore size distribution (PSD) increases from 2 nm to 10 nm, the optimal RH for CO2 mineralization (RHopt) shifts from 25% to 90%.

Full size image

RH controls the water saturation degree of the mesopores which critically governs CO2 adsorption capacity (Fig. 4b). The most intriguing observation is that the highest CO2 uptake occurs at the onset of capillary condensation, where the mesopore starts to fill with density-fluctuating metastable water, creating an ideal docking site for CO2 adsorption. Under such circumstances, the adsorbed CO2 exhibits “dissolved-like” states with a low diffusion coefficient but an exceptionally high concentration compared to CO2 solubility in bulk liquid water. This observation enables us to establish the Kelvin-like relationship between the optimal RH for CO2 adsorption and the mesopore size distribution, which is useful to predict the optimal RH for fast CO2 mineralization in random material systems with specific pore size distribution (Fig. 4c): minerals with smaller pores achieve efficient carbonation at relatively low RH, while those with larger pores require higher RH for optimal performance. Considering that the formed calcium carbonates and other products during the carbonation process change the pore size distribution persistently, a more effective solution in experiments commences with dynamic RHopt (i.e., time-dependent RHopt according to the carbonation degree) to fit the pore size evolution and maximize the entire carbonation efficiency. On the other hand, to enhance the CO2 mineralization in field experiments where the humidity control is far from trivial, our model suggests the careful control of the pore size distribution of the CO2-reactive minerals to achieve high-efficiency carbonation. For instance, when the environment RH is 60%, the optimal carbonation efficiency will be obtained with an average pore size of ~4 nm. It is also important to note that most alkaline solids with porous structures exhibit a polydisperse pore size distribution rather than a monodisperse one, as discussed in this work. Under these realistic conditions, determining the optimal RH becomes more complicated. From our perspective, for solids with a relatively concentrated pore distribution, the optimal RH can be selected based on the characteristics of these pore sizes. Conversely, for solids with a widely distributed pore size, a dynamically controlled RH should be employed to facilitate carbonation across different pore sizes.

Future work derived from this study will focus on two main areas. First, we aim to apply the proposed model to various mineral solids, including calcium silicate hydroxide, dicalcium silicate, and tricalcium silicate. The surface textures of these materials can significantly influence the water adsorption isotherm, which may, in turn, impact the water content required for capillary condensation. Understanding these factors is crucial for determining the optimal RH for CO2 adsorption. The second aspect of our future work will involve extending the current model to polydisperse porous systems. We will develop a more robust model to describe the optimal RH for different porous media. Ultimately, this enhanced model will be applied in large-scale settings to improve the efficiency of industrial carbon mineralization processes.

Methods

Force field and models

In this work, the CLAYFF force field40 is employed to describe the atomistic interactions between CH, CO2, and water molecules. Numerous research studies have shown the capability of CLAYFF to precisely capture the solid/liquid interface behaviors in an alkaline system41,42. The incorporation of CO2 potential in CLAYFF has been widely employed and its reliability in predicting its adsorption on wetted surfaces of clay-based materials is discussed by Cygan et al43. The optimized CLAYFF force field parameters including CO2 potentials are presented in Supplementary Table 1. It should be noted that force fields are disabled to precisely capture the CO2 solubility in the water-rich phase and water solubility in the CO2-rich phase under extremely high pressure44,45. However, our research investigates CO2 adsorption at a low pressure of 10 bar, where the majority of CO2 molecules reside at the gas-liquid interface, with limited CO2 fully dissolved in the water (although we categorized interfacial CO2 as “dissolved CO2” based on its coordination number with water molecules). Therefore, the accuracy of reproducing the CO2-water phase diagram is not a critical factor in validating our simulation results.

A 2 × 3 × 4 supercell of CH molecular structure46 was constructed and relaxed under an isobaric-isothermal ensemble at 298 K and 1 bar for 1 ns to reach full equilibrium. Then, a flat surface was obtained by cleaving the (0 0 1) surface of the CH, after which the vacuum spaces of 2 nm, 2.5 nm, 3 nm, 3.5 nm, 4 nm, and 10 nm were built to reproduce the mesopores in between CH grains. We continuously increased the water film thickness in CH slit pores by hand to mimic increasing RH until the maximum water intake was achieved. The relationship between RH and adsorbed water film thickness on the CH walls is described by the Frenkel−Halsey−Hill equation33, the two constants of which were determined by fitting water adsorption results in experiments (Supplementary Fig. 4a and Supplementary Note 5; Supplementary Methods). The water contents and corresponding RHs are illustrated in Supplementary Table 2.

CO2 adsorption

The adsorption of CO2 in CH channels employed the GCMC methods47. 100 attempts of insertion, removal, or exchange of CO2 molecules were manipulated through GCMC methods every 1 ps, during which the CO2 molecules were able to freely diffuse in the CH nanochannel. The whole system was relaxed under canonical NVT ensemble at 300 K during the CO2 adsorption process to maintain stability. We employed a timestep of 1 fs for the GCMC simulation and conducted 25 million Monte Carlo moves to assess when the system could achieve full equilibrium. We found that equilibrium could be reached after 5 million Monte Carlo moves (Supplementary Note 3; Supplementary Methods). Therefore, all confined GCMC simulations were equilibrated for 5 million moves, followed by slow converging simulations for an additional 5 million steps to ensure proper convergence. The configurational-biased insertion, deletion, or reinsertion probability was set at 0.125 for CO2, with a biased molecular translation probability of 0.375 and a maximum displacement of 0.5 Å. The biased molecular rotation probability was 0.5, with a maximum rotation of 0.05 rad. During the GCMC simulations, a canonical NVT ensemble at 300 K was employed for the equilibration of the entire system. The amount, distribution, and trajectory of adsorbed CO2 molecules were recorded every 1 ps. The chemical potentials for CO2 adsorption at 300 K under different pressures are shown in Supplementary Table 3. Detailed information about chemical potential is discussed in Supplementary Note 2. Supplementary Methods. All the GCMC simulations were performed in LAMMPS software.

Adsorption energy

The adsorption energy of CO2 in the CH pore with water film was calculated through:

$${E}_{{{\rm{ads}}}}={E}_{{{\rm{total}}}}-{E}_{{{\rm{CH}}}}-{{nE}}_{{{{\rm{CO}}}}_{2}}$$
(5)

where \({E}_{{total}}\) is the total potential energy of the CH slab with CO2 adsorption. \({E}_{{CH}}\) and \({E}_{{{CO}}_{2}}\) are the potential energies of the CH slab with water film and a single CO2 molecule, respectively. \(n\) is the number of adsorbed CO2 molecules. Specific methods for calculating \({E}_{{CH}}\) and \({E}_{{{CO}}_{2}}\) are presented in the Suppl. Note 1. Supplementary Methods. To record the adsorption energy variation with respect to CO2 surface coverage, the configurations of CH with CO2 adsorption were output every 1 ps (GCMC step). The potential energy at a certain step was then calculated through energy minimization.

Diffusion coefficient

The diffusion coefficient of CO2 was measured by the mean squared displacement (MSD). After the CO2 adsorption in the CH channel reached equilibrium, the system was relaxed with an NVT ensemble for another 10 ns, during which the trajectories of all atoms were recorded. Based on the trajectory data, the time-dependent \({MSD}(t)\) of CO2 was calculated and the diffusion coefficient of CO2 molecules (\({D}_{{{CO}}_{2}}\)) was obtained by measuring the slop of MSD through the Einstein relation:

$${D}_{{{{\rm{CO}}}}_{2}}=\frac{1}{6}{{\mathrm{lim}}}_{t\to \infty }\frac{{{\rm{MSD}}}(t)}{t}$$
(6)

Carbonation experiments

To determine the optimal RH for efficient carbonation of CH, the CH powder of analytical grade was carbonated at different RHs of 10%, 30%, 55%, 75%, and 98%. The CH samples were cured at the target RH environments (controlled by saturated solutions) with nitrogen protection gas for 5 months to ensure the inner humidity equilibrium with the environment before they were carbonated at a CO2 pressure of 0.05 MPa for 3 h following a “semi-dry”48 procedure. After vacuum freeze-drying for 48 h, the carbonated samples were prepared for qualitative phase analysis. The phase composition was identified by X-ray diffraction (XRD) using a Rigaku SmartLab 9 kW diffractometer with Cu Kα radiation (λ = 1.54 Å). The scanning covered a 2θ range of 5–60° with a step size of 0.02° and a rate of 2°/min. The Rietveld method was adopted for phase quantitation with a weighted residual (Rwp) value of less than 10%. The pore structure analysis was carried out using an automatic specific surface area and porosity analyzer (Micromeritics ASAP 2020Plus). Nitrogen gas was chosen as the adsorption gas after the samples were degassed for 10 h.

Water sorption experiments

Water vapor sorption isotherms were measured gravimetrically at 20 °C using a vacuum gas/vapor sorption analyzer (BSD-VVS). The CH and cement paste samples were vacuum-dried at 60 °C for 48 h to remove residual moisture before vapor sorption. The RH (0–95%) was precisely controlled by mixing the dry argon gas with water-saturated argon flow. The sample was continuously weighted through a high-precision ( ± 0.1 μg) weighing instrument as the RH was adjusted. At each RH level, the vapor sorption continued until the weight change was less than 0.1 mg/ 60 min, ensuring the equilibrium of sorption at each RH.