Continuous decoupled redox electrochemical CO₂ capture

Abstract

Electrochemical CO₂ capture driven by renewable electricity holds significant potential for efficient decarbonization. However, the widespread adoption of this approach is currently limited by issues such as instability, discontinuity, high energy demand, and challenges in scaling up. In this study, we propose a scalable strategy that addresses these limitations by transforming the conventional single-step electrochemical redox reaction into a stepwise electrochemical-chemical redox process. Specifically, the hydrogen evolution reaction (HER) at the cathode and the oxidation of a redox carrier at the anode are employed to modulate the pH of the electrolyte, thereby facilitating effective CO₂ capture. By decoupling the electrochemical swing for CO₂ capture from redox carrier regeneration in both temporal and spatial domains, this approach mitigates unwanted side reactions and enhances system stability. Our results demonstrate a stable CO₂ capture process sustained for over 200 h, with a electrical work of 49.16 kJ_e mol^-1 CO₂ at a current density of 10 mA cm^-2. Furthermore, a scaled-up system capable of producing approximately 0.4 kg of pure CO₂ per day maintained stable operation for 72 h, highlighting the potential feasibility of this method for large-scale decarbonization applications.

Introduction

Direct carbon dioxide (CO₂) capture from industrial sources or the atmosphere plays a crucial role in managing global CO₂ emissions. However, it faces a significant challenge due to the high energy consumption associated with current methods^1,2,3. Electrochemical CO₂ capture has emerged as a promising alternative that efficiently utilizes intermittent renewable energy resources without relying on traditional thermal processes, such as chemical absorbent scrubbing or high-pressure-driven membrane separation. This approach offers the potential for low-power CO₂ purification and improved energy efficiency^4,5. One key advantage of electrochemical CO₂ capture is its ability to separate CO₂ from gas streams through an electricity-controllable electro-swing system. Unlike conventional methods, this technique does not require heating, making it highly flexible for capturing CO₂ at different times and locations^6,7.

There are two main types of electrochemical CO₂ capture methods that have been extensively studied. The direct method involves the electrochemical generation of nucleophilic agents in organic solvents via electro-reduction⁸. These nucleophilic agents react with CO₂ to form adducts, capturing low concentrations of CO₂. The CO₂ is later released and purified through the electro-oxidation of these adducts. Despite its potential, this method faces challenges, such as high ohmic resistance and interference from water in organic solvents, which limit its efficiency⁹.

The indirect methods, including pH-swing^10,11,12 and metal-amine complexing electro-swing^13,14, use absorbents like alkali or amines to capture CO₂. Desorption occurs when redox components are electrically regenerated, which displaces the CO₂. These methods benefit from lower ohmic resistance and can operate in aqueous solutions. In addition, the use of organic redox mediators in these systems typically enhances electrode kinetics on graphite electrodes. This design avoids common issues like flooding in gas diffusion electrodes¹⁵ and dendrite formation or corrosion in copper electrodes¹⁶.

However, a critical limitation of electrochemical CO₂ capture systems, particularly those using organic redox couples, is their instability during continuous CO₂ absorption-desorption cycles. When exposed to real CO₂ sources containing oxygen (O₂), such as atmospheric air or flue gas, redox molecules can degrade, limiting the long-term application of these systems⁵. Addressing this instability is essential for advancing electrochemical CO₂ capture technologies for practical use.

Recent advancements have introduced several innovative strategies to mitigate the effects of oxygen-side reactions in electrochemical carbon capture systems. For direct electrochemical carbon capture methods, it remains challenging to overcome the coupling between the oxygen tolerance of redox carriers and their binding constants with CO₂. Some advanced studies have reported that hydrogen bonding can be employed to develop redox carriers that exhibit both oxygen tolerance and favorable CO₂ binding constants^17,18. For indirect electrochemical carbon capture methods, strategies like electrochemical rebalancing¹⁹ and solid electrolyte reactors²⁰ have been proposed to develop oxygen-tolerant electrochemical carbon capture systems. In addition, extensive research has focused on creating O₂-tolerant electrochemical redox molecules^21,22 and absorbent systems²³, which demonstrate good oxygen resistance. However, these technologies still face the complex challenge of balancing oxygen tolerance, operational continuity, and energy consumption for carbon capture.

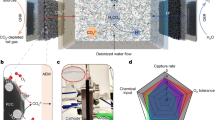
In this paper, we present an approach to decoupled redox electrochemical CO₂ capture, which enables continuous and stable CO₂ capture in O₂-containing flue gas. This method separates the conventional single-step electrochemical reaction into two processes: electrochemical and chemical redox reactions. Electrochemical reactions are used to modulate the pH at the anode and cathode, allowing for efficient CO₂ capture and desorption. Specifically, at the cathode, the hydrogen evolution reaction (HER) produces an alkaline solution, while at the anode, the oxidation of an organic redox mediator (QH₂) generates an acidic solution. The alkaline solution absorbs low concentrations of CO₂, forming bicarbonate ions. These ions migrate through an anion exchange membrane, driven by an electric field, to the acidic region at the anode, where high-purity CO₂ is desorbed. The redox mediator at the anode is then regenerated via spontaneous hydrogenation in a separate tower, a process that does not require electrical energy (Fig. 1). This design enables each module to operate independently, facilitating continuous CO₂ capture.

Fig. 1: Schematic diagram of the decoupled redox electrochemical CO₂ capture system.

In the electrolytic system, hydrogen evolution reactions occurring at the cathode increase the alkalinity of the solution, facilitating the absorption of low-concentration CO₂. At the anode, the electrochemical oxidation of AQDSH₂ acidifies the solution, promoting the desorption of high-purity CO₂. Bicarbonate ions generated at the cathode migrate to the anode through the anion exchange membrane, maintaining charge balance and providing a carbon source for the CO₂ desorption reaction at the anode. In the regeneration tower, the oxidized AQDS is regenerated through a spontaneous chemical hydrogenation reaction with H₂ over a Pt/C catalyst.

By decoupling the electrochemical CO₂ capture process from the regeneration of the redox mediator both spatially and temporally, this strategy effectively reduces the impact of oxygen on the regeneration process. In this study, we developed and validated a laboratory-scale decoupled redox electrochemical CO₂ capture (DREC) system. We established a thermodynamic theoretical model for the DREC system and demonstrated a scaled-up electrochemical carbon capture system capable of continuous and stable CO₂ capture in oxygen-containing environments.

Results and discussions

Concept and verification of DREC system

The decoupled redox electrochemical CO₂ capture (DREC) system employs an asymmetric electrolysis design consisting of three modules: an electrolysis module, a CO₂ capture module, and a redox regeneration module. In the electrolysis module, the hydrogen evolution reaction (HER) at the cathode increases the solution’s alkalinity, facilitating CO₂ absorption in the capture module. Simultaneously, the anode utilizes an organic redox mediator (QH₂) in its reduced state. At the anode, QH₂ undergoes electrochemical oxidation, releasing H⁺ ions and acidifying the solution through a reversible proton-coupled electron transfer (PCET) reaction. Following this, the oxidized form, Q, is regenerated by H₂ in the redox regeneration module, catalyzed by Pt/C, to restore QH₂. This regeneration process occurs spontaneously without the need for electrical input. The hydrogen oxidation reaction, characterized by rapid kinetics, is mediated by anthraquinone disulfonate (2,7-AQDS). Meanwhile, bicarbonate ions (HCO₃^-) formed at the cathode migrate through an anion exchange membrane (AEM) to the anode, where they react with H⁺ ions to release pure CO₂.

This asymmetric design decouples the sites of CO₂ absorption-desorption from the redox regeneration process, eliminating the need for frequent electrode replacement as required in traditional electrochemical CO₂ capture systems. In addition, it prevents direct contact between oxygen on the absorption side and the anodic redox mediator, which would otherwise reduce efficiency. It overcomes the slow kinetics of H₂ oxidation at the gas diffusion anode.

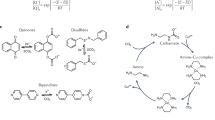
We began by establishing the selection criteria for the redox mediator in the DREC system (Fig. 2A). The organic redox mediator at the anode must satisfy thermodynamic requirements under CO₂ dissolution equilibrium to maintain an optimal pH for efficient CO₂ absorption and desorption. Thus, the mediator must be stable in an aqueous CO₂ environment, possess a redox potential higher than H₂/H⁺, and enable reversible proton-coupled electron transfer (PCET) reactions. In addition, energy consumption for CO₂ capture is primarily affected by the potential range, which varies with pH (∆E_pH and ∆E_pH’ in Fig. 2B), and the intrinsic potential difference (∆E₀ in Fig. 2B). To minimize energy consumption, we aim for a low intrinsic potential difference (∆E₀) while meeting the other necessary criteria. We selected 2,7-AQDS as the redox mediator due to its low reduction potential (− 0.1265 V vs. SHE at pH 6, Fig. 2B, red line), high solubility (1.34 mol L⁻¹ in a phosphate-mixed solution; Supplementary Fig. 1), and excellent electrochemical stability and reaction kinetics (Supplementary Figs. 2, 3)²⁴. It can be efficiently reduced by H₂ using metal-based catalysts^25,26, such as the Pt-based catalysts employed in this study. The 2e⁻/2H⁺ PCET reaction of 2,7-AQDS effectively drives CO₂ desorption at pH 6. At pH values above 11, the reduced form of quinone, hydroquinone, deprotonates before electrochemical oxidation and exhibits a pH-independent reduction potential (Fig. 2C). This behavior is determined by the pKa of the redox-active center and can be fine-tuned through molecular design to accommodate various pH conditions.

Fig. 2: Concept verification of the DREC system.

A Selection criteria for active substances in anodic oxidation-reduction. B Cyclic voltammogram of AQDS (red line) and the HER (blue line) scanned at 50 mV s⁻¹ on a glassy carbon electrode and a platinum-plated nickel mesh electrode. The difference between the two CV scans indicated by the red solid line and the red dashed line represents a pH difference of 0.5 in the anolyte. The difference between the two CV scans indicated by the blue solid line and the blue dashed line represents a pH difference of 1.49 in the catholyte. C Pourbaix diagram of 2,7-AQDS. Data are fitted to three solid lines with slopes of − 59.3 mV pH⁻¹, − 28 mV pH⁻¹, and 0 mV pH⁻¹, corresponding to two-, one- and zero-proton processes, respectively. The data shown are an average from three experimental runs; the error bars indicate the standard deviation. D LSV curve of the HER cathode (the blue line is measured under the mixture gas of 15% CO₂ and 85% N₂, and the yellow line is measured under the mixture gas of 15% CO₂, 80% N₂, and 5% O₂). The electrolyte (1 M KHCO₃) is injected with a mixture of gas at 40 mL min⁻¹ for 30 min before the test. Throughout the test, the same mixture of gas was maintained. The potential at the intersection point of the dot-dash line and the dashed line is − 0.545 V. E Stability test of the HER cathode under different O₂ concentrations. The electrolyte is injected with an oxygen-containing gas mixture. The concentration of O₂ was measured by the O₂ concentration sensor. All figures have not been IR-corrected.

Since AQDS operates efficiently below pH 7 and offers proton buffering capabilities, we selected a K₂HPO₄/KH₂PO₄ buffer for the anode and a KHCO₃ buffer for the cathode. These buffers maintain appropriate pH levels for CO₂ desorption and absorption, enabling low-voltage operation with minimal pH fluctuation. The small pH variations observed between the outlet of catholyte and anolyte during electrolysis further demonstrate the strong proton buffering capacity of the electrolyte (Supplementary Fig. 4).

We then assessed the impact of oxygen on the cathode during CO₂ absorption. A simulated gas mixture containing 15% CO₂, 80% N₂, and 5% O₂, representative of typical flue gas composition from coal-fired power plants, was employed. Results from cathode linear sweep voltammetry (LSV) tests under both O₂-free and O₂-containing conditions showed nearly identical curves (Fig. 2D). No obvious effect of oxygen on our electrochemical process was observed. The stability of cathodic constant current electrolysis was further validated across a range of oxygen concentrations (0–20%, Fig. 2E), demonstrating the DREC system’s robust performance in O₂-containing CO₂ environments.

While oxygen could be reduced at the potential of H₂/H⁺, the low solubility of oxygen in water (~ 0.6 mg L⁻¹ under atmospheric conditions or simulated flue gas with 5% O₂) plays a critical role in maintaining electrolysis stability (Supplementary Fig. 5). On the anode side, where CO₂ desorption occurs, AQDSH₂ is exposed to a pure CO₂ atmosphere. The anion exchange membrane (AEM) effectively acts as a barrier, preventing dissolved oxygen from the cathode from reaching the anode, with oxygen levels measured at 0 mg L⁻¹ on the anode side (Supplementary Fig. 5). This design ensures that AQDSH₂ is not oxidized by oxygen in the CO₂ capture process, eliminating the degradation issues typically observed in prior electrochemical carbon capture systems using quinones as redox couples, which were susceptible to side reactions with O₂. Constant current tests for both the anode and cathode demonstrated stability over a 72-hour period (Supplementary Fig. 6). In addition, the system showed stable operation even under high current density conditions, further confirming its durability in practical applications (Supplementary Fig. 7).

Matching of electrochemical oxidation and chemical reduction of redox mediator

The relative redox potentials of H₂ and AQDS indicate that the hydrogenation of AQDS is thermodynamically favorable. We monitored the reduction of 2,7-AQDS by H₂ using in situ UV-vis spectroscopy (Fig. 3A, B). The presence of electron-donating phenolic hydroxyl groups facilitated electron transfer within the AQDS system through the p-π conjugated network, decreasing the transition energy and causing a redshift in the absorption band (from 328 nm to 390 nm). This redshift aligns with previous reports and confirms the formation of AQDSH₂ following hydrogen reduction²⁷.

Fig. 3: Matching verification of the chemical reduction reaction and electrochemical oxidation reaction.

A Schematic diagram of the in situ UV‒vis monitoring system. B In situ UV‒vis spectra obtained during AQDS hydrogenation. C Schematic showing the potential monitoring system for hydrogenation reduction. D OCV curve of the AQDS hydrogenation reduction process. The electrolyte was 100 mL of 0.1 M AQDS in phosphate buffer. The catalyst loading volume was 50 mL. The H₂ flow rate was 30 mL min⁻¹. The temperature was 50 °C. The electrolyte was injected with Ar during the tests. E The Q/QH₂ ratio during the hydrogenation process was calculated with the Nernst equation. The dots are reaction data, and the line reflects a linear fit to the data. F Schematic of the full-cell electrolysis system. G, H Constant voltage electrolysis test of the full cell under different pump flow rates. The initial electrolyte was fully oxidized to 0.1 M AQDS in phosphate buffer and 1 M KHCO₃. Hydrogen gas was introduced for hydrogenation reduction at 20 min.

Next, we tracked the hydrogenation reaction rate by monitoring the open circuit potential of the anode (Fig. 3C, D). Using the Nernst equation, we calculated the QH₂/Q ratio based on the reaction potential (Fig. 3E and Supplementary Note 1). The initial reaction rate was relatively slow due to the adsorption of hydrogen gas on the catalyst surface. However, as the surface became saturated with hydrogen, the reaction rate stabilized. We modeled the reaction process to estimate the rate of AQDSH₂ production, which was found to be 0.0627 M h⁻¹. This corresponds to a maximum current of 1.41 A for electrochemical oxidation. It is important to note that this observed rate was influenced by both internal and external diffusion limitations, meaning it reflected only the rate of AQDSH₂ production within the decoupled capture system and not the intrinsic hydrogenation rate of AQDS.

In addition, we verified the compatibility of the hydrogenation and electrochemical oxidation reactions within the full cell. By applying a constant cell voltage of 1.5 V, within the water stability window, we determined the maximum achievable current (Fig. 3F–H). As the liquid flow rate increased from 200 to 1000 mL min⁻¹, the cell current gradually rose and then plateaued. This initial increase was attributed to improved mass transfer on the electrode surface as flow rates increased, which enhanced the overall mass transfer and boosted cell current. However, as the flow rate continued to rise, the current increase diminished, indicating that the system was nearing the mass transfer limit under the test conditions.

Long-term operation at higher flow rates was restricted by the pump equipment’s limitations. At a flow rate of 1000 mL min⁻¹, we achieved a maximum current density of 160 mA cm⁻². However, higher flow rates led to greater parasitic energy consumption. We estimated that energy loss from the pump during fluid delivery was approximately 2.55 and 20.11 kJ_e mol⁻¹ CO₂ at a flow rate of 200 and 1000 mL min⁻¹, respectively (Supplementary Note 2).

The stability of the anode was verified over 15 days of continuous electrolytic oxidation and hydrogen catalytic reduction (Fig. 4A). Proton nuclear magnetic resonance (¹HNMR) spectra showed no additional peak signals with no observed shifts (Fig. 4B), indicating the stability of 2,7-AQDS against chemical reduction by hydrogen in acidic aqueous solutions. These results were corroborated by carbon nuclear magnetic resonance (¹³CNMR) spectroscopy and liquid chromatography-mass spectrometry (LC-MS) (Fig. 4C and Supplementary Fig. 8). Through cyclic voltammetry (CV) tests using a glassy carbon electrode, no additional redox peaks were observed within the potential range of − 0.4 to 0.4 V versus the standard hydrogen electrode (SHE) (Fig. 4D). This confirms that 2,7-AQDS exhibits both electrochemical and chemical stability during prolonged electrolysis. Furthermore, scanning electron microscopy (SEM) images (Supplementary Fig. 9) confirm that the catalyst’s morphology remains unchanged after extended reduction, indicating the robustness of the catalyst under prolonged operation. Compared to direct electrochemical hydrogen oxidation using a gas diffusion electrode (GDE), our method effectively mitigates the problematic “flooding” process commonly observed at the gas-liquid-solid interface during the hydrogen oxidation reaction (HOR)^15,28.

Fig. 4: Stability test of AQDS during a stepwise electrochemical-chemical redox reaction.

A Single-cell potential stability test in phosphate buffer solution at a current density of 10 mA cm⁻² for 15 days. B ¹HNMR spectra of AQDS recorded in D₂O, showing AQDS after different reaction times of 48, 96, 144, 192, 240, 288, and 336 h. C ¹³CNMR spectra of AQDS recorded in D₂O, showing AQDS after different reaction times of 48, 96, 144, 192, 240, 288, and 336 h. D CV curve of 0.1 M AQDS scanned at 50 mV s⁻¹ on a glassy carbon electrode.

The hydrogen used in the redox regeneration module theoretically originates from the electrolysis cathode. To validate the hydrogen cycle concept, we designed a laboratory-scale testing device (Supplementary Fig. 10). During 24 h of constant current electrolysis, the volume of hydrogen gas in the system remained unchanged (Supplementary Fig. 10). This demonstrates that the hydrogen produced at the cathode is fully recycled within the redox regeneration module, with no detectable loss of hydrogen throughout the system, (Supplementary Fig. 10), demonstrating that the hydrogen generated at the cathode can be fully recycled in the redox regeneration module without any system-wide hydrogen loss. In addition, we measured the amount of hydrogen produced and consumed during the cathodic and anodic reactions (Supplementary Fig. 11A–C). The hydrogen evolution reaction (HER) efficiency at the cathode was 99.5%, while the hydrogen consumption efficiency in the redox regeneration module was 99.7%. The ratio of hydrogen production to consumption was ~ 99.8%, confirming the feasibility of the hydrogen cycle concept in the DREC system.

Demonstration and validation of a laboratory DREC system

The laboratory DREC system demonstrated stable electrolysis voltage over a 200 h period in 15% CO₂, 80% N₂, 5% O₂ environment, maintaining an average voltage of 0.507 V at a current density of 10 mA cm⁻² (Fig. 5A). To ensure the purity of the desorbed CO₂, we release CO₂ at a partial pressure of 1 bar. CO₂ absorption and desorption efficiencies were determined to be 99.6% and 99.5% (Fig. 5B, Cand Supplementary Figs. 12–14), respectively. Carbon removal efficiency is 21.76% (Fig. 5D), corresponding to energy consumption for CO₂ electrolysis was approximately 49.16 kJ_e per mole of CO₂ (Fig. 5E). Compared to other advanced electrochemical carbon capture techniques^{19,20,21,23,29,30,31,32}, our system exhibited lower energy consumption (Supplementary Figs. 15, 16). Carbon removal efficiency is defined as the ratio of the CO₂ concentration at the system’s inlet to its outlet at low concentrations (Eq. 5).

Fig. 5: The performance of DREC system under different current densities.

A Electrolysis durability test at a constant current density of 10 mA cm⁻² for simulated flue gas capture for a total period of 200 h. B Absorption efficiencies at different current densities. C Desorption efficiencies at different current densities. D Carbon removal efficiency of DREC system at different current densities. The carbon removal efficiency is calculated using Eq. 5. The error bars indicate that each group was subjected to three repeated experiments. E Energy consumption of DREC system at different current densities. The energy consumption is calculated using Eq. 8.

Subsequently, we evaluated the electrochemical CO₂ capture performance of the full cell under higher current densities. With increasing current density, we observed a rise in the pH of the catholyte outlet, corresponding to a higher CO₂ absorption rate and improved carbon removal efficiency (Supplementary Fig. 17). At 50 mA cm⁻², absorption and desorption efficiencies decreased slightly to 95.8% and 94.7%, respectively, while the carbon removal efficiency is 63.23% with an average voltage of 0.814 V. This corresponded to an energy consumption of 82.93 kJ_e mol⁻¹ for CO₂ capture (Fig. 5B–Dand Supplementary Figs. 18, 19). At a higher current density of 120 mA cm⁻², the absorption and desorption efficiencies further declined to 89.09% and 84.49%, respectively, with an average voltage of 1.25 V, resulting in an energy consumption of 142.7 kJ_e mol⁻¹ for CO₂ capture. The carbon removal efficiency can reach 92.78% (Fig. 5B–Dand Supplementary Figs. 20, 21).

The reduction in electrolysis efficiency at higher current densities was primarily attributed to the competitive transport of anions such as CO₃²⁻ and OH⁻ in the catholyte, which competed with HCO₃⁻ for transport towards the anode. Although an anion exchange membrane selective for HCO₃⁻ was employed, this competition persisted, especially as cathode alkalinity and operation time increased, leading to a drop in efficiency. Nevertheless, the system maintained relatively high efficiency (greater than 84%) due to the membrane’s strong selectivity for HCO₃⁻. Higher current densities enhance carbon removal efficiency and absorption rates; however, this comes at the cost of increased energy consumption. In addition, we evaluated the membrane’s permeability to AQDS, finding that over a 21-day period, the AQDS permeance was 5.16 × 10⁻³mol m⁻² h⁻¹ (Supplementary Fig. 22). The presence of SO_x and NO_x in real flue gases will also impact the system (Supplementary Fig. 23). Therefore, the development of catalysts that are tolerant to NO_x and SO_x will be crucial for advancing the industrial application of the DREC system in the future. In future applications, these factors will need to be carefully balanced.

The cathode in the DREC system facilitates the transfer of bicarbonate ions (HCO₃^-) to the anode, where they react with protons (H⁺) to form water, establishing a water balance within the system. Overextended operational periods, this balance may shift, resulting in water loss at the cathode and accumulation at the anode. However, water vapor is typically carried out by gases into the atmosphere, which mitigates water accumulation. Experimental results indicated that during a 15-day CO₂ capture process with a gas flow rate of 20 ml min⁻¹, water loss at the anode averaged approximately 1.93 ml per day. In industrial applications, flue gas absorbed at the cathode contains water vapor (H₂O), which theoretically increases water content at the cathode. Thus, maintaining water equilibrium in the system is a complex challenge. Established methods, such as membrane separation^33,34, offer potential solutions for managing water balance in future industrial-scale applications.

Thermodynamic model and energy consumption evaluation

The theoretical model analysis covered the entire CO₂ capture process to evaluate energy consumption (refer to Supplementary Note 3). The analysis primarily focused on the equilibrium relationships of carbonates and phosphates (Supplementary Table 2), excluding the effects of anthraquinone. Unlike previous models^11,14,35, this model introduces a theoretical framework for continuous CO₂ capture without the need for electrode exchange. The model assumes that electrochemical acidification/alkalization and desorption/absorption processes occur independently.

Here, we quantify the amount of CO₂ absorbed or desorbed by measuring the change in dissolved inorganic carbon (∆DIC). Total alkalinity (TA) is defined based on charge balance. In our system, we assume that bicarbonate ions transfer through the anion exchange membrane from the cathode to the anode, accompanied by an equal molar transfer of electrons. As a result, TA remains constant in our model, and ∆DIC is equal to the concentration of electrons transferred. Our model confirms that the DREC system can capture CO₂ from sources with varying concentrations, such as 10–15% in flue gas or approximately 400 ppm in ambient air (Supplementary Fig. 24), and desorb CO₂ at 1 bar. The ∆DIC can be calculated based on the number of electrons transferred, which allows us to determine the pH of the anolyte and catholyte. Using the Nernst equation, we then calculate the system’s theoretical minimum energy consumption. The minimum theoretical electrical energy required by the system is 12.28 kJ_e mol⁻¹ of CO₂ for a 15% CO₂ concentration and 23.35 kJ_e mol⁻¹ for 400 ppm CO₂ (Supplementary Figs. 25–27). Because of the asymmetric structure of the DREC system, we conducted further analysis, which demonstrates that the membrane potential also affects the system’s energy consumption (Supplementary Fig. 28).

Performance of a scaled-up DREC system

To demonstrate the practical applicability of our approach, we developed a demonstration system for CO₂ capture using a stacking strategy, capable of generating approximately 0.4 kg of pure CO₂ per day (Fig. 6A). The electrolysis system was compact and modular, consisting of three stacked cells with a total effective geometric surface area of 1008 cm², compared to 4 cm² for the lab-scale system. The sizes of the modules can be adjusted to accommodate different capture quantities. During a 72 h test period, the system consistently captured CO₂, operating stably at an average voltage of 0.95 V and a current density of 10 mA cm⁻² (Fig. 6B), with an energy consumption of approximately 92.93 kJ_e mol⁻¹ CO₂. Furthermore, CO₂ absorption and desorption tests revealed that simulated flue gas with a CO₂ concentration of 15% was absorbed in the cathode, while 100% CO₂ was desorbed from the anode. The CO₂ absorption and desorption efficiencies were approximately 100% and 98.5%, respectively, with a capture-removal efficiency of around 34% (Fig. 6C–F, Eq. 5).

Fig. 6: Scale-up and performance.

A Optical image and schematic of a demonstration system. B Electrolytic durability test for the demonstration system operated at a constant current density of 10 mA cm⁻². C Flow rate of the CO₂ absorption tower inlet and outlet. The dashed line represents the fitted curve of the flow rate at the outlet of the CO₂ absorption tower. D Concentrations of CO₂ at the inlet and outlet of the absorption tower. E Flow rates of the CO₂ desorption tower inlet and outlet. The dashed line represents the fitted curve of the flow rate at the outlet of the CO₂ desorption tower. F Concentrations of CO₂ at the outlet of the desorption tower.

Despite the successful scale-up, a disparity in energy consumption between the scaled-up system and the laboratory-scale system was observed, due to amplification effects. We anticipate that further reductions in energy consumption and improvements in capture efficiency can be achieved through optimized reactor design, implementation of comprehensive heat exchange networks, and fine-tuning of operational parameters. Overall, the preliminary validation of the decoupled redox electrochemical carbon capture strategy has been achieved.

The most established method for CO₂ capture from flue gas is amine scrubbing, where organic amines absorb low concentrations of CO₂, followed by desorption at temperatures between 120–140 °C. The regeneration heat requirement ranges from approximately 132–150 kJ_th mol⁻¹ CO₂³⁶. Heat exchange optimization can somewhat reduce this energy demand. Other carbon capture technologies, such as solid adsorption and membrane separation, aim to lower overall energy consumption by either using solid adsorbents or leveraging membrane selectivity, thereby avoiding the high thermal regeneration burden associated with solvents. Our system introduces an electrochemical decoupled strategy, utilizing a pH-swing mechanism to bypass the high energy costs of thermal regeneration. Given its potential integration with renewable energy sources in the future, our system offers a promising solution for carbon capture.

It is worth noting that thermal-driven technologies, such as amine scrubbing use thermal work for desorption. In contrast, membrane separation and electrochemical carbon capture technologies rely on electrical work to capture CO₂. A direct comparison between electrical work and thermal work across different techniques is challenging. Therefore, we have indicated the different types of separation work in the table (Supplementary Table 3) to facilitate a more equitable assessment of each technology.

In summary, we have developed an electrochemical CO₂ capture strategy that decouples the traditional single-step electrochemical redox process into a stepwise electrochemical-chemical redox mechanism. This approach enables continuous and stable CO₂ capture via pH swings at the electrode, effectively avoiding undesired O₂ side reactions. We demonstrated the efficacy of this system in a 200 h lab-scale experiment, achieving an energy consumption of approximately 49.16 kJ_e mol⁻¹ CO₂, and in a scaled-up 72 h experiment, achieving 92.93 kJ_e mol⁻¹ CO₂. Further optimization of performance is possible by designing molecular structures with reduction potentials closer to the hydrogen evolution reaction (HER), employing more efficient anion exchange membranes, and dynamically optimizing process parameters. This work presents a perspective on electrochemical CO₂ capture and offers potential solutions to long-standing challenges of scalability and high energy consumption in this field.

Methods

Materials

Chemicals such as potassium bicarbonate (KHCO₃), potassium dihydrogen phosphate (KH₂PO₄), and dipotassium hydrogen phosphate (K₂HPO₄), all of analytical grade, were procured from Shanghai Aladdin Bio-Chem Technology Co., Ltd. 9,10-Anthraquinone-2,7-disulfonic acid (AQDS, 97%) was purchased from HuaXia Technology Co., Ltd. The Pt/C granular catalyst (1 wt% loading, diameter 0.7 mm) was supplied by Shanxi Rock New Materials Co., Ltd. All chemicals were used without further purification. The anion exchange membrane (FAA-3-PK-75) with a thickness of 75 ± 5 μm was purchased from SCI Materials Hub. It was soaked in a 1 M KHCO₃ solution for 24 h and then washed with deionized water three to four times before use. Deionized water with an electrical resistivity of 18.25 MΩ·cm at 25 °C was used as the solvent to prepare the electrolyte solutions. CO₂, N₂, and a mixed gas (80% N₂, 15% CO₂, 5% O₂), all with 99.999% purity, were sourced from the Chengdu Heping Gas Plant.

Structure of the cell

The electrolytic cell was designed as a sandwich-type reactor, comprising two stainless steel plates, two polytetrafluoroethylene (PTFE) plates, and two graphite plates. The anode and cathode chambers were separated by an anion exchange membrane (FAA-3-PK-75). Graphite plates with serpent-like flow channels were employed to regulate the flow of reactants and products. Platinum-plated nickel mesh, with a geometric surface area of 4 cm², served as the cathode for the hydrogen evolution reaction. The anode electrode was composed of pretreated graphite felt, also with an area of 4 cm². The graphite felts were pretreated by soaking in 98% H₂SO₄ at 60 °C for 6 h, followed by soaking in deionized water for 4 h, and then vacuum-dried for 3 days.

Characterization

¹HNMR and ¹³CNMR spectra were obtained using Bruker AV II-600 MHz. The NMR spectra were recorded in D₂O (99.9%) to suppress the water signal. The half-cell stability test was conducted in an oxygen-free glovebox. Daily quantitative sampling was performed, and after vacuum drying in the glovebox, a measured amount of D₂O was added to the samples, which were then sealed in NMR tubes. The tubes were further sealed with parafilm and sent for testing.

Scanning electron microscopy (SEM) was performed using a Thermo Scientific HITACHI REGULUS 8230 at an accelerating voltage of 5.0 kV. A polaron sputtering gun was employed to coat the samples with a 25 nm gold film to enhance their electrical conductivity.

In situ UV-Vis spectroscopy was conducted using a PerkinElmer Lambda 750S spectrophotometer (USA), covering the wavenumber range of 300–600 nm. The reduction tower was loaded with 5 mL of catalyst, and the temperature was maintained at 50 °C. During the experiment, 1 mM AQDS in phosphate buffer was pumped from the tank into both the reduction tower and the flow-through cuvette at a flow rate of 100 mL min⁻¹. Simultaneously, hydrogen gas was introduced into the reduction tower at a flow rate of 30 mL min⁻¹.

Solubility measurement

A phosphate mixture solution (0.8 M KH₂PO₄ and 0.2 M K₂HPO₄) was used as the test environment for the solubility test. Different amounts of AQDS were added to 10 mL of the mixed solution and fully dissolved until there was no precipitate; then, standard solutions of 5 × 10⁻⁵ M, 1 × 10⁻⁴M, 1.2 × 10⁻⁴M, 1.4 × 10⁻⁴M, 1.6 × 10⁻⁴M and 1.8 × 10⁻⁴M concentrations after dilution were prepared. The absorbance within the wavelength range of 300–600 nm was measured by means of an ultraviolet spectrophotometer (PerkinElmer Lambda 750S, USA) with a wavelength interval of 0.5 nm and an optical path length of the quartz cuvette of 10 mm. The peak absorbance values of different concentrations of AQDS at 328 nm were selected for fitting to plot a standard regression curve²⁷. The sample consisted of 5 mL of a mixed solution with AQDS, reaching a saturation state after 24 h of equilibrium. There was still a small amount of solid insoluble matter. After resting, the supernatant was filtered and diluted to a constant volume, and the absorbance was measured with the same method. The peak absorbance at 328 nm was used to calculate the maximum solubility of AQDS in the mixed solution by means of the standard regression curve.

Dissolved oxygen test

To evaluate the effectiveness of the anion exchange membrane in isolating oxygen, we measured the dissolved oxygen concentration in an H-cell. The H-cell was divided into two chambers, separated by the anion membrane. One chamber was filled with 1 M KHCO₃ solution and continuously supplied with a mixed gas (15% CO₂, 80% N₂, 5% O₂) at a flow rate of 40 mL min⁻¹. The other chamber contained 0.1 M AQDS in a phosphate buffer solution (0.8 M KH₂PO₄ and 0.2 M K₂HPO₄). Initially, the solution was exposed to atmospheric conditions for 3 h. Subsequently, the mixed gas was bubbled into the AQDS chamber for an additional 3 h. To simulate practical application conditions, the solution was then bubbled with pure CO₂ to remove any remaining oxygen and achieve degassing. The dissolved oxygen concentration in the solution decreased to nearly 0 mg L⁻¹. To maintain a stable CO₂ environment, CO₂ gas was continuously bubbled into the upper portion of the solution. Dissolved oxygen concentrations were monitored using a dissolved oxygen detector (INESA Scientific Instrument Co., Ltd., JPB607A).

The permeance of AQDS test

The AQDS permeation experiment was conducted in an H-cell. One compartment contained a 0.1 M AQDS phosphate solution, while the other contained a 1 M KHCO₃ solution. The area of the anion exchange membrane (AEM) was 4.9 × 10⁻⁴ m². After sampling from the KHCO₃ solution side, the concentration of AQDS was measured using UV-vis spectroscopy to calculate the permeance of AQDS.

Hydrogen evolution and consumption efficiency

For the hydrogen evolution efficiency test, N₂ gas is used as a carrier gas and introduced into the cathode to sweep out the H₂. The flow rate of the mixed gas and the concentration of H₂ are then measured using a flow meter and gas chromatograph (GC). For the hydrogen consumption efficiency test, H₂ is introduced into the reduction tower, where it mixes with N₂ upon exiting. The flow rate of the mixed gas and the concentration of H₂ are similarly measured using a flow meter and GC.

CO₂ absorption and desorption

For CO₂ absorption measurements, the catholyte was purged with 15% CO₂, 5% O₂ and 80% N₂. The exit gas was passed sequentially through a drying tube, a gas flow sensor, and a CO₂ sensor to measure the total gas flow rate and CO₂ concentration. Two magnetic pumps were used to circulate both the catholyte and anolyte solutions.

For CO₂ desorption measurements, pure CO₂ gas was introduced into the anolyte chamber, and the flow rate was measured using a gas flow sensor. The exit gas was then passed through a drying tube, a gas flow sensor, and a CO₂ sensor to determine the total gas flow rate and CO₂ concentration. The amount of desorbed CO₂ was calculated by multiplying the difference in flow rates between the inlet and outlet by the CO₂ concentration.

Electrochemical characterization

Cyclic voltammetry (CV) measurements were performed at room temperature using a CHI660E electrochemical workstation (CH Instruments). All electrochemical data were exported in TXT or CSV format. No iR compensation was applied to any of the electrochemical tests. A glassy carbon electrode with a 3.0 mm diameter was employed as the working electrode in all three-electrode CV tests. The reference electrode was an Ag/AgCl electrode, presoaked in a 3.5 M KCl solution, while a platinum mesh (1 × 1 cm²) served as the counter electrode. The reference electrode was calibrated prior to the electrochemical measurements. The reference electrode was immersed in a 3.5 M potassium chloride standard solution, and its potential was calibrated by comparing the measured potential with the theoretical potential at room temperature. Prior to testing, the solution was degassed with argon for 30 min, and argon was continuously purged throughout the experiment to maintain an inert atmosphere. The glassy carbon electrode was polished sequentially with 0.5 μm and 0.03 μm alumina powders to ensure a smooth surface. The electrolyte volume is 100 mL. For the stability test, the electrolyte consisted of 1 mM AQDS in a phosphate buffer (0.8 M KH₂PO₄ and 0.2 M K₂HPO₄). In the potential comparison experiment (Fig. 2B), the electrolyte was 0.1 M AQDS in the same phosphate buffer.

To construct the Pourbaix diagram, 1 mM AQDS solutions (100 mL) were prepared in various pH buffers, using sulfuric acid (1 M, pH 0), HSO₄⁻/SO₄²⁻ (0.1 M, pH 1–2), AcOH/AcO⁻ (0.1 M, pH 2.65–5), H₂PO₄⁻/HPO₄²⁻ (0.1 M, pH 5.3–8), HPO₄²⁻/PO₄³⁻ (0.1 M, pH 9.28–11.52), and KOH (0.1 M, pH 13). The pH of each solution was adjusted with 1 M H₂SO₄ or 0.1 M KOH and measured using a pHS-3E pH meter (INESA Scientific Instrument Co., Ltd.), which was calibrated using buffer solutions with pH values of 9.18, 6.86, and 4.00. The slope of the linear fit of the plot of E0 versus pH was used to determine the ratio of the proton number to the electron number (m/n), with the slope ratio of 0.059 approximating this value.

RDE measurements were conducted at room temperature using an AutoLab PGSTAT302N electrochemical workstation. A glassy carbon electrode with a 5.0 mm diameter was used as the working electrode, along with an Ag/AgCl reference electrode and a platinum mesh (1 × 1 cm²) as the counter electrode. The reference electrode was presoaked in a 3.5 M KCl solution. Argon gas was introduced into the system to degas the solution for 30 min and was maintained throughout the tests. The glassy carbon electrode was polished sequentially with 0.5 μm and 0.03 μm alumina powders and rinsed with deionized water before use. The electrolyte volume is 100 mL. The electrode was rotated at speeds of 2800, 2400, 2000, 1600, 1200, 800, 600, and 400 r.p.m., while the potential was swept linearly from 0 V to − 0.8 V (vs. Ag/AgCl) at a scan rate of 5 mV s⁻¹. The diffusion-limited current densities at -0.8 V were plotted against the square root of the rotation rate (ω) and fitted using a straight line. The slope of the fit, defined by the Levich equation, was used to determine the diffusion coefficient (D) of AQDS, yielding a value of 4.09 × 10⁻⁶cm²s⁻¹.

The inverse of the current at overpotentials of 32, 42, 52, 61, 71, and 81 mV was plotted against the reciprocal of the square root of the rotation rate, and the data were fitted with a straight line. The intercept of the fit gave the inverse of the kinetic current (i_K). A plot of log(i_K) versus overpotential was linearly fitted, with a slope of 50 mV, consistent with the Butler–Volmer equation. The x-intercept of this fit provided the exchange current (i₀), which was used to calculate the standard rate constant (k₀) for AQDS, giving a value of 3.2 × 10⁻³cm s⁻¹.

Linear sweep voltammetry (LSV) curves were obtained at room temperature using a CHI660E in a single cell. The platinum-plated nickel mesh (1 × 1 cm²) was used as the working electrode for all three-electrode LSV tests. An Ag/AgCl reference electrode (presoaked in 3.5 M KCl solution), and a platinum net counter electrode (1 × 1 cm²) were used for the LSV tests. The scan rate was 1 mV s⁻¹. The electrolyte (100 mL) was 1 M KHCO₃.

Hydrogen circulation verification

The electrolysis module, along with all pipeline interfaces, was sealed with epoxy resin to prevent hydrogen leakage. Prior to electrolysis, AQDS was pre-reduced to AQDSH₂ using external hydrogen, and the system was subsequently purged with hydrogen. Hydrogen gas produced at the cathode was stored in a buffer tank and circulated to the redox regeneration module via an H₂ gas circulation pump, where it was utilized for AQDS hydrogenation. During 0.04 A constant current electrolysis, the pressure in the hydrogen buffer tank was monitored using the drainage method. If hydrogen was consumed, the liquid level in the detection water column would rise as the buffer tank pressure dropped, enabling quantification of net hydrogen consumption by measuring the change in liquid column volume.

Hydrogen reaction rate test

In the lab-scale system, the reduction tower was filled with 50 mL of Pt/C particle catalyst, having a loading density of 0.45 g mL⁻¹. The anolyte comprised 100 mL of a 0.1 M AQDS phosphate buffer, which circulated between the reduction tower and a reservoir. The H₂ flow rate was set at 30 mL min⁻¹, and the system operated at 50 °C. The potential of the solution was monitored in real time using an electrochemical workstation. A glassy carbon electrode (3.0 mm diameter) was employed as the working electrode, while an Ag/AgCl reference electrode (pre-soaked in a 3.5 M KCl solution) and a platinum mesh counter electrode (1 × 1 cm²) were used for the test.

Half-cell measurement

Half-cell measurements were conducted at room temperature using a CHI660E electrochemical workstation (CH Instruments) in an H-cell. A platinum-plated nickel mesh (1 × 1 cm²) was used as the working electrode for the cathode test, and a carbon felt electrode (1 × 1 cm²) was used for the anode test. An Ag/AgCl reference electrode (pre-soaked in a 3.5 M KCl solution) and a platinum mesh counter electrode (1 × 1 cm²) were employed. The catholyte (250 mL) was 1 M KHCO₃, bubbled with a gas mixture (80% N₂, 15% CO₂, 5% O₂). The anolyte (250 mL) was a 0.1 M AQDS/phosphate buffer (0.8 M KH₂PO₄ and 0.2 M K₂HPO₄). An anion membrane (FAA-PK-3-75) with a thickness of 75 ± 5 μm separates two chambers. It was soaked in a 1 M KHCO₃ solution for 24 h and then washed with deionized water three to four times before use.

Full-cell measurement

Measurements for the full cell were conducted using a direct current power supply (ITECH 6911, ITECH Electronic Co., Ltd.). An anion exchange membrane (FAA-3-PK-75) with a thickness of 75 ± 5 μm was selected. It was soaked in a 1 M KHCO₃ solution for 24 h and then washed with deionized water three to four times before use. The effective area of the electrode is 4 cm². The anolyte consisted of 100 mL of a 0.1 M AQDS/phosphate buffer solution, composed of 0.8 M KH₂PO₄ and 0.2 M K₂HPO₄, while the catholyte was 100 mL of 1 M KHCO₃. Both the anolyte and catholyte were introduced into the cell through 3 mm diameter PFET tubing, controlled by two magnetic pump systems (Lead Fluid, CT3001F). The reduction tower was loaded with 50 mL of catalyst and maintained at 50 °C. The anolyte was pumped into the reduction tower, and the electrolyte, along with hydrogen, flowed from the top of the tower back to the anode chamber. The hydrogen flow rate was set at 30 mL min⁻¹. Unless otherwise specified, the electrolyte flow rate is 200 mL min⁻¹.

Calculation of CO₂ absorption or desorption, carbon-removal, hydrogen evolution and consumption efficiency

The CO₂ absorption and desorption efficiency is defined as the ratio of the actual CO₂ absorbed or desorbed to the theoretical CO₂ absorption or desorption under the corresponding current. The CO₂ absorption or desorption efficiency was determined based on Faraday’s law and thermodynamic principles (Eqs. 1–4).

$${Q}_{{{CO}}_{2}}=\left|{\sum }_{{n=t}_{i}}^{{t}_{f}}({V}_{{{CO}}_{2}}^{{base}}-{V}_{{{CO}}_{2}}^{n})\times \Delta t\right|$$

(1)

$${n}_{0}=\frac{{It}}{{zF}}$$

(2)

$${Q}_{{the}}=\frac{{n}_{0}{RT}}{P}$$

(3)

$$\eta=\frac{{Q}_{{{CO}}_{2}}}{{Q}_{{\mbox{the}}}}$$

(4)

where Q_CO2 is the amount of absorbed or desorbed CO₂, t_f is the final time, t_i is the start time, ${{{\rm{V}}}}_{{{{\rm{CO}}}}_{2}}^{{{\rm{base}}}}$ is the flow rate of inlet CO_2, ${{{\rm{V}}}}_{{{{\rm{CO}}}}_{2}}^{{{\rm{n}}}}$ is the instantaneous volumetric flow rate of outlet CO₂ at nth data recording time t_n, n₀ is the theoretical number of moles of absorbed or desorbed CO₂ calculated by means of the Faraday formula, z is the amount of charge transferred by the molecule of the substance, which is 1 in this system, P is the gas pressure, R is the ideal gas constant, T is the temperature in Kelvin, and Q_the is the theoretical amount of absorbed or desorbed CO₂.

The carbon removal efficiency is defined as the ratio between the CO₂ outlet concentration and the CO₂ inlet concentration. The carbon-removal efficiency was calculated by means of Eq. 5.

$${\eta }_{C}=1-\frac{{{Q}_{{out}}C}_{{out}}}{{{Q}_{{in}}C}_{{in}}}$$

(5)

where Q_in and Q_out are the CO₂ flow rates at the inlet and outlet of the absorption tower, respectively. C_in and C_out are the concentrations of CO₂ in the inlet and outlet concentrations of the CO₂ absorption tower, respectively.

The hydrogen evolution and consumption efficiency are defined as the ratio of the hydrogen generated at the cathode and consumed at the anode to their theoretical values under the corresponding current. These efficiencies are calculated using Faraday’s law and the laws of thermodynamics (Eqs. 6–7).

$${Q}_{{H}_{2}}=\,\left|{\sum }_{n={t}_{i}}^{{t}_{f}}({V}_{{H}_{2}}^{{base}}-{V}_{{H}_{2}}^{n})\times \Delta t\right|$$

(6)

$${\eta }_{H}=\frac{{Q}_{{H}_{2}}}{{Q}_{{the}}}$$

(7)

where Q_H2 is the actual amount of hydrogen measured by gas chromatography, t_f is the final time, t_i is the start time, ${V}_{{H}_{2}}^{{base}}$ is the flow rate of inlet H_2, ${V}_{{H}_{2}}^{n}$ is the instantaneous volumetric flow rate of outlet H₂ at nth data recording time t_n, and Q_the is the theoretical hydrogen volume. The hydrogen evolution efficiency and hydrogen reduction efficiency were calculated to be 99.5% and 99.7%, respectively.

Calculation of energy consumption

The electrolysis energy consumption of the cell was estimated by means of Eq. 8.

$${W}_{E}={Pt}=\frac{U{F}{{n}}_{0}}{\eta }$$

(8)

where P is the electrolytic power and t is the time. U is the average cell voltage of the electrolytic process under a specified current density, F is the Faraday constant (96485 C mol⁻¹), η is the average current efficiency, and n₀ is the number of electrons transferred.