Introduction

Renowned for their high porosity and structural diversity, metal-organic frameworks (MOFs) have become a promising class of materials for a range of applications, including gas storage1,2,3, catalysis4,5,6, and drug delivery7,8. A variety of MOFs with unique structures and novel functionalities have been investigated and synthesized over the past decades, pushing boundaries of MOFs across various industries and research areas9,10. The most distinctive characteristic and greatest advantage of MOFs lie in their modular nature. The diverse combinations of metal nodes, organic linkers and their geometric topologies make MOFs highly tunable, offering numerous experimentally reported structures11,12 and virtually unlimited chemical search space13,14.

Given the large number of candidate structures, researchers have made considerable efforts to search for the top-performing MOFs for specific applications. The most commonly attempted method is high-throughput screening (HTS)15,16,17, which explores and compares every structure in a database. However, HTS shows limitations with the increased size of the database, and as such, optimization methods such as genetic algorithms18,19,20 and Bayesian optimizations21,22,23 have been employed for more efficient exploration of the MOF search space. Recently, generative models have been developed to design materials by learning the intrinsic distribution of the training dataset, and then generating new materials from this space. Various generative models, including variational autoencoders (VAEs)24,25 and generative adversarial networks (GANs)26,27, are actively being studied for diverse materials generation tasks.

Although such methods have been used to design MOFs with user-desired properties, the range of the target properties is highly restricted in terms of flexibility. Most previous works have focused primarily on numeric target characteristics, such as pore diameter (e.g., 15 Å) or adsorption capacity (e.g., 40 g/L). However, non-numeric data, such as pore morphology28,29 and thermal/chemical stability30,31 are also of great interest, especially for experimentalists, and these properties have not been widely incorporated in this context. Additionally, handling text-based data facilitates users to communicate with the machine learning models, and thereby significantly lowers the barrier to utilizing such technology32,33,34. Nevertheless, the conditioning on diverse modalities of data for deep generative models targeted at porous materials generation has not been explored yet.

To remedy this issue, diffusion models offer an innovative approach, as they have gained numerous attention for their versatile conditioning capabilities34,35,36,37,38. These models have been actively applied in the field of materials generation with drug-like molecules39,40, proteins41,42 and small crystals43 being main targets. When it comes to generating MOFs using diffusion models, Park et al.44 focused on the generation of MOF linkers rather than entire structures, while Fu et al.45 reduced the structural complexity by applying coarse-grained representation. Nonetheless, the structural diversity and validity of the generated samples remain lacking, and the consideration of the target property for inverse design has been limited to only numeric data (e.g., CO2 capacity). This highlights the necessity for a data representation that can better capture the intrinsic characteristics of porous materials, along with a novel architecture that enables flexible conditioning.

In this work, we propose MOFFUSION, a multi-modal conditional diffusion model that generates MOFs with careful attention to the three-dimensional (3D) shape of the pore structures (Fig. 1). A database composed of 247,742 hypothetical MOF structures was used for the training, which were generated using PORMAKE13 (a MOF construction software) and further geometry optimized using LAMMPS software46. We applied a signed distance function (SDF)37,47,48 for the input representation, marking the first application of 3D modeling techniques for the generation of MOFs. The suitability of SDF to describe MOFs and to capture essential features of porous materials was verified through the high structural validity of the generated samples.

Fig. 1: MOFFUSION Overview.
figure 1

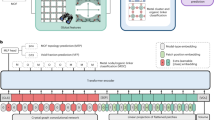
a Signed distance function (SDF) representation of MOFs. Negative SDF values represent the interior of the pore surface, while positive values represent the exterior of the pore surface. b A graphical illustration of the noising and denoising process of SDFs. c Model architecture of MOFFUSION. Within MOFFUSION, a denoising 3D U-Net is used for the diffusion process, and the MOF Constructor is used for the construction of MOFs from the generated SDFs. VQ-VAE is used for data compression and restoration, but it is omitted from the visualization for clarity. MOFFUSION exhibits the conditioning of diverse modalities of data including numeric, categorical, and text data. The model scheme was prepared using Adobe Illustrator.

Full size image

Within MOFFUSION, latent diffusion model architecture and attention algorithms were employed to address the challenges of the limited flexibility of conditioning targets. The ability of our model to conditionally generate MOFs based on diverse modalities of data, including numeric data, categorical data, text, and even their combinations, was validated. As a representative numeric data, MOFFUSION was conditioned on hydrogen working capacity and its capability to generate structures with the desired hydrogen capacity was validated through Grand Canonical Monte Carlo (GCMC) simulations. MOFFUSION also demonstrated outstanding performance in handling categorical data, achieving high accuracy in generating MOFs with targeted geometric topologies. Furthermore, its capability to condition with text data was validated by generating MOFs with desired characteristics based on input prompts. Lastly, MOFFUSION’s ability to account for multiple target properties during conditional generation was confirmed, and its inherent capability of generating MOFs with user-tailored pore shapes was further demonstrated.

Results

SDF representations for periodic crystals

Modeling 3D shapes is an active research area, particularly in the fields of animation and the creation of 3D assets in virtual environments49. Of the various data types used to represent 3D geometries, SDFs offer an implicit encoding of object surfaces by measuring the signed distances between 3D coordinate queries to their closest surface (Fig. 1a). SDFs have proven to be a versatile representation (e.g., controllable resolution, and small memory requirements), with a particular strength in accurately modeling the shape of the surfaces.

The pore structure is an essence of porous materials, differentiating them from the other substances. The morphology of the pore structure plays a critical role in determining the overall characteristics of the material. In the case of MOFs, the importance of the pore structure on their chemical properties have been widely observed across various applications, including gas storage50, separation51,52, and even catalysis53. Therefore, utilizing information about the continuous shape of MOF surfaces is crucial in understanding their intrinsic nature and thereby their microscopic/macroscopic characteristics. However, most data representations of MOFs and other porous materials for machine learning (e.g., graph representation54) have predominantly focused on the discrete location of atoms or their connectivity. In this context, considering the information on their 3D surfaces could bring a new paradigm in processing porous materials with machine learning models. Therefore, SDFs, known for its capability of delicately describing surfaces, can serve as an appropriate input representation for generating porous materials.

In MOFFUSION, we employed SDFs to describe porous materials for the first time in their generation. SDFs have typically been applied to finite objects, such as 3D assets, and their implementation in repeating systems with periodic boundary conditions (PBCs) has been limited especially in the field of machine learning. Therefore, we used our own methodology to obtain SDFs from the crystal system with considering PBCs, as described in the Supplementary Note #1-1. The procedure for the preparation of periodic SDFs includes conducting the sampling of SDFs in the supercell of the structure, and then taking the minimum value among the replicated SDF sampling points. From the crystal structure and the periodic SDF of MOF-5 shown in Supplementary Fig. 1, it can be verified that the periodic SDF well describes the periodicity of the crystalline structure by capturing the connectivity across the cell boundaries. Notably, the resolution of SDFs is tunable, and we used a resolution of 323 (i.e., sampling a given unit cell by dividing each axis into 32) to balance representation accuracy with memory constraints. We qualitatively validated that a resolution of 323 was sufficient for accurately representing the intrinsic pore structures of various representative MOFs (Supplementary Fig. 2). It is worth noting that during the generation process using PORMAKE, a widely used tool for the generation of hypothetical MOFs, we limited the maximum cell length of the generated structures to 60 Å. Therefore, the length of one grid lattice is no longer than 2 Å, ensuring the most chemical bonds are allocated to more than one grid. However, a finer grid will lead to more detailed pore morphology, which will enhance the overall performance of the workflow.

MOFFUSION architecture

The overall scheme of the MOFFUSION architecture is illustrated in Fig. 1c. MOFFUSION basically follows the architecture of a latent diffusion model and is mainly composed of three parts: a vector quantized-variational autoencoder (VQ-VAE), a diffusion model, and a MOF Constructor. Detailed explanation about the diffusion model part will be covered in the Methods section, and the other two parts will be discussed more extensively in this section and in the Supplementary Note #2.

A VQ-VAE, known for its high training stability and model robustness55, is employed within MOFFUSION for the data compression and restoration (Fig. 2a). Notably, within the convolutional layers of the VQ-VAE architecture, periodic padding (or circular padding) was used to account for the periodicity of MOFs during the processing. The embedding space of the trained VQ-VAE into 2D space is depicted in Fig. 2b, using t-distributed stochastic neighbor embedding (t-SNE)56. The SDFs of MOFs with the top 10 most frequently occurring topologies in the database were assessed, showing that the SDFs of MOFs with the same topologies are clustered and distinguishable from others. This supports that the VQ-VAE was successfully trained, effectively capturing geometric features of SDFs during mapping them into the latent space. Further analysis of the trained VQ-VAE can be found in the Supplementary Note #2-1.

Fig. 2: VQ-VAE for data compression and restoration.
figure 2

a The architecture of VQ-VAE used within MOFFUSION for latent mapping of SDFs to a lower dimension. The VQ-VAE is composed of encoder and decoder, with a codebook used for vector quantization for mapping into a discrete latent space. b A t-SNE plot for MOFs with the top 10 most frequently appearing topologies. Source data are provided as a Source Data file.

Full size image

While new SDFs are being generated through the diffusion model, the actual demand is for MOF structures rather than SDFs themselves. As a result, MOFFUSION features a unique architecture that includes an additional neural network, named MOF Constructor, which maps generated SDFs to MOF structures. MOF Constructor is a ResNet57-based classification model that returns the corresponding topology and building blocks of the given input SDF. MOF Constructor exhibited high prediction accuracy, exceeding 80 % for every building blocks (topology, metal node, organic node, and edge) in the top-5 predictions (Supplementary Fig. 6c). The information on the predicted building components can then be used to generate actual MOF structures using PORMAKE software. Detailed model architecture and in-depth investigation on MOF Constructor can be found in the Supplementary Note #2-3.

Generation performance comparison with precedent models

The generation performance of MOFFUSION was assessed and compared with several precedent models for MOF generation. SMVAE24 is a multi-component VAE architecture that used template-based representation for describing MOFs. MOFDiff45 is a coarse-grained diffusion model which represented the building blocks of MOFs using a coarse-grained manner, further applying assembly algorithm as a post-processing step. GHP-MOFassemble44 is another diffusion model approach for the generation of MOFs, but it was not considered for comparison as it focused on generating organic linkers, rather than the whole structure, and inserted them into pcu topology with fixed metal nodes.

We built a dataset of 247,742 hypothetical MOFs with diverse topologies and building blocks to train MOFFUSION. Our database comprised of 605 different topologies, 432 metal node, 51 organic nodes, and 220 organic edges, spanning a wide diversity of MOF building components, especially in geometric topologies and types of metal nodes (Table 1). Unlike Perov-558 for perovskites, or Carbon-2459 for carbon materials, there exist no publicly shared dataset for MOF generation tasks. All precedent research used their own datasets for training and it is unfeasible to re-train every model with a shared dataset due to the differences in their detailed methodologies. This presents limitations in thoroughly comparing the performance between different models. However, a comparison was conducted as fairly as possible, by focusing solely on the output structures obtained from 10,000 generation attempts for each trained model. The structural validity of the generated MOFs and property statistics for various chemical properties were evaluated, which are widely used metric for the comparison of generative models in materials generation43 (Table 1). The structure was deemed valid if it could be generated using PORMAKE (which accounts for building block compatibility and steric hindrance), and if it successfully underwent geometry optimization without failure. Additionally, property statistics entail an earth mover’s distance (EMD) of chemical properties between the training set and the generated data, assessing the capability of the model in generating realistic samples. Detailed explanations on the evaluation metrics can be found in the Supplementary Note #3-3.

Table. 1 Comparison of dataset diversity and generation performance of MOFFUSION with precedent models
Full size table

MOFFUSION achieved a structure validity of 81.7%, which is higher than other baseline models, as shown in Table 1. The high validity of MOFFUSION stems from its novel architecture and the benefits of SDFs, which provide a deep understanding of the geometric nature of MOFs. The uniqueness and novelty of structures are additional metrics often considered for evaluating generative models. Uniqueness indicates how non-redundant the generated structures are, while novelty measures the percentage of generated structures not included in the training data. For the structures generated using MOFFUSION, 79.9 % were found to be valid and unique, while 58.4% were valid, unique, and novel. This validates MOFFUSION’s capability to generate new structures unseen during the training. However, uniqueness and novelty were not compared with other models, as their respective papers did not report these specific values, except for MOFDiff who reported that its proportion of valid, novel, and unique structures was 30.0%.

MOFFUSION also significantly outperforms baseline models in the property statistics of all three properties (PLD, surface area, and density). The properties distributions of the structures generated through MOFFUSION were almost identical to those comprising the training dataset, as illustrated in Supplementary Fig. 8. This demonstrates MOFFUSION’s ability to effectively learn the probability distribution of the training data, confirming the outstanding similarity between the generated structures and those in the training set in terms of their chemical behavior.

In addition, the interatomic distances of the generated structures were compared with the experimental structures comprising the Open Chemistry Database (OChemDB60). The metal-oxygen bond distances in the generated structures from MOFFUSION showed similar distributions to those of the structures from OChemDB, which further validates the reliability of the generated structure and the entire generation workflow (Supplementary Fig. 9). Furthermore, an ablation study on the SDFs was performed to assess the significance of representing structures as SDFs, as shown in the Supplementary Note #3-4. The comparison with a diffusion model that directly predicts the building block entities highlights that representing structures using SDFs played a significant role in the overall performance of MOFFUSION.

Conditional generation on numeric data

As mentioned earlier, the primary challenge posed in this work was the restricted flexibility in the target properties of porous materials generation, a limitation commonly found in previous inverse design methodologies. While other generative models targeted for MOFs used separate prediction models for target property prediction in their latent space, MOFFUSION employs a classifier-free guidance approach for conditional generation. By directly integrating conditioning into the generative model, classifier-free guidance offers several advantages, including simplicity, flexibility and efficiency in training61. The conditional generation capability of MOFFUSION was tested on diverse data modalities, and the detailed conditioning scheme of each modality can be checked in Supplementary Fig. 11.

First, conditioning on numeric data was evaluated. Among various numeric target properties, gas adsorption capacity was targeted as a representative example. Gas adsorption is of significant interest for MOFs due to their large pore volume and surface area compared to other porous materials. We specifically focused on hydrogen gas, a promising future energy source62,63. The conditional model was trained for hydrogen working capacity (WC), determined by a pressure swing between 5 bar and 100 bar at 77 K. Structures were generated with target WC values of 5, 15, 25, and 35 g/L for evaluation, with a total of 1000 generation attempts for each target. The generated structures exhibited distinctive distributions of WC, with peaks located near the respective target values (Fig. 3). Additionally, adsorption isotherms of representative samples were assessed through GCMC simulations as a sanity check, confirming that structures generated with larger target values exhibited larger WC, and vice versa. Details on hydrogen adsorption simulations can be found in the Supplementary Note #5-2.

Fig. 3: Conditional generation targeted on hydrogen working capacity.
figure 3

The conditional generation capability of MOFFUSION targeted on hydrogen working capacity was tested as a representative example of handling numeric data. Working capacity was calculated based on a pressure swing between 5 bar and 100 bar at 77 K. Structures were generated with target working capacities of 5, 15, 25, and 35 g/L, with a total of 1000 generation trials for each target value. The generated structures exhibited distinctive hydrogen working capacity distributions according to their respective target values. The adsorption behavior of the generated samples was further validated through Grand Canonical Monte Carlo (GCMC) simulations, and their adsorption isotherms were visualized. Within the adsorption isotherms, solid lines are fitted from the dual-site Langmuir model. Source data are provided as a Source Data file.

Full size image

A comparison of MOFFUSION with the genetic algorithm would be valuable, as the latter has been investigated for a similar objective (i.e., the generation of MOFs with desired hydrogen capacity). The genetic algorithm and MOFFUSION share similarities, as both utilize a fixed set of building block for the generation of MOFs. Although the training of MOFFUSION may take considerable time (e.g., several days), in the inference phase, the user can generate a large number of structures (e.g., 10,000) in a few minutes. In contrast, the genetic algorithm necessarily requires numerous cycles for the property of the generated MOFs to converge, which took roughly one week in the workflow from Park et al.18 Furthermore, the genetic algorithm requires entirely new cycles for each different target value (e.g., 5, 15, 25, and 35 g/L), whereas MOFFUSION does not require re-training, making MOFFUSION a more efficient option.

In addition to hydrogen WC, we also evaluated our model on conditioning with pore diameter. We targeted the largest cavity diameter (LCD), which is straightforward, yet one of the most important parameters of MOFs. Structures were generated with 4 different target LCD values of 5, 15, 25, and 35 Å, and the generated structures showed clearly distinctive distributions according to their target values (Supplementary Fig. 12). From these experiments, we validated MOFFUSION’s capability for conditional generation with numeric properties. Notably, we tested both on a simple geometric parameter (LCD) and a relatively complicated and computationally expensive parameter (hydrogen WC), confirming that a wide range of properties can be targeted according to the user’s interest.

Conditional generation on categorical data

Some properties of materials are categorical, which means they can be classified into several labels (or classes) according to certain criteria. A notable example is the magnetism of materials, where materials can be classified as ferromagnetic, paramagnetic and diamagnetic64. For porous materials, properties such as pore dimensionality, thermal/chemical stability and synthesizability are of great interest to both experimentalists and computational scientists65,66. However, these categorical properties are rarely investigated with the purpose of inverse design.

As a case study for the conditional generation of categorical data, MOF topology was selected as the conditioning target. Among the 605 topologies comprising the dataset, the ability of MOFFUSION to generate samples with a certain desired topology was evaluated. As illustrated in Fig. 4a, the latent diffusion model successfully generated SDFs that accompanied the geometric features of the desired topology. The output MOF structures obtained through MOF Constructor exhibited the target topology, achieving an accuracy of 96.0 % in an experiment conducted on 10 randomly selected target topologies with 1000 generation trials each. In a subsequent test focused on metal nodes, MOFFUSION demonstrated its capability to selectively generate structures with the desired metal node (Supplementary Fig. 13). Through these tests, in addition to numeric data, the ability of MOFFUSION to perform conditional generation for categorical data was verified, and its potential extension to other categorical properties is promising.

Fig. 4: Conditional generation with various data modalities.
figure 4

a Conditional generation on categorical data. Through conditional generation tested on topology, MOFFUSION showed exceptional capability in generating SDFs and corresponding MOFs with desired topologies (achieved 96.0 % in accuracy). Generation examples with pcb and lta as target topologies are illustrated. Unit cell boundaries are omitted from the visualization of periodic SDFs. b Conditional generation on text. Capability of MOFFUSION of conditioning with text data was verified. From the experiments conducted on void fraction and topology, MOFFUSION successfully generated structures according to the context given as a natural language. Source data are provided as a Source Data file.

Full size image

Conditional generation on text data

Natural language processing (NLP) is a field of artificial intelligence that focuses on the interaction between humans and computers using natural language67. NLP is a rapidly evolving field with applications across various domains, such as healthcare68 and education69. Understanding human language is also crucial for generative models, as it can significantly lower the barrier for users to access these models. Especially, it empowers nonspecialists without domain knowledge to express desired features through their natural language, thus significantly reducing the difficulty of the entire generation procedure70. It is our opinion that conditional generation based on natural language written as text is one of the directions that generative models will ultimately pursue.

We examined MOFFUSION for the conditional generation based on text data, as one of the first attempts at text-based conditional generation of porous materials. We prepared training data in the form of text containing the information about the void fraction and topology of MOFs (Supplementary Fig. 14a). We utilized SciBERT71, a pre-trained language model for scientific text, to process the text with the expectation that the pre-trained scientific literature would help it understands scientific terms such as ‘void fraction’. As illustrated in Supplementary Fig. 11, we added an additional projection layer to handle the text embedding obtained from SciBERT, tailoring it more specifically to this task. The information processed through the projection layer was integrated into the denoising process of MOFFUSION using cross-attention algorithms72.

Figure 4b illustrates the conditional generation of MOFFUSION trained with text data. With the use of input prompts, MOFFUSION successfully generated structures with the desired void fraction and topology, respectively. Notably, text-based topology conditioning achieved a high accuracy of 88.6% in experiments with random 10 topologies, a value comparable to those obtained by directly utilizing categorical data. Further details on text conditioning, as well as the description on the SciBERT tokenizer can be found in the Supplementary Note #4-4.

The capability of MOFFUSION for text conditioning in MOF generation was verified in this section. Although we used simplified text data with a fixed format for training, one future direction is to use more flexible text formats. The incorporation of flexible training text data would allow users to employ unrestricted and more colloquial input prompts, thereby facilitating smoother communication. Additionally, the utilization of large language models (LLMs) presents an attractive approach for both generating and processing text data73,74. In practice, several previous works have reported the integration of LLMs into materials science, aiming to achieve user-friendly interfaces and applications75,76,77,78. Otherwise, in contrast to our use of the frozen SciBERT model, fine-tuning the language model specifically for the materials domain could also be a promising method for improving the overall performance and enabling more versatile text conditioning.

Multi-target conditioning

Up to this point, MOFFUSION’s capability to handle various data modalities has been demonstrated. While analysis has been focused on a single target property thus far, this section evaluates the conditional generation of MOFFUSION targeting multiple properties simultaneously. The initial focus was on two numeric properties: void fraction and surface area. The conditioning mechanism is the same as in the case of conditioning on a single numeric property (i.e., concatenating a numeric tensor, as depicted in Supplementary Fig. 11), but the number of properties (therefore the number of tensors to concatenate) has increased to two. Conditional generation was tested on two different sets of target values, and the generated structures exhibited distributions of the target properties clustered around their respective target value set (Fig. 5a). This validates that MOFFUSION is capable of handling both void fraction and surface area at the same time during conditional generation.

Fig. 5: Multi-target conditioning and Pore Crafting.
figure 5

a Conditional generation targeted on void fraction (VF) and surface area (SA) simultaneously. The distributions of the generated structures with target values set of VF = 0.6 and SA = 5000 m2/g (blue), and VF = 0.3 and SA = 3000 m2/g (red) are represented. Each condition underwent 1000 generation trials, with star marks indicating the respective target points. Gray points represent the distribution of structures from the training dataset. b Conditional generation targeted on metal nodes and the largest cavity diameter (LCD). Two metal nodes, N206 and N599, were tested with combinations of three target LCD values (5, 15, and 25 Å). Similar to previous experiments, a total of 1000 generation trials were conducted for each condition. c Pore crafting of MOFFUSION to generate structures with user-tailored pore morphology. Structures featuring (i) an empty center pocket, and (ii) a 1D pore channel were successfully generated. Source data are provided as a Source Data file.

Full size image

Subsequently, multi-conditioning targeted on two properties with different modalities was further examined. The type of metal node and LCD were targeted, representing a combination of categorical data and numeric data. Notably, this kind of combination can be particularly interesting for the experimentalists. There could be situations where experimentalists need to fabricate structures exhibiting specific characteristics using particular (or restricted) building components. For instance, one might need a structure composed of Cu paddle wheels (e.g., due to their abundance or its chemical nature such as open metal sites) with a pore size of 15 Å (e.g., for separation purposes). However, it may not be straightforward for experimentalists to determine which topology and organic linker would be appropriate for this task. In such cases, conditioning both on building blocks and target properties could provide valuable guidance.

Similar to the case of considering each single target, pore diameter (a numeric data) was conditioned by concatenating a numeric tensor, while metal node (a categorical data) was processed with an encoder before its incorporation into the diffusion model (Supplementary Fig. 11). Figure 5b illustrates the generation results for two target nodes (N206, N599) and three target pore diameters (5, 15, and 25 Å). MOFFUSION generated structures with desired nodes with an accuracy of 39.1 %, and generated structures exhibited significantly distinctive distributions of LCD with peaks located at the desired target values. This highlights the successful conditioning of MOFFUSION on multi-targets with different modalities, and verifies its ability to handle multiple target data during the generation task.

User-tailored pore generation

In the field of generative models, preserving a designated portion of the original data with modifying or regenerating the rest is often a key focus. In image processing, this process is known as inpainting79, and in 3D objects generation, it is referred to as shape-completion80. By inspired by such studies, we devised an intrinsic feature of MOFFUSION of tailoring the pore structures of the structures being generated. Similarly with designating the region (or portion) that want to be preserved during inpainting or shape-completion, by designating the region within the unit cell where pore to be located, users can finely tune the pore morphology of the structures being generated. We named this process as ‘pore crafting’.

For pore crafting, we employed the blended diffusion methodology proposed by Avrahami et al.81. In their work, to generate a seamless result where the masked region complies with the original image, progressively generated noisy images were kept blended with the corresponding noisy version of the original image of the masked region. We followed similar procedures, where placing pores in a desired region is analogous to blending a given image with a blank sketchbook. During the diffusion process, a region designated to become a pore is kept blended with a latent representation of an empty SDF, resulting in an output that features an empty void in the desired region.

Figure 5c provides qualitative analysis of MOFFUSION’s pore crating capabilities. For the convenience of users, the desired pore region can be specified using the range of the fractional coordinates of each axis. For example, to obtain structures with an empty pocket located at the center, the region of x: [0.25, 0.75], y: [0.25, 0.75], z: [0.25, 0.75] is designated as a desirable pore region. It can be visually confirmed that structures with pockets located in the centers were successfully generated as desired. For the case of a 1D pore channel, a query of x: [0.25, 0.75], y: [0, 1], z: [0.25, 0.75] was provided, resulting in the generation of structures with a channel penetrating the y-axis.

While the generation of structures with desired chemical properties is of great interest, finely tailoring the pore morphology of porous materials is one of the ultimate goals in materials science, which holds immense potentials. For example, through the fine tailoring of pore structures, porous materials with optimal pore morphologies can be designed for much efficient gas storage or separation, and the catalytic activity of the material can be delicately controlled by adjusting the exposure of active sites. Additionally, more precise delivery and release of the drugs could be feasible through target drug-specific pore engineering. MOFFUSION handles this task for the first time, and we hope that this work serves as a cornerstone for achieving comprehensive materials generation with user-tailored pore morphologies.

Discussion

In this work, we present MOFFUSION, a multi-modal conditional diffusion model for the flexible conditioning of metal-organic frameworks generation. To accurately capture the pore morphologies of MOFs, MOFFUSION uses SDFs as an input representation of MOFs, marking the first attempt to utilize SDFs for generative models in the context of porous materials. MOFFUSION’s generation performance significantly outperformed existing methods, demonstrating the novelty of its architecture and the effectiveness of SDFs in describing porous materials. Additionally, MOFFUSION’s capability to handle various data modalities, including numeric, categorical, text, and their combinations is validated. Lastly, we showcase its ability to generate structures with user-tailored pore structures, which holds unlimited potential in various applications.

One observation made throughout the workflow is that, as with other generative models, MOFFUSION performs well with interpolation problems but faces relatively more difficulties with extrapolation. In other words, when there are many data points near a target property value, the model performs well in conditionally generating materials with the desired property, resulting in a sharp distribution in the target property of the generated samples. However, if there are not enough data points near the target value, conditional generation still works but tends to produce a relatively broader distribution. Specifically, the distribution often shifts toward regions where data points are more abundant, and this further emphasizes the necessity of preparing a well-distributed training dataset.

One plausible way to further enhance the versatility of MOFFUSION is by incorporating additional channels (in addition to SDFs) that focus more on chemical features. As SDFs mainly focus on the physical shape of the pore structures, there could exist some limitations in delicately capturing the chemical behavior at the atom-scale. In particular, as shown in Supplementary Fig. 6d of the Supplementary Information, the main reason for the reduction in the accuracy of MOF Constructor was a confusion between similar-looking functional groups. Therefore, to improve MOFFUSION’s performance in understanding the deeper chemical nature, an additional channel that effectively captures the intrinsic chemistry of MOFs could be helpful. An energy grid82, which calculates the interaction energy between probe gas and the given structure at each grid point, is a simple and attractive candidate for this purpose. Furthermore, explicit consideration of translational and/or rotational invariance could be an option worth considering for enhancing the overall performance of the architecture.

Accounting for the synthesizability of structures is also an interesting future direction. A primary challenge in materials design using generative models is the gap between hypothetical structures and those exist in the real world. Guiding the generation process toward the structures likely to be synthesized is considered a practical solution, but assessing the synthesizability of structures in a virtual space is a complex problem. Several metrics have been proposed to estimate the synthetic likelihood of hypothetical MOFs, often based on energy criteria, although these methods are not perfect65. However, we hope to emphasize again that, once a new method for predicting synthesizability is developed, it can be easily incorporated into MOFFUSION’s conditional generation process. Whether the new method predicts the synthesizability as a numeric value (e.g., based on the relative energies of structures), or classifies it (e.g., highly likely, likely, less likely, or not likely), MOFFUSION’s flexible conditioning can accommodate any approach and enable the generation of structures with a high synthetic likelihood. We anticipate the MOFFUSION will find broader application in various meaningful areas or serve as a foundation for developing more versatile and practical methodologies.

Methods

Details on diffusion process

Diffusion model is a branch of probabilistic models that learns a data distribution by denoising a Gaussian variable. It involves two key processes: (1) the forward process (or noising process) and (2) the reverse process (or denoising process), which operate in opposite directions. Within the forward process, which is denoted as \(q\left({X}_{0:T}\right)\), a data sample X is gradually converted into pure Gaussian noise. This transformation is in the form of a Markov chain, which can be expressed as follow:

$$q\left({X}_{0:T}\right)=q\left({X}_{0}\right){\prod}_{t=1}^{T}q\left({X}_{t}|{X}_{t-1}\right),$$
(1)
$$q\left({X}_{t}|{X}_{t-1}\right)={{{\mathcal{N}}}}\left({X}_{t};\sqrt{1-{\beta }_{t}}{X}_{t-1},{\beta }_{t}I\right),$$
(2)

where \({\beta }_{t}\) is a hyperparameter for the noise scheduling. Utilizing the reparameterization trick, X can be sampled at any given time step t during the forward process:

$$q\left({X}_{t}|{X}_{0}\right)={{{\mathcal{N}}}}\left({X}_{t};\sqrt{{\bar{\alpha }}_{t}\varepsilon }{X}_{0},\left(1-{\bar{\alpha }}_{t}\right)I\right),{where} \, {\alpha }_{t}=1-{\beta }_{t},\,{\bar{\alpha }}_{t}={\prod}_{s=1}^{t}{\alpha }_{s},$$
(3)
$${X}_{t}=\sqrt{\bar{\alpha }}{X}_{0}+\sqrt{1-{\bar{\alpha }}_{t}}\varepsilon,\varepsilon \, { \sim } \, {{{\mathcal{N}}}}\left({{{\bf{0}}}},\,{{{\boldsymbol{I}}}}\right)$$
(4)

In the reverse process, which is denoted as \({p}_{\theta }\left({X}_{0:T}\right)\), a data sample is reconstructed by gradually removing noise from a pure Gaussian. This reverse process is also characterized as a Markov chain and is learned using the parameter θ:

$${p}_{\theta }\left({X}_{0:T}\right)=p\left({X}_{T}\right) {\prod}_{t=1}^{T}{p}_{\theta }\left({X}_{t-1}|{X}_{t}\right),$$
(5)
$${p}_{\theta }\left({X}_{t-1}{|X}\right)={{{\mathcal{N}}}}\left({X}_{t-1};{\mu }_{\theta }({X}_{t},t),{\sigma }_{t}^{2}{{{\boldsymbol{I}}}}\right),$$
(6)

where \({p}_{\theta }\left({X}_{T}\right)={{{\mathcal{N}}}}\left({X}_{T};{{{\boldsymbol{0}}}},{{{\boldsymbol{I}}}}\right)\) denotes the standard Gaussian distribution, \({\mu }_{\theta }\left({X}_{t},t\right)\) indicates a denoising network parameterized by θ, and \({\sigma }_{t}^{2}\) is a variance depending on the time step. \({X}_{t-1}\) can be sampled as follows:

$${X}_{t-1}={\mu }_{\theta }\left({X}_{t},t\right)+{\sigma }_{t}\epsilon,\varepsilon \, { \sim } \, {{{\mathcal{N}}}}\left({{{\bf{0}}}},\,I\right)$$
(7)

Then, \({\mu }_{\theta }({X}_{t},t)\) can be simplified as following using the approach proposed by Ho et al.83

$${\mu }_{\theta }\left({X}_{t},t\right)=\frac{1}{\sqrt{{\alpha }_{t}}} \left({X}_{t}-\frac{{\beta }_{t}}{\sqrt{1-{\bar{\alpha }}_{t}}}{\varepsilon }_{\sigma }\left({X}_{t},\,t\right)\right)$$
(8)

where \({\epsilon }_{\sigma }({X}_{t},t)\) is a neural network that predicts noise from the noisy input \({X}_{t}\). \({\epsilon }_{\sigma }({X}_{t},t)\) is trained aiming to minimize the mean squared error between the predicted noise and the actual noise ϵ, as follows:

$$L={{||}{\epsilon }_{\sigma }\left({X}_{t},t\right)-\epsilon {||}}_{2}^{2}$$
(9)

Meanwhile, various conditions (\({c}_{b}\)) was introduced into the generation process, resulting in the reverse process as formulated with \({p}_{\theta }({X}_{t-1}{|X},\,{c}_{b})\), and the final objective for the training is defined as below:

$$L={{||}{\epsilon }_{\sigma }\left({X}_{t},t,\,{c}_{b}\right)-\epsilon {||}}_{2}^{2}$$
(10)

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.