Network structure influences the strength of learned neural representations

Kahn, Ari E.; Szymula, Karol; Loman, Sophie; Haggerty, Edda B.; Nyema, Nathaniel; Aguirre, Geoffrey K.; Bassett, Dani S.

doi:10.1038/s41467-024-55459-5

Download PDF

Article
Open access
Published: 24 January 2025

Network structure influences the strength of learned neural representations

Nature Communications volume 16, Article number: 994 (2025) Cite this article

5060 Accesses
2 Citations
2 Altmetric
Metrics details

Subjects

Abstract

From sequences of discrete events, humans build mental models of their world. Referred to as graph learning, the process produces a model encoding the graph of event-to-event transition probabilities. Recent evidence suggests that some networks are easier to learn than others, but the neural underpinnings of this effect remain unknown. Here we use fMRI to show that even over short timescales the network structure of a temporal sequence of stimuli determines the fidelity of event representations as well as the dimensionality of the space in which those representations are encoded: when the graph was modular as opposed to lattice-like, BOLD representations in visual areas better predicted trial identity and displayed higher intrinsic dimensionality. Broadly, our study shows that network context influences the strength of learned neural representations, motivating future work in the design, optimization, and adaptation of network contexts for distinct types of learning.

Neurocomputational mechanism of real-time distributed learning on social networks

Article 16 February 2023

Constructing graphs from genetic encodings

Article Open access 24 June 2021

Long- and short-term history effects in a spiking network model of statistical learning

Article Open access 09 August 2023

Introduction

Human experience is composed of events, words, and locations that occur in sequences, following predictable patterns. For example, heading to work each day, your route is formed by a series of intersections, as could be conveyed in turn-by-turn directions. Over time, you construct a mental map of not just the intersections but also the route. Likewise, when speaking to a colleague, you predict syllables and words based on your knowledge of the language and scholarly field, as evident in your ability to fill in gaps in the sounds and words that reach you due to, for example, background noise. Even when watching a film, our minds synthesize a temporal sequence of scenes into a multifaceted set of interactions between characters and events. The formation of such mental representations depends upon our ability to detect hidden interactions and to transform them into a predictive model.

Building such statistical models is central to human cognition^1,2,3, because it allows us to accurately predict and respond to future events. One of the most prominent cues to underlying structure is the set of transition statistics between elements, such as how frequently one word precedes another in a lexicon. This cue has been extensively studied in the field of statistical learning⁴, and used to demonstrate that syllable transitions can help demarcate word boundaries as infants learn language^5,6. Such statistical learning occurs in both infants (see ref. ⁷ for an overview) and adults⁸ and is thought to be a fundamental, domain-general learning mechanism because it arises from various sorts of sequences—from tones⁹ and shapes¹⁰ to motor actions¹¹. Human learners likewise exhibit sensitivity to statistics between non-adjacent elements in a sequence^12,13. Despite these strands of evidence, a comprehensive understanding of such non-adjacent statistics is challenging due to the number of possible statistical relations on which human learners might rely.

To study the role of non-adjacent probabilities in statistical learning, one particularly promising approach explicitly models a collection of events and the transitions between them as a graph^14,15. Here nodes in the graph represent events and edges represent possible transitions between any two events. By formally mapping transition probabilities to a graph, one can study how the graph’s topological properties influence human learning. Practically, an experimenter can construct a sequence of events by a walk on the graph, and then assess the participant’s ability to predict upcoming items by measuring their response time to a cover task as the events proceed one by one. Studies of this ilk have demonstrated that topological features impacting learnability include the type of walk¹⁶ and whether the graph contains densely interconnected subsets or modules of nodes¹⁷, a property characteristic of many real-world networks shown to efficiently convey information². Specifically, when graphs contain modular organization, people respond more quickly to transitions between stimuli within the same module than to transitions between stimuli across modules¹⁶. Further, when modularity is eliminated in a controlled fashion (for example, when compared to a locally-equivalent lattice graph), responses are globally slowed. Interestingly, it remains unknown what neural processes might explain the relation between graph topology and behavior.

In contrast to prior work exploring neural representations of items within the same graph^18,19, here we designed a study to ask whether neural representations of stimuli systematically differed between different graph structures. In particular, given the ability of modular structure to efficiently convey information², we hypothesized that the presence of modular structure would lead to robust neural representations, whereas the lack of modular structure would lead to weak neural representations. As a comparison structure, we chose a ring lattice graph, which allowed us to control for local degree while eliminating modularity. For a viewer standing at any given node and viewing immediate neighbors, both of these graphs appear identical, only differing when one can observe the high-level structure or when constructing multi-step predictions. To test our hypothesis, we measured BOLD fMRI activity while participants learned to predict and respond to sequences of abstract shapes. We found that modular structure led to improved discriminability between the neural activity patterns of stimuli, as well as higher intrinsic dimensionality, when compared to the ring lattice. These results demonstrate that neural representations differ systematically in response to different graph structures. Moreover, the work suggests that robust behavior may depend upon our ability to extract organizational patterns such as graph modularity. More broadly, our findings underscore the need to characterize how networks of information shape human learning.

Results

Thirty-four participants (11 male and 23 female) were recruited from the general population of Philadelphia, Pennsylvania USA. All participants gave written informed consent and the Institutional Review Board at the University of Pennsylvania approved all procedures. All participants were between the ages of 18 and 34 years (M = 26.5 years; SD = 4.73), were right-handed, and met standard MRI safety criteria. Two of the 34 participants were excluded because they failed to learn the shape-motor associations (one failed to complete the pre-training; one answered at-chance during the second session), and one additional participant was excluded because we did not accurately record their behavior due to technical difficulties. Hence, all reported analyses used data from thirty-one participants.

Task

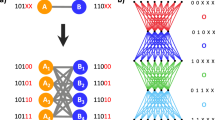
Each participant completed 2 sessions of a visuo-motor response task in an MRI scanner while BOLD activity was recorded. The visuo-motor task consisted of a set of shapes, a set of motor responses, and a graph which both served to map the shapes to responses and to generate trial orderings. Each node in the graph was associated with a shape and a motor response. For the former, we designed a set of 15 abstract shapes (Fig. 1a, left) to be visually discriminable from one another and to evoke activity in the lateral occipital cortex. For the latter, we chose the set of all 15 one- or two-button motor responses on a five-button response pad (Fig. 1a, right). We assigned participants to one of two conditions: a modular graph condition (n = 16) or a ring lattice condition (n = 15) (Fig. 1b, left). Each trial corresponded to a node on the graph, and trial order was determined by a walk between connected nodes. However, subjects were not informed that there would be any such regularity to the order of stimuli. A three-way association between node, shape, and motor response was generated, at random, for each participant: each of the 15 graph nodes was assigned a unique shape and a unique motor response, both chosen at random from the set of shapes and the set of motor responses, respectively (Fig. 1b, right). The mappings of shapes and motor responses were independent of one another, and randomized between participants, allowing us to separate the effects of shape, motor response, and graph.

**Fig. 1: The structure of the graph learning experiment, which incorporated visual stimuli and motor responses on two graph topologies.**

The experiment extended over 2 days. Session one occurred on the first day and session two occurred on the second day. Session one consisted of five task runs, and each run consisted of a training block and a recall block. Session two consisted of eight runs of four recall blocks each (Fig. 1c, top). During each training block, five squares were shown on the screen, horizontally arranged to mimic the layout of the response pad. On each trial, two redundant cues were presented: (1) a shape was shown in all five squares, and (2) the associated motor response was indicated by highlighting one or two squares in red. Either cue alone was sufficient to pick the correct response. The shape was displayed 500 ms earlier than the motor movement in order to encourage participants to learn the visuo-motor pairings. Participants completed 300 trials at their own pace: each trial would not advance until the correct motor response was produced. Once produced, the shape for the next trial would immediately appear, and 500 ms later the square(s) corresponding to the next required motor response would be highlighted. During each recall block, the shape alone was displayed in the center of the screen, and participants were given 2 s to produce the correct motor response by memory. No motor cue was given, unless the participant answered incorrectly: in the latter case, the correct response was shown below the shape for the remainder of the 2 s (Fig. 1c, bottom).

Subjects accurately learn visuo-motor associations

We measured response accuracy to verify that participants learned the task structure and the visuo-motor associations. For participants to attain high response accuracy during the training blocks, they must simply respond to the motor commands presented to them; in contrast, for participants to attain high response accuracy during the recall blocks, they must correctly learn the shape-motor associations. In the training blocks of session one, we observed a mean accuracy of 89.1% by run five, suggesting that participants could produce the motor response with high accuracy when explicitly cued (Fig. 2a, left). In the recall blocks of session one (Fig. 2a, center), we observed a mean accuracy of 74.4% by run five (chance was 6.67%), indicating that participants could also produce the motor response with some accuracy despite the absence of any motor cue. At the beginning of session two, the recall accuracy was slightly lower (at 70.8%), but by the end of session two, the recall accuracy was 96.0%, demonstrating robust recall of motor responses (Fig. 2a, right). Collectively, these data demonstrate that participants were able to learn the motor response assigned to each visual stimuli over a 2-day period. See Supplementary Fig. 3 for individual participants.

**Fig. 2: Participant behavior in the graph learning experiment.**

Whereas response accuracy allows us to assess the learning of visuo-motor associations, response time allows us to assess each participant’s expectations regarding event structure and the underlying graph that encodes that structure. If a participant is able to learn the underlying graph structure, then they can predict which shapes might be coming next (those directly connected to the current shape in the graph), and will respond more quickly. Consistent with this intuition, we found that response times steadily decreased during training, from approximately 1.18 s during run one to approximately 1.01 s during run five (Fig. 2b, left). During the recall blocks, response times depended on the participant’s ability to (1) predict upcoming stimuli and (2) recall the shape-motor association. We found that response times decreased during the recall blocks of session one (1.07 s on run one to 1.00 s on run five; Fig. 2b, center) and of session two (from 0.97 s on run one to 0.89 s on run eight; Fig. 2b, right), demonstrating improvement in prediction and/or recall speed. See Supplementary Fig. 4 for individual participants.

Graph representational structure is not decodable Independently from stimulus and motor structure

Given the behavioral evidence for participant learning, we asked how motor response, shape, and graph were represented in the brain. In what follows, we will describe these three domains in turn. We first sought to find direct evidence of representation of graph structure. We hypothesized that, in-line with prior work, we should be able to decode consistent, subject-specific patterns of activity associated with graph structure in the MTL²⁰. We hypothesized that, if the hippocampus was directly encoding graph structure, we should be able to reliably decode node identity from neural patterns on any given trial. Node identity is fully conflated for each individual subject with visual appearance and motor response, but these three aspects should be separable across participants: if the relationship between patterns of evoked BOLD activity in a given brain region is due to graph structure—rather than response or visual associations—then we should be able to find a consistent pattern of relationships preserved across participants based on graph structure (Fig. 3a).

**Fig. 3: Graph structure is not directly decodable.**

We began by asking whether we could decode trial identity in the hippocampus. To measure the representation of trial information in the brain, we decoded trial identity from patterns of evoked BOLD activity using multi-voxel pattern analysis (MVPA). Each trial evokes a pattern of brain activation, which can be viewed as a point in high-dimensional space, where each dimension corresponds to a different voxel’s BOLD activation. For each of these activation patterns, we used a trained classifier to predict what trial was being experienced by the subject, and we assessed the veracity of that prediction using cross-validation to predict trials in a held-out run (see “Methods”). We examined classification accuracy in left, right, and a bilateral hippocampal gyrus region of interest (ROI) by training a classifier on data from the respective laterality corresponding to seven of the session two recall runs, and by testing our prediction on the remaining run. Data consisted of LS-S β weights resulting from a contrast of the regressor for each trial to a nuisance regressor of all other trials. We find that we were able to decode node identity above-chance in the left hippocampus for lattice graph subjects (t₁₄ = 2.22; p < 0.05) (Fig. 3b), though not for modular graph subjects, and the difference between the two groups is not significant (t₂₉ = 1.51; p < 0.14). Notably, the MTL is prone to low signal-to-noise-ratio fMRI signals due to anatomy²¹, which can be improved by imaging with a reduced field of view at a cost of our ability to infer graph effects elsewhere in the brain; thus this finding may simply suggest a limitation of our whole-brain signal.

Even if we cannot reliably decode trial identity within the hippocampus, it may be that graph structure is encoded more robustly elsewhere in the brain. For each participant, we conducted a whole-brain searchlight where for each voxel we computed the mean RDM in the neighborhood of that voxel, thereby producing a 105-dimensional vector for each voxel composed of the upper right entries in the 15-by-15 RDM. We then calculated the correlation coefficient between that vector and the mean vector of the same voxel in the remaining participants who had been trained on the same graph type. Finally, we took the mean of these correlations across all subjects. This process is similar in principle to that of estimating a lower bound on the noise ceiling²². The resulting map should highlight voxels that displayed similar representational dissimilarity patterns across participants solely due to graph structure, without making any assumptions about the representations themselves or about the dissimilarity pattern. We observed no clear region in which representational structure was shared across participants (Fig. 3c). This variation is perhaps intuitive, as graph structure is experienced indirectly through a sequence of steps between nodes, and also variably in the sense that each participant experienced a different walk through the network. Hence, it is natural to expect high variability in how each participant encodes the graph structure.

High intersubject variability can exist alongside high intrasubject reliability. To understand the potential relation between the two, we measured intrasubject reliability by the consistency of RDMs across runs within each subject. We performed a similar procedure to our earlier searchlight, with the one key difference being that we estimated the correlation between the RDM for each run and the mean of the RDMs for the other runs, in the neighborhood of each voxel. This approach provided us with a consistency map for each subject, and we averaged these consistency maps across subjects (Fig. 3d). We observed two regions of high consistency that overlap with the motor and visual regions, primarily centered on the postcentral gyrus, as well as on the lateral occipital cortex (LOC), regions which we a priori expected to reflect representations of motor and visual aspects of each trial, respectively. This finding suggests that any consistent representation of graph structure may overlap with stimulus shape or motor response encodings; thus, we next asked whether graph structure might nonetheless influence representational structure of stimuli elsewhere, as suggested by previously observed behavioral sensitivity to graph structure.

Representational structure in motor cortex follows response patterns

We next turned our attention to representation of motor response in the brain. Prior work suggests that we should be able to decode consistent, subject-specific patterns of activity associated with each of the 15 one- and two-finger motor responses in both primary and somatosensory motor cortices^23,24,25. We hypothesized that we could reliably decode the associated motor movement from the neural pattern on any given trial, and that the relationships between those neural patterns would be preserved across participants.

As expected, we could predict the identity of the current trial with an accuracy above chance for all 31 participants. That is, the BOLD patterns evoked within each subject in response to finger movements were highly consistent across trials and highly distinct for each movement. Prediction accuracy was above chance for the left hemisphere postcentral gyrus ROI, and for a right hemisphere postcentral gyrus ROI and a bilateral postcentral gyrus ROI in all but one subject (Fig. 4a). Specifically, we found that the left-hemisphere classification accuracy was significantly higher than the right hemisphere classification accuracy, as expected given that task responses were performed with the right hand (two-sided paired t-test; t₃₀ = 6.55; p < 4 × 10⁻⁷). Interestingly, classifying held-out runs using data from both hemispheres did not provide a statistically greater accuracy than classifying using data from the left hemisphere alone (two-sided paired t-test; t₃₀ = −0.64, p = 0.53). These results demonstrate that trial information was robustly represented in the BOLD signal in postcentral gyrus, and that we could decode this information with MVPA, particularly in the hemisphere contralateral to the motor response.

**Fig. 4: Motor responses decoded from the postcentral gyrus.**

While robust, we observed that classification accuracy varied from 5.9% to 17% across subjects in the bilateral postcentral ROI. What drives these differences in classification accuracy? We hypothesized that individual differences in task performance effected differences in classification accuracy. We therefore asked whether our ability to classify trials for a participant was dependent on that participant’s mean response time or mean response accuracy. To answer this question, we used the participant behavior on the recall blocks in session two, which represented post-training task performance (Fig. 4b). We found that response time was a significant predictor of classification accuracy (Table 1), such that classification accuracy was higher for participants with higher average response times than for participants with lower average response times (OLS; β = 0.0191, SE = 0.009, t₂₇ = 2.13, p < 0.043). We did not observe a relationship between classification accuracy and response accuracy (OLS; β = −0.06, SE = 0.081, t₂₇ = −0.73, p = 0.47). The interaction between graph condition and response time was additionally not significant (OLS, β = −0.015, t₂₇ = −1.362, p < 0.19, 95% CI: −0.038 to 0.008). Given that the postcentral gyrus encodes information about motor movements, it is not surprising that the timing of those movements impacted our ability to decode their evoked activity, as increased response times provide a longer readout of activity patterns.

Table 1 OLS regression results for classification accuracy

Full size table

Our classification results suggested that evoked patterns of activity were highly reliable across runs within single subjects. Prior results have suggested that activation patterns vary appreciably between subjects²⁴, but that the relationships between activation patterns are conserved. That is, the distance between representations should be consistent between subjects, even if the specific voxel-wise patterns differ. To assess the preservation of inter-representation differences across subjects, we estimated a representational dissimilarity matrix (RDM) for each subject using a cross-validated Euclidean metric (see “Methods”). In this matrix, we let i, j index pairs of movements, and we let the ij-th matrix element indicate the dissimilarity of movement i’s representation from movement j’s representation. We then averaged the RDMs across participants (Fig. 4c), separately for the two graph conditions (modular and ring lattice). We found that differences in motor representations were preserved across participants and graph conditions, and reflected the movements involved: representations of two-finger movements were consistently more dissimilar to representations of one-finger movements than they were to themselves (two-sided independent t-test; t₉₃ = 9.45, p < 3 × 10⁻¹⁵), and likewise one-finger movement representations were more dissimilar to two-finger movements than they were to themselves (independent t-test; t₅₈ = 4.70, p < 2 × 10⁻⁵). These data demonstrate not only that subjects exhibited reliable patterns of activity evoked by each motor response across the experiment, but also that the relationship between those patterns was reliable between subjects within postcentral gyrus.

Although we chose to consider the postcentral gyrus motivated by prior work, we also performed an exploratory analysis to identify other regions whose motor RDMs were highly similar across participants. For each participant, we repeated the approach from Fig. 3c, conducting a whole-brain searchlight for similar motor representational dissimilarity patterns across participants, without making any assumptions about the representations themselves or about the dissimilarity pattern. We found two regions that exhibit high intersubject similarity after thresholding to control the FWER at p < 0.05 (see “Methods”): a region encompassing both pre- and postcentral gyrus bilaterally (Fig. 4d) and a region in the cerebellum (Supplementary Fig. 2). Thus by constructing an RDM organized by movement, but not by shape or node identity, we identify three regions (precentral gyrus, postcentral gyrus, and cerebellum) which exhibited reliable cross-subject relationships between evoked patterns of activity.

Representational structure in visual cortex reflects both stimulus and graph type

Following our decoding of motor responses, we asked whether visual regions housed reliable encodings of shape identity both within and between participants. Our stimuli were chosen to produce differentiable representations in the lateral occipital cortex (LOC)²⁶. In prior work, the LOC was shown to exhibit task-dependent decorrelations in the neural representations of shape stimuli²⁷. We therefore hypothesized that if the architecture of the graph altered the perception or encoding of stimuli, then that dependence would manifest in LOC. Using data from a separate localizer run, we were able to localize the LOC for each subject by applying a general linear model (GLM) with the following contrast: BOLD responses to a novel set of shape stimuli versus BOLD responses to phase-scrambled versions of those shapes. Note that these novel shapes were generated using the same process as that for the shapes in the training and recall blocks. We then intersected the two largest clusters from the localizer with a surface-defined LOC ROI and ordered the voxels in this intersection by their z-statistics from the localizer contrast. We chose the 200 voxels with the highest z-scores from each hemisphere to define left and right ROIs, and we chose the top 600 voxels to define a bilateral ROI. We then studied whether stimulus coding in this ROI exhibited similar properties to the motor representations we could reliably decode in postcentral gyrus.

As before, we first wished to verify that trial-by-trial representations were consistent within subjects. We found that we could predict trial identity on a held-out run remarkably well across all participants and ROI choices (Fig. 5a). We averaged the classification accuracy across all 8 folds and observed that it was greater than chance (6.67%) for all participants. We also observed higher classification accuracy in participants trained on the modular graph than in participants trained on the lattice graph (Mixed ANOVA, F(1, 29) = 14.14, p < 8 × 10⁻³). Although the above classification accuracy was averaged only over correct trials, the classifier was trained on all trials, and we wished to verify that this choice did not bias our results. Re-running the analysis but only training on correct trials, we found that classification accuracy was again higher for participants trained on the modular graph than for participants trained on the lattice graph (Mixed ANOVA, F(1, 29) = 18.488, p < 2 × 10⁻⁴). These data demonstrate that trial identity could be reliably decoded within-subject from activity within LOC.

**Fig. 5: Trial identity decoded from the lateral occipital cortex.**

To evaluate whether classification accuracy differed by graph, we fit a linear regression model that predicted classification accuracy from both response time and graph condition (Fig. 5b and Table 1). We found that graph condition (modular versus ring lattice) was a statistically significant predictor of classification accuracy (OLS, estimated increase of 5.3% for the modular graph, t₂₇ = 2.15, p < 0.042, 95% CI: 0.002–0.104). This result suggests that there are fundamental differences in learned representations between the two training regimens. In contrast to our findings in the postcentral gyrus, the classification accuracy in LOC was not significantly predicted by response time (OLS, β = 0.024, t₂₇ = 1.13, p < 0.27, 95% CI: −0.019 to 0.067), ruling out the possibility of our results being driven solely by behavior. The interaction between graph condition and response time was not significant (OLS, β = −0.006, t₂₇ = −0.227, p < 0.83, 95% CI: −0.059 to 0.048). Thus we find that graph structure induced a significant difference in our classification accuracy of trials, and that difference, as is evident in Fig. 5b, was not driven by response time differences alone.

Given the reliable patterns of activity in LOC, we next computed a mean RDM in the LOC across subjects as in Fig. 4c, but arranged the RDM by shape rather than by motor command. Crucially, this RDM was not a reordering of the mean motor response RDM, as the correspondence between shapes and motor responses was distinct for each subject. In computing the mean RDM, we averaged data separately for modular and ring lattice conditions. Across both graphs, we found a consistent distance relationship between shape representations, which we find to be significant when comparing the modular and ring lattice RDMs (Kendall’s τ = 0.390, p < 3.81e−9, note the symmetry between the upper and lower triangles of Fig. 5c). This finding suggests that the sensitivity of the LOC to individual shape features was shared across subjects.

The analyses we have described thus far focused on the LOC. Next, similar to Fig. 4d), we performed an exploratory analysis to determine whether other areas of the brain displayed RDMs that were consistent across subjects when the RDMs were arranged by shape. We computed the correlation between a single subject’s shape RDM and the average shape RDM across all other subjects, in the neighborhood of each voxel (Fig. 5d). As before, we took the mean of this correlation estimated for all subjects, and applied a threshold to control the FWER at p < 0.05 (see “Methods”). We observed a single region of high between-subject similarity. As expected, this region was centered on the LOC and extended posteriorly through early visual cortex. Interestingly, we observed no other regions where RDMs were consistent between subjects when arranged by shape. These results largely mirror our findings with motor response activity patterns. However, here we demonstrate that by simply rearranging our RDM we can instead isolate relationships between activity driven by visual properties of the stimuli. Intriguingly, we observe a difference in decoding accuracy between graph conditions, suggesting that graph structure modulates the encoding of individual stimuli in LOC.

Representation and dimensionality differ between graph structures

By searching for regions which exhibited significant intrasubject reliability across runs, we identified two regions in which RDMs were consistent across blocks for individual subjects. We then organized the RDMs according to stimulus shape and motor command, and confirmed that these regions exhibited significant intersubject reliability in which patterns of representational dissimilarity were shared across participants. This inter-subject similarity was likely driven by aspects of trial identity: one- and two-finger movements for the motor response, and aspect ratio or curvature for stimulus shapes. This suggests that any consistent representation of graph structure may spatially overlap with stimulus shape or motor response encodings.

Consistent with this suggestion, we observed that graph type was a significant predictor of classification accuracy in LOC (Fig. 5a, b), whereby classification accuracy was greater in the modular condition than in the lattice condition. One possible explanation for this observation is that trial types were more distinguishable from one another due to more distinct representations: when a subject experienced the modular graph, the representation of shape one may simply have been further away from the representation of shape two in representational space. To evaluate the validity of this possible explanation, we calculated the average distance between representations in the bilateral LOC ROI by computing a Euclidean distance RDM for each run, and then taking the mean of the upper-right off-diagonal elements for each subject (Fig. 6a, left). We observed that discriminability was significantly greater in the modular graph than in the lattice graph (two-sided independent t-test; t₂₉ = 3.04, p = 0.005). That is, the modular condition induced more separable mean activity patterns between pairs of trial types than did the lattice condition.

**Fig. 6: Effects of graph structure on representation.**

Another possible explanation for the greater classification accuracy observed in the modular graph is that trial-to-trial replicability may be higher when a subject experiences the modular graph: a given shape may evoke a more consistent neural representation on each appearance of that shape. To evaluate this possibility, we calculated the average consistency of representations in the same bilateral LOC ROI by taking the mean representation for each run and trial type, and then calculating the mean distance of that representation from the representations of the other runs (Fig. 6a, right). We observed that patterns were more consistent in the modular graph than in the lattice graph, as evident in lower distances between trial repetitions (two-sided independent t-test; t₂₉ = 3.60, p < 0.002). Taken together, these two findings suggest that the modular graph leads to more distinguishable and consistent trial representations, which in turn could drive the heightened classification performance.

The observed increase in neural discriminability in LOC suggests that behavioral discriminability might similarly differ between graph conditions. To test for this possibility, we recruited an additional group of subjects and trained them on the same set of stimuli associated to either a modular or lattice graph. We then tested whether subjects could more quickly discriminate between stimuli presented on the modular graphs than between the same stimuli presented on the lattice graph (Supplementary Fig. 5). We found that response times when discriminating between shape pairs were highly correlated with their representational distance in LOC (Mixed-Effects Model, t₉₃ = 4.33, p < 0.0001). Notably, though, we did not observe a significant difference based on graph type (Mixed-Effects Model, mean = 0.07 ms, t₄₈ = 0.866, p < 0.392). These behavioral results suggest that while subjects in the modular condition exhibited more distinguishable LOC activity patterns than did subjects in the lattice condition, these differences in stimulus representation do not directly relate to behavioral distinguishability of stimuli.

A third possible explanation for the greater classification accuracy observed in LOC in the modular graph is the dimensionality of the representation. If one graph topology allows a participant to encode representations in a higher dimensional space, then those representations could also be made more distinct from one another. Note that our ability to classify trials using an SVM relies on finding a hyperplane separating the trial types. Intuitively, if the trial types lie in a higher-dimensional space, then finding a separating hyperplane becomes an easier task than if the trial types lie in a low-dimensional space. To determine whether dimensionality plays a role in the LOC’s representations, we computed a quantity called the separability dimension, which measures the fraction of binary classifications that can be implemented using our trial types (see refs. ^28,29 and “Methods” for details). While our previous neural discriminability finding examined the ability to distinguish between pairs of trial types, dimensionality addresses the ability to distinguish between larger groupings of trial types, where higher dimensionality enables encoding increasingly complex relationships between trial types. Consistent with our intuition, we found that dimensionality was higher in the modular graph condition than in the ring lattice condition (Fig. 6b). Interestingly, this difference was apparent in LOC where we observed a difference in classification accuracy between graph conditions, but not present in the postcentral gyrus where we observed no difference in classification accuracy between graph conditions (Supplementary Fig. 1).

Functional connectivity during learning predicts subsequent decoding

Thus far, we have examined differences in stimulus representations within individual regions of the brain after subjects have successfully learned to perform the task. We have observed significant differences in stimulus-evoked activity patterns in the LOC between subject groups: that is, more robust decoding accuracy alongside heightened intrinsic dimensionality of the associated neural activity in subjects exposed to the modular graph. Moreover, there exists significant within-group variability in decoding accuracy: that is, differences unrelated to the statistical structure of the graph traversals encountered. Thus, we asked whether individual differences in decoding accuracy could be explained by distinct patterns of connectivity between the aforementioned regions during learning. For example, motor activity in postcentral gyrus might be directly driven by visually-evoked activity in LOC, or it might be simultaneously driven by predictive mechanisms in the MTL. Moreover, communication between the MTL and LOC might reflect the degree to which subjects are learning the underlying statistical structure, versus simply learning to robustly respond to each stimulus at it is encountered.

To address how regional interactions during task acquisition contributed to day 2 learned stimulus representations, we computed the degree of static functional connectivity between brain regions during each learning block on day 1 of the experiment. We focused on the three pairwise connections between the regions in which we primarily expected involvement for the current task: left LOC, left postcentral gyrus, and left MTL. We then averaged these FC values for each subject for each of the three region pairs, providing a per-subject summary of regional interactions during task acquisition. We fit mixed-effects linear regression models which predicted day 2 classification accuracy in each of the three regions (left hippocampus, left LOC, and left postcentral gyrus) as a function of all three day 1 FC values.

We observed that individual differences in classification accuracy on day 2 could be predicted by differences in FC during learning after correcting for multiple comparisons (Table 2). In postcentral gyrus, increased decoding accuracy was predicted by higher LOC/postcentral FC as well as by lower LOC/MTL FC during learning. Intriguingly, this relationship was reversed for hippocampal decoding, where increased decoding accuracy was predicted by lower LOC/postcentral FC and by higher LOC/MTL FC, alongside MTL/postcentral FC being a negative predictor of hippocampal decoding. In LOC, only MTL/postcentral FC was predictive of decoding accuracy, with higher FC predicting higher decoding accuracy. These findings suggest that individual differences in FC during task acquisition are predictive of later differences in strength of stimulus representation among brain regions crucial to the performance of this task, perhaps reflecting distinct roles of involvement of the MTL among participants.

Table 2 Functional connectivity predicts decoding accuracy

Full size table

Discussion

Humans deftly learn the networks of interactions underlying complex phenomena such as language or music³⁰. Behavioral and neural evidence demonstrates that the way we learn and represent stimuli is modulated by the temporal structure in which we experience those stimuli^31,32. Moreover, recent studies indicate that humans may learn to represent the interaction network itself. For example, when stimuli are grouped into clusters, a phenomena commonly observed in natural settings², learner response times to those stimuli are modulated by whether adjacent stimuli are situated in the same cluster, even when all transition probabilities (and thus predictive information) are held constant¹⁶. This effect is shown to be robust to types of stimuli³³ and significant topological variation³⁴. Moreover, learners respond more swiftly to a sequence drawn from a topology with such clusters compared to a topology without such clusters¹⁷. Collectively, these findings suggest that humans can learn properties of graph structure such as modular organization, and can leverage that structure to create more effective predictions. Converging neuroimaging evidence suggests that neural representations of stimuli encode properties of the interaction networks, including cluster identity¹⁸ and graph distance between items^19,35. To date, however, it remains unclear how such graph-induced representation structure differs when the same elements are arranged in a distinct organizational pattern.

In the current study, we addressed this question by training human subjects to respond to sequences of paired visual and motor stimuli. We then tested whether representations of those stimuli differed when we performed a controlled manipulation of the sequence. Specifically, each subject learned a sequence based on either a modular graph or a ring lattice graph, in both cases with no explicit knowledge of the underlying graph. Subjects underwent 1 day of training followed by a second day in which they were asked to produce the motor response associated with each visual stimulus in the sequence. We found that we could reliably decode stimulus identity from the neural representation in both postcentral gyrus and lateral occipital cortex. Further, we observed consistent representation structure of our stimulus set across subjects in these regions, when comparing motor response in postcentral gyrus and stimulus shape in lateral occipital cortex. Within lateral occipital cortex, but not postcentral gyrus, our classification ability was modulated by graph type, with the modular graph leading to significantly higher classification scores than the ring lattice graph. This classification difference due to graph was accompanied by changes in the representation structure: modular representations were both more consistent across trials and more separable between different trial types than were representations from the ring lattice graph. Finally, we found that representations in lateral occipital cortex from the modular graph exhibited higher separability dimension than did those from the ring lattice graph. Taken together, these results show how graph structure can modulate learned neural representations of stimuli, and that modular structure induces more effective (discriminable) representations of stimuli than does ring lattice structure.

Modular graphs enable effective neural representations

There is strong theoretical justification to expect more robust representations to arise from the modular graph than from other non-modular graphs. Using information theory, prior work has shown that graph organizations characterized by hierarchical modularity facilitate efficient transmission of information². Perhaps due to that functional affordance, this type of organization is commonly observed in many real-world networks such as those of word transitions, semantic dependencies, or social relationships. The informational utility of hierarchically modular networks arises in part from the fact that such networks exhibit high entropy, thereby communicating large amounts of information. It also arises in part from the expectations that humans form about clustered structures: preferentially predicting transitions that remain within a cluster, thereby accurately foreshadowing upcoming stimuli³⁶. Here in our study, the modular graph composed of three clusters of five nodes is more highly clustered than the ring lattice graph. This fact can be clearly seen visually, but it can also be quantified by the clustering coefficient, which is defined as the fraction of a node’s neighbors that are connected to one another. The average clustering coefficient of the modular graph is 0.7 and of the ring lattice graph is 0.5. Indeed, we found that participants formed more robust representations of stimuli from the modular graph than from the lattice graph. In other words, the modular graph is more similar to graphs encountered in the real world, to which our expectations are tuned, and is also better capable of conveying its structure.

Response time differences do not explain LOC graph effects

Decoding accuracy in postcentral gyrus was significantly predicted by mean subject response time, explaining some of the observed between-subject variance. This is not particularly surprising, if only because a longer response time would lead to a longer and thus perhaps more robust readout of neural activity. Nonetheless, fully ruling out a non-spurious connection between response time and decoding accuracy would require careful controls. Crucially though, we find that this relationship was not significant in LOC, eliminating a potential confound in explaining our difference in classification accuracy between graph types. In fact, Fig. 5b suggests a clear modulation of graph type on top of any (non-significant) response time effects.

Neural representations from modular graphs are high dimensional

We observed that the neural representations developed during exposure to a sequence drawn from a modular graph tend to be high dimensional. Prior work has shown that high dimensionality of neural representations is associated with faster learning and more efficient stimulus embedding²⁹. Here, we extend the current knowledge in the field by demonstrating that more efficient graph structures lead to higher dimensional neural representations. It is possible that this association between topology and dimensionality arises from the fact that the modular graph can be neatly separated into clusters; coding by cluster could allow the brain to use a high-dimensional embedding. The nature of this higher-dimensional encoding remains a topic for future study, and could be pursued by investigating the learning of a variety of graphs with and without hierarchical structure.

Graph-dependent adaptation decorrelates shapes

Our observation—that graph topology can be used to decorrelate neural responses to shape—is of particular relevance to the study of neural adaptation. An oft-hailed mechanism of neural adaptation is the decorrelation of neural responses among stimuli^37,38. Such decorrelation is thought to allow the brain to become attuned to task-relevant distinctions between stimuli³⁹. Prior work has observed decorrelation in BOLD responses to visual stimuli in the lateral occipital cortex (Mattar et al.²⁷). Specifically, this study found that training on two classes of stimuli caused representations evoked by the two classes in the lateral occipital cortex to decorrelate from one another. Such increased neural separability of stimuli may support behavioral discrimination between important stimulus classes.

Here in our study, all subjects learned the same set of 15 previously unseen shapes. Basic visual properties of the shapes are expected to drive the BOLD response in the lateral occipital cortex²⁶. However, if these properties alone drive the BOLD response, then we would expect similar representational structure between activity patterns in both modular and ring lattice subjects. Instead, we found that we could more accurately classify stimuli from neural representations when participants experienced sequences determined by the modular graph than when they experienced sequences determined by the ring lattice, suggesting that BOLD responses are driven by non-visual factors. This classification difference was accompanied by two observed differences in pattern distance: First, activation for a given trial type was more stable across trials in the modular graph than in the ring lattice graph, as evidenced by the lower mean pattern distance between trial repetitions. Second, activation was more distinct between trials of different types: the average distance between different trial types was higher in the modular graph than in the ring lattice graph. In summary, we observe that graph structure drives a difference in representation fidelity, inducing both more reliable and more separable patterns.

Motor cortex displays strong organizational patterns

The approach that we use here—representational similarity analysis or RSA—has been commonly used to understand how neural representations of stimuli are encoded. Rather than asking which neurons or voxels encode a stimulus, we can study how the patterns of neurons or voxels relate across stimuli. Further, we can compare neural distances to those predicted by real-world stimulus properties, elucidating which real-world properties drive the brain’s organization. For instance, the same single-digit finger movement in different people elicits vastly different patterns of neural activation in primary motor cortex, while the relationship between activity patterns of different fingers is highly conserved across people²⁴. Prior work has demonstrated that everyday usage patterns predict motor representations better than musculature, a result that fundamentally underscores the importance of relationships rather than the movements themselves. Similar findings have also been reported for motor sequences²⁵.

Here in our study, we recorded neural activity of both single- and multi-finger movements, and found that these relationships were highly preserved between participants and between graphs (Fig. 4c). This observation raises an intriguing question for further study: Why is the difference in representational dimensionality between conditions observed in LOC but not in motor cortex? Strikingly, in the postcentral gyrus we found a clear separation of one-finger and two-finger response patterns, where one-finger response patterns were similar to other one-finger response patterns, and two-finger response patterns were similar to other two-finger response patterns. We note that our ROI encompasses a larger area than that used in prior work²⁴, and studies of multi-finger sequences, while distinct from multi-finger movements, have observed that these increasingly complex movements elicit distinct representations in areas further from the central sulcus²⁵. Further investigation is necessary to determine whether (and to what degree) the dissimilarity patterns we observed are influenced by differences in cortical location of one-finger and two-finger motions.

Functional connectivity reveals distinct patterns of regional interactions

While the current study has primarily focused on between-group differences driven by the statistics of modular vs. ring lattice graph traversals, we observed significant variability in classification accuracy both between and within groups. This variability existed even in the hippocampus, despite previous work suggesting hippocampal involvement in similar tasks^4,40,41. It is not particularly surprising that subjects might exhibit variability in hippocampal recruitment. Although the task in this study was designed to encourage prediction of upcoming stimuli, participants can also perform the task solely through learning shape-motor associations. Moreover, the complexity of learning such associations in the current study may have competed for attention with learning to predict upcoming stimuli.

Indeed, we found that classification accuracy in hippocampus and postcentral gyrus exhibit inverse patterns of association with FC during task acquisition. Whereas high LOC/postcentral FC and low LOC/MTL FC predicts high postcentral classification accuracy, we observe the opposite for hippocampus classification accuracy. This finding suggests that increased FC between visual and motor regions is reflective of heightened reliance on robust stimulus representations directly within motor cortex, and in turn less reliance on hippocampal representation. By contrast, increased FC between visual cortex and MTL reflects a later role for MTL in predicting upcoming stimuli, perhaps reflecting competing mechanisms for task performance that vary across subjects. Future research might elucidate the degree to which these functional connections track separable processes, and/or relate to distinct patterns of behavior reflecting differing roles of the hippocampus in tasks that benefit from—but do not require—robust prediction.

Moreover, the relationship between FC during task acquisition and subsequent stimulus representation suggests that the two measures may be reflective of a single learning process. To better understand this process, future work might examine the dynamics between FC and representation during learning. If, as we hypothesize, the increase in FC between visual and motor regions is directly related to the strength of regional representations, then we would expect that FC would shift alongside local representations during the learning process. In the current study, we measured FC and representation in isolation: FC was measured during the learning process, and representational structure was measured only after it was assumed that participants had robustly learned the task structure. In future work, additional measurements of representational structure while learning over an extended time scale could serve to clarify this relationship, as well as elucidate a trade-off between hippocampal and visuo-motor predictive representations across the learning process.

Limitations

Prior work on learning modular structure has found that graph information such as cluster identity is represented in the medial temporal lobe (MTL)^18,42, an area also shown to encode distances between items¹⁹. In the current study, we did not observe any graph-dependent effects in the MTL, but instead in the lateral occipital cortex. A number of factors could give rise to this difference. First, prior studies, to our knowledge, did not show evidence that graph structure was directly encoded. Metrics such as distance and cluster identity pool over many trials, and may allow for greater power to detect graph-related effects in the presence of noise. Indeed, the MTL is prone to low signal-to-noise-ratio fMRI signals due to anatomy²¹. This can be improved by imaging with a reduced field of view, but at a limitation of our ability to infer graph effects elsewhere in the brain. Another possibility is that our analysis is constrained by the number of subjects in our analysis. While we observed robust decoding results in LOC as well as in postcentral gyrus, suggesting that we should be capable of decoding robust within-subject representational structure, the limited sample size in the current study allows the possibility of mis-estimation of effect sizes⁴³. Future work may be well-served by increased sample size, as demonstrated by the more robust behavioral effects of graph structure typically observed in larger behavior-only studies^16,17. Additionally, our task is relatively complex. Behavioral work on graph learning has frequently required participants to learn image orientations^16,20 or to anticipate motor responses¹⁷ but here participants must learn a mapping between both images and motor responses. Indeed, participants are still learning the shape-motor response pairings up through the end of the second session, as response accuracy continues to increase (Fig. 2b, right). The complexity of the task, requiring participants to learn not only visual stimuli but the stimulus-motor response pairings as well, could require additional training for the MTL to detect temporal regularities. Given that plasticity in the lateral occipital cortex can be driven by demands of stimulus discriminability²⁷, additional training may be needed for the hippocampus to extract temporal statistics.

Conclusion

In this study, we expand upon prior behavioral evidence in graph learning, where graphs with modular structures produce faster response times in learners, suggesting that those learners can form more accurate predictions. Learners were successfully able to learn and recall a mapping of 15 novel shapes to motor movements, combining behavioral paradigms from prior graph learning work. We observed that modular graphs enable more consistent and distinct representations when compared to a ring lattice, and in turn allow better prediction of what a participant is responding to using machine learning. This representational difference was present in the lateral occipital cortex, a region sensitive to properties of the visual stimuli used in this task, and was accompanied by increased dimensionality of representations, a feature known to accompany effective learning. Our results motivate future work to better understand the nature of these representational changes, as well as generalizability to broader sets of graph structures.

Citation diversity statement

Recent work in several fields of science has identified a bias in citation practices such that papers from women and other minority scholars are under-cited relative to the number of such papers in the field^{44,45,46,47,48,49,50,51,52}. Here we sought to proactively consider choosing references that reflect the diversity of the field in thought, form of contribution, gender, race, ethnicity, and other factors. First, we obtained the predicted gender of the first and last author of each reference by using databases that store the probability of a first name being carried by a woman^48,53. By this measure (and excluding self-citations to the first and last authors of our current paper), our references contain 13.18% woman(first)/woman(last), 7.12% man/woman, 26.79% woman/man, and 52.92% man/man. This method is limited in that (1) names, pronouns, and social media profiles used to construct the databases may not, in every case, be indicative of gender identity and (2) it cannot account for intersex, non-binary, or transgender people. Second, we obtained predicted racial/ethnic category of the first and last author of each reference by databases that store the probability of a first and last name being carried by an author of color^54,55. By this measure (and excluding self-citations), our references contain 6.03% author of color (first)/author of color(last), 14.19% white author/author of color, 22.81% author of color/white author, and 56.98% white author/white author. This method is limited in that (1) names and Florida Voter Data to make the predictions may not be indicative of racial/ethnic identity, and (2) it cannot account for Indigenous and mixed-race authors, or those who may face differential biases due to the ambiguous racialization or ethnicization of their names. We look forward to future work that could help us to better understand how to support equitable practices in science.

Methods

Participants

Thirty-four participants (11 male and 23 female) were recruited from the general population of Philadelphia, Pennsylvania USA. All participants gave written informed consent and the Institutional Review Board at the University of Pennsylvania approved all procedures. All participants were between the ages of 18 and 34 years (M = 26.5 years; SD = 4.73), were right-handed, and met standard MRI safety criteria. Two of the thirty-four participants were excluded because they failed to learn the shape-motor associations (one failed to complete the pre-training; one answered at-chance during the second session), and one additional participant was excluded because we did not accurately record their behavior due to technical difficulties. Hence, all reported analyses used data from thirty-one participants.

Task

Stimuli

Visual stimuli were displayed on either a laptop screen or on a screen inside the MRI machine using PsychoPy v3.0.3 and consisted of fifteen unique abstract shapes generated by perturbing a sphere with sinusoids using the MATLAB package ShapeToolbox (Fig. 1a, left). Each shape consisted of two sinusoidal oscillations. Each oscillation could vary in amplitude (either 0.2 or 1), angle (0, 30, 60, or 90 degrees), frequency (2, 4, 8, 10, or 12 cycles/2π), and the second oscillation could also vary in phase relative to the first oscillation (0 or 45 degrees). Out of the set of 3200 permutations, we selected a set of 15 visually distinct shapes for the main experiment. A second set of 15 visually distinct shapes was selected from the same set for the localizer. The same set of stimuli was used for all participants, albeit in different order. Five variations of each shape were also created through scaling and rotating (scale/rotation pairs were 100%/0 degrees, 95%/5 degrees, 100%/10 degrees, 95%/15 degrees, and 100%/20 degrees) and the appearance of variations was balanced within task runs so as to capture neural activity invariant to these properties.

Each shape was paired with a unique motor response. Possible motor responses spanned the set of all fifteen one- or two-button chords on a five-button response pad (Fig. 1a, right). The five buttons on the response pad corresponded to the five fingers on the right hand: the leftmost button corresponded to the thumb, the second button from the left corresponded to the index finger, and so on. In addition to the shape cue, motor responses were explicitly cued by a row of five square outlines on the screen, each of which corresponded to a button on the response pad. Squares corresponding to the cued buttons turned red; for instance, if the first and fourth squares turned red, a correct response consisted in the thumb and ring finger buttons being pressed.

Participants were assigned one of two graph types: modular or ring lattice. Both graph types were composed of fifteen nodes and thirty undirected edges such that each node had exactly four neighbors (Fig. 1b, left). Nodes in the modular graph were organized into three densely connected five-node clusters, and a single edge connected each pair of clusters. Each node in a participant’s assigned graph was associated with a stimulus-response pair (Fig. 1b, right). While the stimulus and response sets were the same for all participants, the stimulus-response-node mappings were random and unique to each participant. This mapping was consistent across runs for an individual participant. The order in which stimuli were presented during a single task run was dictated by a random walk on a participant’s assigned graph; that is, an edge in the graph represented a valid transition between stimuli. No other meanings were ascribed to edges. Walks were randomized across participants as well as across runs for a single participant. Two constraints were instituted on the random walks: (1) all walks were required to visit each node at least ten times, and (2) walks on the modular graph were required to include at least twenty cross-cluster transitions. Subjects were not told about the underlying graph type and statistical organization.

Pre-training

Prior to entering the scanner, participants performed a “pre-training” session during which stimuli were displayed on a laptop screen and motor responses were logged on a keyboard using the keys “space”, “j”, “k”, “l”, and “;”. Participants were provided with instructions for the task, after which they completed a brief quiz to verify comprehension. To facilitate the pre-training process, shape stimuli were divided into five groups of three. First, participants were simultaneously shown a stimulus and its associated motor response cue, and then were asked to press the associated button(s) on the keyboard. Next, participants were shown the stimulus alone and asked to perform the motor response from memory. If they did not respond within 2 s, the trial was repeated. If they responded incorrectly, the motor response cue was displayed. Once the participant responded correctly, the same procedure was repeated for the other two stimuli in the subset. Then, participants were instructed to respond to a sequence of the same three stimuli, presented without response cues. The sequence was repeated until the participant responded correctly for 12 consecutive trials. This entire process was repeated for each three-stimulus subset. The three stimuli in a given subset were always chosen so that none were adjacent to one another in the graph dictating the order of the sequence used during the “Training” stage (see below).

Training

During the first scanning session, participants completed five runs each consisting of a “training” and “recall” block inside the MRI scanner. A training block consisted of 300 trials and was designed to elicit learning of graph structure as in ref. ¹⁷. During each trial, participants were presented with a visual stimulus consisting of a row of five square outlines, each of which contained the same abstract shape (Fig. 1c). Five hundred milliseconds later, one or two of the squares turned red. Using a five-button controller, participants were required to press the button(s) corresponding to the red squares on the screen. If a participant pressed the wrong button(s), the word “Incorrect” appeared on the screen. The following stimulus did not appear until the correct buttons were pressed. Participants were instructed to respond as quickly as possible. Sequences were generated via random walks on the participants’ assigned graphs.

Recall (session one)

At the end of each training run, participants completed 15 additional “recall” trials during which each shape was presented without a motor response cue, requiring participants to recall the correct response. This block was intended to measure stimulus-response association learning, as well as to prepare participants for the extended recall phase in session two. A brief instructional reminder was displayed before the start of the block. On each trial, the target stimulus was displayed in a single large square in the center of the screen. Participants were given 2 s to respond to each stimulus; if they did not respond within this time, the trial was marked as incorrect. If they responded incorrectly, the trial was marked as incorrect and the motor response cue was displayed below the shape for the remainder of the 2 s. If they responded correctly, the outline of the square containing the shape turned green. The orderings of all recall trials were also determined by walks on the participants’ assigned graphs. Trials were shown with a variable ITI between presentations. The ITIs in each block varied between 2 and 4 s (mean = 2.8 s, total 42 s) with an additional 6 s delay separating the end of the last recall trial in a block from the start of the first training trial in the subsequent run.

Recall (session two)

During the second session, participants completed eight recall runs, each comprised of four recall blocks of 15 trials, for 60 trials per run. These extended recall runs were designed to allow measurement of the neural patterns of activation associated with each of the stimuli. Each constituent recall block was identical to the recall blocks presented in session one. To generate a continuous walk for each run (across the four blocks), the first block in each run began on a randomly selected node, and each subsequent block in the run was rotated to be contiguous with where the last set ended. This process ensured that the full 60 trials within a block constituted a valid random walk, despite not being generated as a single walk. Blocks 1, 2, and 4 followed a random walk, whereas the third block followed a Hamiltonian walk, in which every node was visited exactly once. Across the full run of 60 trials, each node was required to be visited at least twice. If not, the walk for the run was discarded and a new walk was generated. For the modular graph, the Hamiltonian walk proceeded clockwise on runs 1, 3, 5 and 7 and counter-clockwise on runs 2, 4, 6, and 8. On the ring lattice, the Hamiltonian walk was not generated with any directionality. Hamiltonian and random walks were analyzed together.

Imaging

Acquisition

Each participant underwent two sessions of scanning, acquired with a 3T Siemens Magnetom Prisma scanner using a 32-channel head coil. In session one, two pre-task scans were acquired as participants rested inside the scanner, followed by five task scans and two post-task resting-state scans. In session two, two pre-task scans were acquired, followed by eight task scans, two post-task resting-state scans, and lastly an LOC localizer. Imaging parameters were based on the ABCD protocol⁵⁶. Each scan employed a 60-slice gradient-echo echo-planar imaging sequence with 2.4 mm isotropic voxels, an iPAT slice acceleration factor of 6, and an anterior-to-posterior phase encoding direction; the repetition time (TR) was 800 ms and the echo time (TE) was 30 ms. A blip-up/blip-down fieldmap was acquired at the start of each session. A T1w reference image was acquired during session one using a MEMPRAGE sequence⁵⁷ with 1.0 mm isotropic voxels, anterior-to-posterior encoding, and a GRAPPA acceleration factor of 3⁵⁸; the repetition time (TR) was 2530 ms and the echo times (TEs) were 1.69 ms, 3.55 ms, 5.41 ms, and 7.27 ms. A T2w reference image was acquired during session two using the variable flip angle turbo spin-echo sequence (Siemens SPACE⁵⁹) with 1.0 mm isotropic voxels, anterior-to-posterior phase encoding, and a GRAPPA acceleration factor of 2; the repetition time (TR) was 3200 ms and the echo time (TE) was 565 ms. A diffusion-weighted scan was also acquired at the end of session two. The acquisition followed the ABCD protocol with 1.7 mm isotropic voxels, an iPAT slice acceleration factor of 3, and an anterior-to-posterior phase encoding direction; the repetition time (TR) was 4200 ms and the echo time (TE) was 89 ms, and b-values were 500 (6 directions), 1000 (15 directions), 2000 (15 directions), and 3000 (60 directions). The total acquisition time per scan was 7:29 min and consisted of 81 slices.

Preprocessing

Results included in this manuscript come from preprocessing performed using fMRIPrep 20.1.0 (Esteban et al.⁶⁰^,⁶¹; RRID:SCR_016216), which is based on Nipype 1.4.2 (Gorgolewski et al.⁶²^,⁶³; RRID:SCR_002502).

Anatomical data preprocessing

A total of 1 T1-weighted (T1w) images were found within the input BIDS dataset. The T1-weighted (T1w) image was corrected for intensity non-uniformity (INU) with N4BiasFieldCorrection⁶⁴, distributed with ANTs 2.2.0 [ref. ⁶⁵, RRID:SCR_004757], and used as T1w-reference throughout the workflow. The T1w-reference was then skull-stripped with a Nipype implementation of the antsBrainExtraction.sh workflow (from ANTs), using OASIS30ANTs as target template. Brain tissue segmentation of cerebrospinal fluid (CSF), white-matter (WM), and gray-matter (GM) was performed on the brain-extracted T1w using fast [FSL 5.0.9, RRID:SCR_002823, ref. ⁶⁶]. Brain surfaces were reconstructed using recon-all [FreeSurfer 6.0.1, RRID:SCR_001847, ref. ⁶⁷], and the brain mask estimated previously was refined with a custom variation of the method to reconcile ANTs-derived and FreeSurfer-derived segmentations of the cortical gray-matter of Mindboggle [RRID:SCR_002438, ref. ⁶⁸]. Volume-based spatial normalization to two standard spaces (MNI152NLin2009cAsym, MNI152NLin6Asym) was performed through nonlinear registration with antsRegistration (ANTs 2.2.0), using brain-extracted versions of both the T1w reference and the T1w template. The following templates were selected for spatial normalization: ICBM 152 Nonlinear Asymmetrical template version 2009c [Fonov et al.⁶⁹, RRID:SCR_008796; TemplateFlow ID: MNI152NLin2009cAsym], FSL’s MNI ICBM 152 nonlinear 6th Generation Asymmetric Average Brain Stereotaxic Registration Model [Evans et al.⁷⁰, RRID:SCR_002823; TemplateFlow ID: MNI152NLin6Asym].

Functional data preprocessing

For each of the 18 BOLD runs per participant (across all tasks and sessions), the following preprocessing was performed. First, a reference volume and its skull-stripped version were generated using a custom methodology of fMRIPrep. Head-motion parameters with respect to the BOLD reference (transformation matrices, and six corresponding rotation and translation parameters) are estimated before any spatiotemporal filtering using mcflirt [FSL 5.0.9, ref. ⁷¹]. BOLD runs were slice-time corrected using 3dTshift from AFNI 20160207 [ref. ⁷², RRID:SCR_005927]. A B0-nonuniformity map (or fieldmap) was estimated based on two (or more) echo-planar imaging (EPI) references with opposing phase-encoding directions, with 3dQwarp Cox and Hyde⁷² (AFNI 20160207). Based on the estimated susceptibility distortion, a corrected EPI (echo-planar imaging) reference was calculated for a more accurate co-registration with the anatomical reference.

The BOLD reference was then co-registered to the T1w reference using bbregister (FreeSurfer) which implements boundary-based registration⁷³. Co-registration was configured with nine degrees of freedom to account for distortions that remained in the BOLD reference. The BOLD time-series (including those to which slice-timing correction had been applied) were resampled onto their original, native space by applying a single, composite transform to correct for head-motion and susceptibility distortions. These resampled BOLD time-series will be referred to as preprocessed BOLD in original space, or just preprocessed BOLD. The BOLD time-series were resampled into several standard spaces, correspondingly generating the following spatially-normalized, preprocessed BOLD runs: MNI152NLin2009cAsym and MNI152NLin6Asym.

Several confounding time-series were calculated based on the preprocessed BOLD: framewise displacement (FD), DVARS, and three region-wise global signals. FD was computed using two formulations: absolute sum of relative motions (Power et al.⁷⁴) and relative root mean square displacement between affines (Jenkinson et al.⁷¹). FD and DVARS are calculated for each functional run, both using their implementations in Nipype [following the definitions by ref. ⁷⁴]. The three global signals are extracted within the CSF, the WM, and the whole-brain masks. Additionally, a set of physiological regressors were extracted to allow for component-based noise correction [CompCor, ref. ⁷⁵]. Principal components are estimated after high-pass filtering the preprocessed BOLD time-series (using a discrete cosine filter with 128 s cut-off) for the two CompCor variants: temporal (tCompCor) and anatomical (aCompCor). tCompCor components are then calculated from the top 5% variable voxels within a mask covering the subcortical regions. This subcortical mask is obtained by heavily eroding the brain mask, which ensures it does not include cortical GM regions. For aCompCor, components are calculated within the intersection of the aforementioned mask and the union of CSF and WM masks calculated in T1w space, after their projection to the native space of each functional run (using the inverse BOLD-to-T1w transformation). Components are also calculated separately within the WM and CSF masks. For each CompCor decomposition, the k components with the largest singular values are retained, such that the retained components’ time series are sufficient to explain 50% of variance across the nuisance mask (CSF, WM, combined, or temporal). The remaining components are dropped from consideration.

The head-motion estimates calculated in the correction step were also placed within the corresponding confounds file. The confound time series derived from head motion estimates and global signals were expanded with the inclusion of temporal derivatives and quadratic terms for each⁷⁶. Frames that exceeded a threshold of 0.5 mm FD or 1.5 standardized DVARS were annotated as motion outliers. All resamplings can be performed with a single interpolation step by composing all the pertinent transformations (i.e., head-motion transform matrices, susceptibility distortion correction when available, and co-registrations to anatomical and output spaces). Gridded (volumetric) resamplings were performed using antsApplyTransforms (ANTs), configured with Lanczos interpolation to minimize the smoothing effects of other kernels⁷⁷. Non-gridded (surface) resamplings were performed using mri_vol2surf (FreeSurfer).

Many internal operations of fMRIPrep use Nilearn 0.6.2 [ref. ⁷⁸, RRID:SCR_001362], mostly within the functional processing workflow. For more details of the pipeline, see the section corresponding to workflows in fMRIPrep’s documentation.

Analysis

Behavioral analysis

We analyzed response time and accuracy performance measures for all participants, across both sessions, to ensure that participants were learning the intended visuo-motor associations. For session one, training and recall blocks in each run were analyzed separately. For session two, each run of four recall blocks was analyzed as a whole. To assess response times, we computed the mean response time for each run and participant across all correct trials. For training blocks, in line with previous work^16,17, we excluded trials with response times >3 SDs away from the mean for that run and participant, as well as those under 100 ms or over 3 s. We computed response accuracy as the fraction of trials for which participants responded correctly on the first attempt (training blocks) or correctly within 2 s (recall blocks). We then calculated the mean of these values, both within-group (modular vs. ring lattice) and across all participants, to arrive at mean values for each run (Fig. 1).

LS-S trial modeling

In our analysis, we hypothesize that the pattern of activation within a brain region in response to a condition contains information about that condition, beyond the information conveyed by the mean (unimodal) activation in that region. This approach, generally referred to as MVPA (Multi-Voxel Pattern Analysis), views each trial in the BOLD acquisition as a single point in an N-dimensional space, where N is the number of voxels in our region of interest, and the activity of each voxel during each trial provides coordinates in this N-dimensional space. Given a point for each trial, we can investigate how those points relate to one another.

Typically, BOLD timeseries are not used directly for MVPA. Instead, a typical choice for features is the resulting beta weights having fit a GLM to the data. In rapid event-based designs, such as ours, it has been suggested that running a separate GLM for each event, where all other events are represented by a single nuisance regressor (a strategy typically known as LS-S), leads to more stable estimates of beta weights^79,80. We used LS-S to derive a map of beta weights for each event, and for our analyses used the resulting Z-statistic map.

Our GLM was implemented in nipype using FSL first-level analysis routines, using the outputs (volumes and confounds) from fMRIPrep. All processing took place with BOLD data mapped into MNI152NLin2009cAsym at native resolution. Our model consisted of a double-gamma HRF plus derivatives, modeling 24 motion parameters (6-dof plus their 6 derivatives, as well as squared parameters). We used smoothing of FWHM=5mm and a high-pass cutoff of 60 s. Due to non-steady-state BOLD effects, we removed the first 10 TRs (or 8 s) from each run. For each recall run, this process left us with 59 instead 60 trials, as the first trial overlapped with the non-steady-state period.

To implement LS-S, we ran 59 separate first-level analyses for each recall run—one for each trial. Each GLM consisted of the 24 motion parameters, one column for the “target” event, one column for the “nuisance” events (i.e., all remaining 58 events), and additional regressors for any motion outlier volumes as indicated by fMRIPrep. All columns were then convolved with the double-gamma HRF plus derivatives. We then discarded the “nusiance” regressor, and combined the 59 “target” parameter estimates across the separate first-level analyses to create our activation map across all 59 trials. These activation maps could then be used as the points in an N-dimensional space for our pattern-based analyses.

LOC localizer

To enable robust analysis of LOC activation, participants completed a localizer run at the end of the second scanning session. This run consisted of 120 stimulus presentations and 120 phase-randomized control images, with the goal of localizing a region most sensitive to the contrast between the two. To prevent any interference from the previous learning phases, a separate set of 15 shapes were generated in the same fashion as those used in the earlier runs. These images were presented as follows: the run consisted of 30 blocks, and blocks were grouped into 10 sets of 3. Each set of 3 blocks consisted of, in order, a block of 12 stimuli, a block of 12 phase-randomized stimulus images, and a 12 s blank screen, for 36 s in total. Each stimulus or image was shown in the center of the screen for 0.8 s, with a 0.2 s ISI. Participants were instructed to passively view the sequence of images without responding. To control for the transition structure and the number of times each stimulus was shown, we first generated 16 connected Hamiltonian walks, for a total of 240 trials. The 240 trials were then split in half, with the first 120 assigned to object trials, and the second 120 assigned to phase-randomized trials. These 120 trials were then split between the 10 blocks, such that block 1 contained object trials 1–12 and phase-randomized trials 1–12, etc. We ran a GLM modeling shapes vs. phase-randomized trials for each subject to identify voxels that were selective to the shapes but not their phase-randomized counterparts. This GLM used the same set of nuisance regressors and same HRF convolution as in our LS-S analysis. This provided us with a z-scored contrast for each participant, which was used to select voxels for an LOC ROI.

MVPA classification

To test whether a region coded for differences amongst trial types, we checked whether a linear classifier could predict the trial type of each recall trial based on its decoded activity pattern after being trained on independent examples of those trial types from the same subject. We used a linear SVM to predict which of the 15 trial types was most likely, and computed accuracy as the fraction of correct categorizations. Classification was performed via LinearSVC in scikit-learn. We increased the maximum number of iterations to allow convergence but otherwise used default parameters. In order to improve SVM performance, standard practice is that each feature should be zero-centered and of similar variance. Accordingly, we z-scored the weights for each voxel within each of the eight runs for a given participant. To reduce overfitting, we performed classification by cross-validation across runs. That is, given eight runs, we trained on seven of the eight runs, and then predicted trial identity on the remaining held-out run, and repeated for all eight runs. Cross-validated accuracy was then compared to chance performance, which here is 1/15.

Behavior and classification

We hypothesized that classification accuracy might vary between modular and ring lattice graph types. Graph type has been shown to affect average response times, so we sought to test whether graph type and/or response time modulated classification accuracy. For each participant, we fit MVPA classification accuracy as a function of that participant’s mean response times on session two recall trials, in order to determine whether classification accuracy depended on response time. We fit an OLS model of classification_accuracy ~ response_time*graph. Response time was taken as the mean response time, on correct trials (both within 2 s, and with the correct response), across all 480 trials comprising the eight recall runs. graph was 0 for ring lattice and 1 for modular subjects. To verify whether response accuracy predicted classification accuracy, we fit a similar model of classification_accuracy ~ response_accuracy*graph where response accuracy ranges from 0 (missing all trials) to 1 (being perfect recall).

Representational dissimilarity matrices

We can categorize trials according to three independent attributes. First, we can use shape or, the visual appearance of the trial. Next, we can use motor movement, as in the fingers used to produce the response. Last, we can use graph location, or which other trials can precede and follow, temporally embedding the trial within either the modular or the ring lattice graph. We hypothesized that all three attributes would contribute to the neural activation evoked by a trial, and moreover contribute to how the patterns of neural activation related between trials.

For instance, we might expect that two trials share a similar representation if both responses use the ring finger. Specifically, we would predict that the trials which used “thumb + ring” and “index + ring” would be more similar to one another than trials which used “thumb + pinky” and “index + ring”. Visual attributes can also impact representations—although our shapes were chosen to all be distinguishable, undoubtedly some of the shapes share features that others do not. Finally, graph structure may influence representation. If two nodes are in the same graph cluster, that cluster may be represented as well, heightening the neural similarity of those two nodes.

For a given participant, all three of these organizations are consistent—a node is always paired with both the same motor movement and the same shape—and so similarity is driven by a combination of these factors that we cannot fully disentangle. However, when we compare across participants, pairings vary: shape A might be “thumb” for participant one, and “pinkie” for participant two. We can therefore separate which factors drive representational similarity when we compare across participants. Comparing shapes A and B across all participants should no longer depend on the assigned motor actions, or on the location within the graph.

We asked where in the brain, and under which organization of trials, did participants have similar organizations to one another, using the concept of a noise ceiling bound. For each subject, we estimated an RDM based on a cross-validated Euclidean metric: First, within each run, we averaged LS-S beta weights for trial type, resulting in 15 activation patterns for that run. We then calculated the squared Euclidean distance between patterns, cross-validated across runs: for runs j and k, and trial types u and v, \({d}_{u,v}^{2}=\frac{1}{n(n-1)}{\sum }_{j\ne k}({x}_{ju}-{x}_{jv}){({x}_{ku}-{x}_{kv})}^{T}\), resulting in a 15 × 15 RDM for each subject. Next, we divided each matrix by its largest element, such that it ranged from 0 (all diagonal elements) to 1 (largest element), to enable cross-subject comparison. We then arranged the RDM for each subject based on the modality of comparison—either by node, motor response, or shape, such that this ordering would be consistent across subjects. Finally we took the mean of RDMs across participants separately for modular and ring lattice groups.

Intersubject RDM similarity

To determine which brain regions contained similar representational structure across subjects, we conducted a whole-brain searchlight in which we correlated RDMs across subjects. First, for each subject, PyMVPA was used to calculate the Euclidean-distance RDM in a three-voxel radius around each voxel. The upper right triangle of the RDM was then taken, providing a 105-dimensional vector for each voxel. Next, for each subject, we correlated the RDM vector with an average vector across all other subjects, resulting in a Pearson correlation coefficient for that voxel and subject. Before comparing, RDMs were reordered to follow either graph, motor response, or shape ordering. Finally, we averaged correlation coefficients across subjects to create a map of similarity.

To statistically threshold the resulting maps, we performed a randomized null model procedure, similar to that used in ref. ²², in order to control the familywise error rate (FWER). We repeated our RDM similarity procedure 1000 times, each time randomizing the RDM ordering by rearranging rows and columns in the RDM, separately for each subject. We then computed the mean lower bound map and found the absolute value of the largest magnitude correlation coefficient in each volume, giving us a sample distribution of 1000 correlation coefficients. We chose the 95th percentile of this sample distribution as our cutoff, and thresholded our whole-brain maps using this cutoff. Conceptually, each randomization is similar to reassigning the shape, motor, and visual correspondences for each subject. Thus, the null model procedure is identical for thresholding our similarity maps for shape, motor command, and node, and we therefore identified a single significance threshold which was used in all three maps.

Intrasubject RDM consistency

Whereas the intersubject RDM similarity described above identifies shared representational organization, intrasubject consistency can potentially identify a broader set of regions: those for which representational organization is consistent for each subject, even if the representational structure differs between subjects. Therefore, instead of comparing between subjects, we compare between runs for each subject. We employ a similar procedure to our intersubject RDM similarity: for each run, we correlate the RDM of that voxel with the mean RDM of the other seven runs, giving us a Pearson correlation coefficient for that voxel and run. We take the mean across runs to create a whole-brain map for each subject. Finally, we average those maps across subjects to identify where we observe heightened intrasubject consistency. To estimate ROI differences in intrasubject consistency, we employ a similar procedure. However, instead of operating on a whole-brain searchlight, we use our bilateral LOC ROI. Again, we calculate an RDM for each run, and then compare that RDM with the mean of the other seven runs.

Intrasubject pattern consistency

RDM similarity measures stability of relationships across runs. We may also be interested in stability of the patterns themselves. For each subject, we compute a per-run mean pattern for each of 15 trial types. We then measure the distance, using squared Euclidean distance, between that pattern and the same subject’s pattern in each of the other seven runs. We average this distance across all trial types and run combinations to arrive at a consistency value for that subject.

Dimensionality

To estimate dimensionality, we adapted the procedure taken in Tang et al.²⁹. We take our ability to split our data between arbitrary groupings of classes as a measure of its intrinsic dimensionality: high-dimensional data will allow more separable groupings than low-dimensional data. We begin by enumerating over both the number of classes, m, and permutations of m classes. For each value of m, there are \(\left(\begin{array}{c}15\\ m\end{array}\right)\) combinations of trial types, and for each combination, there are 2^m−1 unique ways to divide those trial types into two groups. Dimensionality is estimated as the fraction of these assignments which we find to be linearly separable. In practice, this means that for a given value of m, we choose m out of 15 trial types, and then assign a binary label ("+” or “ − ”) to each of the m trial types. We then train an SVM to separate the “+” from the “ − ” trial types, and calculate the fraction of assignments above a threshold. However, in following ref. ²⁹, we note that, for fMRI data, this full calculation is computationally intractable and the between-subject differences can be understood from the mean classification score, rather than thresholding a classification as correct. We therefore choose a representative subsample of possible combinations and binary assignments for each value of m.

Functional connectivity analysis

In order to compute functional connectivity, fMRIprep outputs were further preprocessed using XCP Engine 1.2.1 to perform confound regression and residualizing of physiological artifacts from individual BOLD images⁸¹. This included a confound reduction module relying on anatomical component-based correction (aCompCor) to mitigate effects of subject motion on timeseries data⁸². For each of the left LOC, postcentral gyrus, and MTL ROIs, we extracted the preprocessed BOLD signal from the voxels constituting each ROI and averaged using FSL’s fslmeans function to obtain one time series per ROI. We measured the functional connectivity of each pair of ROIs by calculating the product-moment correlation coefficient (Pearson r) for the associated time series^83,84, obtaining a 3 × 3 functional connectivity adjacency matrix for each fMRI scan. All negative correlation values were set to zero⁸³, as negative product-moment values are more sensitive to motion artifacts, and it has been shown that setting negative edges to zero can thus improve reliability of functional connectivity measures. Functional connectivity values for each subject were averaged across the five learning runs, to provide a per-subject measure of functional connectivity for each of the three ROI pairs, and then z-scored across subjects. Classification accuracy was similarly averaged across the eight recall runs for each subject, resulting in three functional connectivity values and three classification accuracy values for each subject. To investigate the relationship between functional connectivity during learning and classification accuracy during recall, we fit a linear mixed-effects model including a full random-effects structure (classification accuracy ~ LOC-MTL FC + LOC-Postcentral FC + Postcentral-MTL FC + (1 + LOC-MTL FC + LOC-Postcentral FC + Postcentral-MTL FC ∣ Subject), one model for each of the three regions in which we were predicting classification accuracy. p values were corrected for multiple comparisons using the Benjamini-Hochberg false-discovery rate procedure⁸⁵.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

Data supporting this study are available at https://osf.io/sdwe3/https://doi.org/10.17605/OSF.IO/SDWE3.

Code availability

Code supporting this study is available at https://osf.io/sdwe3/ and https://github.com/ariekahn/graph-learning-code.

References

Gershman, S. J. & Niv, Y. Learning latent structure: carving nature at its joints. Curr. Opin. Neurobiol. 20, 251–256 (2010).
Article CAS PubMed PubMed Central MATH Google Scholar
Lynn, C. W., Papadopoulos, L., Kahn, A. E. & Bassett, D. S. Human information processing in complex networks. Nat. Phys. 1–9. https://www.nature.com/articles/s41567-020-0924-7 (2020).
Tervo, D. G. R., Tenenbaum, J. B. & Gershman, S. J. Toward the neural implementation of structure learning. Curr. Opin. Neurobiol. 37, 99–105 (2016).
Article CAS PubMed MATH Google Scholar
Schapiro, A. & Turk-Browne, N. B. Statistical learning. Brain Mapp. 3, 501–506 (2015).
Article MATH Google Scholar
Saffran, J. R., Aslin, R. N. & Newport, E. L. Statistical learning by 8-month-old infants. Science 274, 1926–1928 (1996).
Article ADS CAS PubMed Google Scholar
Pelucchi, B., Hay, J. F. & Saffran, J. R. Statistical learning in a natural language by 8-month-old infants. Child Dev. 80, 674–685 (2009).
Article PubMed MATH Google Scholar
Saffran, J. R. & Kirkham, N. Z. Infant statistical learning. Annu. Rev. Psychol. 69, 181–203 (2018).
Article PubMed Google Scholar
Saffran, J. R., Newport, E. L. & Aslin, R. N. Word segmentation: the role of distributional cues. J. Mem. Lang. 35, 606–621 (1996).
Article Google Scholar
Saffran, J. R., Johnson, E. K., Aslin, R. N. & Newport, E. L. Statistical learning of tone sequences by human infants and adults. Cognition 70, 27–52 (1999).
Article CAS PubMed Google Scholar
Kirkham, N. Z., Slemmer, J. A. & Johnson, S. P. Visual statistical learning in infancy: evidence for a domain general learning mechanism. Cognition 83, B35–B42 (2002).
Article PubMed MATH Google Scholar
Monroy, C., Gerson, S. & Hunnius, S. Infants’ motor proficiency and statistical learning for actions. Front. Psychol. 8, 2174 (2017).
Article PubMed PubMed Central MATH Google Scholar
Gómez, R. L. Variability and detection of invariant structure. Psychol. Sci. 13, 431–436 (2002).
Article PubMed MATH Google Scholar
Newport, E. L. & Aslin, R. N. Learning at a distance I. Statistical learning of non-adjacent dependencies. Cogn. Psychol. 48, 127–162 (2004).
Article PubMed MATH Google Scholar
Karuza, E. A., Thompson-Schill, S. L. & Bassett, D. S. Local patterns to global architectures: influences of network topology on human learning. Trends Cogn. Sci. 20, 629–640 (2016).
Article PubMed PubMed Central Google Scholar
Karuza, E. A. The value of statistical learning to cognitive network science. Top. Cogn. Sci. 14, 78–92 (2022).
Article PubMed MATH Google Scholar
Karuza, E. A., Kahn, A. E., Thompson-Schill, S. L. & Bassett, D. S. Process reveals structure: how a network is traversed mediates expectations about its architecture. Sci. Rep. 7, 12733 (2017).
Article ADS PubMed PubMed Central Google Scholar
Kahn, A. E., Karuza, E. A., Vettel, J. M. & Bassett, D. S. Network constraints on learnability of probabilistic motor sequences. Nat. Hum. Behav. 2, 936–947 (2018).
Article PubMed PubMed Central MATH Google Scholar
Schapiro, A. C., Turk-Browne, N. B., Norman, K. A. & Botvinick, M. M. Statistical learning of temporal community structure in the hippocampus. Hippocampus 26, 3–8 (2016).
Article PubMed Google Scholar
Garvert, M. M., Dolan, R. J. & Behrens, T. E. A map of abstract relational knowledge in the human hippocampal–entorhinal cortex. eLife 6, e17086 (2017).
Article PubMed PubMed Central Google Scholar
Schapiro, A. C., Rogers, T. T., Cordova, N. I., Turk-Browne, N. B. & Botvinick, M. M. Neural representations of events arise from temporal community structure. Nat. Neurosci. 16, 486–492 (2013).
Article CAS PubMed PubMed Central Google Scholar
Olman, C. A., Davachi, L. & Inati, S. Distortion and signal loss in medial temporal lobe. PLoS ONE 4, e8160 (2009).
Article ADS PubMed PubMed Central Google Scholar
Nili, H. et al. A toolbox for representational similarity analysis. PLoS Comput. Biol. 10, e1003553 (2014).
Article PubMed PubMed Central MATH Google Scholar
Shen, G. et al. Decoding the individual finger movements from single-trial functional magnetic resonance imaging recordings of human brain activity. Eur. J. Neurosci. 39, 2071–2082 (2014).
Article PubMed MATH Google Scholar
Ejaz, N., Hamada, M. & Diedrichsen, J. Hand use predicts the structure of representations in sensorimotor cortex. Nat. Neurosci. 18, 1034–1040 (2015).
Article CAS PubMed Google Scholar
Yokoi, A., Arbuckle, S. A. & Diedrichsen, J. The role of human primary motor cortex in the production of skilled finger sequences. J. Neurosci. 38, 1430–1442 (2018).
Article CAS PubMed PubMed Central Google Scholar
Drucker, D. M. & Aguirre, G. K. Different spatial scales of shape similarity representation in lateral and ventral LOC. Cereb. Cortex 19, 2269–2280 (2009).
Article PubMed PubMed Central MATH Google Scholar
Mattar, M. G., Olkkonen, M., Epstein, R. A. & Aguirre, G. K. Adaptation decorrelates shape representations. Nat. Commun. 9, 3812 (2018).
Article ADS PubMed PubMed Central Google Scholar
Rigotti, M. et al. The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590 (2013).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Tang, E. et al. Effective learning is accompanied by high-dimensional and efficient representations of neural activity. Nat. Neurosci. 22, 1000–1009 (2019).
Article CAS PubMed MATH Google Scholar
Lynn, C. W. & Bassett, D. S. How humans learn and represent networks. Proc. Natl Acad. Sci. USA 117, 29407–29415 (2020).
Article ADS MathSciNet CAS PubMed PubMed Central MATH Google Scholar
Chen, J. et al. Shared memories reveal shared structure in neural activity across individuals. Nat. Neurosci. 20, 115–125 (2017).
Article CAS PubMed MATH Google Scholar
Boggia, J. & Ristic, J. Social event segmentation. Q. J. Exp. Psychol. 68, 731–744 (2015).
Article MATH Google Scholar
Tompson, S. H., Kahn, A. E., Falk, E. B., Vettel, J. M. & Bassett, D. S. Individual differences in learning social and nonsocial network structures. J. Exp. Psychol. Learn. Mem. Cogn. 45, 253–271 (2019).
Article PubMed MATH Google Scholar
Karuza, E. A., Kahn, A. E. & Bassett, D. S. Human sensitivity to community structure is robust to topological variation. Complexity 2019, 1–8 (2019).
Article MATH Google Scholar
Rmus, M., Ritz, H., Hunter, L. E., Bornstein, A. M. & Shenhav, A. Humans can navigate complex graph structures acquired during latent learning. Cognition 225, 105103 (2022).
Article PubMed PubMed Central Google Scholar
Lynn, C. W., Kahn, A. E., Nyema, N. & Bassett, D. S. Abstract representations of events arise from mental errors in learning and memory. Nat. Commun. 11, 2313 (2020).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Wang, X.-J., Liu, Y., Sanchez-Vives, M. V. & McCormick, D. A. Adaptation and temporal decorrelation by single neurons in the primary visual cortex. J. Neurophysiol. 89, 3279–3293 (2003).
Article PubMed MATH Google Scholar
Gutnisky, D. A. & Dragoi, V. Adaptive coding of visual information in neural populations. Nature 452, 220–224 (2008).
Article ADS CAS PubMed MATH Google Scholar
Clifford, C. W. G. et al. Visual adaptation: neural, psychological and computational aspects. Vis. Res. 47, 3125–3131 (2007).
Article PubMed MATH Google Scholar
Tompson, S. H., Kahn, A. E., Falk, E. B., Vettel, J. M. & Bassett, D. S. Functional brain network architecture supporting the learning of social networks in humans. NeuroImage 116498. http://www.sciencedirect.com/science/article/pii/S1053811919310894 (2020).
Stachenfeld, K. L., Botvinick, M. M. & Gershman, S. J. The hippocampus as a predictive map. Nat. Neurosci. 20, 1643–1653 (2017).
Article CAS PubMed MATH Google Scholar
Schapiro, A. C., Gregory, E., Landau, B., McCloskey, M. & Turk-Browne, N. B. The necessity of the medial temporal lobe for statistical learning. J. Cogn. Neurosci. 26, 1736–1747 (2014).
Article PubMed PubMed Central Google Scholar
Button, K. S. et al. Power failure: why small sample size undermines the reliability of neuroscience. Nat. Rev. Neurosci. 14, 365–376 (2013).
Article CAS PubMed MATH Google Scholar
Mitchell, S. M., Lange, S. & Brus, H. Gendered citation patterns in international relations journals. Int. Stud. Perspect. 14, 485–492 (2013).
Article Google Scholar
Dion, M. L., Sumner, J. L. & Mitchell, S. M. Gendered citation patterns across political science and social science methodology fields. Political Anal. 26, 312–327 (2018).
Article MATH Google Scholar
Caplar, N., Tacchella, S. & Birrer, S. Quantitative evaluation of gender bias in astronomical publications from citation counts. Nat. Astron. 1, 0141 (2017).
Article ADS Google Scholar
Maliniak, D., Powers, R. & Walter, B. F. The gender citation gap in international relations. Int. Organ. 67, 889–922 (2013).
Article MATH Google Scholar
Dworkin, J. D. et al. The extent and drivers of gender imbalance in neuroscience reference lists. bioRxiv https://www.biorxiv.org/content/early/2020/01/11/2020.01.03.894378; https://www.biorxiv.org/content/early/2020/01/11/2020.01.03.894378.full.pdf (2020).
Bertolero, M. A. et al. Racial and ethnic imbalance in neuroscience reference lists and intersections with gender. Preprint at bioRxiv https://doi.org/10.1101/2020.10.12.336230 (2020).
Wang, X. et al. Gendered citation practices in the field of communication. Ann. Int. Commun. Assoc. https://doi.org/10.1080/23808985.2021.1960180 (2021).
Chatterjee, P. & Werner, R. M. Gender disparity in citations in high-impact journal articles. JAMA Netw. Open 4, e2114509 (2021).
Article PubMed PubMed Central Google Scholar
Fulvio, J. M., Akinnola, I. & Postle, B. R. Gender (im)balance in citation practices in cognitive neuroscience. J. Cogn. Neurosci. 33, 3–7 (2021).
Article PubMed Google Scholar
Zhou, D. et al. Gender diversity statement and code notebook v1.0. https://doi.org/10.5281/zenodo.3672110 (2020).
Ambekar, A., Ward, C., Mohammed, J., Male, S. & Skiena, S. Name-ethnicity classification from open sources. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 49–58, https://doi.org/10.1145/1557019.1557032 (ACM, 2009).
Sood, G. & Laohaprapanon, S. Predicting race and ethnicity from the sequence of characters in a name. Preprint at arXiv https://doi.org/10.48550/arXiv.1805.02109 (2018).
Casey, B. J. et al. The Adolescent Brain Cognitive Development (ABCD) study: imaging acquisition across 21 sites. Dev. Cogn. Neurosci. 32, 43–54 (2018).
Article CAS PubMed PubMed Central MATH Google Scholar
van der Kouwe, A. J. W., Benner, T., Salat, D. H. & Fischl, B. Brain morphometry with multiecho MPRAGE. NeuroImage 40, 559–569 (2008).
Article PubMed Google Scholar
Griswold, M. A. et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 47, 1202–1210 (2002).
Article PubMed MATH Google Scholar
Mugler, J. P. et al. Optimized single-slab three-dimensional spin-echo MR imaging of the brain. Radiology 216, 891–899 (2000).
Article PubMed MATH Google Scholar
Esteban, O. et al. fMRIPrep: a robust preprocessing pipeline for functional MRI. Nat. Methods https://doi.org/10.1038/s41592-018-0235-4 (2018).
Esteban, O. et al. fmriprep. Software https://doi.org/10.5281/zenodo.852659 (2018).
Gorgolewski, K. et al. Nipype: a flexible, lightweight and extensible neuroimaging data processing framework in python. Front. Neuroinform. 5, 12318 (2011).
Article MATH Google Scholar
Gorgolewski, K. J. et al. Nipype. Software https://doi.org/10.5281/zenodo.596855 (2018).
Tustison, N. J. et al. N4itk: Improved n3 bias correction. IEEE Trans. Med. Imaging 29, 1310–1320 (2010).
Article PubMed PubMed Central MATH Google Scholar
Avants, B. B., Epstein, C. L., Grossman, M. & Gee, J. C. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 12, 26–41 (2008).
Article CAS PubMed MATH Google Scholar
Zhang, Y., Brady, M. & Smith, S. M. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imaging 20, 45–57 (2001).
Article CAS PubMed MATH Google Scholar
Dale, A. M., Fischl, B. & Sereno, M. I. Cortical surface-based analysis: I. Segmentation and surface reconstruction. NeuroImage 9, 179–194 (1999).
Article CAS PubMed MATH Google Scholar
Klein, A. et al. Mindboggling morphometry of human brains. PLoS Comput. Biol. 13, e1005350 (2017).
Article PubMed PubMed Central MATH Google Scholar
Fonov, V. S., Evans, A. C., McKinstry, R. C., Almli, C. R. & Collins, D. L. Unbiased nonlinear average age-appropriate brain templates from birth to adulthood. NeuroImage 47, S102 (2009).
Article Google Scholar
Evans, A. C., Janke, A. L., Collins, D. L. & Baillet, S. Brain templates and atlases. NeuroImage 62, 911–922 (2012).
Article PubMed Google Scholar
Jenkinson, M., Bannister, P., Brady, M. & Smith, S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage 17, 825–841 (2002).
Article PubMed MATH Google Scholar
Cox, R. W. & Hyde, J. S. Software tools for analysis and visualization of fmri data. NMR Biomed. 10, 171–178 (1997).
Article CAS PubMed MATH Google Scholar
Greve, D. N. & Fischl, B. Accurate and robust brain image alignment using boundary-based registration. NeuroImage 48, 63–72 (2009).
Article PubMed MATH Google Scholar
Power, J. D. et al. Methods to detect, characterize, and remove motion artifact in resting state fmri. NeuroImage 84, 320–341 (2014).
Article PubMed MATH Google Scholar
Behzadi, Y., Restom, K., Liau, J. & Liu, T. T. A component based noise correction method (CompCor) for BOLD and perfusion based fmri. NeuroImage 37, 90–101 (2007).
Article PubMed Google Scholar
Satterthwaite, T. D. et al. An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting-state functional connectivity data. NeuroImage 64, 240–256 (2013).
Article PubMed MATH Google Scholar
Lanczos, C. Evaluation of noisy data. J. Soc. Ind. Appl. Math. Ser. B Numer. Anal. 1, 76–85 (1964).
Article MathSciNet MATH Google Scholar
Abraham, A. et al. Machine learning for neuroimaging with scikit-learn. Front. Neuroinform. 8, 71792 (2014).
Article MATH Google Scholar
Mumford, J. A., Turner, B. O., Ashby, F. G. & Poldrack, R. A. Deconvolving BOLD activation in event-related designs for multivoxel pattern classification analyses. NeuroImage 59, 2636–2643 (2012).
Article PubMed Google Scholar
Lee, S. & Kable, J. W. Simple but robust improvement in multivoxel pattern classification. PLoS ONE 13, e0207083 (2018).
Article PubMed PubMed Central MATH Google Scholar
Ciric, R. et al. Mitigating head motion artifact in functional connectivity MRI. Nat. Protoc. 13, 2801–2826 (2018).
Article CAS PubMed PubMed Central MATH Google Scholar
Ciric, R. et al. Benchmarking of participant-level confound regression strategies for the control of motion artifact in studies of functional connectivity. NeuroImage 154, 174–187 (2017).
Article PubMed MATH Google Scholar
Mahadevan, A. S., Tooley, U. A., Bertolero, M. A., Mackey, A. P. & Bassett, D. S. Evaluating the sensitivity of functional connectivity measures to motion artifact in resting-state fMRI data. NeuroImage 241, 118408 (2021).
Article PubMed Google Scholar
Zalesky, A., Cocchi, L., Fornito, A., Murray, M. M. & Bullmore, E. Connectivity differences in brain networks. NeuroImage 60, 1055–1062 (2012).
Article PubMed Google Scholar
Benjamini, Y. & Hochberg, Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B Methodol. 57, 289–300 (1995).
Article MathSciNet MATH Google Scholar

Download references

Acknowledgements

This research was primarily supported by the National Institutes of Mental Health award number 1-R21-MH-124121-01. D.S.B. would also like to acknowledge additional support from the John D. and Catherine T. MacArthur Foundation, the Alfred P. Sloan Foundation, the Institute for Scientific Interchange Foundation, and the Army Research Office (Grafton-W911NF-16-1-0474 and DCIST-W911NF-17-2-0181). G.K.A. would also like to acknowledge additional support from P30 EY001583: Core Grant for Vision Research. The content is solely the responsibility of the authors and does not necessarily represent the official views of any of the funding agencies.

Author information

Authors and Affiliations

Princeton Neuroscience Institute and Department of Psychology, Princeton University, Princeton, NJ, 08540, USA
Ari E. Kahn
Medical Scientist Training Program, University of Rochester School of Medicine and Dentistry, Rochester, NY, 14642, USA
Karol Szymula
Department of Bioengineering, School of Engineering & Applied Science, University of Pennsylvania, Philadelphia, PA, 19104, USA
Sophie Loman, Nathaniel Nyema & Dani S. Bassett
Department of Neurology, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, 19104, USA
Edda B. Haggerty, Geoffrey K. Aguirre & Dani S. Bassett
Department of Electrical & Systems Engineering, School of Engineering & Applied Science, University of Pennsylvania, Philadelphia, PA, 19104, USA
Dani S. Bassett
Department of Physics & Astronomy, College of Arts & Sciences, University of Pennsylvania, Philadelphia, PA, 19104, USA
Dani S. Bassett
Department of Psychiatry, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, 19104, USA
Dani S. Bassett
Santa Fe Institute, Santa Fe, NM, 87501, USA
Dani S. Bassett

Authors

Ari E. Kahn
View author publications
Search author on:PubMed Google Scholar
Karol Szymula
View author publications
Search author on:PubMed Google Scholar
Sophie Loman
View author publications
Search author on:PubMed Google Scholar
Edda B. Haggerty
View author publications
Search author on:PubMed Google Scholar
Nathaniel Nyema
View author publications
Search author on:PubMed Google Scholar
Geoffrey K. Aguirre
View author publications
Search author on:PubMed Google Scholar
Dani S. Bassett
View author publications
Search author on:PubMed Google Scholar

Contributions

A.E.K., G.K.A., and D.S.B. conceived the project and planned the experiments and analyses. A.E.K., K.S., E.B.H., and N.N. performed the experiments and analyses. S.L. replicated the analyses and results. A.E.K. and D.S.B. wrote the manuscript and Supplementary Information. K.S., E.B.H., N.N., G.K.A., and D.S.B. edited the manuscript and Supplementary Information.

Corresponding author

Correspondence to Dani S. Bassett.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Reporting Summary

Transparent Peer Review file

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Kahn, A.E., Szymula, K., Loman, S. et al. Network structure influences the strength of learned neural representations. Nat Commun 16, 994 (2025). https://doi.org/10.1038/s41467-024-55459-5

Download citation

Received: 03 March 2023
Accepted: 12 December 2024
Published: 24 January 2025
DOI: https://doi.org/10.1038/s41467-024-55459-5

Subjects

Abstract

Similar content being viewed by others

Neurocomputational mechanism of real-time distributed learning on social networks

Constructing graphs from genetic encodings

Long- and short-term history effects in a spiking network model of statistical learning

Introduction

Results

Task

Subjects accurately learn visuo-motor associations

Graph representational structure is not decodable Independently from stimulus and motor structure

Representational structure in motor cortex follows response patterns

Representational structure in visual cortex reflects both stimulus and graph type

Representation and dimensionality differ between graph structures

Functional connectivity during learning predicts subsequent decoding

Discussion

Modular graphs enable effective neural representations

Response time differences do not explain LOC graph effects

Neural representations from modular graphs are high dimensional

Graph-dependent adaptation decorrelates shapes

Motor cortex displays strong organizational patterns

Functional connectivity reveals distinct patterns of regional interactions

Limitations

Conclusion

Citation diversity statement

Methods

Participants

Task

Stimuli

Pre-training

Training

Recall (session one)

Recall (session two)

Imaging

Acquisition

Preprocessing

Anatomical data preprocessing

Functional data preprocessing

Analysis

Behavioral analysis

LS-S trial modeling

LOC localizer

MVPA classification

Behavior and classification

Representational dissimilarity matrices

Intersubject RDM similarity

Intrasubject RDM consistency

Intrasubject pattern consistency

Dimensionality

Functional connectivity analysis

Reporting summary

Data availability

Code availability

References

Acknowledgements

Author information

Authors and Affiliations

Contributions

Corresponding author

Ethics declarations

Competing interests

Peer review

Peer review information

Additional information

Supplementary information

Supplementary Information

Reporting Summary

Transparent Peer Review file

Rights and permissions

About this article

Cite this article

Share this article

Search

Quick links