Room-temperature creation and conversion of individual skyrmion bags in magnetic multilayered disks

Abstract

Skyrmion bags, with arbitrary topological charge Q, have recently attracted much interest, since such high-Q topological systems could open a way for topological magnetism research and are promising for spintronic applications with high flexibility for information encoding. Investigation on room-temperature skyrmion bags in magnetic multilayered structures is essential for applications and remains unexplored so far. Here, we demonstrate room-temperature creation and manipulation of individual skyrmion bags in magnetic multilayered disks. Individual skyrmion bags with varying topological charges are identified to remain stable at zero field. Furthermore, we realize intriguing field-driven topological conversion of skyrmion bags, as well as local manipulation of skyrmion bags via magnetic tips. Micromagnetic simulations indicate that the special boundary condition of the disks is responsible for skyrmion-bag formation and stability. These findings provide a platform to investigate individual skyrmion bags in confined multilayered structures, which could be useful for developing high-Q-based topological spintronic devices.

Introduction

Magnetic skyrmions are topologically nontrivial spin textures^1,2,3,4,5, which have attracted widespread interest due to their exotic physics and potential applications in spintronics^6,7,8,9. A magnetic skyrmion has a unitary topological charge Q, defined as^{1,2,3,4,5,6,7,8,9}

$${Q}=1/(4\pi )\iint {{\bf{m}}}\cdot \left({\partial }_{{x}}{{\bf{m}}}\times {\partial }_{{y}}{{\bf{m}}}\right)d{x}d{y},$$

(1)

which counts how many times the normalized local magnetization m winds around a unit sphere. Many different spin textures with varying topological charges have been discovered over the past few years, most of which exhibit a topological charge |Q | ≤ 1, such as meron¹⁰, bimeron¹¹, and skyrmionium^12,13,14,15. In contrast, complex magnetic states with large topological charge have been recently reported, including skyrmion bag^16,17,18,19, hopfion^20,21, skyrmion braid²² and high-order dipolar (anti)skyrmion²³. Magnetic systems with large topological charges have the potential to open avenues for topological magnetism and spintronic applications. A skyrmion bag, being composed of a large skyrmion outer boundary and N inner skyrmions with opposite polarity, can have an arbitrary topological charge Q = N-1^16,24,25. This varying topological charge enables skyrmion bags to achieve higher degree of freedom in information encoding compared to skyrmions^16,24,25,26, making them promising for spintronic applications.

Recently, skyrmion bags have been observed in several single-phase bulk materials, including B20-type FeGe magnets¹⁶, van der Waals magnets Fe_3-xGeTe₂¹⁷, and X-type Sr₂Co₂Fe₂₈O₄₆ hexaferrite¹⁹. However, the relatively intricate growth methods of these single-phase materials as well as the bulk form hinder their applications. Besides, low temperature and/or magnetic field (B) are usually demanded for both creating and stabilizing skyrmion bags in these materials, which is also detrimental for applications. Investigating the stability of skyrmion bags at room temperature and zero field is important. By contrast, magnetic multilayers deposited by magnetron sputtering are appealing due to their advantages such as the ability to stabilize room-temperature skyrmions^27,28,29, finely tunable material parameters²⁷ and the compatibility with standard semiconductor processing technologies²⁷. A few theoretical studies on skyrmion bags in magnetic multilayers have been recently reported in terms of their creation, stability and dynamic behaviors^{26,30,31,32,33}, where two-dimensional systems were considered and the initial configurations were often subjectively assumed to be skyrmion bags. However, experimental investigation on high-Q skyrmion bags in magnetic multilayers is still lacking, and only recently a room-temperature Q = 1 skyrmion bag was observed as the transitional state in Co/Pt multilayers by applying series of magnetic fields and pulse currents¹⁸, without further investigation on skyrmion bags. For industrial applications, it is essential to create skyrmion bags which are stable at room temperature and zero field, and to realize the conversion of skyrmion bags with different topological charges.

It’s well-known that geometric confinement could help to enhance the stability of skyrmions^{27,34,35,36,37}, which can facilitate the realization of room-temperature skyrmions without B^36,37. Many unique spin textures related to skyrmions have been reported in confined structures, such as skyrmion clusters³⁸, skyrmion chains³⁹, target skyrmions¹², and kπ-skyrmions¹⁴. Due to the absence of spins outside the boundary, the confined structure tends to form a chiral edge twist^{34,35,39,40,41,42}. Along with the large surface-bulk ratio⁴⁰, the interaction between skyrmions and boundaries becomes nontrivial^{35,38,39,43,44,45}. However, experimental research on skyrmion bags in confined structures has not yet been reported so far. Confined structures can facilitate the investigation of the manipulation of individual skyrmion bags, as well as the interaction between skyrmion bags and boundaries. For applications, skyrmion bags in confined structures can be utilized for spintronic devices, such as skyrmion bag-based random access memory, random number generator and magnonic crystal^30,37,46.

In this work, we demonstrate room-temperature creation and conversion of individual skyrmion bags in [Ta/CoFeB/MgO]₁₅ ferromagnetic disks. Utilizing the magnetic force microscope (MFM), skyrmion bags with varying topological charges are identified to be created from the net-like domain structures, obtained by applying a small-angle tilted B and then removing it. Step-by-step topological conversions of skyrmion bags with different topological charges via B are also demonstrated. Furthermore, we investigate the local creation and conversion of skyrmion bags by utilizing the local stray fields from the magnetic tips. Micromagnetic simulations reveal the mechanisms of the creation and stability of skyrmion bags, as well as the chirality distribution along the thickness direction. Our findings open the avenue for research on skyrmion bags in confined multilayered structures, which will stimulate further research, as well as applications in skyrmion bag-based spintronic devices.

Results

Fabrication and magnetic characterizations of samples

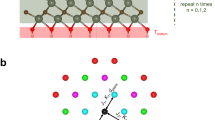
Using standard electron beam lithography and subsequent lift-off technique (detailed fabrication process in Supplementary Fig. 1), we fabricated arrays of ferromagnetic disks with varying diameters (d) ranging from 0.75 to 1.30 μm, which were deposited by ultrahigh vacuum magnetron sputtering (details in Methods). Figure 1a presents the detailed structure of the ferromagnetic disks consisting of substrate/Ta(10 nm)/[Ta(3 nm)/CoFeB(1.1 nm)/MgO(1.0 nm)]₁₅/Ta(2 nm). Here the ferroelectric single-crystal substrate Pb(Mg_1/3Nb_2/3)_0.7Ti_0.3O₃ (PMN-PT) is used to facilitate future research on electric-field manipulation of magnetism. The multilayered structure [Ta/CoFeB/MgO]₁₅ has been demonstrated to stabilize room-temperature skyrmions after being magnetized by a slightly tilted in-plane (IP) B⁴⁷. More importantly, the heavy metal/CoFeB/MgO structures can be designed for the electrical detection of spin textures via CoFeB/MgO-based magnetic tunnel junctions (MTJs)⁴⁸.

Fig. 1: Sample structure and magnetic properties.

a Schematic of the ferromagnetic disk configuration. b 3D AFM image of the 1.1 μm disk array. c STEM image of the cross-section of a d = 1.1 μm disk. d Normalized OOP (blue) and IP (red) magnetic hysteresis loops of the continuous multilayer. e IP wave vector k dependence of the frequency difference ∆f with the error bar obtained from the standard error of Lorentzian fitting. The solid line indicates a linear fitting, used to determine the strength of i-DMI.

Figure 1b shows a representative three-dimensional atomic force microscope (AFM) image of the 1.1 μm disk array. Scanning transmission electron microscopy (STEM) was performed to show the cross-section of the 1.1 μm disk (Fig. 1c). The multilayered stack exhibits sharp interfaces and periodical Ta/CoFeB/MgO trilayer structure. To obtain the macroscopic magnetic properties of the multilayers, the same [Ta/CoFeB/MgO]₁₅ multilayers were also deposited on the unprocessed substrates. Figure 1d shows the out-of-plane (OOP) and IP magnetic hysteresis loops of the continuous multilayer (details in Methods). Our sample exhibits very weak effective magnetic anisotropy since the magnitudes of the saturation fields of the IP and OOP hysteresis loops are comparable⁴⁹. This has been shown to be crucial for the coexistence of high-order dipolar skyrmions and antiskyrmions in continuous multilayers²³. The typical sheared shape of the OOP hysteresis loop indicates the spontaneous creation of domain textures such as stripe domains due to strong dipolar interaction, which can help to enhance the stability of skyrmions⁴⁷. The evolution of the magnetic domain structure in the continuous [Ta/CoFeB/MgO]₁₅ multilayer with B can be found in Supplementary Fig. 2.

The interfacial Dzyaloshinskii–Moriya interaction (i-DMI) is essential for stabilizing chiral spin textures in the asymmetric multilayers^27,28,29 and its strength D can be obtained by the Brillouin light scattering (BLS)^50,51. The IP wave vector k dependence of the frequency difference ∆f between the anti-Stokes and Stokes peaks is presented in Fig. 1e (raw BLS spectra in Supplementary Fig. 3). The relation between ∆f and D can be described as^50,51

$$\varDelta {f}=\frac{2{\gamma }{D}}{\pi {{M}}_{s}}{k}{,}$$

(2)

where γ is the gyromagnetic ratio and M_s is the saturation magnetization. To avoid possible instrument frequency offsets, ∆f is averaged for the positive and negative magnetic fields. D value around 0.27 mJ m⁻² can be extracted from the slope by a linear fitting of ∆f and k, which is comparable to those reported in the literature^47,52.

Creation of zero-field stable skyrmion bags

We propose a two-step method for room-temperature creation of zero-field skyrmion bags in the confined disks. First, the disk arrays were magnetized by a 7 kOe saturation B with a tilted angle θ (schematic illustration in Fig. 2a). We utilized MFM to image the magnetic domain structure in the 1.2 μm disk arrays at remanent states with θ = 0, 15, 45 and 90°, respectively. It’s interesting to observe that the remanent states are dominated by a net-like domain structure consisting of loops and their connections to the boundaries of the disks with θ = 15° (the schematic of “loop” and “connection” in Fig. 2b), while a labyrinthine-stripe domain structure is observed at other tilted angles (Supplementary Fig. 4a–d). For disk arrays with other sizes, the net-like domain structure is also presented for θ = 15° (Supplementary Fig. 4e). It should be mentioned that this net-like domain structure is comparable to the “loop-like” state reported in the van der Waals magnet FeGeTe¹⁷ and the “net domain” structure reported in Co/Pt multilayers¹⁸, which are served as the seed states for the creation of skyrmion bags and skyrmioniums, respectively. However, they were both presented in continuous films rather than in confined structures, with the method and mechanism differ from ours. Since the small-angle tilted B has been shown to create skyrmion lattices in continuous films^47,53, the emergence of the net-like domain structure in our confined disks could be understood as the combination of the skyrmion lattice and the confined structure (schematic illustration and detailed discussion in Supplementary Fig. 4f). Due to the geometric confinement, an incomplete skyrmion lattice, i.e., the net-like domain structure, is obtained in the disks.

Fig. 2: Creation of skyrmion bags in confined disks by magnetic fields.

a Schematic of the tilted B applied to the sample. θ is the tilted angle. b Creation of Q = 1, 2, 3 skyrmion bags by applying an OOP magnetic field to the net-like domains (the remanent states after applying a tilted saturation B of 7 kOe with θ = 15°) in the 1.3 μm disks. c Observation of skyrmion bags with varying topological charges in disks with different d at zero field. d Statistical probability distribution of zero-field magnetic states observed in disk arrays with varying d, determined by averaging over more than 19 nominally identical disks for each d. Labyrinthine stripes (LS), Q = 0, 1, 2, 3 skyrmion bags (Q = 0, 1, 2, 3) are colored blue, green, yellow, orange, and cyan, respectively. The color bar represents the MFM phase shift.

Second, we applied a small OOP magnetic field to the net-like domain structures and found the formation of skyrmion bags. Figure 2b shows the conversion process of the net-like domain structure to skyrmion bags with different topological charges in three d = 1.3 μm disks. The net-like domain structure on the left (label A) and in the middle (label B) contain two and three complete loops inside the disks, respectively. As B increases from 0 to 16 mT, the connections between the loops and the edge of the disks shrink gradually while the loops maintain their structural integrity. Zero-field stable skyrmion bags with topological charges Q = 1 and Q = 2 were obtained after removing B. As for the disk on the right (label C), five complete loops are identified in the initial net-like domain structure, with two of them being partially located at the edge. As B increases to 11 mT, one of the loops breaks and others shrink. The remaining four loops shrink further and the surrounding connections diminish gradually at 16 mT. Finally, a stable skyrmion bag with Q = 3 is observed at zero field. More MFM images are shown in Supplementary Fig. 5a. Therefore, by applying a tilted B and then removing it, we can obtain an intermediate state with the net-like domain structure, which can be utilized to induce the formation of skyrmion bags via applying an appropriate OOP magnetic field. Furthermore, these skyrmion bags can remain stable at B = 0 mT, which could be attributed to the enhanced stability from the geometric confinement^{12,27,34,35,36,37} (we will provide a detailed discussion in the Discussion section).

We have also investigated disk arrays with different sizes using the aforementioned two-step method. Skyrmion bags with varying topological charges were created and persist at zero field in disk arrays with d from 1.05 to 1.30 μm (Fig. 2c; more results in Supplementary Fig. 5b). Many Q = 0 skyrmion bags, usually known as skyrmioniums and target skyrmions, first appear in the 1.05 μm disks. Skyrmioniums have been shown to exhibit no skyrmion Hall effect due to their zero net topological charge^16,18, and are suggested as an alternative to skyrmions as the storage element. As d increases, skyrmion bags with higher topological charges are observed at zero field. Q = 0, 1 skyrmion bags are identified in the 1.1 μm disks while Q = 0, 1, 2 skyrmion bags are all found in the 1.2 μm disks. When d increases to 1.3 μm, Q = 0 skyrmion bags can no longer persist at zero field and Q = 3 skyrmion bags begin to appear. Figure 2d shows the statistical probability distribution of stable zero-field magnetic domain structures in disk arrays with varyinfg d, which is determined by averaging over more than 19 nominally identical disks for each d. The larger disks are required to stabilize skyrmion bags with higher topological charges. Furthermore, the instability of skyrmion bags notably increases when d increases to 1.3 μm and correspondingly the probability of labyrinthine-stripe domain structure increases to 42% (Fig. 2d). We will analyze the dependence of skyrmion bags with different topological charges on disk size in the Discussion section.

Topological conversion of skyrmion bags via magnetic field

Investigation on the conversion of skyrmion bags with varying topological charges is important. Figure 3a–c exhibits the representative step-by-step conversions of Q = 1, 2, 3 skyrmion bags to skyrmioniums via applying OOP magnetic fields (more results in Supplementary Fig. 6). The initial states of Q = 1, 2, 3 skyrmion bags at zero field are obtained through the two-step method described above. Figure 3a shows the Q = 1 skyrmion bag maintains its structural integrity and shrinks in size gradually with B increasing from 0 to 26 mT, and transforms into a skyrmionium at 31 mT. For the initial Q = 2 skyrmion bag (Fig. 3b), the bottom two loops begin to merge at 26 mT and a Q = 1 skyrmion bag is presented at 31 mT, which then transforms into a skyrmionium at 39 mT. Figure 3c presents the conversion process from the Q = 3 skyrmion bag to the skyrmionium. Therefore, higher-Q skyrmion bags tend to collapse into energetically favorable skyrmioniums upon reaching the critical fields.

Fig. 3: Field-driven topological conversion of skyrmion bags.

Process of topological conversions from the initial states Q = 1 skyrmion bags (a), Q = 2 skyrmion bags (b), and Q = 3 skyrmion bags (c) to skyrmioniums under B with d = 1.3 μm for a–c. d Evolutions of skyrmioniums under positive and negative magnetic fields, respectively. Two initial states in d are from the same d = 1.05 μm disk, created by B. The color bar represents the MFM phase shift.

We further investigate the evolutions of skyrmioniums with B (Fig. 3d). First, we applied a positive OOP magnetic field to the disk, which is parallel to the magnetization of the skyrmionium core. The loop domain of the skyrmionium with magnetization antiparallel to the field shrinks in size while maintaining a complete topological structure as B increases to 26 mT. At 29 mT, the skyrmionium collapses into one skyrmion. It should be mentioned that we have observed in some disks the breaking process of the loop domain of skyrmionium and the formation of a small horseshoe-shaped domain, which subsequently shrinks into a skyrmion (Supplementary Fig. 7a). Next, the skyrmionium was created again in the same disk and a negative OOP magnetic field was applied (details in Supplementary Fig. 7b). The loop domain of the skyrmionium expands and stretches along one direction (approaching the boundary) as the negative B increases to 13 mT. At −14 mT, the loop opens a gap at the boundary and a horseshoe-shaped domain appears. A reverse stripe domain with magnetization parallel to B is formed originating from the boundary and the horseshoe-shaped domain splits into two stripe domains at −17 mT (detailed process in Supplementary Fig. 7b). Subsequently, these three stripe domains expand and interconnect with each other, leading to the appearance of two elongated skyrmion-like domains. These two domains shrink to form two skyrmions at −33 mT.

These results indicate that the skyrmioniums in confined disks exhibit different annihilation pathways under positive and negative magnetic fields. When B is parallel to the skyrmionium core, skyrmionium collapses into skyrmion through the interior of the disk. In contrast, skyrmionium transforms into skyrmion through the edge of the disk with B antiparallel to the skyrmionium core. It should be mentioned that the evolutions of skyrmioniums under positive and negative magnetic fields have been reported in low-temperature bulk magnet FeGe disks¹². In that work, the relative orientations between the magnetic fields and skyrmiomium cores corresponding to the two pathways are opposite to our case. This could be due to the different types of the magnetic anisotropies in bulk materials and multilayers, leading to the differences in the orientation distributions of magnetic domains, thereby resulting in different evolution behaviors under B.

Local manipulation of skyrmion bags with MFM tips

As shown above, by performing MFM imaging, the creation and step-by-step topological conversions of skyrmion bags in ferromagnetic disks can be realized via applying uniform external magnetic fields. Considering that the MFM tip can generate a local magnetic stray field^54,55, we have also investigated the local effects of MFM tips on skyrmion bags. We performed multiple zero-field MFM scanning over the 1.2 μm disk array with a region of 12 × 12 μm² (schematic illustration in Fig. 4a and details in Methods). The magnetic tips used for our experiments were found to have varying magnitudes of stray fields for different batches (details in Methods). A MFM tip with the maximum stray field of approximately 200 Oe (at the apex of the tip; Methods and Supplementary Fig. 8) was used to scan the disk array up to 8 times. The disk array was magnetized with the tilted saturation B before MFM scanning.

Fig. 4: Local manipulation of skyrmion bags via MFM tips.

a Schematic of the MFM scanning configuration. Creation of Q = 0 skyrmion bags (b), Q = 1 skyrmion bags (c), and Q = 2 skyrmion bags (d) induced by several MFM tip scans. e Conversion of Q = 1 skyrmion bags to Q = 0 skyrmion bags after the second scan. f Conversion of Q = 2 skyrmion bags to Q = 1 skyrmion bags after the fifth scan. Low-moment MESP-LM-V2 tips (Bruker) with stray fields of around 200 Oe (at the apex of the tips) were used in b–f. The number of the scan is marked above the disks and the color bar represents the MFM phase shift.

After the first scanning, we obtain skyrmion bags as well as other domain structures in different disks, such as domain structures with morphology close to skyrmion bags (Supplementary Fig. 9). Figure 4b–d shows that subsequent multiple tip scanning processes can induce the formation of complete skyrmion bags from the domain structures with morphology close to skyrmion bags. Figure 4b exhibits the creation of a skyrmionium from a horseshoe-shaped domain after the second scan. The stray field generated by the MFM tip facilitates the connection of the two ends of the horseshoe-shaped domain to form a complete loop domain during the scanning process. This process can be interpreted as follows: one end of the horseshoe-shaped domain (with magnetization opposing the tip’s stray field) is pushed away from the position of the scanning tip by the stray field, thereby overcoming the potential barrier between the two ends, leading to their connection. Similarly, we obtain a domain close to the Q = 1 skyrmion bag after the first scan (Fig. 4c). After the second scan, a complete Q = 1 skyrmion bag is identified, in which one of the loops is distorted. Then the distorted loop domain returns to normal after the third scan. Figure 4d shows the formation process of a Q = 2 skyrmion bag. Upon completion of the first scan, a domain emerges exhibiting three loops, analogous to the Q = 2 skyrmion bag. However, one of the three loops is connected to the edge. The stray field during the second scan induced the magnetic reversal of the connections between this loop and the edge (turning from light to dark, Fig. 4d). It is noteworthy that this process demonstrates the “cutting effect” of the local stray field on magnetic domains, analogous to the report that the local stray field cuts the labyrinthine domains into isolated skyrmions⁵⁴. Subsequently, the loop domain with magnetization opposing the stray field is pushed to the middle of the disk and a Q = 2 skyrmion bag is obtained after the third scan.

The above representative results demonstrate the local creation of Q = 0, 1, 2 skyrmion bags via tip scanning, which persist in the subsequent multiple scans (Supplementary Fig. 9). Most of the disks are in the states of skyrmion bags with varying topological charges after three scans (Supplementary Fig. 9). It should be noted that, for the skyrmion bags observed after the first scanning, their conversion towards the lower topological charge are also observed in the subsequent few scans. Figure 4e shows the conversion from a Q = 1 skyrmion bag to a Q = 0 skyrmion bag after the second scan. The conversion from a Q = 2 skyrmion bag to a Q = 1 skyrmion bag was finished after the fifth scan (Fig. 4f). This process also demonstrates the aforementioned cutting effect, where the local stray field induces the flipping of the domains that connect internal skyrmions within the skyrmion bag. For all disks, after the fifth scan, three additional scans were performed and no change of the domain structures was observed (Supplementary Fig. 9). This suggests that for tips with a maximum stray field of approximately 200 Oe, the manipulation effects occur during the initial few scanning processes, after which the magnetic domain structures tend to stabilize.

We have also investigated the effect of magnetic tips with a larger stray field of 350 Oe (from another batch, Supplementary Fig. 8) and the same disk arrays were scanned. Skyrmion bags are identified with Q = 1 and Q = 0 after the first scan and only Q = 0 skyrmion bags persist after multiple scans (Supplementary Fig. 10). It’s clear that magnetic tips with larger stray fields can further reduce the topological charge of the skyrmion bags. It can be anticipated that tips with sufficiently strong stray fields could cut the Q = 0 skyrmion bags into stripe domains or even skyrmions. Our results illustrate that the stray field generated by the magnetic tips can manipulate the local creation and topological transition of skyrmion bags.

Discussion

We have demonstrated room-temperature creation and conversion of skyrmion bags in confined magnetic multilayered structures. The stability of skyrmion bags at zero field in our disks can be attributed to the competition among the exchange interaction, dipolar interaction, magnetic anisotropy and interfacial DM interaction. In particular, geometric confinement could contribute to their enhanced stability. Since the boundary condition is a direct manifestation of the geometric confinement effect, it’s important to investigate the role of the boundary condition on the creation and stability of skyrmion bags in the confined disk. Based on the STEM measurements of the cross-section of the disk (Supplementary Fig. 11), a reasonable boundary condition for disks is established, i.e., a circular region with high uniaxial anisotropy constant K_u at the edge of the disk with gradual increase of K_u from the inside to the edge (details in Supplementary Fig. 11). Based on this boundary condition, micromagnetic simulations were performed to understand the mechanism of the creation and stability of skyrmion bags in our confined disks (details in Methods). We simulated the creation process of skyrmion bags induced by B and their stability at zero field (Fig. 5a). Three different initial states are analogous to the three net-like domains in Fig. 2b. Increasing the positive OOP magnetic field applied to the initial net-like domains, the connections between loops and edges of the disks shrink and finally break to form skyrmion bags, which can persist at zero field. The simulation results are consistent with the experimental results (Fig. 2b).

Fig. 5: Micromagnetic simulations of formation, stability and chirality of skyrmion bags.

a Simulated images of the formation process of Q = 1, 2, 3 skyrmion bags in d = 1.3 μm disks via B. b Disk diameter (d) dependence of the total energy density (f_tot) of skyrmion bags with different topological charges Q. For each d, four initial structures (skyrmion bags with Q = 0, 1, 2, 3) are relaxed to the final states at zero field and only the structures that can remain stable are shown here. Q = 0, 1, 2, 3 skyrmion bags (Q = 0, 1, 2, 3) are colored blue, purple, red, and orange, respectively. c Simulated images of a Q = 1 skyrmion bag in the d = 1.3 μm disk and the cross-sectional view (top to bottom) of the area marked by the white line. d Simulated distributions of m_z (upper panel, indicated by the color bar) and IP magnetization (lower panel, indicated by the color wheel) in different magnetic layers for the skyrmion bag in c. The arrows show the directions of the magnetization vectors (upper panel) and IP magnetization components (lower panel). The color bars in a, c and d all represent the OOP magnetization component m_z.

Based on the simulation results above, we point out that this boundary condition (the established circular high- K_u region) is crucial for the creation and stability of skyrmion bags. The higher K_u allows the magnetization opposing the OOP magnetic field in this region to flip more easily and quickly in alignment with the field as the field increases⁵⁶. Therefore, the boundary condition facilitates the formation of an annular out-of-plane domain near the disk boundary, through which the net-like domain structures transform into skyrmion bags. Furthermore, after the creation of skyrmion bags, the high-K_u region acts as a potential barrier to block the connection between inner skyrmions and the boundary, which explains the stability of skyrmion bags at zero field. To further verify the necessity of the special boundary condition in the formation process of skyrmion bags, we have simulated the evolution of the magnetic domain structure in the disk without the edge-gradient region. From the same initial state (the net-like domain), the loops and connections contract together as B increases, so that no skyrmion bag is formed (Supplementary Fig. 12).

To understand the sensitive dependence of the creation and stability of skyrmion bags with different topological charges on disk size d as shown in Fig. 2d, we have performed micromagnetic simulations. The stability of skyrmion bags with different Q in disks of varying d at zero field were investigated (Supplementary Fig. 13). Only the skyrmion bags with Q = 0 remain stable when d = 1.0 μm while Q = 3 skyrmion bags can already remain stable when d increases to 1.3 μm (Supplementary Fig. 13), which is generally consistent with the experimental results (Fig. 2d). Skyrmion bags with higher topological charges gradually become stable as the disk size increases. To further understand the underlying mechanism, we have calculated the total energy density f_tot of skyrmion bags as a function of d, as shown in Fig. 5b. For the Q = 0 skyrmion bag, the f_tot – d curve exhibits a “V” shape. As d decreases from 1.1 μm, the rapid increase of f_tot leads to the rapid decline in the stability of the Q = 0 skyrmion bag. When d increases from 1.1 μm, the gradual increase of f_tot, which eventually surpasses that of the skyrmion bags with higher topological charges, decreases the stability of the Q = 0 skyrmion bag. This indicates that there is an optimal size range (centered at around 1.1 μm) for the stability of Q = 0 skyrmion bag, which explains the experimental observation of no stable Q = 0 skyrmion bags with d < 1.05 μm or d > 1.2 μm at zero field. For other higher-Q skyrmion bags, we found that their f_tot – d curves generally show a decreasing trend as d increases, indicating that the stability of higher-Q skyrmion bags requires larger disk sizes. These curves can be understood by analogy to the left part of the “V”-shaped curve of the Q = 0 skyrmion bags. It’s expected that as d continues to increase, the Q = 1, 2, 3, and even higher-Q skyrmion bags will successively begin to show an increasing trend of f_tot for sufficiently large d. Therefore, skyrmion bags with specific topological charge each have their own stability ranges of d. The analysis of the contribution of each energy term to f_tot further elucidates the behavior of the “V”-shaped curve (Supplementary Fig. 14).

Since our multilayered stack comprises 15 repeating periods, strong dipolar interaction helps to stabilize skyrmion bags at room temperature^29,47,52. We have calculated the IP distribution of the dipolar interaction energy density (Supplementary Fig. 15a), which reflects the effect of the disk’s circular symmetry. Meanwhile, in the OOP direction, the dipolar interaction competes with the interfacial DM interaction to determine the chirality of skyrmion bags^47,52,57. Taking the Q = 1 skyrmion bag as a representative example, we have performed layer-resolved micromagnetic simulations. The cross-section of the domain wall (as shown by the dashed lines) from top to bottom (Fig. 5c), and the OOP and IP magnetization components of the three representative layers are obtained (Fig. 5d). Taking the domain wall corresponding to the white arrows in Fig. 5d (lower panel) as an example, in the bottom layer, the IP magnetization components inside the domain walls are nearly parallel along the radial direction, indicating that Néel-type domain walls are stabilized. From the bottom up, the IP tangential magnetization components increase gradually. In the 10th layer, the IP magnetization components are oriented almost along the tangential direction, indicating a transition to the Bloch-type domain walls. The domain walls transition back to the Néel-type when approaching the top layer, however, the chirality is reversed to that in the bottom layer. Similar chirality distributions are also present in other domain walls.

This result reveals that a hybrid chiral domain wall structure is present for skyrmion bags in our 15-period sample, analogous to the hybrid chiral structures reported for skyrmions in the multi-period multilayers^47,52,57. The magnetization inside the domain walls tends to reorient to form a flux-closure structure in the thickness direction due to the strong dipolar interaction⁵⁷, and the presence of DMI lifts the Bloch-type layer toward the top surface^52,57. We have computed the corresponding topological charge of the magnetic textures within each layer, as shown in Supplementary Fig. 15b. For each layer, the topological charge is close to 1, confirming the distribution of the Q = 1 skyrmion bag along the thickness direction. The effect of different D values on the chiral structure of domain walls in skyrmion bags is shown in Supplementary Fig. 16.

Based on our proposed mechanism (the established boundary condition), we have investigated the effects of different material parameters on skyrmion bags (Supplementary Fig. 17). The results show that the established boundary condition facilitates the stability of skyrmion bags over a wide range of material parameters. Additionally, guidance on the required disk sizes for different parameters is provided. In addition, we have simulated the process of local creation of skyrmion bags via MFM tips (Supplementary Fig. 18). The simulation results support our experimental findings.

In summary, we have observed the room-temperature creation of individual skyrmion bags with varying topological charges in magnetic multilayered disks. Through MFM measurements combined with micromagnetic simulations, we have demonstrated that skyrmion bags can be created from the net-like domains via B in [Ta/CoFeB/MgO]₁₅ ferromagnetic disks. The special boundary condition, a high-K_u region at the edge of the disk, is essential for skyrmion-bag formation and stability. We have also investigated the step-by-step topological conversions of skyrmion bags under B, and local formation and manipulation of skyrmion bags during magnetic tip scanning. Our work provides a method for investigating room-temperature individual skyrmion bags in confined multilayered structures, which can extend to other geometries and materials. The investigation on the boundary condition of the disk will stimulate further research on the interaction between skyrmion bags and boundaries. What’s more, the magnetron sputtering growing technique is compatible with industry and CoFeB/MgO structures can be conveniently designed for electrical detection via CoFeB/MgO-based MTJs. These findings could facilitate the high-Q-based topological spintronic applications.

Methods

Sample preparation

Ferromagnetic disks were fabricated using electron beam lithography followed by deposition of the multilayer stacks and subsequently lift-off process. More details about the fabrication process are shown in Supplementary Fig. 1. The multilayer stacks Ta(10 nm)/[Ta(3 nm)/Co₄₀Fe₄₀B₂₀(1.1 nm)/MgO(1.0 nm)]₁₅/Ta(2 nm) were deposited by magnetic sputtering at room temperature with a base pressure better than 4 × 10⁻⁵ Pa without B. The bottom 10 nm Ta was deposited as the buffer layer to improve the interface quality and a 2 nm Ta capping layer was used to prevent oxidation of the stack. The stacks were annealed at 300 °C for 0.5 h in a vacuum furnace (3 × 10⁻⁵ Pa) at zero field after the lift-off process.

Magnetic property measurement system

OOP and IP magnetic hysteresis loops for the continuous multilayer were measured via a magnetic property measurement system (MPMS 7 T; Quantum Design).

Magnetic force microscopy

MFM measurements were performed at room temperature by an Infinity Asylum Research AFM. The low-moment magnetic tips (MESP-LM-V2, Bruker) were used in our work. The tip transfer function (TTF) method was used to obtain the magnitudes of stray fields of the tips (details in Supplementary Fig. 8) and we found varying values of stray fields for different batches. MFM images were taken in a standard two-pass tapping/lift mode with a lift height of 80 nm, using the MFM tips with a smaller stray field (maximum value of around 200 Oe with zero lift height and less than 40 Oe with the lift height of 80 nm). When investigating the local effects of MFM tips on skyrmion bags, multiple zero-field MFM scanning using the standard two-pass tapping/lift mode over the 1.2 μm disk array with a region of 12 × 12 μm² was performed. Magnetic textures were primarily influenced by MFM tips during the tapping mode⁵⁴, in which the MFM tip was in contact with the sample surface. Therefore, for each MFM scanning, magnetic textures were switched in the tapping mode (if any) and then the magnetic images were obtained in the lift mode with a proper lift height (to reduce the impact of the stray field on imaging).

Scanning transmission electron microscopy

For TEM measurements, a d = 1.1 μm disk was selected and a focused ion beam system (Zeiss Auriga) was used to cut out a cross-sectional lamella with a thickness of less than 100 nm at the center of the disk. TEM observations were subsequently performed on a double aberration-corrected microscopy (Titan Cubed Themis G2 300) at an acceleration voltage of 300 kV.

Brillouin light scattering

Brillouin light scattering (BLS) is a process that involves inelastic scattering of photons and magnons in a magnetic film. Two Damon-Eshbach (DE) spin waves (magnetostatic surface spin wave) with opposite propagation directions will be generated on the upper and lower surfaces of the magnetic layer when an IP magnetic field (larger than the IP saturation field) is applied. The incident light scatters with these two DE waves respectively, corresponding to the Anti-Stokes process and Stokes process. The frequencies of these two DE spin waves can be determined by measuring the energy of the scattered photons. Interfacial DMI favors certain spatial chirality, which can cause a relative frequency offset of these two DE spin waves. The DMI strength can be obtained by measuring the dispersion relationship of DE spin waves under different wave vectors. Our BLS measurements were performed by using a single-mode solid-state laser with a power of 30 mW and a wavelength of 532 nm. A JRS Sandercock-type multipass tandem Fabry–Pérot interferometer was used to analyze the back-scattered light collected. An IP magnetic field of 310 mT was applied, which was perpendicular to the IP wave vector (DE mode configuration).

Micromagnetic simulation

The GPU-accelerated micromagnetic simulation software MuMax3⁵⁸ is used to perform the simulations. The magnetization distribution of the magnetic domain structure can be represented as M = M_s (m₁, m₂, m₃), where m_i denotes the constituent of unit magnetization vector m in the orientation of the local coordinate axis i. The transient magnetization domain structure is described by the Landau-Lifshitz-Gilbert (LLG) equation⁵⁹:

$$(1+{\alpha }^{2})\frac{\partial {{\bf{M}}}}{\partial {t}}=-\gamma {{\bf{M}}}\times {{{\bf{H}}}}_{{{\rm{eff}}}}-\frac{\gamma \alpha }{{{M}}_{s}}{{\bf{M}}}\times ({{\bf{M}}}\times {{{\bf{H}}}}_{{{\rm{eff}}}}),$$

(3)

where α is the damping constant, γ is the gyromagnetic ratio, and H_eff is the effective magnetic field, which can be described by the following equation:

$${{{\bf{H}}}}_{{{\rm{eff}}}}=\frac{-1}{{\mu }_{0}{{M}}_{{{\rm{s}}}}}\frac{\partial {F}_{{{\rm{tot}}}}}{\partial {{\bf{m}}}},$$

(4)

where μ₀ and F_tot represent the vacuum permeability and total free energy, respectively. The total free energy can be written as

$${F}_{{{\rm{tot}}}}={F}_{{{\rm{dem}}}}+{F}_{{{\rm{ani}}}}+{F}_{exc}+{F}_{{{\rm{dmi}}}},$$

(5)

where F_dem, F_ani, F_exc, and F_dmi are the demagnetization energy, magnetic anisotropy energy, exchange energy and Dzyaloshinskii-Moriya interaction (DMI) energy, respectively. The uniaxial anisotropy energy is used for our sample, the magnitude of which is determined by

$${{F}}_{{{\rm{ani}}}}=\int \!\!\!\iint (-{{K}}_{{{\rm{u}}}}{{m}}_{3}^{2})d{V},$$

(6)

where K_u is the uniaxial anisotropy constant. The exchange energy can be expressed as

$${F}_{{{\rm{exc}}}}=\int \!\!\!\iint {A}_{ex}[{(\nabla {m}_{1})}^{2}+{(\nabla {m}_{2})}^{2}+{(\nabla {m}_{3})}^{2}]dV,$$

(7)

where A_ex is the nearest-neighbor Heisenberg exchange constant. The interfacial DMI for our sample can be expressed as

$${F}_{{{\rm{dmi}}}}=\int \!\!\!\iint [D({m}_{3}\nabla \cdot {{\bf{m}}}-{{\bf{m}}}\cdot \nabla {m}_{3})]dV,$$

(8)

where D is the effective interfacial DMI constant.

To speed up the simulations, the effective medium approach is used to model the multilayer film as a single uniform layer²⁹. The mesh size is 5 × 5 × 5 nm. The following magnetic parameters adopted from Ta/CoFeB/MgO multilayers are used for the simulations: A_ex = 2.0 × 10⁻¹¹ J m⁻¹, K_u = 4.6 × 10⁵ J m⁻³, M_s = 8.6 × 10⁵ A m⁻¹, D = 0.4 mJ m⁻², α = 0.01, γ = 2.2 × 10⁵ mA⁻¹s⁻¹. The temperature in our model is set as T = 0 K. Considering the local inhomogeneity created during the growth process of the multilayer, we have adopted a grain structure for simulations. The grain size is set to be 60 nm and K_u is set to fluctuate randomly by 15% within each grain. To match the actual boundary condition of the disk, a circular high-K_u region is established at the edge of the island, where K_u gradually increases from the inside to the outside (More details in Supplementary Fig. 11). Specifically, the width of the annular region is around 1/8 of the disk’s diameter, in which the magnitude of K_u gradually increases to 1.5 times its original value. When investigating the chirality distribution of the domain walls within skyrmion bags, we have simulated the domain walls of the stable Q = 1 skyrmion bags in the 1.3 μm disk for different D values of 0.2, 0.3, 0.4, 0.5 mJ m⁻², and obtain the corresponding cross-sections of the domain walls in Supplementary Fig. 16.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.