Introduction

High energy resolution (ER) semiconductors with high detection efficiencies are exceptionally important in the detection and localization of weak X-ray and gamma-ray isotopes in the fields of nuclear security, industrial inspection and medical imaging1. The detection efficiency of a radiation detector is determined by the probability that each interacting quantum of radiation inside the detector volume will give rise to a detectable pulse. A high detection efficiency enables minimization of the time required for searching for and identifying weak radiation sources, enhancing the overall efficiency in radiation detection tasks. Semiconductor materials with direct conversion promise a relatively high ER response and an improved spatial resolution, positioning them as the next generation of radiation detection materials. To address the emerging challenges and growing demands in the aforementioned applications, novel radiation detection materials and related technologies must be promptly developed. Nevertheless, enhancing the detection efficiency of state-of-the-art semiconductor detectors for high-energy gamma rays, particularly in terms of the detector thickness, presents a nontrivial challenge compared with conventional scintillators of inch-size2,3,4. For instance, the thickness of commercially available CdZnTe and CdTe detectors has now been limited to approximately 1.5 cm due to device optimization constraints and charge transport deficiencies3,4,5,6,7,8.

The use of perovskite semiconductor detectors with extraordinary charge transport properties and high radiation hardness seemingly favors thicker detectors with increased detection efficiency9,10,11,12,13,14,15. Substantial progress has been made in enlarging the volume of single crystals, with diameters now surpassing 1 inch16,17,18,19. However, despite these advancements, the reported effective detector thickness remains constrained to approximately 5 mm, which is significantly inferior to that of the conventional semiconductor CdZnTe and scintillators such as LaBr3: Ce. This highlights the current gap in the ability to achieve perovskite detectors with larger volumes, especially thickness exceeding 1 cm (Supplementary Table 1).

A single-crystal device mitigates the carrier trapping and recombination occurring at the grain boundaries. Note that the impurity levels in perovskite single crystals are typically orders of magnitude higher (~5 N) than those in conventional semiconductors (~7 N or more)9,20,21. High impurity levels, approximately in the range of 1015-1017 cm−3 corresponding to the mentioned purity levels, may impede the width of depletion layer, consequently reducing the mean free drift path of photogenerated carriers22. Despite the inherent defect tolerance of perovskites, both intrinsic and extrinsic defects are unexpectedly abundant in perovskites, which surely alternate the charge transport efficiency on a macroscopic scale. As previously shown23, electron transport was found to be inferior to hole transport, probably because of charge trapping, immensely hindering the detector performance of thicker crystals. Nevertheless, the carrier transport dynamics in centimeter-thick perovskite detectors have not yet been experimentally investigated.

The unipolar device regime for perovskite detectors was first introduced in 2021 in our previous work. This approach involves screening the electron signal and spatially weighting the hole signal10,16. The unipolar design16 effectively confines the signal induction region for the hole carriers, thereby eliminating the dependence of the signal amplitude on the interaction depth. This regime has been validated to increase the detector performance for larger thicknesses. For instance, a 4.6 mm thick CsPbBr3 detector fabricated with a pixelated configuration achieved a high ER of 1.4% at 662 keV. However, it is worth mentioning that the development of unipolar detectors for perovskite semiconductors is still in its early stages, with two configurations (pixelated and quasi-hemispherical) reported thus far. Therefore, substantial efforts are needed to increase the detection efficiency. Currently, the response behavior of detectors with effective detector thicknesses greater than 1 cm remains elusive.

In this work, we present a virtual Frisch grid (VFG) CsPbBr3 detector with a high detection efficiency in hole-only mode and demonstrate excellent detector performance for a thickness of up to 2.2 cm. We develop rational procedures for the design and fabrication of centimeter-thick perovskite VFG detectors, addressing the fundamental aspect of the charge transport dynamics when the detector thickness exceeds 1 cm. The ER for 137Cs 662 keV gamma rays is optimized to 1.5% and 2.2% for VFG CsPbBr3 detectors with thicknesses of 10.2 mm and 22.1 mm, respectively. The mobility-lifetime product of hole carriers is estimated to be ~2.5 × 10−2 cm2V−1. In particular, a hole carrier multiplication mechanism possibly associated with Auger recombination during the charge transport processes is revealed. Through transient pulse analysis, we investigate individual carrier drift processes and propose a physical model for the anomalous gain observed in the initial biasing stage, which may be applicable to other halide perovskite counterparts.

Results

Principle and fabrication of virtual Frisch grid detector

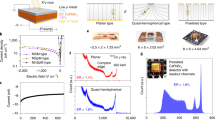
Figure 1a illustrates the design of the CsPbBr3 VFG detector. A columnar or cylindrical-shaped crystal could be fabricated through mechanical processing. A metal grid ring is embedded near the collecting cathode, which is separated by a thin insulating layer. The anode and cathode electrodes are eutectic Ga-In alloy (EGI) and Au, respectively. Detailed fabrication process was schemed in Supplementary Fig. 1. The efficacy of the unipolar detector regime in suppressing low-energy tails, which are commonly observed in ambipolar planar detectors, was demonstrated (see Supplementary Fig. 2). For instance, ambipolar planar detectors with thicknesses of ~5 mm and ~20 mm exhibited the pronounced tails in the energy spectra under an uncollimated 137Cs gamma ray source (Supplementary Fig. 2c, d).

Fig. 1: Physical design and fabrication of the VFG CsPbBr3 detector.
figure 1

a Scheme of the VFG detector. The Ga-In alloy (EGI) was used as the anode, and Au was used as the cathode in the VFG detector. b Simulated two-dimensional distribution of the weighting potential of the Au cathode with detector dimensions of 4.5 × 4.5 × 10 mm3 according to the Shockley–Ramo theorem, the observation plane was in the middle of the side. c–h CsPbBr3 single crystals and as-fabricated VFG detectors with various dimensions of 4.0 × 4.0 × 10.2 mm3, 5.0 × 7.0 × 17.3 mm3 and 6.5 × 7.0 × 22.1 mm3. i Absorption characteristics of CsPbBr3 crystal with thicknesses ranging from 1 to 30 mm for high energy photons. j–l Gamma ray spectroscopic response of the 10.2 mm (detector I), 17.3 mm (detector II) and 22.1 mm (detector III) thick VFG detectors under an uncollimated 137Cs source, respectively. The applied voltages were 1050 V, 3400 V, and 1700 V, respectively. m Linearity response of detector I under uncollimated 57Co and 137Cs source simultaneously. n Summary of the energy resolution achieved by perovskite semiconductors for 137Cs 662 keV gamma ray source. CsPbBr3 grown by melt method: 12.85%54, 9.91%55, 3.8%20, 2.0%56, 1.8%16, 1.4%16, 1.4%16; CsPbBr3 grown by solution method: 12.20%57, 11.47%58, 11%59, 7.31%60, 7.20%61, 5.5%62,63; hybrid perovskites by solution method: 6.7%64, 6.5%34, 5.9%65, 2.9%17, 1.7%66.

Full size image

In quasi-hemispherical detector, a higher electric field is concentrated at the small-area point cathode. However, deviation from the ideal hemispherical detector shape may induce variation in transient pulse shapes, ultimately leading to deficiencies in charge collection. The pixelated configuration represents a widely used design for various semiconductor detectors. The small pixel effect and uniform electric field improve the pulse shape uniformity and facilitate subsequent digital pulse processing. However, a multichannel readout scheme is required for depth correction and charge sharing24,25, which has not yet been technically addressed for perovskite detectors due to the lack of specialized readout electronics. In contrast, the VFG detector requires only a single readout channel, resembling the planar detector and greatly simplifying the readout electronics.

The VFG configuration has proven to be an effective approach in increasing the detection efficiency26,27, while leveraging the benefits of the small pixel effect28. The weighting potential distribution of a columnar crystal with dimensions of 4.5 × 4.5 × 10 mm3 was calculated (Fig. 1b). It is found that the VFG configuration becomes effective unipolar sensing when the side length of the columnar is set to approximately half or less than half of the length of the crystal. A hemispherical-like equipotential arch converges near the collecting cathode region, and the arches are generally confined within a hemisphere with a characteristic diameter approximately equal to the side length of the columnar crystal.

VFG CsPbBr3 detectors were then fabricated using high quality single crystals with various thicknesses of 10.2 mm, 17.3 mm and 22.1 mm (Fig. 1c–h and Supplementary Figs 2, 3). Notably the entire crystal volume was active for charge collection, with specific volumes of 163 mm3, 605 mm3 and 1006 mm3. These volumes are substantially higher than those reported in previous work16, indicating a higher absorption efficiency for 662 keV gamma-ray photons (Fig. 1i). For high energy 662 keV photons, the absorption efficiencies of CsPbBr3 crystals with thicknesses of 1, 5, 10, 20, and 30 mm were calculated as 4.2%, 19.4%, 35.1%, 57.6%, 72.2%, respectively (Fig. 1i). Specifically, the total and photoelectric absorption efficiencies calculated for 25 mm thick CsPbBr3 crystals confirmed their high stopping power for high energy gamma ray photons (Supplementary Fig. 2 and Supplementary Table 2).

Moreover, the introduction of an insulating layer hardly disturbs the current–voltage characteristics on the reverse side of the Schottky type detector (Supplementary Fig. 4). Taking advantage of the small pixel effects and excellent hole transport properties, these three large-volume VFG detectors have manifested highly energy resolved responses to 137Cs 662 keV gamma rays (Fig. 1j–l), with a champion ER of 1.9% for the 10.2 mm thick VFG detector under an electric field of 103 Vmm−1. The ERs of the 17.3 mm and 22.1 mm thick VFG detectors were 3.5% and 8.9%, respectively, which were still impressive considering their large volumes but moderate electric fields of 196 Vmm−1 and 77 Vmm−1 respectively. These performances contrast sharply with the unresolved full energy peaks in ambipolar planar detectors in the thicknesses of 5 mm and 20 mm (Supplementary Fig. 2c, d). The excellent linearity of gamma ray response was confirmed by measuring the multiple characteristic energies from 57Co and 137Cs sources (Fig. 1m). The ERs of VFG detectors with the thicknesses of 10.2 mm and 22.1 mm were further improved to 1.5% and 2.2% for 662 keV through digital pulse discrimination, as discussed below. Surprisingly, there was hardly any charge trapping of hole carriers, confirming an exceptionally long mean free drift path of hole carriers. Overall, the spectral performance of centimeter thick CsPbBr3 VFG detectors we proposed still ranks among the highest, even when compared to those of thinner perovskite detectors, distinguishing uniquely in both energy resolution and detection efficiency (Fig. 1n).

Virtual Frisch Grid detectors measurement and simulation

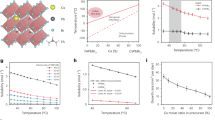
In parallel, according to the Shockley–Ramo theorem29, we investigated the distributions of the weighting potentials of the Au cathode, EGI anode and Frisch ring respectively (Fig. 2a–c). The signal induction processes on each electrode strongly depend on the depth of the gamma ray interaction. The Au cathode showed notable unipolar features when the height of the Frisch ring exceeded the side length of the crystal column, whereas simultaneously, the linearly distributed weighting potential (Fig. 2d) on the unshielded EGI anode was gradually suppressed and finally transformed into a unipolar feature when the side was fully shielded. Accordingly, Frisch ring heights of 5 mm, 6 mm and 6.5 mm with fabrication errors of ~±0.5 mm were chosen for the 10.2 mm, 17.3 mm and 22.1 mm thick VFG detectors, respectively. The distribution of the weighting potential of the Frisch ring exhibited a bipolar feature (Fig. 2c) given the assumption that carriers would likely not terminate on the Frisch ring. The two-dimensional distribution of the weighting potential of the Frisch ring is demonstrated in Fig. 2e.

Fig. 2: Simulation and signal analysis of the VFG CsPbBr3 detectors.
figure 2

a–c Simulated weighting potential distributions of the cathode, anode and Frisch ring, respectively, for various heights of the Frisch ring. d, e Simulated two-dimensional distribution of the weighting potential of the EGI anode and Frisch ring; the observation plane was in the middle of the side length. The detector dimensions in a–e were 4.5 × 4.5 × 10 mm3. f Operation scheme of the VFG detector. Note that positive and negative biases could be applied to the EGI anode and Au cathode, respectively. g Typical pulse shapes collected from the cathode, anode and Frisch ring. h Typical 137Cs gamma ray spectra from the EGI anode and Au cathode in detector I. i Bias-dependent 137Cs gamma-ray spectra from the Au cathode. j Time-dependent 137Cs gamma ray spectra from the Au cathode at a total bias of 1000 V.

Full size image

To further optimize the physical design of the VFG detector, the thickness of the insulating layer, which is considered one of the most important parameters, varied from 0.01 mm to 0.2 mm (Supplementary Fig. 5). Technically, a thinner insulating layer leads to better electrostatic shielding and a more condensed distribution of the weighting potential near the collecting electrode; however, there is a risk of excess leakage current or discharge occurring at the corner area of Au and Frisch ring. Conversely, a more divergent distribution of the weighting potential was revealed when the thickness of the insulating layer was increased to beyond 0.1 mm, indicating a decreased shielding ability. Therefore, a ~20 µm insulating layer was chosen for all three VFG detectors.

During operation, positive and negative voltages were applied to the EGI and Au electrodes respectively, while the Frisch ring was grounded (Fig. 2f). Typical pulses from the two electrodes and the Frisch ring (Fig. 2g) were recorded by a digitizer, which originated from a single gamma ray interaction event. The pulse shape from the EGI anode resembled that in ambipolar planar detectors20. On the Au cathode, the signal was not induced immediately upon the gamma ray interaction, which differed from the signal on the EGI anode. The pulse started to rise only when the charges drifted very close to the equipotential arch (Fig. 1b). This feature resembles that in unipolar pixelated detectors16. The carrier drift time was determined by taking the time difference between the start of the anode pulse and the end of the cathode pulse (Supplementary Fig. 6)26,27,29. Interestingly, owing to the charge noncollection feature, the Frisch ring showed a bipolar pulse shape, in accordance with its weighting potential distribution in Fig. 2c.

Exploiting unipolar sensing, the gamma ray spectrum collected on the Au cathode of VFG detector I demonstrates a clear full energy peak of 662 keV gamma rays with a peak-to-Compton ratio of approximately 2. In comparison, the simultaneous energy spectrum of the EGI anode was not well resolved (Fig. 2h). This characteristic is consistent with previous unipolar devices of CdZnTe and TlBr25,30. By increasing the applied voltage, the ER at 662 keV improved from ~6% to <2%, implicating increased charge collection efficiency (Fig. 2i). Furthermore, the VFG detector could operate stably over time after the stabilization process (Fig. 2j).

Gain effect and space charge accumulation effect

Owing to the inactive nature or shallow levels of most defect-related electronic states near the band edge, perovskite materials are generally regarded as defect-tolerant materials9,21. However, evidence has revealed strong defect activities in halide perovskite materials, which may cause various forms of instability stemming from their low transition energy31,32. The carrier transport kinetics involves charge diffusion and drift processes. Under a high electric field, in principle, a steady carrier transport process is preferable for long-term stability. Compared with charge drift, charge diffusion is generally inconsequential on account of the relatively small carrier mobility thus low diffusion coefficient in perovskite materials23,33. Carrier drift processes were investigated via a time-of-flight approach here. The stimulation source was single γ-ray photons from a 137Cs γ-ray source with an extremely low flux (<103 photons·s−1·cm−2), which contrasts with previous studies that used intense pulsed lasers (1012 photons·s−1·cm−2)34. Each gamma-ray photon with an energy of 662 keV generates approximately 1.25 × 105 electron‒hole (e-h) pairs considering the average ionization energy (εpair) of ~5.3 eV in CsPbBr335. The extremely low quantity of e-h pairs is highly sensitive to trace amounts of electrically active defects during long drift processes over centimeters. The pulse shape could be altered based on variations in the quantity of carriers in motion owing to charge trapping/detrapping or other kinetic processes36. Therefore, precise measurement of the pulse height, which is proportional to the generated charges of e-h pairs, clearly elucidates the carrier transport or trapping kinetics.

Accordingly, the temporal response of the gamma ray spectra was measured by NIM modules, and individual pulses were simultaneously digitized (Fig. 3). The quantity of generated charges, in terms of the channel number, changed with time under a constant external electric field. Surprisingly, we observed a distinct shift tendency for the EGI anode and the Au cathode (Fig. 3a, b). Specifically, the spectral response of the Au cathode gradually improved within 2,700 s. The ER at 662 keV improved from an initial value of ~20% to ~9%, whereas the channel number of the full-energy peak showed a dramatic blueshift from 4143 to 5300, with a percentage increase of ~28%. On the contrary, the EGI anode showed a slight change in the spectral response, with the ER changing from 6.2% to 5.1%. However, the channel number of the full-energy peak decreased from 2947 to 2795, a decrease of ~5%. We also found that the time required for a stabilized response depended on the applied voltage or thickness, in which a weaker applied voltage or a larger detector thickness likely prolonged the stabilization process (Supplementary Figs. 7–9). Note that this anomalous time-dependent response appeared only in the initial biasing stage, and after this stabilization period, both the Au cathode and the EGI anode ultimately demonstrated a stable response without a change in the channel number (Supplementary Fig. 10).

Fig. 3: Temporal response of the VFG CsPbBr3 detectors.
figure 3

a, b Time-dependent 137Cs gamma-ray spectra for Au cathode and EGI anode at a total bias of 1400 V from detector III. The collection time for each spectrum was 540 s. c, d Typical pulses from the Au cathode and EGI anode collected at the beginning c and in the final stable operation stage d from detector I, respectively. Both events were selected with similar interaction depth near the anode region. e, f Scatter plots of the amplifier amplitude and preamplifier amplitude of the Au cathode signals, corresponding to the beginning e and final stable operation stage f, respectively. A total voltage of 400 V was used here for the flat baseline in c–f.

Full size image

To reveal the actual charge transport processes in the bulk, the transient pulses from individual γ-ray interactions were digitized and analyzed. Figure 3c, d depict the typical pulses in the initial and stable stages respectively. The EGI anode seemingly retained its pristine pulse shape after stabilization. However, the pulse shape from the Au cathode (Fig. 3c) deviated from its predicted shape with an extremely lagged rising edge. The prolongation of the rise time by ~30% (46 μs initially compared to 32 μs stabilized) also caused a dispersed distribution of the pulse height (Fig. 3e). In conventional compound semiconductors, gradual spectrum degradation in terms of polarization is usually observed due to charge trapping-detrapping37,38,39. However, the seeming charge trapping-detrapping influence unambiguously disappeared in subsequence (Fig. 3d). In the stable stage, the pulse shape corresponded well with the predicted shape, leading to a centralized distribution of the pulse height and thus a better ER (Fig. 3f).

Position sensing and pulse shape analysis

After bias stabilization, the response of the VFG CsPbBr3 detector was studied via digital pulse shape analysis. The coincident pulses from the EGI anode, Frisch ring and Au cathode upon individual gamma ray interactions were collected (Fig. 4). Two-dimensional depth sensing was achieved via drift time analysis25. Overall, four general depth positions with unique pulse shapes were discriminated (Fig. 4a, d–g). Position i and ii are near the anode and cathode regions outside and inside the hemispherical-like equipotential arch, respectively. Position iii and vi are both outside the equipotential arch and approximately neighbor the side wall of the column. A total of ~4 × 104 events with the shaped amplitude of the Au cathode above the noise levels were triggered and collected. Approximately half of these events had coincident signals on the EGI anode, whereas the remaining half did not. A typical event is illustrated in Fig. 4d, e. A spatial γ ray response was attainable based on this position sensing analysis, with the specific energy spectra for positions i and ii distinguished in Fig. 4c, b, respectively. Notably, the ER at 662 keV was achieved as 1.5% without any depth correction (Fig. 4c). The scatter plot of the drift time and pulse amplitude implied the uniform charge collection across the thickness free of hole carrier trapping. The charge collection uniformity at position ii deteriorated due to the inadequate weighting potential distribution, resulting in an almost linear pulse shape and a relatively short drift time suggesting that interaction occurred near the Au cathode region. In addition, owing to unipolar sensing, the pulse heights of full-energy deposition events were depth-independent, consequently achieving a superior peak-to-Compton ratio of ~6 at position i, which was substantially greater than that reported in previous work16,20.

Fig. 4: Two-dimensional depth sensing and coincident pulse shape analysis.
figure 4

a Schematic diagram of the typical interaction positions. b Energy spectrum achieved from position ii. The inset shows a scatter plot of the pulse amplitude of the Au cathode versus the drift time (viz., interaction depth). c Energy spectrum achieved from position i. Insert was the scatter plot of the pulse amplitude of Au cathode versus the drift time. d–g Typical pulses collected from four different interaction positions. h–k Scatter plot of the Au cathode amplitude, EGI anode amplitude and ACR versus drift time, and the corresponding energy spectrum by cathode signal of 10.2 mm thick detector I with applied bias of 500 V for 137Cs γ ray source. l–o Scatter plot of Au cathode amplitude, EGI anode amplitude and ACR versus drift time, and corresponding energy spectrum of the cathode signal of 22.1 mm thick detector III with an applied bias of 800 V for the 137Cs γ ray source. Note that the triggered signals are those of EGI anode and that the pulse height and drift time are directly measured from digitized pulses. The energy spectra were generated according to the raw statistical distributions of the pulse amplitude without any calibration. The dashed lines in h–j and l–n represent the position of the EGI anode.

Full size image

Furthermore, detailed pulse analysis was directly applied to pulses from the preamplifier considering the possible ballistic deficit caused by the mismatch between the long drift time and constant shaping time15,16,40. The results for detector I and detector III are given in Fig. 4h–k and l–o, respectively. The distribution features were in good agreement with the previous simulation diagrams of the CdZnTe detector41. Remarkably, there was no slowing decay of the full energy edges in either detector with thickness up to 22.1 mm, whereas a slowing decay edge has been commonly observed in thick CdZnTe detectors due to deficiencies in electron transport41. The measured amplitude of the EGI anode showed a nearly linear dependence on the interaction depth. The anode-to-cathode ratio (ACR) indicated a uniform electric field distribution across the thickness. The ER values obtained in Fig. 4k, o were 1.6% and 2.2% for the 10.2 mm and 22.1 mm thick VFG detectors, respectively. The hole carriers demonstrated an extraordinarily long lifetime, which was essentially much longer than 200 μs as indicated in Fig. 4l. This long mean free drift lifetime confirms the feasibility of using inch-thick perovskite semiconductors for high-energy gamma ray detection. The hole carrier mobility can be determined via the maximum drift time method. As indicated in Fig. 4h, the maximum drift time of ~75 μs corresponded to an average hole carrier mobility of 26.7 cm2V−1s−1 for detector I. Similarly, the maximum drift time of ~197 μs corresponded to an average hole carrier mobility of 31.1 cm2V−1s−1 for detector III (Fig. 4l). By combining the extracted μτh in Supplementary Fig. 11, a long hole carrier lifetime of ~804 μs was estimated. Further pulse discrimination or rejection of incomplete charge-collection events41 may significantly improve the ER of VFG CsPbBr3 detectors.

Discussion

We tentatively proposed two mechanisms regarding the unusual phenomenon a peak shifting observed in Fig. 3, the detailed analysis of which was discussed in Supplementary Notes 1–4. For the Au cathode, the increase in the channel number likely results from the gradually enhancement of the charge accumulation effect on the Frisch grid (Supplementary Note 1, Supplementary Figs. 12, 13). As the charge collection process continues, positive charges increasing accumulate on the insulating layer, potentially reaching a dynamic balance between the capture of holes from the bulk and the emission of holes to the metallic Frisch ring. Therefore, the built-in charge accumulation zone expels the hole carriers, eliminating the effects of charge sharing, and finally resulting in a stable gamma-ray response with increased charge collection efficiency (CCE), as expected.

For the EGI anode, one potential mechanism is the gain effect stemming from the defect-assisted Auger recombination process. Considering the formation of ~1.25 × 105 e-h pairs per 662 keV interaction, the concentration of the active Auger recombination centers was evaluated as ~7.1 × 104 cm−3 for a gain factor of 1.05 ± 0.01 (Fig. 3b), and as ~1.4 × 106 cm−3 when assuming a maximum gain factor of 2. The influence of these Auger recombination centers might be concealed during intense irradiation, which generates a significantly larger quantity of e-h pairs, orders of magnitude greater than the extremely low concentration of the centers. Their origin could be assigned to intrinsic point defects such as Br vacancies (VBr), Pb antisites (PbCs), Cs interstitials (Csi) or their complexes, albeit provisionally42,43. These defects likely induce structural distortions, triggering the Jahn–Teller effect and forming defect levels within the bandgap. A prior study also suggested that reduction of octahedral distortions could greatly suppress Auger recombination44. Likewise, such Auger recombination has been reported in other halide semiconductors, such as HgI245.

The gain phenomenon is commonly observed in our melt-grown CsPbBr3 single crystals and could be validated based on the charge collection efficiency method (Supplementary Note 2, Supplementary Fig. 14). To further confirm this process, ultrafast pump-probe transient reflection (TR) measurements were performed on our melt-grown CsPbBr3 crystals, commonly used in characterizing Auger recombination in metal halide perovskites46,47 (Supplementary Note 3). TR spectra captured at short decay times (Supplementary Fig. 15) clearly reveal antisymmetric peaks with a positive peak at 512 nm, a negative peak at 523 nm, and a center point at 518 nm. These features correspond to the bleaching of the exciton transition, ground state bleaching (exciton absorption peak) and bandgap absorption, respectively48,49. The broad low-energy tail of the exciton absorption peak at 523 nm indicates continuous charge transfer within closely spaced energy levels50. Additionally, the triexponential decay observed at 523 nm indicates the presence of three-body Auger recombination processes.

Furthermore, a physical model is proposed here for interpreting the effect of the Auger recombination process on charge transport (Supplementary Note 4, Supplementary Fig. 16). The maximum channel number Ch (representing the induced charge quantity Q) resulting from Auger recombination is as follows, with a detailed derivation provided in the Supplementary Note 4,

$$\frac{{{{{\rm{Ch}}}}}_{\max }}{{{{{\rm{Ch}}}}}_{0}}=\frac{{Q}_{\max }}{{Q}_{0}}=\left(A+1\right)\cdot \left(1+\frac{{\lambda }_{{{{\rm{e}}}}}}{L}\cdot {{\mathrm{ln}}}\left(1-\frac{{AL}}{{AL}+{\lambda }_{{{{\rm{e}}}}}+A{\lambda }_{{{{\rm{e}}}}}}\right)\right),$$
(1)

where A is the probability of Auger recombination, λe is the mean free drift path of an electron and is equal to µτeE, and L is the thickness45. As A varies between 0 and 1, the gain factor, determined as Chmax/Ch0 changes between 1 and 2. The gain factor depends on the mean free drift path of the electron carriers and applied bias (Supplementary Fig. 17), which well supports the bias-dependent spectral changes shown in Supplementary Fig. 8.

In summary, we introduced a VFG detector configuration for perovskite CsPbBr3 detectors, achieving a high intrinsic detection efficiency and an effective volume of up to 1 cm3 for gamma-ray detection. The effective thickness of the fabricated VFG detectors ranged from 10 mm to over 22 mm, with the champion ER being 1.9% at 662 keV. By incorporating depth interaction discrimination, the ER was improved to 1.5% for the 10.2 mm thick detector, and 2.2% for the 22.1 mm thick detector. The hole mobility-lifetime product was evaluated to be above 10−2 cm2V−1. Systematic investigation of the charge transport dynamics via a time-of-flight technique, stimulated by single gamma ray photons, revealed the charge accumulation effect and the gain effect associated with hole carrier multiplication, possibly caused by defect-assisted Auger recombination. These two effects resulted in anomalous dynamic changes in the energy-resolved gamma ray-spectra. Notably, both of these mechanisms were validated for all VFG detectors and the gain effect was also reproducibly observed in the spectral-grade CsPbBr3 detectors, with the gain factor ranging from 1 to ~1.5. Notably, these effects could be mitigated by a bias stabilization process.

Furthermore, the assembly of developed individual VFG detectors into arrays51 may enable practical realization of large-volume and high-performance detector systems, potentially competing with the current radiation detection systems. These results are anticipated to expedite the deployment of low-cost perovskite detectors in applications such as nuclear safety and nuclear medicine imaging, where both high ER and high detection efficiency are crucial.

Methods

Single crystal growth and wafer processing

High quality CsPbBr3 single crystals were grown by Bridgman method20. High-purity CsBr (5 N, Sigma-Aldrich) and PbBr2 (5 N, Sigma-Aldrich) were purchased for the synthesis of polycrystalline CsPbBr3 without further purification. Approximately 100 g of the starting materials in a 1:1 molar ratio was loaded into a quartz ampoule with the outer diameter of 25 mm and inner diameter of 20 mm and sealed under a vacuum of 5 ×10−4 Pa. The ampoule was placed in a two-zone tube furnace, gradually heated up to ~600 °C over 12 h, and held at that temperature for 24 h for complete reaction. Afterward, the ampoule was cooled down to room temperature over 24 h.

The synthesis and growth were done in the same fused silica tube to reduce unintended contamination that might occur in multistep process. The synthesized CsPbBr3 polycrystals were subsequently used for single crystal growth. The ampoule was placed in a custom-built six-zone vertical Bridgman furnace and heated to the appropriate temperature in 10 h to obtain a temperature gradient of ~10 K·cm−1. Initially, the ampoule was moved to an overheating temperature of 590 °C and maintained for 12 h to homogenize prior to crystal growth. The crystal growth was then carried out by slowly lowering the ampoule along the furnace axis at a rate of 1 mm·h−1. After the growth, the furnace was quickly cooled to 200 °C with a rate of 20 °C · h−1, followed by a slower cooling to room temperature at a rate of 3 ~ 5 °C · h−1 to account for the phase transitions. The typical temperature profile across the six-zone vertical Bridgman furnace and the as-grown CsPbBr3 crystal ingot with diameter of 20 mm are shown in Supplementary Fig. 18.

The as-grown CsPbBr3 single crystals were cut into specific shapes using a diamond wire saw (STX-202A, Shenyang Kejing Auto-instrument Co., Ltd.). The crystals dimensions are 4.0 × 4.0 × 10.2 mm3, 5.0 × 7.0 × 17.3 mm3 and 6.5 × 7.0 × 22.1 mm3, respectively. The crystal surfaces were then polished and refined using 1000, 2000, 5000, and 12,000 mesh SiC sandpapers to achieve a smooth and flat surface. Finally, the crystals were cleaned with toluene before metallization on the surface.

Fabrication of the virtual Frisch grid detector

The top electrode was prepared by spreading EGaIn liquid (Ga:In = 75:25, by weight) on the surface. The bottom electrode was prepared using gold conductive adhesive paint. The planar detector was wrapped with polytetrafluoroethylene film around 20 μm on the side, which served as an insulating layer. Near the bottom electrode, the conductive copper tape was used as a Frisch ring to cover the film. Finally, copper wires were connected to the three electrodes using silver conductive adhesive paint (Supplementary Fig. 1). After electrodes deposition and connection with carrier board, the VFG detectors were then encapsulated into paraffin wax to hinder atmosphere. After encapsulation, the VFG detectors were kept at room temperature and ambient condition.

Simulation of the electric field and weighting potential

ANSYS Maxwell was used to simulate the distribution of the electric field and weighting potential distribution for detector with dimension of 4.5 × 4.5 × 10 mm3 that was almost identical to the size of detector I. Based on the Shockley–Ramo theorem29, for instance, to obtain the weighting potential distribution of Au cathode, the potential on the Au electrode is set at unit potential (VAu = 1 V) while the potential at EGI and Frisch ring electrodes is set to zero potential (VEGI = Vring = 0 V). The electric field simulation was carried out by setting the voltage of +900 V on EGI anode and −100 V on Au cathode, which was in accordance with the actual voltage of detector I for operation.

Electrical properties and gamma ray response measurement

The current-voltage characteristics were measured in a shielded box by a Keithley 6517B electrometer. The applied voltage ranges from −500 V to 500 V. The qualitatively on/off response was performed under a LED white light source. The gamma ray response was tested under various γ-rays sources, 57Co γ ray source with activity of ~20 µCi and 137Cs γ ray source with activity of 1 µCi. The energy resolution was calculated by the percentage ratio between the full width at half maximum (FWHM) and the photopeak channel number. The mobility-lifetime product of hole carrier μτ was estimated according to the single-carrier Hecht equation52,53, \(\eta=\frac{Q}{{Q}_{0}}=\mu \tau \frac{V}{{d}^{2}}(1-{e}^{-\frac{{d}^{2}}{\mu \tau V}})\), and η is the charge collection efficiency (CCE), Q and Q0 is the maximum and theoretical saturated position of the photopeak, respectively, d is the detector thickness and V is the applied voltage. For gamma ray response measurement, 57Co and 137Cs sources were irradiated from the top electrode. During test, the VFG device was connected with eV-550 charge sensitive preamplifier. The output of the preamplifier was then shaped by ORTEC 572A amplifier, digitized by a dual 16K-input multichannel analyzer (ORTEC-927) and read into MAESTRO-32 software to generate energy spectrum. The shaping time used in this work was 10 μs.

Transient pulses digitalization and analysis

Transient pulses data acquisition was performed with a multi-channel 80 MHz waveform digitizer with 16-bit accuracy. For each triggered event, the raw waveforms from preamplifiers were stored from Au cathodes, EGI anode and Frisch ring. Then a digital CR-RC4 filtering shaper with CR constant of 5 µs was used for filtering the signal from Au cathode and EGI anode. The amplitudes of the shaped pulses were then compiled into a histogram to generate the energy spectrum. The measurement was performed in ambient conditions at ~20 °C.