Abstract
Humans can flexibly change rules to categorize sensory stimuli, but their performance degrades immediately after a task switch. This switch cost is believed to reflect a limitation in cognitive control, although the bottlenecks remain controversial. Here, we show that humans exhibit a brief reduction in the efficiency of using sensory inputs to form a decision after a rule change. Participants classified face stimuli based on one of two rules, switching every few trials. Psychophysical reverse correlation and computational modeling reveal a reduction in sensory weighting, which recovers within a few hundred milliseconds after stimulus presentation. This reduction depends on the sensory features being switched, suggesting a constraint in routing the sensory information flow. We propose that decision-making circuits cannot fully adjust their sensory readout based on a context cue alone, but require the presence of an actual stimulus to tune it, leading to a limitation in flexible perceptual decision making.
Similar content being viewed by others
Introduction
Successful sensory-guided behavior relies on the ability to transform relevant sensory signals into appropriate action plans that meet task demands. Decades of work have investigated this behavior using perceptual decision-making tasks with fixed stimulus-action mapping, such as the direction discrimination of stochastic moving dots1. Under these conditions, many aspects of behavior, such as choices, reaction times (RTs), and confidence associated with choices, can be accurately explained by a class of models that accumulate sensory evidence toward a decision bound1,2,3,4. These models have been further supported by the findings of neural activity in multiple brain regions that reflect similar computational processes4,5,6.
An important problem that has not been addressed in these frameworks is how the brain flexibly selects relevant sensory information depending on the behavioral context7. Our tasks in the real world are diverse and variable, and our brains must constantly adjust the association of sensory inputs and actions. Recent neurophysiological studies have begun to investigate this selection process by employing task designs that require participants to switch between two perceptual tasks, such as color versus motion discrimination of colored random dot motions8,9,10,11,12. These studies have found that neural population signals reflect flexible sensory gating8,13,14,15. Simultaneously, modeling frameworks using recurrent neural networks (RNNs) have been developed to account for neural activity8,16. RNNs often instantiate selection mechanisms through internal dynamics that switch the flow of sensory information according to external task context signals.
However, humans exhibit notable behavioral limitations in switching tasks that are absent in these network models. Immediately after a task switch, decisions often become less accurate and slower17,18,19,20, even when the switch is predictable21 or explicitly cued22. This switch cost is considered an important property of the brain’s mechanisms of cognitive control23,24. A common explanation is that the brain needs time to reconfigure its internal state for a switched rule18,21,25,26 or to suppress the effect of the previous task rule arising from inertia27 or priming28 from the previous internal state. If preparation time is insufficient, this control process interferes with the subsequent decision-making process and affects task performance18. Interestingly, however, even when sufficient time is given after a task switch is cued, humans still exhibit substantial switch costs (residual switch cost;21,29,30,31,32), suggesting that the brain is unable to fully adjust its internal state based on external cues alone. This has also been explained as a limitation in cognitive control: either participants fail to engage in a task until the task begins29, they cannot fully switch attention33,34,35, or the task stimuli themselves are required to recall the stimulus-response mapping36,37,38. However, a satisfactory explanation for why a contextual cue is insufficient for the brain to switch its state internally is still lacking. This fundamental constraint on task switching provides an important clue regarding how neural circuits implement computational flexibility.
Here, we show that such switch costs in perceptual decision-making reflect a reduction in the efficiency of using sensory inputs to form a decision immediately after a task switch. This efficiency reduction cannot be ameliorated by longer task preparations, but quickly recovers to the baseline level within a few hundred milliseconds after stimulus presentation. Furthermore, the magnitude of the switch cost substantially depends on the specific sensory features to be switched, discordant with the idea that the cost is primarily caused by the transition of abstract cognitive states. These findings were obtained by employing advanced behavioral measurement and modeling techniques to study perceptual decision-making39,40,41,42. In this task, participants switched categorization rules for parametrically morphed facial stimuli that had stochastic evidence fluctuations during stimulus presentation. Psychophysical reverse correlation and computational modeling revealed an initial reduction in sensory weighting that resulted in a switch cost. We suggest that when switching relevant sensory dimensions, decision-making circuits cannot fully adjust their sensory readout based on an abstract context cue alone, but require the presence of an actual stimulus to fine-tune the readout for certain sensory features.
Results
Switch cost independent of stimulus strength and task preparation time
We developed a context-dependent face categorization task, in which participants classified a face stimulus based on one of two task rules. We used face categorization because previous studies successfully explained the behavior using a simple evidence accumulation model39,40 and the high-dimensional nature of face stimuli allowed us to easily introduce flexibility in the task, such as switching between identity and expression categorization43,44,45.
In each trial, participants first fixated on a central fixation point whose color indicated the task rule, then viewed a face stimulus sampled from a two-dimensional (2D) morphed face space, and reported the face category by making a saccade to one of the two targets as soon as they were ready (Fig. 1a, b). The two rules correspond to the two axes of 2D space (e.g., identity vs. expression; Fig. 1a). The category boundary was at the center of each axis (0% morph level) and the stimulus became easier as the distance from the boundary (absolute value of the morph level) increased. Importantly, on each trial, the morph levels of the face stimulus fluctuated randomly every 106.7 ms around the sampled point in the 2D space (Fig. 1b inset), allowing us to estimate how participants temporally weighted each stimulus frame to make a decision (i.e., psychophysical reverse correlation;46). Each face frame transition was interleaved with a mask image so that the fluctuations remained subliminal. This task design allowed us to quantitatively compare differences in decision-making processes between the trials immediately following a rule switch (i.e., switch trials) and the remaining non-switch trials (Fig. 1c; task switched every 2–6 trials following truncated exponential distribution).
a A two-dimensional face stimulus space. Each axis corresponds to one of the two categorization rules (e.g., identity vs. expression; left column). In each rule, a category boundary divides the stimulus space into two halves, which were associated with two saccade targets (right column). Six out of the eight participants performed identity vs. expression categorization, while the remaining two performed identity vs. age categorization (Supplementary Fig. 1). The prototype faces were from the Tsinghua Facial Expression Database72 and presented with permission. b Participants initiated each trial by fixating on a central point whose color indicated the current task rule. Shortly after, two target points appeared, followed by a sequence of face stimuli. In the sequence, the morph levels of face stimuli were randomly updated every 106.7 ms—drawn from a Gaussian distribution with a mean chosen for each trial and a standard deviation of 20% morph level along both task-relevant and orthogonal axes—providing noisy sensory evidence (inset). Participants reported the stimulus category by making a saccade to one of the two targets as soon as they were ready. Reaction time was defined as the time between the stimulus onset and the saccade onset. c Two task contexts were switched every 2–6 trials (truncated exponential distribution). The trials immediately following a rule switch were defined as switch trials (red), while the remaining trials were classified as non-switch trials (black).
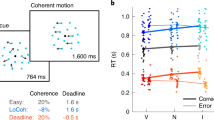
After sufficient training, participants could switch task rules immediately with minimal reduction in their choice accuracy, but their RTs were substantially longer during the switch trials. The psychometric function along the task-relevant axis appeared to be slightly worse in switch trials, but the difference between switch and non-switch trials did not reach statistical significance (Fig. 2a left; change in logistic regression slope α1,switch = −1.1 ± 0.5 in Eq. (2), mean ± S.E.M. across participants; t(7) = −2.3, p = 0.053, Cohen’s d = −0.8, 95% CI = [−2.18, 0.02], relative support for null hypothesis BF01 = 0.547, indicating anecdotal evidence for the alternative hypothesis, two-tailed t-test; see Supplementary Fig. 1 for individual participants). The participants also had negligible lapse rates for the easiest stimuli (≤ 1.2% for all participants), suggesting that they did not show much confusion of the task rule. Mean RTs were faster for easier stimuli as in typical perceptual tasks (Fig. 2a right; the slope of hyperbolic tangent function β2 = 5.2 ± 0.4, Eq. (3); t(7) = 14.3, p < 0.001, Cohen’s d = 5.1, 95% CI = [4.37, 6.10]), but they were systematically longer in switch trials (Fig. 2a; the offset of chronometric function β0, switch = 0.17 ± 0.02, Eq. (3); t(7) = 8.7, p < 0.001, Cohen’s d = 3.1, 95% CI = [0.12, 0.22]; ~ 170 ms longer on average across stimulus strengths).
a Reaction times (RTs) increased for all stimulus strengths in the switch trials (right; β0, switch = 0.17 ± 0.02 in Eq. (3), mean ± S.E.M. across participants; t(7) = 8.7, p < 0.001, Cohen’s d = 3.1, 95% CI = [0.1, 0.2], two-tailed t-test), while choice accuracy was not significantly different between the switch and non-switch trials (left; α1,switch = −1.1 ± 0.5 in Eq. (2); t(7) = −2.3, p = 0.053, Cohen’s d = −0.8, 95% CI = [−2.18, 0.02], BF01 = 0.547, two-tailed t-test). Smooth lines are fit by a logistic function (left; Eq. (2)) and a hyperbolic tangent function (right; Eq. (3)). Plots for individual participants are shown in Supplementary Fig. 1e. (b) Choice accuracy and RTs did not depend on the stimulus strength along the task-orthogonal axis. c, d The RT increase was independent of the stimulus strengths both along the task axis (c) and orthogonal axis (d). e, f The increase in RTs was present mostly in the first trial after a task switch (e) and did not strongly depend on the number of non-switch trials before the switch (f). The plots are the average of all the stimulus strengths. g Participants could prepare for the switched rule after fixating on a context cue until stimulus onset (top). This cue-stimulus interval (CSI) approximately followed a truncated exponential distribution in the experiment (bottom). h The increase in RTs after a task switch occurred both for the trials with short (left) and long (right) CSIs. Trials were split at the median CSI (0.72 s). i Overall increase in RTs (estimated by fitting a hyperbolic tangent curve to the chronometric function; Eq. (3) in Methods) was stable across the range of CSIs. The line is a linear regression averaged across participants. j Psychometric (top) and chronometric (bottom) functions in the 2D space revealed no congruency effect in our task. The stimuli in the second and fourth quadrants of the face space were incongruent, as they were associated with the opposite targets between the two tasks. Participants did not show much lower accuracy or longer RTs for these stimuli. a–f, h–j Data are presented as mean values ± S.E.M. across participants (a-f, h, i); Data are presented as mean values across participants (j); n = 8 participants.
Notably, the increase in average RTs was independent of the stimulus difficulty. We computed the difference in average RTs between the switch and non-switch trials and confirmed that it was not correlated with stimulus difficulty (Fig. 2c; F(5, 42) = 1.4, p = 0.247, η2 = 0.142, BF01 = 5.26, one-way ANOVA). The increase in RTs occurred regardless of the direction of task switching (e.g., identity to expression or expression to identity; details are discussed in a later section) but was only apparent in one trial following a switch, and a statistically clear effect could not be observed thereafter (Fig. 2e; p ≥ 0.154 for all subsequent trials before the next task switch, two-tailed t-test). Also, the number of non-switch trials preceding a switch did not have a statistically clear effect on the RT increase (Fig. 2f; F(3, 28) = 1.9, p = 0.156, η2 = 0.168, BF01 = 2.27 indicating anecdotal evidence for the null hypothesis). Overall, participants correctly switched the task rule and largely maintained choice accuracy, but their average RTs increased uniformly across a range of stimulus difficulties at the moment of the task switch.
However, this increase in average RTs cannot be explained by the additional time required to prepare for switching rules. Importantly, the RT increase occurred even when we varied the preparation time allotted to participants for a task switch. In our task, the fixation point color indicated the task rule to the participants, and a stimulus was presented after a variable duration following the participants’ fixation onset (cue-stimulus interval, CSI: range, 0.45–1.50 s; median, 0.72 s; truncated exponential distribution; Fig. 2g). If the CSI is not long enough for participants to prepare for a task switch, shorter CSIs should result in less task preparation and a delay in initiating the decision-making process. However, the RT increase was large even for trials with longer CSIs (Fig. 2h, i; long CSI (> 0.72 s) trials, β0, switch = 0.15 ± 0.02, Eq. (3)). Thus, participants tended to spend an additional 150–170 ms after stimulus onset to make a decision in the switch trials, despite the much longer and variable preparation time available before stimulus onset.
This persistent behavioral effect of task switching has been termed the residual switch cost21,29,30,31. If CSIs are shorter than the range we used (e.g., < 0.5 s;30), the switch cost can become more substantial, which likely reflects the time participants needed to prepare for a new task (task set reconfiguration;18) or suppress previous rules27,47. However, it remains controversial as to why the cost persists as a residual switch cost with a longer preparation time29,43,48.
One hypothesis is that the stimulus itself triggers the reconfiguration of task rules36,37,38. However, the stimuli in our task contained no clues to task rules, as they were sampled from the same 2D face space in both contexts. If participants perceived stronger sensory signals along the task-relevant axis as a task cue (e.g., clearly happy or sad faces triggered the use of the expression rule), higher morph levels would lead to smaller switch cost, but as shown above, the increase in RTs was independent of stimulus strength (Fig. 2a, c). The increase in RTs was also independent of the morph levels of the task-orthogonal axis (Fig. 2b, d; F(5, 42) = 0.6, p = 0.684, η2 = 0.069, BF01 = 18.5, one-way ANOVA), ruling out the possibility that stronger task-orthogonal inputs caused task confusion. Furthermore, there were only 0.01 ± 0.02 s RT differences between stimuli associated with the same and opposite targets (i.e. congruent and incongruent stimuli) in the two contexts (Fig. 2j; congruent stimuli, RT = 1.07 ± 0.04 s; incongruent stimuli, RT = 1.06 ± 0.04 s), suggesting that cognitive conflict at the response level does not explain the observed switch cost.
Then, why does task switching prolong RTs regardless of stimulus strengths without largely affecting choice accuracy? Previous studies established a simple evidence accumulation model that accurately accounted for choices and RTs during face categorization39,40. Such a modeling approach is suitable for examining the mechanistic components that explain the observed behavioral changes after task switching. Furthermore, random stimulus fluctuations in our task (Fig. 1b inset) enabled us to test whether and how participants changed the weighting of sensory evidence for their decisions in the switch trials. In the next section, we demonstrate that RTs increase owing to a brief initial reduction in sensory weighting.
Brief initial reduction in sensory processing efficiency explains switch cost
We performed a psychophysical reverse correlation39,46 to examine how temporal stimulus fluctuations influenced participants’ behaviors in the switch and non-switch trials. In brief, we calculated the difference in average morph fluctuations between trials in which participants chose one target over the other (Eq. (4)). The amplitudes of the resulting psychophysical kernels reflect the degree to which sensory fluctuations at each moment influenced the participants’ choices; thus, they are informative for estimating how participants weigh sensory evidence to make a decision39. The kernels were aligned to either the stimulus onset or the timing of the participants’ saccadic responses (Fig. 3a, b; see Supplementary Fig. 2 for individual participants).
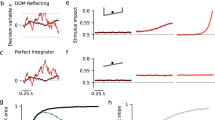
a Psychophysical kernels (Eq. (4)) along the task axis aligned to stimulus onset (left) and participants' response (right). The dynamics of the kernels for the non-switch trials (black) were similar to those observed previously and consistent with a bounded evidence accumulation mechanism39. The kernels for the switch trials (red), by comparison, showed a brief reduction in amplitude at stimulus onset. Plots for individual participants are shown in Supplementary Fig. 2. b The kernels along the task-orthogonal axis were near zero, indicating that the orthogonal information did not influence participants' decisions in both switch and non-switch trials. c An evidence accumulation model that accounts for both switch and non-switch trials. The model receives fluctuating sensory information, integrates the evidence toward decision bounds and, when it reaches a bound, commits to the choice associated with that bound. Reaction time is the sum of bound crossing time and non-decision time, including sensory and motor delays. In switch trials, we added a brief reduction in sensory weight (inset). d, e The model accurately fits choices (d, top), mean reaction times (d, bottom), and reaction time distributions (e; cumulative distributions are shown for visualization) for both switch and non-switch trials. f, g The same model accurately explains the patterns of the psychophysical kernels. The data traces are the same as in a. a, b, d–g Data are presented as mean values ± S.E.M. across participants; model predictions are presented as mean values across participants; n = 8 participants.
In the non-switch trials, we found dynamic kernel patterns consistent with linear evidence accumulation. The kernel aligned to stimulus onset showed a gradual decrease in amplitude, whereas the kernel aligned to the participants’ saccade revealed a characteristic peak a few hundred milliseconds before the saccade (black lines in Fig. 3a). Although these patterns seem to imply the dynamic weighting of sensory evidence, previous studies have shown that they can be fully explained by a bounded evidence accumulation mechanism with a constant sensory weight39,40. In this model (Fig. 3c), sensory fluctuations are linearly accumulated toward the upper or lower bound. When the accumulated evidence reaches a bound, this bound determines the choice. RTs are modeled as the time required to accumulate evidence plus the time irrelevant to decision-making (non-decision time), including sensory and motor delays.
This evidence accumulation model accurately fit the psychometric (Fig. 3d top) and chronometric functions (Fig. 3d bottom) of the non-switch trials as well as the RT distributions (Fig. 3e; R2 = 0.85 ± 0.02 for choice and RT distributions in non-switch trials; see Methods for the derivation of R2). The same model also quantitatively explained the psychophysical kernels. Using the fitted model parameters, we simulated the model responses to randomly generated stimulus fluctuations and computed the psychophysical kernels of the model (thick gray lines in Fig. 3f; R2 = 0.87). This model explains the gradual reduction of the kernel aligned to the stimulus onset (Fig. 3f, left) because there is a temporal gap between the bound crossing and the report of a decision (i.e., the non-decision time). This non-decision time renders a later portion of the stimulus fluctuations irrelevant to the decision. Because the timing of the bound crossing varies across trials, the model predicts a gradual reduction in the effect of stimulus fluctuations over time39. The model also explained the peak of the kernel aligned with the participants’ saccade (Fig. 3f, right). This peak arises because, near the time of bound crossing, tiny stimulus fluctuations can push the decision variable beyond the bound and dictate the decision. Therefore, at that moment, the effect of stimulus fluctuations becomes substantial and peaks. After this peak, the kernel drops sharply to zero because of the non-decision time39,49.
Now, in the switch trials, we found that the kernel aligned to the stimulus onset showed a characteristic reduction in amplitude during the first 200–300 ms after stimulus onset compared to that of the non-switch trials (red lines in Fig. 3a; t(7) = 3.8, p = 0.007, Cohen’s d = 1.35, 95% CI = [0.01, 0.03], two-tailed paired t-test on the first two stimulus frames). The amplitude reduction was approximately 43% (Eq. (5)) from the non-switch trials, and then recovered over time. The amplitudes of this kernel reduction were not significantly different between long and short cue-stimulus intervals (CSI ≤ 0.72 s vs. > 0.72 s; t(7) = −0.52, p = 0.621, Cohen’s d = −0.18, 95% CI = [−0.9, 0.6], BF01 = 2.66 indicating anecdotal evidence for the null hypothesis). Aside from this initial reduction, there was no noticeable difference in the kernels between switch and non-switch trials.
Inspired by the observed kernel patterns, we added a dynamic sensory weighting function to the evidence accumulation model (Fig. 3c inset; Eq. (14)). The weight was constant in the non-switch trials; however, in the switch trials, it is a ramp function that starts with an initially reduced amplitude winit at stimulus onset and recovers to the baseline level at time trecover. While this function modulates sensory evidence, our model is agnostic of whether such modulation occurs during sensory processing or during the conversion of sensory information into accumulated evidence (see Discussion section). Hereafter, we collectively refer to this as a reduction in the efficiency of processing sensory evidence. To test if this efficiency reduction alone was sufficient to account for the behavioral changes in the switch trials, we started with the model parameters fitted to the non-switch trials and allowed the model to change only these two additional parameters (winit and trecover) to fit the behavioral data in the switch trials.
This extended model accurately accounted for participants’ choices (Fig. 3d top), mean RTs (Fig. 3d bottom), and RT distributions in the switch trials (Fig. 3e; R2 = 0.80 ± 0.03 for choice and RT distributions in switch trials). The fitted parameters showed approximately half the amplitude of sensory sensitivity at the stimulus onset on switch trials (winit = 0.38 ± 0.12) that recovered in a few hundred milliseconds (trecover = 562 ± 159 ms). This led to a reduction in the amplitude of the simulated psychophysical kernels, which was in good agreement with the observed data (Fig. 3g; R2 = 0.58). This reduced sensory weight delayed the time required to reach a bound, resulting in longer average RTs. Note that these model outcomes also depended on how the weighting function modulated noise in the accumulation process (Eq. (15) and (16)), as discussed in Supplementary Fig. 3. In contrast to RTs, choice accuracy was almost unaffected because the reduction in sensory weight was transient and sufficient evidence could be accumulated during the subsequent long integration time. Overall, this simple addition to the decision-making model quantitatively accounted for behavioral patterns in switch trials.
We further confirmed that no other mechanisms accounted for the observed behavioral results. Multiple parameters in the evidence accumulation model can increase RTs; however, changing these parameters yields choice accuracy, RTs, and psychophysical kernels that are distinct from the observed data (Fig. 4 and Supplementary Fig. 4). For example, increasing the non-decision time in the model (Fig. 4a) prolongs RTs uniformly across stimulus strengths without affecting choice accuracy, thus explaining the observed choice and mean RTs (Fig. 4b), but it fails to account for the patterns of the psychophysical kernels (Fig. 4c). A longer non-decision time does not produce an initial reduction in the onset-aligned kernel but shifts the peak of the response-aligned kernel that reflects the timing of the bound crossing. However, this pattern was not observed in the actual data.
a A model that explains switch cost by increasing non-decision time. This could happen either due to a longer duration of executing action after committing to a choice or a longer delay before initiating the evidence accumulation. In contrast to our main model (Fig. 3c), rule switch does not affect the accumulation time in this model. b, c The model successfully explains the lack of change in accuracy (b, left) and the prolonged reaction times irrelevant to stimulus strength (b, right), but fails to explain the patterns of psychophysical kernels (c). A longer non-decision time shifts the peak of the response-aligned kernel, while it does not lead to the initial drop of the kernel aligned to the stimulus onset. d A model that explains switch cost based on task preparation. It assumes that a fixed amount of time (following a Gaussian distribution) is required to prepare for a task switch after cue onset. If this preparation time takes longer than a cue-stimulus interval (CSI), it overlaps with an initial part of the stimulus sequence, which is ignored in the decision-making process. e The task preparation model fails to fit the initial reduction of the stimulus-aligned kernel for long CSIs (> 0.72 s). f The model also fails to explain that the increase in reaction times is largely stable across CSIs. The black dots are the data (same as those in Fig. 2i). The blue line is the fit of the task preparation model averaged across participants. The orange line is the fit of the main model (Fig. 3c). g All alternative models we tested had greater Bayesian information criterion (BIC) than our main model, indicating that the main model best fitted the data. The alternative models not explained here are described in Supplementary Fig. 4. b, c, e, f Data are presented as mean values ± S.E.M. across participants; model predictions are presented as mean values across participants; n = 8 participants.
Another alternative is a leak in the evidence accumulation process (Supplementary Fig. 4b), which leads to a reduced amplitude of the kernel near the onset of the stimulus39. However, this results in an increase in RTs for difficult stimuli because they require more time to reach a bound and are thus more affected by leakage. This change in RTs is inconsistent with the observed data. Similarly, increasing the decision bound or decreasing the sensory sensitivity (drift rate) (Supplementary Fig. 4c-e) led to longer RTs, but their patterns and effects on choice accuracy and psychophysical kernels were distinct from the data. In brief, higher decision bounds improve the overall accuracy and increase RTs, especially for more difficult stimuli (Supplementary Fig. 4c). Lower sensory sensitivities deteriorate overall accuracy and increase RTs, especially for easier stimuli (Supplementary Fig. 4d). A combination of the two evenly increases RTs for all difficulty levels with little effect on choice accuracy. However, it reduces the overall amplitude of the psychophysical kernels39, instead of only reducing the initial part of the kernel (Supplementary Fig. 4e). Overall, none of these alternative model parameters satisfactorily account for the effects of task switching, and the fitting qualities of these models estimated as the Bayesian information criterion (BIC) were consistently greater than our main model (Fig. 4g), indicating poorer fits.
Our modeling framework could also quantitatively confirm that the observed switch cost is not owing to the lack of sufficient task preparation time prior to the stimulus presentation (Fig. 4d-f). Suppose that participants need time to prepare for a task switch based on a context cue, and if the preparation time exceeds a cue-stimulus interval (CSI), they cannot initiate decision formation and therefore would ignore the initial part of the stimulus sequence (Fig. 4d). We modeled the preparation time as a Gaussian distribution and fitted the switch trials. This model showed poorer fitting performance (task preparation model vs. main model: ΔBIC = 57.6; positive BIC indicates better fits by the main model). As expected, the model predicted a smaller reduction in the initial portion of the stimulus-aligned kernel with longer CSIs, which was inconsistent with the data (Fig. 4e). Accordingly, the model systematically deviated from the data, which did not show clear dependence of the increase in RTs on CSIs (Fig. 4f).
Finally, we found no evidence of interference from the task-irrelevant rule. Because our stimuli had the same degree of stimulus fluctuations along the task-orthogonal axis, we could perform a psychophysical reverse correlation using these orthogonal fluctuations. The resulting kernels had nearly zero amplitude throughout the stimulus presentation period (Fig. 3b). This suggests that the initial weight reduction was not due to residual attention or faulty accumulation of task-orthogonal information.
Altogether, we showed that longer RTs in the switch trials occurred because of the reduced efficiency of processing sensory evidence at stimulus onset, which recovered within a few hundred milliseconds. This reduction was evident in psychophysical kernels, and our modeling framework confirmed that this mechanism alone was sufficient to explain all aspects of behavioral changes from non-switch to switch trials.
Task switching impairs choice accuracy when stimulus duration is limited
A key implication of the above observations is that task switching influences evidence accumulation in perceptual decision-making. However, it did not have a clear influence on choice accuracy, unlike findings from multiple previous studies12,21, because participants were able to continue accumulating evidence after the sensory weight recovered, thus maintaining performance at the expense of longer RTs (Fig. 3c). This interpretation predicts that when the stimulus duration is externally constrained by the environment, participants should now show impaired accuracy in switch trials. In contrast, the accuracy would not change if the increased RTs were due to a process irrelevant to decision formation, such as motor preparation.
To test this prediction, we conducted a modified experiment (Fig. 5a) in which we fixed the stimulus duration to 320–640 ms (in steps of 106.7 ms stimulus frames, following a geometric distribution), while keeping the other experimental parameters identical. In line with our prediction, we observed reduced choice accuracy in the switch trials (Fig. 5b; see Supplementary Fig. 5 for individual participants; change in logistic regression slope α1, switch = −1.5 ± 0.3, Eq. (6); t(6) = −4.9, p = 0.003, Cohen’s d = −1.8, 95% CI = [−2.2, −0.7], two-tailed t-test). The psychophysical thresholds were systematically higher in switch trials for a range of the CSIs (Fig. 5c; F(1, 51) = 29.0, p < 0.001, ANOVA with linear mixed-effects model), and this did not depend on the CSIs (F(3, 51) = 0.3, p = 0.838, BF01 = 22.2). Furthermore, we still observed a small increase in RTs in the switch trials (Fig. 5d; the offset of chronometric function β0, switch = 0.03 ± 0.01, Eq. (3); t(6) = 4.7, p = 0.004, Cohen’s d = 1.8, 95% CI = [0.01, 0.05], two-tailed t-test; ~ 30 ms longer on average across stimulus strengths). This was expected from the model because the probability of reaching a decision bound before stimulus termination should be lower in switch trials. Thus, task switching affects decision formation, leading to longer RTs or lower accuracy, depending on the accessibility to further sensory inputs.
a Our main model (Fig. 3c) predicts that, if participants are prohibited from accumulating more evidence, task switching will directly affect choice accuracy since the reduced weight cannot be compensated for by longer reaction times. To test this prediction, we performed a modified version of the face categorization task in which the stimulus duration was fixed (following a truncated exponential distribution; range, 320–640 ms in 106.7 ms steps). The remaining task parameters were kept identical to those of the main task. b Participants showed reduced choice accuracy after a task switch, consistent with our prediction. Plots for individual participants are shown in Supplementary Fig. 5. c The psychophysical thresholds (i.e., the morph level at 81.6% correct rate according to Eq. (6)) were consistently larger in switch trials across the range of the cue-stimulus intervals (CSI), similar to the main task (Fig. 2i). The trials were divided into four quantiles. d Reaction times were still longer in the switch trials. This was also expected from the model. b–d Data are presented as mean values ± S.E.M. across participants (b, d); Data are presented as mean values across participants (c); n = 7 participants.
Switch cost depends on sensory features to be switched
Thus far, the results indicate that task switching reduces the early weighting of sensory information for evidence accumulation, which recovers after stimulus presentation. A key implication is that the switch cost in our tasks occurs during the interaction between sensory and decision-making processes rather than within cognitive control mechanisms that switch internal states according to context cues. In this last section, we report a separate line of observations that further substantiate this claim; even under similar task-switching designs with similar task difficulty, the magnitude of the switch cost dramatically varies depending on the sensory features that participants were asked to switch.
We compared three different context-switching tasks: our main reaction-time version of the face categorization task (Fig. 6a), a face (identity) versus color switching task (Fig. 6b), and a motion versus color task (Fig. 6c). Motion versus color tasks have often been used to study context-dependent decision making8,9,50. In our task, participants viewed stochastic moving dots colored purple or green and reported either the overall direction of motion or the dominant color. As an intermediate between this and the face categorization task, we designed a face versus color categorization task (Fig. 6b). In this task, participants reported either the identity or the color of the face. In all tasks, stimuli were defined in 2D space, and participants categorized the stimuli based on one of the two axes. The basic task structure, including the frequency of the rule switch and the duration of the CSI, was kept identical across tasks. Furthermore, participants’ overall choice accuracy and RTs were comparable across the tasks (Fig. 6d), and their performance was similar between the two task rules in each task (Supplementary Fig. 6a). This ensures that the overall task difficulty or imbalance in task difficulty between the two rules27,47 does not affect the switch cost.
a The main face task as in Fig. 1a. b Facial identity vs. color discrimination task. The identity task was similar to that of the main face task. In the color context, participants categorized the color of face images into red or green. The face images were from the NimStim Face set73, but the panel uses images from the Tsinghua Facial Expression Database72 due to copyright issues. Consent was obtained for the use and publication of the face images. c Color vs. motion direction discrimination task8,9. Participants either judged the net direction of random dot motions (left or right) in the motion context or judged the dominant color of the dots (purple or green) in the color context. d The increase in reaction times after rule switch was different among tasks. The conventions are the same as in Fig. 2a. Plots for individual participants are shown in Supplementary Fig. 7. e The magnitudes of switch cost were similar between the two directions of rule switch in each task (e.g., switching from identity to expression categorization versus switching from expression to identity). f Graphical illustration of the cost of switching from/to different features shows that the pairs of features being switched determine the magnitude of switch cost. The numbers adjacent to arrows indicate the increase in reaction times (β0, switch in Eq. (3)), which are also represented by the darkness and thickness of arrows. Note that the expression task was replaced with the age categorization in some participants (Supplementary Fig. 1). d–f Data are presented as mean values ± S.E.M. across participants; n = 8 participants in the main face task, n = 7 participants in the face vs. color task, and n = 7 participants in the color vs. motion task.
Despite this carefully tailored comparison, we found substantial differences in the switch costs across the three tasks (Fig. 6d; Supplementary Fig. 6b). As demonstrated earlier, in our main face categorization, participants showed an increase of approximately 170 ms in overall RTs across a range of stimulus difficulties. By contrast, the motion versus color task had a much smaller rule switch effect ( ~ 43 ms increase in overall RTs; the difference from the main face task: t(13) = −5.3, p < 0.001, Cohen’s d = −2.7, 95% CI = [−0.18, −0.08], two-tailed t-test; see Supplementary Fig. 7b for individual participants). The face versus color task had an intermediate level of the rule switch effect ( ~ 113 ms increase in overall RTs; the difference from the main face task: t(13) = −2.3, p = 0.041, Cohen’s d = −1.2, 95% CI = [−0.110, −0.003]; see Supplementary Fig. 7a for individual participants). In all tasks, the effect on choice accuracy was limited.
We also found that the increases in RTs did not have a significant difference between both directions of the rule switch (i.e., from context 1 to 2 versus from context 2 to 1) in all three tasks (Fig. 6e; the offset of chronometric function β0, switch in Eq. (3) between switch directions: p ≥ 0.393, BF01 ≥ 2.03 across all tasks indicating anecdotal evidence for the null hypothesis, two-tailed paired t-test). Indeed, the RT increases in the three experiments were better explained as the costs associated with the pairs of features to be switched rather than as the costs associated with a feature being switched from or switched to (pair cost vs. from feature cost: ΔBIC = 12.12; pair cost vs. to feature cost: ΔBIC = 11.83; positive BIC indicates better fits by the pair-cost model; see Methods). Several previous studies have reported altered RTs when switching to the judgment of facial expressions from other judgments, and interpreted the results as the prioritization of biologically significant features43,44,45. However, this effect was not observed in our experiments, probably because our face stimuli involved only mild changes in emotion, which did not trigger expression-specific effect.
The dependency of the switch cost on specific perceptual tasks (Fig. 6f) supports the idea that the cost cannot be explained as switching between abstract contextual states in a manner independent of the specific sensory features to be discriminated. Rather, the cost can reflect the difficulty of switching between different sensory readouts, which aligns with our finding of the recovery of sensory processing efficiency after stimulus onset. A comparison of the three tasks alone does not allow us to determine what kinds of sensory features are more difficult to switch between. We speculate that switching features with more overlapping sensory representations can be costly as faces and colors are both encoded in the ventral visual areas (see Discussion section), although it is a formidable challenge to experimentally prove this idea. Nonetheless, the results demonstrate that rule switching is costly not merely because the system requires the transitioning between abstract contextual states.
Discussion
Humans show a reduction in the accuracy or speed of perceptual decisions after a task rule switch, which has been attributed to top-down cognitive control that requires time to adjust its process17,18,23. What is puzzling, however, is that even when sufficient time is given, people still exhibit substantial switch costs21,29,30,31,32,43. We revisited this long-standing observation using recent behavioral measurements and modeling techniques developed to study perceptual decision-making39,40,41,42. We found that there was a reduction in the efficiency of processing sensory evidence at the moment of task switching, which recovered within a few hundred milliseconds after stimulus presentation (Fig. 3a). By incorporating this efficiency reduction into an evidence accumulation model, we could accurately explain multiple aspects of the behavioral data in both the switch and nonswitch trials (Fig. 3c–g). Furthermore, we found that the cost depended substantially on the type of sensory feature to be switched, even when the task structure remained the same (Fig. 6). We suggest that a critical limitation in perceptual decision-making is the flexible switching of the sensory readout, which cannot be fully adjusted based on a context cue alone, but requires the presence of a stimulus to be properly tuned.
Our key finding is attributing the effect of task switching to a process that uses sensory information to form a decision, in contrast to the dominant idea that switch costs reflect the process of switching abstract cognitive states. The costs we observed seem to be unrelated to the processes of recalling a task rule; we did not find that stimuli with higher strength (e.g., a clearly happy face) along either the task or orthogonal axes facilitated or hindered task switching (Fig. 2c, d), implying that the stimuli themselves36 or the conjunction of stimuli and context cues37,38 did not facilitate rule recall. The reduced efficiency appeared to be limited to the first few hundreds milliseconds (Fig. 3a), which corresponds to an early phase of evidence accumulation51,52. Thus, the effect is unlikely to be related to the conflicting action plans between the two rules. Indeed, we did not observe clear congruency effects (Fig. 2j) or interference from task-orthogonal sensory information (Fig. 3b). This is also consistent with recent findings showing a delay in the early components of event-related potentials after a task switch34,35. We also ruled out the possibility of sensory adaptation, priming, or history effects53,54 because we did not find significant correlations between the stimulus strength of previous trials and the RT increase (Supplementary Fig. 8). Taken together, we suspect that the reduced efficiency is primarily related to the transformation of sensory information into the decision variable.
Then, why does the processing efficiency decrease after task switching for certain perceptual tasks and why does it recover quickly after stimulus onset? While speculative, we hypothesize that this reflects the precision limit of top-down control in adjusting the readout of sensory information to form decision evidence based on context cues alone. After the presentation of a task context cue, decision-making circuits can partially adapt their state to the switched rule so that the task-relevant sensory dimension becomes effective without interference from the previously relevant sensory dimension (Fig. 3b). However, the circuits cannot optimally tune the readout to convert sensory information into the decision variable with an abstract cue alone; an influx of actual sensory information is needed to guide the circuits to adjust the readout. The difficulty of tuning the readout depends on the specific pair of rules the brain has to switch (Fig. 6). We have yet to specify what factors dictate this difficulty, but we speculate that it is costlier to switch the readout from two overlapping sensory representations such as two face axes or face and color, both of which are encoded in the ventral visual areas55,56. This interpretation is consistent with previous reports43. For example, switching between visual and auditory tasks shows no residual switch cost57,58, whereas switching between male and female voice discrimination tasks shows a substantial residual switch cost59.
This interpretation is different from, and complements, recent compelling theories using RNNs, which propose that switch costs arise because of the extra process of making transitions between two abstract task states in neural spaces23,25. Such an adjustment of the internal state would explain task preparation triggered by cue onset. We instead focused on residual switch cost (Fig. 2h, i) and explained it as the recovery of sensory weight triggered by stimulus onset (Fig. 3), which depended on the specific sensory features to be switched (Fig. 6). These results suggest that switch cost also reflects the interaction between sensory and decision-making systems. We consider rule switching in perceptual tasks to be a multifaceted process that involves both state transition in associative brain areas and adjustment in readout through communication between associative and sensory areas7.
Our interpretation is also partly related and also distinct from other previously proposed hypotheses regarding the source of the residual switch cost. We highlight the most notable hypotheses here. First, some previous studies have suggested that residual switch costs arise because participants occasionally fail to engage and wait until stimulus onset to prepare for a rule switch29. This claim was made because RTs in switch trials are sometimes as fast as those in non-switch trials, in which participants could be fully prepared. However, such broad distributions of RTs can be produced by noisy evidence accumulation mechanisms without assuming engaged or disengaged states (Fig. 3e). Furthermore, the engagement account does not explain why failure arises in some perceptual tasks but not in others (Fig. 6). Second, several previous studies used the drift-diffusion model to examine switch cost and found effects on non-decision time after a rule switch60,61,62. Indeed, the patterns of the psychometric and chronometric functions appeared as if there was a change in non-decision time (Fig. 4a, b). It was only through fine-grained analyses of psychophysical reverse correlations that we correctly attributed them to the initial reduction in sensory weighting (compare Fig. 4c with Fig. 3g). Finally, some previous studies proposed that humans have limited ability to shift their attention to a relevant stimulus dimension before a stimulus appears34,35,43. This idea is most relevant to our hypothesis and could be pointing to the same process we have proposed. We hope that further neurophysiological investigation will reveal more fine-grained mechanistic accounts for this key limitation in the interaction of sensory and decision-making systems.
This study identified a specific process that gives rise to switch costs, but it should be noted that switch costs likely result from multiple factors whose relative contributions depend on task details17,18,20,31,63,64. For example, studies using shorter CSIs than ours have identified part of switch cost that was strongly dependent on the CSI22. This likely reflects a process more directly related to internal preparation based on contextual cues23,25. On a related note, when there are multiple cues for one context, a cue change alone without task switching degrades behavioral performance, known as the cue switch cost28,37,38,65. Such cue-encoding mechanisms are beyond the scope of our decision-making models. Regarding response encoding, the congruency effect or response conflict is often observed along with switch costs47,66,67, whereas our behavioral results lacked these effects (Fig. 2j). These are typically associated with tasks using firmly established associations between stimuli and responses, such as the Stroop task27. The lack of these effects in our design might stem from arbitrary associations between face stimuli and saccade directions. We expect that the diverse effects of task switching observed in previous studies can be investigated by extending our quantitative modeling framework to different task structures.
This study focused on switching between perceptual tasks, but similar principles may apply to other cognitive tasks. The residual switch cost has been reported in many non-perceptual tasks, such as number or lexical categorizations18. Although the sensory readout may not be a major bottleneck in these tasks, the process of converting sensory inputs into decision evidence may still require fine adjustments in circuit computations in these tasks. Although top-down control can partially align these circuit computations with a given task demand, detailed computations may require further adjustments after a stimulus is presented and the circuits start to operate, leading to limited behavioral performance unique to biological neural networks.
Method
Participants and experimental setup
Twenty human participants (20–40 years old, 7 males and 13 females, students or employees at the Chinese Academy of Sciences) were recruited for the experiments. Our participant sampling strategy did not factor in gender, as it was unlikely to influence the basic perceptual decision-making processes we studied. All participants had normal or corrected-to-normal vision and were naïve to the purpose of the experiment. Written informed consent was obtained from all participants prior to experiments. Each participant was compensated 60 CNY per hour for their time. All experimental procedures were approved by the Institutional Review Board of the Center for Excellence in Brain Science and Intelligence Technology, Institute of Neuroscience, Chinese Academy of Sciences.
The main context-dependent categorization task (Fig. 1) included eight participants, while the fixed duration task (Fig. 5), the face versus color task (Fig. 6b), and the motion versus color task (Fig. 6c) included seven participants each. Eight participants took part in more than one experiment. For the latter three tasks, we initially recruited four, five, and three participants, respectively. Upon reviewers’ request, we performed additional data collection during the revision and added three, two, and four participants to the experiments to make the total sample size seven. Here, we report the results combining these data collected post hoc, as there was not a sufficient sample size to perform statistical tests independently. The results did not change as a consequence of adding participants to the sample post hoc. Our sample sizes were relatively small because we sought to collect a large number of trials from each participant (1500–3000 trials per participant; a total of 79,480 trials in this study) after extensive practice sessions (~ 2000 training trials per participant prior to data collection). This was aimed to obtain as much reliable behavioral data as possible from individual participants68. Using a post-hoc sensitivity analysis, we estimated that our sample size (7–8) could detect an effect with 80% power if the standard deviation across participants was less than 75% of the effect size69. When statistical tests did not show significance, we supplemented our analysis with the Bayes factor (BF01, relative likelihood of the data under the null hypothesis compared to the alternative hypothesis) and interpreted the results cautiously. According to cthe onvention, BF01 between 1 and 3.2 suggests anecdotal evidence for the null hypothesis, between 3.2 and 10 indicates substantial evidence, and between 10 and 100 reflects strong evidence70.
Throughout the experiments, participants were seated in a height-adjustable chair in a semi-dark room with their chin and forehead supported by a tower-mounted chinrest. The chinrest had a fixed position to ensure a stable viewing distance (57 cm) from the cathode-ray-tube monitor (17-inch IBM P77 and 21-inch SUN GDM-5010P; 75 Hz refresh rate; 1024 × 768 pixels screen resolution). Stimulus presentation was controlled using the Psychophysics Toolbox71 and MATLAB (v2019b, MathWorks, MA, USA). Eye movements were monitored using a high-speed infrared camera (Eyelink; SR Research, Ottawa, Canada). The gaze position was recorded at 1 kHz. Data was analyzed using MATLAB (v2019b, MathWorks, MA, USA).
Task designs
Context-dependent face categorization task
To investigate flexible task switching, we designed a context-dependent face categorization task (Fig. 1a, b). We chose face categorization because previous studies successfully explained behavior using a simple evidence accumulation model with psychophysical reverse correlation40. Furthermore, face stimuli can be naturally categorized along multiple sensory dimensions such as identity, expression, and age, making them suitable for studying flexible rule switching.
Participants categorized faces defined in a two-dimensional (2D) face space (Fig. 1a) according to one of two categorization rules. Categorization rules were switched every 2–6 trials within the experimental blocks and were indicated by the color of a fixation point such that participants were always informed of the rule. The two rules were facial identity versus expression categorization for six of the eight participants who participated in this experiment, and facial identity versus age categorization for the remaining two of the eight participants. We used these two conditions to ensure that the switch cost effects were not due to specific types of facial features. For the identity rule, participants categorized faces into one of two facial identities. For the expression and age rules, participants categorized faces as happy/sad or old/young. As the behaviors of these two groups were comparable (Supplementary Fig. 1), we averaged the results in the main section.
Each trial began when participants fixated on a fixation point at the center of the screen (diameter, 0.5∘). The color of the fixation point was either cyan or magenta, cuing one of the two categorization rules. After a short delay (150–300 ms, truncated exponential distribution), two white target dots appeared 7∘ above and below the fixation point. Shortly thereafter (300–1200 ms, truncated exponential distribution), a face stimulus (size, ~ 4∘ × 4∘) appeared on the screen parafoveally (stimulus center, 1.5∘ to the left of the fixation point). We placed the stimuli parafoveally to encourage participants to judge the face stimulus as a whole, rather than focusing on local features. Participants reported the category of the presented face by making a saccade to one of the two targets whenever they were ready (reaction-time task). Associations between face categories and target positions were counterbalanced across participants in each context. The stimulus was extinguished immediately after saccade initiation. If participants did not make a decision within 5 s, the trial was aborted (< 0.2% trials for all participants). Distinct auditory feedback was delivered for correct and incorrect choices. When the face was ambiguous (i.e., 0% morph level, halfway between the two prototypes on the morph continuum), the correct feedback was delivered in a random half of the trial. Following feedback, the next trial began after a 1.2 s inter-trial interval.
We created a 2D face space by continuously morphing four prototype faces. The prototype faces were obtained from the Tsinghua Facial Expression Database72 and the NimStim Face set73, which contains photographs of the same identities with different expressions. To create young/old prototypes, we used free software74 that synthesizes younger or older faces from an original photograph. Morphed facial images were created from the prototype faces using a custom program40. The program linearly interpolates the positions of manually defined anchor points on the facial images and the textures inside the tessellated triangles defined by the anchor points. This algorithm can also independently morph different facial features (eyes, nose, and mouth). In Figures 1, 5, 6, images from the NimStim Face set used in the experiments were replaced with images from the Tsinghua Facial Expression Database to avoid copyright issue. Permission was obtained for the use of the images from the Tsinghua Database.
Using our custom morphing program, we generated two stimulus axes from four prototypes (e.g., images of happy person A, sad person A, happy person B, and sad person B), but we took extra caution in making the two axes orthogonal (factorial)75. For example, the morph axis connecting the happy and sad faces of identity A (AH, AS) is not equivalent to the morph axis connecting the happy and sad faces of identity B (BH, BS). The factorization of the two axes requires the construction of the following two morph vectors and morphing faces along these two axes:
The center of the face space (0% morph level along both stimulus axes) is the average of all four faces (\(\frac{{A}_{H}+{A}_{S}+{B}_{H}+{B}_{S}}{4}\)) and ± 100% morph levels for each axis correspond to the addition or subtraction of the above vectors to the average face. On each trial, we sampled one morph level from the following 11 levels for both axes regardless of the categorization rules: −96%, −48%, −24%, −12%, −6%, 0%, +6%, +12%, +24%, +48%, +96%. As shown in Supplementary Fig. 1a,b, the participants had roughly equal discriminability along the two axes.
We added random temporal fluctuations in morph levels to the sampled value in each trial to examine how participants weighted the evidence conferred by the face stimuli over time (i.e., psychophysical reverse correlation). The morph level was randomly sampled every 106.7 ms (eight monitor frames) from a Gaussian distribution with a standard deviation (SD) of 20%. This fluctuation duration provided us with sufficiently precise measurements of participants’ weighting characteristics in their ~ 1 s decision time, while the duration was long enough to ensure a subliminal transition of morph levels. Between the two morphed face images, we interleaved a noise mask (phase randomization of 0% morph face) with a smooth cosine transition function during the eight monitor frames40. This mask prevented participants from noticing fluctuations in morph levels during stimulus presentation. Random fluctuations were applied independently to each facial feature (eyes, nose, and mouth) along both the task and orthogonal axes while keeping the average morph level constant within a trial. Although the independent fluctuations across facial features allowed us to examine the spatial weighting of evidence40, most of our analyses used the average morph levels of the three features because our primary goal was to test temporal weighting. The psychophysical kernels for the individual features are shown in Supplementary Fig. 9.
We collected data from eight participants for this task (24,358 trials in total; 3045 ± 125 trials per participant). Prior to the main data collection, the participants underwent extensive training (on average, 5 sessions with 2,200 trials) to ensure stable behavioral accuracy under both rules.
Fixed stimulus duration task
In the reaction-time (RT) task described above, participants showed longer RTs in the switch trials, but their choice accuracy was maintained, possibly because they were able to collect more evidence with additional RTs. Therefore, we designed an alternative task (Fig. 5a) in which we limited the stimulus duration to test whether choice accuracy deteriorated when the collection of additional evidence was prohibited.
In each trial, a stimulus was presented for a variable duration (truncated exponential distribution; range, 320–640 ms, in steps of 106.7 ms; mean, 416 ms). This distribution has a flat hazard rate and minimizes the participants’ ability to anticipate the end of a stimulus76. The fixation point disappeared with stimulus termination as the go cue. Participants had to select a target within 0.7 s after the go cue (the proportion of timeout trials: < 7.4% for all participants). The RTs in this task were defined as the time interval between the stimulus offset and saccadic response. The remaining task parameters, including the stimulus design and duration of the CSI, were identical to those in the RT task.
Seven participants performed this fixed-duration task (21,513 trials in total; 3,073 ± 107 trials per participant). Three also participated in the RT task with the same facial stimulus set. All participants received extensive training before main data collection (on average, 5 sessions with 3,000 trials).
Motion versus color and face versus color categorization tasks
To test whether similar degrees of switch costs occur with perceptual tasks using simpler sensory features, we performed motion versus color categorization of colored stochastic moving dots (8,9,50; Fig. 6c). In the motion task, participants reported whether the dots were overall moving to the left or right by making a saccade to one of the two targets positioned to the left or right of the fixation point. In the color task, participants reported whether the majority of the dots were purple or green by choosing one of the same two targets. The two targets were colored purple and green to indicate the association. The overall trial structure was similar to that of the RT version of the face task. To avoid interference with color judgment, task contexts were conveyed by the shape of the fixation point rather than by its color (white triangle or cross). A random dot stimulus appeared within a 6∘ circular aperture centered at the fixation point. It consisted of three independent sets of moving dots displayed in consecutive frames77. Each set of dots was shown for one video frame and then replotted three frames later (Δt = 40 ms; density, 16.7 dots/deg2/s). When replotted, a subset of dots was offset from their original location (speed, 5 ∘/s), whereas the remaining dots were placed randomly. The colors of the dots were chosen to be equiluminant green (L = 20.0, x = 0.386, y = 0.494) or purple (L = 20.0, x = 0.224, y = 0.182).
The stimulus strength of the motion (motion coherence) was defined as the percentage of dots moving coherently in the correct direction. The stimulus strength of the color (color coherence) was defined as the difference between the percentage of green and purple dots8,50. For example, +100% color coherence meant all the dots were green,-100% color coherence meant all the dots were purple, and 0% color coherence meant that green and purple dots were equally likely to be present. On each trial, a motion coherence was chosen from the following set: −51.2%, −25.6%, −12.8%, −6.4%, −3.2%, 0%, +3.2%, +6.4%, +12.8%, +25.6%, +51.2%. A color coherence was chosen from a different set to match the difficulty with the dots task: −100.0%, −51.2%, −25.6%, −12.8%, −6.4%, 0%, +6.4%, +12.8%, +25.6%, +51.2%, +100.0%. For visualization purposes (Fig. 6d, e, right panel), we scaled the eleven stimulus strengths of each task to range from −1 to 1 and denoted it as relative stimulus strength.
We also performed a face versus color categorization task as a control (Fig. 6b). In this task, participants categorized a colored facial stimulus according to its facial identity or color. As in the motion versus color task, the task contexts were indicated by the shape of the fixation point (white triangle or cross). Two prototype facial identities were chosen from the NimStim Face set73, and the faces were uniformly colored with a value in the CIE-1931 xy color space linearly interpolated between the two prototype colors. Because we found that the participants had different color-discrimination thresholds, we chose different prototype colors for different participants to match the task difficulty between the face and color contexts. These prototypes were red (set 1: x = 0.374, y = 0.274; set 2: x = 0.371, y = 0.318; set 3: x = 0.369, y = 0.339; set 4: x = 0.368, y = 0.350) and green (set 1: x = 0.361, y = 0.443; set 2: x = 0.365, y = 0.400; set 3: x = 0.366, y = 0.378; set 4: x = 0.367, y = 0.368). The luminance of each image pixel was kept constant. The stimulus strength of color was defined as the distance from the prototypes; each prototype corresponded to-100% and 100% strength, and the intermediate values were their linear interpolation. We had 11 levels: −96%, −48%, −24%, −12%, −6%, 0%, +6%, +12%, +24%, +48%, +96%. To approximate the fluctuations in sensory evidence that occurred in the other tasks, we introduced a random variation in color to a stimulus. The color strengths were randomly sampled from a Gaussian distribution with an SD of 20% and updated every 13.3 ms (one monitor frame). This rapid fluctuation mimicked the stochasticity of color strength in the motion versus color task, where the color of each dot was resampled in every monitor frame.
Seven participants performed the motion versus color task (20,583 trials in total; 2940 ± 15 trials per participant), and seven participants performed the face versus color task (13,026 trials in total; 1,861 ± 81 trials per participant). Participants received extensive training for each task before main data collection (on average, 4 sessions with 2,000 trials).
Data analysis
Psychometric and chronometric functions
Throughout the analyses, we defined the trials immediately after a rule switch as switch trials and the rest of the trials as non-switch trials. The first trial of each experimental block was excluded. We confirmed that history effects such as post-error slowing78 did not affect our conclusions (Supplementary Fig. 8a,b).
To quantify the differences in the participants’ behavioral performance between the switch and non-switch trials, we fitted the following logistic function to the choice data for each participant:
where logit(p) = log(p/(1 − p)), s is the morph level (ranging from -1 to 1) and I is an indicator variable that is 0 for non-switch trials and 1 for switch trials. α0 and α1 are regression coefficients reflecting choice bias and accuracy in non-switch trials, whereas α0,switch and α1,switch reflect the difference in bias and accuracy between non-switch and switch trials.
The difference in the mean RTs between the switch and non-switch trials was evaluated using a hyperbolic tangent function:
where T denotes mean RTs, β1 and β2 are regression coefficients that reflect the dependency of RTs on stimulus strength, and β0 is a stimulus-independent term. Because the increase in RTs for switch trials was nearly independent of stimulus strength (Fig. 2c), we used β0,switch as a metric to quantify the overall increase in RTs in switch trials (ΔRT in Figs. 2i, 4f, 6f).
Psychophysical reverse correlation
To quantify the effect of stimulus fluctuations on choice, we performed psychophysical reverse correlations39,46. Psychophysical kernels K(t) were calculated as the difference in the average fluctuations of the morph levels, conditional on the participants’ choices, as follows:
where s(t) represents the morph level of the facial stimulus at time t. Although the morph levels fluctuated independently for the three facial features (eyes, nose, and mouth), we averaged them for each stimulus frame to focus on the effects of temporal fluctuations. When averaging, we weighted the fluctuations of each feature according to the fitted sensitivity parameters of that feature in the drift-diffusion model (ke, kn, km in Eq. (10); see below) so that a more informative feature makes a larger contribution to the kernel. The psychophysical kernels for the individual features are shown in Supplementary Fig. 9, and are consistent with our main conclusions. We used trials with low average morph levels (average level 0–12%), in which there was a sufficient number of trials for both choices. For trials with nonzero average morph levels, the average was subtracted from the fluctuations. We used fluctuations up to the median RT aligned to the stimulus or saccade onset to ensure that at least half of the trials contributed to the kernels at all times. Three-point boxcar smoothing was applied to the kernels for denoising, but the unsmoothed data were used to calculate the fitting accuracy of model psychophysical kernels.
We also generated psychophysical kernels for the motion versus color task and the face versus color task (Fig. 6; Supplementary Fig. 6b). In the motion versus color task, stimuli were stochastically generated, but this stochasticity was not explicitly defined by the experimenters, unlike the stimulus fluctuations in the main face task. We therefore estimated their stimulus fluctuations post-hoc. For the motion, we followed past works39,79 and performed a motion energy analysis to generate the relative energy for leftward and rightward motion from random dot positions. We used the same filter parameters as in Okazawa et al.39. For the color, we calculated the proportion of dots with the correct colors. In the face versus color task, the color was explicitly defined as a color value at each stimulus frame. Because these fluctuations happened at a much faster time scale (one stimulus frame: 13.3 ms) than the face fluctuations, we used additional smoothing; for color signals, we applied 20-point boxcar smoothing to frame-by-frame values and, for motion signals, we applied 5-point smoothing to the outputs of the motion energy model.
Testing the effect of cue-stimulus interval on behavior
Our tasks had a variable delay between the onset of participants’ fixation—when they recognized the current task rule based on the fixation point—and stimulus presentation (range, 0.45–1.50 s; median, 0.72 s; roughly followed truncated exponential distribution but depended on participants’ fixation onset; Fig. 2g). This cue-stimulus interval (CSI) allowed participants to prepare for rule switching. To test the effect of CSIs on RTs (Figs. 2i, 4f), we divided trials into seven groups based on CSIs and calculated the difference in RTs between the switch and non-switch trials (ΔRT) for each group. ΔRT was quantified as β0,switch in Eq. (3). A direct comparison of raw RTs between switch and non-switch trials yielded similar results. We performed a linear regression between CSIs and β0,switch for each participant, then averaged the results across participants (Fig. 2i).
The effect of the CSIs on the reduction in psychophysical kernels was examined by dividing the trials into two groups based on the median CSI. We focused on the first two stimulus frames of the kernels and defined the reduction in kernel amplitude for the switch trials as
where \({\bar{K}}_{{{{\rm{switch}}}}}\) and \({\bar{K}}_{{{{\rm{non}}}}{{-}}{{{\rm{switch}}}}}\) represent the averaged kernel amplitudes over the first and second stimulus frames for non-switch and switch trials, respectively.
Discrimination threshold in the fixed stimulus duration task
To test whether the choice accuracy was affected by CSIs in the fixed stimulus duration task, we plotted the discrimination thresholds of the switch and non-switch trials, each divided into four quantiles of CSIs (Fig. 5c). For each quantile, we fitted the following logistic function to the choice data:
where ∣s∣ is the absolute morph level (ranging from 0 to 1), α1 is a regression coefficient reflecting the slope of a psychometric function in non-switch trials, and α1,switch reflects the change in the slope in switch trials. From the fitted curve, we calculated the discrimination threshold, which is defined as the stimulus strength at 81.6% correct rate79.
Testing the dependency of switch cost on features to be switched
We performed three combinations of rule switching tasks (identity versus expression/age, identity versus color, and motion versus color switch; Fig. 6) to examine the dependency of switch cost on stimulus features. We sought to determine whether the increases in RTs after a rule switch depended on the stimulus features that participants judged before the switch, the features after the switch, or the combination of them. We defined the increase in RTs (using β0,switch in Eq. (3)) for each participant n and for each switch condition (switching from feature i to j) as ΔRTi→j,n, then constructed the following three models to explain it.
Eq. (7) and Eq. (8) accounts for ΔRTi→j,n as a cost associated with switching from a feature i (Ci) or a cost associated with switching to a feature j (Cj), whereas Eq. (9) assumes a cost for a pair of features i and j (Ci,j) regardless of the switching direction. We estimated these cost parameters using linear regression to all participants’ data in all three tasks and determined the fitting accuracy using the Bayesian information criterion (BIC).
Model fit and evaluation
To examine the computational mechanisms underlying the behavioral differences between the switch and non-switch trials, we fitted several variants of evidence accumulation models to the data. Previous studies showed that face categorization behavior without a rule switch can be accurately explained by a drift-diffusion model that linearly accumulates spatiotemporal evidence39,40. Therefore, we fitted this model to non-switch trials and attempted to explain the switch trials using additional mechanisms.
Drift-diffusion model for non-switch trials
To fit the non-switch trials, we employed a model previously developed for face categorization behaviors39,40. The model receives spatiotemporal fluctuations in morph levels, linearly accumulates evidence toward an upper or lower bound, and commits to the choice associated with the bound when it is reached. RT is the sum of the time required to reach a bound and the additional non-decision time (Fig. 3c).
In our task, the morph levels of the three facial features (eyes, nose, and mouth) fluctuated along both the task and orthogonal axes, resulting in six morph levels. However, because participants rarely confused the task rule (Fig. 2a) and did not show influences from task-orthogonal information (Fig. 2b), we assumed that only the task axes contributed to forming the momentary evidence (μ(t)) in each context:
where s1e, s1n, s1m, s2e, s2n, s2m are the morph levels of the individual facial features along the task axis, and k1e, k1n, k1m, k2e, k2n, k2m are the sensitivities associated with them. The sensitivities for each feature were parameterized independently for each context because facial features can be weighted differently for different tasks40,80.
Momentary evidence is then accumulated over time to form the decision variable (v):
where η(τ) represents internal (neural) noise in the sensory, inference, or integration processes, assumed to follow a Gaussian distribution with mean 0 and SD σ(t). Under these assumptions, the probability that the decision variable has value v at time t satisfies the Fokker-Planck equation:
where p(v, t) denotes the probability density. The accumulation process started from zero evidence and continued until the decision variable reached one of the two boundaries (± B) indicating two choices. Thus, the above partial differential equation has initial and boundary conditions as follows:
where δ(v) denotes the Dirac delta function. The diffusion noise (σ(t)) was set to 1 and the bound and drift rate were defined in a unit of diffusion noise. The bound-crossing time was convolved with the distribution of non-decision time, which was defined as a Gaussian distribution with a mean of T0 and an SD of \({\sigma }_{{T}_{0}}\), to calculate the RT. The SD, \({\sigma }_{{T}_{0}}\), was always set to one-third of T0 to reduce the number of the free parameters81.
In total, the model had eight free parameters (k1e, k1n, k1m, k2e, k2n, k2m, B, T0) to fit the non-switch trials. The majority of the parameters accounted for the sensitivities of the three facial features in each rule, and by averaging the fluctuations of the three features, the model could be reduced to four parameters (k1, k2, B, T0; one sensitivity parameter for each task context). This reduced model performed equally well in fitting the behavioral data and yielded similar results, except that it did not account for feature sensitivities. Nevertheless, we used the 8-parameter model for the main results to conform to our previous study40. The model had the same bound height (B) and non-decision time (T0) in the two contexts. This was justified by the fact that the participants had similar psychometric and chronometric functions in both contexts (Supplementary Fig. 1a,b).
We fitted the model to the participants’ choices and RT distributions using maximum likelihood estimation. Given a set of parameters, the stimulus fluctuations in each trial were used to calculate the RT distributions of the two choices according to the aforementioned model formulation. From these distributions, we derived the likelihood of observing the participants’ choices and RTs. Summing the likelihoods across all the trials yielded the total likelihood of the parameter set. We used a simplex search method (fminsearch in MATLAB) to determine the parameter set that maximized the summed likelihood. To avoid local maxima, we repeated the fitting process using multiple initial parameter sets and selected the largest overall likelihood as the final result. Fitting was performed for each participant, and included trials with all stimulus strengths. The fitting curves shown in Figures 3 and 4 represent the averages across the participants. The fitting performance of the model was quantified using the coefficient of determination (R2) for the joint distributions of choices and RTs. For each morph level, we generated the RT distribution for each choice (bin size, 100 ms) and computed R2 between the data and model outputs after concatenating the bins of all morph levels and choices.
The reduction in initial sensory weighting in switch trials
To account for the reduced effect of initial stimulus fluctuations in the switch trials (Fig. 3a), we added a dynamic sensory weighting function to the drift-diffusion model (Fig. 3c)39,82. Assuming that sensory weight drops after a task switch and recovers gradually during stimulus presentation, we modeled the sensory weight at each time t (w(t)) in the switch trials as a ramp function:
where winit is the initial value and trecover is the time required for the weight to return to baseline. This weighting was constant in non-switch trials.
Sensory weighting can affect evidence accumulation in two ways. First, it can modulate only the signal component (i.e., drift rate) of the accumulation. This can be formulated by extending Eq. (11) as:
Second, it can modulate the diffusion noise along with the drift rate:
These two forms make different assumptions regarding the noise source. If noise arises during the accumulation process, the weighting function does not affect the noise (Eq. (15)), but if noise arises in the sensory process or in the process of converting sensory information into evidence, weighting can also be applied to the noise (Eq. (16)). In Supplementary Fig. 3, we tested both forms and found that the latter explained the behavioral data well. This is consistent with previous findings that noise in perceptual decision making is largely due to sensory or inference processes83,84,85. Therefore, we used the latter form in our main results.
To fit this model to the switch trials, we changed only the parameters for weight reduction (winit, trecover) during the maximum likelihood estimation for individual participants. All other parameters were fixed at the values fitted to the non-switch trials. This poses strong constraints on the model because only two parameters were used to account for behavioral changes in the switch trials. We also confirmed that the model parameters converged to similar values when all parameters were simultaneously fitted to the switch trial data.
The above formalism (Eq. (14)) assumed a linear recovery of sensory weight, but we found that different forms of recovery fitted the data similarly well. For example, we examined an exponential recovery function:
The mean BIC of this exponential model across participants was 14,515, whereas the mean BIC of our main model was 14,516. Thus, the exact form of the recovery function was not critical in our model.
Alternative models
To examine whether other mechanisms could explain the observed switch costs, we simulated a variety of alternative models. Because sensitivity (k), bound height (B), and non-decision time (T0) in the drift-diffusion model affect RTs, we first examined whether any of these parameters accounted for the data in the switch trials. Similar to the model with initial weight reduction, we started with the model parameters fitted to the non-switch trials, and then allowed the model to adjust these parameters to fit the switch trials using maximum likelihood estimation (non-decision time: Fig. 4a–c; sensitivity and bound height: Supplementary Fig. 4c-e).
We also tested whether a leak in evidence accumulation explains the results (Supplementary Fig. 4b), because it increases RTs and leads to lower kernel amplitudes early in trials owing to the gradual loss of information over time. The drift diffusion model with a leak rate (λ) becomes an Ornstein-Uhlenbeck process86, whose Fokker-Planck equation is
A larger leak rate indicates a greater loss of information over time.
To further examine whether task preparation after receiving the context cue interfered with evidence accumulation and led to the observed switch cost, we extended our model to include task preparation time (Fig. 4d). This extended model assumes that, after participants fixated on the fixation point indicating a rule switch, they needed a fixed amount of time (modeled as a Gaussian distribution with mean Pm and SD Psd) to prepare for the switch. Since evidence accumulation starts only after this preparation time, an early period of the stimulus sequence does not influence the participants’ decisions if this period overlaps with the preparation time. The key difference from the main model is that the duration of this ineffective stimulus period depends on the CSI, which varied across trials in our task. The model was allowed to adjust Pm to fit the switch trials using the same maximum likelihood estimation. The SD, Psd, was maintained at one-third of Pm, because we found that Psd takes an extremely large value when fitted as a free parameter to account for the switch cost in trials with long CSIs, making the model inappropriate as a hypothesis for task preparation.
We compared the performances of all fitted models using Bayesian information criterion (BIC) (Fig. 4g), which was calculated based on the log-likelihood of all trials and participants. ΔBIC in Fig. 4g are the differences in BIC between alternative models and our main model, and the positive values indicate poorer fit performances of the alternative models.
Generating model psychophysical kernels and RT distributions
Because the above model formulation could specify choices and RTs, but not psychophysical kernels, we relied on Monte Carlo simulations to estimate the model kernels. We created 105 simulated trials with 0-12% morph levels with the same morph fluctuation parameters as in the main task (SD, 20%), and generated the responses of the fitted models to these simulated stimulus patterns. We then used the model choices and RTs to calculate their psychophysical kernels, as we did for the human data (thick gray lines in Figs. 3f-g, 4c, and 4e). Thus, the model kernels were not directly fitted to the participants’ kernels, but were generated from an independent set of stimulus fluctuations, making the comparison of data and models informative. Similarly, the RT distributions of the models (Fig. 3e) were generated from simulations with an independent set of morph fluctuations to ensure an accurate comparison of the data and models.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
The raw psychophysical data generated in this study have been deposited on Zenodo at https://doi.org/10.5281/zenodo.1416258087.
Code availability
The codes for behavioral analysis in this study are available on Zenodo at https://doi.org/10.5281/zenodo.1416258087.
References
Shadlen, M. N. & Kiani, R. Decision making as a window on cognition. Neuron 80, 791–806 (2013).
Forstmann, B. U., Ratcliff, R. & Wagenmakers, E.-J. Sequential sampling models in cognitive neuroscience: Advantages, applications, and extensions. Annu. Rev. Psychol. 67, 641–666 (2016).
Ratcliff, R., Smith, P. L., Brown, S. D. & McKoon, G. Diffusion decision model: Current issues and history. Trends Cogn. Sci. 20, 260–281 (2016).
Gold, J. I. & Shadlen, M. N. The neural basis of decision making. Annu. Rev. Neurosci. 30, 535–574 (2007).
O’Connell, R. G. & Kelly, S. P. Neurophysiology of human perceptual decision-making. Annu. Rev. Neurosci. 44, 495–516 (2021).
Hanks, T. D. & Summerfield, C. Perceptual decision making in rodents, monkeys, and humans. Neuron 93, 15–31 (2017).
Okazawa, G. & Kiani, R. Neural mechanisms that make perceptual decisions flexible. Annu. Rev. Physiol. 85, 191–215 (2023).
Mante, V., Sussillo, D., Shenoy, K. V. & Newsome, W. T. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013).
Siegel, M., Buschman, T. J. & Miller, E. K. Cortical information flow during flexible sensorimotor decisions. Science 348, 1352–1355 (2015).
Sasaki, R., Kumano, H., Mitani, A., Suda, Y. & Uka, T. Task-specific employment of sensory signals underlies rapid task switching. Cereb. Cortex 32, 4657–4670 (2022).
Suda, Y. & Uka, T. The NMDA receptor antagonist ketamine impairs and delays context-dependent decision making in the parietal cortex. Commun. Biol. 5, 690 (2022).
Tsumura, K., Aoki, R., Takeda, M., Nakahara, K. & Jimura, K. Cross-hemispheric complementary prefrontal mechanisms during task switching under perceptual uncertainty. J. Neurosci. 41, 2197–2213 (2021).
Pagan, M. et al. Individual variability of neural computations underlying flexible decisions. Nature https://doi.org/10.1038/s41586-024-08433-6 (2024).
Soldado Magraner, J.Mante, V. & Sahani, M. Inferring context-dependent computations through linear approximations of prefrontal cortex dynamics. Preprint at https://www.biorxiv.org/content/10.1101/2023.02.06.527389v1 (2023).
Flesch, T., Juechems, K., Dumbalska, T., Saxe, A. & Summerfield, C. Orthogonal representations for robust context-dependent task performance in brains and neural networks. Neuron 110, 1258–1270 (2022).
Yang, G. R., Joglekar, M. R., Song, H. F., Newsome, W. T. & Wang, X.-J. Task representations in neural networks trained to perform many cognitive tasks. Nat. Neurosci. 22, 297–306 (2019).
Kiesel, A. et al. Control and interference in task switching-A review. Psychol. Bull. 136, 849–874 (2010).
Monsell, S. Task switching. Trends Cogn. Sci. 7, 134–140 (2003).
Karayanidis, F. et al. Advance preparation in task-switching: Converging evidence from behavioral, brain activation, and model-based approaches. Front. Psychol. 1, 25 (2010).
Koch, I., Gade, M., Schuch, S. & Philipp, A. M. The role of inhibition in task switching: A review. Psychon. Bull. Rev. 17, 1–14 (2010).
Rogers, R. D. & Monsell, S. Costs of a predictable switch between simple cognitive tasks. J. Exp. Psychol. Gen. 124, 207–231 (1995).
Meiran, N. Reconfiguration of processing mode prior to task performance. J. Exp. Psychol. Learn. Mem. Cogn. 22, 1423–1442 (1996).
Musslick, S. & Cohen, J. D. Rationalizing constraints on the capacity for cognitive control. Trends Cogn. Sci. 25, 757–775 (2021).
Flesch, T., Nagy, D. G., Saxe, A. & Summerfield, C. Modelling continual learning in humans with Hebbian context gating and exponentially decaying task signals. PLoS Comput. Biol. 19, e1010808 (2023).
Jaffe, P. I., Poldrack, R. A., Schafer, R. J. & Bissett, P. G. Modelling human behaviour in cognitive tasks with latent dynamical systems. Nat. Hum. Behav. 7, 986–1000 (2023).
Ardid, S. & Wang, X.-J. A tweaking principle for executive control: Neuronal circuit mechanism for rule-based task switching and conflict resolution. J. Neurosci. 33, 19504–19517 (2013).
Allport, D. A.Styles, E. A. & Hsieh, S. in Attention and Performance XV: Conscious and Nonconscious Information Processing (ed. Umiltà, C., Moscovitch, M.) Ch. 17 (MIT Press, Cambridge, Massachusetts, 1994).
Mayr, U. & Kliegl, R. Differential effects of cue changes and task changes on task-set selection costs. J. Exp. Psychol. Learn. Mem. Cogn. 29, 362–372 (2003).
de Jong, R. in Control of Cognitive Processes: Attention and Performance XVIII (ed. Monsell, S., Driver, J.) Ch. 15 (MIT Press, Cambridge, Massachusetts, 2000).
Meiran, N., Chorev, Z. & Sapir, A. Component processes in task switching. Cogn. Psychol. 41, 211–253 (2000).
Monsell, S. & Mizon, G. A. Can the task-cuing paradigm measure an endogenous task-set reconfiguration process? J. Exp. Psychol. Hum. Percept. Perform. 32, 493–516 (2006).
Li, B., Li, X., Stoet, G. & Lages, M. Exploring individual differences in task switching. Acta Psychol. 193, 80–95 (2019).
Longman, C. S., Lavric, A., Munteanu, C. & Monsell, S. Attentional inertia and delayed orienting of spatial attention in task-switching. J. Exp. Psychol. Hum. Percept. Perform. 40, 1580–1602 (2014).
Elchlepp, H., Best, M., Lavric, A. & Monsell, S. Shifting attention between visual dimensions as a source of switch costs. Psychol. Sci. 28, 470–481 (2017).
Elchlepp, H., Lavric, A. & Monsell, S. A change of task prolongs early processes: Evidence from ERPs in lexical tasks. J. Exp. Psychol. Gen. 144, 299–325 (2015).
Koch, I. & Allport, A. Cue-based preparation and stimulus-based priming of tasks in task switching. Mem. Cogn. 34, 433–444 (2006).
Logan, G. D. & Bundesen, C. Very clever homunculus: Compound stimulus strategies for the explicit task-cuing procedure. Psychon. Bull. Rev. 11, 832–840 (2004).
Schneider, D. W. & Logan, G. D. Modeling task switching without switching tasks: A short-term priming account of explicitly cued performance. J. Exp. Psychol. Gen. 134, 343–367 (2005).
Okazawa, G., Sha, L., Purcell, B. A. & Kiani, R. Psychophysical reverse correlation reflects both sensory and decision-making processes. Nat. Commun. 9, 3479 (2018).
Okazawa, G., Sha, L. & Kiani, R. Linear integration of sensory evidence over space and time underlies face categorization. J. Neurosci. 41, 7876–7893 (2021).
Waskom, M. L., Okazawa, G. & Kiani, R. Designing and interpreting psychophysical investigations of cognition. Neuron 104, 100–112 (2019).
Fetsch, C. R. The importance of task design and behavioral control for understanding the neural basis of cognitive functions. Curr. Opin. Neurobiol. 37, 16–22 (2016).
Elchlepp, H., Monsell, S. & Lavric, A. How task set and task switching modulate perceptual processes: is recognition of facial emotion an exception? J. Cogn. 4, 36 (2021).
Schuch, S., Werheid, K. & Koch, I. Flexible and inflexible task sets: Asymmetric interference when switching between emotional expression, sex, and age classification of perceived faces. Q. J. Exp. Psychol. 65, 994–1005 (2012).
Berger, N., Richards, A. & Davelaar, E. J. Delayed reconfiguration of a non-emotional task set through reactivation of an emotional task set in task switching: An ageing study. Cogn. Emot. 33, 1370–1386 (2019).
Ahumada Jr, A. J. Perceptual classification images from Vernier acuity masked by noise. Perception 25, 2–2 (1996).
Yeung, N. & Monsell, S. Switching between tasks of unequal familiarity: The role of stimulus-attribute and response-set selection. J. Exp. Psychol. Hum. Percept. Perform. 29, 455–469 (2003).
Schneider, D. W. Investigating a method for reducing residual switch costs in cued task switching. Mem. Cogn. 44, 762–777 (2016).
Zylberberg, A., Ouellette, B., Sigman, M. & Roelfsema, P. R. Decision making during the psychological refractory period. Curr. Biol. 22, 1795–1799 (2012).
Kang, Y. H. R. et al. Multiple decisions about one object involve parallel sensory acquisition but time-multiplexed evidence incorporation. Elife 10, e63721 (2021).
Okazawa, G., Hatch, C. E., Mancoo, A., Machens, C. K. & Kiani, R. Representational geometry of perceptual decisions in the monkey parietal cortex. Cell 184, 3748–3761 (2021).
Roitman, J. D. & Shadlen, M. N. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J. Neurosci. 22, 9475–9489 (2002).
Kiyonaga, A., Scimeca, J. M., Bliss, D. P. & Whitney, D. Serial dependence across perception, attention, and memory. Trends Cogn. Sci. 21, 493–497 (2017).
Urai, A. E., De Gee, J. W., Tsetsos, K. & Donner, T. H. Choice history biases subsequent evidence accumulation. Elife 8, e46331 (2019).
Chang, L. & Tsao, D. Y. The code for facial identity in the primate brain. Cell 169, 1013–1028 (2017).
Chang, L., Bao, P. & Tsao, D. Y. The representation of colored objects in macaque color patches. Nat. Commun. 8, 2064 (2017).
Lukas, S., Philipp, A. M. & Koch, I. The role of preparation and cue-modality in crossmodal task switching. Acta Psychol. 134, 318–322 (2010).
Fintor, E., Stephan, D. N. & Koch, I. The interplay of crossmodal attentional preparation and modality compatibility in cued task switching. Q. J. Exp. Psychol. 72, 955–965 (2019).
Monsell, S., Lavric, A., Strivens, A. & Paul, E. Can we prepare to attend to one of two simultaneous voices? J. Exp. Psychol. Hum. Percept. Perform. 45, 966–982 (2019).
chuch, S. & Konrad, K. Investigating task inhibition in children versus adults: A diffusion model analysis. J. Exp. Child Psychol. 156, 143–167 (2017).
Schmitz, F. & Voss, A. Decomposing task-switching costs with the diffusion model. J. Exp. Psychol. Hum. Percept. Perform. 38, 222–250 (2012).
Ging-Jehli, N. R. & Ratcliff, R. Effects of aging in a task-switch paradigm with the diffusion decision model. Psychol. Aging 35, 850–865 (2020).
Koch, I., Poljac, E., Müller, H. & Kiesel, A. Cognitive structure, flexibility, and plasticity in human multitasking-An integrative review of dual-task and task-switching research. Psychol. Bull. 144, 557–583 (2018).
Ruge, H., Jamadar, S., Zimmermann, U. & Karayanidis, F. The many faces of preparatory control in task switching: Reviewing a decade of fMRI research. Hum. Brain Mapp. 34, 12–35 (2013).
Arrington, C. M. & Logan, G. D. Episodic and semantic components of the compound-stimulus strategy in the explicit task-cuing procedure. Mem. Cogn. 32, 965–978 (2004).
Monsell, S., Yeung, N. & Azuma, R. Reconfiguration of task-set: Is it easier to switch to the weaker task? Psychol. Res. 63, 250–264 (2000).
Hyafil, A., Summerfield, C. & Koechlin, E. Two mechanisms for task switching in the prefrontal cortex. J. Neurosci. 29, 5135–5142 (2009).
Smith, P. L. & Little, D. R. Small is beautiful: In defense of the small-N design. Psychon. Bull. Rev. 25, 2083–2101 (2018).
Lakens, D. Sample size justification. Collabra: Psychol. 8, 33267 (2022).
Kass, R. E. & Raftery, A. E. Bayes factors. J. Am. Stat. Assoc. 90, 773–795 (1995).
Brainard, D. H. & Vision, S. The psychophysics toolbox. Spatial Vision 10, 433–436 (1997).
Yang, T. & Yang, Z. et al. Tsinghua facial expression database—A database of facial expressions in Chinese young and older women and men: Development and validation. PLoS One 15, e0231304 (2020).
Tottenham, N. et al. The NimStim set of facial expressions: Judgments from untrained research participants. Psychiatry Res. 168, 242–249 (2009).
Alaluf, Y., Patashnik, O. & Cohen-Or, D. Only a matter of style: Age transformation using a style-based regression model. ACM Trans. Graph. 40, 1–12 (2021).
Folstein, J. R., Gauthier, I. & Palmeri, T. J. How category learning affects object representations: not all morphspaces stretch alike. J. Exp. Psychol. Learn. Mem. Cogn. 38, 807–820 (2012).
Ghose, G. M. & Maunsell, J. H. R. Attentional modulation in visual cortex depends on task timing. Nature 419, 616–620 (2002).
Britten, K. H., Shadlen, M. N., Newsome, W. T. & Movshon, J. A. The analysis of visual motion: A comparison of neuronal and psychophysical performance. J. Neurosci. 12, 4745–4765 (1992).
Purcell, B. A. & Kiani, R. Neural mechanisms of post-error adjustments of decision policy in parietal cortex. Neuron 89, 658–671 (2016).
Kiani, R., Hanks, T. D. & Shadlen, M. N. Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. J. Neurosci. 28, 3017–3029 (2008).
Schyns, P. G., Bonnar, L. & Gosselin, F. Show me the features! Understanding recognition from the use of visual information. Psychol. Sci. 13, 402–409 (2002).
Churchland, A. K., Kiani, R. & Shadlen, M. N. Decision-making with multiple alternatives. Nat. Neurosci. 11, 693–702 (2008).
Levi, A. J., Yates, J. L., Huk, A. C. & Katz, L. N. Strategic and dynamic temporal weighting for perceptual decisions in humans and macaques. eNeuro 5, 5 (2018).
Brunton, B. W., Botvinick, M. M. & Brody, C. D. Rats and humans can optimally accumulate evidence for decision-making. Science 340, 95–98 (2013).
Waskom, M. L. & Kiani, R. Decision making through integration of sensory evidence at prolonged timescales. Curr. Biol. 28, 3850–3856 (2018).
Drugowitsch, J., Wyart, V., Devauchelle, A.-D. & Koechlin, E. Computational precision of mental inference as critical source of human choice suboptimality. Neuron 92, 1398–1411 (2016).
Bogacz, R., Brown, E., Moehlis, J., Holmes, P. & Cohen, J. D. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychol. Rev. 113, 700–765 (2006).
Luo, T., Xu, M., Zheng, Z., & Okazawa, G. Data and Code for “Limitation of switching sensory information flow in flexible perceptual decision making” (v1.0.0). Zenodohttps://doi.org/10.5281/zenodo.14162580 (2024).
Acknowledgements
We thank Roozbeh Kiani, Bin Min, Yiteng Zhang, and Tianming Yang for their discussions and comments on earlier versions of the manuscript. We thank Jiahao Wu for his assistance with data collection. This work was supported by the National Science and Technology Innovation 2030 Major Program (2021ZD0203703, G.O.), Strategic Priority Research Program of the Chinese Academy of Sciences (XDB1010202, G.O.), National Natural Science Foundation of China (32371077, G.O.), and the National Natural Science Fund for Excellent Young Scientists Fund Program (overseas, G.O.).
Author information
Authors and Affiliations
Contributions
G.O. designed the study. T.L., M.X., and Z.Z. performed the experiments and collected the data. T.L. analyzed the data. T.L. and G.O. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Harrison Ritz, and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Luo, T., Xu, M., Zheng, Z. et al. Limitation of switching sensory information flow in flexible perceptual decision making. Nat Commun 16, 172 (2025). https://doi.org/10.1038/s41467-024-55686-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-55686-w