Abstract
The implementation of large-scale universal quantum computation represents a challenging and ambitious task on the road to quantum processing of information. In recent years, an intermediate approach has been pursued to demonstrate quantum computational advantage via non-universal computational models. A relevant example for photonic platforms has been provided by the Boson Sampling paradigm and its variants, which are known to be computationally hard while requiring at the same time only the manipulation of the generated photonic resources via linear optics and detection. Beside quantum computational advantage demonstrations, a promising direction towards possibly useful applications can be found in the field of quantum machine learning, considering the currently almost unexplored intermediate scenario between non-adaptive linear optics and universal photonic quantum computation. Here, we report the experimental implementation of quantum machine learning protocols by adding adaptivity via post-selection to a Boson Sampling platform based on universal programmable photonic circuits fabricated via femtosecond laser writing. Our experimental results demonstrate that Adaptive Boson Sampling is a viable route towards dimension-enhanced quantum machine learning with linear optical devices.
Similar content being viewed by others
Introduction
The realization of a universal quantum computer is one of the most challenging tasks faced by the quantum information community. Among the possible platforms, photon-based architectures have some special properties, namely the capability of being transmitted over long distances and a strong robustness to decoherence, which have enabled their application for communication and cryptography tasks1. However, photonic systems are inherently characterized by the challenge given by the need of introducing photon-photon interactions between photonic quantum states. While recent experimental progress has been made in this direction2,3,4,5,6,7,8,9, further technological advancements are required for the implementation of highly efficient nonlinear gates. The difficulty of carrying out this class of operations is a major challenge in the realization of photonic universal quantum computation with the gate-based model10, since it requires at least two-qubit operations. Several alternative schemes have already been proposed to overcome this limitation, each with its own strengths and weaknesses. For instance, the universal scheme based on linear optics by Knill, Laflamme, and Milburn11 (KLM) requires adaptive measurement procedures, in which the outcomes of intermediate measurements can drive the rest of the computation, together with ancillary resources that preclude efficient implementations on a large scale. Other approaches exploit nonlinear effects to realize quantum gates but their implementation is challenging12,13. More recent schemes tailored to reduce the resource overhead of the KLM scheme consist in the preparation of large entangled states of many qubits and adaptive measurements on single qubits in the so-called measurement-based quantum computing framework14 or on sub-systems in the fusion-based quantum computing variant15. These schemes thus translate the experimental challenge from applying two-qubit gates to preparing appropriate entangled resource states and performing suitable adaptive measurements.
In parallel, in the era of noisy intermediate-scale quantum (NISQ) devices, other approaches have been explored to demonstrate quantum computational advantage with photons. These strategies have focused on simpler architectures using only linear optical operations and non-adaptive single-photon detection. The Boson Sampling16 and Gaussian Boson Sampling17 computational models are believed to be non-universal and require to generate samples from classically-hard-to-simulate probability distributions such as the ones that regulate the photon-counting statistics of indistinguishable particles at the outputs of random interferometers. Nowadays, many experiments have provided evidence of reaching the quantum advantage regime for this specific sampling task18,19,20, stimulating, on the one hand, the debate about possible classical strategies to mimic the results21,22,23, and, on the other hand, the investigation of possible use-cases of such simplified photonic processors for applications beyond the original task24,25,26,27. Starting from the linear-optics-based Boson Sampling model16, it is known that, either by adding enough nonlinearities28 or enough ancillary photons and adaptivity11, it is possible to recover universal quantum computation models.
In this context, the intermediate regime between non-universal, linear-optics-based schemes and universal computation still needs to be thoroughly explored. Indeed, such an intermediate scenario where a moderate amount of adaptivity is added to linear optics could disclose interesting computational applications within the reach of current photonic technologies. Recent works showed the possibility of enlarging the spectrum of applications by employing intermediate measurements and adaptivity in a standard linear optical quantum experiment. Particular attention in this direction has been devoted to the field of quantum machine learning (QML): photonic implementations of reservoir computing and extreme learning machines have been proposed29,30,31 and first proof-of-principle experiments have been reported32,33. Other proposals involve the definition of the quantum optical analogues of neural networks, which can be trained to assess specific tasks34,35,36,37. Notably, a recent work38 introduced a scheme for QML, which starts from the photonic Boson Sampling paradigm and then adds measurements and adaptivity on a subset of the optical modes.
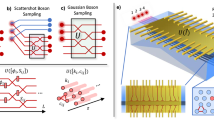
In particular, one may use as a feature map, i.e. the encoding of classical data in quantum states, the output of a Boson Sampling interferometer with n input photons in m optical modes when a subset of r photons is measured in k < m modes. Each photon detected in the k channels activates a unitary transformation on the remaining modes such that there is a correspondence between the configuration p = (o0, o1, ⋯ , ok-1) of the possible ways to detect r < n photons in k modes, that is the input classical data of the feature map, and the interferometer implementing a transformation Up. Then, the state \(\vert {\psi }_{{{\boldsymbol{p}}}}\rangle\) describing n − r photons in the m − k modes after Up is interpreted as the quantum encoding of the classical data associated to p (see also Fig. 1a). This scheme, which we define as Adaptive Boson Sampling (ABS), can be employed as a subroutine for nonlinear kernel estimations as well as to perform classification tasks via full quantum information processing38.
a The algorithm aims at solving a binary classification problem: in a 2D plane filled with different shapes, the goal is to classify the items according to the color feature. b Each point of the dataset is encoded in a quantum state \(\vert {\psi }_{{{\boldsymbol{p}}}}\rangle\), according to the optical circuit output mode, with which such state is triggered. Actually, in the ABS theoretical scheme, the detection of a photon, exiting from U0, in one of the lower modes determines a specific adaptive transformation Up that cooperates in the generation of the state \(\vert {\psi }_{{{\boldsymbol{p}}}}\rangle\). c The dataset is classified using a kernel method, specifically a Support Vector Machine. The kernel elements, defined as the overlap square moduli, can be directly derived from the sketched linear optical circuit, in which Vp is composed of U0 and Up. The square modulus of the overlap can be experimentally obtained through a measurement post-selection of the fraction of coincidences in which photons leave the circuit from the same modes as they entered. d Another way to evaluate the kernel arises from a post-selection reconstruction of the states with a tomography protocol, exploiting the projective unitary T that acts on the adaptive modes. This is the case of the experiment we implement here. After that, the kernel is provided to a classical hardware, which manages the binary classification task.
In this work, we discuss and report on the experimental implementation of the ABS paradigm via post-selection for QML purposes with systems of growing complexity. In particular, we implement the feature map procedure described previously by employing universal (here, universal refers to the fact that these circuits can implement any linear optical computation, not any quantum computation) and fully reprogrammable integrated optical circuits fabricated via the femtosecond-laser-writing method39,40. Our experimental implementation of the ABS paradigm uses two different platforms. The first experiment was carried out on a universal 6-mode integrated photonic circuit where we injected two photons generated by a spontaneous parametric down-conversion source. Then, we scaled up the size of the ABS by injecting two and three photons on a universal 8-mode photonic chip coupled to a bright semiconductor quantum dot source, which allowed us to perform a more sophisticated scheme both in terms of kernel size and quantum state dimension. In particular, the number of measured modes k was k = 3 for the 6-mode chip while k = 6 and k = 5 for the 8-mode device (depending on the dimensionality of the produced output state). We make use of the implemented quantum kernel to successfully carry out different classification tasks of 1D and 2D datasets. Finally, we discuss the scaling and future applications of such an approach.
Results
Background
In this section, we review the main concepts behind the ABS paradigm, as well as the model we consider for designing the experiment. The ABS model requires photon-counting measurements on a subset of outputs of a standard Boson Sampling experiment38. Furthermore, the scheme includes adaptive operations that are activated by the measurement outcomes. Let us now introduce the formalism of such a computational model. Let n be the total number of input photons that are injected in a m-port interferometer. We indicate with n = (n0, n1, ⋯ , nm-1) the string, which describes the arrangement of the \(n=\mathop{\sum }_{i=0}^{m-1}{n}_{i}\) photons in the m input ports. Adaptive measurements are then carried out on k < m modes by detecting r < n photons. The string defined as p = (o0, o1, ⋯ , ok-1), such that \(r=\mathop{\sum }_{j=0}^{k-1}{o}_{j}\), indicates the output photons configuration detected at the k modes. Each outcome in p activates a unitary operation on the modes that are not measured, in such a way that there will be a relationship between p and the adaptive interferometer Up (see Fig. 1). The output state of the device is then a multi-photon state of n − r photons encoded in the m − k modes. Hereafter we identify an ABS device through these parameters [m, n, d, D]. The parameter \(d=\left(\begin{array}{c}m-k+n-r-1\\ n-r\end{array}\right)\) is the dimension of the Hilbert space of the output state. The last parameter D indicates the number of classical strings that can be encoded in the ABS, which corresponds to the number of performed adaptive measurements.
The ABS scheme finds applications in the quantum machine learning context as previously demonstrated in ref. 38. In particular, the ABS feature maps can be employed for kernel-based methods. The quantum device computes the kernel between two data p and q as shown in Fig. 1c. The quantum algorithm requires to apply the circuit \({U}_{{{\boldsymbol{q}}}}^{{\dagger} }\) (\({U}_{{{\boldsymbol{p}}}}^{{\dagger} }\)) to q (p) every time the data p (q) is measured. The kernel element estimation will be given by the number of times the input state of the protocol is detected at the output, divided by the total number of rounds. Such a procedure allows for an efficient estimation of kernels from single-photon counts as demonstrated in ref. 38.
In this work, we experimentally investigate the feature map scheme illustrated in Fig. 1b and apply it to a kernel estimation task. As we will show in the following, the kernel will be computed through quantum tomography (see Fig. 1d) and quantum state fidelity rather than through the direct overlap estimation presented in Fig. 1c. Such a choice allows us to take into account experimental imperfections that could lead to the generation of imperfect states. However, quantum state tomography is a viable route only at low dimensionality while, at higher dimensions, i.e. larger number of photons and modes, the approach of Fig. 1c remains the most efficient way to compute kernels. Furthermore, the state fidelity is mathematically equivalent to the overlap estimation only for output states with high levels of purity.
The present implementation relies on the emulation of the ABS dynamics through post-selection, allowing us to investigate the properties and functionalities triggered by the addition of adaptivity in a Boson Sampling experiment. Such a limitation derives from the current technological challenges in implementing fast enough reconfigurability on the scale of integrated optical circuits41. However, we stress that the results obtained after the post-selection and processing cannot be reproduced with a single, non-adaptive Boson Sampling instance.
Experimental apparatus and data analysis
In the following, we report the results of the experimental implementation of ABS feature maps of increasing dimension by making use of m-mode universal integrated optical circuits and single-photon sources based both on parametric down-conversion and semiconductor quantum dots. As we will describe in what follows, we experimentally demonstrate four ABS schemes of increasing complexity following two main guidelines. On the one hand, we provide a demonstration of the ABS paradigm in a two-photon setting, by employing established components allowing for high quality interference between the photons (Platform A), thus providing a first assessment of the algorithm operation with readily available technology. On the other hand, to further benchmark and assess the capabilities of the method, we employ state-of-the-art components (Platform B) achieving implementations of the ABS paradigm of increasing complexity (B1, B2, B3), given the relevance of the method in view of long-term applications. The two platforms are shown in Fig. 2. Both integrated photonic devices, specifically a six- and eight-mode universal fully reconfigurable circuits, are fabricated through femtosecond laser writing40,42. The on-chip operations are controlled by thermo-optical phase shifters, through the application of external voltages over the 30 and 56 heaters on each integrated device. In particular, the optical circuits were developed according to the universal design reported in ref. 43, in which variable beam-splitters and phase shifters enable the implementation of arbitrary unitary transformations. Our platforms are then exploited as a proof-of-principle for the application of a QML feature map based on the ABS paradigm. At this stage, the time response of the reconfiguration of the circuits is not fast enough to permit an active modulation of the circuit based on the measurement outcomes; this implies that we performed the experiment in post-selection.
a Platform A. Such a platform used for 2-photon experiments in 6 modes, exploits a parametric down-conversion source that generates pairs of photons at 785 nm and a 6-mode universal programmable integrated optical circuit. The two photons are synchronized in time through delay lines. Polarization controllers and filters are employed to have fully indistinguishable photons. The operations of the chip are controlled via a power supply that applies currents to the heaters of the device. Finally, the time-to-digital converter processes the single-photon detector counts that are then analyzed for the experiment. b Platform B. In the second platform, we employ a semiconductor quantum dot source and an 8-mode universal programmable chip. The brightness of the source enables the implementation of up to 3-photon experiment. This time the photons emitted by the same quantum dot at different pump pulses are synchronized by a time-to-spatial demultiplexer in three different channels. Photon-detection has been performed by either avalanche photodiodes or by superconducting nanowire detectors. Photon number resolution in some of the experiments has been added by employing a probabilistic scheme based on mode-splitting via fiber beam-splitters. Legend: BBO (Beta-Barium Borate), F (frequency filter), HWP (half-wave plate), PBS (polarizing beam-splitter), PC (polarization compensation), APD (avalanche photodiode), TDC (time-to-digital converter), DMX (demultiplexing), SNSPD (superconducting nanowire single-photon detectors), BS (beam-splitter).
In platforms A and B1, the circuit was programmed to demonstrate the experimental feasibility of the ABS protocol as described in ref. 38, following a structure with a cascaded set of adaptive unitaries Ui. This choice led to particularly symmetric configuration, in order to maximize the interference between the input photons while keeping the bunching probability at the output low and enhance the detection probability of coincidence events in post-selection. Specifically, as shown in Fig. 3, the adaptive portion of each Ui was placed on the same diagonal, while the rest of the Mach-Zehnder Interferometers are all set at π/4 both for the internal and external phases.
a The experiment implements an ABS scheme [6, 2, 2, 3]. The circuit is encoded in a 6-mode universal programmable chip. In particular, we have a six-mode U0 and then three adaptive transformations Ui. The phase shifters ϕ (rectangles in the figure) and beam-splitter reflectivities θ (circles) are set to angles θ, ϕ = π/4 except for the θi of the Ui highlighted in red, orange and yellow that depends on the detection of one photon in the oj. Pairs of indistinguishable photons generated by parametric down-conversion evolve in such an interferometer and a qubit tomography conditioned on the detection oi is performed in the green part of the circuit. b Comparison between the numerically simulated kernel and the experimental one, the latter computed via the mutual state fidelity between the states reconstructed at the output of the programmable integrated optical circuit. c Experimental \({\rho }_{i}\) density matrices for the quantum states ρ1 (top) and ρ2 (bottom). We retrieved the density matrix by performing the qubit tomography with a tunable beam-splitter and phase-shifter. Uncertainties due to photon-counting statistics are smaller than the image scale. d 3-photon experiment in the 8-mode device. In this scenario we have r = 2 photons detected in 6 adaptive modes. We have a total amount of 15 transformations each of them triggered by the detection of two photons in a pair of the 6 outputs. The optical circuit is divided into an 8-mode unitary U0, and five transformations Ui, activated and combined according to the configurations of the r photons detected in the 6 output modes. The reflectivity values of the beam-splitters θi in red, orange, yellow, teal, and violet, depend on where the ancillary photons are detected, according to the formula displayed in the figure. e Comparison of the 15 × 15 kernels computed according to the theoretical modeling which assumes an imperfect single-photon source and the kernel reconstructed from the states measured at the output of the ABS scheme [8, 3, 2, 15]. Both experiments were carried out with APDs.
Platform A
As initial step, we employ an integrated device with m = 6 modes, designed to work with single-photon states at a wavelength of λ = 785 nm. The single-photon source is a nonlinear crystal, that generates pairs of highly indistinguishable photons via the parametric down-conversion process. The parameters [m, n, d, D] are [6, 2, 2, 3]. We injected one photon in mode 3 and the other in mode 6 and we restricted to the scenarios for which one photon is detected in one of the three modes (2,3,6). Such a measurement maps the strings pi, p1 = (1, 0, 0), p2 = (0, 1, 0) and p3 = (0, 0, 1), into the qubits \(\vert {\psi }_{{{{\boldsymbol{p}}}}_{i}}\rangle\) encoded as one-photon in the modes 4 and 5 of the device. Note that o0 is always zero due to the interferometer connectivity, since photons enter from modes 3 and 6, meaning that we can encode only 3 different strings p. The adaptive transformations Ui are implemented by tuning the reflectivities θi of the beam-splitters highlighted in Fig. 3. These angles depend on the strings pi as \({\theta }_{i}=\frac{\pi }{2}\mathop{\sum }_{j=0}^{j=i-1}{o}_{j}\), where the oj is the number of photons (0 or 1) detected in the modes 1, 2, 3 and 6 for j = 0, j = 1, j = 2, j = 3 respectively (see also Fig. 3a). Intuitively, the adaptive rule for the reflectivities works as follows: for example, if we measure o3 = 1 we will apply the interferometer unitary U3 which has θ1 = θ2 = θ3 = 0. In other words, the reflectivity of the i-th adaptive unitary will depend on the results of photon-counting measurements of the other photons in the previous modes, i.e. up to the i-th mode. The reconfigurable circuit is set to implement one of the Ui and we perform tomography of dual-rail encoded single-photon qubit states in the modes 4 and 5 conditioned on the presence of the other photon in the corresponding detector oi. Such a tomography allows us to estimate the density matrices ρi of the three qubits and the state fidelity \({{{\mathcal{F}}}}_{i}\) with the expected state, as well as to compute the 3 × 3 kernel through the mutual quantum state fidelity \(K({{{\boldsymbol{p}}}}_{i},{{{\boldsymbol{p}}}}_{j})={{\mathcal{F}}}({\rho }_{i},{\rho }_{j})\) (see Supplemental Information). The fidelities with the theoretical pure qubits generated by an ideal ABS circuit, i.e. with perfect photons indistinguishability and perfect settings of the circuit are \({{{\mathcal{F}}}}_{1}=0.981\pm 0.003\), \({{{\mathcal{F}}}}_{2}=0.999\pm 0.001\), \({{{\mathcal{F}}}}_{3}=0.998\pm 0.002\). These values confirm a very good agreement with the expectation and thus a very good level of photon indistinguishability as well as chip control. In Fig. 3b, we report the results regarding kernel estimation, while in panel c, the density matrices reconstructed from the tomography for the states ρ1 and ρ2. Further details about data analysis, measurements, and comparison with theoretical models can be found in the Supplemental Information.
Platform B
As the following step, we have performed additional experiments by using a bright quantum dot single-photon source, a time-to-spatial demultiplexer, a programmable 8-mode integrated photonic device, avalanche photo-diodes (APD) and a Single Quantum Eos system of superconductive nano-wires single-photon detectors (SNSPDs) (see Fig. 2b). By adopting this advanced apparatus we could investigate the capacity to enlarge the size of the kernels by exploring the Hilbert space of multi-photon states. The m = 8 chip configuration is depicted in Fig. 3d and was designed to operate with single-photon states at the wavelength λ = 927 nm. The generation and preparation stage allows for the synchronization of up to 3 photons generated by the same quantum dot source at different time pulses. A preliminary two-photon experiment with such a platform has been carried out and the results are reported in Supplemental Information. In the following, we show the ABS paradigm with three-photons.
B1- The first ABS encoded in this second platform aims at enlarging the number of adaptive measurements by directly exploiting the larger circuit depth given by the 8-mode device, and at increasing the number of photons injected in the interferometer. Here, the detection is at first performed by APDs as in the previous platform. In particular, we injected 3 photons in the interferometer: this implies that the number of classical strings p that can be encoded is at least \(D=\left(\begin{array}{c}6\\ 2\end{array}\right)=15\), which are the possible ways to measure 2 photons in the k = 6 adaptive channels discarding the configurations which feature two photons in the same mode. This means that this ABS scheme is labeled as [8, 3, 2, 15] and encodes 15 classical strings into 15 dual-rail encoded qubits, describing the state of the third remaining photon exiting the interferometer from modes 6,7. Thus, we implement 15 different adaptive unitaries Ui each of them associated with a different position of the pair of detected photons. More precisely, we employ as an adaptive rule for the reflectivities of the beam-splitters the same formula of the previous experiment. This time, each pair of detected photons activates a different configuration of the 5 angles θi. In such a scenario, we obtain a 15 × 15 kernel that summarizes the mutual overlaps of the 15 dual-rail qubits encoded in modes 6 and 7 of the chip, reconstructed via quantum state tomography. In Fig. 3e, we report the experimental kernel and the comparison with the expected results according to the theoretical modeling of an imperfect single-photon source. Such a model takes into account both the partial distinguishability of the photons generated by the source and the multiphoton contributions due to a second-order non-zero correlation function44,45,46 (further details can be found in the Supplementary Note 6). The average measured fidelity between the density matrices measured in the experiment and the ones calculated according to the model is \(\bar{{{\mathcal{F}}}}=0.94\pm 0.02\).
As a following step, the integrated circuit was programmed with a different geometry, as shown in Fig. 4, in order to design an adaptive scheme that could be used in a machine-learning context. Here we increase the depth of the static unitary U0 and consider a smaller two (three) mode adaptive operation Ui. In this case, U0 was chosen by drawing a random interferometer in such a way that sufficient statistics could be recorded in a post-selected regime. In addition, the adaptive transformation Ui was designed in order to gradually span the underlying feature space: such an approach was inspired by classical kernel methods, specifically Gaussian kernels47. This will allow us to showcase a practical use of quantum states obtained via the ABS scheme and its corresponding kernels, in terms of a classification task.
a The [8, 3, 2, 15] ABS scheme of platform B2. We synchronize n = 3 photons emitted from the quantum dot source and we process them in the m = 8 mode universal integrated circuit. The optical circuit is divided into an 8-mode randomly extracted unitary U0 and a 2-mode adaptive unitary Ui. Triggered by the detection of r = 2 photons in the 6 adaptive modes oj, the reflectivity value of the beam-splitter θi assumes 15 different values allowing for the reconstruction of 15 × 15 kernels. The green part of the circuit highlights the tomography station in which the dual rail qubit encoded in the remaining photon conditioned on the detection of the r photons in the other oj outputs is analyzed. On the right panel, we report the comparison between the 15 × 15 kernel simulated according to the theoretical model and the experimental one. b The [8, 3, 3, 15] scheme that encodes classical data in qutrit states (platform B3). The 8-mode U0 is followed by 3-mode adaptive Ui in which the reflectivity of two beam-splitters has been properly programmed in order to implement 15 different unitaries as before. Triggering on the detection of r = 2 photons in the 5 adaptive modes oj, considering both configurations in which photons are bunched in the same mode or are output from different modes, a 15 × 15 kernel has been reconstructed. The green part of the circuit is again the tomography station that analyzes the three-rail qutrit. The right panel reports the comparison between the 15 × 15 kernel simulated according to the theoretical model and the experimental one. c Experimental ρi density matrices for qutrits ρ1 and ρ2 to which correspond the following fidelity with the expected theoretical state, F1 = 0.995 ± 0.001 and F2 = 0.953 ± 0.010. The experimental density matrices are reconstructed by measuring in the tomography stage the generalized Pauli operators. Both experiments reported here were carried out with SNSPDs.
B2- We then implemented an alternative [8, 3, 2, 15] scheme reported in Fig. 4a. This time we made use of superconductive nanowire single photon detectors (SNSPDs), having higher detection efficiency at 927 nm. The goal of this further experiment is to engineer the adaptive operations to generate kernels which can be useful for classification. Here, again, we have 15 different unitaries Ui each of them associated with a different pair of detected photons in the adaptive modes. At variance from the previous scenario, the programmable device has been divided into two sections, one implementing a fixed and randomly extracted transformation U0 and the other a 2-mode adaptive unitary Ui (Fig. 4a). The transformations have been designed in order to obtain a 15 × 15 kernel resembling the characteristics of a Gaussian one. In particular, depending on the string p = (o0, …, o5) measured in the adaptive modes, both the reflectivity of the beam-splitter and the phase in Ui vary as \({\phi }_{i}={\theta }_{i}=\frac{k+\mathop{\sum }_{t=1}^{j}(5-t)}{5}\), where (k, j) are the indices of the outputs in which the two photons are detected. The kernel is estimated as before after performing, in post-selection conditions, a tomography of the dual-rail encoded qubit in modes 2 and 3. In the right panel of Fig. 4a, we report the experimental kernel and the expected one. In this case, the average observed fidelity is \(\bar{{{\mathcal{F}}}}=0.987\pm 0.003\) (see Supplemental Information). These results validate the capability of the Adaptive Boson Sampling scheme, implemented on a hybrid photonic platform, to engineer kernels by properly designing the set of implemented transformations and the correspondence between output states ρi with output strings pi mapped into the post-selection modes.
B3- Finally, we implemented a third experiment aimed at increasing the number of final output modes, in this case to a dimension d = 3 thus leading to qutrit states. Moreover, unlike the previous experiments, we also measured the events which feature bunching in the adaptive modes. We added an in-fiber beam-splitter at output mode 6 and, whenever we wanted to resolve a two-photon bunched state in one of the outputs of U0, we programmed the bottom part of the chip to direct such mode to the pseudo-number resolving configuration. This implies that the number of classical strings p that can be encoded here is \(D=\left(\begin{array}{c}5+2-1\\ 2\end{array}\right)=15\), which are the possible ways to measure r = 2 photons in the k = 5 adaptive channels by also considering the configurations with two photons in the same mode. In this way, we implemented a [8, 3, 3, 15] scheme: here, the 15 different adaptive unitaries - each of them associated with a different pair of detected photons - were again designed in order to obtain a feature map leading to a kernel similar to a Gaussian one. The structure of the optical circuit is similar to configuration B2 and is reported in Fig. 4b. The reflectivities of the beam-splitters and the phases in the Ui vary as in the previous scheme B2 for i ∈ [0, 10], \({\phi }_{i}={\theta }_{i}=\frac{k+\mathop{\sum }_{t=1}^{j}(4-t)}{5}\), where (k, j) are the indices of the outputs in which the two photons are detected, while, for i > 10, \({\phi }_{i}={\theta }_{i}=\frac{11+j}{5}\), where j is the output index where both photons are detected. Notably, unlike the previous experiments we now encode the output states as a single photon state in a superposition of three spatial modes. With this choice we implement a three-dimensional encoding, i.e. a qutrit, and to reconstruct its quantum state we thus need to carry out a measurement of the generalized Pauli operators in modes 1, 2, 3. In the right panel of Fig. 4b, we report the experimental kernel and the comparison with the expected results according to the theoretical modeling of an imperfect single-photon source. In this case, in Fig. 4c, we also report an example of the reconstructed density matrices for two states while the fidelity with the expected qutrit states, obtained averaging over the 15 quantum states being realized in the experiment, is \(\bar{F}=0.963\pm 0.005\). Further details are reported in Supplemental Information.
Classification of data via Adaptive Boson Sampling
Let us now show some practical applications of the ABS scheme for data classification, a prototypical machine-learning task. The key idea here is to use the feature map generated by the ABS paradigm in the context of a Support Vector Machine (SVM). In this framework, the machine is trained using the quantum kernels derived from the ABS output states. The kernels can be estimated through the inner product K(p, q) = ∣〈ψq∣ψp〉∣2 as proposed in the original theoretical work38 (see Fig. 1c), or via the state fidelity \(K({{\boldsymbol{p}}},{{\boldsymbol{q}}})={{\mathcal{F}}}({\rho }_{{{\boldsymbol{p}}}},{\rho }_{{{\boldsymbol{q}}}})\) as we did in the experiment. Note that the two estimates are equivalent for pure states. In the following, we use the quantum kernels collected in the experiment to solve binary classification problems for both 1D and 2D datasets.
i) 1D dataset classification. We consider a dataset comprising 15 labeled points, each of them to be encoded in feature maps implemented in the platforms B2 and B3. The dataset consists of 15 1D data points xp with a binary label yp ∈ (−1, 1). The labels are assigned so that the dataset is not linearly separable (see Fig. 5a). Each data point is assigned to one of the 15 measurement outcomes of post-selected modes, indicated in Fig. 4 and to the corresponding outcome quantum state, qubits for platform B2 and qutrits for platform B3, according to the quantum feature map given by the ABS. Then, the quantum kernel will be represented the 15 × 15 matrix shown in Fig. 4. The dataset is randomly divided into a training set and a test set with the following train-test split: 80% for training and 20% for the test. Due to the limited size of the dataset, to ensure that the choice of training and test set does not favourably bias the accuracy of the classification, we employ cross-validation by averaging the accuracy A of the model on the test set over 100 possible random partitions of the data in training and test sets. The results obtained via this cross-validation procedure with the two experimental kernels, corresponding to qubit and qutrit states, are A = 0.90 and A = 0.80 respectively, thus achieving successful classification. We also report in the histograms in Fig. 5 b, c the performances of other 50 kernels obtained in scenarios B2 and B3 with different assignments of the post-selected modes to the adaptive operations. We report in the Supplementary Note 4 more details about the procedure by which these further kernels are obtained.
a Example of classification of the 1D dataset performed by the SVM with the two quantum experimental kernels obtained from qubit states and qutrit states. The labels yi of the dataset are shown in the colors green and gray, while the symbols ‘o’ and ‘x’ indicate the training and test set, respectively. The background color represents the result of the classification. b–c Histograms of the average accuracy for classification with kernels collected in the experiment by choosing different assignments of the post-selected modes to the adaptive operation. For each kernel, the accuracy is averaged over 100 random partitions of data into training and test sets. In b results for qubits' kernels and in c the qutrits case. d–e Classification of a 2D dataset done with a preliminary clustering algorithm (K-means) followed by the application of a SVM with the two quantum experimental kernels obtained from d qubit states and e qutrit states. The correct label yi of the dataset is shown with the color (green/gray) of the symbols (‘o’: training set, ‘x’: test set). The background color represents the result of the classification.
ii) 2D dataset classification. We then apply the ABS kernel matrices to classify a dataset with more data points and higher dimensionality. We consider a 2D dataset of 200 data points ri with label yi ∈ (−1, 1) generated with the make_moons() function of the scikit-learn Python library. The dataset is again not linearly separable in a 2D space (see Fig. 5d). In order to classify the dataset with the quantum kernels and the SVM, one needs to associate to each data point from the continuous space ri a discrete index xp ∈ [0, 14] so that the kernel element associated to each pair of data (ri, rj) is K(ri, rj) = K(xp(ri), xq(rj)) = K(p, q). This map can be obtained through a standard clustering algorithm, such as the K-means algorithm48. Thus, we create 15 clusters via pre-processing the data via a K-means algorithm. Then, each data point ri is associated with the corresponding cluster centroid index xp. At this stage, the dataset {r, y} is randomly divided into training set and test set according to the proportions 80% and 20% and the SVM is trained with the quantum kernels. Again, we use the experimental data collected in platforms B2 and B3, and the output accuracy A is averaged over 100 different partitions of the data in training and test sets, in a cross-validated fashion. The results obtained with the two experimental kernels corresponding to qubit and qutrit states are A = 0.65 and A = 0.90 respectively (see Fig. 5d, e), thus achieving successful classification.
Scaling up the approach
In the previous sections we have demonstrated how ABS photonic platforms can be employed in the context of quantum machine learning and, more precisely, of kernel-based methods. Let us now discuss how this approach scales when increasing the dimension of the Hilbert space, i.e. when increasing the number of modes and the number of photons.
Given that brute-force classical simulation algorithms can simulate the proof-of-concept quantum experiments performed in this work38, it is natural to investigate how the ABS approach would perform when scaled up to the quantum computational advantage regime. Note that, while we considered quantum feature maps that encode classical data into single-qubit and single-qutrit quantum states as a proof-of-concept demonstration, this is not a limitation of the ABS paradigm. Indeed, allowing for additional unmeasured modes at the output of the ABS provides a natural encoding of classical data into larger Hilbert spaces composed of exponentially higher qubits or qudits dimensions. Moreover, the ABS quantum subroutine of kernel estimation becomes BQP-complete in the regime of many adaptive measurements (see subsection “Complexity-theoretic foundations of quantum machine learning with adaptive Boson Sampling" in Methods). Concerning experimental realizations, imperfections like photon losses and partial distinguishability can undermine the complexity of the problem. Specifically, in an ABS regime with a constant number k of adaptive measurements, the impact of losses will be similar to the case of Boson sampling. We leave to future work the investigation of the possibility of using the ABS paradigm also allowing for some photon loss, that is, keeping as useful events also those when a fraction of the photons are not detected. This method follows a similar approach to the one pursued when studying the complexity of standard Boson Sampling in the presence of photon loss49. Furthermore, since ABS substantially relies on multiphoton interference effects, similarly to its standard version, one can rely on previous results known in the literature to identify the regimes in which the ABS framework remains intractable for a classical computer50,51,52,53,54,55. Hence, it can be expected that as ABS devices are scaled up to more complex instances, they will be capable of solving problems that are intractable for classical computers, as long as the kernels can be efficiently estimated in the quantum regime.
Note that in the case of output states over many modes, the tomographic method used in our experiments to characterize the output quantum states (and estimate the quantum kernel matrix element in particular) is no longer viable, but the kernel matrix can still be estimated efficiently using a different design within the same platform, increasing the depth of the linear optical computation (see Fig. 1c). Such a deeper adaptive circuit provides an estimate of the kernel as a state overlap, that is, for near pure states, mathematically equivalent to the estimates through state fidelity. The advantage of this approach is to obtain a scalable strategy for kernel estimation from single-photon counts that we foresee as essential for the applications of the ABS scheme in the quantum machine learning field. Similarly, the use of post-selection in our experiments allows for the emulation of adaptive behaviour, i.e., by selecting only the output measurements that fulfil the control photon distribution, but its probabilistic nature requires a large overhead in sample complexity. This underlines the technological necessity of genuine adaptivity for scaling up ABS devices.
Finally, our classical data encoding strategy, which involves mapping clustered classical data to measurement outcomes that are randomly sampled by the quantum scheme, can be easily generalised to larger ABS instances.
When scaling up the ABS scheme, the outcome space becomes exponentially sized, which requires binning the outcome space and assigning clustered classical data to binned (rather than single) outcomes. As a consequence, the classical data are effectively mapped to mixed states, namely an ensemble of pure output states each given by a single adaptive output, and kernel estimation can also be done efficiently for binned outcomes using the ABS scheme, when the number of bins is a polynomial in the number of input photons56. Note that while binned outcomes may lead to efficient simulation of Boson Sampling, this is only known to be the case when the number of bins is constant57. Moreover, as the number of adaptive measurements increases, one expects that simulating binned ABS becomes harder (see Supplementary Note 7). We leave for future work a more detailed investigation on the simulability criteria of binned ABS.
That being said, other data encoding strategies are available for addressing larger datasets with near-term ABS devices, such as encoding classical data into non-adaptive initial interferometer parameters (U0 in Fig. 1b)58. The combination with hybrid techniques, where classical pre-processing of the input data can be used to map it into the adaptive bit-strings as we have demonstrated in this work, could further increase the complexity of the problems an ABS platform addresses.
Another strategy for increasing the complexity and the range of applications could be the adoption of a fully quantum approach based on a variational scheme, where the data encoding strategy remains but the output part of the circuit is supplied with a parametrized linear optical circuit. As explained more in detail in Supplementary Note 8, through this procedure the classification of labeled classical data p can be performed entirely by the quantum device. We leave these challenges for future works.
Discussion
We have demonstrated experimentally a new approach to photonic quantum computations beyond Boson Sampling, where the inclusion of adaptive measurements increases the complexity of the output distribution. Indeed, ABS has two key features: a) evolution conditioned on the measurement of a subset of the evolved photons: this leads to a non-linear evolution of the remaining output photons, b) feedforward conditioned on the measurement outcomes. In our experiment we have demonstrated feature a), and emulated feature b) by performing a post-processing of the output of many linear optical instances carried out with different unitaries.
Notably, we employed an integrated photonic platform with up to eight modes combined with quantum dot sources and superconducting detectors, processing up to three single photons, to obtain a quantum kernel matrix from the output states. Such a matrix is the primer for classical optimisation routines defining the solution of data classification problems. As a proof-of-concept demonstration, we applied the quantum kernel matrix to the successful classification of non-trivial 1D and 2D datasets of points and observed in particular an improved accuracy of the quantum classification task when increasing the output Hilbert space dimension. There, the adaptivity of the evolution was emulated using post-selection, which may be improved by the use of faster phase shifters together with fiber delay lines to enable active modulation of the setup. It is worth noting that the ABS scheme has the potential to go beyond quantum kernel methods (see Supplementary Note 7), which may display a limited advantage over classical strategies59,60.
While Boson Sampling has been deeply investigated, the adaptive variant addressed in this work opens a new path toward the near-term application of current state-of-the-art photonic platforms. In particular, the inclusion of adaptive measurements in non-universal models like Boson Sampling has been proven to lead to universal quantum computing11,16. As a future investigation, an interesting direction would be to address the extension of such adaptive schemes for quantum machine learning in the Gaussian Boson Sampling framework, where recent experiments have reported large scale implementations18,20. As such, we expect ABS devices to be applicable to other optimization tasks and, given the rapid development of integrated photonics and near-deterministic single-photon sources, we foresee ABS being applied more generally to other types of large-scale problems in the near future.
Methods
Complexity-theoretic foundations of quantum machine learning with adaptive Boson Sampling
In this section, we give complexity-theoretic foundations for the classical hardness of the computational task of quantum kernel estimation performed by ABS devices, when those are scaled to larger instances.
In particular, we show that the computational subroutines performed by ABS devices are generic instances of the problem of estimating the overlap of quantum states at the output of two quantum computations up to inverse-polynomial additive precision, defined formally as follows:
Definition 1
(APPROX-QCIRCUIT-OVER). Given a description of two quantum circuits C and \({C}^{{\prime} }\) acting on n qubits with m gates and on \({n}^{{\prime} }\) qubits with \({m}^{{\prime} }\) gates, respectively, where \(m,{n}^{{\prime} },{m}^{{\prime} }\) are polynomials in n with \({n}^{{\prime} }\ge n\), and each gate acts on one or two qubits, and two numbers a, b ∈ [0, 1] with b − a > 1/poly(n), distinguish between the following two cases: the overlap \({{\rm{Tr}}}[(\vert \psi \rangle \langle \psi \vert \otimes {{\mathbb{I}}}_{{n}^{{\prime} }-n})\vert {\psi }^{{\prime} }\rangle \langle {\psi }^{{\prime} }\vert ]\) is greater than b, or smaller than a, where we have defined \(\vert \psi \rangle :=C{\vert 0\rangle }^{\otimes n}\) and \(\vert {\psi }^{{\prime} }\rangle :={C}^{{\prime} }{\vert 0\rangle }^{\otimes {n}^{{\prime} }}\).
This computational task captures the power of quantum computers:
Lemma 1
APPROX-QCIRCUIT-OVER is BQP-complete.
Proof
The following probability estimation problem is a canonical BQP-complete problem61 (actually, both problems are formally PromiseBQP-complete).
Definition 2
(APPROX-QCIRCUIT-PROB). Given a description of a quantum circuit Q acting on q qubits with poly(q) gates, where each gate acts on one or two qubits, and two numbers α, β ∈ [0, 1] with β − α > 1/poly(q), distinguish between the following two cases: measuring the first qubit of the state \(Q{\vert 0\rangle }^{\otimes q}\) yields 1 with probability ≥β or ≤α.
Now, note that APPROX-QCIRCUIT-OVER is at least as hard as APPROX-QCIRCUIT-PROB because any instance (q, Q, α, β) of the latter is an instance \((n,{n}^{{\prime} },C,{C}^{{\prime} },a,b)\) of the former with n = 1, \(C={{\mathbb{I}}}_{1}\), \({n}^{{\prime} }=q\), \({C}^{{\prime} }=Q\), and (a, b) = (α, β).
Moreover, we can use the SWAP test62, in which the output probability of the outcome 1 when comparing the states \(\vert \phi \rangle\) and \(\vert \psi \rangle\) is given by \(\frac{1}{2}-\frac{1}{2}| \langle \phi | \psi \rangle {| }^{2}\), to show that any instance \((n,{n}^{{\prime} },C,{C}^{{\prime} },a,b)\) of APPROX-QCIRCUIT-OVER can be converted efficiently to an instance (q, Q, α, β) of APPROX-QCIRCUIT-PROB with \(q=2{n}^{{\prime} }+1\), \(Q=(H\otimes {{\mathbb{I}}}_{2{n}^{{\prime} }}){{\rm{cSWAP}}}(H\otimes C\otimes {{\mathbb{I}}}_{{n}^{{\prime} }-n}\otimes {C}^{{\prime} }){\vert 0\rangle }^{\otimes (2{n}^{{\prime} }+1)}\) (where the controlled-SWAP gate swaps the qubits 1 + k and \(1+k+{n}^{{\prime} }\) for \(k=1\ldots {n}^{{\prime} }\) when the first qubit is \(\vert 1\rangle\)), and \((\alpha,\beta )=(\frac{1}{2}-\frac{1}{2}b,\frac{1}{2}-\frac{1}{2}a)\).
This shows that both problems are computationally equivalent and completes the proof.□
The computational power of ABS interferometers over m modes, in the regime of poly(m) adaptive measurements, is given by the computational power of linear optical computations using single-photon states and vacuum states in input, together with photon-number measurements and feed-forward, which in turn is captured by the complexity class BosonPadap16. Crucially, the Knill–Laflamme–Milburn scheme for universal quantum computing based on dual-rail encoding shows that BosonPadap = BQP11,16, i.e., any quantum circuit acting on q qubits may be simulated by an ABS interferometer over m = poly(q) modes, with n = poly(q) input single photons and k = poly(q) adaptive measurements. With Lemma 1, this implies that quantum kernel estimation based on ABS interferometers is a BQP-complete problem. In other words, quantum kernel estimation using ABS is hard for classical computers unless BQP = BPP.
While this makes the existence of an efficient classical algorithm for ABS quantum kernel estimation unlikely, we emphasize that it does not rule out that the learning task solved using quantum kernel estimation might be efficiently solved by another classical algorithm bypassing the need for kernel estimation.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
The custom codes for this study that support the findings are available from the corresponding authors upon request.
References
Flamini, F., Spagnolo, N. & Sciarrino, F. Photonic quantum information processing: a review. Rep. Prog. Phys. 82, 016001 (2018).
Volz, J., Scheucher, M., Junge, C. & Rauschenbeutel, A. Nonlinear π phase shift for single fibre-guided photons interacting with a single resonator-enhanced atom. Nat. Photonics 8, 965–970 (2014).
Feizpour, A., Hallaji, M., Dmochowski, G. & Steinberg, A. M. Observation of the nonlinear phase shift due to single post-selected photons. Nat. Phys. 11, 905–909 (2015).
Tiarks, D., Schmidt, S., Rempe, G. & Dürr, S. Optical π phase shift created with a single-photon pulse. Sci. Adv. 2, e1600036 (2016).
Hacker, B., Welte, S., Rempe, G. & Ritter, S. A photon-photon quantum gate based on a single atom in an optical resonator. Nature 536, 193–196 (2016).
Stolz, T. et al. Quantum-logic gate between two optical photons with an average efficiency above 40%. Phys. Rev. X 12, 021035 (2022).
Kuriakose, T. et al. Few-photon all-optical phase rotation in a quantum-well micropillar cavity. Nat. Photonics 16, 566–569 (2022).
De Santis, L. et al. A solid-state single-photon filter. Nat. Nanotechnol. 12, 663–667 (2017).
Staunstrup, M. J. R. et al. Direct observation of a few-photon phase shift induced by a single quantum emitter in a waveguide. Nat. Commun. 15, 7583 (2024).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, 2010).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Chang, D. E., Vuletić, V. & Lukin, M. D. Quantum nonlinear optics - photon by photon. Nat. Photonics 8, 685–694 (2014).
Dutt, A., Mohanty, A., Gaeta, A. L. & Lipson, M. Nonlinear and quantum photonics using integrated optical materials. Nat. Rev. Mater. 9, 321–346 (2024).
Briegel, H. J., Browne, D. E., Dür, W., Raussendorf, R. & den Nest, M. V. Measurement-based quantum computation. Nat. Phys. 5, 19–26 (2009).
Bartolucci, S. et al. Fusion-based quantum computation. Nat. Commun. 14, 912 (2023).
Aaronson, S. & Arkhipov, A. The computational complexity of linear optics, in Proceedings of the 43rd annual ACM symposium on Theory of Computing, edited by ACM, Press pp. 333–342. https://doi.org/10.1145/1993636.1993682 (2011).
Hamilton, C. S. et al. Gaussian boson sampling. Phys. Rev. Lett. 119, 170501 (2017).
Zhong, H. S. et al. Quantum computational advantage using photons. Science 370, 1460–1463 (2020).
Zhong, H. S. et al. Phase-programmable gaussian boson sampling using stimulated squeezed light. Phys. Rev. Lett. 127, 180502 (2021).
Madsen, L. S. et al. Quantum computational advantage with a programmable photonic processor. Nature 606, 75–81 (2022).
Martínez-Cifuentes, J., Fonseca-Romero, K. M. & Quesada, N. Classical models may be a better explanation of the Jiuzhang 1.0 Gaussian Boson Sampler than its targeted squeezed light model. Quantum 7, 1076 (2023).
Oh, C., Liu, M., Alexeev, Y., Fefferman, B. & Jiang, L. Tensor network algorithm for simulating experimental gaussian boson sampling, http://arxiv.org/abs/2306.03709 [quant-ph] (2023).
Stanev, D., Giordani, T., Spagnolo, N. & Sciarrino, F. Testing of on-cloud gaussian boson sampler “borealis” via graph theory, http://arxiv.org/abs/2306.12120 [quant-ph] (2023).
Arrazola, J. M. & Bromley, T. R. Using gaussian boson sampling to find dense subgraphs. Phys. Rev. Lett. 121, 030503 (2018).
Schuld, M., Brádler, K., Israel, R., Su, D. & Gupt, B. Measuring the similarity of graphs with a gaussian boson sampler. Phys. Rev. A 101, 032314 (2020).
Banchi, L., Fingerhuth, M., Babej, T., Ing, C. & Arrazola, J. M. Molecular docking with gaussian boson sampling. Sci. Adv. 6, eaax1950 (2020).
Jahangiri, S., Arrazola, J. M., Quesada, N. & Killoran, N. Point processes with gaussian boson sampling. Phys. Rev. E 101, 022134 (2020).
Spagnolo, N., Brod, D. J., Galvao, E. F. & Sciarrino, F. Non-linear boson sampling. npj Quantum Inf. 9, 3 (2023).
Nokkala, J. et al. Gaussian states of continuous-variable quantum systems provide universal and versatile reservoir computing. Commun. Phys. 4, 53 (2021).
Innocenti, L. et al. Potential and limitations of quantum extreme learning machines. Commun. Phys. 6, 118 (2023).
García-Beni, J., Giorgi, G.L., Soriano, M. C. & Zambrini, R. Scalable photonic platform for real-time quantum reservoir computing. Phys. Rev. Appl. 20, 014051 (2023).
Spagnolo, M. et al. Experimental photonic quantum memristor. Nat. Photo 16, 318–323 (2022).
Suprano, A. et al. Experimental property reconstruction in a photonic quantum extreme learning machine. Phys. Rev. Lett. 132, 160802 (2024).
Steinbrecher, G. R., Olson, J. P., Englund, D. & Carolan, J. Deterministic optimal quantum cloning via a quantum-optical neural network. npj Quantum Inf. 5, 60 (2019).
Ewaniuk, J., Carolan, J., Shastri, B. J. & Rotenberg, N. Realistic quantum photonic neural networks. Adv. Quantum Technol. 6, 2200125 (2023).
Stanev, D., Spagnolo, N. & Sciarrino, F. Deterministic optimal quantum cloning via a quantum-optical neural network. Phys. Rev. Res. 5, 013139 (2023).
Wright, L. G. & McMahon, P. L. The capacity of quantum neural networks, in Conference on Lasers and Electro-Optics. p. JM4G.5. https://opg.optica.org/abstract.cfm?URI=CLEO_SI-2020-JM4G.5 (Optica Publishing Group, 2020).
Chabaud, U., Markham, D. & Sohbi, A. Quantum machine learning with adaptive linear optics. Quantum 5, 496 (2021).
Osellame, R., Cerullo, G. & Ramponi, R. Femtosecond laser micromachining: photonic and microfluidic devices in transparent materials, Vol. 123. https://doi.org/10.1007/978-3-642-23366-1 (Springer, 2012).
Corrielli, G., Crespi, A. & Osellame, R. Femtosecond laser micromachining for integrated quantum photonics. Nanophotonics 10, 3789–3812 (2021).
Wang, J., Sciarrino, F., Laing, A. & Thompson, M. G. Integrated photonic quantum technologies. Nat. Photonics 14, 273–284 (2020).
Gattass, R. R. & Mazur, E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2, 219–225 (2008).
Clements, W. R., Humphreys, P. C., Metcalf, B. J., Kolthammer, W. S. & Walmsley, I. A. Optimal design for universal multiport interferometers. Optica 3, 1460–1465 (2016).
Ollivier, H. et al. Hong-ou-mandel interference with imperfect single photon sources. Phys. Rev. Lett. 126, 063602 (2021).
Pont, M. et al. Quantifying n-photon indistinguishability with a cyclic integrated interferometer. Phys. Rev. X 12, 031033 (2022).
Valeri, M. et al. Generation and characterization of polarization-entangled states using quantum dot single-photon sources. Quantum Sci. Technol. 9, 025002 (2024).
Yang, J. et al. Parameter selection of gaussian kernel svm based on local density of training set. Inverse Probl. Sci. Eng. 29, 536–548 (2021).
MacQueen, J. Some methods for classification and analysis of multivariate observations, in Proceedings of the fifth Berkeley symposium on mathematical statistics and probability, Vol. 1 pp. 281–297 (Oakland, CA, USA, 1967).
Aaronson, S. & Brod, D. J. Bosonsampling with lost photons. Phys. Rev. A 93, 012335 (2016).
Oszmaniec, M. & Brod, D. J. Classical simulation of photonic linear optics with lost particles. N. J. Phys. 20, 092002 (2018).
García-Patrón, Raúl, Renema, J. J. & Shchesnovich, V. Simulating boson sampling in lossy architectures. Quantum 3, 169 (2019).
Oh, C., Noh, K., Fefferman, B. & Jiang, L. Classical simulation of lossy boson sampling using matrix product operators. Phys. Rev. A 104, 022407 (2021).
Oh, C., Lim, Y., Fefferman, B. & Jiang, L. Classical simulation of boson sampling based on graph structure. Phys. Rev. Lett. 128, 190501 (2022).
Oh, C., Jiang, L. & Fefferman, B. On classical simulation algorithms for noisy boson sampling http://arxiv.org/abs/2301.11532 [quant-ph] (2023).
Leverrier, A. & Garcia-Patron, R. Analysis of circuit imperfections in bosonsampling. Quantum Inf. Comput. 15, 489–512 (2015).
Chabaud, U. et al. Photonic quantum kernel methods beyond Boson Sampling, in preparation.
Seron, B., Novo, L., Arkhipov, A. & Cerf, N. J. Efficient validation of boson sampling from binned photon-number distributions. Quantum 8, 1479 (2024).
Gan, B. Y., Leykam, D. & Angelakis, D. G. Fock state-enhanced expressivity of quantum machine learning models. EPJ Quantum Technol. 9, 16 (2022).
Huang, H. Y. et al. Power of data in quantum machine learning. Nat. Commun. 12, 2631 (2021).
Jerbi, S. et al. Quantum machine learning beyond kernel methods. Nat. Commun. 14, 1–8 (2023).
Zhang, S. Bqp-complete problems. In Handbook of Natural Computing, (eds Rozenberg, G., Bäck, T. & Kok, J. N.) pp. 1545–1571 https://doi.org/10.1007/978-3-540-92910-9_46 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2012).
Buhrman, H., Cleve, R., Watrous, J. & De Wolf, R. Quantum fingerprinting. Phys. Rev. Lett. 87, 167902 (2001).
Acknowledgements
This work is supported by the ERC Advanced Grant QU-BOSS (QUantum advantage via non-linear BOSon Sampling, Grant Agreement No. 884676), the PNRR MUR project PE0000023-NQSTI (Spoke 4 and Spoke 7) and the European Union’s Horizon Europe research and innovation program under EPIQUE Project (Grant Agreement No. 101135288). U.C. thanks P.E. Emeriau, A. Sohbi, E. Kashefi and D. Markham for interesting discussions. Fabrication of the femtosecond laser-written integrated circuits was partially performed at PoliFAB, the micro and nano-fabrication facility of Politecnico di Milano (https://www.polifab.polimi.it). M.G., F.C. and R.O. wish to thank the PoliFAB staff for the valuable technical support.
Author information
Authors and Affiliations
Contributions
F.H., E.C., G.R., T.F., A.S., T.G., G.Ca., N.S., S.K., M.P., C.L., F.C., M.D., U.C., and F.S. developed the theoretical framework and conceived the experimental scheme. R.A., N.D.G., M.G., F.C., G.Co., and R.O. fabricated the photonic chip and characterized the integrated devices using classical optics. F.H., E.C., G.R., T.F., A.S., T.G., G.Ca., N.S. and F.S. carried out the quantum experiments and performed the data analysis. All the authors discussed the results and contributed to the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Hoch, F., Caruccio, E., Rodari, G. et al. Quantum machine learning with Adaptive Boson Sampling via post-selection. Nat Commun 16, 902 (2025). https://doi.org/10.1038/s41467-025-55877-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-55877-z
This article is cited by
-
Experimental quantum-enhanced kernel-based machine learning on a photonic processor
Nature Photonics (2025)