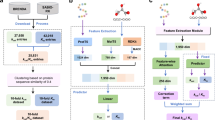
Abstract
The pursuit of obtaining enzymes with high activity and stability remains a grail in enzyme evolution due to the stability-activity trade-off. Here, we develop an isothermal compressibility-assisted dynamic squeezing index perturbation engineering (iCASE) strategy to construct hierarchical modular networks for enzymes of varying complexity. Molecular mechanism analysis elucidates that the peak of adaptive evolution is reached through a structural response mechanism among variants. Furthermore, this dynamic response predictive model using structure-based supervised machine learning is established to predict enzyme function and fitness, demonstrating robust performance across different datasets and reliable prediction for epistasis. The universality of the iCASE strategy is validated by four sorts of enzymes with different structures and catalytic types. This machine learning-based iCASE strategy provides guidance for future research on the fitness evolution of enzymes.
Similar content being viewed by others
Introduction
Enzymes are frequently applied in the food, textile, papermaking, medicine, energy, and chemical industries to promote the production of high-value products1. However, natural enzymes often cannot meet the requirements of industrial production due to poor stability and low activity under complex processing conditions. Designing more effective enzymes can help address severe risks to human populations, such as energy shortages, environmental degradation, and food shortages. In addition, the stability and activity trade-off frequently arises during the process of enzyme evolution. To date, research on industrial enzyme stability based on rational design has mainly focused on various factors that influence interactions of amino acids, such as hydrophobic interactions, hydrogen bonds, salt bridges, protein surface charges, disulfide bonds, and metal ions1,2,3. Improving and controlling the level of enzymatic activity is the overarching goal of enzyme engineering research, typically achieved through strategies such as introducing mutations at the active site and optimizing them for the target substrate4. Other methods, such as channel engineering, modification of dynamic properties, editing recognition elements (such as loops), and targeting allosteric sites, have also proven successful5,6,7. In previous studies, researchers have concentrated on static local interactions3,4,5,6,7. However, general methods for identifying key regulatory residues outside the active site are not yet perfect. Owing to the multifaceted and intricate nature of enzymes, there are no unified rules to guide strategies for improving the stability and activity of industrial enzymes of varying degrees of complexity and catalytic mechanism. Moreover, the effective binding between enzymes and polymeric substrates is a complex and unpredictable process, which presents challenges for identifying mutations that enhance activity and stability, such as the binding mode of polyethylene terephthalate (PET) hydrolase and PET polymers. It is beneficial to identify the substrate binding mode to improve stability and activity. Additionally, balancing the trade-off between stability and activity presents an additional challenge.
The extraordinary proficiency exhibited by enzymes is ascribed to the intricate network of amino acid interactions, harmonizing communication among diverse regions of the protein to realize its functional potential. A profound comprehension of the intricate interrelations between enzyme sequence, structure, dynamics, and function holds the promise of substantially amplifying the catalytic capabilities of enzymes8. Industrial enzymes undergo functional evolution dictated not merely by dominant structures but predominantly by the dynamics of the enzymes. Dynamics, as a key regulatory parameter, play an important role in forming functions or adapting to environments. Nevertheless, investigations into the evolutionary trajectories of enzyme performance have predominantly focused on a limited number of protein families and individual enzymes2,3,9,10. A conspicuous lacuna persists in the formulation of universally applicable strategies efficaciously augmenting the performance of enzymes across varying structural complexities and types.
The fitness landscape provides a perspective on the molecular underpinnings of laboratory evolution. Intricate intramolecular interactions between amino acids, reconfigured by evolution, lead to non-additive effects on protein fitness known as epistasis11,12. Epistasis includes sign epistasis and amplitude epistasis13. Sign epistasis refers to the scenario where a mutation exhibits contrasting effects when present in isolation versus in conjunction with other mutations. Conversely, magnitude epistasis denotes a mutation’s consistent effects whether occurring in isolation or in combination with other mutations13,14. Positive epistasis occurs when the combined effect of mutations is more beneficial than their individual effects, driving the evolutionary trajectory of the protein. In contrast, negative epistasis arises from antagonistic mutations that detrimentally affect protein fitness. Moreover, epistasis is delineated into short-range and long-range mutation effects. While interactions in short-range epistasis are intuitively evident in structure, elucidating the mechanisms governing supra-additive effects between amino acids positioned at spatially distant locations requires further refinement. Therefore, investigating how amino acid interactions based on conformational dynamics influence protein epistasis holds paramount significance.
Machine learning (ML) depends on the examination and learning patterns within datasets to modify the model parameters, enabling the prediction of samples. It is increasingly utilized in computer-assisted protein research. Models predicting protein fitness evolution can be mainly divided into sequence-based prediction models and structure-based prediction models15. Most ML-based protein fitness prediction models are supervised, using numerical representations of protein sequences as features and the corresponding observed fitness as labels, such as eUniRep, ECNet, and Mutcompute16,17,18,19. There are also unsupervised inferring probabilistic models using multiple sequence alignments like Potts-Models. Most sequence-based models are built using linear equations or learning algorithms, which limit the potential to predict nonlinear effects. In contrast, nonlinear models can account for higher-order genetic interaction effects. Therefore, models like EVmutation20, which considers residue pair interactions based on Potts-Models, and DeepSequence VAE21, which considers interactions among all residues, have been developed. Unsupervised prediction models cannot utilize evolutionary data from tested variants available during directed evolution, which may limit their accuracy in guiding protein engineering.
In this study, we use layered modularization to modify enzymes of varying complexity and construct hierarchical modular networks for secondary structures, supersecondary structures, and domains, respectively. We develop a multi-dimensional conformational dynamics mediated isothermal compressibility-assisted dynamic squeezing index perturbation engineering (iCASE) strategy to guide the rapid evolution of enzymes (Fig. 1). To validate the applicability of this strategy to enzymes of varying structural complexities, we employ the monomeric enzyme protein-glutaminase (PG), xylanase (XY) with a typical super-secondary TIM barrel (β/α)8 structure, and hexamer glutamate decarboxylase (GADA) as models for our study. Additionally, a dynamic response predictive model using structure-based supervised ML is established to forecast the function and fitness of other enzymes. Finally, we select MTGase (transferase, α + β), laccase (oxidoreductase, all β), and PET hydrolase PES-H1 (hydrolase, α/β) to further validate the generality of the iCASE strategy, and the stability and activity are synergistically improved. These design principles can inform the development of industrially robust biocatalysts for various enzymes.
There is a negative correlation between the isothermal compressibility (βT) and melting temperature (Tm). The dynamic squeezing index (DSI) is positively correlated with activity. The mutations obtained by using this strategy can quickly reach the peak of the fitness landscape. Finally, Dynamic response predictive models based on machine learning for protein function and fitness were built, verified, and evaluated.
Results
Enzyme modification with varying complexity by the iCASE strategy
The iCASE strategy is a combination of stability and activity modification strategy for the selection of globally optimal mutants. For simple-structured enzymes, we employed a secondary structure-based iCASE strategy for enzyme engineering, using PG to validate the results. PG (EC 3.5.1.44) is a monomeric enzyme that specifically converts glutamine residues of proteins or peptides into glutamate and releases ammonia22. Initially, the hot fluctuation regions α1 (amino acids 8–19), loop2 (amino acids 20–41), α2 (amino acids 42–55), and loop6 (amino acids 102–113) were selected based on the fluctuations in isothermal compressibility (βT) (Fig. 2a). The results of molecular docking showed that S35, S72, and S108 formed hydrogen bonds with the ligand. The loop2 and loop6 were flexible regions near the active site, which might have been beneficial for activity modification (Supplementary Fig. 1a). Subsequently, we proceeded to refine the selection criteria of mutation sites within high-fluctuation regions. By combining modifications to the activity, we developed an indicator dynamic squeezing index (DSI) coupled with the active center to improve the activity of enzymes with varying degrees of complexity. The residue with a DSI > 0.8 was selected as a candidate, representing 20% of the residues with the highest score (Fig. 2b). Moreover, changes in free energy upon mutations (ΔΔG) were predicted using Rosetta 3.13 (Supplementary Table 1). Lastly, 11 mutants (G41I, R45K, A46K, H47F, H47L, M49E, M49L, M49Y, S105E, L106E, and L106W) were screened for use in wet experiments.
a The βTs of PG, XY, and GADA under different pressures. b The DSI values of residues of PG. The color-coded DSI mapped onto the 3D structure was displayed in the top right. The specific activity (c) and melting temperature (d) of the wild-type PG and mutants. Reactions were performed in triplicate; Data were presented as mean values ± SD. Data were analyzed by ANOVA and t-test, using the two-tail test. *p < 0.05, **p < 0.01, and ***p < 0.001. The p values of G41I, R45K, H47L, M49E, M49L, L106E, K48R/M49L, K48R/M49E, H47L/K48R, K48E/M49L, K48E/M49E, H47L/K48E, M49E/S81E, and M49L/S81E were 8.82 × 10−1, 2.30 × 10−1, 6.08 × 10−6, 8.75 × 10−5, 1.32 × 10−5, 6.80 × 10−3, 3.32 × 10−2, 5.95 × 10−5, 4.73 × 10−2, 3.80 × 10−5, 1.63 × 10−4, 7.12 × 10−3, 2.73 × 10−3, and 4.88 × 10−1 in (c), respectively. The p values of G41I, R45K, H47L, M49E, M49L, L106E, K48R/M49L, K48R/M49E, H47L/K48R, K48E/M49L, K48E/M49E, H47L/K48E, M49E/S81E, and M49L/S81E were 1.66 × 10−7, 2.92 × 10−6, 2.55 × 10−4, 1.06 × 10−8, 4.34 × 10−2, 6.88 × 10−4, 1.13 × 10−6, 1.01 × 10−4, 2.80 × 10−5, 2.81 × 10−3, 3.17 × 10−5, 3.38 × 10−2, 1.68 × 10−2, and 7.36 × 10−8 in (d), respectively. e The shortest path analysis of the wild type XY and mutant R77F/E145M/T284R. f The shortest path analysis of the wild-type GADA and mutant D40E/N47F/H167F. Source data are provided as a Source Data file.
As shown in Fig. 2c, d, and Supplementary Data 1, the single-point mutants H47L, M49E, and M49L showed 1.42-fold, 1.29-fold, and 1.82-fold improvements in specific activity, respectively, with slightly increased thermal stability compared to the wild type. The mutants H47L, M49E, and M49L were then combined with the previously identified positive mutants K48E, K48R, and S81E to generate double mutants23. Compared to the wild type, the best double-point mutation K48R/M49E exhibited a 1.74-fold increase in specific activity and nearly unchanged stability, one of the highest comprehensive performances. Other double-point mutations (such as K48E/M49L, K48E/M49E, and M49E/S81E) had different degrees of improvement in the specific activity. The multiple-sequence alignment analysis showed that the mutant sites K48R and M49E were not conserved (Supplementary Fig. 2a). This strategy can quickly screen the minimum mutation set to obtain high stability and activity mutants.
To explore the performance of the iCASE strategy on higher-structure enzymes, we used the supersecondary-structure-based iCASE strategy for enzyme engineering, with XY as the object of investigation. The alkaline-resistant XY (EC 3.2.1.8) from Bacillus halodurans S7 presents a classical TIM barrel (β/α)8 and catalyzes the degradation of the xylan into xylo-oligosaccharides24,25,26. The βTs of secondary structures of the TIM barrel were calculated and high-fluctuation regions were identified as loop3 (amino acids 75-83), α2b (amino acids 84–96), α3c (amino acids 130–155), loop18 (amino acids 278–289), α7a (amino acids 290–293), and α7b (amino acids 295–318) (Fig. 2a). As shown in Supplementary Fig. 1b, loop3 and loop18 were flexible loops close to the substrate. Subsequently, 13 single-point mutants were selected as ultimate variants using DSI and Rosetta free energy calculations (Supplementary Fig. 3a and Supplementary Table 1). The best triple-point mutant R77F/E145M/T284R exhibited a 3.39-fold increase in specific activity and an increase in Tm of 2.4 °C (Supplementary Data 1). Moreover, it could be observed that the three mutation sites (R77, E145, and T284) were not conserved by multiple sequence alignment (Supplementary Fig. 2b).
Given that the XY in this study is tolerant to salt and alkali, we further investigated the effects of pH and salt on enzyme stability and activity. The optimal pH for both wild type and R77F/E145M/T284R was 9.0 (Supplementary Table 2). The wild type was rapidly inactivated, with a half-life of only 6.62 min, whereas the R77F/E145M/T284R exhibited a significantly extended half-life of 5 h (Supplementary Fig. 4). The radius of gyration (Rg) of R77F/E145M/T284R was lower than that of the wild type at pH 9.0, indicating that R77F/E145M/T284R had a more compact structure. Additionally, the catalytic efficiency of R77F/E145M/T284R was significantly improved, being 1.41 times that of the wild type (Supplementary Table 3). The binding affinity between R77F/E145M/T284R and the substrate was improved under high temperature and alkaline conditions, thus improving the catalytic efficiency. The substitution of the negatively charged Glu at position 145 with Met at pH 9.0 reduced electrostatic repulsion, decreased electrostatic energy, and increased van der Waals interactions, thereby enhancing enzyme stability (Supplementary Fig. 4). The substitution of hydrophobic amino acids for charged residues accelerated the folding process of the enzyme27. The stability and catalytic efficiency of R77F/E145M/T284R were superior to that of the wild type under different salt concentration conditions. The constant-pH MD simulations results revealed that the electrostatic energy and solvent accessible surface area (SASA) of R77F/E145M/T284R was lower than that of the wild type (Supplementary Fig. 4), indicating that the mutations optimized protein electrostatic interactions, thereby improving protein stability28,29,30,31,32,33. The salt ion interactions were explored with the wild type and R77F/E145M/T284R using MD simulations. Na+ cations were mainly concentrated on the enzyme surface and affected the stability and catalytic efficiency of the enzyme. According to the MD simulations results of XYWT and R77F/E145M/T284R, the decrease in electrostatic repulsion and electrostatic energy of R77F/E145M/T284R led to a decrease in SASA. Given the significant positive correlation between ΔCp and SASA34, the decrease in ΔCp (−77.91 J/(°C g)) resulted in enhanced stability of R77F/E145M/T284R27,34,35.
To further explore the performance of the iCASE strategy in more complex polymerase enzymes, we employed the hexamer GADA (EC 4.1.1.15) from E. coli as the research object, with the dimer serving as the functional unit36. GADA catalyzes the decarboxylation of l-glutamate to yield γ-aminobutyric acid (GABA) and releases CO237. To investigate the interface interactions, we selected the interface contacts in dimers as follows: loop1 (amino acids 27–38), loop2 (amino acids 54–57), loop3 (amino acids 65–70), loop4 (amino acids 298–301), loop5 (amino acids 315–319), α2 (amino acids 39–53), α3 (amino acids 70–78), α4 (amino acids 91–107), α5 (amino acids 126–146), α6 (amino acids 165–172), α9 (amino acids 322–334), and α10 (amino acids 335–346). As shown in Fig. 2a, the screened high-fluctuation regions on the interface of GAD were α2, α9, α6, and α3, respectively. The α6 was a crucial region near the substrate binding site (Supplementary Fig. 1c). Combined with DSI screening and Rosetta free energy calculations of the high-fluctuation regions, 16 mutants were obtained for experimental verification (Supplementary Table 1). The results implied that the specific activity of five mutants (D40E, A42M, A42W, N47F, and H167F) significantly increased, with the D40E mutant showing the highest increase of up to 89.37% (Supplementary Data 1). The mutant A42W implied the highest Tm of 49.8 °C, which was 7.8 °C higher than that of the wild type. Ultimately, five promising mutants (D40E, A42M, A42W, N47F, and H167F) were selected for combination mutagenesis to further improve the GADA performance.
The best mutation D40E/N47F/H167F showed a 2.34-fold increase in the specific activity and a Tm increase of 2.0 °C compared with the wild type. The positive mutation rates of mutants based on multiple structural domain modifications were 71%. Within the three mutation sites analyzed, it was observed that sites 40 and 47 were not conserved while site 167 was conserved (Supplementary Fig. 2c). The successful modification for such higher-order mutations underscores the potential of our approach. Moreover, the stability and anti-aggregation of PG, XY, and GADA were evaluated under industrial conditions, respectively. The results indicated that the stability and anti-aggregation of the high-performance mutants obtained through the iCASE strategy have improved compared to the wild type, demonstrating that the iCASE strategy helps enhance enzyme stability under industrial conditions (Supplementary Figs. 4 and 5).
Fitness landscape analysis based on conformational dynamics
To elucidate the conformational dynamics mechanism underlying the increased thermal stability and activity of the mutants, we analyzed the characteristics of structural changes using MD simulations. The root mean square deviation (RMSD), Rg, and root mean square fluctuation (RMSF) of mutants K48R/M49E, R77F/E145M/T284R, and D40E/N47F/H167F were lower than those of the wild type, indicating that the introduced mutations lead to a tighter protein packing, which may contribute to the stability of the transition state (Supplementary Figs. 6 and 7). A similar trend was observed in the dynamic cross-correlation map (DCCM) analysis. Compared to the wild-type PG, the substitution of Arg and Glu residues in mutant K48R/M49E increased the positively correlated residue movements, which exhibited a positive effect on enzyme stability (Supplementary Fig. 8a, b). The increase in dynamic correlation strength indicated a stronger residue interaction network. In the mutant R77F/E145M/T284R, a more positive dynamics correlation between residues was observed in the super-secondary structure region (Supplementary Fig. 8c, d). According to the interface contact regions in the DCCM, there were more positive correlations between residue movements in the mutant D40E/N47F/H167F, indicating increased stabilization of the mutant (Supplementary Fig. 8e, f). The impact of mutations based on the iCASE strategy on correlation was largely orthogonal, suggesting that this orthogonal dynamic relationship may be crucial not only for the higher-order epistasis of PG, XY, and GADA but also for the evolution of other natural enzymes and designed enzymes.
The principal component analysis (PCA) results indicated that the first 20 principal components (PCs) in the wild type PG and K48R/M49E accounted for 59.7% and 66.9% of the total contribution, respectively (Supplementary Fig. 9). Specifically, in the wild type PG, the total contribution of the first two PCs (PC1 and PC2) was 22.6%, whereas in the mutant K48R/M49E, the total contribution of the first two PCs reached 33.5%. These differences in the distribution of conformational states (represented by color-coded dots), implied that the conformation of K48R/M49E was more compact than that of the wild-type PG. Similar results were obtained in mutants R77F/E145M/T284R and D40E/N47F/H167F (Supplementary Figs. 10 and 11). As shown in Supplementary Fig. 12, the mutant K48R/M49E, R77F/E145M/T284R, and D40E/N47F/H167F displayed a narrower conformational space than their corresponding wild types. These results agree with the experimental data.
Additionally, the substrate formed three hydrogen bonds with the wild type PG, while two additional hydrogen bonds between K48R/M49E with the substrate (Supplementary Fig. 13). The distance between the hydrogen bond formed between the substrate and S108 of K48R/M49E was reduced, suggesting that the mutation had a stronger binding affinity for the substrate, leading to an increase in enzyme activity. We also investigated the potential substrate entry channels within the wild-type PG and mutant K48R/M49E. The length and curvature of the substrate channel in the mutant K48R/M49E were decreased by 2.00 Å and 0.38 Å, respectively, indicating that a short and straight substrate channel facilitated the entry of substrate molecules and the release of product molecules (Supplementary Fig. 14 and Supplementary Table 4). A similar trend was observed in mutants R77F/E145M/T284R and D40E/N47F/H167F. These are consistent with the experimental results. These findings demonstrate the potential for the rational design of mutants with improved activity and stability, and provide insight into the structure-function relationship of this enzyme.
The shortest path map is a promising computational method to capture the influence of relevant distant residues38. The shortest path analysis of the three mutation sites in XY revealed that there was no significant difference between the wild type and the mutant, indicating that the same pathways were involved in long-range interactions within the protein molecules (Fig. 2e). However, the shortest path analysis results revealed that three mutation sites in mutant D40E/N47F/H167F in GADA exhibited a shorter path compared to the wild type, illustrating that the long-range interaction pathway responsible for the allosteric regulation of protein molecules has been shortened in the mutant. As a result, the mutant requires fewer amino acid interactions to achieve improved functional properties (Fig. 2f).
Next, we focused on understanding the evolutionary processes that generated the activity and stability of enzymes with different degrees of complexity. We constructed the evolutionary pathways based on both activity and stability, gaining insights into the diverse routes that evolution could follow (Fig. 3a–c). In the active evolutionary pathway analysis, the mutants obtained using this strategy quickly reached their peak. As shown in Fig. 3a, the K48R and M49E mutants of PG exhibited positive effects when present alone (with activities 1.54-fold and 2.29-fold that of the wild type, respectively). Cooperative activity was observed between K48R and M49E, resulting in an activity 2.74-fold greater than that of the wild type, illustrating the occurrence of magnitude epistasis. Similar results were observed for XY, including the mutants R77F/T284R, N136F/T284R, E153L/T264R, and E145M/T284R (Fig. 3b). Mutation T284R was individually beneficial in activity. When T284R was combined with the other mutants (R77F, N136F, E145M, and E153L), the overall performance of the combinatorial mutants in the activity was further improved. In addition, the PG mutants H47L/K48R, H47L/K48E, K48R/M49L, and M49L/S81E exhibited signs of epistasis, that is from being deleterious to beneficial or vice versa39. In the case of GADA, the mutant D40E/N47F/H167F was considered to have a single maximum across the entire landscape, without any alternative local maxima (Fig. 3c). This indicated a clear evolutionary path with a single optimal solution for this particular enzyme. During the process of stability evolution, intermediate local maxima were often observed in PG, XY, and GADA, possibly because of the trade-off between stability and activity, where stability is sacrificed to some extent during the evolutionary process to achieve greater enzyme activity. The enhanced positive dynamic correlation in mutant variants revealed a stronger residue interaction network. PCA of the enzyme’s conformational landscape revealed that the introduction of mutations increases the conformational freedom of protein. The synergistic interplay between dynamic interactions and conformational dynamics resulted in this non-additive interaction, accelerating enzyme evolution.
The adaptive landscape of PG mutants (a), XY mutants (b), and GADA mutants (c) for thermal stability and activity, respectively. The number at the center of each node indicates its activity or stability multiple relative to the wild type. Red circles represent mutants with enhanced activity, while blue circles denote mutants with reduced activity. Orange circles denote mutants with enhanced stability, while gray circles indicate mutants with reduced stability. The edge of the connected node represents a single mutational step. The black line exhibits a path that leads to an increase in the fitness of the previous node and is evolutionarily reachable. The light gray solid line represents a path that results in an increase in fitness, however, it is inaccessible due to the decrease in the fitness observed in the previous node. The light gray dashed line represents a path that is unreachable due to the decrease of the fitness of the previous node. The correlations between ΔβT and Tm of PG mutants (d), XY mutants (e), and GADA mutants (f), respectively. Source data are provided as a Source Data file.
We further evaluated the correlation between compressibility and stability of the mutants (Fig. 3d–f). The ΔβT showed a negative Pearson correlation with Tm, with Pearson coefficients of r = −0.52, −0.53, and −0.64 for the three enzymes, respectively, consistent with our hypothesis that decreasing the βT could improve the stability. Additionally, we analyzed the changes in the DSI values of mutants and found that mutants with increased activity exhibited larger DSI values, indicating a high coupling between the mutation sites and the activity center (Supplementary Fig. 15). This result suggested that a high level of coupling with the active sites was favorable for improving activity.
Machine learning-based dynamic response predictive model
To expand the applicability of the iCASE strategy, considering the design-build-test-learn framework, we established the supervised dynamic response predictive model to predict protein function and fitness by utilizing evolutionary data and assay-labeled data. The workflow used to build, verify, and evaluate the model is illustrated in Fig. 4a. We evaluated the model’s performance using Spearman’s ρ across ten datasets with different numbers of variants (Supplementary Table 5). These ten datasets contained data on single, double, and multiple substituted variants. We selected seven features (βT, DSI, RMSD, Rg, SASA, hydrophobicity, and charge) related to enzyme function and fitness evolution as input. Specifically, βT measures the fluctuation of protein structure, RMSD assesses parameters of protein structure change and stability, Rg indicates protein compactness, SASA, and charge influence protein-solvent interactions affecting stability and activity, hydrophobicity impacts protein folding and stability, and DSI quantifies the coupling strength between amino acid residues in protein networks and considers the impact of combinatorial mutations and epistasis on fitness. We compared three nonlinear regression models (k-nearest neighbors, support vector regression, and random forest regression) and linear regression on their performance for ten datasets. The random forest regression model consistently demonstrated superior performance across nine datasets, and thus, it has been adopted as the default method (Fig. 4b). Subsequently, the VIP values of each feature in the ten datasets were calculated, and it was found that five features contribute significantly to enzyme function and fitness evolution (Fig. 4c). Therefore, βT, DSI, RMSD, Rg, and SASA were selected as input features.
a Workflow for dynamic response predictive model building, verifying, and evaluating. b Performance of different methods for ten datasets. c The VIP values of different variables (βT, DSI, RMSD, Rg, SASA, hydrophobicity, and charge) for ten datasets. d Performance of the dynamic response predictive model based on the random forest model for ten datasets with different data sizes. e Performance of high N datasets (beta-lactamase and PABP (RRM domain) singles) for training data sizes 48, 96, 144, 192, and 240. f The interpolation results for ten datasets. g The extrapolation results of two datasets (PABP (RRM domain) and protein-glutaminase) by training on single substituted variants and predicting higher substituted variants. The training datasets of PABP (RRM domain) and protein-glutaminase were 1188 and 45, and the test datasets were 2000 and 35. Source data are provided as a Source Data file.
The dynamic response predictive model successfully captured the influences of mutations in low-throughput experiments on the stability of beta-glucosidase (ρ = 0.74, N = 21), ubiquitin (ρ = 0.90, N = 30), beta-lactamase (ρ = 0.80, N = 30), RML lipase (ρ = 0.78, N = 28), FYN (SH3 domain) (ρ = 0.79, N = 55), trypsin (ρ = 0.82, N = 23), Hepatitis C NS5A (ρ = 0.83, N = 240). Furthermore, in high-throughput experiments, the model demonstrated robust performance in predicting fitness for beta-lactamase (ρ = 0.86, N = 4998) and poly-A binding protein (PABP) (RRM domain) (ρ = 0.76, N = 1188), including double and multiple substitutions. These results indicated that this model can be utilized for designing proteins with improved stability or fitness (Fig. 4d). The model’s performance in predicting the activity of RML lipase and trypsin was 0.62 and 0.47, respectively. For high-throughput datasets, the overall model performance increases as the training dataset increases (Fig. 4e). In addition to the training dataset of 48 in beta-lactamase, this may be the selection of mutants that may favor our correlation. Furthermore, the out-of-box prediction performance was evaluated across ten datasets, with most out-of-bag (OOB) scores being above 0.4 (Supplementary Fig. 16a). Using PABP and PG to train on singly substituted variants and predict more highly substituted variants, the OOB scores were 0.60 and 0.21, respectively (Supplementary Fig. 16b). Furthermore, the interpolation performances were greater than 0.60 on most datasets (Fig. 4f).
To evaluate the ability of the model to predict the epistasis of combined mutations in low and high N datasets, we examined the model’s substitutional extrapolation ability on two datasets by training on single substituted variants and predicting higher substituted variants. The enrichment scores of PABP (Ntrain = 1188, Ntest = 2000) and the thermostability of PG variants (Ntrain = 45, Ntest = 35) were used to validate the extrapolation performances of the model. The extrapolation performances of PABP and PG were 0.72 and 0.60, respectively (Fig. 4g). The extrapolation performances of PABP showed no significant change with the increase of the training dataset (Supplementary Fig. 16c). The results indicated that the model exhibited a robust ability to capture epistasis for both low and high N datasets. Extrapolation performance also depends on the degree to which epistasis contributes to the fitness landscape40. The prediction results for PG may be influenced by the presence of more diverse effects (both deleterious and beneficial) or non-additive effects in multi-site combinatorial mutations.
Validation of the iCASE strategy transferability
Furthermore, we applied the iCASE strategy to different types of enzymes, selecting transferases, oxidoreductase, and hydrolases for validation. We selected microbial transglutaminase (MTGase, α + β), laccase (all β), and PET hydrolase (PES-H1, α/β) from different SCOP structural classifications as our study subjects. Firstly, highly active and stable mutants of microbial transglutaminase (MTGase, EC 2.3.2.13) were constructed. Seven potential mutants A212P, R215L, D221T, A216I, S246H, V252L, and S303P were selected according to the iCASE strategy (Supplementary Fig. 17a–c). The Tm values of mutants S246H, A212P, D221T, and R215L increased by 1.5 °C, 1.4 °C, 0.9 °C, and 0.5 °C, respectively (Supplementary Fig. 17d). The specific enzyme activities of all seven mutants were improved, with R215L exhibiting a 3.48-fold increase compared to the wild type, which was one of the mutants with the best comprehensive performance (Supplementary Fig. 17e). A representative oxidoreductase, laccase (EC 1.10.3.2) derived from Bacillus subtilis is an all-β type protein. Six mutants were obtained by using the iCASE strategy. The Tm values of mutants H86W, S91T, G321P, G323N, and G324H increased by 1.3 °C, 4.1 °C, 5.1 °C, 2.6 °C, and 1.8 °C, respectively (Supplementary Fig. 18a). The specific activities of H86W, S91T, G321P, and G324H were 1.52, 1.08, 1.18, 3.36, and 1.33 times that of the wild type, respectively (Supplementary Fig. 18b).
Furthermore, we also selected a canonical PET hydrolase (PES-H1, EC 3.1.1.101) with a canonical α/β-hydrolase fold for verification41. The iCASE strategy is used to identify the high fluctuation regions α3 (94–110, interface contact region), α6 (184–192), and loop5 (60–65) (Fig. 5a). Moreover, we conducted the molecular docking of the wild type in complex with the substrate 3PET (three repeating PET units). As shown in Fig. 5b, two hydrogen bonds were formed between the substrate and G65 and S130 in the wild type. Hydrophobic interactions were formed between the substrate and residues I178 and L209. Additionally, H129 and H208 formed salt bridges with the substrate in the wild type. The loop5 is the critical flexible region of PES-H1 that interacts with 3PET. Subsequently, the DSI and free energy on these regions were calculated (Fig. 5c). Combined with the results of the prediction model, 9 single-point mutants were selected for wet experimental verification.
a The βTs of PES-H1 under different pressures (1 bar, 100 bar, 500 bar, 1000 bar, 2000 bar, and 4000 bar). n = 3 independent simulations. Error bars represent the means ± SE of βT for PES-H1 under different pressures. b Molecular docking of PES-H1 with 3PET. Hydrogen bonds were depicted by solid blue lines, hydrophobic interactions were illustrated with dashed gray lines, and salt bridges were denoted by dashed yellow lines. c The DSI values of residues of PES-H1. The specific activity (d) and melting temperature (e) of the wild-type PES-H1 and mutants. Reactions were performed in triplicate; Data were presented as mean values ± SD. Data were analyzed by ANOVA and t-test, using the two-tail test. *p < 0.05, **p < 0.01, and ***p < 0.001. The p values of T63H, A64F, S97R, R98L, G99A, Q103L, D107W, S185N, N190L, T63H/A64F, T63H/R98L, A64F/R98L, A64F/S185N, T63H/A64F/R98L, and T63H/A64F/S185N were 1.11 × 10−6, 2.20 × 10−6, 2.08 × 10−5, 1.82 × 10−5, 3.60 × 10−6, 1.16 × 10−7, 1.85 × 10−7, 1.35 × 10−5, 3.93 × 10−1, 1.62 × 10−3, 2.61 × 10−4, 2.66 × 10−3, 8.25 × 10−3, 2.75 × 10−4, and 3.61 × 10−4 in (e), respectively. f Scanning electron microscope images of the treated PET film. PET film was incubated with enzyme in 1 mL of 50 mM glycine-NaOH buffer (pH 9.0) at 70 °C for 4 h. Reactions were performed in triplicate. Source data are provided as a Source Data file.
The nine mutants all exhibited an increase in enzymatic activity, with T63H showing a particularly remarkable 11.09-fold improvement (Fig. 5d). Additionally, the stability of the mutants T63H, A64F, R98L, and S185N was enhanced, with T63H and A64F displaying a significant increase in Tm by 7.5 °C, and the Tm of T63H reaching 85.9 °C (Fig. 5e). At 70 °C, the residual activity of the positive mutants was higher than that of the wild type, indicating that the positive mutant exhibited greater stability (Supplementary Fig. 19). The stability and anti-aggregation of the wild type and T63H were assessed under industrial conditions (70 °C, pH 9.0). T63H exhibited superior stability and anti-aggregation compared to the wild type (Supplementary Fig. 20). In addition, T63H demonstrated superior performance in hydrolyzing low-crystallinity (<15%) PET films. The PET film treated with the wild type displayed a slightly rough surface, while the PET film treated with the mutant T63H exhibited a surface that was rough and porous (Fig. 5f). The weight loss of PET film treated with T63H for 12 h at 70 °C was 94%, nearly achieving complete degradation of the PET film (Supplementary Fig. 21).
To further investigate the mechanism of PET hydrolysis, we conducted molecular docking and MD simulations of wild type and T63H in complex with the substrate 3PET, respectively. T63H formed an extra hydrogen bond with the substrate compared to the wild type (Supplementary Fig. 22a–d). This result suggested that T63H had a stronger binding affinity for the substrate, leading to an increase in enzyme activity. In the wild type, hydrophobic interactions were formed between the substrate and residues I178 and L209, while in T63H, these interactions involved not only I178 and L209 but also residues N212 and T213. Additionally, H129 and H208 formed salt bridges with the substrate in both the wild type and T63H. The binding free energy of the T63H complex was −66.43 kJ/mol, which was 19.73 kJ/mol lower than that of the wild type (Supplementary Fig. 22e). The energy decomposition analysis revealed the pivotal roles played by amino acids L209, I178, W155, R91, and H129 (Supplementary Fig. 22f). These validation results indicate that the iCASE strategy has the potential to rationally design mutants with higher activity and stability, quickly screen for high-performance single-point mutants, accelerate the search for fitness evolutionary peaks, and provide insights into the structure-function relationship of enzymes.
Discussion
Given the sophisticated structures of enzymes, the computational prediction of mutations that can generate greater functions is challenging. In this study, we developed a design strategy to evolve the thermal stability and activity of enzymes with varying degrees of complexity, using the iCASE strategy based on multi-dimensional conformational dynamics. As illustrated in our previous research23,42, the differences in stability between the wild type and mutants could be elucidated by examining the evolving features of βT through computational analysis. The increase in activity can be attributed to the characteristic spectral changes in the DSI, which are closely correlated with the dynamics of the active center. Our successful implementation of a dynamics-based design methodology highlights the significance of considering protein dynamics and conformational interactions in the engineering of enzymes using this approach. This strategy systematically introduced mutations in specific regions, greatly reducing the experimental effort needed to achieve a high positive rate, and overcoming the stability and activity trade-off.
The iCASE strategy was employed to validate three enzymes with different structures and catalytic mechanisms: microbial transglutaminase (MTGase, α + β), laccase (all β), and PET hydrolase (PES-H1, α/β). It was found that high-performance single-point mutants could be rapidly screened using this strategy. In particular, the optimal single-point mutant R215L for MTGase achieved a specific activity of 109.99 U/mg, which was higher than that of the combinatorial mutant R57L/Y198F/F259W modified by cavity engineering strategy previously reported43. The iCASE strategy could be widely applied to the rational design of enzymes with different structures and types. In industrial applications involving conditions such as high temperatures, extreme pH, and high salt concentrations, the iCASE strategy was utilized to screen and mutate charged residues to optimize the surface charge of enzymes, thereby improving long-term stability (e.g., thermostability and anti-aggregation) and activity of the enzymes under industrial conditions.
By systematically analyzing the evolutionary pathways of enzymes with varying levels of complexity, we found that some feasible evolutionary paths exist in the vicinity of the local optima. However, the most probable path to globally optimal fitness is often hindered by widespread fitness valleys. The reason for this phenomenon may be the hindrance caused by competitive interactions, which obstruct the overall optimization of the system and give rise to numerous local maxima, leading to a frustrating effect44. The result showed that the experimentally determined enzyme activity landscape exhibited a degree of frustration, as individually beneficial mutants often proved mutually incompatible, resulting in a rugged fitness landscape. Additionally, it is important to note that the landscape described here was generated through constant selection for a single activity or stability and thus cannot be directly compared to evolutionary pathways leading to functions. However, the landscape may be subject to significant changes due to evolving environmental conditions or varying selection pressures45.
The dynamic response predictive model is a supervised structure-based model, covering proteins of different types and structures. Similar to ProteinMPNN46, starting from the protein structure, we calculated feature values using protein structure information, considering dynamic structure information, and verified the key feature values that affected enzyme function and fitness evolution. Among these, the DSI feature quantified the coupling strength between amino acid residues in the protein network and considered the impact of combinatorial mutations and epistasis on fitness. The model demonstrated robust performance on ten datasets with different data sizes. Further experiments on combined mutation datasets showed that the iCASE strategy could generalize from low-order mutants to high-order mutants. The dynamic response prediction model performed better than EVmutation on the datasets trypsin, FYN (SH3 domain), ubiquitin, and beta-glucosidase20. The performances of the dynamic response prediction model on the datasets beta-lactamase, ubiquitin, and hepatitis C NS5A were better than that of Augment EV mutation Potts, Augmented DeepSequence VAE, Augmented eUniRep, Augmented transformer, etc. The performance on the dataset PABP (RRM domain) was similar to that of Augment EV mutation Potts40. The model holds promise for further applications in enzyme engineering for the function and fitness evolution of other enzymes. To gain more valuable insights into proteins, it is recommended that dynamic response predictive models be integrated with other methods within high-throughput annotation platforms for omics data analysis.
Methods
Isothermal compressibility analysis
The Gibbs free energy (ΔG) between the native and unfolded varies of the protein with pressure and temperature in reversible reactions as follows:
In constant temperature, Eq. (1) has the Taylor second-order expansion as follows:
Where ΔG0 and ΔV0 stand for reference conditions, p and p0 are the pressure and standard atmospheric pressure, respectively, and βT is the isothermal compressibility47. βT is one of the vital parameters to assess protein stability.
The crystal structure of PG (PDB ID: 2ZK9), XY (PDB ID: 2UWF), GADA (PDB ID: 1XEY), MTGase (PDB ID: 3IU0), laccase (PDB ID: 1GSK), and PES-H1 (PDB ID: 7CUV) were used as the initial model, respectively. The structures of the mutants were predicted by AlphaFold248. MD simulations were performed using Amber 20 with an FF14SB force field. The system was solvated in a 15 Å cubic using TIP4PEW water box with neutralizing ions. The temperature was maintained at 310 K, and pressure was set to 1 bar, 500 bar, 1000 bar, 2000 bar, and 4000 bar, respectively. The MD simulation was run for 50 ns. Structure analysis was performed using PyMOL 3.0. RMSD, Rg, and RMSF were calculated with the cpptraj tool. DCCM, PCA, and free energy landscape (FEL) were analyzed using Bio3D49. βT was analyzed using simulation data according to Zheng et al.23,42.
Dynamic squeezing index analysis
DSI was employed to evaluate the intensity of coupling between residues within the protein network. Specifically, the DSI score between residue “i” and the active center was determined by the ratio of the volume fluctuation of residue “i” when the active center (within 5 Å around the center of mass) was perturbed to the volume fluctuation of residue “i” when all amino acids were perturbed8,50,51. It was expressed as:
Based on linear response theory8,52, MD simulations were performed using AMBER 20 to calculate volume fluctuation. The potential sites were selected with DSI > 0.8.
Construction, expression, and purification of mutants
Site-directed mutations were performed using the Fast Mutagenesis Kit. Primer sequences were summarized in Supplementary Data 2. The PG, XY, GADA, MTGase, laccase, PES-H1, and their mutants were induced in E. coli BL21 (DE3) at OD600 0.6 with 0.5 mM isopropyl β-D-thiogalactoside for 20 h at 16 °C. Following ultrasonic cell disruption, crude extracts were obtained by centrifugation at 10,000 r/min for 20 min. The enzyme was eluted with different concentrations of imidazole using an AKTA protein purification system (GE Healthcare, NJ, USA) in conjunction with a 1 mL His Trap FF nickel column.
Determination of enzyme properties
The enzymatic activity of PG was determined according to Zheng et al.23. Ten microliter of enzyme solution was transferred into 96-well plates to react with 100 μL of 10 mM Cbz–Gln–Gly for 30 min at 37 °C. Then, 100 μL of 10% trichloroacetic acid was added to terminate the reaction. Subsequently, 12 μL of reaction solution was mixed with 60 μL of chromogen solution A (40.46 g/L phenol and 0.15 g/L sodium nitroprusside), 30 μL of chromogen solution B (49.94 g/L KOH), and 60 μL of chromogen solution C (20.004 g/L K2CO3 and 83.3% (v/v) NaClO), followed by incubation for 20 min at 37 °C. The enzymatic activity was calculated from the absorbance at 630 nm determined.
XY assay was carried out using the dinitrosalicylic acid (DNS) method53. One hundred microliter of diluted enzyme solution was mixed with 700 μL of 1% corn cob xylan (pH 9.0) and allowed to react for 10 min at 70 °C. The reaction was terminated by adding 700 μL of DNS, and heating at 100 °C for 10 min. After cooling to room temperature, sample absorbance was measured at 540 nm. The enzymatic activity was calculated according to the absorbance.
GADA assay was measured by the Berthelot method54. 100 μL of enzyme solution was mixed with 1 mL 50 mM sodium glutamate and 10 mM pyridoxal-5’-phosphate (pH 4.8) and allowed to react for 30 min at 37 °C. Then, 500 μL of reaction solution was mixed with 1 mL of 200 mM sodium borate solution (pH 9.0), 1 mL of 6% phenol solution, and 1 mL of 5% sodium hypochlorite solution, then boiled for 10 min. After cooling to room temperature, the absorbance values were read at 630 nm. Finally, the enzymatic activity was calculated according to the absorbance.
The enzyme activity of MTGase was determined by referring to Zhang et al.43. Sixty microliters of the enzyme solution was added to 150 μL of the substrate solution (10 mg/mL CBZ–Gln–Gly, 7 mg/mL hydroxylamine hydrochloride, and 3 mg/mL glutathione, pH 6.0) and incubated at 50 °C for 10 min. Then, 60 μL of 12% trichloroacetic acid was added, and the absorbance was measured at 525 nm.
The activity of laccase was determined as follows: 45 μL of the enzyme solution was added to 255 μL of the ABTS solution and incubated at 60 °C for 20 min. The absorbance values were read at 420 nm.
The enzymatic activity of PET was determined according to Cui et al.55. Eighty microliters of phosphate buffer (100 mM, pH 7.5), 10 μL of para-nitrophenyl butyrate (p-NPB), and 10 μL of enzyme solution were added into an EP tube, gently mixed, and heated at 70 °C for 5 min. Subsequently, 100 μL of ethanol was added to the mixture. The activity was measured at 405 nm. Fifty micrograms of the enzyme were used to degrade the PET film (~45 mg) in 1 mL of 50 mM glycine-NaOH buffer (pH 9.0) at 70 °C for 12 h. Then the weight loss rate of the PET film was measured. The surface morphology of the PET film was identified by scanning electron microscopy using the FEI Quanta 200 (magnification, ×5000).
For thermal stability measurement, 20 μL of enzyme solution and 5 μL of SYPRO orange dye were mixed and added to the 96-well PCR plate. Afterward, the plate was subjected to gradual heating in a real-time quantitative PCR system, starting from 25 °C and increasing at a rate of 1 °C per minute until reaching 95 °C.
PROTEOSTAT protein aggregation assay was used to detect protein aggregation. The protein concentration is approximately 50 μg/mL. Ninty-eight microliter of protein and 2 μL of the diluted PROTEOSTAT detection reagent were mixed and added to the 96-well PCR plate. Incubate the microplate containing test samples in the dark for 15 min. Fluorescence was read at excitation and emission wavelengths of 550 nm and 600 nm, respectively.
Dynamic response predictive model
The random forest, support vector regression, K-nearest neighbors, and linear regression were employed to establish the dynamic response predictive models for enzyme function and fitness, respectively. Ten different-sized datasets (~8700 mutants) were used for training and testing, including beta-glucosidase56, Ubiquitin57, beta-lactamase58, Rhizomucor miehei lipase59, FYN (SH3 domain)60, Trypsin61, Hepatitis C NS5A62, beta-lactamase63, PABP (RRM domain)64, and PG23,51. Then we performed data integration, data cleaning, and feature selection to ensure the quality and relevance of the data. Features for both the wild type and mutations were generated by the simulation software AMBER 20 and GROMACS 2023.4, including βT, DSI, RMSD, Rg, SASA, hydrophobicity, and charge. These features served as input variables, while the function and fitness of the enzymes acted as the target variables. The input data was normalized to ensure that different features had similar scales. Feature selection was performed with the variable importance in projection (VIP), which was calculated based on each feature’s contribution to model performance (the decrease in Gini impurity) during node splitting in the random forest trees. In the inner loop, we utilized five-fold cross-validation for hyperparameter optimization, designating 20% of the training data as validation data. For the outer loop, we implemented five-fold cross-validation to assess the model, averaging the validation results over the randomized data splits. The code is written by Python 3.11 and is accessible through GitHub (https://github.com/zhengnan77/predictive-model)65.
Statistics
All experiments were conducted at least three times and error bars in figures denoted the standard errors. Statistical analysis was performed using a two-way analysis of variance (ANOVA) followed by a t-test.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
All data that support the findings of this study are provided in the Supplementary Information and Source Data file. The crystal structure of PG (PDB ID: 2ZK9), XY (PDB ID: 2UWF), GADA (PDB ID: 1XEY), MTGase (PDB ID: 3IU0), laccase (PDB ID: 1GSK), and PES-H1 (PDB ID: 7CUV) were used in this study. There is no restriction on data availability. Source data are provided with this paper.
Code availability
All codes for the dynamic response predictive model used in this study are available at https://github.com/zhengnan77/predictive-model65. There is no restriction on code availability.
References
Liu, Q. et al. The state-of-the-art strategies of protein engineering for enzyme stabilization. Biotechnol. Adv. 37, 530–537 (2019).
Dou, Z. et al. Data-driven strategies for the computational design of enzyme thermal stability: trends, perspectives, and prospects. Acta Biochim. Biophys. Sin. 55, 343–355 (2023).
Cui, Y. et al. Computational redesign of a PETase for plastic biodegradation under ambient condition by the GRAPE strategy. ACS Catal.11, 1340–1350 (2021).
Wu, T. et al. Reshaping substrate-binding pocket of leucine dehydrogenase for bidirectionally accessing structurally diverse substrates. ACS Catal. 13, 158–168 (2022).
Wang, Z. et al. Computational redesign of the substrate binding pocket of glutamate dehydrogenase for efficient synthesis of noncanonical l-amino acids. ACS Catal. 12, 13619–13629 (2022).
Li, P. & Hammes-Schiffer, S. Substrate-to-product conversion facilitates active site loop opening in yeast enolase: a molecular dynamics study. ACS Catal 9, 8985–8990 (2019).
Mhashal, A. R. et al. Modeling the role of a flexible loop and active site side chains in hydride transfer catalyzed by glycerol-3-phosphate dehydrogenase. ACS Catal. 10, 11253–11267 (2020).
Modi, T. et al. Hinge-shift mechanism as a protein design principle for the evolution of beta-lactamases from substrate promiscuity to specificity. Nat. Commun. 12, 1852 (2021).
Nick Pace, C. et al. Forces stabilizing proteins. FEBS Lett. 588, 2177–2184 (2014).
Pinney, M. M. et al. Parallel molecular mechanisms for enzyme temperature adaptation. Science 371, 2784 (2021).
Fröhlich, C. et al. Epistasis arises from shifting the rate-limiting step during enzyme evolution of a β-lactamase. Nat. Catal. 7, 499–509 (2024).
Buda, K. et al. Pervasive epistasis exposes intramolecular networks in adaptive enzyme evolution. Nat. Commun. 14, 8508 (2023).
Nishikawa, K. K. et al. Epistasis shapes the fitness landscape of an allosteric specificity switch. Nat. Commun. 12, 5562 (2021).
Kim, I. et al. Energy landscape reshaped by strain-specific mutations underlies epistasis in NS1 evolution of influenza A virus. Nat. Commun. 13, 5775 (2022).
Wittmund, M. et al. Learning epistasis and residue coevolution patterns: current trends and future perspectives for advancing enzyme engineering. ACS Catal. 12, 14243–14263 (2022).
Luo, Y. et al. ECNet is an evolutionary context-integrated deep learning framework for protein engineering. Nat. Commun. 12, 5743 (2021).
Shroff, R. et al. Discovery of novel gain-of-function mutations guided by structure-based deep learning. ACS Synth. Biol. 9, 2927–2935 (2020).
Lu, H. et al. Machine learning-aided engineering of hydrolases for PET depolymerization. Nature 604, 662–667 (2022).
Illig, A.-M. et al. A hybrid model combining evolutionary probability and machine learning leverages data-driven protein engineering. Preprint at https://doi.org/10.1101/2022.1106.1107.495081 (2021).
Hopf, T. A. et al. Mutation effects predicted from sequence co-variation. Nat. Biotechnol. 35, 128–135 (2017).
Riesselman, A. J. et al. Deep generative models of genetic variation capture the effects of mutations. Nat. Methods 15, 816–822 (2018).
Chen, X. et al. Protein deamidation to produce processable ingredients and engineered colloids for emerging food applications. Compr. Rev. Food Sci. Food Saf. 20, 3788–3817 (2021).
Zheng, N. et al. Protein-glutaminase engineering based on isothermal compressibility perturbation for enhanced modification of soy protein isolate. J. Agric. Food Chem. 70, 13969–13978 (2022).
Mamo, G. et al. An alkaline active xylanase: insights into mechanisms of high pH catalytic adaptation. Biochimie 91, 1187–1196 (2009).
Yagi, H. et al. Functional characterization of the GH10 and GH11 xylanases from Streptomyces olivaceoviridis E-86 provide insights into the advantage of GH11 xylanase in catalyzing biomass degradation. J. Appl. Glycosci. 66, 29–35 (2019).
Lipsh-Sokolik, R. et al. Combinatorial assembly and design of enzymes. Science 379, 195–201 (2023).
da Silva, F. B. et al. Rational design of chymotrypsin inhibitor 2 by optimizing non-native interactions. J. Chem. Inf. Model. 60, 982–988 (2020).
Strickler, S. S. et al. Protein stability and surface electrostatics: a charged relationship. Biochemistry 45, 2761–2766 (2006).
Gribenko, A. V. et al. Rational stabilization of enzymes by computational redesign of surface charge-charge interactions. Proc. Natl. Acad. Sci. USA 106, 2601–2606 (2009).
Contessoto, V. G. et al. NTL9 folding at constant pH: the importance of electrostatic interaction and pH dependence. J. Chem. Theory Comput. 12, 3270–3277 (2016).
Coronado, M. A. et al. TKSA-MC: a web server for rational mutation through the optimization of protein charge interactions. Protein Pept. Lett. 24, 358–367 (2017).
de Godoi Contessoto, V. et al. Electrostatic interaction optimization improves catalytic rates and thermotolerance on xylanases. Biophys. J. 120, 2172–2180 (2021).
Ngo, K. et al. Improving the thermostability of xylanase A from Bacillus subtilis by combining bioinformatics and electrostatic interactions optimization. J. Phys. Chem. B 125, 4359–4367 (2021).
Myers, J. K. et al. Denaturant m values and heat capacity changes: relation to changes in accessible surface areas of protein unfolding. Protein Sci. 4, 2138–2148 (1995).
Makhatadze, G. I. & Privalov, P. L. Heat capacity of proteins. I. Partial molar heat capacity of individual amino acid residues in aqueous solution: hydration effect. J. Mol. Biol. 213, 375–384 (1990).
Dutyshev, D. I. et al. Structure of Escherichia coli glutamate decarboxylase (GADalpha) in complex with glutarate at 2.05 angstroms resolution. Acta Crystallogr. D Biol. Crystallogr. 61, 230–235 (2005).
Yu, P. et al. Production of gamma-aminobutyric acid in Escherichia coli by engineering MSG pathway. Prep. Biochem. Biotechnol. 48, 906–913 (2018).
Osuna, S. The challenge of predicting distal active site mutations in computational enzyme design. WIREs Comput. Mol. Sci. 11, e1502 (2020).
Weinreich, D. M. et al. Perspective: sign epistasis and genetic costraint on evolutionary trajectories. Evolution 59, 1165–1174 (2005).
Hsu, C. et al. Learning protein fitness models from evolutionary and assay-labeled data. Nat. Biotechnol. 40, 1114–1122 (2022).
Pfaff, L. et al. Multiple substrate binding mode-guided engineering of a thermophilic PET hydrolase. ACS Catal. 12, 9790–9800 (2022).
Zheng, N. et al. Isothermal compressibility perturbation as a protein design principle for T1 lipase stability-activity trade-off counteracting. J. Agric. Food Chem. 71, 6681–6690 (2023).
Zhang, Z. et al. Microstructural, physicochemical properties, and interaction mechanism of hydrogel nanoparticles modified by high catalytic activity transglutaminase crosslinking. Food Hydrocoll. 147, 109384 (2024).
Blanco, C. et al. Molecular fitness landscapes from high-coverage sequence profiling. Annu. Rev. Biophys. 48, 1–18 (2019).
Pressman, A. D. et al. Mapping a systematic ribozyme fitness landscape reveals a frustrated evolutionary network for self-aminoacylating RNA. J. Am. Chem. Soc. 141, 6213–6223 (2019).
Dauparas, J. et al. Robust deep learning-based protein sequence design using ProteinMPNN. Science 378, 49–56 (2022).
Meersman, F. et al. Protein unfolding, amyloid fibril formation and configurational energy landscapes under high pressure conditions. Chem. Soc. Rev. 35, 908–917 (2006).
Jumper, J. et al. Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021).
Grant, B. J. et al. The Bio3D packages for structural bioinformatics. Protein Sci. 30, 20–30 (2021).
Butler, B. M. et al. Conformational dynamics of nonsynonymous variants at protein interfaces reveals disease association. Proteins 83, 428–435 (2015).
Zheng, N. et al. Functional, structural properties and interaction mechanism of soy protein isolate nanoparticles modified by high-performance protein-glutaminase. Food Hydrocoll. 139, 108594 (2023).
Gerek, Z. N. & Ozkan, S. B. Change in allosteric network affects binding affinities of PDZ domains: analysis through perturbation response scanning. PLoS Comput. Biol. 7, e1002154 (2011).
Singh, R. K. et al. Molecular cloning and characterization of a GH11 endoxylanase from Chaetomium globosum, and its use in enzymatic pretreatment of biomass. Appl. Microbiol. Biotechnol. 97, 7205–7214 (2013).
Searle, P. L. The berthelot or indophenol reaction and its use in the analytical chemistry of nitrogen. A review. Analyst 109, 549 (1984).
Cui, L. et al. Excretory expression of IsPETase in E. coli by an enhancer of signal peptides and enhanced PET hydrolysis. Int. J. Biol. Macromol. 188, 568–575 (2021).
Souza, V. P. et al. Protein thermal denaturation is modulated by central residues in the protein structure network. FEBS J. 283, 1124–1138 (2016).
Ermolenko, D. N. et al. Hydrophobic interactions at the Ccap position of the C-capping motif of alpha-helices. J. Mol. Biol. 322, 123–135 (2002).
Firnberg, E. et al. A comprehensive, high-resolution map of a gene’s fitness landscape. Mol. Biol. Evol. 31, 1581–1592 (2014).
Zhang, Z. et al. Inside out computational redesign of cavities for improving thermostability and catalytic activity of Rhizomucor miehei lipase. Appl. Environ. Microbiol. 89, e0217222 (2023).
Di Nardo, A. A. et al. The relationship between conservation, thermodynamic stability, and function in the SH3 domain hydrophobic core. J. Mol. Biol. 333, 641–655 (2003).
Halabi, N. et al. Protein sectors: evolutionary units of three-dimensional structure. Cell 138, 774–786 (2009).
Qi, H. et al. A quantitative high-resolution genetic profile rapidly identifies sequence determinants of hepatitis C viral fitness and drug sensitivity. PLoS Pathog. 10, e1004064 (2014).
Deng, Z. et al. Deep sequencing of systematic combinatorial libraries reveals beta-lactamase sequence constraints at high resolution. J. Mol. Biol. 424, 150–167 (2012).
Melamed, D. et al. Deep mutational scanning of an RRM domain of the Saccharomyces cerevisiae poly(A)-binding protein. RNA 19, 1537–1551 (2013).
Zheng, N. et al. Tailoring industrial enzymes for thermostability and activity evolution by the machine learning-based iCASE strategy. Zenodo https://doi.org/10.5281/zenodo.14166570 (2024).
Acknowledgements
This work was supported by the National Key Research and Development Program of China (2022YFC2105501 (X.X.), 2021YFC2104001 (X.X.)). We are thankful for the support from the high-performance computing cluster platform of the School of Biotechnology, Jiangnan University.
Author information
Authors and Affiliations
Contributions
N.Z. performed the MD simulations and analyzed the simulation results. Z.Z. directed the MD simulations. N.Z., H.Z., Y.D., and S.D. performed the experiments. N.Z. analyzed the experimental data. M.T. and W.F. performed the code work. X.X. and Y.C. directed the study. N.Z. wrote the manuscript, and all authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zheng, N., Cai, Y., Zhang, Z. et al. Tailoring industrial enzymes for thermostability and activity evolution by the machine learning-based iCASE strategy. Nat Commun 16, 604 (2025). https://doi.org/10.1038/s41467-025-55944-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-55944-5