Abstract
The floating phase, a critical incommensurate phase, has been theoretically predicted as a potential intermediate phase between crystalline ordered and disordered phases. In this study, we investigate the different quantum phases that arise in ladder arrays comprising up to 92 neutral-atom qubits and experimentally observe the emergence of the quantum floating phase. We analyze the site-resolved Rydberg state densities and the distribution of state occurrences. The site-resolved measurement reveals the formation of domain walls within the commensurate ordered phase, which subsequently proliferate and give rise to the floating phase with incommensurate quasi-long-range order. By analyzing the Fourier spectra of the Rydberg density-density correlations, we observe clear signatures of the incommensurate wave order of the floating phase. Furthermore, as the experimental system sizes increase, we show that the wave vectors approach a continuum of values incommensurate with the lattice. Our work motivates future studies to further explore the nature of commensurate-incommensurate phase transitions and their non-equilibrium physics.
Similar content being viewed by others
Introduction
The study of quantum phases and quantum phase transitions is one of the central topics in condensed matter, atomic, and high energy physics. Among these, commensurate to incommensurate phase transitions have been actively investigated since the 1980s1,2,3,4,5,6 and have attracted renewed attention recently7,8,9,10,11,12. A pivotal question revolves around the extent of the intermediate incommensurate phase and the potential for a direct chiral transition within the Huse-Fisher universality class1 as a commensurate solid melts into the disordered phase. In the context of spontaneous symmetry breaking, commensurate crystalline states in lattice systems often give hints to the underlying universality class of the phase transitions, such as the Ising and Potts classes13. Nonetheless, Huse and Fisher1 proposed that when different kinds of domain walls exist in commensurate phases, they can introduce chiral perturbations, where the sequence of the domains matters. In such cases, several other possibilities could arise for the phase transition between the disordered and the commensurate ordered phases. These include a direct chiral transition1, a direct first-order transition5, or an intriguing two-step transition across an incommensurate density-wave phase, i.e., the quantum floating phase5,14.
Early efforts in this field focused on probing classical floating phases in the melting of two-dimensional (2D) solids on periodic substrates15,16,17. Later on, Fendley et al.18 proposed a one-dimensional (1D) constrained hard-boson model that hosts a critical quantum floating phase. The constrained model is of particular relevance to the Rydberg atom array quantum simulation platform, which has made significant advancements in recent years19,20,21,22,23,24. Strong blockade interactions between nearby Rydberg atoms directly mimic the constraint in the hard-boson model. Theoretical calculations predict that critical quantum floating phases should exist in the 1D Rydberg atom array system7,8,9,10,25. However, probing the floating phase in the 1D Rydberg system has been proven to be challenging due to the fact that the atoms cannot be placed arbitrarily close to each others, only a very thin sliver of the floating phase on top of the \({{\mathbb{Z}}}_{3}\) phase of the Rydberg chain is accessible experimentally.
In this study, we construct a quasi-1D array of 87Rb atoms arranged in a two-leg ladder and experimentally probe the quantum floating phase. The Rydberg interactions between the two legs of the ladder array in the chosen geometric aspect ratio introduce stronger chiral perturbations (Supplementary Note 4) that yield broad regions of the floating phase in experimentally accessible parameter regimes (Fig. 1b), which greatly facilitate our experimental observations. We provide supporting numerical calculations for the full phase diagram of the ladder system and experimentally measure the various phase regimes. By taking snapshots of the prepared states, we obtain the site-resolved Rydberg density and correlation functions. The dominant wave vectors for the measured correlation functions, extracted through Fourier analysis, offer a clear distinction between commensurate and incommensurate phases. An important feature of the floating phase is that, in the thermodynamic limit, the incommensurate wave vectors continuously depend on the physical parameters14. We experimentally observe that, as system sizes increase, the incommensurate wave vectors tend towards a continuum of values.
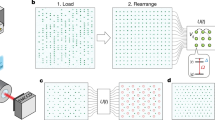
a Atoms are loaded into a two-leg ladder of optical tweezer traps generated using a spatial light modulator (SLM) and rearranged into defect-free patterns by a second set of moving tweezers using a pair of crossed acousto-optical deflectors (AODs). Coherent transitions are driven between the ground state \(\vert g\rangle=\vert 5{S}_{1/2}\rangle\) and the Rydberg state \(\vert r\rangle=\vert 70{S}_{1/2}\rangle\) in each atom with a two-photon transition induced by lasers at 420 nm and 1013 nm. The inset shows a linear detuning sweep Δ(t) at a constant Rabi frequency \({\Omega }_{\max }=2\pi \times 2.5\,\,{\mbox{MHz}}\,\) for preparing the ground states of the phase diagram via adiabatic evolution. Projection of the many-body quantum state into bitstrings of \(\left\vert g\right\rangle\) and \(\left\vert r\right\rangle\) for each atom can be detected on an Electron Multiplying Charge-Coupled Device (EMCCD) camera with the Rydberg state \(\left\vert r\right\rangle\) detected as loss of atom. b The ground-state phase diagram for the Rydberg Hamiltonian [Eq. (1)] in a two-leg ladder is shown with lattice spacings ax = a and ay = 2a. Structure factors S(k) are numerically computed for 1 ≤ Rb/a ≤ 3.5 using DMRG (Supplementary Note 2). The color map depicts the peak height S(ko) at ko = 2π/p with p being the wavelength in units of the lattice constant a, while contour lines show the constant-p lines. The \({{\mathbb{Z}}}_{p}\) orders have constant values of integer p, while the floating phase exhibits a continuously varying p. The black line cut corresponds to experimental parameters chosen in subsequent figures. c Experimentally measured Rydberg densities illustrate the \({{\mathbb{Z}}}_{p}\) orders and the floating phase. The radius of the dashed circle illustrates the Rydberg blockade radius Rb. The \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) orders exhibit Rydberg density oscillations with periods of p = 3 and p = 4 lattice spacings, respectively. The incommensurate floating phase displays no discernible periodicity in density oscillations.
Results
Implementation of the Rydberg ladder
In order to prepare this geometry of atom arrangement, 87Rb atoms are loaded from a magneto-optical trap into a 2D array of optical tweezers generated using a spatial light modulator (SLM). We then rearrange the initially loaded atoms into a defect-free two-legged pattern using a second set of optical tweezers generated by a pair of crossed acousto-optical deflectors (AODs)26. In our system, qubits are encoded in the electronic ground state \(\vert g\rangle=\vert 5{S}_{1/2}\rangle\) and the Rydberg state \(\vert r\rangle=\vert 70{S}_{1/2}\rangle\). The transition between the two states is driven by a two-photon process with two counter-propagating laser beams at 420 nm and 1013 nm shaped into light sheets (Fig. 1a). The coupling between the states and van der Waals interaction between Rydberg states result in the Hamiltonian
where i = 1, 2, …, L and j = 0, 1 are the rung index and the leg index, respectively, Ω is the effective two-photon Rabi frequency, Δ is the two-photon detuning, \({\hat{n}}_{i,j}=\vert {r}_{i,j}\rangle \langle {r}_{i,j}\vert\) is the Rydberg density operator, and \({V}_{{{{\bf{r}}}},{{{{\bf{r}}}}}^{{\prime} }}={C}_{6}/{\left\vert {{{\bf{r}}}}-{{{{\bf{r}}}}}^{{\prime} }\right\vert }^{6}\) is the van der Waals interaction where C6 = 2π × 862690 MHz μm6 and r = iaxex + jayey. In this work, we set the lattice spacings ax = a and ay = 2a (Fig. 1c). The interactions are parameterized by the Rydberg blockade radius \({R}_{b}={({C}_{6}/\Omega )}^{1/6}\), within which the interaction is much larger than the Rabi frequency, and it is thus energetically unfavorable to have more than one Rydberg excitation.
Complex many-body ground states emerge from the interplay between the detuning and the Rydberg interactions (Fig. 1b). For small positive values of detuning Δ/Ω, the system has a low Rydberg state occupancy and displays a featureless disordered ground state. When the detuning becomes large, the Rydberg excitations can occupy one of every p consecutive sites, with p being an integer number and its value determined by Rb/a. Such ordered \({{\mathbb{Z}}}_{p}\) density wave states have been observed experimentally both in 1D and 2D Rydberg arrays19,20,23. In the intermediate values of Rb/a between two different crystalline orders, the proliferation of different types of domain-wall excitations destroys the crystalline orders, but it can still stabilize an algebraically decaying quasi-long-range order that is incommensurate with the lattice spacing a1,9, giving rise to the quantum floating phase (Supplementary Notes 6 and 7). Those density wave states have degeneracies related by translation and mirror symmetries. To facilitate experimental observations, we apply special boundary conditions to add two extra sites on the edges of the ladder array as shown in Fig. 1c, which break the aforementioned symmetries (Supplementary Note 4).
Phase diagram via structure factor
The Rydberg density-density correlation functions can reflect (quasi) long-range orders in density-wave states and the Fourier analysis can extract the dominant wave vectors of these orders. To quantitatively map out the phase diagram, we use the following structure factor:
where mi = ni,1 − ni,0 is the difference between the Rydberg density on the two sites in the ith rung and p2/L2 is an overall normalization factor. Here, p is determined by p = 2π/ko, where L2S(k) peaks at ko. The ordered \({{\mathbb{Z}}}_{p}\) phase and the incommensurate floating phase correspond to p being integer and non-integer values, respectively, and S(ko) converges to non-zero constant values as the system sizes increase. On the other hand, S(ko) goes to zero in the thermodynamic limit for the disordered phase. The phase diagram for our ladder system is shown in Fig. 1b by numerical calculations via density matrix renormalization group (DMRG)27,28,29,30. The maximum value S(ko) is plotted as a function of the physical parameters Δ/Ω and Rb/a. The colormap shows clear differences among commensurate \({{\mathbb{Z}}}_{p}\) ordered phases, incommensurate floating phases, and the disordered phase. Lines of constant p are superimposed to the phase diagram in Fig. 1b. They reveal the wavelength of the density oscillations and thus whether it is commensurate or incommensurate (the validity of using S(k) to extract wave vectors in different phases is demonstrated in Supplementary Note 5). As illustrated, we can see the clear differences between commensurate \({{\mathbb{Z}}}_{p}\) ordered phases (with p = 2, 3, 4, 6) and the incommensurate floating phase that lies between \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) orders or between \({{\mathbb{Z}}}_{4}\) and \({{\mathbb{Z}}}_{6}\) orders. The \({{\mathbb{Z}}}_{5}\) order and in fact \({{\mathbb{Z}}}_{p}\) orders for any odd p ≥ 5 do not exist due to strong inter-leg Rydberg blockade interactions (Supplementary Note 4). We emphasize that determining the phase diagram by mapping out the structure factors, as demonstrated here, has the desirable benefit of being directly measurable in our experiments, in contrast to using the entanglement entropy (Supplementary Note 4).
Characterizing phases via bitstring distributions
Our experimental setup allows many repetitions of the adiabatic preparation process, giving us direct access to snapshots of bitstrings of each atom in \(\vert g\rangle\) and \(\vert r\rangle\) in each observation. We plot the experimentally measured density profiles for \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\), \({{\mathbb{Z}}}_{4}\), and floating phases in Fig. 1c. In each experimental run, the corresponding many-body ground state is prepared by an adiabatic evolution starting from all atoms in the \(\vert g\rangle\) state, followed by an adiabatic sweep similar to the one shown in the inset of Fig. 1a. One can see that the \({{\mathbb{Z}}}_{p}\) order has large occupation of Rydberg states every p-th site on each leg, while the Rydberg density in the floating phase does not have the same repetitive structure in the array. Analysis of the statistical distributions of the read-out configurations provides clear indications of the different many-body phases prepared (Fig. 2). In the case of the disordered state with Δ/Ω = 0, the measured bitstring configurations are likely to be all different, i.e., all the bitstrings occur only once (see Fig. 2a, with a total of 573 samples taken in our experiments). A typical measurement read-out shows no order along the ladder, where a representative snapshot is shown in the florescence image above the histogram plot. In contrast, for the commensurate \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) (588 samples) and \({{\mathbb{Z}}}_{4}\) (599 samples) phases, there is only one particular configuration that occurs much more frequently than all the other configurations (Fig. 2b, d), corresponding to the classical density-wave state with periodicities p = 3 and p = 4, respectively, as shown in the florescence images.
Bottom row: In each of the \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\), floating, and \({{\mathbb{Z}}}_{4}\) phases, the histograms of many-body state occurrence frequency are shown. Top row shows fluorescence images of the \(\left\vert g\right\rangle\) and \(\left\vert r\right\rangle\) bitstrings with the largest occurrence for (b, c, d), and a typical bitstring for (a), where atoms excited to \(\left\vert r\right\rangle\) are detected as atom loss and marked with red circles. The experimental parameters for these phases are along the black line shown in Fig. 1b with Δ/Ω = 3.5. The atoms are arranged in a (2 × 21 + 2) ladder array for all phases with L = 21. a The disordered phase at Δ/Ω = 0, Rb/a = 2.4 is sampled 573 times, with each measured bitstring occurring only once. b The \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) order at Rb/a = 2.1 exhibits a perfect \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) state occurring 24 times out of 588 samples, significantly more frequent than all other states. Blue boxes encircle the \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) unit cells. c The floating phase at Rb/a = 2.35 is measured 600 times, with \({{\mathbb{Z}}}_{4}\) (orange boxes) and \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) (blue boxes) cells appearing alternatively in the most frequent state. Right arrows point to the domain walls where the \({{\mathbb{Z}}}_{4}\) domain changes sublattices (the index i modulo 4 changes for the rungs containing Rydberg states). d The \({{\mathbb{Z}}}_{4}\) phase at Rb/a = 2.7 is sampled 599 times, with perfect \({{\mathbb{Z}}}_{4}\) states occurring most frequently at 33 times. Orange boxes encircle the \({{\mathbb{Z}}}_{4}\) unit cells.
More interestingly, within the floating phase situated between the \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) phase regimes, the most frequently observed bitstring out of 600 samples does not exhibit \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) or \({{\mathbb{Z}}}_{4}\) periodicity. Instead, there are always smaller regions with \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) or \({{\mathbb{Z}}}_{4}\) order appearing alternately, as shown by the alternate orange and blue boxes in the florescence image in Fig. 2c. This observation reveals that the floating phase is not simply a macroscopic superposition of \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) orders. If the melting of the \({{\mathbb{Z}}}_{4}\) order is considered, the domain walls can be identified by observing where the \({{\mathbb{Z}}}_{4}\) domain changes sublattices (Supplementary Note 3). These domain walls, as indicated by the right arrows, are essential for the incommensurate nature of the quantum floating phase (Fig. 1c). In principle, the domain walls should be distributed at equal distances across the entire system for the ground state. However, changing the position of the domain walls incurs only small energy cost in the floating phase, which results in a nearly continuous distribution of states with high occurrences (In the thermodynamic limit, a continuum limit can be defined and continuous translations can be performed on each configuration without any cost in energy. This translation corresponds to an overall phase shift of the incommensurate density wave, and the degeneracy is a manifestation of an emergent global U(1) symmetry.). We observe such a feature in the bitstring distribution in Fig. 2c. This behavior stands in contrast to the commensurate ordered phases, where only one bitstring occurs dominantly. These experimental results are fully consistent with theoretical calculations (see the Supplementary Note 3 for numerical results).
Density-density correlations
The \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\), \({{\mathbb{Z}}}_{4}\), and intermediate quantum floating phases can be further elucidated through a quantitative analysis of the Rydberg density correlations. In Fig. 3a, we present the correlation matrix \(\langle {m}_{i}{m}_{{i}^{{\prime} }}\rangle\) between rungs i and \({i}^{{\prime} }\). In the disordered phase, the diagonal elements of the correlation matrix are non-zero, while the off-diagonal elements quickly decay to zero, accompanied by weak site-dependent fluctuations. This behavior indicates that the correlation length is short in this case. Quantitatively, by averaging the correlation functions over sites with a fixed relative distance \(i-{i}^{{\prime} }\), we show that the mean correlation function \(C(r)=1/{N}_{r}{\sum }_{i-{i}^{{\prime} }=r}\langle {m}_{i}{m}_{{i}^{{\prime} }}\rangle\) (Nr is the number of \((i,{i}^{{\prime} })\) pairs satisfying \(i-{i}^{{\prime} }=r\)) decays to zero immediately for \(| i-{i}^{{\prime} }| > 0\) (first column of Fig. 3b). The numerical results are in good agreement with experimental measurements. Both experimental and numerical structure factors S(k) show a weak signal for density fluctuations, as shown in the first column of Fig. 3c.
a The experimental correlation matrix \(\langle {m}_{i}{m}_{{i}^{{\prime} }}\rangle\) employing the order parameter mi = ni,1 − ni,0 for a system size of L = 21. The presented results correspond to (Δ/Ω, Rb/a) = (0, 2.4) in the disordered phase, (3.5, 2.1) in the \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) phase, (3.5, 2.45) in the floating phase, and (3.5, 2.7) in the \({{\mathbb{Z}}}_{4}\) phase. Black boxes indicate examples of minimal repeating patterns for \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) orders, which repeat every three or four sites, respectively. The floating phase lacks a repeating pattern due to an incommensurate wavelength. b The mean correlator C(r) is determined by averaging correlation functions \(\langle {m}_{i}{m}_{{i}^{{\prime} }}\rangle\) over the same relative distance \(r=i-{i}^{{\prime} }\). Both numerical and experimental results are presented, showing nearly identical oscillation periods. c The structure factor S(k) is derived from the Fourier transform of \(\langle {m}_{i}{m}_{{i}^{{\prime} }}\rangle\) with respect to \(i-{i}^{{\prime} }\). While weak signals are observed in the disordered phase, both numerical and experimental results display robust matching signals for \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\), floating, and \({{\mathbb{Z}}}_{4}\) phases. Some detailed features of the figures such as beat patterns and peak asymmetries are discussed extensively in Supplementary Note 1.
The same analysis is performed for \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\), floating, and \({{\mathbb{Z}}}_{4}\) phases. The integer-period oscillation patterns for \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) phases can be easily read from the correlation matrix, where the correlations oscillate with periodicities of p = 3 and p = 4, respectively. On top of the periodic oscillations, there also exists some amplitude decay for the correlations as the distance increases. The black boxes in Fig. 3a indicate the smallest repeating units: 3 × 3 and 4 × 4 squares for \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) orders, respectively. There is no such repeating unit in the correlation matrix for the quantum floating phase, indicating that its periodicity is not commensurate with the lattice spacing. The mean correlation function in Fig. 3b also shows perfect \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) oscillations for the commensurate phases, while it presents an incommensurate oscillation pattern for the floating phase. The plots of C(r) exhibit excellent agreement with numerical results in the short range, albeit with amplitude decay due to the finite correlation length in our experiments. The experimental data for the three density-wave phases show strong signals of oscillations, which are absent in the disordered phase.
Structure factor analysis across phases
The structure factor in Fig. 3c has peaks at 2π × 8/24, 2π × 7/24, and 2π × 6/24 for the \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\), the incommensurate floating, and the \({{\mathbb{Z}}}_{4}\) phases, respectively, in agreement with numerical results. These particular values for the peak positions can be explained by the finite size of the ladder and our choice of boundary conditions. With finite detuning, a Rydberg excitation is pinned at each of the two edge sites of the ladder since that minimizes the Rydberg blockade energy, as illustrated in Fig. 1c. Under this boundary condition, the Rydberg density waves for \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) orders are both compatible with system sizes satisfying L = 12l − 3, with l being any positive integer number. Because of the Rydberg interactions, the pinning of the Rydberg density wave at the edge sites on a finite lattice restricts arbitrary continuous variation of the wavelength in the floating phase, allowing only l − 1 fractional values of wavelength between the \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and the \({{\mathbb{Z}}}_{4}\) orders. For example, in the \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) phase (p = 24/8) with a system size of L = 21, the most frequently occurring state contains 8 excitations in each leg, while in the \({{\mathbb{Z}}}_{4}\) phase (p = 24/6), it comprises 6 excitations in each leg. In the floating phase between the \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) phases, the most common state consists of 7 excitations in each leg, resulting in a fractional p = 24/7, as confirmed by the results in Fig. 2c. In the large L limit, this series of l − 1 waves with fractional wavelengths continuously interpolates between two crystalline orders with integer values p = 3 and p = 4. In the following, we experimentally explore this trend by constructing ladder arrays of different sizes.
Scaling of structure factors with system size
We vary Rb/a in small steps by changing the lattice constant a and examine the changes in the structure factor S(k) for various system sizes. This experimental cut is indicated by the black line in Fig. 1b at Δ/Ω = 3.5 and Rb/a ranges from 2.1 to 2.8. S(k) is measured for different system sizes L = 21, 33, 45, with its dependence on Rb/a and k presented in Fig. 4a–c. We note that at each value of Rb/a, the corresponding many-body ground state is prepared by an adiabatic sweep starting from all atoms in the \(\vert g\rangle\) state. As we can see, the structure factor exhibits k/2π = 1/3 and 1/4 peak plateaus independent of system sizes, signifying the existence of \({{\mathbb{Z}}}_{3}\times {{\mathbb{Z}}}_{2}\) and \({{\mathbb{Z}}}_{4}\) orders. More importantly, we experimentally observe, in the floating phase, 1, 2, and 3 peak steps for L = 21, 33, and 45, respectively, which are fully consistent with our theoretical expectations. Furthermore, the step locations are observed at the corresponding incommensurate values, also in agreement with theory results. In particular, we observe k/2π = 7/24 for L = 21, k/2π = 10/36, 11/36 for L = 33, and k = 13/48, 14/48, 15/48 for L = 45. As experimental imperfections favor domain wall excitations, incommensurate regimes become wider than numerical results. Our experiments demonstrate that the number of incommensurate steps between crystalline orders increases with the system size, which agrees with the theoretical expectation of its tending towards infinity as the system approaches the thermodynamic limit. Consequently, the dominant wave vector of the quantum floating phase would change continuously with the physical parameters. An example of the structure factor in the large L limit is shown in Fig. 4d using DMRG calculations for L = 141. In this case, the dominant wave vector in the floating phase takes a series of values, nearly forming a continuous curve within a small window between Rb/a = 2.34 and Rb/a = 2.51. In addition, we conducted measurements in the same Rb/a range with fixed Δ/Ω = 0, where the system is always in the disordered phase. The results show very weak peaks in the structure factor, and the signals diminish with increasing system sizes (Supplementary Note 1). These vanishing signals for the disordered phase confirm that the boundary effects do not induce artificial signatures for the existence of density-wave orders in our experiments, and, in particular, the observed peaks in the incommensurate wave vectors are genuine features of the quantum floating phase.
a–c Experimental measurements of S(k) are taken along the Δ/Ω = 3.5 line, as labeled by the black line in Fig. 1b, for system sizes L = 21, 33, 45. The data points cover Rb/a values ranging from 2.1 to 2.8 with a step size of 0.05. The magenta curves represent the peak positions of S(k) obtained from numerical calculations. The experimental data show that the number of peak plateaus allowed in the quantum floating phase increases with system sizes. d Numerical results for L = 141 demonstrate a continuous change in the wave vector of the quantum floating phase in the large L limit.
Discussion
In summary, our utilization of Rydberg-atom ladder arrays has enabled the experimental observation of an incommensurate density wave—the quantum floating phase. Distinct Rydberg density fluctuations are observed in different density-wave states, and the structure factor exhibits strong signatures for the existence of the floating phase. Through systematic tuning of the lattice constant, discrete wave vectors allowed in the quantum floating phase for different system sizes are observed, indicating their convergence to a continuum of incommensurate values in the thermodynamic limit. This experiment underscores the versatility of Rydberg atoms in ladder arrays as highly programmable quantum simulators, facilitating the exploration across various quantum many-body phases. The constructed Rydberg arrays house a broad spectrum of critical lines and points in experimentally accessible regimes, including Ising, Potts, Ashkin-Teller, chiral, Berezinskii-Kosterlitz-Thouless31, Pokrovsky-Talapov32, and Lifshitz critical points33 (see Supplementary Note 8 for details). The \({{\mathbb{Z}}}_{4}\) regime in our system establishes an ideal platform for investigating the Kibble-Zurek mechanism of chiral phase transitions. Our work paves the way for future experimental inquiries into these critical phenomena, and it offers potential applications in diverse contexts, such as quantum simulation of lattice gauge theories34,35,36,37,38, inhomogeneous phases, the Lifshitz regime of lattice quantum chromodynamics39,40, and “chiral spiral-” condensation in interacting fermionic systems41.
Methods
Creation of atom array
In this experiment, we utilize 87Rb atoms captured from a magneto optical trap. The atoms are loaded with 59% probability into optical tweezers generated using 840 nm light, which are created through a phase-only spatial light modulator (SLM, Hamamatsu X15213 series) to generate the trapping potentials with a depth of 10 MHz, as determined by the Stark shift associated with the \(\vert 5{S}_{1/2},F=2,{m}_{F}=-2\rangle\) to \(\vert 5{P}_{3/2},F=3,{m}_{F}=-3\rangle\) transition. Subsequently, we image atoms for 15 ms using near resonant 780 nm light, which is captured through a microscope objective of NA = 0.65 to image onto an EMCCD camera (Andor iXon Ultra) to capture the occupation of each site with 99.5% fidelity. From the atom detection results, atoms are moved using acousto-optic deflectors (AODs) to sort atoms onto the target two-legged pattern with 99.5% sorting fidelity. Following imaging, the atoms are cooled to a temperature of 10 μK and polarized into the \(\vert 5{S}_{1/2},F=2,{m}_{F}=-2\rangle\) state.
Rydberg system
The atomic levels we use in our qubit system are \(\vert g\rangle=\left\vert 5{S}_{1/2},F=2,{m}_{F}=-2\right\rangle\) and \(\left\vert r\right\rangle=\vert 70{S}_{1/2},{m}_{j}=-1/2,{m}_{I}=-3/2\rangle\), which are coherently driven by a two-photon transition induced by lasers at 420 nm and 1013 nm. The 420 nm laser is a frequency-doubled Ti: Sapphire laser (M Squared). We frequency stabilize the laser by locking a frequency sideband generated by an electro-optic modulator to an ultra-low-expansion reference cavity (notched cylinder design, Stable Laser Systems), with finesse \({{{\mathcal{F}}}}=30,000\) at 840 nm. The 1013 nm laser source is a whispering-gallery mode laser (OEwaves—OE3745), which is locked to the same reference cavity with a finesse of \({{{\mathcal{F}}}}=50,000\). The 1013-nm laser is amplified by an fiber amplifier (IPG YAM-100-1013-LP-SF).
We place the Rydberg two-photon transition at a single-photon detuning of δ ≈ 2π × 1 GHz blue detuned from the intermediate state \(\vert 6{P}_{3/2}\rangle\) with Rabi frequencies \(\left({\Omega }_{420},{\Omega }_{1013}\right)=2\pi \times (114,44)\) MHz, and a two-photon Rabi frequency of Ω = Ω420Ω1013/2δ ≈ 2π × 2.5 MHz.
Rydberg pulses
Atoms are adiabatically released from the tweezer traps after initializing them into the ground state \(\left\vert g\right\rangle\). The total time with the traps off is 7 μs. It is during the trap-off time that we apply a Rydberg pulse. The pulse is described by a time-dependent Rabi frequency \(\Omega \left(t\right)\), time-dependent detuning \(\Delta \left(t\right)\), and instantaneous phase \(\phi \left(t\right)\). This is implemented by controlling the amplitude, frequency, and phase of the 420-nm laser using a double-pass acousto-optic modulator configuration.
Rydberg beam shape
We shape both Rydberg excitation beams into 1D top-hats (light sheets) to homogeneously illuminate the plane of atoms. This is done by placing a SLM in the Fourier plane of each Rydberg beam. This allows us to control both phase and intensity on the atoms at the cost of efficiency. The tophat geometry is 75 μm wide in the plane of the atom array and has a waist of 35 μm along the axis normal to the atom array plane.
Data availability
The experimental data generated in this study are provided in the Supplementary Source Data file. Additional data are available from the corresponding author upon request. Source data are provided with this paper.
References
Huse, D. A. & Fisher, M. E. Domain walls and the melting of commensurate surface phases. Phys. Rev. Lett. 49, 793–796 (1982).
Ostlund, S. Incommensurate and commensurate phases in asymmetric clock models. Phys. Rev. B 24, 398–405 (1981).
Howes, S., Kadanoff, L. P. & Den Nijs, M. Quantum model for commensurate-incommensurate transitions. Nucl. Phys. B 215, 169–208 (1983).
Haldane, F. D. M., Bak, P. & Bohr, T. Phase diagrams of surface structures from Bethe-ansatz solutions of the quantum sine-Gordon model. Phys. Rev. B 28, 2743–2745 (1983).
Huse, D. A. & Fisher, M. E. Commensurate melting, domain walls, and dislocations. Phys. Rev. B 29, 239–270 (1984).
Dröse, T., Besseling, R., Kes, P. & Smith, C. M. Plastic depinning in artificial vortex channels: competition between bulk and boundary nucleation. Phys. Rev. B 67, 064508 (2003).
Chepiga, N. & Mila, Frédéric Floating phase versus chiral transition in a 1d hard-boson model. Phys. Rev. Lett. 122, 017205 (2019).
Rader, M & Läuchli, A. M. Floating phases in one-dimensional Rydberg Ising chains. http://arxiv.org/abs/1908.02068 (2019).
Chepiga, N. & Mila, F. Kibble-Zurek exponent and chiral transition of the period-4 phase of Rydberg chains. Nat. Commun. 12, 414 (2021).
Maceira, I. A., Chepiga, N. & Mila, Frédéric Conformal and chiral phase transitions in Rydberg chains. Phys. Rev. Res. 4, 043102 (2022).
Eck, L. & Fendley, P. Critical lines and ordered phases in a Rydberg-blockade ladder. Phys. Rev. B 108, 125135 (2023).
Samajdar, R., Ho, WenWei, Pichler, H., Lukin, M. D. & Sachdev, S. Complex density wave orders and quantum phase transitions in a model of square-lattice Rydberg atom arrays. Phys. Rev. Lett. 124, 103601 (2020).
Wu, F. Y. The Potts model. Rev. Mod. Phys. 54, 235–268 (1982).
Bak, P. Commensurate phases, incommensurate phases and the devil’s staircase. Rep. Prog. Phys. 45, 587 (1982).
Abernathy, D. L., Song, S., Blum, K. I., Birgeneau, R. J. & Mochrie, S. G. J. Chiral melting of the Si (113) (3 × 1) reconstruction. Phys. Rev. B 49, 2691–2705 (1994).
Schreiner, J., Jacobi, K. & Selke, W. Experimental evidence for chiral melting of the Ge (113) and Si (113) 3 × 1 surface phases. Phys. Rev. B 49, 2706–2714 (1994).
Schuster, R. et al. Pokrovsky-Talapov commensurate-incommensurate transition in the Co/Pd(100) system. Phys. Rev. B 54, 17097–17101 (1996).
Fendley, P., Sengupta, K. & Sachdev, S. Competing density-wave orders in a one-dimensional hard-boson model. Phys. Rev. B 69, 075106 (2004).
Bernien, H. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017).
Keesling, A. et al. Quantum Kibble–Zurek mechanism and critical dynamics on a programmable Rydberg simulator. Nature 568, 207–211 (2019).
Labuhn, H. et al. Tunable two-dimensional arrays of single Rydberg atoms for realizing quantum Ising models. Nature 534, 667–670 (2016).
de Léséleuc, S. et al. Observation of a symmetry-protected topological phase of interacting bosons with Rydberg atoms. Science 365, 775–780 (2019).
Ebadi, S. et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 595, 227–232 (2021).
Scholl, P. et al. Quantum simulation of 2D antiferromagnets with hundreds of Rydberg atoms. Nature 595, 233–238 (2021).
Weimer, H. & Büchler, H. P. Two-stage melting in systems of strongly interacting Rydberg atoms. Phys. Rev. Lett. 105, 230403 (2010).
Wurtz, J. et al. Aquila: QuEra’s 256-qubit neutral-atom quantum computer. http://arxiv.org/abs/2306.11727 (2023).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992).
White, S. R. Density-matrix algorithms for quantum renormalization groups. Phys. Rev. B 48, 10345–10356 (1993).
Östlund, S. & Rommer, S. Thermodynamic limit of density matrix renormalization. Phys. Rev. Lett. 75, 3537–3540 (1995).
Fishman, M., White, S., & Stoudenmire, E. M. The ITensor software library for tensor network calculations, SciPost Phys. Codebases, 4 (2022).
Kosterlitz, J. M. The critical properties of the two-dimensional XY model. J. Phys. C Solid State Phys. 7, 1046–1060 (1974).
Pokrovsky, V. L. & Talapov, A. L. Ground state, spectrum, and phase diagram of two-dimensional incommensurate crystals. Phys. Rev. Lett. 42, 65–67 (1979).
Chepiga, N. & Mila, Frédéric Lifshitz point at commensurate melting of chains of Rydberg atoms. Phys. Rev. Res. 3, 023049 (2021).
Bazavov, A., Meurice, Y., Tsai, S.-W., Unmuth-Yockey, J. & Zhang, J. Gauge-invariant implementation of the Abelian-Higgs model on optical lattices. Phys. Rev. D. 92, 076003 (2015).
Zhang, J. et al. Quantum simulation of the universal features of the Polyakov loop. Phys. Rev. Lett. 121, 223201 (2018).
Surace, F. M. et al. Lattice gauge theories and string dynamics in Rydberg atom quantum simulators. Phys. Rev. X 10, 021041 (2020).
Meurice, Y. Theoretical methods to design and test quantum simulators for the compact Abelian Higgs model. Phys. Rev. D. 104, 094513 (2021).
Heitritter, K., Meurice, Y. & Mrenna, S. Prolegomena to a hybrid Classical/Rydberg simulator for hadronization (QuPYTH). http://arxiv.org/abs/2212.02476 (2023).
Pisarski, R. D., Skokov, V. V. & Tsvelik, A. M. A Pedagogical Introduction to the Lifshitz Regime. Universe 5, 48 (2019).
Kojo, T., Hidaka, Y., McLerran, L. & Pisarski, R. D. Quarkyonic chiral spirals. Nucl. Phys. A 843, 37–58 (2010).
Başar, G. & Dunne, G. V. Self-consistent crystalline condensate in chiral Gross-Neveu and Bogoliubov–de Gennes systems. Phys. Rev. Lett. 100, 200404 (2008).
Acknowledgements
We thank K. Heitritter, J. Corona, Milan Kornjača, and members of the QuLAT collaboration for helpful discussions, and Simon Evered for providing helpful feedback on the manuscript. Authors from QuEra Computing Inc. acknowledge the support from the DARPA ONISQ program (grant no. W911NF2010021). S.-W.T. acknowledges the support from the National Science Foundation (NSF) RAISE-TAQS under Award Number 1839153. J.Z. is supported by NSFC under Grants No. 12304172 and No. 12347101, Chongqing Natural Science Foundation under Grant No. CSTB2023NSCQ-MSX0048 and No. CSTB2024YCJH-KYXM0064, and Fundamental Research Funds for the Central Universities under Projects No. 2023CDJXY-048 and No. 2020CDJQY-Z003. Y.M. and, in the early stage of the project, J.Z. were supported in part by the U.S. Department of Energy (DoE) under Award Number DE-SC0019139. Computations were performed using the computer clusters and data storage resources of the UCR High Performance Computing Center (HPCC), which were funded by grants from NSF (MRI-2215705, MRI-1429826) and NIH (1S10OD016290-01A1).
Author information
Authors and Affiliations
Contributions
Y.M. and A.K. initiated the collaborative study on the physics of Rydberg ladders. J.Z. and F.L. proposed the experiment to investigate the quantum floating phase in the Rydberg two-leg ladder system. S.H.C., A.B., B.B., F.H., J.A.-G., A.L., and N.G. built the experimental setup. S.H.C. performed the measurements and analyzed the data. J.Z., F.L., and S.H.C. performed theoretical analysis. All work was supervised by S.T.W., Y.M., and S.W.T. All authors discussed the results and contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interest.
Peer review
Peer review information
Nature Communications thanks Natalia Chepiga and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhang, J., Cantú, S.H., Liu, F. et al. Probing quantum floating phases in Rydberg atom arrays. Nat Commun 16, 712 (2025). https://doi.org/10.1038/s41467-025-55947-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-55947-2