Introduction

Photons, the quanta of light, are massless particles whose energy E is related to their frequency f by Planck’s constant h, through the relation E = hf 1. The most energetic photons ever recorded, with E > 100 TeV, belong to the class of gamma rays, which extend down to E ~ MeV2. Lower energy photons, such as X-rays, have energies around E ~ keV3,4,5. Single photons in the gamma and X-ray ranges are detected using high-energy physics techniques, such as crystal scintillators and photomultiplier tubes6. In the optical domain, where photons typically have energies of E ~ eV, single-photon detection is well-established, utilizing devices like photomultipliers and avalanche photodiodes7. Advancements in superconducting technologies have enabled photon detection in the infrared range (E ~ meV), employing methods such as nanowires8,9, transition-edge sensors10, kinetic inductance detectors5, and Josephson junctions4.

The microwave range, with photon energies around E ~50 μeV ( ~10 yJ), represents the frontier of single-photon detection11. This range has been explored using quantum dots12 and bolometric schemes13,14,15. The development of single-photon detectors (SPDs) in the microwave range has drawn significant interest from the field of quantum technologies. Circuit quantum electrodynamics schemes16 have been proposed17,18 and implemented with qubits19,20,21,22,23,24,25,26.

The demand for microwave SPDs is exemplified in dark matter searches, such as those for axions27,28,29. In particular, dark matter haloscopes30,31,32,33 rely on precision power measurements using low-noise amplifiers. Transitioning to photon detectors is crucial34,35 as they outperform quantum-limited amplifiers and quantum-enhanced measurement techniques, especially at higher frequencies (above a few GHz) where the standard quantum limit of linear amplification significantly hinders sensitivity34,36.

The axion signal, characterized by a stochastic emission of rare photons at frequency fa, depends on the unknown axion mass and has a narrow bandwidth of 10−6fa27. Consequently, suitable photon detectors must exhibit a low dark count rate, wide spectral range, high efficiency, and continuous operation capabilities. Existing microwave photon detectors generally fall short of these requirements, although some recent experiments24,37 have addressed these challenges. Josephson junctions have been proposed and analyzed as threshold detectors for microwave photons38,39,40,41,42,43,44. While they have been realized for detecting high photon rates44, their use in detecting rare photons remains an experimental challenge.

In this work, we demonstrate the detection of single microwave photons with high efficiency and a sub-hertz dark count rate using an underdamped Josephson junction (JJ). The photons are generated via thermal emission from a bulk copper resonator. The experimental scheme and operation principles are illustrated in Fig. 1. The cavity design determines the frequency of the emitted photons, and the emission rate is adjusted from less than one photon per hour to thousands of photons per second by varying the cavity temperature. The photons are collected by the detector using an on-chip impedance-matching line terminated by a JJ. When a photon impinges on the detector, the current-biased JJ switches to the resistive state, producing a detection event. The observed thermal photons depend exponentially on temperature and, when sourced from a single mode, follow a super-Poissonian statistics45,46, providing a unique signature of their nature47.

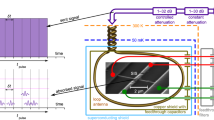
Fig. 1: Description of the experimental scheme.
figure 1

a A microwave cavity is connected to the photon detector, where the former acts as a source of thermal photons and the latter is formed by the Josephson junction, inserted into a coplanar waveguide adapter. b Temperature dependence of the rate of thermal photons emitted by the cavity. With a corresponding temperature change of tens of millikelvin, the photon rate is varied by orders of magnitude. c The tilted washboard potential describes the dynamics of a Josephson junction: the system is superconducting if the wavefunction is confined to a minimum, and resistive if it runs down the potential. The switching to the resistive state can be due to the arrival of a photon, or due to noise, appearing as thermal escape or quantum tunnelling processes, which therefore needs to be suppressed.

Full size image

Results

Experiment concept

The experiment consists of two main components: a photon source and a photon detector, as shown in Fig. 2. The photon source is a cylindrical cavity with a radius of 3.0 cm and a height of 1.2 cm (Fig. 2a). The cavity body is made of oxygen-free, high-conductivity copper, ensuring effective thermalization and a quality factor of approximately 104. The cavity is coupled to two SMA ports: port 1, weakly coupled, is used for characterization, while port 2 is close to critical coupling. The measured S21 transmission of the resonator, shown in Fig. 2b, reveals the first four resonant modes.

Fig. 2: Microwave cavity and photon detector used in this work.
figure 2

a The cavity, critically coupled to the SPD through antenna port 2, while port 1 is weakly coupled and used for characterization purposes. At the center of the cavity, a sketch of the 14 GHz mode shape is shown. b Room-temperature response of the cavity, showing resonant modes starting from the fundamental mode at 8.81 GHz. A comparison with resonances at 17 mK is provided in Fig. 4. (c) Circuit diagram with optical images of the detector connected to the cavity antenna and mounted in the sample holder. SEM image of the Josephson junction with artificial colors: pink - bottom Al electrode, blue - top Al electrode, violet - overlapping areas. The feeding dc lines are also shown, indicating the bias current Ib and measured voltage U. d Picture of the coldest plate of the dilution refrigerator, showing the sample holder within the cryoperm screen and the copper cavity. A SQUID thermometer is mounted on top, with a heating resistor installed below.

Full size image

The detector is an underdamped Al-AlOx-Al Josephson junction connected to the cavity antenna. When a photon is absorbed, the junction switches to the running state, producing a measurable voltage drop of hundreds of microvolts. Figure 2c shows the circuit diagram, chip layout, optical images, and an SEM image of the Josephson junction. The on-chip coplanar line is designed as an impedance transformer from 50 Ω to 200 Ω. Simulations indicate that the matching efficiency exceeds 60% even for junctions with RN values up to 2 kΩ. The detector’s bandwidth is  ~3 GHz around 14 GHz, with a subband near 8.8 GHz linked to internal resonances of the JJ sample.

Microwave signals from cavity port 2 are delivered through a short coaxial cable soldered to the PCB coplanar line, which is bonded to the chip’s coplanar line. Bias and voltage line T-filters consist of feed-through capacitors (1.1 nF, red), on-plate resistors (500 Ω, blue), and external resistors (10 kΩ, not shown). The output voltage is read using a room-temperature AD745 amplifier and analog-to-digital converter.

The setup with the cavity mounted on the coldest plate of a dilution refrigerator is shown in Fig. 2d. The SPD is housed inside cryoperm and superconducting screens to minimize magnetic noise and stray light. A SQUID thermometer on the cavity ensures precise temperature control, while a 5 Ω heating resistor is installed at the cavity base. Measurements of the SPD’s response to the resonator’s signal were conducted by varying the heating temperature from 21 mK to 80 mK, corresponding to heating resistor voltages of 0 mV to 28 mV. The SPD’s copper base is anchored directly to the mixing chamber plate to reduce heat transfer through the SMA connector. SPD switching time measurements were automated, enabling precise feedback for cavity and cryostat plate temperatures.

The SPD was fabricated using the shadow evaporation technique, forming an Al-AlOx-Al trilayer on a Si substrate with an area of 2.5 × 0.7 μm2, see Methods. At 17 mK, the measured critical current is IC = 170 nA, and the normal state resistance is RN = 1480 Ω (Fig. 3a). The chosen parameters balance reduced dark count rates and optimal quantum efficiency, targeting a regime that minimizes thermal activation and quantum tunneling events42. The critical current and damping allow operation in the phase diffusion regime44,48, enhancing performance. The detector response time, determined by the inverse plasma frequency, is below 1 ns. The detector’s dead time, governed by RC filters, is 2–10 ms. An example of a single-shot measurement with 3 ms bias current rise and fall times and a 42 ms switching time is shown in the inset of Fig. 3a.

Fig. 3: Preliminary characterization of the detector.
figure 3

a Current-voltage characteristics of the sample at 17 mK, sequentially measured 10 times to demonstrate setup stability. Inset: Example of a single-shot measurement with bias current rise and fall times of 3 ms each. b Mean switching times of the SPD at 17 mK, showing significant reductions in dark counts due to filtering improvements over several months (dots - experiment, solid curves - theory). Error bars are smaller than the dot size.

Full size image

Sequential measurements of the SPC-73 sample’s current-voltage characteristics confirm setup stability (Fig. 3a). The critical current at 17 mK, IC = 170 nA, approaches the Bardeen-Cooper-Schrieffer (BCS) theoretical limit of 197 nA in the absence of thermal and quantum noise. Figure 3b shows the mean switching time of the SPC-73 sample, demonstrating significant reductions in dark counts through iterative filtering and screening improvements. Theoretical tunneling time predictions38,49,50 (red solid curve) match closely the experimental data after improvements. Stray light mitigation efforts yielded the rightmost curve (red dots), surpassing the standard tunneling time limit. This points to the onset of the quantum phase diffusion regime44, where the dark count rate decreases significantly. Interestingly, the rightmost data align with the classical Kramers’ time predictions51, fitting at 18 mK a critical current value of 191 nA, consistent with the BCS theoretical limit for this sample.

Measuring the cavity resonances

An underdamped Josephson tunnel junction is well-known as a detector of a harmonic signal with a minimum detectable power down to the femtowatt level, by measuring the photon-assisted tunneling (PAT) steps at the inverse branch of a current-voltage characteristic. In this work, we use PAT steps (see Methods) to measure resonant curves of the cavity at low temperatures.

To correctly fit the measured photon rate with the theory, see below, we must properly characterise the cavity quality factors as well as their central frequencies and substitute these values into Eq. (1). The resonator has four resonant frequencies: 8.81 GHz; 13.95 GHz; 16.67 GHz and 17.85 GHz, but the rate of photon emission at frequencies 16.67 GHz and 17.85 GHz is more than one order of magnitude lower than at the other two frequencies. Therefore, when determining the SPD efficiency, only modes at 8.81 GHz and 13.95 GHz were taken into account.

The method for measuring the cavity resonances with using the PAT steps is as follows. First of all we measure a series of IV curves at a frequency close to a resonance with various microwave power values (Fig. 4a). Then we plot the calibration curve that shows the dependence of the current step position on the supplied microwave power in dB at a certain voltage on the SPD (Fig. 4b, blue diamonds). We make an exponential fit of the calibration curve and thus have the dependence of the incident power on the current step position at any value between the measured points (Fig. 4b, red curve). Then, finally, we measure IV curves at a constant supplied microwave power with frequencies varying in the vicinity of the cavity resonance (Fig. 4c). Using the calibration curve obtained at the previous step we transform the positions of the current step into the value of the incident power in dB. Since we make such measurements near the resonant frequency, the incident power strongly depends on the frequency of the microwave signal. The frequency response of the cavity near 8.8 GHz (d) and 13.9 GHz (e) measured by the PAT steps (red curves) are presented in Fig. 4d, e. For comparison, we plot the room temperature frequency response of the cavity, measured with a VNA (blue). We see that the quality factor at low temperature 17 mK increases, as expected, with a simultaneous shift of the resonant frequencies to slightly higher values. Thus, at low temperatures, the quality factor of the 8.81 GHz mode reaches Q1 = 7340, and the one of the 13.9 GHz mode is Q2 = 4650. The measured values of quality factors and central frequencies are used for fitting of the measured photon rate with the theory in Eq. (1), shown in Fig. 5.

Fig. 4: Measurements of cavity resonances by photon-assisted tunneling steps of the SPD.
figure 4

a IV curves at various incident radiation powers and constant frequency of 13.9537 GHz; b Calibration curve to translate the position of current step to dB; c IV curves at various frequencies of incoming radiation and constant power; d,e Comparison of frequency response of the cavity measured at room temperature by VNA (blue) and at 17 mK measured by photon-assisted tunneling steps in SPD (red). d Resonance at 8.8 GHz, e resonance at 13.9 GHz. Both dependences are normalized to the same level so that their maxima are at 0 dB. Blue curves are actually the enlarged curves from Fig. 2b.

Full size image
Fig. 5: Single microwave photon detection.
figure 5

a An event plot of the recorded data is shown at various temperatures of the cavity. b The SPD switching rate, fitted with the theoretical photon rate, using formula (1). The error bars do not exceed the dot sizes due to 5000 averages. The data are fitted with the expected cavity photon rate rc (1) (red solid curve) plus a dark count rate rDC (green dashed line) to extract the efficiency and noise floor of the detector. The black dotted curves show  ± 0.05 η2 spread of the fitting. The values of quantum efficiency η reach  ~ 0.0125 and 0.45 ± 0.05 for 8.81 GHz and 13.9 GHz modes, respectively. c The SPD switching rates versus bias current, measured at the base temperature 17 mK, for various cavity temperatures from 21 to 80 mK.

Full size image

Detecting single photons, thermally emitted from the cavity

The average number of thermal photons in a cavity mode follows the Planck distribution and depends on the modes’ resonance frequency, loaded quality factor, and temperature. Dissipation regulates the photon lifetime, giving rise to an emission rate that can be controlled by coupling an antenna to the mode52. On first approximation, the cavity photon rate rc(T) measured with an SPD can be calculated considering n modes as

$${r}_{{{{{\rm{c}}}}}}(T)=\sum\limits_{i=1}^{n}\frac{{\eta }_{i}}{{\tau }_{i}}\frac{1}{{e}^{h{f}_{i}/{k}_{{{{{\rm{B}}}}}}T}-1}$$
(1)

where fi, τi are the frequencies and the lifetimes of the cavity modes’ photons, respectively; h is the Planck constant, kB is the Boltzmann constant and T is the temperature. The photon lifetime τi = Qi/(2πfi) is extracted from the quality factor Qi of the mode and its central frequency fi. The parameter ηi is the ratio between the thermally available photons of the i-th cavity mode and the detected ones. It depends on the cavity antenna coupling and on the detector quantum efficiency. The fact that the antenna is critically coupled to the cavity means that only a half of available photons exit the cavity and go to the detector. Thanks to the exponential dependence of the rate on the hfi/kBT ratio, at low enough temperatures only a limited number of modes significantly contribute to the rate, allowing us to neglect the effect of higher-order resonances.

To observe the variation of the photon rate and characterise the quantum efficiency and dark count rate of the detector, we measured the temperature dependence of the switching events. To this end, the temperature of the cold plate of a dilution fridge was fixed at about 17 mK, while the cavity, weakly thermally coupled to the plate, was heated by a resistor to a temperature of 21 to 80 mK, precisely controlled using a SQUID noise thermometer. An estimate of a photon-induced current pulse is given in Methods.

In Fig. 5a we present an event plot of the recorded data at various cavity temperatures, from 21 to 62 mK, showing an exponential increase of the switching rate. Figure 5b displays the switching rate versus temperature and its fit. We fit the data with the expected cavity photon rate rc(T) in Eq. (1) plus a dark count rate rDC = 1/τ0, which is the inverse of the mean switching time τ0 taken from the lowest temperature data, to extract the efficiency and noise floor of the detector. For this analysis, the quality factors and resonance frequencies are fixed to the values measured using PAT steps, see Fig. 4. In particular, at f1 = 8.81 GHz, Q1 ≃ 7340, and at f2 = 13.95 GHz, Q2 ≃ 4650. Figure 5b shows a good agreement between the expected cavity photon rate and the experiment. From this data, we verify that only the first two modes contribute to the detector response at these temperatures, while the higher frequency modes are irrelevant. The detection efficiency η2 is as high as 45 ± 5% for the mode f2, with a dark count rate of 0.1 Hz. In this experiment, the estimated efficiency is a convolution between the antenna coupling and the detector efficiency, and is therefore a lower limit. For instance, η1 ≃ 1% is mainly due to the weak coupling of the antenna to the mode f1, as can be deduced from Fig. 2b, as well as SPD coplanar antenna selectivity, aimed to efficiently receive 14 GHz photons. The choice of the antennas’ couplings is tailored to swap the main contribution to rc(T) from f1 to f2 at a temperature of about 50 mK, therefore forming a peculiar cavity response, as shown in Fig. 5b.

In Fig. 5c, the SPD is characterised by measuring its mean switching rate versus bias current for various cavity temperatures. The mean switching rate coincides with the SPD dark count rate at the lowest cavity temperature of 21 mK in the absence of thermal photons, while it is defined by the photon rate at a large cavity temperature. One can see that the switching rate, starting from 0.01 Hz at the smallest bias current, increases by four orders of magnitude when heating cavity up to 80 mK, demonstrating the efficient response to incoming photons. It was checked that the dark count rate nearly does not change at the same cavity temperature variation if the sample is disconnected from the cavity, and also that the response is heavily suppressed if the cavity is connected to the SPD by the port 1.

Since a signature of single-mode thermal photons is their super-Poissonian statistics45, let us study the ratio of the SPD mean switching time τ to its standard deviation σ. It is known that in the case of Poissonian statistics, which is a natural statistics of thermal or quantum dark counts of our detector, this ratio should be equal to unity51. In the inset of Fig. 6 the τ/σ ratio vs temperature is shown. One can see that at low and high temperatures τ/σ is close to unity, proving the Poissonian statistics. At intermediate temperatures, τ/σ is significantly lower than unity, reaching the minimum value of 0.73 at 47 mK. This is evidence of the super-Poissonian distribution of photons, also known as photon bunching.

Fig. 6: Distribution of times between sequential switchings of the SPD at three various temperatures.
figure 6

The experimental data (dots) are fitted by \(\exp (-t/\tau )/\tau\) (dashed curves) without any fitting parameters with the mean switching time τ directly taken from experimental data. Good agreement between fitting and experiment is observed at 21 mK and 80 mK cavity temperatures. One can note super-Poissonian distribution at intermediate cavity temperature 47 mK. Inset: The τ to σ ratio vs cavity temperature, showing deviation from Poissonian statistics.

Full size image

The time intervals between the events are presented as switching time distributions in Fig. 6 and fitted with an exponential distribution (dashed curves). This probability density for noise-induced escapes (or tunneling) across (through) the barrier should represent Poissonian distribution in the form \(w(t)=\exp (-t/\tau )/\tau\)51. One can see that the curve for 21 mK is fitted by the above exponential dependence without any fitting parameter for τ = 9.026 s. The curve for 80 mK is also well-fitted by exponential dependence with τ = 7.214 ms. In all cases, τ is taken directly from the experimental data as the mean time interval between the events. At the same time, at 47 mK, the switching time distribution is better fitted by the power dependence t−α with α = 0.75 (dotted curve) than by the exponential dependence with τ = 0.119 s, at least for intermediate switching times. This is the evidence of quantum chaos47 as natural statistics of thermal photons45, see below. The change from Poissonian distribution at low temperatures to super-Poissonian at intermediate and back to Poissonian at high temperatures can be explained in the following way. At low temperatures, when the thermal photons in the cavity are very rare, the Poissonian statistics is the internal statistics of the detector as, e.g., for noise-induced escapes across a potential barrier51. With temperature increase, the contribution of thermal photons from a single 8.81 GHz mode starts to dominate, which, as argued in45, should demonstrate the super-Poissonian statistics (see the mode contribution vs temperature in Fig. 5b). With further increase of the temperature, the main 14 GHz mode starts to compete with the first one (their contributions become equal at 54 mK), which leads to Poissonization of the thermal photon statistics, according to45. To our knowledge, this is the first direct observation of the super-Poissonian statistics of microwave thermal photons. The observation of super-Poissonian statistics of photons was proposed to be used as a signature of quantum chaos47. Figure 7a shows the results of quantum chaos modeling47, where the authors propose to use photon arrival histograms as a tool for observing quantum chaos. The authors compare the results of numerical simulations, and show that the statistics changes from Poissonian for regular dynamics to super-Poissonian in the case of the quantum chaos appearance. This is exactly the distribution observed in our experiment, shown in Fig. 7b, supporting the slogan: quantum chaos—nonlinear linearity. Here, we should add, that while the cavity represents completely linear resonator, the total system is not linear, since the resonator is weakly coupled to the Josephson junction detector, which is a strongly nonlinear element.

Fig. 7: Comparison of Poissonian and super-Poissonian distributions.
figure 7

a Numerically computed distributions according to47. b Measured switching time distribution (blue dots) of thermal photons from a cavity representing super-Poissonian distribution, fitted with exponent (red dashed curve) and t−α dependence.

Full size image

Discussion

In this work we describe and operate a microwave single photon detector used to observe the clicking and the statistics of thermal photons emitted by a resonator at ultracryogenic temperatures. The Josephson junction-based sensor shows a sub-Hz dark count rate and high efficiency, combined with a reduced operation complexity compared to qubit-based designs23,24. The SPD was used to observe single microwave photons emitted by a single-mode and a multi-mode thermal source, i. e. a copper cavity. Although widely accepted45,53,54, an experimental demonstration of the super-Poissonian statistics of thermal microwave photons was, to our knowledge, missing. The measured photon rate is consistent with thermal emission from the microwave cavity modes, and closely follows the expected temperature dependence. The photon distribution displays a clear reduction of the mean-to-standard deviation ratio when the light is emitted mainly by one mode, which instead remains unitary for dark count and multi-mode emission. The dynamical range of the detector extends from its dark count rate to the kHz range and is currently limited by the acquisition electronics’ speed. The detector dynamics was not further investigated and will be the subject of future works. The SPD efficiency can be better characterised with an on-demand microwave photon source55,56,57,58, to disentangle it from other systematic uncertainties. Future efforts to improve the SPD aim mainly at improving its dark count rate. For instance, a junction with lower IC could enter the phase diffusion regime, which is expected to increase its lifetime, and thereby reduce the dark count rate44. Advancing the screening and filtering of the setup is also foreseen to improve the detector performance. In perspective, this work paves the way to a deeper examination of thermal light’s quantum properties and to their use to study quantum chaos47, ghost imaging59,60,61, and more45. The device itself finds numerous applications in the field of precision physics beyond the Standard Model, as for instance Axion searches34,35. On the one hand, the performance requirements needed to drastically improve current Axion experiments are already met by the current device. On the other hand, these apparata typically include strong magnetic field and long operation times, posing a challenge to the screening and long-term-stability of the detector. Nevertheless, the implementation of single microwave photon detectors such as the one presented here fosters the emergence of next-generation beyond the Standard Model experiments42,62.

Methods

Sample fabrication

The fabrication of a Josephson junction-based single photon detector requires a two-layer process. In the first Ti/Au/Pd multilayer, the contact pads, the antenna, and dc wires were fabricated at the nanofabrication facility of Chalmers university using laser-writer and lift-off technology. In the second layer, we patterned the superconductor-insulator-superconductor (SIS) tunnel junctions with the electron beam lithography. Thereafter, the SIS junction structures made of aluminum were deposited at NNSTU using a well-established shadow evaporation technique63,64 without breaking the vacuum. This technology is typically used for the fabrication of superconducting qubits that ensures long-time operation of the samples.

Shielding of the detector

The shielding of the setup from the environment is straightforward. The detector is readout with dc lines, filtered by the T-filters already described in the main text. Photons are emitted and measured inside the compact volume of the cavity and the detector holder without the need of any microwave cable, thereby ensuring a strong decoupling from the environment. External magnetic fields around the detector are screened by a two-layer cryoperm and superconducting screen. Our experimental setup shows no sensitivity to either the Earth’s magnetic field or nearby magnets.

Photon-assisted tunneling steps

The frequency response of the cavity at low temperatures was measured by using the photon-assisted tunneling steps of the SPD’s IV curves65, see Fig. 4. When the voltage at the junction is slightly lower than the doubled gap voltage, a single electron (quasiparticle) is able to tunnel from one side of the junction to another one. It becomes possible when eV + hf > 2Δ with V, f, Δ being voltage, emission frequency and superconducting energy gap, respectively. This effect appears in the IV curve of the junction as PAT step. The position of this step depends on the power of the incident signal while the voltage depends on its frequency.

Estimation of a single-photon-induced current pulse

Let us demonstrate that the Josephson junction works as a microwave single photon detector when its bias current Ib is slightly lower than the critical current IC. As outlined in Fig. 1, the dynamics of a Josephson junction can be treated as the evolution of a phase particle in a tilted washboard potential. An absorbed photon causes a current pulse ΔI through the junction, overcoming the threshold, and thus leading to the appearance of measurable resistive state with a finite voltage of about 0.4 mV. In the Josephson circuit, the energy hf of the incoming photon is split between the energy of the supercurrent Es stored in the tank circuit and the energy Ed dissipated in the subgap resistor Rqp, approaching RN close to zero voltage, according to quasiparticle IV curve of a tunnel Josephson junction66. Assuming the simple relation between Es and the pulse amplitude ΔI 42, Es = LJJΔI2/2, and taking into account that in parallel RLC-resonant circuit \(Q={R}_{N}{\left(C/{L}_{{{{{\rm{JJ}}}}}}\right)}^{1/2}\), Es/Ed = Q/2π, the current increase due to the photon can be estimated as \(\Delta I=\sqrt{2hf{L}_{{{{{\rm{JJ}}}}}}^{-1}{(1+2\pi /Q)}^{-1}}\), where the junction inductance LJJ depends on the bias current I as \({L}_{JJ}=\hslash /(2e){({I}_{C}^{2}-{I}^{2})}^{-1/2}\). Using the above parameters, for IC = 170 nA the single photon current pulse ΔI is estimated about 60 nA.