Introduction

Vertical structures of layered graphene or transition metal dichalcogenides (TMDs) can be produced very efficiently by simple superposition of individual layers. The twist between the crystals and a possible lattice mismatch leads to 2D moiré superlattices, that may also be accompanied by symmetry breaking and strong bands hybridization effects. In most studied cases, the individual layers present a three- or six-fold rotational symmetry (C3 or C6) which is preserved in the stack. Over the last decade, it has been demonstrated that such systems can exhibit unique physical properties such as unconventional superconductivity, moiré excitons, Wigner crystalline states, and orbital ferromagnetism1,2,3,4,5,6,7,8,9,10,11,12. In twisted bilayer TMDs, flat bands can be possibly generated for “magic” twisted angles and the Coulomb interaction dominates over kinetic energy due to the small group velocity. However, flat bands have been observed only below the valence band maximum (VBM) at the Γ valley and the generation of these electronic structures at the highest occupied states, where original quantum phenomena are supposed to occur, remains an open challenge13,14,15.

Stacking layers from different crystal classes also permits breaking the rotational symmetry of the individual layers, giving rise to original functionalities. In such a case, the original C3 symmetry of the TMDs cannot be preserved anymore16,17,18,19,20,21. Recent works have demonstrated that the C3 symmetry breaking induced on TMDs monolayers deposited onto rectangular lattices such as black phosphorus (bP) or silicon phosphide (SiP) leads to the appearance of a spontaneous photocurrent which can even be spin-polarized under circularly polarized light illumination17,18. Although band hybridization between layers has been evoked to possibly trigger this effect, direct experimental evidence of it is still lacking. Furthermore, the physics behind the C3 symmetry breaking in TMD monolayers remains understudied to date. These questions can be effectively addressed via a direct visualization of the electronic band structure. New developments in micro-angle-resolved photoemission spectroscopy (micro-ARPES) can now provide the necessary space resolution to study these reduced-size heterostructures with the further advantage of providing both a high energy and momentum resolution22,23,24,25,26,27,28,29.

In this work, this technique was used to directly investigate modifications of the electronic structure of monolayer MoS2 deposited on bP due to the reduction in the rotational symmetry resulting from the combination of crystals belonging to different classes. Irrespective of the twist angles, we observe a breaking of the C3 symmetry for the highest occupied MoS2 states and the opening of minigaps at the Γ valley, the properties of which depend on the orientation of the underlying bP layer. In addition, the top valence band at Γ is flat along most of the in-plane directions and undergoes a giant energy renormalization of ~140 meV leading to a switch of the VBM from the K point to the Γ point. All these effects are accounted for by first-principle simulations, indicating they derive from a strong hybridization between the Mo \({d}_{{z}^{2}}\) orbitals of the monolayer and P \({p}_{x}\) orbitals of the substrate. This understanding of the electronic structure modulation in monolayer MoS2 induced by the substrate bP involving rotational symmetry breaking and interlayer hybridization opens up possibilities for generating flat bands with arbitrary twist angles in 2D heterostructures and manipulating anisotropic properties in TMDs.

Results

C3 rotational symmetry breaking and minigap opening

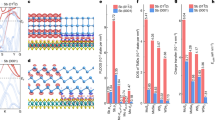
Two MoS2-bP stacks with different twist angles have been fabricated in a glove box by the dry transfer method (see the “Methods” section). A hexagonal boron nitride (BN) flake (thickness ~10 nm) has been used as a substrate, being free of dangling bonds and charge traps. A multilayer crystal of bP (thickness ~20 nm) was then deposited on it, followed by a monolayer of MoS2 (a micrograph of the stack can be seen in Supplementary Fig. 1). The twist angle θ between the layers is defined as the angle between the bP and MoS2 armchair directions (AC) or equivalently in the momentum space as the angle between the bP Γ–X direction and the MoS2 Γ–M direction (anti-clockwise angles are defined as positive), as shown in Fig. 1a. In Fig. 1b, c is given as example the direct and the reciprocal space of a stack with a twist angle of θ = 45°, as well as the superlattice obtained from the lattice coincidence method imposing a reduced strain on the primitive's lattice parameters.

Fig. 1: Schematics of MoS2-black phosphorus (MoS2-bP) superlattice and micro angle-resolved photoemission spectroscopy (micro-ARPES).
figure 1

a–c Schematics of atomic structure and corresponding Brillouin zone (BZ) of MoS2-bP superlattices, with twisted angle θ. The armchair (AC) directions of MoS2 and bP are labeled as dashed lines in panel a. d Schematic of micro-ARPES on MoS2-bP superlattices. e Scanning photoemission microscopy image (SPEM) of MoS2-bP superlattice (θ = 8.5°). The photoemission signals are integrated from the energy range of binding energy 2.1–2.3 eV and momentum range of k// = ±0.4 Å−1. Monolayer MoS2 and MoS2-bP regions are labeled in black and red dashed curves, and the measured points of micro-ARPES are labeled as circular shapes in the regions. The scale bar is 5 μm. f Determination of twisted angle θ. The angle-resolved polarized Raman spectra (ARPRS) of Ag2 vibration mode in bP with fitted curve (top) and the micro-ARPES of monolayer MoS2 at constant energy cuts of kinetic energy at valence band maximum E = EVBM (middle) and E = EVBM−0.8 eV (bottom).

Full size image

Figure 1d depicts the configuration of micro-ARPES measurements on MoS2-bP superlattices. Micro-ARPES experiments were carried out at the Spectromicroscopy beamline of the Elettra synchrotron light source using photons with energies of hν = 27 eV and hν = 74 eV (see the “Methods” section). A scanning photoemission microscopy image (SPEM) of the first MoS2-bP stack is shown in Fig. 1e (see Supplementary Fig. 2 for the optical images and the second stack). One can clearly distinguish the MoS2 and MoS2-bP regions by comparing the total photoelectron intensity in the SPEM with the optical image. The high quality of the MoS2 monolayer both in the BN and bP regions is confirmed by Raman spectra obtained after performing the micro-ARPES experiments (see Supplementary Fig. 3). The AC direction of the bP crystal can be determined by analyzing the angular dependence of the Ag2 peak intensity in angle-resolved polarized Raman spectra (ARPRS, see the “Methods” section), as shown in Fig. 1f. The monolayer MoS2 Γ–K and Γ–M directions can be extracted instead from micro-ARPES constant energy cuts at E = EVBM (kinetic energy at valence band maximum) and E = EVBM−0.8 eV. As a result, a twist angle of θ = 8.5° ± 0.5° is determined for the first MoS2-bP stack and θ = 2.4° ± 0.5° for the second one (see Supplementary Fig. 4 for θ = 2.4°).

In Fig. 2a–c are presented constant-energy cuts of the 3D micro-ARPES intensity maps taken under hν = 74 eV obtained for the pristine monolayer and the two MoS2-bP heterostructures (the Brillouin zone BZ of each material and their relative orientation are depicted in the left panels). The kinetic energy of the top Γ valley (EVBMΓ) has been used as an energy reference. For pristine MoS2, a near-circular shape is observed around Γ for energies close to the EVBMΓ (Fig. 2a) while at lower energies a hexagonal shape appears at higher momenta (see Supplementary Fig. 5). These findings confirm the isotropy of the MoS2 Γ valley and the overall reciprocal space C3 symmetry, taking into account the inequivalence between the K and K’ valleys due to spin–orbit coupling.

Fig. 2: Rotation symmetry breaking, minigap opening, and flat bands at Γ valley of MoS2-bP superlattices.
figure 2

a–c Constant energy cut maps of monolayer MoS2, MoS2-bP superlattices with θ = 8.5° and with θ = 2.4°. The corresponding BZ and orientations are depicted in the left panel. d and e Valence bands of MoS2-bP along AC, AC + 45° and zigzag (ZZ) directions in superlattices with θ = 8.5° (top) and θ = 2.4° (bottom). The valence bands of monolayer MoS2 are given for comparison in the right panel. The bands are fitted by dashed curves. The cut directions are labeled in the BZ inserted in each panel.

Full size image

C3 symmetry breaking in monolayer MoS2 can introduce Berry curvature dipole and valley magneto-electricity30,31. For both MoS2-bP heterostructures, the C3 symmetry is instead broken, as it can be clearly observed in Fig. 2b, c. Constant-energy cuts at E−EVBMΓ = 0 meV and E–EVBMΓ = −100 meV present a significant deformation along the high symmetry directions of the bP crystal, indicating an effective coupling of the MoS2 monolayer with the bP substrate. Moreover, constant energy cuts at E−EVBMΓ = −200 and −300 meV show an uneven spectral weight along the bands. This characteristic is a result of a gap opening, as evident from the band structures presented in Fig. 2d,e. The band structure of pristine monolayer MoS2 shows a parabolic dispersion at Γ from which a hole effective mass of m* = 2.3 ± 0.1me can be extracted by fitting the experimental data. Instead, minigaps are clearly visible in the band structure of MoS2 obtained from the two stacks. As one moves from the AC to the zigzag (ZZ) bP directions, these minigaps shift to larger wave vectors and decrease in width. Intriguingly, the top valence band at Γ bands undergoes a significant transformation, becoming completely flat as shown for the AC ± 45° directions. Along the ZZ direction, a small dispersion is preserved, and the extracted holes' effective masses are m* = 8.1 ± 0.1me in the θ = 8.5° sample and m* = 3.0 ± 0.1me in the θ = 2.4° sample. The origins of MoS2 band modifications and the discrepancy of effective masses along the ZZ direction between the two samples are discussed in the next section.

The observed C3 symmetry breaking, minigap opening, and band flattening in MoS2-bP superlattices are also evident at a photon energy of hν = 27 eV (see Supplementary Figs. 6 and  7). It is worth noting that photoemission signals of bP are too weak to be observed in both samples, even though they have been previously clearly observed in bulk crystals32,33,34,35. Two reasons account for the absence of the bP photoemission signal in MoS2-bP heterostructures. First, the electron mean free path for a kinetic energy of ~20 or ~70 eV is ~5 Å36, comparable to the thickness of the monolayer MoS2 (~6 Å)37, mainly explaining the absence of signal from bP in the MoS2-covered regions. Second, ultrafast surface degradation of bP is unavoidable during the fabrication process38 although this is difficult to quantify. Despite this, it is important to note that the samples are never exposed to the ambient conditions prior to the micro-ARPES measurements, which preserves most of the bP quality, as evidenced by the sharp Raman signal. Moreover, the significant band renormalization observed in the MoS2/bP heterostructure aligns well with our theoretical calculations presented in the following section, suggesting that bP plays a dominant role in the interface coupling even though the photoemission signal of bP is not evident.

Anisotropic properties of the minigaps and orbital hybridization

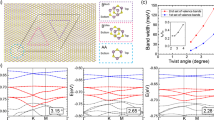
In order to further investigate the anisotropic properties of the minigaps, we extract their size, momentum, and energy position by analyzing micro-ARPES energy distribution curves (EDCs) obtained along different directions of the bP crystal; as an example in Fig. 3a, b are presented EDCs along the AC direction for the two stacks. The minigap width can be estimated from the energy distance between contiguous peaks, as indicated by the double arrow in the figure. In Fig. 3c, the results for the gap momentum position (kGap, obtained using the VBM as reference) as a function of the direction angle, and in Fig. 3d for the energy position (EGap, obtained using the Γ point as reference) are summarized. Both kGap and EGap are determined from EDCs as a function of the k-vector, as the minigap appears at positions where the peak shows an abrupt change, as illustrated in Fig. 3a, b. Both curves present a strong anisotropy which follows the bP symmetry. Furthermore, the EDCs reveal that in the broad direction domain of AC ± 60°, the higher energy peak presents a rather constant energy (see for instance, Fig. 3a, b for the AC direction). This observation indicates a flattening of the top valence band at Γ, to which is associated with a significant increase in the density of states (DOS). The same angular dependence is found for the two stacks indicating that the MoS2-bP twist angle is not critical for the generation of minigaps and flat bands. This result is in strong contrast with the case of twisted TMDs bilayers, where flat bands occur only at discrete twist “magic” angles. Indeed, flat minibands in twisted bilayer WSe₂ were experimentally observed via micro-ARPES in the Γ valley only at twist angles of 5.1°, 5.3°, and 57.4°; no flat minibands were detected in the K valleys, likely due to a reduced interlayer wavefunction overlap13,14,15.

Fig. 3: Anisotropic properties of minigaps and theory calculation of band hybridization in MoS2-bP superlattices.
figure 3

a and b Energy distribution curves (EDCs) extracted from MoS2-bP superlattices with θ = 8.5° in a and θ = 2.4° in b along AC direction from k = 0 Å−1 to k = 0.36 Å−1. The red points and red arrows indicate the peak positions and hybridized gap size, receptively. The highlighted black curves represent the approximate momentum position of the gap. c and d Extracted momentum and energy positions of hybridized minigap from micro-ARPES data and simulated intersection positions from panel g as a function of directions. e The reciprocal space of a MoS2-bP superstructure model with a twist angle of θ = 0°. f The corresponding unfolded band structure projected on the MoS2 (cyan) and bP (red) layers. g The Mo \({d}_{{z}^{2}}\) band (cyan) of monolayer MoS2 around the center of the BZ together with the P \({p}_{x}\) band (yellow) of bulk bP. The bands have been aligned accordingly to density functional theory (DFT) simulations of the heterostructure. h The unfolded bands projected onto Mo \({d}_{{z}^{2}}\) (cyan) and \({d}_{{x}^{2}+{y}^{2}}\) (magenta) and P \({p}_{x}\) orbitals (yellow).

Full size image

To gain more insight into the electronic structure at the Γ valley of MoS2, we performed complementary first-principles simulations of MoS2-bP superstructure models. The band structure of a moiré supercell heterostructure is highly folded, making it challenging to correlate with the individual components. This complexity can be addressed through the use of unfolding methods, which offer a primitive cell-effective band structure that can be compared with ARPES measurements. For heterostructures formed from layers with incommensurate lattice parameters, a supercell can be built using the lattice coincidence method. This method identifies pairs of supercells that can be combined to minimize lattice mismatch, allowing the residual strain to be distributed across one or both layers. The coincidence method is commonly used for 2D heterostructures formed by stacking two hexagonal lattices, such as graphene and h-BN, resulting in a hexagonal supercell. In our work, we extend this approach to heterostructures involving both rectangular and hexagonal lattices. For these general heterostructure models, oblique supercells are obtained, requiring both lattice parameters and angles to align, which significantly reduces the number of feasible supercells for a given strain tolerance (see Supplementary Fig. 8). Figure 3e shows the reciprocal space of a MoS2-bP superstructure model with a twist angle of θ = 0° and Fig. 3f the corresponding unfolded band structure projected on the MoS2 (cyan) and bP (red) layer. The band structure of pristine MoS2 is overlaid as a dashed curve for comparison. The simulation clearly reproduces the minigaps and band flattening in MoS2-bP superlattices observed by micro-ARPES. We further calculated the unfolded bands over a homogeneous mesh of the reciprocal space; an excellent agreement is also observed between the unfolded bands and micro-ARPES when comparing the intensity distribution at equivalent energy cuts (see Supplementary Fig. 9). Remarkably, a strong hybridized feature and additional bands along a direction parallel to Γ−Y at kx = 0.2 Å−1 are formed which we ascribe to hybridized bands and possible moiré effect in the superlattice (see Supplementary Fig. 10).

Figure 3h presents the unfolded bands projected onto Mo\({d}_{{z}^{2}}\) (cyan) and \({d}_{{x}^{2}+{y}^{2}}\) (magenta) and P\({p}_{x}\) (yellow) orbitals, demonstrating that minigaps occur due to avoid band crossing, indicating a rehybridization of MoS2 \({d}_{{z}^{2}}\) and bP\({p}_{x}\) surface orbitals; orbitals with other symmetries (see Supplementary Fig. 11) do not hybridize between the layers. Mo and P atoms are not aligned directly on top of one another, which suggests that hybridization between out-of-plane orbitals may be less significant than expected. Instead, this spatial arrangement allows for an overlap between Mo \({d}_{{x}^{2}+{y}^{2}}\) and P in-plane orbitals, which is less sensitive to the exact relative positions of atoms between the layers. Additionally, an energy and momentum match is achieved between bands with Mo \({d}_{{z}^{2}}\) and P \({p}_{x}\) characters, while these conditions are not satisfied for P \({p}_{y}\) orbitals, which lie at a lower energy level. This result is also confirmed by the simulation of a heterostructure model with a larger twist angle θ = 22° (see Supplementary Fig. 12).

Figure 3g presents the \({{\rm{Mo}}}{d}_{{z}^{2}}\) band of the perfect monolayer MoS2 around the center of the BZ together with the \({p}_{x}\) band of bulk bP; the bands have been aligned accordingly to DFT simulations of the heterostructure. The two surfaces cross in space over a line whose energy and momentum angular dependence, indicated by dashed lines in Fig. 3c, d, follows the positions of the minigaps observed in the experiments. Since the Mo \({d}_{{z}^{2}}\) band is essentially isotropic at the Γ valley, the rotation of the bP layer does not change the shape of the crossing curve but its orientation. As a result, the properties of such band modifications at the Γ valley of MoS2 are determined solely by the in-plane of bP. This simple model explains why the C3 symmetry breaking, the appearance of minigaps, and the flat band at the Γ valence valley are independent of the twist angle between MoS2 and bP. It is important to note that the Mo \({d}_{{z}^{2}}\) and P \({p}_{x}\) band alignment, determined by the work functions and doping levels of MoS2 and bP, plays a critical role in band tuning. This alignment is especially crucial in determining the effective masses of MoS2 bands along the ZZ direction, where the Mo \({d}_{{z}^{2}}\) and P \({p}_{x}\) bands do not present real intersections. As an example, let us consider the two samples shown in Fig. 2d and e: the effective masses of MoS2 bands along the ZZ direction present clearly different values, and we attribute this to slight differences in band alignment between MoS2 and bP, rather than the twist angle. First, the monolayer MoS2 is likely extrinsically doped during the fabrication process, resulting in minor differences in the doping levels of pristine MoS2 between the two samples. Additionally, the thickness of bP in the two samples is not the same, as indicated by the optical contrast, which can also contribute to variations in the P \({p}_{x}\) band. Overall, the band alignment between MoS2 and bP dominates the results of band hybridization in the MoS2-bP heterostructure.

Flat band in the VBM of monolayer MoS2

Another important effect of the interactions with the bP substrate is the displacement of the valence band maximum in the momentum space. Figure 4a–f shows the valence bands and their second derivative along the Γ−K direction in pristine monolayer MoS2 and in the two MoS2-bP heterostructures with different twist angles. The spin–orbit coupling (SOC) splitting at the K point in pristine monolayer MoS2 is observed from the second derivative data shown in Fig. 4d, while it is difficult to discern in the MoS2-bP heterostructure regions, mainly due to band broadening, as the roughness of the bP is greater than that of BN. Independently in all the presented graphs, the energy at VBM has been chosen as reference energy. As expected, in monolayer MoS2 the VBM at K is about 120 meV higher than at Γ, which shows a similar character to the previous reports39,40,41. However, in the MoS2-bP heterostructures, the relative energy positions between Γ and K are inverted, and the VBM occurs at Γ, where the flat band is located, as indicated by the black dashed lines in Fig. 4d–f. The corresponding EDCs obtained at the Γ and K points also clearly demonstrate the VBM renormalization, as presented in Fig. 4g. Once more the magnitude of this effect is the same for the two twist angles. Such flat bands at the VBM can potentially improve the transport properties or thermoelectric properties, such as the Seebeck coefficient in MoS240.

Fig. 4: Flat band in VBM of MoS2.
figure 4

a–c Micro-ARPES from pristine monolayer MoS2 (left) and MoS2-bP superlattices with θ = 8.5° (middle) and θ = 2.4° (right) along the Γ–K direction closest to AC direction. d–f The corresponding second derivatives of panels a–c. The dashed lines represent the highest energy levels at the Γ and K points. g EDCs of pristine monolayer MoS2 and MoS2-bP superlattices taken at momentum positions of Γ and K points. The VBM is indicated by the dashed line.

Full size image

This band normalization can also be observed on the calculated band structure (Fig. 3h) or on the projected density of states (see Supplementary Fig. 13). Monolayer MoS2 is a direct bandgap semiconductor with a gap at K where the highest occupied state has a \({d}_{{x}^{2}+{y}^{2}}\) character and the lowest unoccupied a \({d}_{{z}^{2}}\) character34; the top valence band at Γ is also build from \({d}_{{z}^{2}}\) orbitals. The same characters are preserved in the heterostructure (Fig. 3h), but the relative position of the states is significantly modified. The valence band maximum moves to Γ while both extrema in the K valley remain unchanged.

Discussion

In summary, we have directly investigated the electronic band structure renormalization in monolayer MoS2 at rotational symmetry mismatched interface MoS2-bP by using micro-ARPES and first principle simulations. As a result of a strong band hybridization between the Mo and P orbitals in the heterojunction, the electronic structure of MoS2 gets strongly modified with a breakdown of the C3 symmetry, the opening of anisotropic minigaps, and a flattening of the upper valence band, all irrespective of the twist angle. Moreover, a band renormalization of the order of ~140 meV is realized, which results in a transition of the VBM from K to the flat band occurring at the Γ valley. Our results clearly identify the underlying physics which is at the origin of all these effects—namely the combined effects of band hybridization and strong interlayer coupling with rotational symmetry mismatch at the heterojunction. As a result, our discoveries pave the way for extrapolating these findings to diverse heterostructures, offering a novel avenue to manipulate rotational symmetry and valley renormalization in TMDs, without relying on external pressure or conventional methods of controlling twisted angles. More generally, the flat band generated at the VBM of TMDs offers a highly tunable platform for studying strongly correlated physics, given the large effective masses and relatively strong electron–electron interactions that TMDs exhibit. Notably, previous transport studies have shown that the Fermi level can reach the flat band through effective gating in TMD devices. In the rotation symmetry mismatched MoS2-bP interface we proposed, the anisotropic band flattening at the VBM of MoS2 expands the platform for exploring anisotropic strongly correlated physics in monolayer TMDs. Moreover, the C3 rotational symmetry breaking, which originates from band hybridization, offers the potential for non-linear physics applications, such as the generation of shift current in TMDs-bP-based photovoltaic devices. Overall, our results reveal a wide range of possibilities to discover in TMDs anisotropic behaviors and exotic physical phenomena, such as the appearance of strongly correlated phases associated with flat bands.

Methods

Sample preparation

In the sample fabrication process, we used the dry transfer method to fabricate MoS2-bP superlattices in the glove box. Firstly, multilayer BN, multilayer bP, and monolayer MoS2 were exfoliated onto different silicon oxide–silicon (SiO2-Si) substrates, respectively. The MoS2-bP vertical structures were fabricated by stacking flakes together with high precision under optical microscopy. Firstly, monolayer MoS2 was transferred onto a polycarbonate (PC) film on polydimenthylsilosane (PDMS) stamp. Secondly, the bP flake was well aligned by PDMS-PC-MoS2 and then peeled off from SiO2–Si substrate, forming PDMS-PC-MoS2-bP structure. Thirdly, the BN flake was continually transferred onto PDMS-PC-MoS2-bP and thus giving PDMS-PC-MoS2-bP-BN structure by using a similar way. The PDMS-PC-MoS2-bP-BN was placed on Au/SiO2/Si substrate, and then the PDMS stamp was smoothly peeled off from PC-MoS2-bP-hBN after heating it at ~120 °C. At last, the PC film was removed by washing the PC-MoS2-bP-BN in chloroform solvent, followed by drying in the glove box.

Micro-ARPES experiments

Micro-ARPES measurements of MoS2-bP superlattices were performed at the spectromicroscopy beamline of the Elettra light source in Italy. In order to clean the sample surface, the samples were annealed at ~200 °C for 3 h in the preparation chamber under ultrahigh vacuum before micro-ARPES experiments. The pressure in the experimental chamber was better than 1 × 10−10 mbar during micro-ARPES measurements. At Spectromicroscopy beamline, lineally p-polarized light with a fixed incident angle of 45° was focused to ~600 nm by Schwartzschild objective. Momentum space mapping was carried out by the rotation of a hemispherical analyzer. All the experiments were performed at T = ~ 95 K with photon energy of hν = 27 eV and hν = 74 eV. The overall energy and momentum resolution of the experiment was ~45 meV and 0.005 Å−1.

ARPRS experiments

ARPRS experiments on MoS2-bP superlattices with θ = 8.5° and θ = 2.4° were performed on Renishaw and Horiba Raman spectrometers, respectively. A continuous Argon laser with a wavelength of 514 nm (Renishaw) and 532 nm (Horiba) through ×100 objective lens was used to excite the sample. The incident light passing through a linear polarizer was reflected by a beam splitter. A half-wave plate was positioned between the beam splitter and the objective lens in order to rotate the polarization of the incident light. Another half-wave plate was positioned in the collection path, followed by a linear polarizer to select the polarization of interest from the scattered light, which was subsequently detected by a CCD camera. The samples were rotated at a step of 10° in order to explore Raman anisotropy of black phosphorus, and the MoS2-bP area was chosen for the measurement.

Computational details

DFT calculations have been performed using the OpenMX code42. The exchange-correlation potential was expressed in the generalized gradient approximation using the Perdew–Burke–Ernzerhof (PBE) schema. Norm conserving full relativistic pseudopotentials, including a partial core correction and spin–orbit coupling, was used. Dispersion interactions have been included using the Grimme-D2 method43. A basis set of optimized numerical pseudo-atomic orbitals was employed as provided by the OpenMX 2019 database. Band unfolding has been performed over a homogeneous mesh of the reciprocal space according to the method presented in refs. 44,45. An energy broadening of 50 meV has been employed to produce all band unfolding figures.

For the structure model: MoS2 and bP have incommensurable lattice parameters and therefore a moiré supercell cannot be constructed from a simple superposition of the layers but small lattice deformations must be imposed. For band structure calculation with twist angle θ = 0°, a minimal moiré supercell model for the bP-MoS2 heterostructure on which the AC MoS2 and BP directions are aligned can be built from supercells obtained from the transformation matrix \({\left(\begin{array}{cc}5 & 0\\ 0 & 1\end{array}\right)}_{{{\rm{bP}}}}\) and \({\left(\begin{array}{cc}4 & -4\\ 1 & 1\end{array}\right)}_{{{{\rm{MoS}}}}_{2}}\). To minimize spurious effects on the MoS2 electronic structure, a moiré supercell has been built by imposing all lattice deformations only to the bP slab (a stretch of about 0.4% along a and a strain of about 3.8% along b). A slab of six phosphorous atomic planes provides an accurate representation of the bP electronic structure.