Elliptic anisotropy measurement of the f₀(980) hadron in proton-lead collisions and evidence for its quark-antiquark composition

Abstract

Despite the f₀(980) hadron having been discovered half a century ago, the question about its quark content has not been settled: it might be an ordinary quark-antiquark (${{\rm{q}}}\overline{{{\rm{q}}}}$) meson, a tetraquark (${{\rm{q}}}\overline{{{\rm{q}}}}{{\rm{q}}}\overline{{{\rm{q}}}}$) exotic state, a kaon-antikaon (${{\rm{K}}}\overline{{{\rm{K}}}}$) molecule, or a quark-antiquark-gluon (${{\rm{q}}}\overline{{{\rm{q}}}}{{\rm{g}}}$) hybrid. This paper reports strong evidence that the f₀(980) state is an ordinary ${{\rm{q}}}\overline{{{\rm{q}}}}$ meson, inferred from the scaling of elliptic anisotropies (v₂) with the number of constituent quarks (n_q), as empirically established using conventional hadrons in relativistic heavy ion collisions. The f₀(980) state is reconstructed via its dominant decay channel f₀(980) → π⁺π⁻, in proton-lead collisions recorded by the CMS experiment at the LHC, and its v₂ is measured as a function of transverse momentum (p_T). It is found that the n_q = 2 (${{\rm{q}}}\overline{{{\rm{q}}}}$ state) hypothesis is favored over n_q = 4 (${{\rm{q}}}\overline{{{\rm{q}}}}{{\rm{q}}}\overline{{{\rm{q}}}}$ or ${{\rm{K}}}\overline{{{\rm{K}}}}$ states) by 7.7, 6.3, or 3.1 standard deviations in the p_T < 10, 8, or 6 GeV/c ranges, respectively, and over n_q = 3 (${{\rm{q}}}\overline{{{\rm{q}}}}{{\rm{g}}}$ hybrid state) by 3.5 standard deviations in the p_T < 8 GeV/c range. This result represents the first determination of the quark content of the f₀(980) state, made possible by using a novel approach, and paves the way for similar studies of other exotic hadron candidates.

Introduction

One of the most intriguing puzzles in quantum chromodynamics (QCD), the theory describing the strong interaction, is the phenomenon of confinement. Confinement is the peculiar feature of the QCD color charges that they cannot be separated and are fatefully confined in color-neutral bound states known as hadrons. The mechanism for the color confinement is still not well understood. A hadron can be the usual quark-antiquark (${{\rm{q}}}\overline{{{\rm{q}}}}$) meson or three-quark (qqq) baryon, but it has been suggested that there also exist less conventional, “exotic” forms, such as tetraquarks or meson molecules (${{\rm{q}}}\overline{{{\rm{q}}}}{{\rm{q}}}\overline{{{\rm{q}}}}$), pentaquarks (${{\rm{q}}}\overline{{{\rm{q}}}}{{\rm{q}}}{{\rm{q}}}{{\rm{q}}}$), and dibaryons (qqqqqq)^1,2,3, where q stands for a constituent quark of any flavor. Studies of these exotic states can significantly advance our understanding of how partons can form bound states and in which configurations. This knowledge is fundamental for a deeper understanding of QCD, especially in its nonperturbative regime^4,5.

Exotic hadrons are expected to be short-lived and decay into ordinary hadrons, making it challenging to decipher their original parton structure. The first evidence of a tetraquark or a molecular state, X(3872), was reported by the Belle experiment at KEK⁶. Experiments at the CERN LHC, particularly LHCb, have recently observed several new candidates for tetraquarks and pentaquarks, as discussed, e.g., in ref. ⁷. Those candidates all involve heavy quarks, which implies that their properties can be calculated in nonrelativistic QCD^8,9.

However, similar calculations are hard to perform for hadrons built of only light quarks, as one has to use relativistic QCD in its nonperturbative regime. In particular, the f₀(980) hadron, discovered 50 years ago^10,11,12, has been hypothesized to be an ordinary ${{\rm{q}}}\overline{{{\rm{q}}}}$ meson, a tetraquark state, a ${{\rm{K}}}\overline{{{\rm{K}}}}$ molecule, or a ${{\rm{q}}}\overline{{{\rm{q}}}}$-gluon hybrid state^{13,14,15,16,17,18}. The suggestion that the f₀(980) hadron can be a tetraquark extends beyond the ground-state constituent quark model, and studies of such states would impact our understanding of QCD and color confinement. Despite a multitude of experimental and theoretical works, the nature of the f₀(980) state has not yet been established, as is evident from ref. ¹⁹ and references therein.

This is where high-energy nuclear collisions may come to the rescue. The collisions of lead-lead (PbPb) ions at the LHC aim to recreate the quark-gluon plasma (QGP), widely believed to be the state of matter prevailing in the early universe, when the temperature and energy density were too high to allow for the formation of hadrons. They offer a universal laboratory to study various aspects of QCD, such as the formation of hadrons from the QGP hadronization. A large number of hadron species, presumably including exotic ones, are abundantly produced during and following the phase transition from the QGP to hadronic matter. Indeed, evidence for the production of the X(3872) exotic state in PbPb collisions was reported by the CMS experiment²⁰. The QGP phase transition (hadronization), intimately connected to color confinement, is being extensively studied, both experimentally and theoretically. A viable way to describe hadronization is via the coalescence of quarks, now dressed with gluons over the phase transition, into hadrons. The coalescence model was initially proposed to describe the formation of deuterons in targets exposed to proton beams²¹ and is now commonly used to model hadronization in relativistic nuclear collisions^{22,23,24,25,26}.

In heavy ion collisions, the azimuthal distribution of produced particles is anisotropic. The anisotropy is believed to result from the interactions among quarks and gluons created in these collisions, converting the initial approximately elliptical ("almond-like”) overlap region of the colliding nuclei with a nonzero impact parameter into the anisotropy of particle momenta²⁷. It is noteworthy that the collision geometry anisotropy is generic and also present in head-on heavy ion collisions, as well as in proton-proton (pp) and proton-nucleus collisions, arising from fluctuations in the distribution of constituents inside the colliding objects²⁸. While it initially came as a surprise when momentum anisotropy was first observed in pp^29,30,31,32 and proton-lead (pPb)^{33,34,35,36,37,38,39,40} collisions, it is by now a well-established fact. This momentum anisotropy of quarks is then inherited by the formed hadrons, thus providing information that can be used to experimentally determine the quark content of the hadrons⁴¹, as explained below. Since the anisotropy has been established at the LHC energies in PbPb, pPb, and even pp collisions with high multiplicity of particles produced, any of these colliding systems can be used for this type of measurements.

Azimuthal distributions of particles are often described by a Fourier series⁴²,

$$\frac{{{\rm{d}}}N}{{{\rm{d}}}\phi }\propto 1+{\sum }_{n=1}^{\infty }2{v}_{n}\cos [n(\phi -{\psi }_{n})],$$

(1)

where ϕ is the azimuthal angle of the particle momentum vector and ψ_n is the azimuthal angle of the nth harmonic plane, defined in each event such that ${\sum }_{i}\sin [n({\phi }_{i}-{\psi }_{n})]=0$, where the index i runs over all particles in an event. Details on the reconstruction of the harmonic planes using event observables are given in the Methods section. The coefficients v_n, called anisotropic flow parameters, generally depend on the particle transverse momentum (p_T) and rapidity (y). The v₂ coefficient, called the elliptic flow, describes the dominant anisotropic component. The second-order harmonic plane angle ψ₂ is an approximation of the azimuthal angle of the reaction plane, which is defined by the line connecting the centers of the colliding nuclei and the beam line.

In the coalescence picture, illustrated in Fig. 1, quarks with close spatial positions and momenta are more likely to combine and, therefore, the anisotropic flow coefficients v_n of the formed hadron inherit those of the parent quarks (v_n,q). If n_q quarks with approximately equal momenta combine to form a hadron, the resulting azimuthal distribution is then given by

$$\frac{{{\rm{d}}}{N}_{{{\rm{h}}}}}{{{\rm{d}}}\phi }\propto {\left(\frac{{{\rm{d}}}{N}_{{{\rm{q}}}}}{{{\rm{d}}}\phi }\right)}^{{n}_{{{\rm{q}}}}}\propto {\left[1+{\sum }_{n=1}^{\infty }2{v}_{n,{{\rm{q}}}}({p}_{{{\rm{T}}}}^{{{\rm{q}}}})\cos (n[\phi -{\psi }_{n}])\right]}^{{n}_{{{\rm{q}}}}},$$

(2)

where ${p}_{{{\rm{T}}}}^{{{\rm{q}}}}={p}_{{{\rm{T}}}}/{n}_{{{\rm{q}}}}$, and N_h (N_q) is the multiplicity of hadrons (quarks). For small values of v_n, relevant for the measurement reported in this paper, one can simplify Eq. (2) as

$${v}_{n}({p}_{{{\rm{T}}}})\approx {n}_{{{\rm{q}}}}{v}_{n,{{\rm{q}}}}({p}_{{{\rm{T}}}}/{n}_{{{\rm{q}}}}).$$

This expression is commonly referred to as the number of constituent quarks (NCQ) scaling of the anisotropic flow⁴³. The anisotropic flow of hadrons formed in heavy ion collisions can therefore reveal the NCQ n_q contained in a hadron, conventional or exotic⁴¹. Alternatively, such information can also be extracted by measuring the yields and p_T spectra (or their ratios) of these hadrons in heavy ion collisions, albeit in a more model-dependent way^44,45,46,47.

Fig. 1: Coalescence hadronization.

This picture illustrates the formation of hadrons in heavy-ion collisions in the coalescence model. Hadrons tend to form when the constituent quarks have similar positions and momenta. [Detector image reprinted from ref. ⁶⁹, under a CC BY SA 4.0 license].

The NCQ scaling has been observed to approximately hold for common hadrons in heavy ion collisions at the BNL RHIC^48,49 and at the CERN LHC^38,50,51. It has also been established in pPb collisions at the LHC by the CMS experiment for ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω hadrons^38,52. These observations of the NCQ scaling support the validity of the coalescence hadronization model, at least at low p_T. We note that the NCQ scaling may additionally arise from other mechanisms in the same or an extended p_T range. The empirical observations of the NCQ scaling do not depend, however, on a particular underlying physics mechanism.

This paper presents the first measurement of the elliptic flow of the f₀(980) state. Data from pPb collisions at a nucleon-nucleon center-of-mass energy of $\sqrt{{s}_{{{\rm{NN}}}}}=8.16\,\,{\mbox{TeV}}$ are used. The choice of pPb collisions used in this measurement is driven by the smaller combinatorial background than in PbPb collisions, which simplifies the f₀(980) signal extraction. The elliptic flow coefficient v₂ of the f₀(980) state is determined as a function of p_T. The NCQ scaling of the f₀(980) hadron v₂ coefficient is tested. We demonstrate that the hypothesis of the f₀(980) state being an ordinary ${{\rm{q}}}\overline{{{\rm{q}}}}$ meson is significantly preferred over alternative hypotheses. This novel technique could be used to investigate other exotic hadron candidates. The numeric values from various figures presented in this paper can be found in the HEPData database⁵³.

Results

Analysis of f ₀(980) signal

In this paper, the f₀(980) state is measured in pPb collisions at $\sqrt{{s}_{{{\rm{NN}}}}}=8.16\,\,{\mbox{TeV}}$ by the CMS experiment. The CMS detector is described in Methods. A high-multiplicity data sample collected in 2016 is used, corresponding to an integrated luminosity of 186 nb^−1 54. The charged-particle multiplicity range is chosen to be 185 ≤ N_trk < 250. The N_trk multiplicity observable is defined in ref. ⁵², and its range is chosen to be identical to the one used in that measurement, where significant anisotropic flow has been observed, and to which we compare the NCQ scaling of the f₀(980) measurement. The triggers and event selections are identical to those in ref. ⁵⁵, as discussed in more detail in the Methods section.

The f₀(980) state is reconstructed within the rapidity ∣y∣ ≲ 2.4 via its dominant decay channel, f₀(980)→π⁺π^− 19. The pion mass is assigned to all charged-particle tracks. The combinatorial background is modeled via same-charge-sign pion track pairs and subtracted from the opposite-charge-sign dipion mass spectrum. The resulting distribution is then fit to extract the f₀(980) yield. The fit model includes a sum of three Breit–Wigner functions^56,57,58,59 corresponding to the f₀(980), ρ (770)⁰, and f₂(1270) resonances, and a third-order polynomial for the residual background. Details of the fit procedure are described in the Methods section.

The observed elliptic flow v₂ of the f₀(980) state is extracted by fitting the yield as a function of ϕ. The contamination from nonflow correlations—those unrelated to the nuclear collision geometry—is subtracted. After nonflow-contamination subtraction, the elliptic flow coefficient is denoted by ${v}_{2}^{{{\rm{sub}}}}$. More details can be found in the Methods section.

In order to compare the ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}$ values to the established NCQ scaling for other hadrons, the v_n,q of ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω states measured in the same high-multiplicity range are fit with the following empirical function derived from data:

$$f(K{E}_{{{\rm{T}}}}/{n}_{{{\rm{q}}}})=K{E}_{{{\rm{T}}}}/{n}_{{{\rm{q}}}}\left({p}_{0}+{p}_{1}K{E}_{{{\rm{T}}}}/{n}_{{{\rm{q}}}}\right)\,{{{\rm{e}}}}^{-{p}_{2}K{E}_{{{\rm{T}}}}/{n}_{{{\rm{q}}}}}.$$

(3)

The argument of the function, KE_T/n_q, is related to the kinetic energy per constituent quark, where $K{E}_{{{\rm{T}}}}=\sqrt{{m}^{2}+{\langle {p}_{{{\rm{t}}}}\rangle }^{2}}-m$, 〈p_t〉 is the average p_T of a p_T bin of the corresponding bound state, and m is its invariant mass. The f₀(980) 〈p_t〉 values of the p_T bins are obtained from an exponential fit to the f₀(980) candidate dN/dp_T distribution. The KE_T variable is chosen to describe the NCQ scaling as it yields better agreement with the data than p_T⁴⁹. The NCQ scaling fit is based on the minimization of the χ², assuming that the bin-by-bin uncertainties are uncorrelated, with the coefficients p_i (i = 0, 1, 2) being free parameters of the fit. Details about the n_q extraction and about testing of various quark content hypotheses can be found in the Methods section.

Systematic uncertainties

Systematic uncertainties in the f₀(980) v₂ and ${v}_{2}^{{{\rm{sub}}}}$ are detailed in the Methods section. The correlation of systematic uncertainties between different p_T bins is taken into account by using a covariance matrix in the χ² calculation when extracting n_q. The statistical uncertainty in the f(KE_T/n_q) fit is also included as a systematic uncertainty component in the extracted n_q. The n_q extraction procedure is repeated for variations in the functional form of f(KE_T/n_q), as well as by using p_T instead of E_T in the NCQ scaling expression given by Eq. (3) (as discussed in the Methods section). The resulting difference in n_q from the default value is taken as the corresponding systematic uncertainty. The systematic uncertainties are listed in Table 1. The uncertainty in the 〈p_t〉 of the f₀(980) state has a negligible impact on n_q.

Table 1 Sources and magnitudes of the uncertainties in the extracted n_q of the f₀(980) state in the range p_T < 10 GeV/c

Elliptic anisotropy of f ₀(980)

Figure 2 shows the ${v}_{2}^{{{\rm{sub}}}}$ of the f₀(980) state, which is significantly above zero and exhibits a clear trend of rising and then falling with p_T, reaching a maximum in the 4 < p_T < 6 GeV/c range. Such a trend in p_T has been also observed for other hadrons and is generally considered to come from an interplay between the hydrodynamic expansion at low p_T and partonic energy loss at high p_T.

Fig. 2: Elliptic anisotropy results.

The nonflow-effect-subtracted elliptic anisotropy ${v}_{2}^{{{\rm{sub}}}}$ of the f₀(980) is shown as a function of p_T within ∣y∣ ≲ 2.4 in high-multiplicity pPb collisions. The error bars show statistical uncertainties while the shaded areas represent systematic uncertainties.

Quark content of f ₀(980)

Figure 3 shows a comparison of ${v}_{2}^{{{\rm{sub}}}}/{n}_{{{\rm{q}}}}$ for the f₀(980) state with those of ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω hadrons⁵² as a function of KE_T/n_q. (A similar comparison for ${v}_{2}^{{{\rm{sub}}}}/{n}_{{{{\rm{q}}}}}$ as a function of p_T/n_q can be found in the Methods section.) The two sets of the f₀(980) data points correspond to the n_q = 2 and 4 hypotheses. The red curve shows the NCQ scaling parameterization of the ${v}_{2}^{{{\rm{sub}}}}$ data for these other hadrons (whose n_q values are fixed by their known quark content).

Fig. 3: NCQ scaling of elliptic anisotropy.

The ${v}_{2}^{{{\rm{sub}}}}/{n}_{{{\rm{q}}}}$ of the f₀(980) state (for the n_q = 2 and 4 hypotheses) as a function of KE_T/n_q, compared with those of ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω strange hadrons⁵² in high-multiplicity pPb collisions. The error bars show statistical uncertainties while the shaded areas represent systematic uncertainties. The red curve is the NCQ scaling parameterization of the data for ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω hadrons given by Eq. (3).

To assess the significance of the result, the log-likelihood ratio $-2\ln ({L}_{{n}_{{{\rm{q}}}}=4}/{L}_{{n}_{{{\rm{q}}}}=2})$ is calculated using the ${v}_{2}^{{{\rm{sub}}}}/{n}_{{{\rm{q}}}}$ data and the NCQ scaling expectation between the n_q = 2 and 4 assumptions. Details about the log-likelihood ratio can be found in the Methods section. The measured value is shown by the red arrow in Fig. 4, together with the distributions of the log-likelihood ratio from pseudo-experiments. The ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}$ values are generated according to the NCQ scaling under the n_q = 2 and 4 hypotheses, with a Gaussian smearing to account for the uncertainties. The extracted significance of the n_q = 2 hypothesis over the n_q = 4 hypothesis is 7.7 standard deviations (σ) in the p_T < 10 GeV/c range. As shown in Fig. 3, the NCQ scaling range as delineated by the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$ data extends up to p_T/n_q of 4 GeV/c, whereas for the baryons it is restricted to about 2.5 GeV/c. For the n_q = 2 hypothesis, our high-p_T data start falling out of the measured NCQ scaling p_T/n_q range; for the n_q = 4 hypothesis, however, our data are within that range. Consequently, we extract significance values also for two restricted-p_T ranges: p_T < 8 and 6 GeV/c. The exclusion significances of the n_q = 4 vs. 2 hypotheses in these ranges are 6.3 and 3.1σ, respectively.

Fig. 4: Exclusion significance from n_q = 4.

The log-likelihood ratio distributions for the n_q = 2 and 4 hypotheses from pseudo-experiments, together with the measured value for the f₀(980) state in the 0 < p_T < 10 GeV/c range.

The ${{\rm{K}}}\overline{{{\rm{K}}}}$ molecule, if produced by the coalescence of two kaons, would possess the same v₂ as that of a tetraquark, and is thus practically also ruled out. It is unclear what v₂ a hybrid ${{\rm{q}}}\overline{{{\rm{q}}}}{{\rm{g}}}$ state would attain in pPb collisions because the NCQ scaling has been tested only with ordinary hadrons. If the constituent gluon behaves just like the constituent (anti)quarks, the v₂ of a hybrid ${{\rm{q}}}\overline{{{\rm{q}}}}{{\rm{g}}}$ state would scale as n_q = 3. Such a state would be ruled out with a 3.5σ significance using the p_T < 8 GeV/c range, in which the NCQ scaling is adequately measured for the n_q = 3 case.

The χ² quantity is calculated between the v_n,q data of the f₀(980), with floating n_q, and the NCQ curve in KE_T/n_q in Fig. 3, with the covariance matrix taking into account correlations among uncertainties. Scans of χ² versus n_q are performed, as detailed in the Methods section. Using f₀(980) data within the p_T < 6 GeV/c range (a conservative choice, which ensures that the NCQ scaling holds for the n_q = 2 hypothesis, given that p_T/n_q < 3 GeV/c), the preferred n_q value of the f₀(980) is found to be n_q = 2.40 ± 0.40. Assuming the NCQ scaling extends beyond p_T/n_q ~3 GeV/c, the preferred n_q values of 2.10 ± 0.24 and 2.07 ± 0.21 are extracted in the p_T < 8 and 10 GeV/c ranges, respectively. Indeed, the n_q = 2 hypothesis for f₀(980) is consistent with the NCQ scaling from the other hadrons, with χ² = 4.7 for the 5 data points. Contrary to that, the n_q = 4 hypothesis is inconsistent with the data, as evident from the corresponding χ² = 58, with a Gaussian p value of 3 × 10⁻¹¹. Consequently, we report a strong evidence for the ${{\rm{q}}}\overline{{{\rm{q}}}}$ quark content of the f₀(980) state.

Discussion

The f₀(980) state is observed in the π⁺π⁻ invariant mass distribution of high-multiplicity proton-lead collisions at $\sqrt{{s}_{{{\rm{NN}}}}}=8.16\,\,{\mbox{TeV}}$, using data collected by the CMS experiment in 2016 and corresponding to an integrated luminosity of 186 nb⁻¹. The elliptic flow anisotropy v₂ of the f₀(980) state is measured as a function of p_T up to 10 GeV/c, with respect to the second-order harmonic plane reconstructed from forward/backward energy flow. After subtracting the nonflow contamination, evaluated from ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$ measurements, we obtain the corrected ${v}_{2}^{{{\rm{sub}}}}$ observable. By comparing the ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}$ to those of ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω under the number-of-constituent-quarks scaling hypothesis, we rule out the hypotheses that the f₀(980) is a tetraquark state or a ${{\rm{K}}}\overline{{{\rm{K}}}}$ molecule, in favor of an ordinary ${{\rm{q}}}\overline{{{\rm{q}}}}$ meson hypothesis, at 7.7σ (6.3 or 3.1σ, respectively, if only a restricted range of p_T < 8 or 6 GeV/c is considered). The f₀(980) data in the p_T < 8GeV/c range are found to disfavor a quark-antiquark-gluon hybrid state at 3.5σ. The NCQ of the f₀(980) state, as extracted from a fit to the ${v}_{2}^{{{\rm{sub}}}}$ data, is consistent with the value of 2, characteristic of an ordinary meson. Consequently, we find strong evidence that the f₀(980) hadron is a normal quark-antiquark state. We believe that the results reported in this paper offer a solution to a half-century-old puzzle.

The experimental determination of the quark content of the f₀(980) state with high confidence, using this novel approach, is expected to stimulate further experimental investigations as well as theoretical studies. It paves the way for studies of other exotic hadron candidates using the collective flow scaling approach in high-multiplicity proton-nucleus and heavy ion collisions.

Methods

In this section, we provide experimental details of various steps used in the analysis presented in this paper.

CMS detector

The central feature of the CMS apparatus is a superconducting solenoid of 6 m internal diameter, providing a magnetic field of 3.8 T. Within the solenoid volume are a silicon pixel and strip tracker, a lead tungstate crystal electromagnetic calorimeter (ECAL), and a brass and scintillator hadron calorimeter (HCAL), each composed of a barrel and two endcap sections. Forward calorimeters extend the pseudorapidity coverage provided by the barrel and endcap detectors. Muons are measured in gas-ionization detectors embedded in the steel flux-return yoke outside the solenoid. The silicon tracker measures charged particles within the range ∣η∣ < 2.5. For nonisolated particles of 1 < p_T < 10 GeV/c and ∣η∣ < 1.4, the track resolutions are typically 1.5% in p_T and 25–90 (45–150) μm in the transverse (longitudinal) impact parameter⁶⁰. The procedure followed for aligning the detector is described in ref. ⁶¹.

Trigger

Events of interest are selected using a two-tiered trigger system, a suite of triggers based on particle multiplicity. The first level (level-1), composed of custom hardware processors, uses information from the calorimeters and muon detectors to select events at a rate of around 100 kHz within a fixed latency of 4 μs⁶². At level-1, where tracking information is not available, the events were seeded using a tower count in the ECAL and HCAL barrel calorimeters, by selecting events passing a minimum threshold on the number of active towers. An active tower is defined as a trigger tower with a transverse energy exceeding 0.5 GeV. Trigger towers are built by summing energy deposits in the ECAL and HCAL cells in Δη × Δϕ = 0.087 × 0.087 regions (matching the size of one HCAL cell in the barrel region). The trigger required the tower count to exceed either 115 or 120, depending on the data-taking period.

The second level, known as the high-level trigger, consists of a farm of processors running a version of the full event reconstruction software optimized for fast processing, and reduces the event rate to around 1 kHz before data storage⁵⁴. Several high-level triggers based on the multiplicity of tracks reconstructed either in the pixel detector layers or the full tracker were used for the analysis. The events were first selected requiring more than 125 tracks with p_T > 0.4 GeV/c, ∣η∣ < 2.4, and the distance of closest approach along the beam axis between the track and the interaction vertex of less than 0.12 cm, reconstructed using only the pixel detector. Further, the events were required to have more than 185 tracks reconstructed in the full tracker with the same p_T and ∣η∣ requirements, and with the distance of closest approach less than 0.15 cm. The interaction vertex is required to be within 15 cm of the detector center along the beam direction. Offline, we require the number of reconstructed tracks, N_trk, to be between 185 and 250. The trigger turn-on effect has been shown to have a negligible impact on the result.

More detailed descriptions of the CMS detector, together with a definition of the coordinate system used and the relevant kinematic variables, can be found in refs. ^63,64.

Event selection and reconstruction of the f₀(980) signal

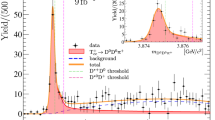
The f₀(980) candidates are reconstructed through the dominant decay channel, f₀(980)→π⁺π^− 19. All charged-particle tracks with p_T > 0.4GeV/c and ∣η∣ < 2.4 passing standard high-purity requirements⁶⁰, and with a distance of closest approach to the interaction vertex divided by its uncertainty of less than 3 in both the direction along the beams and in the plane perpendicular to it, are considered as pion candidates. To improve the mass resolution, we only consider tracks with a relative uncertainty in p_T of less than 10%. The f₀(980) candidates are formed from pairs of tracks of opposite-charge-sign, with the charged pion mass assigned to both. The combinatorial background is estimated from same-charge-sign track pairs and is subtracted from the invariant mass spectrum of the f₀(980) candidates. The spectrum is further corrected for the tracking efficiency as a function of the track p_T and η, as obtained via a hijing v1.0 simulation⁶⁵ followed by the CMS detector response simulation with Geant4⁶⁶. The analysis is performed in bins of ϕ–ψ₂, the azimuthal angle of the f₀(980) candidate relative to that of the second harmonic plane. The latter is reconstructed from the energy deposition in the hadron forward (HF) calorimeter covering 3 < η < 5 in the Pb-going direction (resulting in a better resolution compared to that using the opposite HF calorimeter) and corrected for the nonuniform detector performance by using the procedure described in ref. ⁴². Figure 5 shows an example of the invariant mass spectrum of the f₀(980) candidates within a p_T range of 4–6 GeV/c and a ϕ–ψ₂ range of 0–π/12 (where the ϕ–ψ₂ value is first folded from the full range into the 0–π/2 range to decrease the statistical uncertainty per ϕ − ψ₂ bin).

Fig. 5: Invariant mass fit.

The invariant mass spectrum of opposite-sign pion pairs after the combinatorial background subtraction, for the pair transverse momentum 4 < p_T < 6 GeV/c and the azimuthal angle 0 < ϕ–ψ₂ < π/12, in high-multiplicity pPb collisions. The solid blue curve is the fit result within the fit range marked with vertical blue dashed lines; the orange dashed curve represents the residual background. The solid red curve represents the f₀(980) signal, while the dashed dark-violet and light-green curves correspond to the background contributions from the ρ (770)⁰ and f₂ (1270) resonances, respectively. The ratio between data and the fit result is shown in the lower panel, with the error bars representing statistical uncertainties only. The low-mass region exhibits a nontrivial turn-on behavior and is not included in the fit.

Several resonances are evident in the mass spectrum shown in Fig. 5, including a significant f₀(980) peak at  ~0.98 GeV/c². The mass spectrum is fit with a template composed of three Breit–Wigner functions corresponding to the ρ (770)⁰, f₀(980), and f₂ (1270) resonances, and a third-order polynomial to model the residual background. The fit mass range is chosen to be 0.8–1.7 GeV/c² in order to exclude the contribution from a ρ (1700) peak at high masses and to avoid the low-mass region (<0.8 GeV/c²) exhibiting a nontrivial turn-on behavior. Since only the right tail of the ρ (770)⁰ resonance is included in the fit, the extrapolated peak into the lower mass region does not necessarily represent the true shape of the ρ (770)⁰ resonance. The ϕ-integrated mass spectrum is fit in each p_T interval to obtain the f₀(980) yield and the line-shapes of the three resonances present within the fit window. The resonant line-shapes are then fixed, and the fit of the mass spectrum is repeated in six individual ϕ–ψ₂ bins in the corresponding p_T interval, treating the resonance yields as free parameters. The resultant fit to the example ϕ–ψ₂ bin of the p_T interval is superimposed in Fig. 5, along with the χ² of the fit per degree of freedom (dof).

Extraction of f ₀(980) elliptic anisotropy v₂ values

Figure 6a shows the f₀(980) yield as a function of ϕ–ψ₂ in the 4 < p_T <  6 GeV/c bin as an example. The f₀(980) yield as a function of ϕ–ψ₂ is fit with Eq. (1) with only the n = 2 term to extract the v₂ parameter. The fitted v₂ values are corrected for the harmonic plane resolution, which represents the precision of the reconstructed ψ₂. The resolution is obtained by the three-subevent method⁴² and evaluated in each fine multiplicity interval, and an average resolution is obtained weighted by the corresponding ϕ-integrated yield of f₀(980). The three-subevent method uses the two HFs and the central tracker detector, where the η gaps between the subevents help suppress the nonflow effects. Figure 6b shows the corrected v₂ of the f₀(980) as a function of p_T.

Fig. 6: Elliptic anisotropy before the nonflow effect subtraction.

a The f₀(980) yield in the 4 < p_T < 6 GeV/c range as a function of ϕ–ψ₂ in high-multiplicity pPb collisions. Error bars show statistical uncertainties. The red curve is a fit to Eq. (1) with only the n = 2 term, from which the elliptic anisotropy v₂ parameter is extracted. b The elliptic anisotropy v₂ of the f₀(980) state is shown before the nonflow effect subtraction as a function of p_T within rapidity ∣y∣ ≲ 2.4 in high-multiplicity pPb collisions. The error bars show statistical uncertainties while the shaded areas represent systematic uncertainties.

The v₂ measurement is contaminated by nonflow correlations, such as back-to-back jet pairs, where an f₀(980) candidate is found within a jet and the harmonic plane is reconstructed from hadrons that include the other fragments of the dijet system. Since f₀(980) is a hadron known to likely contain strange quarks, the relative nonflow contribution $({v}_{2}-{v}_{2}^{{{\rm{sub}}}})/{v}_{2}$ to the f₀(980) v₂ is assumed to be the same as that for the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$ meson, in each p_T bin, where ${v}_{2}^{{{\rm{sub}}}}$ represents the elliptic flow after nonflow-effect subtraction. The latter, evaluated using events with low track multiplicity⁵², is fit with a second-order polynomial as a function of p_T. The relative nonflow contribution to the f₀(980) v₂ is evaluated from the fit function at the 〈p_t〉 in each p_T bin and ranges 9–64% for different p_T bins. The nonflow effects are subtracted to obtain the final ${v}_{2}^{{{\rm{sub}}}}$ of the f₀(980) state. The ${v}_{2}^{{{\rm{sub}}}}$ of the f₀(980) is shown in Fig. 2 as a function of p_T.

Systematic uncertainties in f ₀(980) v₂ values

The systematic uncertainties in the f₀(980) yield, and consequently those in the f₀(980) v₂ values, include those from track selection, track efficiency correction, combinatorial background subtraction, residual background parameterization, resonance line-shape modeling, fit range choice, and the harmonic plane resolution. They are summarized in Table 1 and are evaluated as follows.

• Looser and tighter criteria of track selection are applied, and the obtained f₀(980) v₂ results are compared to the default ones, all of which are not corrected for track efficiencies. The uncertainty is 3–22% in the f₀(980) v₂ value, depending on p_T.

• There could be a difference in the detector response between the same-charge-sign and opposite-charge-sign pairs in the same event. To assess this systematic uncertainty, the default combinatorial background spectrum from same-sign pairs is scaled by the ratio of opposite- to same-sign spectra from mixed events (i.e., when the two tracks forming a pair are taken from different events). The effect on the f₀(980) v₂ values is smaller than 3%.

• The residual background is parameterized by second-, fourth-, and fifth-order polynomials besides the default third-order one. The corresponding systematic uncertainty in v₂ is found to be less than 5%.

• The resonance mass peaks are alternatively modeled via a relativistic Breit–Wigner function⁶⁷ and a relativistic Voigt function⁶⁸, which yields a systematic uncertainty in v₂ of less than 2%, except in the highest measured p_T interval, where it reaches 25%. The default fit range (0.8–1.7 GeV/c²) is varied by 0.02 GeV/c² on each side and gives a systematic uncertainty in v₂ of less than 8%.

• The statistical uncertainty in the harmonic plane angle extraction is propagated to the f₀(980) v₂ and treated as a systematic uncertainty, of ~6%.

• An alternative way to estimate the nonflow contribution to the f₀(980) v₂ is by assuming that the absolute nonflow contribution ${v}_{2}-{v}_{2}^{{{\rm{sub}}}}$, instead of the relative $({v}_{2}-{v}_{2}^{{{\rm{sub}}}})/{v}_{2}$ contribution, at a given p_T, is the same as that of the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$ meson. The difference between the ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}$ estimates obtained with the alternative and default methods is treated as the systematic uncertainty in the nonflow-effect subtraction, which is further symmetrized using the larger of the negative and positive variations. The resultant systematic uncertainty band in ${v}_{2}^{{{\rm{sub}}}}$ is then capped between the measured v₂ value and zero, ranging from 1% to 33%, depending on p_T.

• We have also examined the nonflow contribution using D⁰ and Λ data instead of ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$ data. Moreover, we have compared the uncorrected v₂ distribution of the f₀(980) to those of the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω hadrons. The variations observed in these cross-checks are shown to be fully covered by the systematic uncertainty detailed in the previous item.

These various sources of systematic uncertainties are assumed to be independent of each other. The statistical uncertainty is treated as uncorrelated for different p_T bins. The systematic uncertainty arising from the event plane resolution is assumed to be fully correlated between the p_T bins. For each of the other systematic uncertainties, the ${v}_{2}^{{{\rm{sub}}}}$ covariance matrix element for the ith and jth p_T bins is calculated as

$${\sigma }_{i,j}=\frac{1}{{N}_{{{\rm{alt}}}}}{\sum }_{k=1}^{{N}_{{{\rm{alt}}}}}\left({v}_{2,k}^{{{\rm{sub}}}}({p}_{{{\rm{T}}},i})-{v}_{2,{{\rm{default}}}}^{{{\rm{sub}}}}({p}_{{{\rm{T}}},i})\right)\left({v}_{2,k}^{{{\rm{sub}}}}({p}_{{{\rm{T}}},j})-{v}_{2,{{\rm{default}}}}^{{{\rm{sub}}}}({p}_{{{\rm{T}}},j})\right),$$

(4)

where N_alt is the number of alternative methods to extract this systematic uncertainty, and ${v}_{2,{{\rm{default}}}}^{{{\rm{sub}}}}$ is the default value. The overall covariance matrix of the ${v}_{2}^{{{\rm{sub}}}}$ is the sum of the covariance matrices corresponding to the various systematic uncertainties. The uncertainty in the 〈p_t〉 evaluation is estimated using pseudo-experiments and is found to be negligible.

Cross-checks of the NCQ scaling assumption

The uncertainty used in the parametrization of Eq. (3) of the ${v}_{2}^{{{\rm{sub}}}}/{n}_{{{\rm{q}}}}$ data for the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω hadrons is the combined statistical and systematic uncertainties of the fit added in quadrature. The resulting best fit parameters are: p₀ = 0.111 ± 0.004, p₁ = 0.045 ± 0.017, and p₂ = −1.00 ± 0.08. The fit yields a relatively large χ²/dof = 80/34, which indicates that the NCQ scaling is not perfect. To accommodate for this, we increased the uncertainties to achieve the χ²/dof of 1 and found the effect on the n_q result to be negligible.

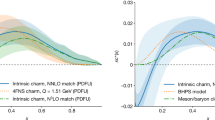
The NCQ scaling can also be parameterized in p_T/n_q. The fit quality is worse, with χ²/dof = 170/34. The NCQ-scaled ${v}_{2}^{{{\rm{sub}}}}/{n}_{{{\rm{q}}}}$ as a function of p_T/n_q is shown in Fig. 7 for the f₀(980) state together with those of the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω hadrons⁵². Using NCQ scaling in p_T/n_q, the extracted significance of the n_q = 2 hypothesis over the n_q = 4 hypothesis is 7.8, 6.2, or 2.4σ, in the p_T < 10, 8, or 6 GeV/c ranges, respectively.

Fig. 7: NCQ scaling of elliptic anisotropy in p_T/n_q.

The ${v}_{2}^{{{\rm{sub}}}}/{n}_{{{\rm{q}}}}$ of the f₀(980) state (for the n_q = 2 and 4 hypotheses) as a function of p_T/n_q is compared with those of the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω strange hadrons⁵² in high-multiplicity pPb collisions. Error bars show the statistical uncertainties while the shaded areas represent systematic uncertainties. The red curve is the NCQ scaling parameterization of the data for the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, Ξ⁻, and Ω hadrons.

To extract the n_q of f₀(980), the χ² of the ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}/{n}_{{{\rm{q}}}}$ data (denoted by $\overrightarrow{y}$) with respect to the NCQ scaling curve (denoted by $\overrightarrow{f}$) is calculated by ${\chi }^{2}={(\overrightarrow{y}-\overrightarrow{f})}^{T}{({C}_{y}+{C}_{f})}^{-1}(\overrightarrow{y}-\overrightarrow{f})$, where C_y is the ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}$ covariance matrix scaled by $1/{n}_{{{\rm{q}}}}^{2}$ and C_f is the covariance matrix between the NCQ scaling function from the fit and the ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}/{n}_{{{\rm{q}}}}$ data. The latter is given by C_f = J ⋅ C_p ⋅ J^T, where C_p is the covariance matrix of the fit parameters and $J=\partial f/\partial \overrightarrow{p}$ is the Jacobian matrix that describes how the fit function value changes with the fit parameters $\overrightarrow{p}$.

Scans of χ² as a function of n_q, treated as a continuous parameter, between the ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}/{n}_{{{\rm{q}}}}$ data and the NCQ scaling curve, are shown in Fig. 8. The three curves correspond to the f₀(980) data for p_T < 6, 8, and 10 GeV/c, respectively. The statistical and systematic uncertainties are included in the χ² calculation with the covariance matrix. The optimal n_q value is determined at the minimum χ², denoted by ${\chi }_{\min }^{2}$, with the uncertainty bracketed by the ${\chi }_{\min }^{2}+1$ level. The corresponding n_q values are listed in Fig. 8, with the uncertainties accounting for the effects of variations in the NCQ fit functional forms and from using p_T/n_q instead of KE_T/n_q, which are relatively small (as detailed in Table 1).

Fig. 8: The χ² scan.

The χ² of the f₀(980) elliptic flow data with respect to the NCQ scaling parameterization, scanned in steps of n_q. The three curves correspond to using f₀(980) data for p_T < 6, 8, and 10 GeV/c, respectively.

Lead-lead collision data from ALICE suggest that the NCQ scaling holds within a precision of 20%^50,51. We vary the overall fit curve of the NCQ scaling by  ±10% and obtain n_q = 1.95 ± 0.22 and 2.19 ± 0.24, respectively, for the positive and negative variations, by using f₀(980) data for p_T < 10 GeV/c. Both these values agree well with the nominal result of n_q = 2.07 ± 0.22, demonstrating the robustness of our result with respect to variations in the NCQ scaling assumption.

The NCQ scaling may be less valid at low p_T where ${v}_{2}^{{{\rm{sub}}}}$ likely reflects hydrodynamic behavior, which is mass dependent. However, excluding the lowest p_T data point has negligible effect on our results.

To examine the effects of imperfect NCQ scaling, we carry out further cross-checks as follows. We fit only the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}\,{v}_{2}^{{{\rm{sub}}}}$ data to obtain an alternative NCQ scaling curve and repeat the analysis. The f₀(980) n_q extracted this way is 2.03 ± 0.22. When we use the nominal NCQ scaling curve with $\Lambda \,{v}_{2}^{{{\rm{sub}}}}$ data, the extracted Λ n_q value is 2.73 ±  0.14. The 2σ deviation from the nominal value of 3 indicates degree of the validity of the NCQ scaling between the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$ and Λ hadrons. Similarly, when we use only the $\Lambda \,{v}_{2}^{{{\rm{sub}}}}$ data to obtain the NCQ scaling curve, the extracted n_q is 2.30 ± 0.22 for the f₀(980) and 2.29 ± 0.18 for the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$ states. We have also tested the NCQ scaling validity on Ω data by using the ${{{\rm{K}}}}_{{{\rm{S}}}}^{0}$, Λ, and Ξ⁻ data for the NCQ scaling fit; the extracted n_q value for Ω is 3.21 ± 0.69.

Exclusion significance determination

The log-likelihood ratio $-2\ln ({L}_{{n}_{{{\rm{q}}}}=4}/{L}_{{n}_{{{\rm{q}}}}=2})$, evaluated as the χ² difference between the n_q = 2 and 4 hypotheses, is calculated for the ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}$ data. We also generate pseudo-data of ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}$ according to the NCQ scaling curve for a given n_q hypothesis. The ${v}_{2}^{{{\rm{sub}}}}$ uncertainties are taken into account by smearing ${v}_{2}^{{{\rm{sub}}}}$ with a Gaussian distribution according to the covariance matrix given by Eq. (4). The corresponding log-likelihood ratio is calculated for the pseudo-data in the same way as for pPb data. The pseudo-experiments yield an expected distribution of the log-likelihood ratio for the two given f₀(980) n_q hypotheses. Each of these distributions is fit with a Gaussian function and the significance of the main hypothesis over the alternative one is extracted as the distance between the Gaussian mean of the alternative distribution (the yellow histogram in, e.g., Fig. 4) and the measured value in data (the red arrow in the same figure), divided by the width of the Gaussian function. The consistency with the main hypothesis can be inferred in a similar way by comparing the value obtained in data with the Gaussian mean and width of the main distribution (the green histogram in the same figure).

The log-likelihood ratio distributions for the n_q = 2 vs. 4 hypotheses for the two restricted p_T ranges are shown in Fig. 9a, b. The log-likelihood ratio distributions for the n_q = 2 vs. 3 hypotheses in the p_T < 8 GeV/c range are shown in Fig. 9c.

Fig. 9: Exclusion significances.

Same as Fig. 4 but using ${{\mbox{f}}}_{0}(980)\,{v}_{2}^{{{\rm{sub}}}}$ data within the restricted ranges p_T < 8 GeV/c (a) and p_T < 6 GeV/c (b). c The expected log-likelihood ratio distributions for n_q = 2 vs. 3 hypotheses from the pseudo-experiments and the observed value for the f₀(980) in data in the p_T < 8 GeV/c range to extract the exclusion significance for n_q = 3.