Introduction

Skyrmions, initially proposed by particle physicist Skyrme in 1961, represent a three-dimensional solitonic particle-like state with topologically protected structures1. Extensive research on skyrmions has been conducted in various physical systems, including Bose-Einstein condensates2,3, quantum fields4, magnetic materials5,6,7,8,9,10,11 and optical systems12. The unique properties of skyrmions, such as their stability and nontrivial topology, make them promising candidates for next-generation data storage, memory devices13,14, sensing15, and optical communication12,16. As an emergent topological texture, skyrmions exhibit a disk-like structure in two dimensions (2D) and a string-like structure in three dimensions (3D) 17. Other intensely studied topological structures, including antiparticles of skyrmions (antiskyrmions)10, fractionalizations of skyrmions (meron and antimeron)17,18,19 and pairs of fractional skyrmions (bimeron)20, have been demonstrated in various experimental materials. Creation of these topological textures in one skyrmion string and direct optical observation of topologically protected structural transformations between distinct 3D string-like skyrmions remains a grand challenge11. In liquid crystals (LCs), significant progress has been made in the study of the structures and dynamics of fractional and full skyrmions21,22,23,24,25,26,27. Due to its intrinsic complexity and larger system size, LC might provide a promising platform for tackling the abovementioned challenge.

When colloidal particles are suspended in an anisotropic LC fluid, a plethora of colloidal self-assemblies are enabled due to long-range elastic interactions28. Thus, the complexity of superstructures can be dramatically increased, and a variety of colloidal assemblies can be realized by using interfaces and topological defects28,29,30,31,32,33,34,35. Using LC to control the dynamic behavior of colloidal particles is another important ongoing research effort36,37,38,39. For instance, hexagonal prisms functionalized with azobenzene dye molecules exhibit elastic monopole moments, which can be rotated and out-of-equilibrium self-assembled by unstructured light40,41. As such, the marriage between LC-based skyrmion topological entities and colloidal self-assembly might be key to realizing exotic states of colloids, such as exquisite assemblies or even complex collective dynamics.

In this work, topologically protected 3D string-like fractional skyrmions, antiskyrmions, and bimerons are created in a nematic LC with the mismatch between different topological patterns. By using continuum simulations and experimental responses of colloidal particles in skyrmion strings, distinct topological configurations of half skyrmions, namely, half-anti-skyrmion (HAS), half-Néel-skyrmion (HNS), and half-Néel-bimeron (HNB), are identified. When the strings are driven out of equilibrium by light irradiation, the topological profiles are continuously transformed between the HAS and HNS through the HNB. These effects are manifested by dancing-like elastic rotations of the colloids, which are explained by theoretical modeling. In addition, a skyrmion string loop is designed to contain four distinct topological profiles along the loop. The shrinkage of the loop enables complex dynamics of the colloidal assembly, and a final jammed assembly is formed to prevent the annihilation of the skyrmion loop. Finally, skyrmion strings with letter shapes “HKUSTC” with both half-skyrmions and half-bimerons are nucleated and used as templates for straight and zigzag colloidal structures. This work opens new possibilities for designing smart materials based on skyrmion-colloid composites.

Results

Emergence of half skyrmions with two different topological structures

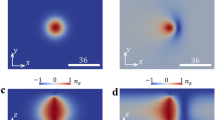
To create skyrmions, the topological pattern consists of alternating splay-bend distortions with a director field designed as \(\hat{{{\bf{n}}}}=\left({n}_{x},{n}_{y},{n}_{z}\right)=(\cos \alpha,\sin \alpha,0)\), where α = πx/L and L = 100 μm is the period, see Methods, Supplementary Figs. 1 and 2 and Supplementary Movie 1. The top surface is of uniform alignment along the y-axis, Fig. 1a. As the sample thickness is ≤20 μm, after a nematic LC of 5CB is injected at room temperature, (Supplementary Fig. 1a) disclination lines with period L are formed42,43,44,45,46,47, Supplementary Fig. 3a, b. If the sample thickness is ~ 50 μm, topologically protected 3D skyrmion strings with period 2L are created, Supplementary Fig. 3c, d48. The coexistence of skyrmions and disclination lines is demonstrated if the sample thickness is in the middle range, Supplementary Fig. 3e, f. If the LC sample is heated to isotropic phase at 35 °C, and then cool down to the nematic phase at 25 °C at a cooling rate of 2 °C/min, more stable half-skyrmions can be obtained. Continuum simulations based on the Landau-de Gennes free energy function are conducted to show the crossover between skyrmions and disclination lines, Supplementary Fig. 3g–i. To investigate the formation mechanism of half skyrmion structures, we measured the twist angle of the director fields, which is the overall rotation angle of directors in the cell thickness direction. Due to the achiral nature of nematic liquid crystals, the twist angle tends to minimize the twist distortion energy. As illustrated in Supplementary Fig. 3j, when the twist angle exceeds |π/2|, twist reversal occurs, resulting in the formation of a singular disclination line49. As the cell thickness is increased to a certain range, to avoid the energy penalty caused by the twist disclinations, an out-of-plane tilt and a high degree of twist distortion are introduced. As shown in Supplementary Fig. 3k, the twist angle gradually increases from 0 to |π|, indicating the transformation of the director fields from a homogeneous region to a highly twisted half-skyrmion region. At the position of the half skyrmion, the twist angle changes discontinuously, accompanied by a 2π jump in the twist angle.

Fig. 1: Topological structures of half-skyrmion strings and colloidal response.
figure 1

a Schematic of the formation of skyrmion strings. The bottom substrate adopts alternating splay-bend distortions, and the top surface is along the y-axis. The skyrmion strings are produced in the splay regions (black). b Micrograph of colloids in skyrmion strings. The point defect of the colloid is on the right-hand side, and \(\hat{{{\bf{p}}}}\) points along the −y-axis (φ  = 180°). The black arrow points at the defect. The violet arrow represents \(\hat{{{\bf{p}}}}\). c\(\,\hat{{{\bf{p}}}}\) points along the y-axis (φ = 0°). d Schematic 3D half-skyrmion string. It is defined as a half-anti-skyrmion (1/2, − 1/2, 0, 0). e A half-skyrmion string is defined as a half-Néel-skyrmion (1/2, 1/2, 0, π). f Schematic vector field of a half-anti-skyrmion (1/2, − 1/2, 0, 0); Red (blue) region shows that the y-component of the director is positive(negative), while the white region shows that the director is in-plane. g Different perspectives of the vector field wrapping the unit sphere. h Schematic vector field of the half-Néel-skyrmion (1/2, 1/2, 0, π). i Corresponding unit sphere. j Simulated topological structures (blue frame from part (b)) of the two half-anti-skyrmions (1/2, − 1/2, 0, 0) formed in the splay regions at x = 0 and x = 2 L. The color represents the component of the director field on the z-axis. k Topological structures (red frame from part (c)) of adjacent half-anti-skyrmions (− 1/2, − 1/2, 0, π) at x = 0 and half-Néel-skyrmions (1/2, 1/2, 0, π) at x = 2L. l Experimental (Exp.) and simulated (Sim.) FCPM images in the vertical cross section through the half skyrmions. The linearly polarized excitation lights for FCPM are marked in yellow. m Mapping of the interaction potential between colloids and half-anti-skyrmions (1/2, − 1/2, 0, 0). The colloid with φ = 180° has minimized potential at location 1 (black dashed line). The arrow represents the locally preferred orientations of the dipoles. n Potential mapping between colloids and half-Néel skyrmions (1/2, 1/2, 0, π). The colloid with φ = 0° is at location 2 (black dashed line). Red solid lines indicate the center of the skyrmion string (x = 0). (Scale bar, 20 μm).

Full size image

In our system, a skyrmion (Nsk, m, γ, F) is defined by four parameters: skyrmion number Nsk, vorticity m, helicity γ, and far-field (F) which is defined as the angle between the top uniform surface and the y-axis. The skyrmion number \({N}_{{sk}}=\frac{1}{4\pi }\iint {{{\rm{d}}}}^{2}\,{{\bf{rn}}}\,\cdot (\frac{\partial {{\bf{n}}}}{\partial x}{{\times }}\frac{\partial {{\bf{n}}}}{\partial y})\), counts how many times the vector field n(r) wraps around a unit sphere15. If the vectors wrap only half of the sphere, it is referred to as a half-skyrmion with skyrmion number \({N}_{{sk}}=\pm \frac{1}{2}\). A bimeron, as a transformed state derived from a skyrmion, is characterized by a texture composed of two half-skyrmions with opposite polarities. A bimeron is characterized by a topological charge of Nsk = ±1. A bimeron is created by rotating the orientations of a skyrmion around an in-plane axis (here, the z-axis) by 90°50. To generate an antiskyrmion, a subsequent 90° rotation of the orientations is necessary. This is achieved by changing the far field (F). Note that, for simplicity, we focus on vectorized n(r), as all the director structures analyzed in this study can be efficiently transformed into vectors, even in cases where n(r) = − n(r), namely, the system’s director field exhibits nonpolar head-tail symmetry.

As a colloidal sphere with a radius of r = 2.5 μm is introduced in LC, it induces a dipolar configuration of the surrounding LC with a topological defect next to it51. \(\hat{{{\bf{p}}}}\) is defined as the structural dipole from the defect toward the sphere, and φ is the angle between \(\hat{{{\bf{p}}}}\) and the y-axis. As a colloid approaches the skyrmion, it is attracted to the skyrmion if the defect is between the colloid and the skyrmion, Supplementary Fig. 4a and Supplementary Movie 2. It is repelled by the skyrmion if the defect is away from the skyrmion, Supplementary Fig. 4b and Supplementary Movie 2. After the colloids are attracted to the skyrmion, two different schemes are shown for the colloidal response in the skyrmion. In the first scenario, the colloids are oriented in the same direction as the topological defects on the right side, φ = 180°, Fig. 1b. The second case shows that the defects of the colloids in the adjacent skyrmions are in opposite directions, φ = 180° and φ = 0° (Fig. 1c).

Since colloids have different responses to skyrmions, their topological textures can be deciphered by continuum simulations (see “Methods”). According to the simulations, skyrmion with colloids of φ = 180° is defined as half-anti-skyrmion (1/2, − 1/2, 0, 0), Fig. 1d, f and Supplementary Fig. 5a. Skyrmion with colloids of φ = 0° is defined as half-Néel-skyrmion (1/2, 1/2, 0, π), Fig. 1e, h and Supplementary Fig. 5b. Note that the half-skyrmion is different from that reported in the literature17, as it is not obtained by splitting the full skyrmion sphere into northern and southern hemispheres along the latitudinal direction but rather by splitting it into eastern and western hemispheres along the longitudinal direction due to geometric constraints from the substrates, as shown in Fig. 1g, i and Supplementary Fig. 6. The vector fields of anti-skyrmion, Néel-skyrmion, half-anti-skyrmion, and half-Néel-skyrmion are shown in Supplementary Fig. 6a–h.

The 3D topological structures of these two different scenarios are also mapped in Fig. 1j, k. The vector field and skyrmion number density are shown in Supplementary Fig. 7. This indicates that the period of the half skyrmion is twice that of the splay-bend surface pattern. To resolve the twist deviation between the top and bottom substrates, the directors twist in the direction perpendicular to the cell thickness while also introducing an out-of-plane tilt within the bulk. A fluorescent confocal polarizing microscope (FCPM) is employed to map the 3D director fields, which is matched with those derived from n(r) simulations52,53,54,55, Fig. 1l.

To gain insight into how colloids respond in half-skyrmions, the interaction potential between a colloidal sphere with a dipolar director and a distorted director (with r ≪ L) is written as56 \({U}_{d}=-8\pi K{r}^{2}(\beta (\hat{{{\bf{p}}}}\cdot \hat{{{\bf{n}}}}){{\boldsymbol{\nabla }}}\cdot \hat{{{\bf{n}}}}-\frac{r}{12}{({{\boldsymbol{\nabla }}}{{\bf{n}}})}^{2})\), where K is the Frank elastic constant and β is the amplitude of dipole director distortions which depends on the strength of the surface anchoring and the elastic constants. The mapping of the interaction potential shows that \(\hat{{{\bf{p}}}}\) points in the − y-direction (φ = 180°) at location 1 in the half-anti-skyrmion (1/2, − 1/2, 0, 0), Fig. 1m, and points in the + y-direction (φ = 0°) at location 2 in the half-Néel-skyrmion (1/2, 1/2, 0, π), Fig. 1n. The location 1 and 2 represent different heights. Note that from the potential mapping, the height of colloid in half-anti-skyrmion (1/2, − 1/2, 0, 0) is higher than that of colloid in half-Néel-skyrmion (1/2, 1/2, 0, π). The prediction of the relative height difference was further supported by experimental validation, as demonstrated in Supplementary Fig. 8a, c.

Half-Néel-bimerons with two different topological structures

As shown in Fig. 2a, another type of skyrmion is formed if uniform alignment is along the x-axis, as shown by the colloidal response in the skyrmions, Fig. 2b. Colloids are oriented as φ = − 135° (Fig. 2b) or − 45° (Supplementary Fig. 9a) in this skyrmion. Colloids can also be oriented as φ = 45° (Fig. 2c) or 135° (Supplementary Fig. 9c) in adjacent skyrmions. By using simulations, the skyrmion of φ = − 135° or − 45° is defined as a half-Néel-bimeron (1/2, 0, 0, − π/2), Fig. 2d, f and Supplementary Fig. 5c. The skyrmion of φ =  135° or 45° is defined as half-Néel-bimeron (1/2, 0, 0, π/2), Fig. 2e, h and Supplementary Fig. 5d. Note that the half-bimeron is different from that reported in the literature20, as it is split into eastern and western hemispheres along the longitude, Fig. 2g, i and Supplementary Fig. 6i–p. The 3D topological profiles of the half-bimerons are mapped in Fig. 2j, k. The 3D mapping of the director fields by FCPM are consistent with n(r) simulation of half bimerons, Fig. 2l. Vector field and skyrmion number density are shown in Supplementary Fig. 10. The interaction potential between the colloid and half-Néel-bimeron (1/2, 0, 0, − π/2) shows that the colloid of φ = − 135° is at location 1, Fig. 2m, and the colloid of φ = − 45° is at location 2 (Supplementary Fig. 9a, b). Likewise, in half-Néel-bimeron(1/2, 0, 0, π/2), the colloid of φ = 45° is located at location 2 (Fig. 2n) and the colloid of φ = 135° is located at location 1 (Supplementary Fig. 9c, d).

Fig. 2: Topological structures of half bimerons and colloidal response.
figure 2

a Schematic of the formation of half-Néel-bimeron. The bottom substrate is an alternating splay-bend distortion, and the top surface is along the x-axis. The half bimerons are produced in the bend regions (violet). b Micrographs of colloids in half bimerons. If the \(\hat{{{\bf{p}}}}\) orientation is φ = − 135°, the half bimeron is defined as the half-Néel-bimeron (1/2, 0, 0, − π/2). The black arrow points at the defect. The violet arrow represents \(\hat{{{\bf{p}}}}\). c If the \(\hat{{{\bf{p}}}}\) orientation is φ = 45°, the half bimeron is defined as the half-Néel-bimeron (1/2, 0, 0, π/2). d 3D half-Néel-bimeron (1/2, 0, 0, − π/2) string. e 3D half-Néel-bimeron (1/2, 0, 0, π/2) string. f Schematic vector field of the half-Néel-bimeron (1/2, 0, 0, − π/2); Red (blue) region shows that the y-component of the director is positive (negative), while the white region shows that the director is in-plane. g Different perspectives of the vector field wrapping the unit sphere. h Schematic vector field of half-Néel-bimeron (1/2, 0, 0, π/2). i Corresponding unit sphere. j Simulated topological profiles (blue frame from part (b)) of the two half-Néel-bimerons (1/2, 0, 0, − π/2) formed in the bend regions at x = L/2 and x = 5L/2. The color represents the component of the director field on the z-axis. k Topological structures (red frame from part (c)) of adjacent half-Néel-bimeron (1/2, 0, 0, π/2) at x = L/2 and half-Néel-bimeron (− 1/2, 0, 0, π/2) at x = 5L/2. l Experimental (Exp.) and simulated (Sim.) images of 3D mapping the half bimerons. The linearly polarized excitation lights for FCPM are marked in yellow. m Mapping of the interaction potential between colloid and half-Néel-bimeron (1/2, 0, 0, − π/2). The colloid with φ = − 135° has minimized potential at location 1 (black dashed line). n Potential mapping between colloid and half-Néel-bimeron (1/2, 0, 0, π/2). The colloid with φ = 45° is at location 2 (black dashed line). Red solid lines indicate the center of the skyrmion string (x = 0). (Scale bar, 20 μm).

Full size image

Elastic dancing of colloids in collective dynamics of skyrmion strings

The half-skyrmions can be driven out-of-equilibrium if the top surface is irradiated with linearly polarized light. For instance, half skyrmions are generated at x = 0, 2 L, …, if the top surface alignment is along the y-axis, Fig. 3a. The half skyrmions are identified as half-anti-skyrmions (1/2, − 1/2, 0, 0) due to colloids ① and ② of φ = 180°, Fig. 3a, b. Manipulation of the irradiated linear polarization drives the half skyrmions to continuously translate along the x-axis, Supplementary Fig. 11. With the translation of the skyrmion string, the colloids start to rotate in the half skyrmion, manifesting the transformation of topological profiles of half skyrmions. At t = 0 s, the half-anti-skyrmion is at x = 0 in the splay region, Supplementary Fig. 12a. Unlike colloids ① and ②, colloid ③ with defects away from the skyrmion string is repelled by the string, Fig. 3b. At t = 205 s, the string moves to the bend region at x = L/2, Fig. 3a and Supplementary Fig. 12b and Supplementary Movies 3, 4. Colloids ① and ② are oriented with φ = 135°, indicating that the half-anti-skyrmion (1/2, − 1/2, 0, 0) is transformed to half-Néel-bimeron (1/2, 0, 0, π/2). Colloid ③ is attracted into the string and adopts φ = 45°, Fig. 3b. At t = 355 s, the string moves to the splay region at x = L, Fig. 3a, Supplementary Fig. 12c and Supplementary Movies 3, 4. Colloid ③ is rotated to φ = 0 in the string, showing that it is a half-Néel-skyrmion (1/2, 1/2, 0, π), which results in colloids ① and ② being repelled off the string, Fig. 3b. With the continued translation of string, colloids ① and ② rotate clockwise (CW) 180° near the string, Supplementary Movie 3. At t = 450 s, colloids ① and ② are attracted to the string with an orientation of φ = − 135° and colloid ③ with an orientation of φ = − 45°, indicating that the skyrmion is half-Néel-bimeron (1/2, 0, 0, − π/2), Fig. 3b, Supplementary Fig. 12d and Supplementary Movies 3, 4. Finally, after the translation of 2 L at t = 638 s, the string is transformed to the original half-anti-skyrmion (1/2, − 1/2, 0, 0), and colloid ③ is again repelled off the string, Fig. 3b, Supplementary Fig. 12e, and Supplementary Movies 3, 4. Throughout the entire translation process, the skyrmion number of the half-skyrmions remains topologically protected as Nsk = 1/2, as shown in Supplementary Fig. 13 and Supplementary Movie 5.

Fig. 3: Dynamical behaviors of colloids in the transformations between half skyrmions and half bimerons.
figure 3

a Image sequence of the colloidal response in the motion of a half-skyrmion string. The black double arrows indicate the top surface alignment. The half skyrmions are transformed in the following order: half-anti-skyrmion (1/2, − 1/2, 0, 0) (t = 0 s), half-Néel-bimeron (1/2, 0, 0, π/2) (t = 205 s), half-Néel-skyrmion (1/2, 1/2, 0, π) (t = 355 s), half-Néel-bimeron (1/2, 0, 0, −π/2) (t = 450 s) and half-anti-skyrmion (1/2, − 1/2, 0, 0) (t = 638 s). The colored trajectories of colloids ①, ② and ③ are shown in the image at t = 638 s. b Image sequence of the rotations of colloids ①, ② and ③ (① in violet frame, ② in red frame and ③ in green frame from part (a)) as the string translates along the x-axis. c Free energy comparison of different half skyrmions. d Temporal dependence of φ for colloids ①, ② and ③. e Mapping of the interaction between colloids ② and ③ with half skyrmion at different time. This explains the colloidal orientations in the translational half skyrmion string. Red solid lines indicate the center of the skyrmion string (x = 0). f Image sequence of the colloidal chain response in the motion of a half-skyrmion string. The half skyrmion strings are transformed following the same order as in part(a). g Zoomed-in images of the collective dynamics of the colloidal chain from part (f). The white arrows indicate the translation direction. Black arrows point at the defects in (b) and (g). HAS (1/2, − 1/2, 0, 0) indicates half-anti-skyrmion, HNS (1/2, 1/2, 0, π) indicates half-Néel-skyrmion, HNB (1/2, 0, 0, − π/2) and HNB (1/2, 0, 0, π/2) indicate half-Néel-bimerons. (Scale bar, 50 μm).

Full size image

The free energy change of the half-skyrmion strings in this process is shown in Fig. 3c. In this process, colloids ① and ② are rotated from φ = 180° to φ = − 180°, while colloid ③ is rotated from φ = 135° to φ = − 135°, Fig. 3d. Besides, elastic rotations of the colloids are well captured by mapping the interaction potential Ud, Fig. 3e. The location 1 and 2 represent different heights. For instance, at t = 0 s, colloid ② is oriented with φ = 180° in half-anti-skyrmion (1/2, − 1/2, 0, 0), and colloid ③ is repelled off the half-anti-skyrmion. At t = 205 s, colloid ② is of φ = 135°, and colloid ③ adopts φ = 45° in half-Néel-bimeron (1/2, 0, 0, π/2). At t = 355 s, colloid ② is off the half-Néel-skyrmion (1/2, 1/2, 0, π), and colloid ③ is of φ = 0° in this half-Néel-skyrmion. At t = 450 s, colloids ② and ③ have φ = − 135° and φ = − 45°, respectively, in the half-Néel-bimeron (1/2, 0, 0, − π/2). At t = 638 s, colloid ② is oriented with φ = 180° in a half-anti-skyrmion (1/2, − 1/2, 0, 0), and colloid ③ is off the half skyrmion. The reversible translation process is shown in Supplementary Fig. 14 and Supplementary Movie 6.

The dynamic behaviors of the colloidal assembly in the translation of half-skyrmion string is remarkably different from that of the individual colloids shown in Fig. 3a–e. For example, at t = 0 s, a colloidal chain (12 colloids) is in the half-anti-skyrmion (1/2, − 1/2, 0, 0), Fig. 3f, g. As the string is transformed to the half-Néel-bimeron (1/2, 0, 0, π/2) at t = 182 s, the colloidal chain is tilted with φ = 135°. At t = 372 s, the string is transformed to half-Néel-skyrmion (1/2, 1/2, 0, π), and the colloidal chain begins to coil downward with the skyrmion string sweeping the colloids. Then, the chain is off the string (at t = 441 s), Supplementary Movie 7. From t = 552 s to t = 603 s, the colloidal chain makes a U-turn into the string as the string is transformed to half-Néel-bimeron (1/2, 0, 0, − π/2). At t = 791 s, the chain is oriented with φ = − 180° in a half-anti-skyrmion (1/2, − 1/2, 0, 0). Note that this collective behavior of the colloidal chain depends on the number of colloids in the chain. When the number of particles is less than 10, such behavior is not observed, as shown in Supplementary Fig. 15 and Supplementary Movie 8. In this case, the colloidal chains assemble and disassemble the kink structures with half skyrmion translation, Supplementary Fig. 15.

Collective dynamics of a half-skyrmion string loop with four distinct topological textures

When the director field on the bottom surface is designed as \(\hat{{{\bf{n}}}}=({n}_{x},{n}_{y},{n}_{z})=(\cos \alpha,\sin \alpha,0)\), where \(\alpha=\frac{\pi \sqrt{{x}^{2}+{y}^{2}}}{L}\), and the top surface is aligned along the y-axis, a skyrmion string loop is created, Fig. 4a, b. By placing colloidal particles in the loop, it is determined that four different topological profiles coexist in the loop following the position order of ⓐhalf-anti-skyrmion (1/2, − 1/2, 0, 0), ⓑhalf-Néel-bimeron (1/2, 0, 0, π/2), ⓒhalf-Néel-skyrmion (1/2, 1/2, 0, π), and ⓓhalf-Néel-bimeron (1/2, 0, 0, − π/2), Fig. 4b. Note that the colloid in the half skyrmion at position ⓐ (in black frame) needs to be rotated π to determine the half skyrmion type because the splay region at ⓐ has a phase difference of π compared to that at position ⓒ (in red frame). In addition, the bend regions at positions ⓑ (in green frame) and ⓓ(in violet frame) have phase differences of π/2 and − π/2, respectively, when compared to those at position ⓒ, Fig. 4b. However, 2 different half skyrmions and 2 different half bimerons maintain a constant skyrmion number of Nsk = 1/2 in the loop, Supplementary Fig. 16.

Fig. 4: Collective dynamics of colloids in a skyrmion string loop.
figure 4

a Schematic of the formation of a half-skyrmion string loop. b The designed director field on the bottom surface and micrographs of four different types of half skyrmions on a loop. The topological profiles of ⓐhalf-anti-skyrmion (1/2, − 1/2, 0, 0), ⓑhalf-Néel-bimeron (1/2, 0, 0, π/2), ⓒhalf-Néel-skyrmion (1/2, 1/2, 0, π) and ⓓhalf-Néel-bimeron (1/2, 0, 0, −π/2) are created in the same loop. The black arrows point at the defects. c Image sequence of colloidal dynamics in the loop shrinkage. The ring radius changes from r = 115μm to r = 15μm. At t = 120 s and t = 152 s, colloid ② and colloid chain ③ are repelled off the loop due to the changes in half skyrmion textures. Colloidal chains ① and ④&⑤ rotate along the CW azimuthal direction in the loop. d Colored trajectories of colloidal chains ① and ④&⑤. e Temporal dependence of the rotation angle for colloidal chains ① and ④&⑤ along the azimuthal direction. f The dependence of the interaction potential between the colloid and loop on the azimuthal angle at t = 0 s. g Mapping of the interaction potential of colloidal chains ① and ④&⑤ with different topological profiles in the loop. (Scale bar, 100 μm).

Full size image

The loop is driven to shrink by light irradiation, Fig. 4c, d and Supplementary Movie 9. At t = 0 s, colloidal chain ① (red circle) is in half-Néel-skyrmion (1/2, 1/2, 0, π); colloid ② and colloid chain ③ (green circles) are in half-Néel-bimeron (1/2, 0, 0, π/2); chains ④ and ⑤ (black circles) are in half-anti-skyrmion (1/2, − 1/2, 0, 0). With shrinkage of the loop, half-Néel-bimeron (1/2, 0, 0, π/2) is transformed to half-Néel-skyrmion (1/2, 1/2, 0, π), resulting in colloid ② and colloid chain ③ are repelled off the loop at t = 120 s and t = 152 s, respectively, Supplementary Movie 9. However, colloidal chains ④ (5 colloids) and ⑤ (3 colloids) assemble into a new 8-colloid assembly at t = 120 s. At t = 152 s, the ④&⑤ 8-colloid chain rotates in the loop to the region of the half-anti-skyrmion (1/2, − 1/2, 0, 0) to be compatible with the local topological texture. Meanwhile, colloidal chain ① (11 colloids) rotates CW in the loop and finally reaches the half-Néel-skyrmion (1/2, 1/2, 0, π) region at t = 152 s. After that, both colloidal chains ① and ④&⑤ rotate CW with changes in the local topological profiles. At t = 244 s, chain ① is in the half-Néel-skyrmion (1/2, 1/2, 0, π), and chain ④&⑤ in the half-anti-skyrmion (1/2, − 1/2, 0, 0). At the final t = 336 s, they are jammed to prevent the annihilation of the half skyrmion string loop, Fig. 4c, d.

For colloids on half skyrmion string loops with radii ranging from 100–200 μm, there are two scenarios of motion during the shrinkage of the loop. One case is similar to the motion of colloids on a straight half-skyrmion string shown in Fig. 3. When the half bimeron moves from the bend region to the next splay region, the colloids in the half-skyrmion are repelled. In the straight half skyrmion string shown in Fig. 3, we can control the speed of the string by adjusting the light intensity so that the colloid can follow the motion of the string. When the string shifts approximately half a period to the bend region, the colloids will be attracted back to the string, Fig. 3. However, for a small-radius half-skyrmion string loop, it is difficult for the colloids to return to the string once they are repelled off because the loop tends to shrink and eventually annihilate due to the small radius. Hence, colloids ② and ③ are left behind after the string is moved, Fig. 4c. In the second case, colloidal chains ① and ④&⑤ show constant CW rotation in the half skyrmion string loop. The rotation angles for colloidal chains ① and ④&⑤ along the azimuthal direction are shown in Fig. 4e.

The mapping of the interaction potential explains the positions of the colloids in the loop during loop shrinkage, Fig. 4f, g. Colloidal chain ① always rotates along the string to the half-Néel-skyrmion (1/2, 1/2, 0, π) to minimize the interaction potential, while the chain ④&⑤ moves to half-anti-skyrmion (1/2, − 1/2, 0, 0), Fig. 4g and Supplementary Movie 9. Their motions in the string avoid local rotations of the colloidal chains, which might cost more elastic energy. The colloidal dynamics during the expansion of the loop are shown in Supplementary Fig. 17 and Supplementary Movie 10.

Templated colloidal assembly by arbitrarily shaped half skyrmion strings

Based on the above findings, colloidal assemblies can be templated by using arbitrarily shaped strings with alternating half skyrmions and half bimerons, Fig. 5. Half skyrmion strings in the shapes of the letters “HKUSTC” are nucleated by using light irradiation, Fig. 5, Supplementary Fig. 18 and Supplementary Movie 11. As an example, with the help of laser tweezers, colloids assemble into linear chains in the half-anti-skyrmion (1/2, − 1/2, 0, 0) region in the letter “U” of Fig. 5i and the half-Néel-skyrmion (1/2, 1/2, 0, π) region in the letter “C” of Fig. 5r. The colloidal assemblies exhibit a zigzag shape in the half-Néel-bimeron (1/2, 0, 0, − π/2) and half-Néel-bimeron (1/2, 0, 0, π/2) (Fig. 5i) regions in the letter “U”.

Fig. 5: Colloidal assemblies on skyrmion strings of arbitrary shapes.
figure 5

Director fields of letters “HKUSTC” are (a) “H”, (d) “K”, (g) “U”, (j) “S”, (m) “T” and (p) “C”. Micrographs of the colloidal assemblies in these letters are shown in parts (b–r). (Scale bar, 20 μm).

Full size image

Discussion

Creation of distinct topological textures in one skyrmion string, direct optical observation and manipulation of the transformations between them are crucial for obtaining a fundamental understanding of the topological nature of skyrmions. Furthermore, what is the response of colloidal particles to the out-of-equilibrium dynamics of skyrmion strings? How does the interplay of topology and geometry in skyrmion strings influence the collective dynamics of colloidal assembly? To answer these questions, in-depth scientific explorations must be conducted. In this work, we use experiments, simulations, and theory to determine stepping stones to provide answers to these fundamental questions.

We create string-like half-skyrmions with distinct topological textures (half-anti-skyrmion, half-Néel-skyrmion, half-Néel-bimerons) by interfacing different topological patterns in a nematic LC. The skyrmion types are identified by using simulations and experimental responses of the colloids in half skyrmion strings. As half-skyrmion strings are driven out-of-equilibrium by light irradiation, the topological textures of half-skyrmions are transformed in the order of half-anti-skyrmion (1/2, − 1/2, 0, 0), half-Néel-bimeron (1/2, 0, 0, π/2), half-Néel-skyrmion (1/2, 1/2, 0, π), half-Néel-bimeron (1/2, 0, 0, − π/2) and half-anti-skyrmion (1/2, − 1/2, 0, 0). All four skyrmion textures are labeled as elements of the second homotopy group, \({\pi }_{2}({{\mathbb{S}}}^{2}/{{{{\mathbb{Z}}}}}_{2})={{{\mathbb{Z}}}}\)24. Since these configurations are homeomorphic in 3D, a half-anti-skyrmion is allowed to change to a half-Néel-skyrmion continuously with a half-Néel-bimeron as the intermediate structure. Due to the complexity of the topological nature of skyrmions, exotic dynamic behaviors of colloidal assemblies have been demonstrated. The colloids are driven to adopt elastic rotations in out-of-equilibrium topologically protected structural transformations. The collective behaviors of colloidal assemblies are remarkably different from that of individual colloids. Depending on the number of colloids in the colloidal chains, the chains not only form coil structures but also assemble and disassemble kink structures during skyrmion string motion. Due to the nonsingular nature of skyrmions, colloids have more freedom to rotate inside and outside of the skyrmions, exhibiting dancing-like exotic dynamic behaviors, which is fundamentally different from the colloidal dynamics in singular disclinations28,35,57.

As the geometry of a half-skyrmion string changes from straight to a loop, four topological textures can be formed in the same loop. The shrinkage of the loop drives the colloidal assemblies to rotate along the loop to be compatible with the local topological profiles. Hence, by manipulating the topology and geometry of half skyrmions, the collective dynamics of colloidal assemblies can be well controlled. Finally, skyrmion strings with arbitrary shapes containing both half skyrmions and half bimerons can be used as templates to program the formation of various exquisite colloidal chains or zigzag structures. The demonstrated effect in this work not only provides insights into skyrmions with changing topologies, geometries, and shapes but also opens opportunities for the development of responsive colloidal composites and smart materials.

Methods

Materials

A 0.01 wt% silica colloid of r = 2.5 μm in radius treated with octadecyl-dimethyl-(3-trimethoxysilylpropyl) ammonium chloride (DMOAP) was added to a nematic LC called 4′-pentyl-4-cyanobiphenyl (5CB), as shown in Supplementary Fig. 1a, b. This doping process results in the formation of perpendicular director alignment and dipolar structures around the colloid within the 5CB, exhibiting a hyperbolic hedgehog on one side of each colloid sphere. The colloidal dispersion in the 5CB was injected into the photopatterned cell at 22 °C. The colloids were manipulated by using laser tweezers from JCOPTIX, China.

Patterned surface alignment

The azo dye SD1, Supplementary Fig. 1c, was purchased from Nanjing Ningcui Optical Technology Co., LTD, and used without additional purification. A solution of SD1 was prepared by mixing it with n,n-dimethylformamide (DMF) solvent at a concentration of 0.2 wt%. Glass substrates were thoroughly cleaned in an ultrasonic bath containing dishwasher detergent, followed by rinsing with isopropyl alcohol and drying in an oven at 85 °C for 15 min. The substrates were further treated in a UV-ozone chamber for 10 min. Next, the SD1 solution was spin-coated onto the treated glass substrates at 3000 rpm for 30 s. The glass plates were then baked at 100 °C for 45 min. Upon exposure to linearly polarized light, the photosensitive azo dye on the glass substrates will align perpendicularly to the direction of linear polarization58. The orientation of the liquid crystal LC director is consistent with the alignment of the azo dye molecules.

The topological pattern is achieved through a maskless photopatterning setup that utilizes a projector display59,60, Supplementary Fig. 2a. The alternating splay-bend pattern is designed with director field \(\hat{{{\bf{n}}}}=({n}_{x},{n}_{y})=(\cos \alpha,\,\sin \alpha )\), where α(x, y) = πx/L and L = 100 μm is the period, Supplementary Fig. 2b. The segment in the rectangular shape starts at the position shown in Supplementary Fig. 2d, and the polarizer rotates starting along the x-axis. The rotation speed of the polarizer in the clockwise sense is set as R1 = 18°/5s. The segments will be displaced along the -y-axis at a speed of R2 = 10 μm/5s, Supplementary Fig. 2d and Supplementary Movie 1. Hence, after π rotation of the polarizer, the designed pattern is obtained, as shown in Supplementary Fig. 2b.

The topological pattern in Fig. 4 with \(\hat{{{\bf{n}}}}=({n}_{x},{n}_{y},{n}_{z})=(\cos \alpha,\sin \alpha,0)\), where \(\alpha=\frac{\pi \sqrt{{x}^{2}+{y}^{2}}}{L}\), Supplementary Fig. 2c, is produced by using the concentric segments shown in Supplementary Fig. 2e. The rotation speed of the polarizer in the clockwise sense is set as R1 = 18°/5s. The segments shrink at a speed of R2 = 10 μm/5s. Thus, the period of this pattern is 100 μm, as shown in Supplementary Fig. 2c.

Sample preparation

The patterned substrate is covered by an additional layer of liquid crystal polymer to minimize the impact of subsequent light irradiation experiments. Monomer RM257, as shown in Supplementary Fig. 1d, purchased from Nanjing Leyao is mixed with toluene at a concentration of 10 wt%. The photoinitiator Irgacure 651 (from Nanjing Leyao) was added at a concentration of 5 wt% RM257. Subsequently, this solution was spin-coated onto the patterned SD1 substrates at 3000 rpm for 30 s. To polymerize the substrates, unpolarized ultraviolet light with an intensity of 1.4 mW/cm2 was used for 30 min. The resulting polymer pattern replicates the pattern of SD1 alignment beneath it.

The top substrate is uniformly aligned, while the bottom substrates adopt different topological patterns. The two substrates are assembled to form a sandwich cell with 50 μm glass spacers separating the two substrates. At 25 °C, nematic LC 5CB was introduced into the cell through capillary force. As the LC filled the cell, skyrmion strings were formed, and the samples were viewed using a polarizing optical microscope. The phase transition process was then carried out using a hot stage (from INSTEC). To drive the sample out-of-equilibrium, a collimated LED (from Thorlabs) emitting at a wavelength of 455 nm and with a light intensity of 510 mW/cm2 at the focus point was used as the light source. The photosensitive azobenzene SD1 molecules on the top substrate would be rearranged by linearly polarized light. Since the bottom substrate of the two-dimensional (2D) topological pattern is layered with a liquid crystal polymer, it remains unaffected by light.

Polarizing optical microscopy

We utilized a SOPTOP CX40P polarized optical microscope (POM) that included a 10x Plan, N.A. = 0.30 objective, and a 50x Plan, N.A. = 0.55 objective to capture optical microscopy images. Using a 9 MP Sony Exmor CMOS Sensor Microscope Camera, we were able to capture images at a resolution of 4096 × 2160 pixels.

Laser scanning fluorescence confocal polarizing microscopy (FCPM)

The anisotropic fluorescent dye N, N′-bis(2,5-di-tert-butylphenyl)-3, 4, 9, 10-perylenedicarboximide (BTBP) (from Sigma‒Aldrich) was mixed in methanol at 0.1 wt%. The BTBP solution was mixed with 5CB at a weight ratio 1:1. Then, methanol was evaporated for 10 h on a hotplate at 90 °C. Imaging was performed with a Leica STELLARIS 8 STED laser scanning confocal fluorescence microscope using lasers with an excitation wavelength of 488 nm and emission wavelength of 530 nm.

We used oil-immersion 40x objective with N.A. = 1.3, 63x objective with N.A. = 1.4 and 100x objective with N.A. = 1.4. We scanned the excitation beam through the sample volume and recorded the fluorescence signal as a function of coordinates. The linear polarization of the beam was defaulted along the x-direction, while the samples were rotated to change the relative angle between samples and polarization directions.

We define the director with respect to polar angle θp and azimuthal angle φa, where \(\hat{{\boldsymbol{n}}}=({n}_{x},{n}_{y},{n}_{z})=(\cos {\varphi }_{a}\,\sin {\theta }_{p},\,\sin {\varphi }_{a}\,\sin {\theta }_{p},\,\cos {\theta }_{p})\). The fluorescence intensity I depend on the angle between n(r) and the controlled excitation beam polarization and the background intensity Iback.

$$I={I}_{{\mathrm{back}}}+{I}_{{\mathrm{norm}}}{\cos }^{2}\left({\varphi }_{a}-\omega \right){\sin }^{4}{\theta }_{p}$$

ω is the angle between linear polarization direction and x-axis, so φa − ω denotes the angle between polarizer and the projection of directors n(r) into xy plane. Computer simulations of the FCPM images are based on the simulation director fields. Simulation images under different incident polarizations are obtained by modifying the value of ω.

Considering the attenuations of excitation intensity with depth, we manually constructed an exponential decay function adding to the background intensity Iback. The exponential decay function is a function of the depth, where \({I}_{{\mathrm{back}}}=0.4\exp \left(2-\frac{2Z}{H}\right)\). Z is the depth of scanning positions, and H is the total thickness of the sample.

Skyrmion string translation distance measurement

Micrographs were processed by ImageJ, and the motion of half-skyrmion strings was processed by tracking the displacement of their motion using the ImageJ MTrackJ Plugin. To calculate the moving distance of the half skyrmions, each step of the trajectory is measured as (xi, yi), and the starting point is (x0, y0). The distance between each step and the starting point is \(\sqrt{{({x}_{i}-{x}_{0})}^{2}+{({y}_{i}-{y}_{0})}^{2}}\).

Numerical simulations

The total free energy Ftotal of a nematic liquid crystal is given by

$${F}_{{\rm{total}}}={\int }_{\! \!\!V}\left({f}_{\!{{\rm{LdG}}}}+{f}_{\!\!{{\rm{el}}}}\right){dV}+{\int }_{\!\!\!\!S}\, \,{f}_{{\rm{surf}}}{dS},$$
(1)

where fLdG is the short-range Landau-de Gennes free energy, fel is the long-range elastic energy, and fsurf is the surface anchoring-induced free energy. The Landau-de Gennes free energy density fLdG is calculated as61

$${f}_{{\rm{LdG}}}=\frac{{A}_{0}}{2} \left(1-\frac{U}{3}\right){{\rm{Tr}}}( {{\boldsymbol{Q}}}^{2})\frac{{A}_{0}U}{3}{{\rm{Tr}}}({{\boldsymbol{Q}}}^{3})+\frac{{A}_{0}U}{4}({{\rm{Tr}}}({{\boldsymbol{Q}}}^{2}))^{2}$$
(2)

where Q is the tensorial order parameter from an ensemble average over unit vector n (representing the molecular orientation), Q = < nn − I/3>. Parameter U controls the magnitude of S of a homogenous static system through

$$S=\frac{1}{4}+\frac{3}{4}\sqrt{1-\frac{8}{3U}}$$
(3)

The Frank-Oseen elastic free energy density for the nematic liquid crystal is expressed as62

$${f}_{{\rm{el}}}^{{\rm{Fo}}}= \frac{1}{2}{K}_{1}{(\nabla \cdot {{\rm{n}}})}^{2}+\frac{1}{2}{K}_{2}{({{\rm{n}}}\cdot \nabla \times {{\rm{n}}})}^{2} \\ + \frac{1}{2}{K}_{3}{({{\rm{n}}}\times \left(\nabla \times {{\rm{n}}}\right))}^{2}-\frac{1}{2}{K}_{24}\nabla \cdot \left[{{\rm{n}}}\left(\nabla \cdot {{\rm{n}}}\right)+{{\rm{n}}}\times (\nabla \times {{\rm{n}}})\right]$$
(4)

where K1, K2, K3 and K24 are the splay, twist, bend and saddle-slay elastic moduli, respectively. To be consistent with the Landau-de Gennes energy, the elastic energy density in the simulation is alternatively written in terms of the Q tensor (in the Einstein summation form)

$${f}_{{el}}^{{Q}}= \frac{1}{2}{L}_{1}({\partial }_{k}{Q}_{{ij}})({\partial }_{k}{Q}_{{ij}})+\frac{1}{2}{L}_{2}({\partial }_{k}{Q}_{{jk}})({\partial }_{l}{Q}_{{jl}})\\ +\frac{1}{2}{L}_{3}{Q}_{{ij}}({\partial }_{i}{Q}_{{kl}})({\partial }_{j}{Q}_{{kl}})+\frac{1}{2}{L}_{4}({\partial }_{l}{Q}_{{jk}})({\partial }_{k}{Q}_{{jl}})$$
(5)

The mapping between constant sets K1, K2, K3, and K24 and L1, L2, L3, and L4 is via

$$\begin{array}{c}{L}_{1}=\frac{1}{2{S}^{2}}[{K}_{2}+\frac{1}{3}({K}_{3}-{K}_{1})]\\ {L}_{2}=\frac{1}{{S}^{2}}({K}_{1}-{K}_{24})\\ {L}_{3}=\frac{1}{2{S}^{3}}({K}_{3}-{K}_{1})\\ {L}_{4}=\frac{1}{{S}^{2}}({K}_{24}-{K}_{2})\end{array}$$
(6)

The anchoring energy fsurf is calculated by the nondegenerate formula, the so-called the Rapini-Papoular63.

$${f}_{\!\!{{\rm{surf}}}}=\frac{{1}}{2}W({{\bf{Q}}} - {{\bf{Q}}}_{{\rm{surf}}})^{2}$$
(7)

where Qsurf is the preferred field of the surface, Qsurf = S(ns ns − I/3), ns is the surface-preferred molecular orientation, and W is the anchoring strength. In our simulations, we assumed that the anchoring conditions on the top and bottom surfaces are strong, and therefore, the directors are almost fixed at the substrates. To simulate the half skyrmions driven out of equilibrium if the top surface is irradiated with linear polarization, we assumed that the Qsurf of the top surface (where there is no pattern) changes linearly from one preferred direction to another during the simulation. After equilibrating the initial state, all rotations are run for a total number of steps of 250000 to ensure that the systems evolve quasistatically. Eq. (1) calculates a thermodynamic potential that determines the stable or metastable solutions of the system. We define a molecular field

$${{\bf{H}}}={-\left[\frac{\delta {F}_{{total}}}{\delta {{\bf{Q}}}}\right]}^{{st}}$$
(8)

where […]st is a symmetric and traceless operator. Assuming that all transitions are quasistatic processes, the evolution of the Q-tensor for bulk points follows

$${\partial }_{t}{{\bf{Q}}}={{{\Gamma }}}_{{{\boldsymbol{s}}}}{{\bf{H}}}$$
(9)

where Γs is the relaxation constant. For surface points, the evolution of Q is governed by

$$\frac{\partial {{\boldsymbol{Q}}}}{\partial t}=-{{{\Gamma }}}_{s}[-{{\boldsymbol{\nu }}}\cdot \frac{\partial F}{\partial \nabla {{\boldsymbol{Q}}}}+{\left\{\frac{\partial {f}_{{surf}}}{\partial {{\boldsymbol{Q}}}}\right\}}^{{st}}]$$
(10)

where the unit vector ν represents the surface normal, constant L1 = 4 × 10−11 N, L2 = 4 × 10−11 N, L3 = 2.88 × 10−11 N, and L4 = 0. The numerical parameters used here are A0 = 1.17 × 105 J/m3 and U = 3.5. To simulate 4′-pentyl-4-cyanobiphenyl (5CB), the elastic constants are K1 = 6 pN, K2 = 3.9 pN, K3 = 8.2 pN and K24 = 7 pN. The characteristic length scale is set to the nematic coherence length, the defect core size, with \({\xi }_{N}=\,\sqrt{{L}_{1}/{A}_{0}\quad }\approx 6.63\,{\mathrm{nm}}\).

The initial configuration for the half bimeron under the topological pattern of alternating splay–bend distortions was generated as follows64:

$${n}_{x}=\,\cos \left\{\pi \left[1+\left(-\frac{x}{L}+\frac{1}{2}\right) \tan {{\rm{\!h}}}\left[\eta \frac{\pi }{H}(x-{x}_{w})\right]\right]\left(1-\frac{z}{H}\right)\right\}$$
(11)
$${n}_{y}= \sin \left\{\pi \left[1+\left(-\frac{x}{L}+\frac{1}{2}\right)\tan{{\rm{\!h}}}\left[\eta \frac{\pi }{H}(x-{x}_{w})\right]\right]\left(\left(1-\frac{z}{H}\right)\right)\right\} \\ \tan{{\rm{\!h}}}\left[\eta \frac{\pi }{H}(x-{x}_{w})\right]$$
(12)
$${n}_{z}= \sin \left\{\pi \left[1+\left(-\frac{x}{L}+\frac{1}{2}\right)\tan{{\rm{\!h}}}\left[\eta \frac{\pi }{H}(x-{x}_{w})\right]\right]\left(\left(1-\frac{z}{H}\right)\right)\right\}\\ {\mbox{sec}}{{\rm{h}}}\left[\eta \frac{\pi }{H}(x-{x}_{w})\right]$$
(13)

where L represents the period of the surface pattern, and H corresponds to the height of the cell thickness. The half bimeron is positioned at x = xw, and the parameter η controls the string thickness depending on the elastic modulus K and the ratio between H/L. Different configurations can be obtained by multiplying a rotation matrix around the rotation axis and the z-axis.

Theoretical analysis

The interaction potential between a colloidal sphere with a dipolar director and a distorted director (with r ≪ L) is written as56 \({U}_{d}=-8\pi K{r}^{2}(\beta (\hat{{{\bf{p}}}}\cdot \hat{{{\bf{n}}}}){{\boldsymbol{\nabla }}}\cdot \hat{{{\bf{n}}}}-\frac{r}{12}{({{\boldsymbol{\nabla }}}{{\bf{n}}})}^{2})\), where K is the Frank elastic constant and β is the amplitude of dipole director distortions that depends on the strength of the surface anchoring.

Since the size of the experiment is larger than the simulation size, to focus on the half-skyrmion region, we first simulate a truncated half-skyrmion structure in a rectangular channel (lx × ly × lz = 600 × 300 × 400) with a splay-bend surface pattern of period L = 2000. We impose equilibrium director fields to calculate the interaction potential between half skyrmions and colloids. To match the experimental scale, we adjust the length scale of the structures to lx  × ly  ×  lz = 30 μm × 15 μm × 20 μm. The parameters used here are K = 7.5 pN and r = 2.5 μm. β is a phenomenological parameter representing the strength that pulls the elastic dipole to the splay regions. The second part of the interaction potential accounts for the mismatch between the ambient director and the fixed director at the particle surface. This component balances the force pulling the elastic dipole toward the splay distortion area. Therefore, to achieve a complementary balance between the two forces, we adjust the value of β = 0.05 throughout the paper.

To determine the preferred orientations of elastic dipoles, minimizing the first part of the interaction potential is necessary. When β is positive, the sign of \(\hat{{{\bf{p}}}}\cdot \hat{{{\bf{n}}}}\) must be the same as the sign of divergence of the local director field \({{\boldsymbol{\nabla }}}\cdot \hat{{{\bf{n}}}}\). Since \(\hat{{{\bf{p}}}}\) and \(\hat{{{\bf{n}}}}\) are unit vectors, \((\hat{{{\bf{p}}}}\cdot \hat{{{\bf{n}}}}){{\boldsymbol{\nabla }}}\cdot \hat{{{\bf{n}}}}\) reaches its maximum when they are either parallel or antiparallel, which depends on the sign of their dot product. By considering these factors, we can determine the optimal orientations of the elastic dipoles, ensuring their alignment with the local director field to minimize the interaction potential.