Introduction

Quantum simulation1,2,3,4,5 with ultracold atoms has enabled the generation and exploration of strongly correlated matter. Itinerant models that are challenging to probe with computer simulations have been successfully studied with optical lattice-based quantum simulators3,6,7. Concurrently, atoms in optical tweezer arrays8,9,10,11 have ushered in a new era of quantum computation12,13,14,15,16,17 and enabled large-scale quantum algorithms with logical qubits18. Essential to both of these platforms is imaging19,20,21 of individual atoms22,23,24,25.

Fast imaging significantly reduces cycle time, which is one of the key figures of merit for quantum simulators and quantum computers. Moreover, quantum error correction, essential to fault-tolerant quantum computation, relies on fast, mid-sequence readout18. Efforts have been made to improve the repetition rate of quantum experiments by greatly accelerating the state preparation of degenerate quantum gases26,27 or by loading tweezers directly from magneto-optical traps and implementing sideband cooling28,29. However, high-fidelity imaging takes hundreds of milliseconds in many machines, which can act as an experimental cycle time bottleneck. Cavity-assisted measurements within tens of microseconds have been demonstrated30 but require complex optics installed inside vacuum. Recently, fast imaging in 8 μs31 (99.5% fidelity) and 20 μs (98.6% fidelity)13,14 have been reported. Yet, neutral atom platforms so far still need much longer readout time than other quantum computing platforms, such as superconducting qubit platforms32,33,34,35.

Another key limitation of imaging systems is their resolution: the diffraction limit of the imaging light can be a significant hurdle to the site-resolved imaging fidelity36. When studying itinerant models, wavelength-scale lattice spacings are used to optimize tunneling3. Even smaller lattice spacings are required to study long-range interactions31, or to realize collective optical effects37. In these cases, the optical point spread functions between neighboring sites may substantially overlap, requiring longer imaging times to distinguish between sites with high fidelity. We used accordion lattices to study the extended Hubbard model in our recent work31 but here we fully characterize the performance of the accordion lattices.

Conventionally, atoms must be localized to the same site throughout the imaging duration, necessitating deep pinning traps and efficient on-site optical cooling. Imaging multiple atoms per single site leads to parity projection: light-assisted collisions22,38,39,40,41 cause pairwise loss of atoms, resulting in the final atom number in a site to be 0 (1) if the initial atom number is even (odd). To avoid this limitation and count the total number of atoms in each site, techniques of expanding the atoms to multiple sites have been demonstrated42,43,44,45,46,47,48. However, direct on-site atom counting would significantly reduce the technical complexity of exploring models with many atoms in a lattice site.

In this work, building upon the free space imaging demonstrated in refs. 31,49, we push the limit of fast site-resolved imaging. We achieve a high fidelity (>99.4%) of distinguishing between 0 and 1 atoms per site within as little as 2.4 μs, bringing neutral atom quantum platforms to be comparable to superconducting platforms in terms of detection time34,35. We elucidate and overcome the detrimental effects of continuous high-saturation imaging of atoms from two directions and experimentally confirm the understanding of the imaging process. Using an accordion lattice, we resolve a small-spacing lattice beyond the diffraction limit. Moreover, we demonstrate parity-projection-free imaging that, for the first time, enables direct atom number detection.

Results

Experimental setup

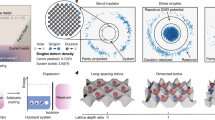
The fast imaging method with accordion lattices presented in this work is primarily developed for our quantum gas microscope that uses magnetic erbium atoms to create strongly correlated lattice models with long-range dipolar interaction50. This enables quantum simulations of extended Hubbard models and recently led to the observation of dipolar quantum solids31. To maximize the magnetic dipolar interaction strength51, we choose a lattice spacing of 266 nm, roughly two times smaller than the lattice spacing used in typical experiments. Both resolving this small lattice spacing optically and laser cooling erbium atoms in lattices during imaging is technically challenging. Therefore, we use accordion lattices52,53,54,55 to increase the spacing of the sites during imaging to a similar regime as optical tweezer arrays. With a spacing of a few microns, the point spread functions of adjacent lattice sites do not overlap. Therefore, we only need to detect as few as 15 photons to identify an atom reliably. We can then completely circumvent trapping and laser cooling during imaging and instead rely on the inertia of the atom to keep it in place as we quickly scatter as many photons as possible13,14,49,56. This scheme not only greatly speeds up the imaging to only a few microseconds, but also removes the complexity of pinning lattices and cooling schemes.

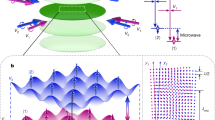
In our experiment we rapidly create Bose-Einstein condensates of erbium (168Er) within a few hundred milliseconds26, and adiabatically load these condensates into tightly spaced retro-reflected lattices31. To image the atoms, we turn off the lattice dynamics by quickly ramping up the tightly spaced lattice and transferring the atoms to an accordion lattice. The accordion lattice is created by projecting beams through a high numerical aperture objective (Supplementary Information (SI)). The accordion lattice spacing is expanded to a few microns in 80 ms. We estimate the loss rate during the lattice transfer and expansion to be smaller than 1% (SI). After quenching off the lattices, we illuminate the atoms from two sides with high-intensity (I ≈ 20Isat, where Isat is the saturation intensity of the transition at 56 mW/cm2) imaging beams (purple arrows in Fig. 1a) for a total of a few microseconds on resonance with the broad 30 MHz transition of erbium at 401 nm and scatter 80 photons per microsecond. Fluorescence photons are captured by the objective and recorded on an Electron Multiplying (EM) Charge-Coupled Device (CCD) camera (Fig. 1c). As a result of a through hole in our custom objective (SI), we collect photons between 0.3 and 0.85 Numerical Aperture (NA). It is worth noting that our imaging scheme injects a significant amount of energy into our system and as a result, the atoms are effectively lost after being imaged. However, if trap depths were to be increased to much larger than the kinetic energy imparted during imaging, it is conceivable to recapture atoms after imaging, albeit at a fairly high temperature.

Fig. 1: Imaging setup.
figure 1

a Our quantum gas microscope consists of a high-resolution objective mounted in vacuum. To perform imaging, we send two counter-propagating beams onto the atoms and set the beam polarization and atom quantization axis to maximize the objective collection efficiency (SI). b we expand the lattice spacing to a few micrometers to perform fast fluorescence imaging in free space without cooling or trapping and obtain single-shot images. c is one such image with a Mott Insulator in the center and checkerboard patterns on the edge—a signature of dipolar interactions between the magnetic atoms used in our quantum gas microscope.

Full size image

Effects of imaging light recoil

Our free space imaging method relies on the atom not moving significantly from its original position during imaging. Therefore, we minimize the imaging duration by maximizing the photon scattering rate to collect enough photons before the atom can drift far enough to be mischaracterized as being in a different lattice site. This is achieved by shining highly saturated imaging beams, on-resonance with a broad transition, onto the atom. As there is no cooling and trapping, the atom is accelerated solely by the recoil of the scattered photons. When illuminated by an imaging beam, the atom undergoes coherent Rabi oscillations between 0 and ℏk units of momentum transfer in the direction of the illuminating light. This continues until spontaneous emission projects the atom, imparting ℏk in the direction of the imaging light and ℏk of momentum in an isotropic random direction. Subsequent scattering events occur in the same manner, with Rabi oscillations between spontaneous emission events, for the duration of imaging. Ideally, to ensure the atom remains spatially localized we want to balance the directional ℏk momentum kick that accompanies the isotropic momentum kick49. We use two deeply saturated counter-propagating beams to circumvent the acceleration along the illumination direction by cancelling out the directional transport from absorption recoil events. Naively, the saturation should prevent fluctuations in relative power from causing mean field motion. Experimentally, however, we find a strong deviation from this picture. When two radiation fields are incident on the atom at the same time, we observe the atom’s momentum during the coherent Rabi drive acts non-trivially; the atom quickly spreads out even if the power of the two beams is carefully balanced. We observe diffusion in momentum that scales with the intensity of the beams, despite the rate of incoherent scattering saturating (Fig. 2b). In addition, a slight beam intensity imbalance for deeply saturated beams causes rapid acceleration in one direction (Fig. 2c), highlighting how detrimental this effect is in realistic, imperfect experimental systems. We observed similar phenomena for a range of relative detunings of the counter-propagating beams and different polarization arrangements. Such behavior was previously reported49, but no explanation was found. Here we take careful consideration of the physics of imaging with counter-propagating beams, in particular, what occurs during the Rabi drive in the time between spontaneous emission events, and explain how our solution of using alternating beams circumvents unwanted transport.

Fig. 2: Alternating pulsed imaging beams result in high imaging fidelity.
figure 2

The spread and bias of atom momentum can reduce imaging fidelity. To prevent atoms from accelerating in one direction, we apply two counter-propagating beams to average momentum kicks. However, when both beams simultaneously illuminate at high intensity (I ≈ 20Isat), we observe rapid spatial spreading due to coherent quantum walks between spontaneous emission events. This process quickly spreads the atomic wave function across many momentum states. For times t ≲ 1/Γ, the dynamics can be approximated by coherent oscillations in the highly saturated regime (I ≫ Isat), which explains key features of the observed behavior. Simulations of the excited state population reveal that the quantum walk causes the momentum to spread over tens of ℏk states (left of a), with excited state population shown in red. In contrast, with alternating beams, the momentum remains confined to ±ℏk (right of a), with excited state population shown in green before spontaneous emission. As a result, the atomic motion during imaging is primarily governed by a diffusive random walk from spontaneous emission events. In b, we simulate the momentum spread after multiple spontaneous emissions using the master equation (SI). For a fixed imaging duration, the momentum spread increases linearly with beam intensity when using two continuous beams while it plateaus with alternating beams, even at higher intensities. Experimental time-of-flight measurements show good agreement with these simulations (solid lines), with error bars representing the standard error of the mean throughout this paper. c displays the measured momentum bias and simulated results (solid lines) for continuous beams, highlighting the increased sensitivity to intensity imbalance with simultaneous beams. Finally, (d) compares averaged images with one beam on (top), both beams on continuously (middle), and alternating beams with no overlap (bottom) at the same total imaging duration. The alternating beam configuration yields sharper images with better separation of histogram peaks, consistent with theoretical predictions.

Full size image

To study this surprising effect, we consider a picture where the atom performs a quantum walk in momentum space57,58. In between spontaneous emission events, when both beams are on at the same time and couple the atom to the same excited mJ state with Rabi frequencies Ω1 and Ω2, the atom goes through quantum walks in momentum space which can be described as a realization of the Su-Schrieffer-Heeger (SSH) model59,60,61,62 (SI). We simulate this model using exact diagonalization63 (Fig. 2a left, SI). At high beam intensities, the Rabi frequency from the imaging beams (Ω), which corresponds to two times the tunneling energy in the SSH model, is larger than the decay rate (Γ). Therefore, the quantum walk spreads the atom wave function to momentum states larger than h/λ, where λ is the imaging wavelength at 401 nm, before spontaneous emission projects the atom’s momentum state. In contrast, by alternatingly pulsing the two beams, the atom coherently oscillates between 0 and  ±h/λ momentum states and does not venture into states with higher momentum until spontaneous emission, limiting the momentum spread per scattered photon. Intuitively, with both beams on simultaneously the atom acts as a conduit to shuttle photons between the two imaging beams and hence takes on a wide spread of momentum to do so; however, with alternating beams only one radiation field has an effect on the coherent drive in a given instance. This not only allows the momentum spread to be narrower but also makes the momentum imbalance very insensitive to beam intensity imbalance, as long as both beam intensities are much higher than Isat. Taking into account spontaneous emission, we arrive at similar results (SI).

To measure the momentum spread in the two imaging configurations, we turn on the beam(s) for a short duration of 0.2 μs and then take an image after 100 μs time-of-flight. We fit the image and plot the width of the Gaussian fit (Fig. 2b). When both beams are on at the same time the width (blue) increases roughly linearly with the Rabi frequency, which is consistent with the simulation (SI). In contrast, when only one beam is on, as in the case of alternatingly pulsed imaging beams, the width (orange) saturates. The spread of momentum states increases the spread of the atom position, directly reducing the imaging fidelity. In addition, we study the enhanced sensitivity at high intensity with continuous beams. Due to the quantum walk interference, any beam intensity imbalance can cause a large bias in the momentum, quickly accelerating the atom along the stronger beam direction and greatly affecting the imaging fidelity (Fig. 2c and SI). As shown in Fig. 2d left, the peak in the middle panel is significantly lower than the one in the bottom panel, since atoms spread out much faster and venture into neighboring sites, resulting in worse fidelity (Fig. 2c right). Therefore, we pulse the beams alternatingly so that as long as each beam is highly saturated and the excited state population is close to 50%, the recoil is relatively insensitive to fluctuations in the beam power.

Our measurements and theory explain why alternating imaging beams give significantly higher fidelity. Hence, from here on, we optimize the imaging in this configuration. We perform a simulation of the atom’s trajectory during imaging and of the fluorescence signal. The simulation takes into account the imaging light’s stochastic recoil events that move the atoms inside and outside of the focal plane as well as several other factors (SI). As atoms are imaged for a longer duration, they spread out further around the original location (Fig. 3a top). On the other hand, more photons are collected so the histograms are separated further, increasing the estimated fidelity (Fig. 3a bottom), ultimately limited by the transition to dark states as discussed in the next section. To confirm the accuracy of our simulation, we compare the average images between the simulation and the experimental data. The accordion lattices are set to different spacings and the imaging beams are set to different durations. We then fit the average image with a Gaussian function and define the spot size as twice the standard deviation (Fig. 3b). The imaging spot size increases for larger accordion spacing because of slight shot-to-shot position fluctuations of the accordion lattice due to air currents (0.065 waves standard deviation)36. In addition, the calculated ground state Wannier functions based on the measured lattice depth and spacing of the accordion lattices also grow larger when the spacing is larger. Furthermore, the simulation takes into account the wavefront error of the objective that was measured before its placement in the vacuum chamber64. The data agrees with the simulation as shown in Fig. 3c, confirming our understanding of the imaging process and facilitating the application of this method to different atoms or molecules.

Fig. 3: Imaging with alternating beams.
figure 3

With alternatingly pulsed beams, the stochastic recoil causes atoms to spread out when the imaging duration is increased, as simulated in the upper panel of (a), where colors represent different simulated traces. To compare the experiment with the simulation, we measure the spot size of our atoms. b is an exemplary image averaged over 30 single-shot images where we expand the accordion lattices to 6 μm spacing and perform free space imaging for 7.2 μs. The image is slightly asymmetric since the beams are along one direction and our objective has aberrations especially when the atom randomly walks out of the focal plane. The image is then cropped into individual sites and 1D profiles are obtained by summing over either the x or y axis. The x and y spot sizes are different since the imaging beams are along only one axis and the objective aberrations are anisotropic (SI). The spot sizes with different accordion lattice spacings and imaging durations are shown in (c). The measured spot sizes of the x and y profiles are plotted with circles with error bars. The respective colored lines correspond to the simulated spot size along the x and y directions. The measurements qualitatively agree with the simulation.

Full size image

Ultra-fast imaging using binarization

The speed of imaging with our EM CCD camera can be further improved using an image processing technique: binarization49. We present a detailed analysis of this technique and obtain imaging fidelities of 99.4% in only 2.4 μs after collecting 15 photons.

The number of photons collected by the imaging system follows a Poisson distribution (Fig. 4a bottom left). Standard practice for fluorescence imaging techniques is to determine optimal cutoffs between different modeled photon count distributions to identify the presence or absence of an atom. In an ideal system, this is done by choosing the cutoff at the minimal overlap between two Poissonian distributions. However, EM CCD cameras introduce additional noise during the EM process and broaden the distribution to twice the original variance (Fig. 4a bottom right) so careful consideration of how to model this noise is necessary to faithfully reconstruct the probability distributions. The imaging magnification is chosen so that each pixel mostly detects only zero or one photon (Fig. 4a blue histograms). Applying a binarization threshold (brown dashed line) to each pixel we can effectively distinguish whether the pixel detected a photon or not and strongly suppress the additional EM noise when summing up pixels to obtain histograms64 (Fig. 4b). Fundamentally, this cut-off method is a post-processing technique that improves signal-to-noise ratio, and hence readout accuracy, by taking advantage of how nonlinear EM noise factors in differently when distinguishing between 0 and 1 photon distributions and between 1 and 2 (or any higher number) photon distributions. We compare the histograms with and without applying binarization when the atoms are imaged for only 2.4 μs. In Fig. 4c, we fit the histograms with two skew-normal distributions (since the photon number is low, the Poisson distribution due to photoelectron number and the Gamma distribution due to EM are both asymmetric) and add a constant background in between the Gaussian peaks to account for erbium’s branching ratio. The infidelity of false positive (red in Fig. 4c) and false negative (blue) errors at different cutoffs are shown. For the case with (without) binarization, we plot the discrete (continuous) distribution. Based on the cumulative distributions, we use gray dashed lines to mark the total count cutoff that minimizes the sum of infidelity for false positives and false negatives. Binarization reduces the variance of the peaks by roughly 1.8 times and increases the fidelity significantly from 97.7% to 99.4%. This improvement in signal-to-noise ratio can be exploited when fast imaging with few photons is desired, such as in tweezer array experiments12,13,14,15,16,17,18.

Fig. 4: Ultra-fast high-fidelity imaging via binarization of Electron Multiplying (EM) CCD counts.
figure 4

EM noise on the EM CCD camera can negatively affect the signal-to-noise ratio (a). Pixels with 0, 1, or 2 initial electrons (left top 3 panels) are amplified via EM, resulting in overlapping probability distributions that make it impossible to precisely distinguish the initial electron number (right top 3 panels). Assuming a Poisson distribution of the initial electron number (left lowest panel in orange), the EM process results in a factor of two more variance (right lowest panel in orange). However, when the photon density per pixel is less than one (the blue panels dominate) setting a binarization threshold (brown dashed line) to each camera pixel enables a near-perfect distinction between 0 and 1 initial electrons. This effectively removes the EM noise and increases the signal-to-noise ratio. An example of binarization is shown in (b), where only 15 photons are collected on the camera within 2.4 μs (3 μm accordion lattice spacing). The histograms are fitted with two skew-normal distributions and a constant offset between the peaks to account for the branching ratio in (c). The infidelity at different cutoffs is estimated based on the fit, assuming the overlapping distributions are accurate representations of the probability distribution in the tails. Binarization increases the estimated fidelity from 97.7% to 99.4% on our EM CCD camera. The maximum fidelity of more than 99.5% can be achieved with only 3 μs imaging duration as shown in (d). The fidelity is mainly limited by the atom transitioning into a dark state during imaging, which we estimate in (e) by preparing a cloud with mostly one atom per site and then performing imaging for 8.8 μs at 4 μm accordion lattice spacing. In addition to two peaks corresponding to 0 and 1 atom per site, we identify significant counts between the peaks with this long imaging duration. The simulated histograms assuming different branching ratios are laid on top of the data, showing an estimated branching ratio of slightly below 5 × 10−5.

Full size image

Our fidelity at long imaging duration (Fig. 4d) is limited by the atom transitioning into intermediate long-lived dark states. Once an atom decays to a dark state, it no longer scatters photons and can be mischaracterized as absent. This chance to decay to dark states (the branching ratio) can be estimated by analyzing the histogram of the counts in between the peaks corresponding to 0 and 1 atoms per site. We simulate the histogram taking into account the stochastic random walk of atoms in and out of the focal plane as well as an assumed branching ratio. The result indicates a branching ratio of slightly less than 5 × 10−5. Similar results are obtained with different imaging durations and accordion lattice spacing. Previous calculations estimated the total branching ratio to dark states to be on the order of 10−4 65 and measurements indicated the ratio to be slightly less than 10−5 66, which is roughly consistent with our estimate. Adding repumper lasers or choosing a transition with a lower branching ratio could further improve imaging fidelity.

Parity-projection-free imaging

This imaging method uniquely enables direct atom number readout without parity projection for the first time. We load multiple atoms per site and measure histograms by summing the raw camera count in a 19 × 19-pixel box (Fig. 5b light blue bars), which shows distinct peaks, allowing different atom numbers to be distinguished. Our simulation (SI) with only the peak heights as free parameters is plotted in orange, where the simulated photon count peak centers corresponding to different numbers of atoms per site match the measured results. The peak shapes are also similar between simulation and experiment. In the simulation, we assume no interactions between atoms on the same site, so the close match between measurement and simulation is evidence that we do not suffer from parity projection due to light-assisted collisions. The simulated fidelity is labeled on top of Fig. 5b. The demonstrated parity-projection-free imaging (Fig. 5a right) has enabled us to observe the sub-Poissonian fluctuation in site occupation of the Mott insulator25,43,67,68 with more than one particle per site, in situ, in Fig. 5c. The fidelity could be further improved by employing the latest camera technology and expanding the accordion lattice further. With qCMOS cameras free from EM noise and proper magnification, we estimate roughly 99% fidelity distinguishing between 1 and 2 atoms per site and more than 95% fidelity distinguishing between 3 and 4 atoms per site. By increasing the dynamic range of the accordion lattice, we would be able to space the atoms further than 4.5 μm and image longer to resolve even larger atom numbers.

Fig. 5: Parity-projection-free imaging.
figure 5

A single-shot image of more than one particle per site is shown in (a). The histogram of the data and the simulation (no free parameters except the peak heights) shows good agreement in (b). The fidelity from the simulation is labeled on top of the graph. In 700 digitized single-shot images, we select three different representative sites with average fillings of 1, 2, and 3 atoms per site, and plot the histogram of the atom number in (c). The Poisson distribution is overlaid in solid lines to contrast the sub-Poissonian statistics we observed, qualitatively showing that we are in the Mott Insulator regime.

Full size image

Discussion

We have thoroughly studied and optimized an imaging method that features an imaging duration of only 2.4 μs, pushing the state-of-the-art readout time of neutral atoms one step closer to that of superconducting qubits34,35. We demonstrated a high fidelity of 99.5% to distinguish between 0 and 1 atoms per site and more than 90% up to 4 atoms per site. Cameras with lower noise and the application of machine learning69,70,71 may further increase the performance of our imaging method. Our technique can be applied to any atom or molecule in optical tweezers or lattices and requires only a few hundred photons scattered, which can be essential for the detection of molecules whose transitions are not fully closed72,73. For tweezers, the already large spacing eliminates the need for accordion lattices, reducing the total imaging duration from the typical value of a few milliseconds to only a few microseconds. Although the survival probability of atoms after imaging in the trap is small, many quantum error correction methods with mid-circuit readout do not require the original imaged atom to be preserved13,14. For small-spacing lattices, the accordion lattice transfer and expansion limit the total imaging duration; however, the duration is still favorable compared to the typical imaging duration of quantum gas microscopes using established techniques that are on the order of half a second. Furthermore, for quantum simulators that do not require an accordion lattice, our fast-imaging technique can be a marked improvement. Moreover, the accordion operation time could still be further reduced to a few milliseconds by increasing lattice depths.

Additionally, we demonstrated that our site-resolved imaging does not suffer from parity projection, which simplifies the technical challenges of studying a wide range of physics, including the measurment of entanglement entropy in 2D to study quantum phase transitions and quantum critical points42,74, multi-band Fermi–Hubbard models75, SU(N) physics76,77,78,79, charge density wave and topological phases like Haldane Insulator80,81,82 with dipolar atoms or molecules, and quantum link model simulations83.