Abstract
Interplay between seismic and aseismic slip could shed light on the frictional properties and seismic potential of faults. The well-recorded 2023 Kahramanmaraş earthquake doublet provides an excellent opportunity to understand their partitioning on strike-slip faults. Here, we utilize InSAR and strong motion data to derive the coseismic rupture during the doublet, ~4-month postseismic afterslip, and slip distributions of two Mw>6.0 aftershocks. Our results show that afterslip appears to be complementary to coseismic slip and aftershocks, accounting for ~11.3% of the coseismic moment. Aftershocks mainly fall within the regions of positive Coulomb stresses caused by afterslip and follow a temporal decay similar to that of afterslip, indicating that aftershock production is the failure of small asperities loaded by the afterslip. The early postseismic afterslip is released ~93.7% aseismically and ~6.3% seismically by aftershocks. Our modeling results thus depict a complex fault system with highly variable slip patterns and stresses.
Similar content being viewed by others
Introduction
Elastic rebound theory states that elastic stress/strain across an active fault accumulated during the interseismic period is released by sudden slip during an earthquake1. Thereafter, strain release continues, which is controlled by postseismic aseismic afterslip2,3,4,5. Seismic and aseismic slip are two main modes of fault behavior, with their spatial distribution shedding some light on the frictional properties of faults and serving as an indicator of the seismic potential6,7,8. Therefore, understanding the partitioning of seismic and aseismic fault slip is the core of seismotectonics6,9.
The East Anatolian Fault Zone (EAFZ) is a ~600-km sinistral strike-slip fault that connects the Dead Sea Fault Zone (DSFZ) to the Karlıova Triple Junction10,11. It accommodates the relative motion between the Arabian and Anatolian plates at a slip rate of ~10 mm/yr on the northeast side to ~4 mm/yr on the southwest side12,13,14,15,16. The EAFZ is divided into several major segments, and each of them is defined by bends, compressional structures, or pull-apart basins, as well as multiple subparallel and seismically active branches10,17,18.
The fault section of the EAFZ stretching from the Erkenek segment (ES) to the Amanos segment (AS) is characterized by a seismic recurrence interval of hundreds to millennia10, high interseismic coupling16,19, moderate strain rate20, and low seismicity rate21,22,23, indicating that it is capable of producing large earthquakes24. At 01:17 on 6 February 2023 (UTC Time), the Mw 7.8 Nurdağı-Pazarcık earthquake struck this section, followed ~11 minutes later by an Mw 6.6 aftershock (hereafter called the 06/02/2023 aftershock). After over 9 h, the Mw 7.7 Ekinözü earthquake occurred ~97 km NNE of the 1st earthquake, which, along with the Mw 7.8 mainshock, is referred to as the Kahramanmaraş earthquake doublet. On 20 February 2023, the Mw 6.3 Antakya aftershock struck the southwestern termination of the Mw 7.8 Nurdağı-Pazarcık earthquake25 (Fig. 1). The series of strong shocks resulted in over 59,000 deaths and 110,000 injuries26,27.
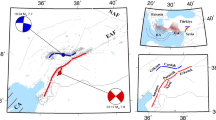
a Seismicity and data used in this study. Strong-motion stations (pale green diamonds) and synthetic aperture radar (SAR) frames of the Sentinel-1 (pale magenta lines) and ALOS-2 (orange lines) satellites are shown in this subplot. Black lines represent the mapped fault traces with small green dots marking segment boundaries. The blue, red, and black beach balls show the focal mechanisms of the 2020 Mw 6.8 Elazığ earthquake, the earthquake doublet, and two strong aftershocks from the United States Geological Survey (USGS), respectively. Yellow dots indicate the relocated aftershocks that occurred within about two months following the Kahramanmaraş earthquake doublet29. White circles represent historical earthquakes with M > 4.5 occurring between 1900 and 201823. AFP African Plate, ATP Anatolian Plate, ARP Arabian Plate, EUP Eurasian Plate, NAF North Anatolian fault, EAF East Anatolian fault, AS Amanos segment, PS Pazarcık segment, ES Erkenek segment, NF Nurdağı fault, SF Sürgü fault, DF Doğanşehir fault, ÇF Çardak fault, YF Yeşilköy fault. b and c are the wrapped interferograms obtained from the Sentinel-1 descending (T021) and ascending (T014) tracks, respectively. d and e are the descending (T077) and ascending (T184) interferograms derived from ALOS-2 data, respectively. f and g are the ~4-month cumulative postseismic deformation along the descending and ascending tracks, respectively. The red and blue colors indicate the displacement towards and away from the SAR satellite, respectively. The background topography data in a-g is sourced from SRTM15 + V2.690. h Normalized coseismic slip distributions of the Mw 7.8 Nurdağı-Pazarcık earthquake on the Erkenek segment and the 2020 Mw 6.8 Elazığ earthquake65, respectively. Pink dots are 18-day relocated aftershocks following the 2020 Mw 6.8 Elazığ earthquake91. ES Erkenek segment, PüS Pürtürge segment, SQR seismically quiescent region.
The 2023 Kahramanmaraş earthquake doublet drew the attention of the community and seismologists around the world. After these two events, back-projection imaging, aftershock relocation, rupture dynamic simulation, multi-point source, and finite fault inversion were rapidly performed to decipher their fault geometries, source parameters, and rupture properties19,25,28,29,30,31,32,33,34,35,36,37,38. A consensus is that the 1st mainshock originated from an unmapped fault branch linked to the Pazarcık segment (PS) and then propagated bilaterally along the EAFZ for about 300 km, which imposed significant positive static stresses on the hypocentral region of the 2nd mainshock33. However, information on the postseismic deformation and mechanism following the Kahramanmaraş doublet is still unclear, limiting our knowledge of the fault slip budget of the EAFZ and the assessment of future seismic hazards. Therefore, a joint analysis of seismic and aseismic fault slips during and after this doublet is necessary. It is also important to understand the mechanical basis of stress buildup and release in continental strike-slip fault zones.
In this study, we utilize the strong-motion observations and Interferometric Synthetic Aperture Radar (InSAR) data from Sentinel-1 and ALOS-2 satellites to invert for the coseismic fault slip associated with the 2023 Kahramanmaraş doublet and two strong aftershocks with Mw>6.0. Additionally, we investigate the postseismic afterslip within the first ~4 months and the interplay between aseismic and seismic fault slip. Finally, we discuss the seismic potential of the surrounding major faults.
Results and discussion
Coseismic rupture during the Kahramanmaraş doublet
The coseismic deformation derived from the Sentinel-1 and ALOS-2 SAR images is utilized to constrain the detailed coseismic slip distribution (see Methods, Supplementary Figs. 1 and 2a). Figure 2a and Supplementary Fig. 3a reveal that the majority of coseismic slip is confined to depths above 15–20 km, consistent with the average seismogenic thickness18. The 2023 Kahramanmaraş earthquake doublet is dominated by sinistral slip, accompanied by minor normal or reverse components, which is consistent with previous studies31,33. The main asperity of the Nurdağı-Pazarcık earthquake is located on the PS with a maximum slip of ~9 m. A more compact asperity with a peak slip of ~10 m is observed on the Çardak fault (ÇF) for the Ekinözü earthquake. Assuming a shear modulus of 30 GPa, the geodetic moments released by the Nurdağı-Pazarcık and Ekinözü earthquakes are ~6.5 × 1020 N·m and ~4.1 × 1020 N·m, respectively, corresponding to moment magnitudes of 7.8 and 7.7. The geodetic moment of the Nurdağı-Pazarcık event is slightly larger than the estimates from the United States Geological Survey (USGS) (5.4 × 1020 N·m) and the Global Centroid Moment Tensor (GCMT) (5.8 × 1020 N·m). And the geodetic moment released by the Ekinözü earthquake is between the seismic moments estimated by the USGS (2.6 × 1020 N·m) and GCMT (4.5 × 1020 N·m).
a Coseismic slip, b kinematic afterslip, c stress-driven afterslip, and d optimal afterslip associated with the 2023 Kahramanmaraş earthquake doublet. SQR, seismically quiescent region. Slip distributions of e the 06/02/2023 Mw 6.6 aftershock and f the Mw 6.3 Antakya aftershock. Note that different colorbars are applied in a–f.
Our preferred coseismic slip distribution is in good agreement with some published coseismic rupture models19,31,32,38,39,40,41, mainly because we all use InSAR data. These models consistently demonstrate that the high slip is concentrated in the shallow crust above depths of 15–20 km, with similar slip magnitudes and patterns. Some detailed discrepancies are attributed to different fault geometries, datasets, and inversion methods. For example, previous models did not consider the contribution of the Sürgü fault (SF) due to the lack of significant displacement discontinuities31,37 and few aftershocks near the SF28,29. To align with the local fault structure10,42, the SF is added to our coseismic model. Results show that SF is characterized by a small slip, possibly due to the 1986 M ~6 earthquake sequence that occurred along this fault22,23,43. The kinematic models without the constraint of InSAR observations show a relatively discrete high-slip region33,34, emphasizing the need for near-field geodetic data.
As shown in Supplementary Fig. 4, the optimal slip model recovers the surface displacements from both the Sentinel-1 and ALOS-2 images satisfactorily. In addition, we conduct a jackknife sensitivity analysis to evaluate the reliability of slip estimation (see Methods). The maximum standard deviation of the slip is ~0.8 m (Supplementary Fig. 5a), which represents only ~8% of the coseismic slip. All of them highlight the reliability of the coseismic slip model of the earthquake doublet constrained by InSAR observations.
Slip distribution of two strong aftershocks
Since the 06/02/2023 aftershock occurred temporally between the Mw 7.8 Nurdağı-Pazarcık and the Mw 7.7 Ekinözü events, it is difficult to directly retrieve its coseismic deformation using InSAR technology. We thus use the strong-motion data (Fig. 1a) to resolve the kinematic slip evolution during the aftershock by the iterative deconvolution and stacking (IDS) method (see Methods). Supplementary Fig. 6 shows that in the first 4 s, the 06/02/2023 aftershock ruptures bilaterally along dip with its major propagation toward the updip direction, featuring a peak slip rate of ~0.4 m/s. Subsequently, it mainly propagates toward the updip and SE directions. However, the moment release becomes weak and dispersed in this stage, probably due to the discontinuous fault structures in this region. The average rupture velocity is slow at ~2.5 km/s. Most of the slip is concentrated within the depth range of 8-24 km, and the total seismic moment is ~9.0 × 1018 N · m (Mw 6.6). The maximum slip is ~1.2 m, which is located ~5.6 km SW of its epicenter (Fig. 2e and Supplementary Fig. 6). The good agreement between the observed and synthetic waveforms validates the robustness of our kinematic model associated with the 06/02/2023 aftershock (Supplementary Fig. 7).
For the Mw 6.3 Antakya aftershock, we estimate its slip distribution with InSAR observations (see Methods, Supplementary Fig. 2c, d). Figure 2f demonstrates the slip distribution of the Antakya aftershock, which is characterized by a dominant sinistral movement with a minor normal component. The high slip is mainly concentrated at depths ranging from 3 km to 15 km, which releases a geodetic moment of ~3.0 × 1018 N · m (Mw 6.3). Notably, InSAR observations may include some contributions from postseismic deformation following the Mw 7.8 Nurdağı-Pazarcık earthquake. Given the small coseismic slip and afterslip (as modeled below) associated with the Nurdağı-Pazarcık event in the Antakya region (Fig. 2), it is reasonable to ignore its postseismic effects. The slip model for the Mw 6.3 Antakya aftershock effectively reproduces the observed InSAR displacements (Supplementary Fig. 8), thereby confirming the validity of this assumption and the robustness of the model.
Kinematic afterslip model
We use the cumulative postseismic line-of-sight (LOS) displacements within the first ~4 months to derive the kinematic afterslip distribution of the 2023 Kahramanmaraş earthquake doublet, following the same strategy as the coseismic inversion (see Methods, Supplementary Figs. 2b, 9, and 10). The spatial distribution of afterslip is illustrated in Fig. 2b. The majority of afterslip occurs in regions with low coseismic slip, spatially complementing the coseismic asperities. Notably, the high-afterslip concentration zone is located on the ÇF, with a maximum slip of ~0.65 m at a depth of ~16 km. The total moment yielded by the kinematic afterslip model is ~1.2 × 1020 N · m, corresponding to a moment magnitude of 7.3.
As demonstrated in Supplementary Fig. 11, the surface LOS displacements predicted by the kinematic afterslip model are basically in agreement with the InSAR observations, suggesting that afterslip is the main driving mechanism for the near-field postseismic deformation ~4 months after the earthquake doublet. The jackknife resampling method is also utilized to assess the sensitivity of the inversion for afterslip (see Methods). The maximum standard deviation of the slip is ~0.03 m (Supplementary Fig. 5b), accounting for only ~5% of the afterslip. This suggests that the InSAR observations are able to constrain the kinematic afterslip distribution well.
Stress-driven afterslip model
To ensure the physical plausibility of the inferred afterslip and reduce the number of free parameters44, we consider a stress-driven forward model for the afterslip of the 2023 Kahramanmaraş earthquake doublet (see Methods). Figure 2c and Supplementary Fig. 3c illustrate the predicted afterslip distribution during the first ~4 months under the frame of the rate-strengthening friction, which releases a geodetic moment of ~1.1 × 1020 N · m (Mw 7.3). The stress-driven afterslip distribution resembles the pattern of kinematic afterslip, with the majority of the afterslip occurring downdip of the coseismic high-slip zones. However, the stress-driven afterslip is found to be more concentrated close to the coseismic asperities, where shear stress increases substantially caused by the mainshocks. The kinematic afterslip model is smoother and fails to capture significant slip gradients. Discrepancies between the kinematic and stress-driven afterslip models may be attributed to heterogeneous frictional parameters on the fault plane32,41,45, smoothness constraints46, inaccuracies in the driving source of the coseismic slip model, and contributions of other postseismic mechanisms47. The surface deformation predicted by the stress-driven afterslip closely matches the cumulative postseismic displacements derived from InSAR data, except for some near-field and far-field noise that the kinematic afterslip model also cannot recover well (Supplementary Fig. 12). Herein, although we do not directly use the InSAR time series to constrain the stress-driven afterslip, the predicted time series for Regions A and B are still in good agreement with the observations (Fig. 3a, c, d). Moreover, the slip uncertainties, as determined through statistical analysis (see Methods), are below 0.22 m (Supplementary Fig. 13a), further validating the robustness of the stress-driven afterslip model.
a Locations of Region A and Region B. The background topography data is sourced from SRTM15 + V2.690. b The trade-off between the reference rate \({V}_{0}\) and frictional parameter \((a-b)\sigma\). The red star marks the optimal values. The cumulative postseismic deformation relative to the first acquisition (light blue dotted lines) and displacements predicted by the stress-driven afterslip model (SAM, light orange dotted lines) and optimal afterslip model (OAM, light green dotted lines) in c Region A and d Region B.
Optimal afterslip model
The stress-driven afterslip simulation excludes shallow afterslip because it requires exceedingly dense grids to accurately resolve near-surface fault patches46. To better model the observed postseismic deformation and quantify the shallow afterslip, we construct a combined model that incorporates both kinematic shallow afterslip and stress-driven deep afterslip (see Methods). Figure 2d and Supplementary Fig. 3d exhibit a superposition of the inferred shallow and deep afterslip due to the Kahramanmaraş earthquake doublet, highlighting the predominance of downdip afterslip, with shallow afterslip primarily concentrated on the ES. The total moment yielded by the combined afterslip model is ~1.2 × 1020 N · m (Mw 7.3), with ~88% attributable to the deep afterslip and ~12% to the shallow afterslip. The afterslip moment represents roughly 11.3% of the coseismic geodetic moment. As illustrated in Supplementary Fig. 14, the InSAR-observed cumulative postseismic transients are explained well by the combined afterslip model, displaying an improved fit compared to the stress-driven afterslip model (Supplementary Table 1), particularly for the near-field deformation. Furthermore, it improves the fit between the observed and modeled InSAR time series (Fig. 3c, d). We thus take the combined afterslip model as the optimal afterslip model for the Kahramanmaraş earthquake doublet. The small slip uncertainties for both shallow and deep afterslip further demonstrate the stability of our combined afterslip model (Supplementary Fig. 13b).
Coseismic and afterslip moment scaling
Figure 4 displays the estimated moments of afterslip and coseismic slip for the Kahramanmaraş earthquake doublet alongside 62 afterslip models from 47 other earthquakes48 (Supplementary Fig. 15 and Table 2). The results reveal that the afterslip moment (Maft0) near-linearly increases with the coseismic moment (M0) of earthquakes, with a gradient of ~1.0 (Fig. 4a). The correlation between Maft0 and M0 of the Kahramanmaraş earthquake doublet also agrees well with this trend. This is because Maft0 is the result of the combined effects of the coseismic area and average slip48. Given that the large uncertainty in the Maft0 estimates due to data and modeling factors can mask the dependence we would expect to see from the observational time window48 (Fig. 4a), we do not attempt to normalize the Maft0 estimates for the observation period but rather consider the individual Maft0 estimates here.
a Comparison between the estimated afterslip moment (Maft0) and coseismic moment (M0). The stars outlined in red and green represent the estimated M0 and Maft0 of the Mw 7.8 Nurdağı-Pazarcık earthquake and the Mw 7.7 Ekinözü earthquake, respectively. Circles and rectangles denote the moments yielded from the kinematic afterslip model (KAM) and the stress-driven afterslip model (SAM), respectively. The estimates for the same earthquake from different studies are connected by red lines. The color scale represents the temporal duration of the data used for each afterslip model. b Comparison between the relative afterslip moment (Mre) and corresponding M0.
Further examination of the relationship between the relative afterslip moment (Mre = Maft0/M0) and corresponding M0 reveals that Mre varies by several orders of magnitude, with 94% of models suggesting a range between 1% and 100% (Fig. 4b). The majority of moment models cluster around 10%, indicating that Maft0 may be an order of magnitude smaller than M0. Interestingly, Mre exhibits a weak negative correlation with M0, indicating that larger events are prone to less Mre. As shown in Fig. 4b, the relative afterslip moments of the Mw 7.8 Nurdağı-Pazarcık earthquake and the Mw 7.7 Ekinözü earthquake are ~0.11 and ~0.12, respectively, consistent with the correlation. Notably, this identified correlation may be due to publication bias48. A wider range of Maft0 variability in smaller earthquakes (Fig. 4), compounded by a bias towards studying smaller earthquakes with greater Maft0, may contribute to the observed pattern48.
Interplay between the coseismic slip, afterslip, and aftershocks
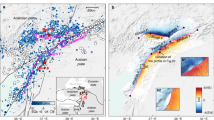
The coseismic and postseismic slip patterns provide valuable insights into how seismic and aseismic fault slip is partitioned6,49. As demonstrated in Fig. 2b–d, the kinematic, stress-driven, and optimal afterslip models all reveal that the short-term afterslip is mainly located downdip of the coseismic rupture. There seems to be little overlap between the coseismic and postseismic zones (Supplementary Fig. 3). Notably, the spatially complementary pattern between the coseismic slip and afterslip is common, which has been widely observed in other events elsewhere5,50,51. To further decipher their interplay, we calculate the Coulomb failure stress changes (\(\Delta {{{\rm{CFS}}}}\)) on the fault planes induced by the coseismic rupture (see Methods). As shown in Fig. 5a, the afterslip is concentrated in regions with positive \(\Delta {{{\rm{CFS}}}}\) due to the mainshocks, indicating that afterslip is indeed triggered by the coseismic slip.
Coulomb failure stress change (\(\triangle {{{\rm{CFS}}}}\)) on the seismogenic fault plane of the earthquake doublet caused by a coseismic slip and b afterslip. SQR seismically quiescent region, AS Amanos segment, PS Pazarcık segment, ES Erkenek segment, NF Nurdağı fault, SF Sürgü fault, DF Doğanşehir fault, ÇF Çardak fault, YF Yeşilköy fault. White contours represent our preferred afterslip distribution, with values exceeding 0.1 m. Yellow dots are the relocated aftershocks within 5 km of the fault plane29. \(\triangle {{{\rm{CFS}}}}\) on c the Mw 6.6 06/02/2023 aftershock fault plane and d the Mw 6.3 Antakya fault plane due to the Mw 7.8 Nurdağı-Pazarcık earthquake. e Relocated background seismicity with depth22. The yellow bars represent the number of background seismicity. Average f coseismic slip and g afterslip with depth associated with the Mw 7.8 Nurdağı-Pazarcık earthquake (red line) and the Mw 7.7 Ekinözü earthquake (green line). The orange bars represent the number of aftershocks.
In addition, we estimate the \(\Delta {{{\rm{CFS}}}}\) triggered by the optimal afterslip distribution. We find that most near-fault aftershocks29 (within a distance of 5 km of the fault plane) fall within the regions of positive \(\Delta {{{\rm{CFS}}}}\) caused by afterslip (~53%) rather than by the mainshocks (~30%) (Fig. 5a, b). This finding is further confirmed by the aftershock catalog from ref. 28., which reveals a higher proportion of aftershocks associated with afterslip (~59%) than with the coseismic slip (~19%). Similar phenomena are also observed in some aftershocks at a distance from the fault planes, which is discussed in a later section. It is no longer surprising that afterslip plays a central role in triggering aftershocks52,53, which has been widely reported elsewhere after other documented earthquakes45,54, such as the 2021 Mw 7.4 Maduo earthquake51 and the 2017 Mw 8.2 Chiapas earthquake50. One extreme view of aftershock production is the rupture of small asperities loaded by afterslip, favored by the similar temporal decay between aftershocks and afterslip54. As shown in Fig. 6c, the temporal evolution of the optimal afterslip model correlates well with aftershocks. Moreover, the spatial relationship between aftershocks and afterslip is found to be complementary over time (Supplementary Fig. 16). We thus argue that afterslip may drive the occurrence of aftershocks. Note that we cannot rule out the possibility of dynamic triggering55. To further understand the seismic and aseismic slip behaviors during the early postseismic period, we estimate the cumulative seismic moment released by aftershocks within ~4 months to be 7.5 × 1018 N · m (Mw 6.5) (Fig. 6d). Here, the frequency-magnitude distribution for the aftershock catalog reveals a completeness magnitude of 1.6 (see Methods), above which all aftershocks are considered. By comparing the aftershock moment with the geodetically derived postseismic moment, we find that ~6.3% of the postseismic afterslip is released by aftershocks. This indicates that the increased stress due to the coseismic slip is mainly released in an aseismic manner.
a Spatial distribution of aftershocks and afterslip. SQR, seismically quiescent region. b Estimation of the completeness magnitude for the aftershock catalog. The aftershock catalog is from the Department of Earthquake, Disaster and Emergency Management Authority of Türkiye (AFAD). c Comparison of the moment yielded by the optimal afterslip model (light green line) with the cumulative number of aftershocks larger than the completeness magnitude (Mc: 1.6) (red line). d Comparison of the temporal moment release for the stress-driven afterslip model (light brown dashed line), optimal afterslip model (light green line), and aftershocks (red line).
We also demonstrate the spatial distribution of background seismicity, aftershocks, as well as the coseismic slip and afterslip along dip (Fig. 5e–g). We find that the relocated background earthquakes along the EAFZ are active within a depth range of 4–22 km22, consistent with the dominant depth range of aftershocks. Additionally, most aftershocks28 are concentrated between the coseismic asperity and postseismic afterslip. Spatially, there exists a complementary distribution among coseismic slip, afterslip, and aftershocks, collectively releasing the accumulated energy during the interseismic period.
Frictional properties
Our obtained coseismic and postseismic slip models associated with the Kahramanmaraş earthquake doublet demonstrate that the frictional behaviors of the EAFZ vary with depth. Under the framework of rate-and-state friction, earthquakes can only occur in locked regions appearing to be rate-weakening, whereas the rate-strengthening zones are dominantly characterized by afterslip6. Therefore, the coseismic slip and afterslip should not overlap significantly, especially when using simple layered crust models56. As shown in Fig. 2 and Supplementary Fig. 3, the coseismic slip is concentrated within a depth range of less than 15–20 km, while the afterslip predominantly occurs downdip of the coseismic high-slip zones, in line with the expected slip pattern. We thus argue for a transition from a rate weakening in the shallow crust (<15–20 km) to a rate strengthening or steadily creeping region at greater depths.
The stress-driven deep afterslip suggests a uniform frictional parameter \((a-b)\sigma\) of 3 MPa (see Methods, Fig. 3b), aligning with the general magnitude order of 10−1-10 MPa derived from afterslip models for other earthquakes45,54,57,58,59,60. For instance, a lower bound of 0.7 MPa was identified for the 2004 Mw 6.0 Parkfield earthquake45, and uniform values of 0.42 MPa and 6.5 MPa were determined for the 2020 Mw 7.8 Simeonof Island, Alaska earthquake54 and the 2015 Mw 7.8 Gorkha (Nepal) earthquake60, respectively. The parameters of \((a-b)\sigma\) and \({V}_{0}\) together control the evolutionary characteristics of afterslip45,46,61. A larger \((a-b)\sigma\) indicates a lower degree of nonlinearity in the afterslip decay61. Variations in frictional properties may be attributed to differences in fault zone materials and physical conditions59. When assuming the effective normal stress \(\sigma=260\) MPa at 20 km under hydrostatic pore pressure conditions62, the corresponding value of the frictional parameter \((a-b)\) is 0.012, which is close to the range of 10−3-10−2 suggested by laboratory measurements63,64.
Future seismic potential
The Mw 7.8 Nurdağı-Pazarcık earthquake ruptured ~300 km along the western EAFZ. This event occurred just 3 years after the devastating 2020 Mw 6.8 Elazığ earthquake that ruptured the central segment of EAFZ22,49,65, leaving a ~40-km seismically quiescent region (SQR)25,29,65 (Fig. 1h). Notably, the aftershock distribution connects these two events below ~10 km, which is consistent with the depth of interseismic seismicity18,29. Therefore, the SQR is located between the surface and ~10 km depth. The optimal afterslip model suggests that the accumulated energy within the SQR is released aseismically through afterslip (Fig. 2d), resulting in a stress shadow (Fig. 5b). Furthermore, it has been found to creep during the interseismic period49. These indicate that the SQR may be characterized by the rate-strengthening property2,66, preventing the coseismic rupture of the 2023 Mw 7.8 Nurdağı-Pazarcık earthquake and the 2020 Mw 6.8 Elazığ earthquake. Consequently, the likelihood of a strong earthquake occurring in this region in the near future is low. It is necessary to mention that the 1893 M ~ 7.1 and 1905 Ms 6.8 Malatya earthquakes occurred near the SQR67. However, in the absence of more precise information on the faulting extent for the 1893 and 1905 events22, it is unclear whether these two earthquakes ever ruptured the SQR, preventing us from further characterizing its slip behaviors and frictional properties.
The extensive rupture of the 2023 earthquake doublet releases accumulated strain and adjusts the stress conditions of surrounding regions68. Therefore, we employ the static \(\Delta {{{\rm{CFS}}}}\) to further comprehend the stress effects caused by the coseismic slip and afterslip of this earthquake doublet (Fig. 7). To analyze the triggering relationship among aftershocks, coseismic slip, and afterslip, we calculate the \(\Delta {{{\rm{CFS}}}}\) map at a depth of 10 km, utilizing the receiver fault’s geometry parameters aligned with the focal mechanism of the Mw 7.8 Nurdağı-Pazarcık earthquake from the USGS. As shown in Fig. 7c, d, aftershocks (in the depth interval of 10 ± 3 km) are mainly concentrated in regions with positive \(\Delta {{{\rm{CFS}}}}\) induced by afterslip rather than by the mainshocks, consistent with the above analysis on the fault plane (Fig. 5a, b). Moreover, \(\Delta {{{\rm{CFS}}}}\) is positive at the north end (Pürtürge) and south end (Antakya) of the seismogenic fault of the Mw 7.8 Nurdağı-Pazarcık earthquake due to the coseismic and postseismic slip. As a result, there may be a risk of strong aftershocks in these areas.
\(\triangle {{{\rm{CFS}}}}\) induced by a coseismic slip and b afterslip on surrounding faults. c \(\triangle {{{\rm{CFS}}}}\) at 10 km depth due to coseismic slip. Purple stars indicate the locations of the two Mw > 6.0 aftershocks. Yellow dots are relocated aftershocks between 7 km and 13 km depth. BF Bozava fault, DSFZ Dead Sea Fault Zone, GF Gerger fault, KF Kahramanmaraş fault, KaF Karataş fault, EnF Engizek fault, MF Malatya fault, NaF Narince fault, SaF Savrun fault, TF Toprakkale fault. d Similar to c, but caused by the optimal afterslip model.
To further investigate the seismic potential of the major faults, we specially select 11 nearby faults as receiver faults. Their fault traces and geometries are referenced from the active faults database in Türkiye42 (Supplementary Table 3). The results reveal that the stress increase due to the coseismic slip exceeds 0.03 bar on the DSFZ (Fig. 7a), bringing the fault closer to failure, while afterslip has little effect on the DSFZ (Fig. 7b). Given the significantly increased \(\Delta {{{\rm{CFS}}}}\) on the DSFZ due to the Kahramanmaraş doublet and the fact that the DSFZ is highly coupled16, it has the potential to generate strong earthquakes and derives more attention. In addition, \(\Delta {{{\rm{CFS}}}}\) due to the coseismic slip and afterslip is positive on the northern faults, including the Gerger fault, the Malatya fault, the Narince fault, and the Pürtürge segment, which may push the next earthquake on these faults. These findings underscore the need for heightened monitoring and preparedness in these regions.
Methods
InSAR data processing
We process the Sentinel-1 SAR data using GMTSAR software69,70. We invoke the differential InSAR (D-InSAR) method to map the coseismic LOS displacements of the earthquake doublet, as well as the Mw 6.3 Antakya aftershock. The chronological information of SAR images is presented in Supplementary Table 4. To account for the topographic phase, we apply the 3-arc-second Shuttle Radar Topography Mission (SRTM) Digital Elevation Model (DEM). The interferograms are multi-looked with a ratio of 8:2 in range and azimuth and filtered using a 200 m-wavelength Gaussian filter. The dense near-field fringes pose a challenge in accurately unwrapping the phase. To mitigate its potential impact, we exclude the region with coherence values below 0.2 to create a near-fault decorrelation mask70 and allow a phase discontinuity when unwrapping with SNAPHU71. We obtain the coseismic deformation associated with the earthquake doublet after geocoding (Supplementary Fig. 1a, b). Notably, the absence of near-fault deformation constraints may hinder the accurate determination of the coseismic slip distribution. Fortunately, the longer wavelength of the ALOS-2 data (~23.6 cm compared to ~5.5 cm for the Sentinel-1) results in better phase coherence and enables accurate phase unwrapping in the proximity of the fault trace. Therefore, we additionally use the ALOS-2 ascending (T184) and descending (T077) downsampled data from the work of ref. 32. to recover the coseismic deformation caused by the Kahramanmaraş earthquake doublet.
To measure the early postseismic deformation associated with the earthquake doublet, we utilize the SBAS-InSAR method72,73 to process the Sentinel-1 SAR data. The ascending track, collected from 9 February 2023 to 3 July 2023, and the descending track, spanning from 10 February 2023 to 22 June 2023 (Supplementary Table 4), are processed accordingly. The interferogram pairs are generated by applying specific thresholds for the temporal baseline (set at 80 days) and the spatial baseline (set at 200 meters) (Supplementary Fig. 9). These interferograms undergo a multi-looking process with a factor of 16:4 (range: azimuth) and are subsequently filtered with a Gaussian filter of 400 meters wavelength. To minimize the impact of poor coherence pixels and retain the stable high-quality regions, we perform a stacking process on the coherence grids of the interferograms and exclude regions with mean coherence less than 0.1. The presence of noise caused by atmospheric perturbations in interferograms limits accurate mapping of the postseismic deformation20. Here, we utilize the Generic Atmospheric Correction Online Service (GACOS) corrections74 and the Common-Scene-Stacking (CSS) method75 to mitigate atmospheric effects. Finally, the time series of postseismic deformation is obtained (Supplementary Fig. 10).
Static coseismic slip inversion
To enhance computational efficiency while preserving essential information, we employ the gradient-based quadtree method to downsample the coseismic deformation fields of the earthquake doublet76. Finally, we retain 5418 and 5129 data samples from the Sentinel-1 ascending and descending orbits, respectively. Equal weights are assigned to the displacements obtained from ALOS-2 data during the inversion.
The steepest descent method (SDM)77 is adopted to estimate the detailed coseismic slip of the earthquake doublet. To calculate the surface displacements caused by fault slip, we employ a rectangular dislocation model embedded in an elastic half-space78. We identify the fault traces by combining previous studies41, relocated aftershocks28,29, coseismic and postseismic deformation (Fig. 1), and geological survey10,42. Eight fault segments, namely the AS, PS, ES, Nurdağı fault, SF, Doğanşehir fault, ÇF, and Yeşilköy fault, are adopted to invert the observed InSAR displacements (Fig. 1 and Supplementary Fig. 1). The dip angles are established based on the work of ref. 32. (Supplementary Table 5), which is grounded in the analysis of aftershock profiles. The fault plane is extended from the surface to 30 km along dip, and then is discretized into 852 rectangular sub-faults with a grid of ~5 km by 5 km. The rake angle is allowed to vary between -40° and 40°. The optimal smoothing factor is determined to be 0.1 based on the L-curve criterion (Supplementary Fig. 2a).
Two strong aftershock slip models
For the Mw 6.6 06/02/2023 aftershock, we use the strong-motion data to resolve its kinematic slip evolution. We access the strong-motion waveform data from the Department of Earthquake, Disaster and Emergency Management Authority of Türkiye (AFAD), and 14 stations with good azimuthal coverage are selected. We integrate the raw strong-motion accelerations twice into displacements and band-pass filter them in [0.02 0.2] Hz to escape the interference by long-period noise and the inadequacies of the theoretical Green functions at higher frequencies79. We apply the automatic inversion scheme based on the iterative deconvolution and stacking (IDS) method80 to determine its refined slip evolution. The rupture initiation (37.29°N, 36.93°E, 14.8 km) is adapted from the high-resolution relocation28. A rectangular fault plane is constructed with the strike and dip of 218° and 85°, respectively, based on the relocated aftershock distribution28. We use the code QSSP81 to calculate the Green’s function based on the CRUST1.0 model82.
For the Mw 6.3 Antakya aftershock, we process the Sentinel-1 SAR images from both ascending (T014) and descending (T021) tracks. The observed LOS displacements are shown in Supplementary Fig. 1c, d. Due to the smaller deformation area of the Mw 6.3 Antakya aftershock, we uniformly downsample its coseismic LOS displacement fields. The SDM approach is invoked to estimate the coseismic slip of the Antakya aftershock. We constrain the curved fault trace with the deformation and active fault datasets42. We determine the dip angle by systematically marching through a series of dips to arrive at the minimum root mean square of residuals (\({{{\rm{RMSR}}}}\)) between InSAR observations and predictions.
where \({d}_{{{{\rm{obs}}}}}\) and \({d}_{{{{\rm{pre}}}}}\) denote the observed and predicted LOS displacements, respectively, and \(n\) is the number of data points. As shown in Supplementary Fig. 2c, the fault plane is determined as dipping to the northwest at 42°, consistent with the focal mechanism from the GCMT (strike/dip: 226°/42°). During the inversion, we divide the fault plane into 80 sub-faults with allowable rake angles between −70° and 30°. The smoothing factor of 0.05 is set to balance the model roughness and data misfit based on the trade-off curve (Supplementary Fig. 2d).
Kinematic afterslip inversion
The postseismic deformation may arise from the contributions of poroelasticity, afterslip, and viscoelastic relaxation83, among which afterslip has been identified as the primary mechanism responsible for the early postseismic deformation spanning from several days to months51,59. We thus perform a pure afterslip model to investigate the postseismic deformation of the earthquake doublet.
In general, the afterslip is distributed updip and downdip of the coseismic rupture. We thus extend the fault plane to 50 km for the postseismic afterslip model to recover the larger range of postseismic deformation (Supplementary Fig. 11). Considering the limitations of the CSS method in mitigating atmospheric noise at the end images59, we exclude the last few scenes to determine the postseismic deformation. We downsample the cumulative postseismic deformation for the ascending (9 February 2023 to 9 June 2023) and descending (10 February 2023 to 10 June 2023) tracks after applying a mask to exclude the region affected by the Mw 6.3 Antakya aftershock. We then estimate the kinematic afterslip based on the cumulative postseismic LOS displacements within the first ~4 months following the strategy of the coseismic slip inversion. The smoothing factor is the same as that in the coseismic inversion (Supplementary Fig. 2b).
Stress-driven afterslip simulation
We simulate the stress-driven afterslip evolution using the Unicycle program57,84,85,86. The fault afterslip controlled by the rate-strengthening simplification could be expressed as45:
where \(\Delta \tau\) is shear stress loading induced by the coseismic rupture; \(\sigma\) is the effective normal stress on the fault; The friction parameter \({V}_{0}\) represents the reference slip rate that controls the timescale of relaxation; \((a-b)\) is the frictional parameter of the rate-and-state friction law.
The coseismic slip model is used as the stress-driving source. We deduce model parameters by seeking the most suitable values that can effectively recover the postseismic deformation, which is determined by minimizing the \({{{\rm{RMSR}}}}\) between InSAR observations and predictions. Through the trial-and-error approach, the best-fitting stress-driven model is identified, achieving a minimum \({{{\rm{RMSR}}}}\) of ~14.3 mm. Meanwhile, the optimal values of the frictional parameter and the reference slip rate are determined to be 3 MPa and 1.3 m/yr, respectively (Fig. 3b).
Optimal afterslip model
Taking into account both the physical reasonableness and the fit to the observed postseismic deformation, we thus develop a combined afterslip model that incorporates the stress-driven deep afterslip and kinematic shallow afterslip46. We first calculate the surface contributions of the optimal stress-driven afterslip model (\({V}_{0}\): 1.3 m/yr; \((a-b)\sigma\): 3 MPa) and remove them from the InSAR observations. We then use the residual LOS displacements to estimate the distribution of shallow afterslip following the strategies of the kinematic afterslip inversion. In order to mitigate potential trade-offs with long-wavelength residuals, we exclude the residual displacements beyond 20 km from the fault trace.
Jackknife sensitivity analysis
We test the reliability of the coseismic slip and kinematic afterslip models using the jackknife resampling method87. We randomly remove 20% of downsampled InSAR data, and then rerun the inversion using the remaining data. Subsequently, we reperform the processes by randomly selecting another 20% of the data. We repeat this process 50 times and then calculate the standard deviations of slip for each fault patch. Supplementary Fig. 5 shows the distribution of standard deviations for the coseismic slip and kinematic afterslip.
Statistical uncertainty analysis
Due to various trade-offs among the parameters of the stress-driven afterslip model, the best-fitting model is only marginally superior to other relatively distinct models. To account for the uncertainties associated with the stress-driven and optimal afterslip models, we select models that are acceptable at the 68% confidence level88, ensuring a \({{{\rm{RMSR}}}}\) below 15.7 mm. Based on these selected models, we systematically calculate the slip uncertainties for each fault patch. Notably, the uncertainties for both the stress-driven and optimal afterslip models are less than 0.22 m, demonstrating the robustness of our afterslip models (Supplementary Fig. 13).
Coulomb failure stress changes
The Coulomb failure stress changes (\(\Delta {{{\rm{CFS}}}}\)) can be calculated based on the following formula:
where \(\Delta \tau\) and \(\Delta {\sigma }_{n}\) represent the changes in shear stress and normal stress, respectively. The effective friction coefficient \({\mu }^{\prime}\) is set at 0.4. A positive value of \(\Delta {{{\rm{CFS}}}}\) indicates that the induced stress changes bring the fault closer to rupture, while a negative \(\Delta {{{\rm{CFS}}}}\) value suggests the opposite effect. Our optimal coseismic slip and afterslip models are used as driving sources to calculate the stress changes due to the mainshocks and afterslip, respectively.
Completeness magnitude of the aftershock catalog
The completeness magnitude represents the lowest magnitude at which all earthquakes in a region are detected and reliably recorded. To accurately estimate the completeness magnitude for the AFAD aftershock catalog, we apply the maximum curvature method using Zmap7 software89. This method analyzes the frequency-magnitude distribution of earthquakes, focusing on the point of maximum curvature on this distribution curve. This point is indicative of the magnitude threshold above which all earthquakes are reliably recorded, and below which some smaller earthquakes might be undetected or omitted due to limitations in the detection capability of the seismic network.
Data availability
The Sentinel-1 SAR data used in this study are downloaded from the Alaska Satellite Facility (ASF, https://search.asf.alaska.edu/). The strong-motion data are available at https://zenodo.org/records/10081034. Sub-sampled LOS displacements from the ALOS-2 used in this study are available at https://doi.org/10.5281/zenodo.8128343. Coseismic and postseismic deformation derived from Sentinel-1 images, slip models, and the aftershock catalog from the AFAD project are available at https://doi.org/10.5281/zenodo.14223396.
Code availability
The SDM code can be found at ftp://ftp.gfz-potsdam.de/pub/home/turk/wang/. The Unicycle open-source software for modeling the stress-driven afterslip is available at https://bitbucket.org/sbarbot/unicycle/src/master/. The Zmap7 software can be found at github: https://github.com/CelsoReyes/zmap7.
References
Reid, H. F. The mechanism of the earthquake, in the California earthquake of April 18, 1906. Rep. State Earthq. Investig. Comm. 2, 16–28 (1910).
Guo, R., Zheng, Y. & Xu, J. Stress modulation of the seismic gap between the 2008 Ms 8.0 Wenchuan earthquake and the 2013 Ms 7.0 Lushan earthquake and implications for seismic hazard. Geophys. J. Int. 221, 2113–2125 (2020).
Milliner, C., Bürgmann, R., Inbal, A., Wang, T. & Liang, C. Resolving the kinematics and moment release of early afterslip within the first hours following the 2016 Mw 7.1 Kumamoto earthquake: implications for the shallow slip deficit and frictional behavior of aseismic creep. J. Geophys. Res. Solid Earth 125, e2019JB018928 (2020).
Perfettini, H. et al. Seismic and aseismic slip on the Central Peru megathrust. Nature 465, 78–81 (2010).
Wang, K. & Fialko, Y. Space geodetic observations and models of postseismic deformation due to the 2005 M7.6 Kashmir (Pakistan) earthquake. J. Geophys. Res. Solid Earth 119, 7306–7318 (2014).
Avouac, J.-P. From geodetic imaging of seismic and aseismic fault slip to dynamic modeling of the seismic cycle. Annu. Rev. Earth Planet. Sci. 43, 233–271 (2015).
Churchill, R. M., Werner, M. J., Biggs, J. & Fagereng, Å. Spatial relationships between coseismic slip, aseismic afterslip, and on-fault aftershock density in continental earthquakes. J. Geophys. Res. Solid Earth 129, e2023JB027168 (2024).
Moreno, M., Rosenau, M. & Oncken, O. 2010 Maule earthquake slip correlates with pre-seismic locking of Andean subduction zone. Nature 467, 198–202 (2010).
Dianala, J. D. B. et al. The relationship between seismic and aseismic slip on the Philippine fault on Leyte island: Bayesian modeling of fault slip and geothermal subsidence. J. Geophys. Res. Solid Earth 125, e2020JB020052 (2020).
Duman, T. Y. & Emre, Ö. The East Anatolian Fault: geometry, segmentation and jog characteristics. Geological Soc. Lond. Special Publ. 372, 495–529 (2013).
Yilmaz, H., Over, S. & Ozden, S. Kinematics of the East Anatolian Fault Zone between Turkoglu (Kahramanmaras) and Celikhan (Adiyaman), eastern Turkey. Earth Planets Space 58, 1463–1473 (2006).
Aktug, B. et al. Slip rates and seismic potential on the East Anatolian Fault System using an improved GPS velocity field. J. Geodyn. 94-95, 1–12 (2016).
Bletery, Q., Cavalié, O., Nocquet, J.-M. & Ragon, T. Distribution of interseismic coupling along the North and East Anatolian Faults inferred from InSAR and GPS data. Geophys. Res. Lett. 47, e2020GL087775 (2020).
Hamiel, Y. & Piatibratova, O. Spatial variations of slip and creep rates along the southern and central Dead Sea Fault and the Carmel–Gilboa Fault System. J. Geophys. Res. Solid Earth 126, e2020JB021585 (2021).
Mahmoud, Y. et al. Kinematic study at the junction of the East Anatolian fault and the Dead Sea fault from GPS measurements. J. Geodyn. 67, 30–39 (2013).
Özkan, A., Yavaşoğlu, H. H. & Masson, F. Present-day strain accumulations and fault kinematics at the Hatay Triple Junction using new geodetic constraints. Tectonophysics 854, 229819 (2023).
Bulut, F. et al. The East Anatolian Fault Zone: Seismotectonic setting and spatiotemporal characteristics of seismicity based on precise earthquake locations. J. Geophys. Res.: Solid Earth 117, B07304 (2012).
Güvercin, S. E., Karabulut, H., Konca, A. Ö., Doğan, U. & Ergintav, S. Active seismotectonics of the East Anatolian Fault. Geophys. J. Int. 230, 50–69 (2022).
Li, S. et al. Source model of the 2023 Turkey earthquake sequence imaged by Sentinel-1 and GPS measurements: implications for heterogeneous fault behavior along the East Anatolian Fault Zone. Remote Sens. 15, 2618 (2023).
Weiss, J. R. et al. High-resolution surface velocities and strain for Anatolia from Sentinel-1 InSAR and GNSS data. Geophys. Res. Lett. 47, e2020GL087376 (2020).
Karabulut, H., Güvercin Sezim, E., Hollingsworth, J. & Konca Ali, Ö. Long silence on the East Anatolian Fault Zone (Southern Turkey) ends with devastating double earthquakes (6 February 2023) over a seismic gap: implications for the seismic potential in the Eastern Mediterranean region. J. Geological Soc. 180, jgs2023–2021 (2023).
Pousse-Beltran, L. et al. The 2020 Mw 6.8 Elazığ (Turkey) earthquake reveals rupture behavior of the East Anatolian Fault. Geophys. Res. Lett. 47, e2020GL088136 (2020).
Tan, O. A homogeneous earthquake catalogue for Turkey. Nat. Hazards Earth Syst. Sci. 21, 2059–2073 (2021).
Nalbant, S. S., McCloskey, J., Steacy, S. & Barka, A. A. Stress accumulation and increased seismic risk in eastern Turkey. Earth Planet. Sci. Lett. 195, 291–298 (2002).
Barbot, S. et al. Slip distribution of the February 6, 2023 Mw 7.8 and Mw 7.6, Kahramanmaraş, Turkey earthquake sequence in the East Anatolian Fault Zone. Seismica https://doi.org/10.26443/seismica.v2i3.502 (2023).
Dal Zilio, L. & Ampuero, J.-P. Earthquake doublet in Turkey and Syria. Commun. Earth Environ. 4, 71 (2023).
Hussain, E., Kalaycıoğlu, S., Milliner, C. W. D. & Çakir, Z. Preconditioning the 2023 Kahramanmaraş (Türkiye) earthquake disaster. Nat. Rev. Earth Environ. 4, 287–289 (2023).
Ding, H. et al. High-resolution seismicity imaging and early aftershock migration of the 2023 Kahramanmaraş (SE Türkiye) Mw 7.9 & 7.8 earthquake doublet. Earthq. Sci. 36, 1–16 (2023).
Güvercin, S. E. 2023 earthquake doublet in Türkiye reveals the complexities of the East Anatolian Fault Zone: insights from aftershock patterns and moment tensor solutions. Seismol. Res. Lett. 95, 664–679 (2024).
Goldberg, D. E. et al. Rapid Characterization of the February 2023 Kahramanmaraş, Türkiye, Earthquake Sequence. Seismic Record 3, 156–167 (2023).
He, L. et al. Coseismic kinematics of the 2023 Kahramanmaras, Turkey earthquake sequence from InSAR and optical data. Geophys. Res. Lett. 50, e2023GL104693 (2023).
Jia, Z. et al. The complex dynamics of the 2023 Kahramanmaraş, Turkey, Mw 7.8-7.7 earthquake doublet. Science 381, 985–990 (2023).
Liu, C. et al. Complex multi-fault rupture and triggering during the 2023 earthquake doublet in southeastern Türkiye. Nat. Commun. 14, 5564 (2023).
Melgar, D. et al. Sub- and super-shear ruptures during the 2023 Mw 7.8 and Mw 7.6 earthquake doublet in SE Türkiye. Seismica https://doi.org/10.26443/seismica.v2i3.387 (2023).
Meng, J. et al. Surface deformations of the 6 February 2023 earthquake sequence, eastern Türkiye. Science 383, 298–305 (2024).
Okuwaki, R., Yagi, Y., Taymaz, T. & Hicks, S. P. Multi-scale rupture growth with alternating directions in a complex fault network during the 2023 South-Eastern Türkiye and Syria earthquake doublet. Geophys. Res. Lett. 50, e2023GL103480 (2023).
Ren, C. et al. Supershear triggering and cascading fault ruptures of the 2023 Kahramanmaraş, Türkiye, earthquake doublet. Science 383, 305–311 (2024).
Xu, L. et al. The 2023 Mw 7.8 and 7.6 earthquake doublet in southeast Türkiye: Coseismic and early postseismic deformation, faulting model, and potential seismic hazard. Seismol. Res. Lett. 95, 562–573 (2023).
Mai, P. M. et al. The Destructive Earthquake Doublet of 6 February 2023 in South‐Central Türkiye and Northwestern Syria: Initial Observations and Analyses. The Seismic Record 3, 105–115 (2023).
Xu, L. et al. The overall-subshear and multi-segment rupture of the 2023 Mw7.8 Kahramanmaraş, Turkey earthquake in millennia supercycle. Commun. Earth Environ. 4, 379 (2023).
Zhang, Y. et al. Geometric controls on cascading rupture of the 2023 Kahramanmaraş earthquake doublet. Nat. Geosci. 16, 1054–1060 (2023).
Emre, Ö. et al. Active fault database of Turkey. Bull. Earthquake Eng. 16, 3229–3275 (2018).
Taymaz, T., Eyidog̃an, H. & Jackson, J. Source parameters of large earthquakes in the East Anatolian Fault Zone (Turkey). Geophys. J. Int. 106, 537–550 (1991).
Rousset, B., Barbot, S., Avouac, J.-P. & Hsu, Y.-J. Postseismic deformation following the 1999 Chi-Chi earthquake, Taiwan: Implication for lower-crust rheology. J. Geophys. Res. Solid Earth 117, B12405 (2012).
Barbot, S., Fialko, Y. & Bock, Y. Postseismic deformation due to the Mw 6.0 2004 Parkfield earthquake: Stress-driven creep on a fault with spatially variable rate-and-state friction parameters. J. Geophys. Res. Solid Earth 114, B07405 (2009).
Jin, Z., Fialko, Y., Yang, H. & Li, Y. Transient deformation excited by the 2021 M7.4 Maduo (China) earthquake: Evidence of a deep shear zone. J. Geophys. Res. Solid Earth 128, e2023JB026643 (2023).
Zhao, B. et al. Dominant Controls of Downdip Afterslip and Viscous Relaxation on the Postseismic Displacements Following the Mw7.9 Gorkha, Nepal, Earthquake. J. Geophys. Res. Solid Earth 122, 8376–8401 (2017).
Churchill, R. M., Werner, M. J., Biggs, J. & Fagereng, Å. Afterslip moment scaling and variability from a global compilation of estimates. J. Geophys. Res. Solid Earth 127, e2021JB023897 (2022).
Cakir, Z. et al. Arrest of the Mw 6.8 January 24, 2020 Elaziğ (Turkey) earthquake by shallow fault creep. Earth Planet. Sci. Lett. 608, 118085 (2023).
Guo, R., Zheng, Y., Xu, J. & Jiang, Z. Seismic and aseismic fault slip associated with the 2017 Mw 8.2 Chiapas, Mexico, earthquake sequence. Seismol. Res. Lett. 90, 1111–1120 (2019).
Tang, X., Guo, R., Xu, J. & Zheng, Y. Role of poroelasticity and viscoelasticity during the postseismic deformation of the 2021 Mw 7.4 Maduo, China, earthquake. Seismol. Res. Lett. 94, 2192–2201 (2023).
Frank, W. B., Poli, P. & Perfettini, H. Mapping the rheology of the Central Chile subduction zone with aftershocks. Geophys. Res. Lett. 44, 5374–5382 (2017).
Gualandi, A., Serpelloni, E. & Belardinelli, M. E. Space–time evolution of crustal deformation related to the Mw 6.3, 2009 L’Aquila earthquake (central Italy) from principal component analysis inversion of GPS position time-series. Geophys. J. Int. 197, 174–191 (2014).
Zhao, B. et al. Aseismic slip and recent ruptures of persistent asperities along the Alaska-Aleutian subduction zone. Nat. Commun. 13, 3098 (2022).
Hardebeck, J. L. & Harris, R. A. Earthquakes in the shadows: Why aftershocks occur at surprising locations. Seismic Record 2, 207–216 (2022).
Hillers, G., Ben-Zion, Y. & Mai, P. M. Seismicity on a fault controlled by rate- and state-dependent friction with spatial variations of the critical slip distance. J. Geophys. Res. Solid Earth 111, B01403 (2006).
Muto, J. et al. Coupled afterslip and transient mantle flow after the 2011 Tohoku earthquake. Sci. Adv. 5, eaaw1164 (2019).
Tian, Z., Freymueller, J. T. & Yang, Z. Spatio-temporal variations of afterslip and viscoelastic relaxation following the Mw 7.8 Gorkha (Nepal) earthquake. Earth and Planetary Science Letters 532, 116031 (2020).
Wang, K. & Bürgmann, R. Probing Fault Frictional Properties During Afterslip Updip and Downdip of the 2017 Mw 7.3 Sarpol-e Zahab Earthquake With Space Geodesy. J. Geophys. Res. Solid Earth 125, e2020JB020319 (2020).
Wang, K. & Fialko, Y. Observations and modeling of coseismic and postseismic deformation due to the 2015 Mw 7.8 Gorkha (Nepal) earthquake. J. Geophys. Res.: Solid Earth 123, 761–779 (2018).
Zhuo, Z., Freymueller, J. T., Xiao, Z., Elliott, J. & Ronni, G. Early postseismic deformation of the 29 July 2021 Mw 8.2 Chignik earthquake provides new constraints on the downdip coseismic slip. Preprint at https://doi.org/10.22541/essoar.168988434.40307775/v1 (2023).
Kaneko, Y., Fialko, Y., Sandwell, D. T., Tong, X. & Furuya, M. Interseismic deformation and creep along the central section of the North Anatolian Fault (Turkey): InSAR observations and implications for rate-and-state friction properties. J. Geophys. Res. Solid Earth 118, 316–331 (2013).
Marone, C. Laboratory-derived friction laws and their application to seismic faulting. Annu. Rev. Earth Planet. Sci. 26, 643–696 (1998).
Mitchell, E. K., Fialko, Y. & Brown, K. M. Velocity-weakening behavior of Westerly granite at temperature up to 600 °C. J. Geophys. Res. Solid Earth 121, 6932–6946 (2016).
Konca, A. Ö. et al. From interseismic deformation with near-repeating earthquakes to co-seismic rupture: A unified view of the 2020 Mw 6.8 Sivrice (Elazığ) eastern Turkey earthquake. J. Geophys. Res. Solid Earth 126, e2021JB021830 (2021).
Yue, H. et al. The 2016 Kumamoto Mw = 7.0 Earthquake: A Significant Event in a Fault–Volcano System. J. Geophys. Res. Solid Earth 122, 9166–9183 (2017).
Ambraseys, N. N. Temporary seismic quiescence: SE Turkey. Geophys. J. Int. 96, 311–331 (1989).
Dai, X. et al. Coseismic slip distribution and Coulomb stress change of the 2023 Mw 7.8 Pazarcik and Mw 7.5 Elbistan earthquakes in Turkey. Remote Sens 16, 240 (2024).
Sandwell, D., Mellors, R., Tong, X., Wei, M. & Wessel, P. Open radar interferometry software for mapping surface Deformation. Eos, Trans. Am. Geophys. Union 92, 234–234 (2011).
Xu, X. et al. Refining the shallow slip deficit. Geophys. J. Int. 204, 1867–1886 (2016).
Chen, C. W. & Zebker, H. A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Optical Soc. Am. A 18, 338 (2001).
Berardino, P., Fornaro, G., Lanari, R. & Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 40, 2375–2383 (2002).
Schmidt, D. A. & Bürgmann, R. Time-dependent land uplift and subsidence in the Santa Clara valley, California, from a large interferometric synthetic aperture radar data set. J. Geophys. Res. Solid Earth 108, 2416 (2003).
Yu, C., Li, Z., Penna, N. T. & Crippa, P. Generic atmospheric correction model for interferometric synthetic aperture radar observations. J. Geophys. Res. Solid Earth 123, 9202–9222 (2018).
Tymofyeyeva, E. & Fialko, Y. Mitigation of atmospheric phase delays in InSAR data, with application to the eastern California shear zone. J. Geophys. Res. Solid Earth 120, 5952–5963 (2015).
Jónsson, S. N., Zebker, H., Segall, P. & Amelung, F. Fault slip distribution of the 1999 Mw 7.1 Hector Mine, California, earthquake, estimated from satellite radar and GPS measurements. Bull. Seismol. Soc. Am 92, 1377–1389 (2002).
Wang, R. et al. The 2011 Mw 9.0 Tohoku earthquake: comparison of GPS and strong‐motion data. Bull. Seismol. Soc. Am. 103, 1336–1347 (2013).
Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 75, 1135–1154 (1985).
Guo, R. et al. Kinematic slip evolution during the 2022 Ms 6.8 Luding, China, earthquake: compatible with the preseismic locked patch. Geophys. Res. Lett. 50, e2023GL103164 (2023).
Zheng, X. et al. Automatic Inversions of Strong-Motion Records for Finite-Fault Models of Significant Earthquakes in and Around Japan. J. Geophys. Res. Solid Earth 125, e2020JB019992 (2020).
Wang, R., Heimann, S., Zhang, Y., Wang, H. & Dahm, T. Complete synthetic seismograms based on a spherical self-gravitating Earth model with an atmosphere–ocean–mantle–core structure. Geophys. J. Int. 210, 1739–1764 (2017).
Laske, G., Masters, G., Ma, Z. & Pasyanos, M. E. CRUST1.0: An updated global model of Earth’s crust (EGU General Assembly, 2012).
Bürgmann, R. & Dresen, G. Rheology of the lower crust and upper mantle: Evidence from rock mechanics, geodesy, and field observations. Annu. Rev. Earth Planet. Sci. 36, 531–567 (2008).
Barbot, S. Slow-slip, slow earthquakes, period-two cycles, full and partial ruptures, and deterministic chaos in a single asperity fault. Tectonophysics 768, 228171 (2019).
Barbot, S., Moore, J. D. P. & Lambert, V. Displacement and stress associated with distributed anelastic deformation in a half‐space. Bull. Seismol. Soc. Am. 107, 821–855 (2017).
Moore, J. D. P. et al. Imaging the distribution of transient viscosity after the 2016 Mw 7.1 Kumamoto earthquake. Science 356, 163–167 (2017).
Melgar, D. et al. Seismogeodesy of the 2014 Mw6.1 Napa earthquake, California: Rapid response and modeling of fast rupture on a dipping strike-slip fault. J. Geophys. Res.: Solid Earth 120, 5013–5033 (2015).
Perfettini, H. & Avouac, J.-P. Modeling afterslip and aftershocks following the 1992 Landers earthquake. J. Geophys. Res. Solid Earth 112, B07409 (2007).
Wiemer, S. A software package to analyze seismicity: ZMAP. Seismol. Res. Lett. 72, 373–382 (2001).
Tozer, B. et al. Global bathymetry and topography at 15 arc sec: SRTM15+. Earth Space Sci. 6, 1847–1864 (2019).
Melgar, D. et al. Rupture kinematics of 2020 January 24 Mw 6.7 Doğanyol-Sivrice, Turkey earthquake on the East Anatolian Fault Zone imaged by space geodesy. Geophys. J. Int. 223, 862–874 (2020).
Acknowledgements
This work was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB 41000000, J.X.), the National Natural Science Foundation of China (42394112, R.G.), the Group Project of Natural Science Foundation of Hubei Province (2023AFA040, R.G.), the Open Fund of Hubei Luojia Laboratory (230100015, S22H640201, R.G.), and the Open Fund of Wuhan Gravitation and Solid Earth Tides National Observation and Research Station (WHYWZ202210, Y.Z.).
Author information
Authors and Affiliations
Contributions
R.G. conceived the study. R.G., X.T., Y.Z., W.Z., M.Q., and X.Z. performed the data process and modeling. R.G., X.T., and Y.Z. wrote the original manuscript. R.G., X.T., Y.Z., W.Z., M.Q., J.X., J.Z., X.Z., and H.S discussed, commented on, and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Guo, R., Tang, X., Zhang, Y. et al. Seismic versus aseismic slip for the 2023 Kahramanmaraş earthquake doublet. Nat Commun 16, 959 (2025). https://doi.org/10.1038/s41467-025-56350-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-56350-7