Introduction

Irrigation increases crop yield and currently accounts for more than 70% of total human freshwater use1. Irrigation-related water withdrawal and application have substantial impacts on global and regional water, energy, and biogeochemical cycles2,3,4,5, and therefore can change the magnitude and pattern of some meteorological conditions6,7,8. Notably, irrigation has a cooling effect on near-surface temperature9,10, especially during hot extremes11,12. For that reason, irrigation has been proposed as a potential land management strategy for balancing extreme heat escalation under anthropogenic climate change12,13,14.

Most previous studies only focused on temperature differences, ignoring that human comfort is also affected by heat dissipation15. Evaporative cooling is one of the main ways humans lose heat16, and air humidity and wind speed greatly influence evaporation efficiency17. These metrics can also be altered by irrigation18,19, suggesting that irrigation-induced impacts on human comfort during heat stress may be complex. Multiple moist-heat metrics were developed to quantify the compound effects of different meteorological conditions on heat stress20,21, and some of them have been used in irrigation-related studies. For example, over intensely irrigated regions in India, the wet-bulb temperature (Tw) was simulated to increase due to irrigation, despite a lowering of the temperature22,23. In addition to the ignorance of changes in air humidity, existing modelling studies generally use a static irrigated land map and rely on a single Earth System Model (ESM), which can introduce uncertainties in their results.

To address these limitations, we launched the Irrigation Model Intercomparison Project (IRRMIP) to comprehensively explore the impacts of irrigation expansion on climate and water resources during the 20th century. The IRRMIP protocol consists of two transient AMIP-style24 historical climate experiments, one with and one without irrigation expansion, during the period 1901–2014. Here we analyse IRRMIP simulations from six ESMs to study the impacts of irrigation expansion on historical (moist-)heat stress. We calculate several moist-heat metrics based on 3-hourly 2-m air temperature (T2m), 2-m air relative humidity, and 10-m wind speed. By comparing the results from different experiments and periods, we separate the effects of irrigation expansion and other forcings on high percentiles of these metrics. We aim at consolidating the understanding of irrigation-induced impacts on (moist-)heat stress, facilitating the inclusion of these impacts in future local land-use and land-management planning.

Results

Irrigation expansion drives the increase in water withdrawal

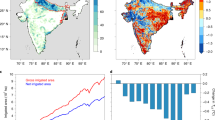
Global area equipped for irrigation has experienced substantial expansion from 1901 to 2014, increasing almost sixfold from 0.5 × 106 km2 to around 3 × 106 km2 (Fig. 1a). Expansion mainly happened in some irrigation hot spots, including South Asia (SAS), East Asia (EAS), and Central North America (CNA) (Fig. 2a). In 1901, most of the global irrigated land was concentrated over the regions where rice is the main staple food, such as India, China, and Japan (Fig. S3a). Since 1901, irrigated land has risen slowly over many regions until the 1950s, followed by an accelerated increase during the second half of the century (Fig. 1a). Until 2014, the irrigated areas in India and China experienced intensification and expansion, with some grid cells having a ≥40% (of the grid cell area) increase in irrigated area (Fig. 2a, b). Over North America, some new densely irrigated grid cells appear in CNA, while for other regions, the expansion is limited (mostly below 10% of the grid cell area).

Fig. 1: Historical increase in area equipped for irrigation and simulated irrigation water withdrawal.
figure 1

a Global and regional time series of area equipped for irrigation (AEI) in 1901–2014. The area equipped for irrigation data is from the Land-Use Harmonization phase 2 (LUH2) project57, and the grid cells corresponding to IPCC reference regions are indicated in Fig. 2a. b Simulated mean global irrigation water withdrawal (IWW) with (blue: tranirr) by all six models and without (red: 1901irr) irrigation expansion by five models (except IPSL-CM6). The line indicates the median value of six (or five) models and the range indicates the maximum and minimum values. Note that IWW of CNRM-CM6-1 is applied as an external input, which is the irrigation fluxes from a global reconstructed hydrological dataset based on simulations34, and for the 1901irr experiment of IPSL-CM6, irrigation is switched off. c–h Global and regional IWW (tranirr) simulated by CESM2 (c), CESM2_gw (d), NorESM (e), E3SM (f), CNRM-CM6-1 (g), and IPSL-CM6 (h).

Full size image
Fig. 2: Spatial pattern of irrigation expansion and simulated irrigation water withdrawal in different periods.
figure 2

a Increase in irrigated fraction between 1901 and 2014, and the IPCC reference regions71 used in the analysis. b Irrigated fraction in the year 2014 (Irrigated fraction in the year 1901, 1941, and 1981 could be found in Fig. S3a–c). The grid resolution is the simulation resolution of CESM2, CESM2_gw, and NorESM (0.9° × 1.25°). c, d Multi-model mean simulated annual irrigation water withdrawal (IWW) with transient irrigation extent (tranirr) during the first 30 years (1901–1930: (c) and the last 30 years (1985–2014: (d). The figure showing results from all individual models can be found in Fig. S15. Multi-model mean simulated annual IWW with fixed irrigation extent (1901irr) during the two periods can be found in Fig. S3e, f.

Full size image

The spatial pattern of simulated irrigation water withdrawal (IWW) is in agreement with the distribution of the area equipped for irrigation (Fig. 2c, d). India is still the most intensively irrigated region, consisting of many grid cells (0.9° × 1.25°) with more than 250 mm yr−1 of IWW. The six IRRMIP models simulate a broad range of global IWW (900–4000 km3 yr−1 after the year 2000), but the temporal trend of simulations with transient irrigation extent (hereafter referred to as tranirr) generally aligns with that of the area equipped for irrigation. Consistent with a previous review5, simulated annual IWW during the post-2000 period ranges from  ~900 to  ~4000 km3 yr−1 (Fig. 1c–h), due to different representations of irrigation in these models. CESM2, CESM2_gw, and NorESM2 show high similarity because they share the same atmosphere and land models, with comparably small differences in specific sub-models (see Supplementary Note 1).

Based on IWW and irrigated area, we select several regions, including West North America (WNA), CNA, North Central America (NCA), Mediterranean (MED), West Central Asia (WCA), SAS, EAS, and Southeast Asia (SEA) (Fig. 2a), to calculate regional irrigation water quantities (Fig. 1c–h). SAS is the region with the highest IWW in all models, but its relative importance varies. For example, after the year 2000, SAS accounts for around one-third of global IWW simulated by CESM2 (32.4–35.8%), CESM2_gw (31.4–35.1%), E3SM (27.5–41.8%), and NorESM (32.8–35.1%), but in IPSL-CM6, this fraction is less than one-fourth (16.0–20.4%). WCA consumes the second-highest quantity of IWW, even though its area equipped for irrigation is less than EAS. This indicates that simulated IWW is dependent not only on the area equipped for irrigation but also on other factors, such as background climate conditions.

Different feedback from heat and moist-heat stress to irrigation expansion

Here we focus on T2m, HUMIDEX (HU: Eq. (2)), and Tw (Eq. (4)) warm extremes, as many other metrics are weighted average values of T2m and Tw. Changes in high percentiles of these three metrics could be interpreted as the impacts of irrigation expansion and other forcings on dry heat stress (T2m), human comfort (HU), and humid heat stress (Tw) (Table 1). In the tranirr experiment, climate change, land use change, and irrigation expansion, are all transient throughout the simulation period, and in the 1901irr experiment, the only difference is that irrigation extent is fixed at the level in year 1901 (simulation protocol of IRRMIP can be found in Supplementary Note 2). By comparing the last-30-year of tranirr (tranirr(1985–2014)) to the first-30-year of 1901irr (1901irr(1901–1930)), we can quantify the impacts of all forcings (greenhouse gas emissions, land use and land management change, irrigation expansion, etc.). Similarly, the difference between the first- and the last-30-year periods of 1901irr (1901irr(1901–1930) and 1901irr(1985–2014)) gives the impacts of all forcings minus irrigation expansion. Finally, by subtracting the outputs of tranirr(1985–2014) from 1901irr(1985–2014), we obtain the impacts of irrigation expansion.

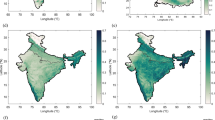
Table 1 Approach to separate the impacts of different forcings
Full size table

We first calculate the 99.9th percentile values (one-in-1000 time steps warm event) of three metrics in three exp_periods (1901irr(1901–1930), 1901irr(1985–2014) and tranirr(1985–2014)), and take the one of 1901irr(1901–1930) as the reference (Fig. 3a–c). Several irrigation hot spots, like SAS, WCA, NCA, and CNA, are also extreme heat hot spots, with a 99.9th percentile value of T2m exceeding 40 °C in many grid cells. Other forcings cause a general warming signal (+0.5 to +2 °C, see Fig. 3g), except in some areas over SAS and EAS, which may be attributed to the increasing aerosol concentrations25,26. Irrigation expansion has substantial cooling impacts in heavily irrigated grid cells (>1 °C) and weaker impacts over surrounding grid cells (<0.5 °C) (Fig. 3j). This cooling effect creates regional irrigation-induced ‘cooling islands’ against the global warming background, like the Indo-Gangetic Plain and several grid cells in Central USA (Fig. 3d). Irrigation expansion’s cooling impacts on the extreme value of HU are much less substantial in magnitudes (Fig. 3k), as a result of the increased humidity, and the ‘cooling islands’ do not exist if HU is picked as the indicator (Fig. 3e). Interestingly, Tw extreme value is only affected by irrigation expansion in limited regions, like several pixels in WCA, CNA, and the Mediterranean, but over other traditional hot spot regions like SAS and EAS, the impacts are negligible (Fig. 3l).

Fig. 3: Heat and moist-heat extremes and impacts of different forcings on them.
figure 3

a–c Multi-model mean absolute values of the 99.9th percentile values of 2-m air temperature (T2m: a), HUMIDEX (HU: b), and wet-bulb temperature (Tw: c) of the first 30 years (1901–1930) in the simulations without irrigation expansion (1901irr). d–l Multi-model mean impacts of all forcings (ALL: greenhouse gas emissions, land use and land management change, irrigation expansion, etc.) (d–f), all forcings except irrigation expansion (ALL-IE: g–i), and irrigation expansion (IE: j–l) on the 99.9th percentile values of T2m (d, g, j), HU (e, h, k), and Tw (f, i, l). Impacts are calculated by subtracting the values in the new exp_period by those in the reference exp_period (see Table 1). Hatches indicate that signals (>0.1 or <−0.1) are agreed by ≥5 of 6 models (results for the individual models are presented in Supplementary Fig. S16–21). Results for other extreme event percentiles (the 99th and 99.5th) are shown in in Supplementary Figs. S28–36.

Full size image

To quantify the changes in extreme heat events frequency, we then calculate the probability ratio (PR: Eq. (5) and Table 1) of T2m, HU, and Tw warm extremes between different exp_periods (Fig. 4, S4–6). We find that the pattern of these impacts is similar to those on the absolute value of heat extreme events (Fig. 3). Other forcings, especially greenhouse gas emissions, contribute to a warmer world, with  >4 times increased frequency for the events of all three metrics in most grid cells in tropical and sub-tropical regions (Figs. S4f, S5f, and S6f). Most models agree that irrigation expansion substantially reduces the frequency of T2m extremes, especially in SAS, WCA, and CNA (Fig. 4a, d, g and S4i). However, its impacts on HU and Tw are much less pronounced and are also less consistent among models (Fig. 4b, c, e, f, h, i, S5i and S6i). Similarly, for Tw, the dampening impacts of irrigation on extreme high events disappear over the most intensely irrigated area like India and are reversed to an intensifying effect in the Central CNA and WCA, where the 99.9th percentile Tw event happens ≥2 times more often due to irrigation expansion (Fig. 4c, f).

Fig. 4: Changes in the frequency of (moist-)heat extreme events induced by irrigation expansion.
figure 4

a–i Impacts of irrigation expansion (IE) on the frequency of the events in which 2-meter air temperature (T2m: a, d, g), HUMIDEX (HU: b, e, h), and wet-bulb temperature (Tw: c, f, i) exceed their 99.9th percentile values of the first 30 years (1901–1930) in the simulations without irrigation expansion (1901irr) (shown in Fig. 3a–c). The spatial coverage include three regions: 130–60°W and 20–60°N (a–c), 20°W–50°E and 20–60°N (b–f), 50–120°E and 5–45°N (g–i). The location of these regions can be found in Fig. 3j–l. Impacts are quantified by probability ratio (PR: Eq. (5)) which is calculated by dividing the events frequencies in the new exp_period by those in the reference exp_period (see the lowest row in Table 1), and the values are the sixth root of the product of PR calculated from the outputs of six ESMs. Hatches indicate that signals (>1.2 or <1/1.2) are agreed by ≥5 of 6 models (results of individual models can be found in Fig. S22–27). Results of other metrics can be found in Fig. S7. In Fig. S4–6, the impacts of all forcings (ALL), all forcings except irrigation expansion (ALL-IE), and IE on the frequency of the events in which T2m, HU, and Tw exceed their 99th, 99.5th, 99.9th percentile values during 1901–1930 in the simulations 1901irr are shown (results of other metrics can be found in Supplementary Figs. S37–42).

Full size image

The more extreme the T2m heat events are, the more pronounced irrigation expansion-induced impacts become (Fig. S4). The impacts of irrigation expansion on T2m are mainly limited to irrigation hot spots for the 99th percentile heat event, e.g., large changes in PR (that is,  >2 times less likely) are only found in North India and Central USA (Fig. S4g). When the events get more extreme (99.5th percentile and 99.9th percentile), the affected areas expand around these hot spots and also appear in other regions like Europe and East China (Fig. S4h, i). The slight cooling impacts on HU are also more pronounced when events get more extreme (Fig. S5), and the warming effects on Tw do not change substantially (Fig. S6). We also calculate irrigation expansion’s impacts on other moist-heat metrics (Fig. S7, description of metrics can be found in Supplementary Note 3). We find that the significance of irrigation expansion’s impacts on the apparent temperature is similar to HU, and as for other moist-heat metrics, the magnitude and consistency depend on the weight of Tw and T2m.

We calculate the average annual hours (weighted by areas) exposed to extreme events of the grid cells with more than 40% (of the grid area) irrigation expansion (Fig. 5). The average annual hours exposed to T2m extreme events show a slight increase in the first half of the century, then increases rapidly between 1950 and 1980, and keeps steady in the last decades. Irrigation expansion causes a decreasing trend in the hours exposed to heat extremes in heavily irrigated regions, in spite of global warming. However, for HU, the cooling impacts of irrigation expansion are quite small, thus the hours exposed to extreme HU events still increase, but at a slightly slower speed than those without irrigation expansion. Interestingly, the hours exposed to Tw extreme events for both 1901irr and tranirr remain almost unchanged until 1980. After 1980, this starts to rise rapidly. In the case of tranirr, the hours are slightly higher than 1901irr, indicating the intensifying impact of irrigation expansion over these grid cells. Since T2m extremes are the most substantially affected events, we also calculate the average annual hours exposed to different magnitude of T2m extreme events (the 99.0th, the 99.5th and the 99.9th percentile events) over different groups of grid cells (with 0–20%, 20–30%, 30–40%, and more than 40% of irrigation expansion) (Fig. S8). Despite the difference in magnitudes, irrigation expansion has similar reducing impacts on all degrees of T2m extreme events, which become more substantial with the extent of irrigation expansion.

Fig. 5: Increase in annual hours exposed to (moist-)heat extreme events over the grid cells with the most substantial irrigation expansion.
figure 5

a–c Time series of the annual hours over the grid cells with ≥ 40% of irrigated fraction increase (in the year 2014 compared to the year 1901) of 2-m air temperature (T2m: a), HUMIDEX (HU: b), and wet-bulb temperature (Tw: c) warm extremes. The warm extremes are defined as the period when T2m, HU, and Tw exceed their 99.9th percentile values of the first 30 years (1901–1930) in the simulations without irrigation expansion (1901irr). Lines indicate the median value among six models and ranges indicate the middle four of six models. Curves were smoothed using Savitzky-Golay filtering (order = 2, window = 15)72. The range of the y-axes are different for three sub-plots. Results of various extreme events of T2m over grid cells with different extent of irrigation expansion is shown in Fig. S8, and similar results of HU and Tw can be found in Figs. S43–44.

Full size image

Irrigation expansion-induced impacts on energy fluxes

T2m generally has positive correlation with the land surface temperature and sensible heat flux (SHF)27, and land surface temperature directly determines the upwelling longwave radiation flux (LWup). Results show that both LWup (Fig. 6a) and SHF (Fig. 6b) decrease due to irrigation expansion, which explains its cooling impacts. Based on surface energy balance, the sum of SHF and LWup could be calculated as Eq. (1):

$${{LW}}_{{up}}+{{SHF}}={{SW}}_{{down}}-{{SW}}_{{up}}+{{LW}}_{{down}}-{{LHF-R}}$$
(1)

where SWdown and SWup denote the down/upwelling shortwave radiation, LWdown is the downwelling longwave radiation, LHF is the latent heat flux, and R means the residual term which includes the heat storage and fluxes in ground, water, vegetation, as well as anthropogenic heat sources and sinks.

Fig. 6: Impacts of irrigation expansion on land surface energy fluxes.
figure 6

a–f Impacts of irrigation expansion on upwelling longwave radiation (LWup: a), sensible heat flux (SHF: b), latent heat flux (LHF: c), downwelling shortwave radiation (SWdown: d), upwelling shortwave radiation (LWup: e), and downwelling longwave radiation (LWdown: f). Impacts are calculated by subtracting the values in the new exp_period by those in the reference exp_period (see Table 1 row 3). Hatches indicate that signals (>0.5 or <−0.5 W/m2) are agreed by ≥5 of 6 models.

Full size image

It is known that irrigation practices substantially increase LHF due to enhanced evapotranspiration7,10,28 (Fig. 6c), but its impacts on other radiative fluxes are less pronounced (Fig. 6d–f), which align with previous studies10,28,29. In general, increase in LHF is the main reason for irrigation’s cooling impacts, which, however, also is the origin of negative impacts of higher humidity. Some other measures could be considered to provide additional cooling while avoiding the moistening effects, like enlarging the albedo (increasing SWup)13, and the most importantly, reducing greenhouse gas concentrations (decreasing LWdown). In addition, switching from low-efficiency irrigation to high-efficiency irrigation may also help reducing exposure to moist-heat stress30.

Discussion

Six ESMs simulate a broad range of IWW (~900 to  ~4000 km3 yr−1 after the year 2000) with a median value of around 1500 km3 yr−1 (Fig. 1), which is lower than the value of 2761 km3 yr−1 reported for the period 2005–200731. Most models, especially those which have CLM5 as their land model, substantially underestimate the global IWW, which could be attributed to its over-conservative irrigation water demand calculation28. A new modification has been made by implementing different irrigation techniques28, in which the non-effective water consumption is more comprehensively considered, outperforming substantially compared to the original module at global or regional levels. In E3SM a slightly higher IWW is simulated, possibly due to the higher spatial resolution and its added features like surface/groundwater demand separation32, and an interactive surface water withdrawal module33. The overestimation of CNRM-CM6-1 originates from an external dataset reconstructed with a global hydrological model34, in which the irrigation water abstraction from groundwater is not limited by water resources35. In IPSL-CM636, a constraint is imposed on IWW based on the water availability, with the parameters sensitivity tests and calibration, showing a superior performance of reproducing global IWW despite the slight underestimation. Overall, the implementation of irrigation techniques, groundwater withdrawal, water resources management, water availability, and the calibration and validation of irrigation-related parameters, should all be considered in the next generation of irrigation representations in ESMs.

Despite the wide range of simulated IWW, ESMs used in this study agree that irrigation has a cooling impact on local hot extremes, which is consistent with previous studies10,12,13. This cooling impact has the potential of mitigating the heat exposure of both local inhabitants and crops37. However, reduced temperature does not decrease the frequency of moist-heat stress by a similar magnitude, and most ESMs even believe that historical irrigation expansion has an intensifying impacts on Tw extremes in some regions like the Central USA and West Asia (Fig. 3l), possibly endangering local population. Different from the cooling impacts on temperature extremes, the impacts of irrigation on moist-heat extremes are less substantial. As mentioned above, over two intensely irrigated regions, India and East China, extreme events of Tw do not show pronounced changes in both magnitude and frequency (Figs. 3 and 4) due to irrigation expansion. Two previous studies, a global one using the Goddard Institute for Space Studies (GISS) climate model23 and a regional one based on Massachusetts Institute of Technology Regional Climate Model38, found that irrigation increases the average values Tw more substantially than the extreme values over the same regions. It implies that the most extreme Tw events may not happen during the heavily irrigated season. Thus, we calculate multi-year mean monthly IWW during the period 1985–2014 of tranirr experiment (Fig. S9), monthly maximum T2m, HU, and Tw during the same period but of 1901irr experiment (Fig. S10–12), which confirms this hypothesis. In India, high IWW appears in April to June, high T2m extremes exist in May to June, while HU peaks from June to August, and Tw from July to August. This temporal mismatch has also been argued by some researchers39,40, both regarding heat and moist-heat extremes. Irrigation expansion-induced impacts on annual mean, maximum, minimum temperature (Fig. S13) and specific humidity (Fig. S14) also show that Tw is more substantially affected where both annual maximum temperature and specific humidity match temporally the irrigation season, like WCA and CNA. However, if limiting the study period to irrigation season, some studies still found evidence of irrigation-induced warming on Tw extremes in India22,41. Over East China, in contrast, the most intense irrigation season generally overlaps with the peak season for T2m, HU, and Tw, and a previous study has attributed weak impacts of irrigation in this area to a lower intensity of AEI expansion than India and local climatic conditions41.

Similar to previous ESM-based impact studies regarding moist-heat metrics42,43, we use temperature, moisture, and wind speed at the grid-cell level which are averaged based on values from different land cover tiles. Thus, coarse-resolution simulations’ suitability to calculate human heat metrics may be questionable, as sub-grid scale extreme values could be masked. Constrained by computational resources, conducting long-term high-resolution global simulations at less than 100 km resolution is very expensive. In addition, the impacts of agricultural irrigation on neighbouring non-irrigated areas, especially urban areas with high population density, should be investigated more comprehensively. A previous study highlighted the higher exposure of cities surrounded by irrigated cropland in India to moist-heat stress, as a combined consequence of irrigation and urban heat island effect41. Unfortunately, urban regions are still poorly resolved in current coarse-resolution ESMs. Despite these limitations, those simulations remain important for understanding the spatial distribution and temporal trend of irrigation-induced impacts on moist-heat stress. Furthermore, previous studies have assessed the suitability of various moist-heat metrics based on their correlation with local mortality datasets, and discovered that the optimal metric varies among countries and cities44,45. The range of moist-heat metrics presented here enables finely tailored investigation of irrigation’s impacts on environmental health at local scales. Note that both HU and Tw are designed for human beings, so the results here are not suitable for detecting irrigation-induced impacts on crops and natural plants, which requires better understanding of interactions between plant growth, temperature, and humidity.

In summary, our study stresses an over-optimism regarding irrigation’s health benefits, which ignores the impacts of increased air humidity on human comfort. Different metrics extremes have various feedback to irrigation expansion, highlighting the importance of better understand the most suitable metrics for people with different races, genders, ages, health conditions, etc. As a metric commonly used in outdoor activities guidance, Tw extreme events are even intensified by irrigation expansion in some regions. Under global warming scenarios, intolerable Tw events will occur more frequently, especially in South Asia, Central North America, and East Asia46. Even more troublesome, the maximum Tw is tied to atmospheric buoyancy, which is determined by global mean surface temperatures47,48. Tw will increase to the new irrigated value, and scale with global mean temperature changes16. This calls for better monitoring of local moist-heat metrics to inform exposed communities of the potential danger, and the exploration of potential solutions.

Methods

Participating ESMs and simulation protocol

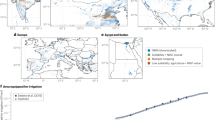
Six combinations of state-of-art Earth system models (ESMs) and irrigation parametrizations are used in this study: the Community Earth System Model version 2 (CESM2)49, CESM2 with groundwater withdrawal and flow representation (CESM2_gw)?50, the Institut Pierre-Simon Laplace Climate Model version 6 (IPSL-CM6)51 with a newly developed irrigation scheme36, the Norwegian Earth System Model version 2 (NorESM2)52, the Energy Exascale Earth System Model Version 2 (E3SMv2)53 with active two-way coupled irrigation scheme33, and the Centre National de Recherches Météorologiques Climate Model version 6 (CNRM-CM6-1)54,55. Irrigation is represented in different ways in these models, which can be divided into two categories: soil-moisture-based schemes and external forcing applications (only for CNRM-CM6-1). Differences between soil-moisture-based irrigation modules relate to irrigation triggers, start time, duration, amount, and the method of water application. The employed ESMs provide the option to customise irrigation-related parameters, but in this study, all ESMs used default parameter values. CESM2, CESM2_gw, and NorESM2, share identical or similar land system models, which explains why they show strong consistency between each other. However, their differences in atmospheric models and features in the irrigation scheme, still represent an added value to this study. More detailed description of ESMs and their irrigation representations could be found in Supplementary Note 1.

We design two historical experiments in this study: with (tranirr) and without (1901irr) historical irrigation expansion. The simulations of both experiments follow the protocol of AMIP simulations in CMIP6 with the same input data56, which means that the ocean model is switched off and sea surface temperatures are prescribed. To better capture the signal of irrigation extent increase in the 20th century, we select a simulation period of 1901–2014. The only difference between the two experiments is that in tranirr, irrigation extent is transient, while in 1901irr, the irrigation extent is fixed at the level in the year 1901. One exception is IPSL-CM6, where irrigation is entirely switched off for 1901irr, and we include outputs of this ESM in the analysis as in the year 1901, irrigated fraction is very limited (Fig. S3a). The land-use map and time-series data used in these simulations are from the Land-Use Harmonization phase 2 project (LUH257), in which all crop management activities-related data, including irrigated land distribution, is obtained from the History Database of the Global Environment 3.2 (HYDE 3.2)58. The irrigated land data from HYDE 3.2 during the period 1901–2014 has multiple sources: for the period pre-1960, the data is collected directly from the global historical irrigation data set (HID)59, and for the post-1960 period, the numbers are calculated by multiplying the term “area equipped for irrigation" in FAO statistics60 by the fraction of actual irrigated area in area equipped for irrigation from HID.

Climate extremes

Most models report output variables at the 3-hourly frequency to enable analysis of sub-daily extremes, but CNRM-CM6-1 only provides daily mean, maximum, and minimum values, so we calculate several moist-heat metrics based on daily maximum temperature and minimum air relative humidity to calculate the maximum metrics consistent with a previous study61, thereby assuming that the lowest relative humidity occurs when the temperature is maximum.

HUMIDEX (HU) is a feel-like heat stress metric developed in the late 1970s, and it was first used for the meteorological service in Canada62. It is calculated as Eq. (2):

$${{{\rm{HU}}}}={T}_{{{{\rm{C}}}}}+\frac{5}{9}\left(\frac{{e}_{{{{\rm{RH}}}}}}{100}-10\right)$$
(2)

where TC is the temperature at 2-meter height (°C), eRH (Pa) is the vapour pressure calculated based on relative humidity (RH) and saturated vapour pressure (es in Pa), as shown in Eq. (3):

$${e}_{{{{\rm{RH}}}}}={{{\rm{RH}}}}{e}_{{{{\rm{s}}}}},$$
(3)

HU is still used by the Canadian Centre for Occupational Health and Safety (CCOHS) to inform the general public if the weather conditions may be comfortable based on the following thresholds: 20–29, 30–39, 40–45, and over 46 represent the warning of ’little discomfort’, ’some discomfort’, ’great discomfort’, and ’dangerous’, respectively63.

Tw is a measure of heat stress considering the maximum potential evaporative cooling impact64. It can be measured by a thermometer covered in water-soaked cloth over which air is passed65. The calculation of Tw is very computationally expensive, so we employ a simplified method66, as indicated in Eq. (4):

$${T}_{{{{\rm{W}}}}}= {T}_{{{{\rm{C}}}}}\arctan (0.151977\sqrt{{{{\rm{RH}}}}+8.313659})\\ +\arctan \left({T}_{{{{\rm{C}}}}}+{{{\rm{RH}}}}\right)-\arctan ({{{\rm{RH}}}}-1.676331)\\ +0.00391838{{{{\rm{RH}}}}}^{3/2}\arctan (0.023101{{{\rm{RH}}}})-4.68035$$
(4)

Based on previous studies64,67, when Tw is over 31 °C, physical labour becomes impossible, and exposure to Tw exceeding 35 °C for more than 6 h is dangerous even for healthy individuals. However, the maximum evaporative cooling (swamp cooler) is not easy to approach, as in previous heatwave events, high casualties already existed even if the Tw is less than 28 °C68. Other metrics described in Supplementary Note 3 are also calculated based on simulations by all six models, except that we do not calculate the apparent temperature from CNRM-CM6-1 outputs, given the lack of the appropriate wind speed variable.

Data processing

Outputs from E3SM, IPSL-CM6, and CNRM-CM6-1 are firstly regridded to the resolution of CESM2, CESM_gw, and NorESM (0.9° × 1.25°) (original resolution can be found in Supplementary Note 2), and then the moist-heat metrics are calculated (Eqs. (2) and (4)). After calculating the moist-heat metrics, we further processed the results to separate the impacts of irrigation expansion from other forcings. We first calculated irrigation expansion’s impacts on the absolute values of extreme events as well as surface energy fluxes. We select two periods, the first 30 years (1901–1930) and the last 30 years (1985-2014), for both simulations (tranirr and 1901irr) to calculate the impacts of all forcings, all forcings except irrigation expansion, and irrigation expansion, on near-surface climate (see Table 1). We assume that the difference between the results during 1901–1930 of 1901irr and those during 1985–2014 of tranirr represent the consequence of all forcings. The difference between the results during the two periods for the 1901irr simulations is assumed to be the consequence of other forcings. The difference between these two simulations during the 1985–2014 period is assumed to represent the impacts of irrigation expansion as the only difference between them is whether irrigation extent is transient.

Apart from the absolute value of extreme events, we also calculate the probability ratio (PR) for several extreme events, which has been used in previous studies to show the changes in climate extreme events frequency12,69. The extreme events defined in this study are based on percentile values, e.g., a 99th percentile event means that in the reference period, it happens once per 100 time steps (3 h per 300 h for 3-hourly outputs), or in other words, it indicates the 1% time steps with the most extreme values. Considering that outputs from CNRM-CM6-1 is at a daily frequency, we select the 92nd, 96th, and 99.2nd percentile events for this ESMs to represent the 99th, 99.5th, and 99.9th percentile events simulated by other ESMs. This is based on an assumption that those extreme events calculated based on maximum temperature and minimum humidity last 3 h during the day, so a 92nd percentile value means 8 days per 100 days and then 24 h per 2400 h, which is equal to 3 h per 300 h for 3-hourly outputs. The PR is calculated as:

$${{{\rm{PR}}}}=\frac{{P}_{{new}}({X}_{{ext}})}{{P}_{{ref}}({X}_{{ext}})},$$
(5)

where Pnew(Xext) is the probability of a certain kind of extreme event (Xext) during the new exp_period and Pref(Xext) is the probability of the same kind of event during the reference exp_period. Let us assume, for example, that the 99th percentile value of T2m is 33 °C in the reference exp_period, meaning the extreme events are the ones with T2m > 33 °C: if the frequency of these events is 4% in the new exp_period, then the PR is 4. Thus, a PR of more than 1 indicates that this event occurs more frequently in the new exp_period compared to the reference exp_period, and vice versa. Similar to absolute values, we also select two periods (1901–1930 and 1985–2014) for both tranirr and 1901irr, then calculate the PR between them for the 99.0th, 99.5th, and 99.9th percentile events for T2m, HU, and Tw. To further investigate the temporal trend of irrigation expansion’s impacts, we calculated the mean value of annual hours exposed to warm extremes for four groups of grid cells, with irrigation expansion of 0–20%, 20–30%, 30–40%, and more than 40%.