Deterministic multi-phonon entanglement between two mechanical resonators on separate substrates

Abstract

Mechanical systems have emerged as a compelling platform for applications in quantum information, leveraging advances in the control of phonons, the quanta of mechanical vibrations. Experiments have demonstrated the control and measurement of phonon states in mechanical resonators, and while dual-resonator entanglement has been demonstrated, more complex entangled states remain a challenge. Here, we demonstrate rapid multi-phonon entanglement generation and subsequent tomographic analysis, using a scalable platform comprising two surface acoustic wave resonators on separate substrates, each connected to a superconducting qubit. We synthesize a mechanical Bell state with a fidelity of ${{{{\mathcal{F}}}}}=0.872\pm 0.002$, and a multi-phonon entangled N = 2 N00N state with a fidelity of ${{{{\mathcal{F}}}}}=0.748\pm 0.008$. The compact, modular, and scalable platform we demonstrate will enable further advances in the quantum control of complex mechanical systems.

Introduction

Mechanical systems have significantly smaller footprints than existing circuit quantum electrodynamics (cQED) systems at similar frequencies¹, potentially long lifetimes², and a large number of accessible microwave-frequency modes^3,4,5,6. Mechanical systems have been operated in the quantum limit^7,8, with explorations of quantum information storage and processing^2,9,10,11,12 and quantum sensing^13,14,15. Additional achievements include the quantum control of mechanical motion^5,7,16, entanglement between macroscopic mechanical objects^{17,18,19,20,21,22}, coupling between surface acoustic waves (SAW) and qubits^{3,23,24,25,26}, the deterministic emission and detection of individual SAW phonons as well as phonon-phonon entanglement^27,28,29, and the transmission of quantum information^{27,28,29,30,31}, among other demonstrations^32,33,34. Mechanical systems have also been investigated as a platform for interconnecting microwave qubits with optical photons^{35,36,37,38,39} and spin assemblies⁴⁰, with the potential for realizing long-distance quantum communication. Many of these advances have been enabled through the integration of superconducting qubits with mechanics, affording the quantum control of highly linear mechanical modes as well as straightforward quantum measurement.

Here, we demonstrate the deterministic generation and distribution of multi-phonon entanglement between two physically separated mechanical modes. We use a modular architecture, in which the two mechanical resonators are fabricated on separate piezoelectric substrates and electrically coupled to a pair of superconducting qubits on a third, non-piezoelectric substrate. This design supports the generation of complex entangled states as well as straightforward quantum tomography, with potential applications in quantum random access memory^9,41, quantum error correction¹¹, quantum sensing and high-precision measurements^{42,43,44,45,46}

Results

Device design and characterization

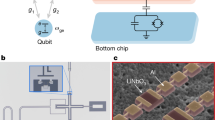
The experimental layout is shown in Fig. 1. Our device comprises two nodes, each node including a mechanical SAW resonator inductively coupled via a variable coupler¹⁶ to a frequency-tunable superconducting Xmon qubit^47,48. The two qubits are capacitively coupled to one another, supporting entangling gates. The two SAW resonators (R_A and R_B) are fabricated on separate lithium niobate (LN) substrates, while the qubits (Q_A and Q_B), couplers (G_A and G_B), and their associated readout resonators and control lines, are fabricated on a sapphire substrate. The two LN dies are sequentially aligned and attached to the sapphire substrate, using a non-galvanic flip-chip assembly⁴⁹. Each mechanical resonator includes a central interdigitated transducer (IDT) and two acoustic mirrors, situated on either side of, and immediately adjacent to, the transducer. Each acoustic mirror is an array of two hundred 10 nm-thick parallel aluminum lines, forming a Bragg mirror with a  ~ 50 MHz-wide acoustic stop-band, centered on the respective mechanical resonator frequencies of 3.027 GHz (R_A) and 3.295 GHz (R_B). The free spectral range (FSR) of each acoustic resonator is designed to be slightly larger than mirror stop-band, confining a single acoustic mode in each resonator. By virtue of the piezoelectric response of the LN substrates, applying an electrical signal to either IDT generates symmetric, oppositely-directed surface acoustic waves, whose retro-reflection by the two mirrors forms a single Fabry-Pérot resonance, generating a sympathetic electrical response at the corresponding IDT. In Fig. 2a we show the calculated SAW resonator transmission, mirror stopband, and IDT admittance for each resonator, using their design parameters. Each superconducting qubit is coupled to its respective mechanical resonator via a variable coupler, whose coupling strength is controlled externally by magnetic flux bias of an rf-SQUID¹⁶, with the coupler connected to the respective IDT through an air-gap inductive coupler. The three-die assembly is mounted in an aluminum box with wire-bond electrical connections and external magnetic shielding, operated in a dilution refrigerator with a base temperature of about 10 mK.

Fig. 1: Device layout, lumped circuit model, and optical micrographs.

a False-color optical micrograph of a device identical to that used in the experiment. Two lithium niobate (LN) dies (light blue) each support one mechanical resonator R_A and R_B (left and right; purple), and are flip-chip bonded to a larger sapphire substrate, the latter including two qubits Q_A (blue) and Q_B (orange), their associated variable couplers G_A and G_B (green), and all readout resonators and control lines. b Equivalent lumped-element circuit diagram. The air-gap inductive coupling between the sapphire wiring (green) and LN wiring (black) allows non-galvanic contacts between the LN dies and the sapphire substrate⁴⁹. c Optical micrograph of assembled device. The two LN dies are 4.5 × 2 mm², and the larger sapphire substrate is 15 × 6 mm². The  ~ 5 μm air gap between the LN and sapphire dies is set by lithographically-defined epoxy standoffs⁴⁹. More details can be found in the Methods section.

Fig. 2: Device modeling and characterization.

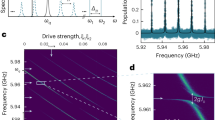
a Numerically-calculated SAW resonator (R_A and R_B) characteristics. Solid lines (blue and orange) show SAW resonator electrical transmission ∣S₂₁∣ in linear scale (left) and green dashed lines indicate the acoustic mirror reflection coefficient ∣Γ∣, with the vertical axis in dB (right), together with the real part of the IDT admittance Re(Y_IDT) (S) (purple dashed line), all calculated using the coupling-of-modes (COM) model⁵⁹. b Qubit interaction with mechanical resonators, measured by monitoring either qubit’s excited state probability P_e (color scale) with time (vertical axis) while tuning the qubit frequency across the IDT bandwidth (horizontal axis). Interaction is measured separately for each qubit-resonator pair; response agrees well with the model using measured parameters. Blue and orange arrows indicate SAW resonant response, centered on the vacuum-Rabi exchanges of single quanta between the qubit and resonant mode. Pink arrow in right panel indicates Q_A idle frequency. c Simultaneous vacuum-Rabi swaps between each mechanical resonator and the associated qubit, with qubits set to the frequencies indicated by the blue and orange arrows in panel b. Solid lines are simulation results based on separate measurements of the mechanical lifetimes and qubit coherence times (See Supplementary Fig. 1). Inset shows pulse sequence (coupler control pulses not shown). Qubit populations for each data point are extracted from 3000 repetitions. Statistical uncertainties for all qubit populations are smaller than the readout infidelities (See Supplementary Table 1).

We first characterize each node by measuring the qubit-resonator interactions, measured as a function of time versus qubit frequency (see Fig. 2b). Each qubit is initially excited to its $\left\vert e\right\rangle$ state by a tuned microwave π pulse, following which the coupling between the qubit and resonator is turned on. When the qubit is tuned into resonance with the corresponding acoustic mode, qubit-resonator Rabi swaps give rise to the expected chevron patterns (Fig. 2b). Outside the  ~ 50 MHz acoustic mirror stop band, visible in Fig. 2a (dashed green line), but within the IDT emission band of  ~ 600 MHz (shown by the larger calculated admittance, dashed purple line), the qubit decays rapidly by acoustic emission that escapes through the mirrors. When the qubit is tuned outside the IDT emission band (left and right margins of either plot in panel b), the qubit lifetime increases rapidly due to the reduced phonon emission rate, due to the smaller admittance (purple dashed line in panel a).

The system supports multiplexed Rabi swap measurements, shown in Fig. 2c. Each qubit is set to its idle frequency of 3.245 GHz (3.557 GHz), a microwave π pulse applied, and the qubits then tuned into resonance with their corresponding mechanical resonators while both variable couplers are turned on, yielding simultaneous parallel swaps. The swap times for nodes A and B are 42 ns and 35 ns, respectively. We next use the qubits to measure the mechanical resonator lifetimes at the single-phonon level, by swapping an excitation from the qubit into the resonator and then measuring the decay of the resulting one-phonon state as a function of time, for both nodes A and B. The resonators’ energy relaxation times extracted from the measurements are ${T}_{1,A}^{m}=380\pm 8$ ns and ${T}_{1,B}^{m}=270\pm 3$ ns. The dephasing time for each resonator is then measured by exciting either qubit with a π/2 microwave pulse and swapping the qubit superposition state into the corresponding resonator, then measuring the decoherence time with a Ramsey fringe measurement¹⁶. We find dephasing times of ${T}_{2,A}^{m}=709\pm 16$ ns and ${T}_{2,B}^{m}=527\pm 6$ ns, approximately twice the T₁ times (see Supplementary Fig. 1). The corresponding quality factors for the resonators are Q_A ≈ 7200 and Q_B ≈ 5600, roughly twice the value for single-mode SAW resonator in ref. ¹⁶. The improvement is possibly due to a modified SAW resonator geometry as well as more thorough surface cleaning of the LN substrates (see Methods).

Mechanical Bell state

We then use the qubits to prepare entangled mechanical resonator states, distributed across the two LN dies, as illustrated in Fig. 3a. In ref. ²¹, a two-resonator mechanical Bell state was prepared, then measured dispersively using a single-qubit Ramsey measurement. Here we use direct swaps between the resonators and their respective qubits for state analysis, using short pulse sequences with improved state fidelity. Following a protocol similar to ref. ⁵⁰ (pulse sequence shown in Fig. 3b), we prepare a mechanical Bell state by exciting qubit Q_A and performing a half-swap to qubit Q_B, generating a two-qubit Bell state $(\left\vert eg\right\rangle+\left\vert ge\right\rangle )/\sqrt{2}$. We then bring each qubit into resonance with its corresponding mechanical resonator, and turn on the variable couplers to perform full qubit-resonator swaps, ideally resulting in a dual-resonator Bell state $(\left\vert 10\right\rangle+\left\vert 01\right\rangle )/\sqrt{2}$. Note this method is not negatively impacted by the different swap times for nodes A and B (44.8 ns and 36.4 ns, respectively). To analyze the resulting entangled resonator state, coherent displacement pulses ${\hat{D}}_{A}$ and ${\hat{D}}_{B}$ are applied to each resonator, following which the qubits interact resonantly with their corresponding resonators, followed by simultaneous two-qubit state readout^50,51. By varying the interaction time τ, we can map out the two-qubit state probabilities P_gg, P_ge, P_eg and P_ee as a function of time, shown for zero displacement (${\hat{D}}_{A}={\hat{D}}_{B}=0$) in panel c. These data show coherent swaps between the resonators and qubits while P_ee remains zero, consistent with the expectation that only a single phonon is shared between the two resonators. Panel d shows the populations for the resonators, corresponding to the fit solid lines in c. By performing similar measurements with a total of 15 × 15 different combinations of displacement pulses ${\hat{D}}_{A}$ and ${\hat{D}}_{B}$ (see Methods), we reconstruct the Bell state using convex optimization. The resulting density matrix ∣ρ∣ is shown in Fig. 3e, with a fidelity ${{{{\mathcal{F}}}}}=\sqrt{{{{{\rm{Tr}}}}}({\rho }_{{{{{\rm{Bell}}}}}}\cdot | \rho | )}=0.872\pm 0.003$ to the ideal Bell state ρ_Bell, close to our simulated result, which predicts a fidelity ${{{{\mathcal{F}}}}}=0.92$ (see Methods). The infidelity is dominated by the resonator lifetime combined with a reduced qubit T₁ when each qubit is coupled to its resonator (see Methods and Supplementary Table 1).

Fig. 3: Deterministic mechanical Bell state generation and tomography.

a Principle: A two-qubit Bell state $(\left\vert eg\right\rangle+\left\vert ge\right\rangle )/\sqrt{2}$ is generated in the qubits, then swapped coherently into the resonators, generating the entangled mechanical state $(\left\vert 10\right\rangle+\left\vert 01\right\rangle )/\sqrt{2}$. b Left of dashed line, pulse sequence to generate, then swap, a Bell state; right, Wigner tomography pulses, where the optional pulses for R_A and R_B indicate classical displacement pulses. c Joint qubit state probabilities with no displacement pulse, extracted from 2,000 repetitions. Solid lines are fits, yielding joint resonator occupation probabilities in d. e Density matrix from Wigner tomography of mechanical Bell state (solid colored bars), yielding a state fidelity ${{{{\mathcal{F}}}}}=0.872\pm 0.002$ to the ideal Bell state (dashed bar outlines). The density matrix is reconstructed from tomography measurements. All error bars and uncertainties represent one standard deviation.

Mechanical NOON state

We finally display the capabilities of this system for generating and measuring multi-phonon entangled states, doing so for an N = 2 N00N state shared between the two mechanical resonators. Our protocol is illustrated in Fig. 4a, with the corresponding pulse sequence in panel b. We use a similar process to Fig. 3 to prepare a two-qubit Bell state $(\left\vert eg\right\rangle+\left\vert ge\right\rangle )/\sqrt{2}$, then use a microwave π pulse to selectively excite each qubit to its second excited state $\left\vert f\right\rangle$, yielding the entangled qutrit state $(\left\vert fg\right\rangle+\left\vert gf\right\rangle )/\sqrt{2}$ (stage 1 in Fig. 4a). We then tune each qubit’s f ↔ e transition into resonance with the corresponding resonator, and perform a full swap, resulting in the four-fold entangled state $(\left\vert eg10\right\rangle+\left\vert ge01\right\rangle )/\sqrt{2}$ (stage 2 in Fig. 4a). We note that during the f ↔ e swap with the resonator, the e ↔ g transition also falls inside the active SAW transducer bandwidth, but detuned from the resonator transition and outside the mirror bandwidth of  ~ 50 MHz; the qubit $\left\vert e\right\rangle$ state thus decays in parallel by emitting unwanted, non-resonant phonons via the transducer, competing with the desired f → e transition. There is thus a trade-off between the qubit-resonator coupling strength and this unwanted phonon emission. This issue could be alleviated by reducing the IDT bandwidth so that the e ↔ g transition is outside the IDT emission bandwidth, due to qubit anharmonicity, e.g. by adding more IDT finger pairs. In our experiment, we carefully control both couplers to maximize the final N00N state fidelity.

Fig. 4: Multi-phonon entanglement generation and tomography.

a Illustration of N00N (N = 2) state generation process. We first generate an entangled qutrit state $(\left\vert fg\right\rangle+\left\vert gf\right\rangle )/\sqrt{2}$ ($\left\vert f\right\rangle$ is the qubit 2nd excited state), followed by a two-step swap from the qubits into the mechanical resonators, yielding a $(\left\vert 20\right\rangle+\left\vert 02\right\rangle )/\sqrt{2}$ N00N state. The corresponding pulse sequence is shown in b; following state preparation, tomography is performed in a manner analogous to that for the Bell state tomography. c, d Qubit coincidence probability measurements and corresponding joint resonator population distribution. For the N00N N = 2 state, the oscillations in P_eg and P_ge are approximately $\sqrt{2}$ faster than for the analogous Bell state measurements in Fig. 3b; P_ee remains zero as expected. Qubit populations for each data point are extracted from 5,000 repetitions. e Density matrix resulting from Wigner tomography of multi-phonon entangled state, with a state fidelity ${{{{\mathcal{F}}}}}=0.748\pm 0.008$ to the ideal $(\left\vert 20\right\rangle+\left\vert 02\right\rangle )/\sqrt{2}$ N00N state; measured density matrix ρ is shown with solid color bars, while dashed outlines show the simulated result (see Methods).

In the last step, each qubit’s e ↔ g transition is brought into resonance with its corresponding resonator, swapping the remaining qubit excitation into the resonator, ideally resulting in a final state $\left\vert gg\right\rangle \otimes (\left\vert 20\right\rangle+\left\vert 02\right\rangle )/\sqrt{2}$. This protocol can be extended to $(\left\vert N0\right\rangle+\left\vert 0N\right\rangle )/\sqrt{2}$ states by iterating the first two steps. Alternatively, we can generate $(\left\vert N0\right\rangle+\left\vert 0M\right\rangle )/\sqrt{2}$ N00M states, if one qubit is initially excited to its $\left\vert f\right\rangle$ state while the other qubit remains in $\left\vert e\right\rangle$.

We analyze the final resonator state using Wigner tomography, similar to the Bell state analysis. The evolution of the two-qubit state probabilities for zero displacement are shown in Fig. 4c; the corresponding joint resonator population distribution is shown in panel d. We see that the P_eg and P_ge oscillations are approximately $\sqrt{2}$ faster than the corresponding oscillations for the Bell state in Fig. 3b, while the measured P_ee remains zero, consistent with the expectation that detection of a phonon by one qubit precludes detection by the other qubit. Using a total of 261 different combinations of tomography displacement pulses, we use convex optimization to reconstruct the density matrix ρ, shown in Fig. 4e. We find a state fidelity ${{{{\mathcal{F}}}}}=\sqrt{{{{{\rm{Tr}}}}}({\rho }_{{{{{\rm{N00N}}}}}}\cdot | \rho | )}=0.748\pm 0.008$ to the ideal N = 2 N00N state ρ_N00N, in reasonable agreement with our simulation fidelity of ${{{{\mathcal{F}}}}}=0.745$ (see Methods). The unwanted phonon emission mentioned above, together with the short mechanical resonator lifetimes, limit our ability to generate higher N N00N states.

Discussion

In conclusion, we deterministically entangle two macroscopic mechanical resonators on separate substrates, using two independently-controlled superconducting qubits to synthesize and then analyze multi-phonon states, including high-fidelity phonon Bell and N00N states. This platform is scalable, supporting simultaneous entanglement of larger numbers of mechanical resonators, enabling e.g. the direct synthesis of Greenberger-Horne-Zeilinger (GHZ) and W states, as well as synthetic cat states. Using larger SAW cavities with smaller free spectral ranges, each qubit could access multiple acoustic resonances, opening the possibility for multi-mode quantum information processing with small form-factor acoustic devices (see Supplementary Fig. 4). Our architecture promises further insight into the fundamental science of entangled mechanical systems, as well as an approach to distributed quantum computing. This hybrid quantum system would clearly benefit from increased coherence lifetimes for the SAW resonators, which will be essential for implementing more complex quantum operations^11,52,53. This could be achieved by better material growth⁵⁴, different device designs, or possibly lowering the frequency of the SAW resonators⁵⁵.

Methods

This section provides detailed information on device fabrication, theoretical modeling, and numerical simulations.

Device fabrication

Each acoustic device is fabricated on a LiNbO₃ substrate, which is first cleaned using 80 ^∘C Nanostrip to remove organic contaminants. The transducer and acoustic mirrors are then fabricated by patterning a single layer of 10 nm thick aluminum using a PMMA bilayer liftoff process. The transducers each have 10 finger pairs with a 180 μm aperture, with a design pitch of 642 nm for node A and 584 nm for node B, while the acoustic mirror pitches are 667 nm and 605 nm, respectively. The distance between the acoustic mirror pairs are  ~ 75 μm for node A and  ~ 70 μm for node B. For the qubit die, we first deposit a 100 nm thick aluminum base layer on the sapphire substrate, patterned with optical lithography followed by a plasma etch. Next, a 200 nm thick SiO₂ crossover support is patterned using optical lift-off. The qubit and coupler Josephson junctions are then deposited using a standard Dolan bridge technique with bilayer PMMA, with an angled deposition by electron beam evaporation with an intermediate oxidation step. To create galvanic contacts between the junctions and ground plane, we use a bandage layer process with ion milling. The crossover metalizations are completed together with bandage layer. In the final step, we pattern 5 μm thick standoffs on the sapphire substrate using photo-definable epoxy. The acoustic and qubit chips are then aligned and flip-chip assembled with spacing defined by the standoffs⁴⁹.

Joint state tomography of two mechanical resonators

We perform joint Wigner tomography by applying coherent resonant microwave pulses to resonators R_A and R_B, using Gaussian pulses with complex amplitudes α_j, j = A, B, where the mean phonon number in each pulse is ∣α_j∣², with phase distributed over an origin-centered circle in the complex plane. The corresponding displacement operators are given by ${\hat{D}}_{j}(-{\alpha }_{j})={\hat{D}}_{j}^{{{{\dagger}}} }({\alpha }_{j})=\exp ({\alpha }_{j}^{\star }{\hat{a}}_{j}-{\alpha }_{j}{\hat{a}}_{j}^{{{{\dagger}}} }),\,j=A,B$ where ${\hat{a}}_{j}$ is the phonon destruction operator for resonator R_j.

Given an initial joint mechanical resonator density matrix ρ_m, the displacement pulses generate a displaced density matrix

$${\rho }_{D}={\hat{D}}_{A}(-{\alpha }_{A}){\hat{D}}_{B}(-{\alpha }_{B}){\rho }_{m}{\hat{D}}_{A}({\alpha }_{A}){\hat{D}}_{B}({\alpha }_{B}).$$

(1)

Following the displacement pulses, each qubit interacts with its respective mechanical resonator, from which we can establish the diagonal elements of ρ_D by fitting the time-dependent two-qubit state population traces as in Fig. 3. The joint mechanical resonator density matrix ρ_m can then be found by inverting Eq. (1) using convex optimization, while constraining ρ_m to be Hermitian, positive semi-definite, and trace of 1. In the joint resonator density matrix reconstruction for the N00N state, we assume a maximum of two excitations in each resonator, so we zero-pad ρ_m for phonon indices larger than 2 (note we do not limit the total number of excitations in both resonators).

For the analyses in Figs. 3 and 4, we use displacement pulses distributed over a circle in the complex plane, ${\alpha }_{j,k}=| {\alpha }_{j}| \exp (i 2\pi k/N),\,j=A,B,\,k=0,1,\ldots,N-1$. For analyzing the two-resonator Bell state, we use ∣α_A∣ = 0.35 (∣α_B∣ = 0.26) with N = 15, for a total of 15 × 15 = 225 pulse combinations. For the N00N state analysis, we use ∣α_A,B∣ = 0.3 with N = 6, together with ∣α_A,B∣ = 0.5 with N = 15 for a total of 261 pulse combinations. Uncertainties for the reconstructed density matrices are calculated using a bootstrap method⁵⁶, randomly selecting with replacement a subset of the pulse combinations and repeating the reconstruction 10 times.

Numerical simulations

Our system is well-modeled by the Hamiltonian

$$H= \sum\limits_{j=A,B}\left[{H}_{{Q}_{j}}+{\omega }_{{R}_{j}}{a}_{j}^{{{{\dagger}}} }{a}_{j}+{g}_{ge,j}({s}_{ge,j}^{{{{\dagger}}} }{a}_{j}+h.c.)+{g}_{ef,j}({s}_{ef,j}^{{{{\dagger}}} }{a}_{j}+h.c.)\right] \\ +{g}_{q}({s}_{ge,A}^{{{{\dagger}}} }{s}_{ge,B}+h.c.).$$

(2)

In this Hamiltonian, we model each qubit as a frequency-tunable, three-level anharmonic oscillator, with

$${H}_{{Q}_{j}}=\left[\begin{array}{ccc}0&0&0\\ 0&{\omega }_{ge,j}(t)&0\\ 0&0&{\omega }_{gf,j}(t)\end{array}\right],$$

(3)

for j = A, B. The mechanical resonators have fixed frequencies ${\omega }_{{R}_{j}}$, j = A, B. The coupling strength between each qubit and its respective mechanical resonator is g_ge,j and g_ef,j, depending on whether we are coupling the g ↔ e or the e ↔ f qubit transitions, with corresponding qubit operators ${s}_{ge,j}=\left\vert g\right\rangle \left\langle e\right\vert$ and ${s}_{ef,j}=\left\vert e\right\rangle \left\langle f\right\vert$. The qubit-qubit coupling strength is g_q = 8.6 MHz, and is used for preparing the initial qubit Bell states. We use independently-measured system parameters, as given in Supplementary Table 1, for the Lindblad master equation simulations, which are performed using the open-source Python package QuTiP⁵⁷. We note that during the qubit-mechanical resonator Rabi swaps, the qubit T₁ is shortened, probably dominated by unwanted IDT emission outside the mirror bandwidth ( ~ 50 MHz). Using independently-measured mechanical ${T}_{1}^{m}$ and ${T}_{2}^{m}$, in Fig. 2c we fit the qubit T₁ during the e ↔ g swap. Simulation results are in good agreement with experimental data.

Qubit readout correction

Two-qubit measurement corrections⁵⁸ are applied to all the qubit measurement data. We measure both qubits simultaneously using a multiplexed readout pulse. Prior to each experiment, we measure the two-qubit readout visibility matrix, by preparing the two qubits in the fiducial states $\{\left\vert gg\right\rangle,\left\vert ge\right\rangle,\left\vert eg\right\rangle,\left\vert ee\right\rangle \}$, followed by a two-qubit readout. The visibility matrix V is defined as the transformation between the measured probability vector (P_meas) and the expected probability vector (P_exp) for the different fiducial states, P_meas = VP_exp. A typical visibility matrix is:

$$V=\left(\begin{array}{cccc}{F}_{gg,gg}&{F}_{gg,ge}&{F}_{gg,eg}&{F}_{gg,ee}\\ {F}_{ge,gg}&{F}_{ge,ge}&{F}_{ge,eg}&{F}_{ge,ee}\\ {F}_{eg,gg}&{F}_{eg,ge}&{F}_{eg,eg}&{F}_{eg,ee}\\ {F}_{ee,gg}&{F}_{ee,ge}&{F}_{ee,eg}&{F}_{ee,ee}\end{array}\right)=\left(\begin{array}{cccc}0.954&0.042&0.027&0.002\\ 0.022&0.939&0.000&0.028\\ 0.024&0.003&0.955&0.037\\ 0.001&0.017&0.018&0.934\end{array}\right),$$

(4)

where F_a,b represents the fidelity of preparing the two-qubit state in $\left\vert a\right\rangle$ and measuring the two-qubit state in $\left\vert b\right\rangle$. By inverting the visibility matrix we obtain the measurement-corrected two-qubit probability vector P_corr = V⁻¹P_meas.