Introduction

Electron transport in solids with a flat dispersion can be dominated by Coulomb interactions if the kinetic energy, set by the bandwidth, is relatively much smaller. From a local Hubbard interaction picture, adding electrons is hindered by the large repulsive Coulomb potential (U) if the band is half-filled, resulting in a Mott˘Hubbard insulating state1. If there is another band nearby, a charge-transfer insulator2, with gap Δ defined as the energy between the upper Hubbard band and the second nearby band, will emerge while Δ < U. In this case, excitation no longer hops between adjacent unit cell sites with on-site interaction energy U, but transfers from the anion to cation atoms within a unit cell with charge-transfer energy Δ, which is determined by the electronegativity differences between cation and anion. The relative size of U and Δ determines the nature of the insulator and significantly affects emerging phases, like high-temperature superconducting states3. However, traditional charge-transfer insulators usually have complicated band structures and offer little tunability of U, Δ, bandwidth, and carrier density, impeding investigation into the interplay between these parameters and the various resulting correlated phases.

In recent years, two-dimensional (2D) moiré heterostructures have arisen as a potential solution to this problem. 2D moiré heterostructures exhibit great tunability over the carrier density, electronic structure, and have allowed for the exploration of strongly correlated physics4, like superconductivity5,6,7,8,9,10, correlated insulators6,11,12,13,14,15, and anomalous magnetic states6,16,17. In particular, Mott insulators15,17,18,19 and generalized Wigner crystal states20,21 have been realized at half or fractional filling of a moiré flat band in twisted transition metal dichalcogenides (TMDs). In this work, we use transport measurement to investigate correlated phases associated with the Γ-valley hole-side moiré flat band in another twisted TMD, TDB-WSe2. We find that the K-valley, in the absence of electric field, is below the Γ-valley and that its position in energy is highly tunable by a perpendicular electric field. As the Γ-valley moiré flat band splits at half filling, instead of finding a Mott˘Hubbard insulator, we observe a correlated phase with a tunable gap, Δ, between the K-valley and the upper Hubbard Γ-valley. Distinct from the conventional charge transfer insulator, where the gap Δ is between anion to cation, the excitation in this new state happens between different valleys. We denote this exotic state of matter as a valley charge-transfer insulator. Intriguingly, we are able to close the gap by tuning the K-valley to be above the Γ-valley at large displacement fields. This allows us to induce a phase transition and to observe a coexistence of a Γ-valley splitting and a K-valley metallic state.

Results

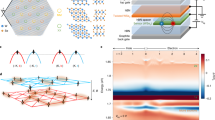
Figure 1 a illustrates the dual-gated TDB-WSe2 device structure. Our stacks were first fabricated by the “pick up and tear” method22,23 and then dropped onto pre-patterned, Hall bar-configured, Pt electrodes to achieve good Ohmic contact24(see method for details). For the twist angle, we choose an angle near 60° so that there is an AA-stacking, twist interface25 between the two inner layers. This allows the band hybridization18 between layers to dominate near the K point, as opposed to forbidden tunneling due to spin anti-alignment26. In the main text, we focus on one sample with a twist angle of 55.5° (see SI for similar phenomena on more samples with slightly different twist angles). The right panel of Fig. 1a depicts our TDB-WSe2 lattices in real space, where the hexagon denotes lattice sites where the Γ-valley flat band mainly resides (see Supplementary Fig. 1). Due to the symmetry of the stacking, the Γ-valley flat bands exhibit a relativistic graphene-like dispersion with a Dirac crossing located at the K point of the moiré Brillouin zone25.

Fig. 1: Interplay between Γ-valley flat band and K-valley band in TDB-WSe2.
figure 1

a Left: schematic of the device structure. Right: illustration of the moiré pattern TDB-WSe2 with twist angle 60∘ − θ. b Schematic band structures of TDB-WSe2, based on our DFT results, at a twist angle near 60∘ without (top) and with (bottom) displacement fields. The blue and red lines represent Γ- and K- valley bands, respectively. The width of the top Γ-valley ba`sistance, Rxy, as a function of Vtg and Vbg measured at B = 0 T and B = 2 T, respectively (T = 1.5 K). The yellow and black dashed lines trace the evolution of the half-filling correlated insulating states. For c the white and blue dashed lines trace the evolution of the  −1/3ns filling states with black and blue arrows pointing on corresponding feature in Rxy. The magenta dashed line highlights a boundary where the K-valley crosses the Fermi level. The gray color in c represents the off-region. The corresponding Hall resistances in (d) in this off-region are also mainly noise. e Rxx as a function of Vbg at four typical Vtg values, which display a half-filling peak at each line and another at  −1/3ns for Vtg = −5.6 V. The curves are offset for clarity. The horizontal gray dashed lines correspond to zero resistance for each curve. The gray-shaded region on the right side denotes the mobility edges. f Map of Rxx as a function of temperature and band filling measured at Vtg = −5 V. g Rxx as a function of temperature at different band fillings, highlighting the activation of the half-filling correlated insulator and the metallic behavior at densities away from half-filling.

Full size image

Figure 1 b shows the schematic band structures of TDB-WSe2 without (top panel) and with (bottom panel) displacement field (D) as calculated from density functional theory (DFT) (see Supplementary Figs. 1, 2, 3, and 4 in SI). In contrast to twisted bilayer WSe218,27, where the Γ-valley flat bands are buried more than 140 meV below the valence band maximum (VBM), due to the stronger interlayer hybridization the Γ-valley flat bands (blue curves) in TDB-WSe2 rise up to the VBM when D = 0 V/nm. Moreover, the Γ- and the K-valley bands are very close in energy with considerable overlaps, but hybridization between these two bands remains small because the two are rooted in different atomic orbitals of the metal and chalcogen atoms25. With increasing D, the K-valley bands (red curves) split, and the VBM shifts to one of the K-valley bands, while the Γ-valley flat bands remain almost unaffected. These unique features of the electronic band structure, induced by the moiré potential, allow us to study the interplay between correlated states in the Γ-valley flat band and K-valley states.

To begin investigating this interplay, we first measure Rxx (B = 0 T) and Rxy (B = 2 T) while sweeping the top (Vtg) and bottom (Vbg) gates, Fig. 1c, d. A prominent resistive peak in Rxx, marked by the yellow dashed line, is observed along the constant half-filling density, which we denote as  −ns, corresponding to one hole per moiré unit cell. The Rxy around this feature changes sign three times, indicating a correlated insulating state that deviates strongly from the single-particle band structure18. Tracing the n/ns = −1 peak to larger negative Vtg values, the resistance first gradually decreases (up to Vtg ≈ −8 V), and then quickly collapses to a small residual resistance peak traced by the black dashed line. The Rxy in this region, black arrow Fig. 1d, exhibits slightly higher values than the background, but without sign change. Similar dependence also appears at −1/3ns filling, marked by white and blue dashed lines. This trend is highlighted in the Rxx versus Vbg curves under four different Vtg values from −5.6 V to −9 V in Fig. 1e.

To further verify the correlated insulating nature of the state at half-filling, we show the temperature dependence of Rxx near this doping regime in Fig. 1f, g. Above a critical temperature, TC ≈ 12 K, the sample shows a metallic behavior. Below TC, as the sample is cooled the resistance at half-filling increases in a manner consistent with a thermally activated insulator. When it is doped slightly away from half-filling, the insulating behavior changes to metallic. Intriguingly, we also observe a small resistance peak (magenta dashed line, Fig. 1c) which intersects with both the n/ns = −1 and  −1/3 insulating states at their transition points. We have measured similar phenomena in other devices with similar twist angles (Supplementary Fig. 5). We hypothesize that this feature is related to an evolution of the band structure, which may destroy the correlated state.

Following this hypothesis, we draw a cartoon phase diagram of the gate-gate behavior in terms of D and the band filling (n/ns) in Fig. 2a. Our reasoning for this model is as follows: first we consider the system without electron interactions in (Fig. 2b) under zero and finite D. As shown in Fig. 1b, D has little effect on the Γ-valley band but can significantly broaden the K-valley bandwidth and shift its position in energy upwards. At a critical displacement field, Dc, the K-valley (red dashed line, Fig. 2b) reaches the Fermi level, whose position also determines the doping density n. When n is lower (higher), the Fermi level is further from (closer to) the K-valley band and thus there is a larger (smaller) resulting Dc, explaining the phase boundary defined by the D = Dc line in Fig. 2a. In this picture when D < Dc only the Γ-valley will be filled. However, when D > Dc, carriers will reside in both the Γ- and K- valleys.

Fig. 2: Displacement field and doping response of the correlated phases in TDB-WSe2.
figure 2

a Schematic phase diagram of TDB-WSe2 resulting from the theoretical model in (b–d). Here, Γx and Kx denote the nature of the corresponding bands with x = Me, x = MI, and x = BI denoting metallic, Mott˘Hubbard insulating and band insulating states, respectively. b Single particle band illustration: at a carrier concentration n (n/ns ≠ −1), the upper edge of the K-valley band touches the Fermi level when D = Dc. In a single particle picture, for D < Dc, only Γ-valley is filled; and for D > Dc, both K-valley and Γ-valley are filled. c, d At half-filling, n/ns = −1, the Γ-valley flat band splits into the upper and lower Hubbard band via strong Coulomb interaction. c and d correspond to the sample under a small and large D, respectively. e Resistance versus displacement field and band filling, replotted from the same dataset in Fig. 1c all the dashed lines follow the same coloring definition as in Fig. 1c gray color represents the off region and white color represents the regions not measured.

Full size image

Next, we consider what happens when we add Coulomb interactions into the model (Fig. 2c). At half-filling, the Γ flat band splits into lower (LHB) and upper (UHB) Hubbard bands. Because the difference in energy between the Γ- and K- valleys (from DFT, see SI) is small, the LHB lies below the K-valley band. As a consequence, a charge-transfer insulator with a gap Δ smaller than U is formed between the K-valley maximum and the UHB minimum. Thus we assign this gap as a correlated insulating state, where D can continuously tune the size of Δ all the way to zero. Experimentally, we observe the results of this model as we tune from the insulating state (D < Dc) to the metallic state (D = Dc) where the K-valley touches the UHB and closes the gap (intersection of the yellow and magenta dashed lines in Fig. 2e).

Finally, in Fig. 2d, we examine what happens to the correlated insulating states when the K-valley begins to overlap with the UHB (i.e., D > Dc). As a result of this overlap, additional Δn carriers are needed to fill the K-valley in order to keep the Γ-valley band at half-filling. Intuitively, a larger D will shift the K-valley further up in energy and will result in a larger Δn. With this understanding in mind, we look back on Fig. 1c and re-plot it as a function of D and (n/ns) in Fig. 2e with the same colored dashed lines as in Fig. 1c marking the main features. In agreement with the theoretical phase diagram (Fig. 2b), we find a critical value of D, Dc, above which the resistance of the correlated states at n = −ns and  −1/3ns will collapse. The correlated behavior, marked by a black line in Fig. 2e, corresponds to the Γ-valley band being in the Mott˘Hubbard state concomitant with the K-valley band being in a metallic state, as suggested by Fig. 2d. Because the two bands overlap in energy, the behavior observed in electronic transport is metallic (see temperature dependence in Supplementary Fig. 6). Similarly, the correlated insulating state seen at  −1/3ns filling also diminishes to small resistance peaks, marked by the dashed blue line in Fig. 2e.

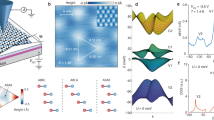
To further prove the validity of the phase diagram presented in Fig. 2a and the existence of a charge-transfer insulator state, we examine the sample under perpendicular magnetic fields. Figure 3a, b shows the Rxx and Rxy values versus n and B up to 14 T with Vtg fixed at −7 V (see Supplementary Figs. 7 and 8 for other values of Vtg and similar behavior in another device). With sweeping Vbg, the constant Vtg = −7 V line crosses the magenta dashed line in Fig. 1c. As a result, in the low-doping region D is much larger than Dc and the K-valley band is at the VBM. So the observed Landau fan (red lines, Fig. 3a) originates from the K-valley band edge. Starting from the lowest Landau level −2, both odd and even-integer quantum Hall states are observed, suggesting a full lifting of the spin-valley degeneracy. As we move to higher carrier density, we observe a second set of Landau fans (purple lines) whose trajectories point towards the Γ-valley band edge. Different from the Mott insulator phase in tbWSe218, we find that the charge-transfer insulator peak (located at n ~ 7 × 1012 cm−2) in TDB-WSe2 survives up to 14 T.

Fig. 3: Magneto-transport on the K- and Γ-valley bands in TDB-WSe2.
figure 3

a, b Rxx and Rxy as a function of carrier density, n, and magnetic field, B, at Vtg = −7V (T = 1.5K). c, d Rxx and Rxy versus n and B at Vtg = −10 V (1.5 K). e Temperature-dependent quantum oscillations ΔRxx versus 1/B at three representative positions. From red to blue, the temperatures are 1.5, 2.3, 3, 3.9, 4.7, 5.7, 7, 9, and 12 K. f Normalized amplitude versus T for three representative points: (a, b, c). Solid lines fit the Lifshitz–Kosevich formula.

Full size image

Upon increasing D further by fixing Vtg at  −10 V (Fig. 3c, d), we enter the D > Dc region where only the correlated metallic state is observed. This state exists up to high magnetic field without sign change in the corresponding Rxy. Similar to Vtg = −7 V, as a result of the sample residing in the D > Dc region, we observe two sets of Landau fans originating from the Γ and K-valley bands. As compared to Vtg = −7 V, we also observe that the separation in carrier density between these two sets of Landau fans increases, in agreement with the predicted shift of the K-valley band from DFT. Notice that there is a set of curved Landau fans, which cross the correlated metallic state and may be pointing toward full filling of the K-valley. We speculate that the slope of these fans is affected by the simultaneous filling of the Γ-valley band. To further confirm the origin of the Landau fans, we extract the effective mass of each region by measuring the temperature-dependent SdH oscillations (Fig. 3e) at three fixed Vtg and Vbg values, marked as a, b, and c. To determine the effective mass, we used the Lifshitz–Kosevich formula \(A(T)={A}_{0}\frac{2{\pi }^{2}{k}_{{{\rm{B}}}}T/\hslash {\omega }_{c}}{\sinh (2{\pi }^{2}{k}_{{{\rm{B}}}}T/\hslash {\omega }_{c})}\), where \({A}_{0}=4\exp (-2{\pi }^{2}{k}_{{{\rm{B}}}}{T}_{D}/\hslash {\omega }_{c})\), ωc = eB/m*c is the cyclotron frequency, TD = ℏ/2πkBτq is the Dingle temperature, ℏ is the reduced Planck’s constant, and kB is the Boltzmann constant. Figure 3f shows the normalized amplitude versus temperature at a, b, and c. Indeed, the fits show that the effective masses at a and b, associated with the K-valley fans, are lighter (0.39me and 0.52me, me is the bare electron mass) while the effective mass at c, related to the Γ valley fans, is heavier (1.14me), as expected from theory.

Finally, we investigate the displacement field-induced metal-insulator phase transition of the charge-transfer insulator. Figure 4a displays the resistance along the constant half-filling line versus D and temperature. It unambiguously shows an insulator-metal phase boundary around D = 0.38 V/nm (for similar transitions in other devices, see Supplementary Fig. 9). In Fig. 4b, we plot a series of R−T curves below and above the phase boundary in Fig. 4a. The curves for D values ranging from  −0.06 V/nm to 0.36 V/nm exhibit an insulating behavior at temperature below 12 K, with resistances increasing with decreasing temperature. This behavior becomes weaker with increasing D, up to 0.36 V/nm where the R−T curve is nearly flat. Upon further increasing of D from 0.4 V/nm to 0.6 V/nm, we see a smooth transition from an insulating state to a metallic one. To quantify this change, we extract the activation gap Δ for each curve in Fig. 4c (see fittings in Supplementary Fig. 10). We observe a maximum gap size of 1.8 meV at D = 0, which decreases monotonically with increasing D until D = 0.4 V/nm, where the metallic states from the K-valley band dominate the transport behavior. Although a phase transition from a Mott insulator state to a metallic state has been theoretically and experimentally reported in twisted TMDs28,29,30,31, the mechanism is due to the increasing bandwidth of the moiré flat band under finite D. However, for TBD-WSe2, small D does not change the Γ-valley bandwidth and, therefore, we attribute this tunable gap to the rising of the K-valley, in accordance with our theoretical model discussed in Fig. 2. Thus we have demonstrated a tunable phenomena in moiré heterostructures: a charge-transfer gap in TDB-WSe2, where a phase transition at n/ns = −1 is induced by D and the result of this gap closing between the Γ flat band and the K-valley band.

Fig. 4: Displacement field tunable charge-transfer insulator gap and insulator-metal phase transition in TDB-WSe2.
figure 4

a Rxx as a function of D and T at n/ns = −1. b Rxx versus T curves for D ranging from −0.06 V/nm to 0.6 V/nm. The Rxx − T dependence changes smoothly from insulating to metallic behavior with D at low T. c Δ versus displacement field at n/ns = −1. Error bars reflect the uncertainty in determining the linear region for the fit.

Full size image

Discussion

Going beyond the established moiré control paradigm of tuning bandwidths, our work establishes an additional control knob—the valley degree of freedom. With this, we demonstrate valley-enabled control of many-body phases of matter, including correlated Mott˘Hubbard and charge transfer states. The continuous control of phase transitions between different correlated states and metals using purely displacement fields is a unique application of this valley-enabled control. This phenomenon elevates TDB-WSe2, and similar TMD structures, as novel platforms significantly expand on the available moiré materials engineering. Owing to the widely tunable band structure, TDB-TMDs can provide model systems to systematically explore other emergent electronic phases, such as the realization of correlated insulators as potential parent states to unconventional superconductors (analogous to charge-transfer cuprates3), exciton condensates, and potentially even spin-liquid states32.

Methods

Sample fabrication

We used the pick-up transfer method22 to fabricate the twisted double bilayer WSe2 (TDB-WSe2) devices. All the flakes including bilayer WSe2, hexagonal boron nitride (hBN), and few-layer graphite were mechanically exfoliated from the bulk crystal on Si substrates with a 285 nm oxide layer. We fabricated prepatterned leads by first preparing a stack of hBN/Graphite as the bottom gate, and then evaporating a Hall-bar-shaped Cr/Pt (1/20 nm) metallic leads on the hBN layer. To fabricate the twisted TDB-WSe2 stack, we picked up another hBN(25–50 nm) flake and used it to pick up the TDB-WSe2 flakes by the “pick up and tear” method22,23. The hBN/TDB-WSe2 stack was then dropped onto the pre-patterned Pt leads. Lastly, a metal top gate was evaporated on the top layer h-BN.

DFT calculation on the bandstructure

In order to assess the electronic properties of TDB-WSe2 system, we performed the first principle calculations based on density functional theory (DFT) as implemented in the Vienna ab initio simulation package (VASP)33. The pseudo-potentials approach under the framework of the projected augmented-wave method (PAW) was used to perform the first principal Ab initio calculations34. Plane-wave basis sets with cutoff energy equal to 500 eV were employed. The generalized gradient approximation (GGA) under the Perdew-Burke-Ernzerhof (PBE) scheme was used to model the exchange-correlation interaction35. Due to the large size of the moiré supercells, only the Γ point was considered in all the self-consistent calculations. A slab model was used with vacuum thickness more than 15 Å to avoid the artificial interaction between the periodic slabs. To cover the Van der Waals interaction between the adjacent layers, Tkatchenko–Scheffler method was applied during the relaxation36. All the structures were fully relaxed until the largest Hellmann Feynman force on each atom converged to values smaller than 0.01 eV/Å. For figures like charge density distributions and atomic structure visualization, we used the VESTA code37.

To model the TDB-WSe2 systems, we placed the bilayer WSe2 over the bilayer WSe2 with twisted angles between the constituent bilayer WSe2 to be (60 − θ) degrees. In our work, we specifically focused on the systems with θ = 5.08° and 4.4°. Extensive DFT calculations were performed both in the absence and presence of displacement fields. Spin-orbit interactions were included in all the calculations.