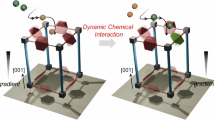
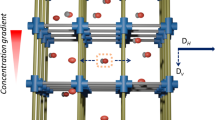
Abstract
In the realm of heterogeneous catalysis, the diffusion of reactants into catalytically active sites stands as a pivotal determinant influencing both turnover frequency and geometric selectivity in product formation. While accelerated diffusion of reactants can elevate reaction rates, it often entails a compromise in geometric selectivity. Porous catalysts, including metal-organic and covalent organic frameworks, confront formidable obstacles in regulating reactant diffusion rates. Consequently, the chemical functionality of the catalysts typically governs turnover frequency and geometric selectivity. This study presents an approach harnessing diffusion length to achieve improved selectivity and manipulation of reactant-active site residence time at active sites to augment reaction kinetics. Through the deployment of a thin film composed of a porous metal-organic framework catalyst, we illustrate how programming reactant diffusion within a cross-flow microfluidic catalytic reactor can concurrently amplify turnover frequency (exceeding 1000-fold) and enhance geometric selectivity ( ~ 2-fold) relative to conventional nano/microcrystals of catalyst in one-pot reactor. This diffusion-programed strategy represents a robust solution to surmount the constraints imposed by bulk nano/microcrystals of catalysts, marking advancement in the design of porous catalyst-driven organic reactions.
Similar content being viewed by others
Introduction
Porous heterogeneous catalysts, like zeolites, metal-organic frameworks (MOFs) and covalent-organic frameworks (COFs) are widely researched for organic conversions1,2,3. The growing interest particularly in MOFs, constructed by linking metal ion/cluster with functionalized organic ligand, stems from their well-organized confined active sites, which are sterically and electronically tunable4,5,6. The extensive chemical diversity and predictable structure-property relationships of MOF-based catalysts have significantly expanded their applications, including in the areas such as enantiomer/size-selective catalysis, electrocatalysis, and photocatalysis7,8,9,10,11,12,13,14,15. Nonetheless, a persistent challenge for porous catalysts is the limitation imposed by mass transfer or diffusion16,17. Often all the catalytic sites are not accessible due to substantial diffusion barrier (surface barrier and large diffusion length), leading to lowering of conversion efficiency16. Further, poorly regulated diffusion leads to smaller geometric selectivity. Therefore the overall efficiency of porous catalysts remains underestimated. Although the diffusion mechanism18,19,20 is well-explored in theory and simulation for porous materials, access to the highest efficiency, selective catalysis in practice remains a complex challenge.
In typical catalytic reaction, whether batch or fixed-bed types, a range of MOF particle sizes is utilized. This size heterogeneity can significantly reduce both the turnover frequency (TOF) and geometric selectivity (which is the hallmark feature of MOF catalysis21,22,23). The underlying reasons are as follows: in porous heterogeneous catalysts, active sites are located both on the surface and within the bulk. When the catalyst has a very high surface-to-volume ratio (particle size < 10 nm), the reaction rate is governed by the surface active sites. For catalysts with a very low surface-to-volume ratio (particle size >10 μm), the very high reactant diffusion barrier allows the reaction only at the surface active sites. Within the intermediate particle size range, the diffusion rate controls the reaction outcome, influencing both TOF and selectivity. This relationship is depicted in Fig. 1a, b, demonstrating that for a specific catalytic reaction, there is a critical particle size or diffusion length (Lc) at which geometric selectivity is maximum (i.e. selectivity is controlled by diffusivity only). However, achieving this critical point in a conventional catalytic reaction appears unattainable. It is also noteworthy that maximizing geometric selectivity inherently leads to reduction in TOF; a trade-off intrinsic to any porous material-based catalytic reaction. Note that the diffusion length (LD) is the maximum distance of the active site from the catalyst particle surface; hence it is shown as the radius of spherical particle. The rate of diffusion will vary depending on the reactant geometry, catalyst pore size, dimensionality and chemical functionality. In Fig. 1b, reactants of different sizes can fit into the pores of the catalysts and diffuse at different rate.
a Schematic illustration of porous heterogeneous catalyst (MOF) in a conventional reaction set up, b diffusion length-dependent turn-over frequency (TOF, solid line) and geometric selectivity (dotted line) profiles for a catalytic reaction; red and green arrow indicate diffusion for A and B reactants, size A > B, the half spheres represent a model porous catalyst particle, c (i) schematic illustration of the diffusion controlled, microfluidic cross-flow reaction set up, (ii) for a catalyst with LC: plausible flow-rate (F) dependent TOF and geometric selectivity profiles, red and green line indicate reactants of different sizes. SP product selectivity. Following are the power laws for (b) and (c) (ii); TOF\(\propto\) 1/LD3 and TOF\(\propto\) 1/F0.5.
There are elegant chemical pathways (defect density control24,25,26,27, postsynthetic linker modification, exchange28,29,30, and multivariate assembly31,32) that can uplift TOF or geometric selectivity in MOF catalysis. For other types of porous catalysts (e.g. zeolites), the chemical tunability is not always straightforward. Keeping the chemical compositions constant in a MOF catalyst, we have explored the possibility of efficiency (TOF and selectivity) tuning by controlling the diffusion length only. We realized that the primary factors are diffusion length (LD) and reactant-active site residence time (collision frequency). The former can improve geometric selectivity, while the latter can boost TOF. To precisely manipulate LD, we have utilized a monolithic thin film of MOF catalyst with programmable thickness, and mounted in a microfluidic cell (cross-flow) to enhance residence time. This reaction setup is illustrated in Fig. 1c (i). By precisely controlling the LD and residence time, for a condensation reaction we have achieved a >1000 fold increase in TOF and 2-fold enhanced geometric selectivity compared to a chemically equivalent batch reaction using submicron-size particles of catalyst. A straightforward control over LD and residence time allows programming the diffusion of the reactants, which controls the outcome of the reaction, as depicted in Fig. 1c (ii). In the following discussion we have illustrated the working principle and a general strategy to perform the diffusion-programmed catalysis, enabling access to the highest limits of TOF and geometric selectivity for any porous catalyst.
Results
The pore window size, cavity size and chemical environment of MOFs can be engineered precisely and predictively33,34,35,36. By leveraging this chemical and structural tunability, catalytic sites within the pores can be tailored to accommodate specific reactants. This exceptional selectivity in geometry can be regulated by varying the LD of the reactants. Literature suggests that reducing LD (i.e., using smaller particle sizes) enhances the turnover frequency (TOF)37,38,39. However, this increase in TOF comes at the cost of reduced geometric selectivity. To evaluate this statement, we conducted a conventional one-pot reaction using submicron-scale catalyst particles.
We investigated a Knoevenagel condensation reaction catalyzed by a Lewis base (-NH2) housed within a robust MOF pore40,41. The MOF of interest, UiO-66-NH242, composed of Zr4+ and 2-aminobenzendicarboxylic acid (NH2-bdc), was synthesized, with particle sizes43 averaging ~ 500 nm and ~160 nm employed for the catalytic reactions (Supplementary Fig. 1–4). The MOF’s triangular pore window size is ~6 Å and cavity diameter is ~11 Å (Supplementary Fig. 1a, b, experimentally obtained pores size distribution ~ 5 Å and 10 Å, due to structural defect, see later). Ethyl cyanoacetate (Et-CA; 4.5 Å × 10.3 Å) and tert-butyl cyanoacetate (t-But-CA; 5.8 Å × 10.3 Å) were chosen as the small and large nucleophiles40, respectively, reacting with benzaldehyde (6 Å × 4.3 Å) to form ethyl-2-cyano-3phenylacrylate (Et-Acr) and ethyl-2-cyano-3phenylacrylate (t-But-Acr), respectively (Fig. 2a, Supplementary Figs. 5–7). The nucleophiles’ dimensions allow diffusion into the pores, albeit at varying rates due to sieving effects. Molecular dynamics (MD) simulations were employed to estimate diffusivity differences of two nucleophiles within UiO-66-NH2, Supplementary Figs. 8 and 9 (see “Methods” section below). Analysis of mean square displacement (MSD) profiles indicates that Et-CA diffuses approximately ten times faster than t-But-CA (Supplementary Fig. 8). We have also employed biased simulation techniques, specifically umbrella sampling, to estimate the free energy barrier associated with molecular transport across the pore window (Supplementary Fig. 9a). Supplementary Figure 9b indicates that the free energy barrier for t-But-CA is higher than that for Et-CA, likely due to its larger size, suggesting slower pore to pore diffusion of t-But-CA compared to Et-CA. Close-proximity interactions between nucleophiles and MOF pores reveal that the active –CH2 group (marked with * in Fig. 2a) of nucleophiles predominantly interacts with the organic linker rather than the metal node (Supplementary Fig. 9c, d). This –CH2 –NH2 interaction suggests the potential for Lewis base catalyzed reactions.
a Chemical structure of the reactants, * = reactive –CH2 group; DtBut and DEt are the diffusivities of t-But-CA and Et-CA, respectively; b illustration of cross-flow microfluidic reaction using MOF thin film as catalyst, P circulating pump, R reactant and product chamber, yellow dotted line indicates the flow path, right MOF catalyst thin film with controllable thickness, LD diffusion length; c TOF after 24 h at 70 °C for one pot reaction with smaller MOF submicron-sized particles and in cross-flow microfluidic reaction using UiOTF1 (5 mL/min flow-rate), 1 mmol of benzaldehyde and nucleophiles each in 10 mL of ethanol. Conversion % is calculated using 1H NMR.
We anticipated the reaction rate to exceed the diffusion rate, leading to diffusion-controlled TOF and selectivity. At 24 h, we achieved 42 (±2)% and 24% conversions for the smaller and larger nucleophiles, respectively, using the ~160 nm catalyst particles (1 mol% in ethanol, 70 °C; Supplementary Table 1, Supplementary Figs. 10–12). Under similar conditions, the ~500 nm catalyst particles exhibited approximately 50% lower yield but improved selectivity (~25%) for the smaller nucleophile. However, this improvement in selectivity is not deemed significant. Noteworthy, the one-pot reaction contains a large variety of particle sizes (Supplementary Figs. 2 and 3). Hence any significant change in the selectivity by varying the particle sizes is a challenge.
At this point, to regulate TOF and selectivity, we have designed a new reaction methodology. To enhance the TOF, we have done following: (i) a method to improve TOF is by increasing collision frequency (reactant-active site). To achieve this, we designed a microfluidic reactor where the catalyst is supported on a solid surface (vide infra) and the volume of reactant solution in contact with the catalyst is 80 (±4) μL. The small volume ensures that only a limited amount of reactant interacts with the entire catalyst layer at any given time, thereby enhancing reactivity. (ii) The microfluidic cell is connected to a pump that circulates a larger volume of reactant solution. Consequently, both reactants and the formed products circulate in a cross-flow direction along the catalyst bed (thin film). This reaction setup resembles one-pot catalysis reactions, except that the catalyst is placed within a microfluidic cell as a thin film. iii) Reactant flow can be controlled (0.1–15 mL/min) in a cross-flow direction, which helps preventing pore surface blockage.
To enhance the selectivity, the catalyst is deposited as a monolithic thin film with controllable thickness (see “Experimental” section, Supplementary Fig. 13). In the proposed cross-flow setup, concentration gradient is along the film thickness, and hence the thickness is LD. This allows straightforward tuning of the LD, unlike in the one-pot reaction (vide supra). The reaction setup is illustrated in Fig. 2b. Noteworthy those conventional nano/microparticles of MOFs are not suitable for this catalysis reaction. Rather, recently developed MOF thin film growth methodologies, e.g., layer-by-layer epitaxy44,45,46, chemical vapor deposition47, solution atomic layer deposition48, vapor assisted conversion49, and electrochemical50,51 deposition can be applied to make the catalyst layer.
To execute the reaction scheme, we have synthesized UiO-66-NH2 monolithic thin film (UiOTF1 ~ 120 nm thickness) on a Si/SiO2 substrate at room temperature (298 ± 3 K), using a drop casting methodology52 (Supplementary Figs. 14 and 15). This method is suitable for controlling the film thickness with high crystalline orientation (Supplementary Fig. 16). All the films synthesized have similar crystallite sizes (Supplementary Fig. 15) and crystalline orientations (Supplementary Fig. 17). Additionally, the oriented MOF thin film showed rapid adsorption of methanol52 and tert-butanol vapors, confirming its porosity (Supplementary Fig. 18). Using the catalyst thin film UiOTF1 we performed reactions using a similar reactant solution volume as for one-pot reactions, at 70 °C using a flow rate of 5 mL/min (Fig. 2b). We could realize maximum ~96% and 35% formation for the Et-Acr and t-But-Acr after 24 h (TOF ~ 2271 and 790 h−1 respectively, Supplementary Table 2, Supplementary Figs. 19–21). The TOF and selectivity are enhanced by ~1300-fold and 1.5-fold, compared submicron-sized particle based catalysis. These findings, depicted in Fig. 2c, validate the simultaneous enhancement of TOF and selectivity through our proposed strategy. In absence of any chemical modification, these observations are unprecedented17. Subsequently, we elaborate on the underlying principles driving these radical improvements.
To confirm that the reaction is indeed controlled by pore diffusion and that selectivity enhancement is attributable the diffusion length (LD), we have conducted reactions varying film thickness. Increasing film thickness simultaneously increases LD and also amount of active sites. In the absence of diffusion control, the TOF should remain unchanged with increasing thickness. Conversely, a diffusion-regulated reaction should exhibit a quadratically decreasing TOF, assuming the nucleophiles obey Fickian diffusion (TOF \(\propto\) 1/LD2). We synthesized UiOTF2 and UiOTF3 with thickness ~300 (±30) and 400 (±50) nm, respectively (Supplementary Fig. 14). The film TOF vs film thickness profiles for both of the condensation products are shown in Fig. 3a (Supplementary Table 2, under similar reaction conditions). The data clearly show that with increasing thickness TOF decreases and selectivity increases in a nonlinear trend. This supports the notion that the conversion is controlled by intrapore diffusion rather than being surface confined. Furthermore, it is feasible to enhance selectivity by adjusting the film thickness, i.e., LD.
a Catalyst film thickness dependent and (b) flow-rate (F mL/min) dependent TOF and selectivity (SEt/t) profiles for the Et-Acr and t-But-Acr in cross-flow microfluidic reaction. All reactions are done at 70 °C using 1 mmol of benzaldehyde and 1 mmol of nucleophiles each in 10 mL ethanol. Conversion % is calculated using 1H NMR. Error-bars are calculated by carrying out three set of reactions.
Apart from selectivity, the sharp enhancement in TOF can be attributed to the microfluidic reaction set up. Direct evidence of this can be obtained by following experiment: A reaction of Et-CA and benzaldehyde was carried out in one-pot method using the thin film catalysts UiOTF2. After 30 h the conversion was ~50 % (Supplementary Table 3, Supplementary Fig. 23). This markedly lower conversion efficiency compared to the microfluidic reaction, confirms that the effective residence volume for the reactant solution and entire catalyst indeed enhances the TOF.
To verify influence of other factors, e.g. defect density in the powder and monolithic thin films (UiOTF1–3), we compared the infra-red (IR) spectra, nuclear magnetic resonance spectrum (NMR) and X-ray photoelectron spectra (XPS) of those (Supplementary Figs. 24 and 25). The IR spectra indicated that the –COO stretching frequencies (asymmetric and symmetric 1571 and 1382 cm−1, respectively) are similar for thin film and powder catalysts. XPS confirmed that the Zr/N ratio and nature of defects related to dangling –COO are similar53,54 for both the type of catalysts. From solution state 1H-NMR of the disintegrated MOF powder we estimated ~33% missing linker defect (Supplementary Fig. 24b). We have also realized that monodispersed surface-anchored MOF particles can also enhance TOF10,55. We have confirmed that the UiOTF1 is a monolithic thin film, having no evident cracks or islands of crystals (Supplementary Fig. 14a). These above mentioned evidences support that the enhanced TOF is due to the integration of MOFs in a cross-flow microfluidic setup.
After confirming the influence of diffusion and microfluidic reaction set up on the selectivity and TOF, respectively we have performed a flow-rate dependent catalysis reaction. Flow-rate and reactant-catalyst residence time is inversely proportional. In the absence of diffusion control, it is expected that product yield % will linearly decrease with increasing flow-rate. In case of diffusion regulated process, a quadratic decrease of conversion % is expected (vide supra). In Fig. 3b, Et-Acr yield % vs flow-rate profile (4 h reaction at 70 °C) exhibited a nonlinear trend (yield % \(\propto\) (1/F)0.2–0.32), confirming reactant diffusion limited reaction (Supplementary Table 4, Supplementary Figs. 26 and 27). Moreover, t-But-Acr yield % also reduces nonlinearly (Supplementary Table S4, Supplementary Fig. 28) with increasing flow rate and we could observe highest selectivity of 11.5 at a flow-rate of 1 mL/min (Et-Acr yield ~70%). Using similar conditions (solvent, temperature, and concentration) in a one-pot reaction similar TOF and selectivity is not feasible. Noteworthy, the TOF and selectivity vs flow-rate profiles in Fig. 3b resemble Fig. 1b, except diffusion length is replaced by flow-rate. We have shown that by straightforward tuning of flow-rate it is feasible to achieve critical diffusion path (Lc) which allows access to highest selectivity with higher TOF than the conventional methods.
It is evident that for thickness and flow-rate based diffusion control experiments conventional Fickian diffusion is not followed, as the power law diverges from the quadratic norm. This anomalous behavior is indicative of additional factors, e.g., presence of competitive interaction with benzaldehyde and any specific chemical interaction with MOF. These factors inhibit the long-range random walk, leading to a modified TOF expressed as TOF \(\propto\) (1/F)1/(2+α), where α represents the anomalous factor56,57,58.
The above discussed experiments conclude that the TOF and selectivity can be enhanced beyond the conventional limits using the proposed scheme. A comparison of the TOF and selectivity, for similar condition (at similar temperature, solvent and time) one-pot (using 500 nm particle) and cross-flow microfluidic (using UiOTF2) reaction, confirmed >1000 and 2-fold enhancement, respectively (Supplementary Tables 4 and 5, Supplementary Fig. 29). In the next step, we have explored the impact of heterogeneous mixtures (i.e., mixture of Et-CA and t-But-CA) on the reactivity. In Fig. 4 we have illustrated the observed TOF and selectivity for one-pot (1 mol% catalyst) and cross-flow microfluidic (4.2 × 10−3 mol% catalyst, 0.1 mL/min) reactions (Supplementary Tables 6 and 7, Supplementary Figs. 30 and 31). It is evident that competing diffusion of the reactants decreases the total conversion efficiency. However, the selectivity are found to be 5.4, higher than the one-pot reactions using large (4.3) submicron-sized catalyst particles. The improvement in the conversion efficiency is also evident; Et-Acr yield % is similar for one-pot (smaller particle) and cross-flow microfluidics methods, although catalyst mol% differ by >1000-fold. This confirms that even in a heterogeneous mixture of competing reactant diffusion, cross-flow microfluidic reaction using MOF catalyst monolith is superior to the state-of-the-art catalysis reactions while maintaining the crystallinity of the monolithic thin film post-reaction (Supplementary Fig. 16).
Discussion
Metal–organic frameworks (MOFs) are esteemed as exceptional heterogeneous catalysts among the porous materials, owing to their crystallinity, extensive chemical versatility, high surface area, and confinement effects. However, the diffusion-limited TOF and selectivity present significant challenges that continue to impede their catalytic performance. To address these issues, we have engineered a cross-flow microfluidic reaction setup and catalyst monolithic thin film, which allow precise control over reactant diffusion, thereby modulating both TOF and selectivity. This diffusion programmability is exemplified in a Knoevenagel condensation reaction, demonstrating the feasibility of simultaneously enhancing TOF and product selectivity beyond the conventional limits imposed by one-pot or batch reactors, achieving improvements by orders of magnitude. The ability to control diffusion rate allows for continuous tuning of the conversion efficiency, with experiments revealing a sub-diffusive nature of the catalytic reaction. This marks the first proof-of-concept demonstration of diffusion-programmed catalysis in porous materials, representing a significant step forward in the field. The design of microfluidic cell and flow control used in the current work may be improved in future to explore other varieties of organic reactions.
Methods
Characterization techniques
X-ray diffraction
The X-ray diffraction patterns of the powder and thin films were recorded using a Rigaku SmartLab diffractometer using nickel-filtered Cu Kα radiation (λ = 1.5418 Å). Data were collected from 5 to 20° at room temperature (voltage 40 kV, current 200 mA). XRD was recorded in 2θ/θ (step size 0.01, scan rate 0.2°/s) geometry.
Scanning electron microscopy (SEM)
Morphology and cross-section of the thin films and powders were characterized using field emission scanning electron microscopy (FESEM), JEOL JSM-7200F instrument with a cold emission gun operating at 5, 25, and 30 kV.
Infrared (IR) spectroscopy
Infrared reflection absorption spectroscopy (IRRAS) of the thin films and attenuated total reflection (ATR) absorption spectroscopy of the powder were done using the Bruker Vertex 70 v instrument, with a spectral resolution of 2 cm-1. IRRAS results were recorded in grazing incidence reflection mode at an angle of incidence 45° relative to the surface, under vacuum at room temperature. 1-octadecanethiol self-assembled monolayer (SAM) functionalized Au was used for background measurements.
X-ray photoelectron spectroscopy (XPS)
Elemental detection of the powder and thin film was performed using X-ray photoelectron spectrometer (PHI versaProbe III) within an ultrahigh vacuum (1 × 10−9 bar) environment. This instrument was equipped with an Al-Kα X-ray source and a monochromator.
Nuclear magnetic resonance (NMR) spectroscopy
NMR spectra were recorded on a BrukerNanoBay 300 MHz NMR spectrometer. In our experiment, after the reaction, we used a syringe filter to separate the MOF powder catalyst. The entire collected solution was then concentrated and 0.4 mL of CDCl3 was added to check the NMR data. For the cross-flow microfluidic catalysis, we collected the entire solution from the fluidic cell, concentrated and after adding 0.4 mL of CDCl3 we checked the NMR data.
Analysis of mass uptake kinetics
We evaluated the mass uptake rates of thin films grown on quartz crystal microbalance (QCM) sensors functionalized with a MUD-coated gold surface. To probe the system, we used methanol and tert-butanol, under 50 ml/min N2 flow) as test molecules, chosen for their smaller kinetic diameters relative to the pore window size. The QCM sensors with thin-film coatings were mounted within a fluidic cell in a temperature-controlled setup, where vapor uptake rates were measured by monitoring changes in the fundamental frequency over time.
The relationship between mass and frequency for the QCM sensor is governed by the Sauerbrey equation:
Here n represents the overtone order (specifically n = 3, 5, and 7) and c stands for the mass sensitivity constant. For a quartz crystal with a frequency of 5 MHz, the value of c is 17.7 ng cm−2. We analyzed the data under the assumption of Fickian diffusion, which means we considered a constant diffusivity, D, that does not change with varying vapour concentrations.
Molecular dynamic simulation of reactant diffusion
Simulation model
We considered a 1 × 1 × 1 UiO-66-NH2 containing one molecule of Et-CA or t-But-CA individually. Partial charges for the MOF atoms were obtained from earlier report59, and other bond, angle, and dihedral parameters were modeled using OBGMX. The analyte molecules were modeled using Charmm force field generic parameters (CGenFF)60. Simulations for each reactant molecule were conducted in the gas phase, within a rectangular box of dimensions 2.07 × 2.07 × 2.07 nm3.
Simulation method
Each simulation employed periodic boundary conditions (PBC) in all three dimensions. Long-range electrostatic interactions were managed using the particle mesh Ewald (PME) method61 with cubic interpolation, with a 1.2 nm cutoff for short-range electrostatic interactions. The LINCS algorithm62 was used to constrain bonds involving hydrogen atoms. The system was first energy minimized using the steepest descent algorithm, followed by stepwise equilibration over seven steps with gradual temperature increases from 50 K to 300 K, each step lasting 100 ps with a time step of 0.0005 ps. During equilibration, the average temperature was maintained using a V-rescale thermostat63, separately coupling the MOF and analyte molecule. The equilibrated system then underwent a 10 ns NVT production run at 300 K, also maintained by the V-rescale thermostat. All simulations were performed using GROMACS64 version 2018.6 and repeated multiple times to ensure statistical reproducibility. Structure files are provided as UiO-Et and UiO-tBut in pdb format.
Reactant diffusion was analyzed by calculating the mean square displacement (msd) using the ‘gmx msd’ tool, and the corresponding diffusion coefficient (D) was estimated. To understand the chemical interactions between reactant molecules and the MOF, pair correlation functions of active –CH2 groups (see Fig. 2a) were measured relative to specific functionalities in MOF (metal-oxo nodes, organic linkers, and –NH2 group of the organic linkers). Metal-node represents the Zr metal and the linked oxygen atoms, μ3-O and μ3-OH. Whereas the term linker represents all the atoms of the organic linker, i.e., bdc-NH2.
Free energy calculation
To investigate the free energy barrier associated with molecular movement across the MOF pores, we conducted umbrella sampling simulations. These simulations focused on evaluating the energetics of molecular motion across the MOF pore by simulating the movement of a single molecule from one pore window to another. The equilibrated structure from prior simulations was used as the starting point, with the dimensions of the simulation box and MOF remaining unchanged.
Initial configurations for each umbrella sampling window were generated by systematically moving the molecule along the Y-direction through the MOF pore, from one pore window to the next. The Y-direction of the molecule within the pore of the MOF (d) was chosen as the collective variable (CV) for the umbrella sampling. Harmonic potentials with force constants in the range of 7500 kJ/mol/nm2 were found to be optimal for CV values spanning from 0.05 nm to 0.85 nm (with a spacing of 0.05 nm), ensuring sufficient overlap between adjacent windows.
For each umbrella sampling window, the same simulation protocol was applied. The Weighted Histogram Analysis Method (WHAM) [Grossfield, A. WHAM: The Weighted Histogram Analysis Method version 2.0.7, http://membrane.urmc.rochester.edu/content/wham] was then used to analyze the simulation data. WHAM enabled the calculation of unbiased histograms and the corresponding free energy profiles by combining the results from all independent trajectories.
Umbrella sampling simulations were performed for both substrates, Et-CA and t-But-CA, and the resulting free energy profiles were (Fig. S9b) compared to elucidate differences in their molecular transport through the MOF pore.
Data availability
The data that support the findings of this study are available from the corresponding authors upon request. Source data are provided with this paper.
References
Pascanu, V., González Miera, G., Inge, A. K. & Martín-Matute, B. Metal–organic frameworks as catalysts for organic synthesis: a critical perspective. J. Am. Chem. Soc. 141, 7223–7234 (2019).
Guo, J. & Jiang, D. Covalent organic frameworks for heterogeneous catalysis: principle, current status, and challenges. ACS Cent. Sci. 6, 869–879 (2020).
Rogge, S. M. J. et al. Metal–organic and covalent organic frameworks as single-site catalysts. Chem. Soc. Rev. 46, 3134–3184 (2017).
Furukawa, H., Cordova, K. E., O’Keeffe, M. & Yaghi, O. M. The chemistry and applications of metal-organic frameworks. Science 341, 1230444 (2013).
Kitagawa, S. & Matsuda, R. Chemistry of coordination space of porous coordination polymers. Coord. Chem. Rev. 251, 2490–2509 (2007).
Fang, Z., Bueken, B., De Vos, D. E. & Fischer, R. A. Defect-engineered metal–organic frameworks. Angew. Chem. Int. Ed. 54, 7234–7254 (2015).
Jiao, L., Wang, Y., Jiang, H.-L. & Xu, Q. Metal–organic frameworks as platforms for catalytic applications. Adv. Mater. 30, 1703663 (2018).
Seo, J. S. et al. A homochiral metal–organic porous material for enantioselective separation and catalysis. Nature 404, 982–986 (2000).
Greifenstein, R. et al. MOF-hosted enzymes for continuous flow catalysis in aqueous and organic solvents. Angew. Chem. Int. Ed. 61, e202117144 (2022).
Semrau, A. L. et al. Vectorial catalysis in surface-anchored nanometer-sized metal–organic frameworks-based microfluidic devices. Angew. Chem. Int. Ed. 61, e202115100 (2022).
Zhang, T. & Lin, W. Metal–organic frameworks for artificial photosynthesis and photocatalysis. Chem. Soc. Rev. 43, 5982–5993 (2014).
McCarthy, B. D. et al. Analysis of electrocatalytic metal-organic frameworks. Coord. Chem. Rev. 406, 213137 (2020).
Suremann, N. F. et al. Molecular catalysis of energy relevance in metal–organic frameworks: from higher coordination sphere to system effects. Chem. Rev. 123, 6545–6611 (2023).
Stanley, P. M., Haimerl, J., Shustova, N. B., Fischer, R. A. & Warnan, J. Merging molecular catalysts and metal–organic frameworks for photocatalytic fuel production. Nat. Chem. 14, 1342–1356 (2022).
Karmakar, S. et al. Confining charge-transfer complex in a metal-organic framework for photocatalytic CO2 reduction in water. Nat. Commun. 14, 4508 (2023).
Johnson, B. A. & Ott, S. Diagnosing surface versus bulk reactivity for molecular catalysis within metal–organic frameworks using a quantitative kinetic model. Chem. Sci. 11, 7468–7478 (2020).
Yang, D. & Gates, B. C. Catalysis by metal organic frameworks: perspective and suggestions for future research. ACS Catal. 9, 1779–1798 (2019).
Titze, T. et al. Transport in nanoporous materials including MOFs: the applicability of Fick’s laws. Angew. Chem. Int. Ed. 54, 14580–14583 (2015).
Sharp, C. H. et al. Nanoconfinement and mass transport in metal–organic frameworks. Chem. Soc. Rev. 50, 11530–11558 (2021).
Hwang, S., Schneider, D., Haase, J., Miersemann, E. & Kärger, J. Quantifying diffusion-limited catalytic reactions in hierarchically structured porous materials by combining kinetic monte carlo simulations with the two-region model of diffusion. ChemCatChem 14, e202200829 (2022).
Grigoropoulos, A. et al. Encapsulation of Crabtree’s Catalyst in Sulfonated MIL-101(Cr): enhancement of stability and selectivity between competing reaction pathways by the MOF chemical microenvironment. Angew. Chem. Int. Ed. 57, 4532–4537 (2018).
Genna, D. T. et al. Rhodium hydrogenation catalysts supported in metal organic frameworks: influence of the framework on catalytic activity and selectivity. ACS Catal. 6, 3569–3574 (2016).
Roberts, J. M. et al. Urea metal–organic frameworks as effective and size-selective hydrogen-bond catalysts. J. Am. Chem. Soc. 134, 3334–3337 (2012).
Dai, S. et al. Highly defective ultra-small tetravalent MOF nanocrystals. Nat. Commun. 15, 3434 (2024).
Moore, S. C., Smith, M. R., Trettin, J. L., Yang, R. A. & Sarazen, M. L. Kinetic impacts of defect sites in metal–organic framework catalysts under varied driving forces. ACS Energy Lett. 8, 1397–1407 (2023).
Ding, J. et al. Defect engineered metal–organic framework with accelerated structural transformation for efficient oxygen evolution reaction. Angew. Chem. Int. Ed. 62, e202311909 (2023).
He, J. et al. Strategic defect engineering of metal–organic frameworks for optimizing the fabrication of single-atom catalysts. Adv. Funct. Mater. 31, 2103597 (2021).
Chen, W., Cai, P., Zhou, H.-C. & Madrahimov, S. T. Bridging homogeneous and heterogeneous catalysis: phosphine-functionalized metal-organic frameworks. Angew. Chem. Int. Ed. 63, e202315075 (2024).
Liang, Y. et al. A cage-on-MOF strategy to coordinatively functionalize mesoporous MOFs for manipulating selectivity in adsorption and catalysis. Nat. Commun. 14, 5223 (2023).
Karagiaridi, O., Bury, W., Mondloch, J. E., Hupp, J. T. & Farha, O. K. Solvent-assisted linker exchange: an alternative to the de novo synthesis of unattainable metal–organic frameworks. Angew. Chem. Int. Ed. 53, 4530–4540 (2014).
Wang, Y. et al. A tunable multivariate metal–organic framework as a platform for designing photocatalysts. J. Am. Chem. Soc. 143, 6333–6338 (2021).
Xia, Q. et al. Multivariate metal–organic frameworks as multifunctional heterogeneous asymmetric catalysts for sequential reactions. J. Am. Chem. Soc. 139, 8259–8266 (2017).
Rosen, A. S. et al. High-throughput predictions of metal–organic framework electronic properties: theoretical challenges, graph neural networks, and data exploration. npj Comput. Mater. 8, 112 (2022).
Darby, J. P. et al. Ab initio prediction of metal-organic framework structures. Chem. Mater. 32, 5835–5844 (2020).
Fan, W. et al. Fine-tuning the pore environment of the microporous Cu-MOF for high propylene storage and efficient separation of light hydrocarbons. ACS Cent. Sci. 5, 1261–1268 (2019).
Wilmer, C. E. et al. Large-scale screening of hypothetical metal–organic frameworks. Nat. Chem. 4, 83–89 (2012).
Li, P. et al. Synthesis of nanocrystals of Zr-based metal–organic frameworks with csq-net: significant enhancement in the degradation of a nerve agent simulant. Chem. Commun. 51, 10925–10928 (2015).
Kiyonaga, T. et al. Dependence of crystal size on the catalytic performance of a porous coordination polymer. Chem. Commun. 51, 2728–2730 (2015).
Wang, B., Liu, W., Zhang, W. & Liu, J. Nanoparticles@nanoscale metal-organic framework composites as highly efficient heterogeneous catalysts for size- and shape-selective reactions. Nano Res. 10, 3826–3835 (2017).
Hasegawa, S. et al. Three-dimensional porous coordination polymer functionalized with amide groups based on tridentate ligand: selective sorption and catalysis. J. Am. Chem. Soc. 129, 2607–2614 (2007).
Gascon, J., Aktay, U., Hernandez-Alonso, M. D., van Klink, G. P. M. & Kapteijn, F. Amino-based metal-organic frameworks as stable, highly active basic catalysts. J. Catal. 261, 75–87 (2009).
Trickett, C. A. et al. Definitive molecular level characterization of defects in UiO-66 crystals. Angew. Chem. Int. Ed. 54, 11162–11167 (2015).
Schaate, A. et al. Modulated synthesis of Zr-based metal–organic frameworks: from nano to single crystals. Chemistry 17, 6643–6651 (2011).
Liu, J. & Wöll, C. Surface-supported metal–organic framework thin films: fabrication methods, applications, and challenges. Chem. Soc. Rev. 46, 5730–5770 (2017).
So, M. C. et al. Layer-by-layer fabrication of oriented porous thin films based on porphyrin-containing metal–organic frameworks. J. Am. Chem. Soc. 135, 15698–15701 (2013).
Ikigaki, K., Okada, K. & Takahashi, M. Epitaxial growth of multilayered metal–organic framework thin films for electronic and photonic applications. ACS Appl. Nano Mater. 4, 3467–3475 (2021).
Stassen, I. et al. Chemical vapour deposition of zeolitic imidazolate framework thin films. Nat. Mater. 15, 304–310 (2016).
Barr, M. K. S. et al. Solution atomic layer deposition of smooth, continuous, crystalline metal–organic framework thin films. Chem. Mater. 34, 9836–9843 (2022).
Virmani, E. et al. On-surface synthesis of highly oriented thin metal–organic framework films through vapor-assisted conversion. J. Am. Chem. Soc. 140, 4812–4819 (2018).
Zhou, S. et al. Electrochemical synthesis of continuous metal–organic framework membranes for separation of hydrocarbons. Nat. Energy 6, 882–891 (2021).
Zhang, X. et al. Electrochemical deposition of metal–organic framework films and their applications. J. Mater. Chem. A 8, 7569–7587 (2020).
Panda, S., Kundu, S., Malik, P. & Haldar, R. Leveraging metal node-linker self-assembly to access functional anisotropy of zirconium-based MOF-on-MOF epitaxial heterostructure thin films. Chem. Sci. 15, 2586–2592 (2024).
Wang, Y. et al. Missing-node directed synthesis of hierarchical pores on a zirconium metal–organic framework with tunable porosity and enhanced surface acidity via a microdroplet flow reaction. J. Mater. Chem. A 5, 22372–22379 (2017).
Semrau, A. L. & Fischer, R. A. High-quality thin films of UiO-66-NH2 by coordination modulated layer-by-layer liquid phase epitaxy. Chemistry 27, 8509–8516 (2021).
Semrau, A. L. et al. Substantial turnover frequency enhancement of MOF catalysts by crystallite downsizing combined with surface anchoring. ACS Catal. 10, 3203–3211 (2020).
Arkhincheev, V. E. Generalized Fick law for anomalous diffusion in the multidimensional comb model. JETP Lett. 86, 508–511 (2007).
Fomin, S., Chugunov, V. & Hashida, T. Mathematical modeling of anomalous diffusion in porous media. Fract. Diff. Calculus 1, 1–28 (2011).
Crank, J. The Mathematics of Diffusion. 2nd edn, 69–88 (Oxford University Press, 1975).
Yang, Q. et al. Functionalizing porous zirconium terephthalate UiO-66(Zr) for natural gas upgrading: a computational exploration. Chem. Commun. 47, 9603–9605 (2011).
Vanommeslaeghe, K. et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 31, 671–690 (2010).
Darden, T., York, D. & Pedersen, L. Particle mesh Ewald: an N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 98, 10089–10092 (1993).
Hess, B. P-LINCS: a parallel linear constraint solver for molecular simulation. J. Chem. Theory Comput. 4, 116–122 (2008).
Bussi, G., Donadio, D. & Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101 (2007).
Abraham, M. J. et al. GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1-2, 19–25 (2015).
Acknowledgements
We acknowledge the intramural funding at TIFR Hyderabad from the Department of Atomic Energy (DAE), India, under Project Identification Number RTI 4007.
Author information
Authors and Affiliations
Contributions
S.P. and R.H. conceived the idea and planned the experiments, S.P. performed the experiments, characterization, and analysis with guidance from R.H., T.M., and A.K.M. carried out parts of the synthesis, S.S. performed the MD simulation with guidance from J.M., paper draft was prepared with the inputs from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Panda, S., Maity, T., Sarkar, S. et al. Diffusion-programmed catalysis in nanoporous material. Nat Commun 16, 1231 (2025). https://doi.org/10.1038/s41467-025-56575-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-56575-6