Flat-band enhanced antiferromagnetic fluctuations and superconductivity in pressurized CsCr₃Sb₅

Abstract

The spin dynamics and electronic orders of the kagome system at different filling levels stand as an intriguing subject in condensed matter physics. By first-principles calculations and random phase approximation analyses, we investigate the spin fluctuations and superconducting instabilities in kagome phase of CsCr₃Sb₅ under high pressure. At the filling level slightly below the kagome flat bands, our calculations reveal strong antiferromagnetic spin fluctuations in CsCr₃Sb₅, together with a leading s_±-wave and a competing (d_xy, ${d}_{{x}^{2}-{y}^{2}}$)-wave superconducting order. Unlike the general intuition that the flat bands are closely related to the ferromagnetic correlations, here we propose a sublattice-momentum-coupling-driven mechanism for the antiferromagnetic fluctuations enhanced from the unoccupied flat bands. The mechanism is generally applicable to kagome systems where the Fermi level intersects near the flat bands, offering a new perspective for future studies of geometrically frustrated systems.

Introduction

The kagome system has attracted significant research interest due to its highly frustrated nature. In the Mott limit, several theoretical proposals has been made for the possible topological quantum spin liquid phases in spin-1/2 kagome Heisenberg model^1,2,3. On the other hand, extensive investigations have also been carried out based on its unique electronic band structures away from the Mott limit. At the flat-band filling (>4/3 per site), the large degeneracy and nontrivial topology of the partially filled flat band could give rise to ferromagnetic (FM) ground state or fractional quantum Hall states^4,5,6,7; at the van Hove filling (2/3 ± 1/6 per site), the perfect Fermi surface (FS) nesting dominates the instability of the system, yielding exotic phases such as bond orders, density wave (DW), as well as their intertwining with superconducting (SC) orders^{8,9,10,11,12,13,14,15,16,17,18,19}; around the Dirac filling (~2/3 per site), the system could develop topological nontrivial phenomena such as anomalous quantum Hall effect and topological insulating phases^{20,21,22,23,24}. The interplay of electronic dynamics and geometry frustration in the kagome system opens up new frontiers for uncovering a wealth of exotic physical phenomena.

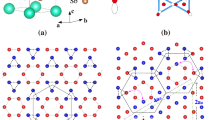
Recently, a new kagome compound CsCr₃Sb₅ was discovered²⁵. This compound features a structure analogous to that of the AV₃Sb₅ (A = K, Rb, Cs) family^26,27, as shown in Fig. 1a. At ambient pressure, CsCr₃Sb₅ exhibits a bad metal behavior and undergoes a DW-like phase transition at around 55 K. The DW phase can be gradually suppressed at pressure larger than 3.65 GPa, accompanied by an SC dome as well as non-Fermi-liquid behavior in the phase diagram. Nuclear magnetic resonance measurements and DFT calculations show that the DW transition is likely to have a magnetic nature^25,28, suggesting the close relation between the spin dynamics and possible unconventional superconductivity (USC) in CsCr₃Sb₅. In contrast to the isostructural AV₃Sb₅ compounds (A = K, Rb, Cs) whose low-energy physics is dominated by the saddle-point patches around the Fermi level (E_F)¹¹, CsCr₃Sb₅ is distinguished by the presence of incipient flat bands (IFBs). This presence has been supported by both experimental studies of angle-resolved photoemission spectroscopy measurements^29,30,31, as well as theoretical studies such as density functional theory (DFT) calculations^25,28, dynamical mean-field theory³², and slave-spin investigations³³. Previous theoretical studies in other systems have shown that the IFBs could substantially contribute to the virtual pair-scattering processes and play vital roles in the USC^34,35,36,37. Moreover, the interband processes between non-Kramers degenerated bands could also contribute to nontrivial quantum geometry and lead to enhanced FM fluctuations and possible spin-triplet SC pairings³⁸. Therefore, the presence of IFBs in CsCr₃Sb₅ offers us a unique opportunity to study the effects of flat-band physics on electronic correlations and superconductivity.

Fig. 1: Crystal and electronic structures for CsCr₃Sb₅ at 5 GPa.

a Crystal structure for CsCr₃Sb₅. b Top view of the kagome Cr-lattice. The local coordinates and atomic d orbitals are also shown for different Cr-sublattices. c Band structures and projected density of states for CsCr₃Sb₅. d The first Brillouin zone and high-symmetry lines for hexagonal CsCr₃Sb₅ lattice. e Fermi surfaces for CsCr₃Sb₅, plotted with FermiSurfer program⁵². The orbital contributions of Cr-d_yz, Cr-d_xz, and Cr-${d}_{{x}^{2}-{y}^{2}}$ in c, e are denoted by red, green, and blue color components, respectively. The crystal structures are constructed with the VESTA program⁵³.

In this paper, we present our first principles and random phase approximation (RPA) calculations for pressurized CsCr₃Sb₅. We begin by conducting RPA investigations on the Wannier-downfolded first-principles Hamiltonian at 5 GPa. To analyze superconducting (SC) instabilities, we employ a set of linearized SC gap equations. Our results indicate that the primary SC pairing channel in the pressurized CsCr₃Sb₅ exhibits s_±-wave symmetry, accompanied by a competing (d_xy, ${d}_{{x}^{2}-{y}^{2}}$)-wave channel. Our theoretical analysis further highlights the essential role of the IFBs in AFM electron correlations. In the following discussions, we introduce a microscopic mechanism for the flat-band-enhanced antiferromagnetic (AFM) fluctuations in CsCr₃Sb₅, which incorporates the sublattice-momentum coupling (SMC) of both occupied dispersive bands and unoccupied IFBs. We note that the electron susceptibilities are treated within the weak-coupling RPA scenario in this paper, thus the AFM spin fluctuations have an itinerant nature and should be understood as SDW modes. This mechanism well explains the observed enhancement of AFM spin fluctuations in numerical calculations. It is also anticipated to be broadly applicable to kagome and other geometrically frustrated systems.

Results

First-principles calculations

We first conducted first-principles structural optimizations on CsCr₃Sb₅ under external pressure of 5 GPa. The relaxation yields a hexagonal lattice with parameters of a  =  5.272 Å, c  = 8.400 Å. The band structures and projected density of states for the optimized structure are shown in Fig. 1c. Evidently, most bands near E_F are mainly contributed by the Cr-d_xz, Cr-d_yz, and Cr-${d}_{{x}^{2}-{y}^{2}}$ orbitals. As shown in Fig. 1e, the d_yz orbitals form a quasi-two-dimensional (Q2D) cylindrical Fermi surface around the Γ point (namely, the α band); while around the L point, the d_xz orbitals strongly hybridize with the d_yz orbitals and form six three dimensional (3D) FS pockets (β band). Surrounding the Q2D cylindrical FS, the ${d}_{{x}^{2}-{y}^{2}}$ orbitals form another set of six separated ridge-shaped FS sheets (γ band). It is notable that at E − E_F ~0.3 eV, the d_xz orbitals hybridize with d_yz and form an extremely flat band within the k_y  = 0 plane (as illustrated by Γ-M-L-A segments). Such a flat band is responsible for the highest DOS peak shown on the right-hand side of Fig. 1c. It can also be shown to arise from the frustrated geometry of the kagome Cr-lattice³⁹ (please refer to Supplementary Materials). In fact, two sets of moderately distorted kagome bands could be recognized from the CsCr₃Sb₅ band structures near E_F (please refer to Supplementary Materials), with filling levels slightly below the IFBs. We will show later that the interband processes between the IFBs and the highest dispersive band (HDB) substantially contribute, and more interestingly, determine the momentum dependence of spin fluctuations and SC orders in CsCr₃Sb₅.

RPA analyses

To explore the instabilities in the pressurized CsCr₃Sb₅, we conducted RPA analyses on the DFT-calculated electronic structures. Our calculations stem from a model Hamiltonian of $H={H}_{0}+{\sum }_{\tau }{H}_{int}^{\tau }$. Here H₀ is the non-interacting Hamiltonian obtained from Wannier downfolding, for which 30 locally defined Cr-3d and Sb-5p atomic orbitals are adopted as initial guess. The interacting ${H}_{int}^{\tau }$ is considered for the Cr sites, and is given by:

$${H}_{int}^{\tau }=U\sum\limits_{i}{n}_{i\uparrow }{n}_{i\downarrow }+{U}^{{\prime} }\sum\limits _{i < j}{n}_{i}{n}_{j}+J\sum\limits _{i < j,\sigma,{\sigma }^{{\prime} }}{c}_{i\sigma }^{{\dagger} }{c}_{j{\sigma }^{{\prime} }}^{{\dagger} }{c}_{i{\sigma }^{{\prime} }}{c}_{j\sigma }+{J}^{{\prime} }\sum\limits _{i\ne j}{c}_{i\uparrow }^{{\dagger} }{c}_{i\downarrow }^{{\dagger} }{c}_{j\downarrow }{c}_{j\uparrow },$$

(1)

where i, j are the d-orbital indices within site τ. It is worth noting that all the obtained Cr-d Wannier orbitals are well-localized (with spreading of only  ~1.5 Ų) and their atomic symmetries are well maintained. Therefore we can adopt symmetry relations that $J={J}^{{\prime} }$, $U={U}^{{\prime} }+2J$, which is also consistent with our constrained RPA (cRPA) results. The bare electron, spin, and charge susceptibilities are then calculated using:

$${{\chi }_{0}}_{st}^{pq}\left({{\bf{Q}}},i{\nu }_{m}\right)=-\frac{1}{N\beta }\sum \limits_{{{\bf{k}}},i{\omega }_{n}}{G}_{sp}\left({{\bf{k}}},i{\omega }_{n}\right){G}_{qt}\left({{\bf{k}}}+{{\bf{Q}}},i{\omega }_{n}+i{\nu }_{m}\right),$$

(2)

$${\chi }_{{{\rm{S}}}}={\chi }_{0}{\left(1-{U}_{{{\rm{S}}}}{\chi }_{0}\right)}^{-1},$$

(3)

$${\chi }_{{{\rm{C}}}}={\chi }_{0}{\left(1+{U}_{{{\rm{C}}}}{\chi }_{0}\right)}^{-1}.$$

(4)

Here we have restricted our calculations to the real part of the iν_m  =  0 term⁴⁰. We shall focus on the property of the susceptibility matrix block χ^dd that contracts with the Coulomb interaction vertices (i.e., pq, st ∈ nonzero U matrix indices), since they will dominate the spin and charge susceptibilities near the critical point.

Figure 2a–c show the calculation results under U  = 0.95 eV, J/U = 0.4, at β  = 1000 eV⁻¹. In Fig. 2a, a set of V-shaped peaks around the M points and a set of ring-shaped peaks surrounding the interior of the first Brillouin zone could be distinguished for the leading eigenvalue of ${\chi }_{0}^{dd}$. Among them, three peaks at Q₁  =  (0.0, 0.41, 0.0), Q₂  =  (−0.06, 0.5, 0.0), and Q₃ =  (0.2, 0.34, 0.0) are intimately connected to the FS nesting. As shown in Fig. 2e, Q₁, Q₂, and Q₃ correspond to the inter-pocket scattering between α and β bands, inter-pocket scattering between different β band FS pockets, and intra-pocket scattering within α band, respectively. As the interactions are switched on, the peaks are generally enhanced in ${\chi }_{{{\rm{S}}}}^{dd}$ and suppressed in ${\chi }_{{{\rm{C}}}}^{dd}$, indicating the dominance of the spin fluctuations over charge ones. Specifically, the peaks at Q₁ and Q₂ exhibit more pronounced amplifications than Q₃. In the context of spin-fluctuation mediated SC paring, the strong enhancement at Q₁ and Q₂ implies strong repulsive pairing interactions between different FS pockets. Note that the pair scatterings of Q₁ favor a sign change between α and β bands, while the scatterings of Q₂ favor a sign change between different FS pockets of β band. The interplay of various scattering processes then indicates a possible competition between different SC orders in CsCr₃Sb₅^40,41.

Fig. 2: Results for RPA analyses.

a–c The largest eigenvalues for calculated bare electron (${\chi }_{0}^{dd}$), spin (${\chi }_{{{\rm{S}}}}^{dd}$), and charge (${\chi }_{{{\rm{C}}}}^{dd}$) susceptibilities, under U =  0.95 eV, J/U  =  0.4, 1/β  =  1 meV. d The RPA phase diagram in terms of the leading instabilities. The purple star denotes the interactions estimated from the constrained RPA method (i.e., U  = 0.95 eV, J/U = 0.4). e Nesting vectors of the Fermi surface, plotted with a superconducting gap of the s_± phase. f–h Superconducting gap functions for the leading solutions.

The spin-fluctuation mediated SC gap symmetries are then investigated by solving the linearized gap equations. As shown in Fig. 2d, under moderate U (0.5–1.2 eV), the leading gap symmetry is mainly tuned by the ratio of J/H. When J/H is large, the system tends to form an SC gap with A_1g symmetry (i.e., the s_±-wave solution shown in Fig. 2f). When J/H is small, on the other hand, the SC gap with E_2g symmetry [the (d_xy, ${d}_{{x}^{2}-{y}^{2}}$)-wave in Fig. 2g, h] takes place as the leading solution. To gain insight into the SC gap symmetry in the experimental system, we performed cRPA calculations to estimate the interaction parameters in the pressurized CsCr₃Sb₅. The average interaction parameters are U  =  0.95 eV and J/U  =  0.4, indicating that the system resides within the s_±-wave region. Fig. 2f illustrates the FS distribution of the gap function for the s_±-wave solution. There is no sign change on the α-pocket, consistent with a common understanding of s-wave. However, within each β FS patch, it reveals an intriguing sign-changing character. In this s_±-wave SC phase, line nodes exist without crystal symmetry breaking. Such a feature could be detected through the deviation of full-gap behavior in heat capacity and penetration depth measurements⁴². Furthermore, for the competing d-wave solution, there is a degree of freedom in forming linear combinations of the d_xy and ${d}_{{x}^{2}-{y}^{2}}$ bases. This can result in nematic d_xy and ${d}_{{x}^{2}-{y}^{2}}$ phases that break the rotational symmetry, or the chiral d ± id phases that break the time-reversal symmetry (TRS)^43,44. The symmetry of SC order in CsCr₃Sb₅ could be further identified via spatial anisotropic experiments such as angle-resolved critical field measurements, as well as TRS-sensitive experiments such as muon spin rotation and polar Kerr effect studies^45,46.

Role of incipient flat bands

From the result of our first-principles calculations, we have manifested the presence of IFBs in CsCr₃Sb₅ (as highlighted in Fig. 3a). Given the fact that these bands contribute to prominent DOS peaks around E_F, it is therefore natural to explore their role in the aforementioned scenario of superconductivity in CsCr₃Sb₅. In fact, the significance of the IFBs has been usually investigated as incipient flat parts of a dispersive band^36,37. Here we emphasize that, even if the full part of the IFBs are flat and unoccupied, they still substantially affect the momentum dependence of spin fluctuations and thus are critical to the SC orders in CsCr₃Sb₅.

Fig. 3: Momentum selective contributions to the spin fluctuations from the unoccupied incipient flat bands (IFBs).

a Band structure for CsCr₃Sb₅. The unoccupied and partially occupied incipient flat bands are highlighted by orange and purple lines, respectively. b The largest eigenvalues for spin and bare electron susceptibility with and without unoccupied IFBs. c, d Leading eigenvalues of the linearized gap equations calculated with and without unoccupied IFBs, respectively.

To elucidate the crucial role of unoccupied IFBs, we conducted calculations both with and without the unoccupied IFBs for comparison. As shown in Fig. 3b, strikingly, the AFM peaks of spin susceptibility ${\chi }_{S}^{dd}$ are significantly suppressed after we exclude the unoccupied IFBs, leaving a rather broad hump around the Γ point. The result clearly demonstrates that the AFM fluctuations are selectively and substantially contributed by the unoccupied IFBs. As a consequence, the spin-fluctuation-mediated SC orders are also significantly altered. Fig. 3c, d depict the leading solutions of linearized gap equations calculated with and without unoccupied IFBs, respectively. It is evident that without the unoccupied IFBs, the AFM spin-fluctuation mediated solutions (e.g., the s_±-wave and the d-wave solutions) are remarkably suppressed. In contrast, owing to the surviving FM fluctuations, two spin-triplet solutions of E_1u (p-wave) and B_1u (f-wave) symmetries are stabilized and turn out to be the leading SC orders.

The IFB-induced enhancement of the AFM spin fluctuations is a ubiquitous feature for Kagome systems where the E_F resides between the flat bands and the dispersive bands. As shown in Fig. 4b, for the kagome Hubbard model at a filling level of n  =  3.6 (i.e., 1.2 electron per site), the spin susceptibility χ_S exhibits a ring-shaped peak set which originates from the two-dimensional cylindrical FS. When we move E_F closer to the flat band by upshifting the filling level to n  =  3.7 and 3.8 (Fig. 4c, d), the size of the ring gradually shrinks as the FS shrinks towards the Γ point. Even more prominently, another set of AFM peaks around the K points emerges and quickly becomes dominant, thus the ring-shaped structure is difficult to be distinguished from the background in Fig. 4d. The ring-shaped structure can be clearly identified in calculations excluding the contributions from the flat bands (Figs. 4e-g) or by switching off the Hubbard U terms (Fig. 4h). In either cases, the AFM peaks around the K points disappear. Therefore the enhancement of AFM fluctuations should be a consequence of the combination of both the flat band and the local Coulomb interaction.

Fig. 4: Flat-band induced enhancement of the AFM spin fluctuations in kagome Hubbard model.

a Band structure of the ideal kagome model. The green, blue, and red dash-dot lines correspond to the Fermi level at filling levels of n  =  3.6, 3.7, and 3.8, respectively. b–g Leading eigenvalues of spin susceptibilities for the kagome Hubbard model under different filling levels, calculated at U  =  2t. b–d are calculated with all three bands, e–g are calculated without the flat band. h Leading eigenvalues of the bare electron susceptibility at filling level of n = 3.8. The black arrows point to the ring-shaped peak sets originating from the Fermi surface nesting, which do not vary upon excluding the flat band, while the AFM peaks around the K points are intimately related to the flat band.

Discussion

To comprehend the embedding mechanism behind the IFB-induced momentum-dependent enhancement of spin fluctuations, we rewrite Eq. (2) into the spectral form that:

$${{\chi }_{0}}_{st}^{pq}({{\bf{Q}}})=-\frac{1}{N}\sum\limits _{{{\bf{k}}},\mu \nu }\frac{f\left({E}_{{{\bf{k}}}+{{\bf{Q}}},\nu }\right)-f\left({E}_{{{\bf{k}}},\mu }\right)}{{E}_{{{\bf{k}}}+{{\bf{Q}}},\nu }-{E}_{{{\bf{k}}},\mu }+{{\rm{i}}}{0}^{+}}\times \langle s| {{\bf{k}}},\mu \rangle \langle {{\bf{k}}},\mu | p\rangle \langle q| {{\bf{k}}}+{{\bf{Q}}},\nu \rangle \langle {{\bf{k}}}+{{\bf{Q}}},\nu | t\rangle,$$

(5)

where f(E) is the Fermi-Dirac distribution function, μ and ν are band indices. For the channels involving unoccupied IFBs (without loss of generality, here we set ν to be the band index for unoccupied IFBs), $f\left({E}_{{{\bf{k}}}+{{\bf{Q}}},\nu }\right)$ is fixed to be 0 and E_k+Q,ν is nearly a constant. Therefore, the Lindhard function [i.e., the $\frac{f\left({E}_{{{\bf{k}}}+{{\bf{Q}}},\nu }\right)-f\left({E}_{{{\bf{k}}},\mu }\right)}{{E}_{{{\bf{k}}}+{{\bf{Q}}},\nu }-{E}_{{{\bf{k}}},\mu }+{{\rm{i}}}{0}^{+}}$ part] has negligible momentum dependence and the AFM feature should mainly emerge from the orbital or site degrees of freedom.

Figure 5a, b show the sublattice character for the ideal kagome bands and CsCr₃Sb₅ mirror-odd downfolded bands (which is responsible for the leading fluctuation channel in CsCr₃Sb₅, see Supplemental Materials for detail), respectively. Evidently, the sublattice degree of freedom is strongly coupled to the momentum and exhibits a similar SMC pattern for both the ideal kagome model and CsCr₃Sb₅. For the flat band, the sublattice-A weight is mainly distributed around the Γ-K₁ line; while for the HDB, the sublattice-A weight peaks around the M₂ point. When the Fermi level cuts the top of the HDB and makes the flat band incipient, the SMC pattern will be encoded in the interband processes and become crucial for the spin fluctuations of the system.

To see how the SMC feature affects the spin susceptibilities in the presence of local Coulomb interactions, let’s consider two processes depicted by the Feynman diagrams in Fig. 5c. As highlighted by the red rectangles in Fig. 5c, the indices of paramagnons [i.e., (${p}^{{\prime} }$, ${q}^{{\prime} }$) or (${s}^{{\prime} }$, ${t}^{{\prime} }$) in Fig. 5c] are restricted to the same site by the locality of Coulomb interactions. The restriction requires that the propagators of both k and k  +  Q must have the same sublattice component. Therefore, for the Dyson series shown in the upper diagram of Fig. 5c, the correlators for intra-sublattice paramagnons are selectively enhanced. And for the SC pairing vertex shown in the lower diagram of Fig. 5c, only intra-sublattice paramagnon correlators are picked out to contribute to the SC pairing. As illustrated in Fig. 5d, in the kagome lattice, the sublattice weight separation in occupied (dispersive) and unoccupied (flat) bands makes the paramagnons of Q  =  Γ inter-sublattice. Thus only intra-sublattice channels at Q ≠ Γ are involved in the diagrammatic summation of Fig. 5c. As a consequence, the AFM fluctuations are selectively enhanced by the local Coulomb interactions.

Fig. 5: Sublattice-momentum coupling as a driving mechanism for the AFM fluctuations.

a, b Band structures and sublattice projections for Cr_A in ideal kagome model and downfolded M_z-odd Wannier Hamiltonian of CsCr₃Sb₅, respectively. c Feynman diagrams for the Dyson series and the pairing vertex of RPA calculations. The locality of the Coulomb interactions is emphasized by the red rectangles. d Schematic illustration for the SMC-driven mechanism of the AFM enhancement in the ideal kagome model: The dominant inter-sublattice correlator at Q =  Γ does not appear in the Wick contractions of the local Coulomb interactions, while the intra-sublattice correlator at Q ≠ Γ does.

The SMC is a general feature for the line graphs of planar bipartite lattices⁵. In fact, similar k-space sublattice weighting could also be observed for other kagome systems such as CsV₃Sb₅ and CoSn^18,47. In CsV₃Sb₅, the SMC manifests as a set of p-type vHSs (where the saddle-point states correspond one-to-one with the sublattice sites), alongside a set of m-type vHSs (where two of the three sublattice components mix at each saddle point). The interplay between the SMC and FS nesting in CsV₃Sb₅ yields a unique sublattice interference character which selectively shapes the contributions of different Coulomb interaction components^11,18. In CsCr₃Sb₅, on the other hand, the kagome IFBs have a more pronounced influence on the system’s low-energy physics. Due to their flatness and unoccupied nature, these IFBs lead to a stronger coupling of the SMC with the locality of Coulomb interactions, which results in a selective impact on the momentum of the leading fluctuation channels. In addition, due to the self-doping effect between the Sb1-p_z orbitals and the Cr-d orbitals, the position of IFBs in CsCr₃Sb₅ is relatively inertia to external pressure, and thus the SMC mechanism is expected to be present in this compound within a wide range of pressure (see Supplementary Materials for details). The SMC in these systems establishes a connection between the reciprocal space band structures and the real-space patterns of Coulomb interactions and spin/charge orders. We anticipate that it can be further utilized to explore a wider variety of novel physical phenomena in geometrically frustrated systems.

In conclusion, we have performed first-principles calculations and RPA investigations on pressurized CsCr₃Sb₅, at an external pressure of 5 GPa. Our calculations reveal strong AFM fluctuations in CsCr₃Sb₅, which mediate a dominating s_±-wave and a competing (d_xy, ${d}_{{x}^{2}-{y}^{2}}$)-wave SC order. Under the dominance of local Coulomb interactions, the k-space sublattice weight separation of occupied bands and unoccupied IFBs inhibits the formation of intra-sublattice FM fluctuations and thus selectively enhances the AFM fluctuations. Such SMC-enhanced AFM mechanism is expected to widely exist in kagome systems where the Fermi level resides between IFBs and dispersive bands, and may also apply to other geometrically frustrated systems.

Methods

First-principles calculations

The first-principles calculations are performed with density functional theory (DFT), as implemented in the Vienna Ab initio Simulation Package (VASP)⁴⁸. The Kohn-Sham wave functions are represented under projected augmented wave (PAW) basis⁴⁹. The crystal structure of CsCr₃Sb₅ is optimized at an external pressure of 5 GPa, with a solid revised Perdew–Burke–Ernzerhof (PBEsol) exchange-correlation functional⁵⁰. For the self-consistent and density of state (DOS) calculations, we employed a 12  × 12 ×  8 and a 24  ×  24  ×  12 Γ-centered k mesh respectively. Our tight-binding Hamiltonian is then constructed via Wannier downfolding⁵¹, where 30 atomic-like projectors of 15 Cr-d and 15 Sb-p are adopted as initial seeds. The local axes are set so that the three Cr sites are connected by successive C₃ rotations, as shown in Fig. 1b. Details of band structure downfolding are given in the Supplemental Materials.

Random-phase approximation analysis

Our RPA calculations begin from the model Hamiltonian that:

$$H={H}_{0}+\sum\limits _{\tau }\left[U\sum \limits_{i}{n}_{\tau,i\uparrow }{n}_{\tau,i\downarrow }+{U}^{{\prime} }\sum\limits _{i < j}{n}_{\tau,i}{n}_{\tau,j}+J\sum \limits_{i < j,\sigma,{\sigma }^{{\prime} }}{c}_{\tau,i\sigma }^{{\dagger} }{c}_{\tau,j{\sigma }^{{\prime} }}^{{\dagger} }{c}_{\tau,i{\sigma }^{{\prime} }}{c}_{\tau,j\sigma }\right.\\ \left.+{J}^{{\prime} }\sum \limits_{i\ne j}{c}_{\tau,i\uparrow }^{{\dagger} }{c}_{\tau,i\downarrow }^{{\dagger} }{c}_{\tau,j\downarrow }{c}_{\tau,j\uparrow }\right],$$

(6)

where H₀ is the bare-election tight-binding Hamiltonian obtained from Wannier downfolding; τ is the Cr site index, i, j are d orbital indices for each Cr. The Coulomb parameters follow the general symmetry relation that $J={J}^{{\prime} }$, $U={U}^{{\prime} }+2J$.

The bare electron susceptibility is calculated using:

$${{\chi }_{0}}_{st}^{pq}({{\bf{q}}},{{\rm{i}}}{\nu }_{m})=-\frac{1}{{N}_{{{\bf{k}}}}\beta }\sum\limits _{n,{{\bf{k}}}}{G}_{sp}({{\rm{i}}}{\omega }_{n},{{\bf{k}}}){G}_{qt}({{\rm{i}}}{\omega }_{n}+{{\rm{i}}}{\nu }_{m},{{\bf{k}}}+{{\bf{q}}}),$$

(7)

where iω_n and iν_m are fermionic and bosonic Matsubara frequencies respectively; p, q, s, t are orbital indices; ${G}_{sp}({{\rm{i}}}{\omega }_{n},{{\bf{k}}})={\sum }_{\mu }\frac{\langle s| {{\bf{k}}},\mu \rangle \langle {{\bf{k}}},\mu | p\rangle }{{{\rm{i}}}{\omega }_{n}-{E}_{{{\bf{k}}},\mu }}$ is the bare electron propagator. We have adopted a 100  × 100  ×  30 Q mesh and $\frac{1}{\beta }=$ 0.001 eV for the calculations.

For spin and charge susceptibilities, we employ a matrix random-phase approximation (RPA) formula that:

$${\chi }_{{{\rm{S}}}}={\chi }_{0}{\left(1-{U}_{{{\rm{S}}}}{\chi }_{0}\right)}^{-1},$$

(8)

$${\chi }_{{{\rm{C}}}}={\chi }_{0}{\left(1+{U}_{{{\rm{C}}}}{\chi }_{0}\right)}^{-1}.$$

(9)

The matrix elements for spin and charge vertices are:

$${{U}_{{{\rm{S}}}}}_{st}^{pq}=\left\{\begin{array}{cc}U,\quad &p=q=s=t,\\ J,\quad &p=q\,\ne\, s=t,\\ J,\quad &p=t\,\ne\, q=s,\\ {U}^{{\prime} },\quad &p=s\,\ne\, q=t,\end{array}\right.\quad {{U}_{{{\rm{C}}}}}_{st}^{pq}=\left\{\begin{array}{cc}U,\hfill \quad &p=q=s=t,\\ 2{U}^{{\prime} }-J,\hfill \quad &p=q \,\ne\, s=t,\\ J,\hfill \quad &p=t \,\ne\, q=s,\\ 2J-{U}^{{\prime} },\quad &p=s \,\ne\, q=t.\end{array}\right.$$

(10)

The superconducting (SC) pairing vertex functions for spin-singlet and spin-triplet channels are then calculated by:

$$ {V}^{{{\rm{singlet}}}}({{{\bf{k}}}}^{{\prime} }q,-{{{\bf{k}}}}^{{\prime} }s;{{\bf{k}}}p,-{{\bf{k}}}t)=\frac{1}{4}{(3{U}_{{{\rm{S}}}}+{U}_{{{\rm{C}}}})}_{st}^{pq} \\ +\left\{\frac{1}{4}{\left[3{U}_{{{\rm{S}}}}{\chi }_{{{\rm{S}}}}({{{\bf{k}}}}^{{\prime} }-{{\bf{k}}}){U}_{{{\rm{S}}}}-{U}_{{{\rm{C}}}}{\chi }_{{{\rm{C}}}}({{{\bf{k}}}}^{{\prime} }-{{\bf{k}}}){U}_{{{\rm{C}}}}\right]}_{st}^{pq}+({{\bf{k}}}p\leftrightarrow -{{\bf{k}}}t)\right\},$$

(11)

$$ {V}^{{{\rm{triplet}}}}({{{\bf{k}}}}^{{\prime} }q,-{{{\bf{k}}}}^{{\prime} }s;{{\bf{k}}}p,-{{\bf{k}}}t)=\frac{1}{4}{\left(-{U}_{{{\rm{S}}}}+{U}_{{{\rm{C}}}}\right)}_{st}^{pq}\\ -\left\{\frac{1}{4}{\left[{U}_{{{\rm{S}}}}{\chi }_{{{\rm{S}}}}({{{\bf{k}}}}^{{\prime} }-{{\bf{k}}}){U}_{{{\rm{S}}}}+{U}_{{{\rm{C}}}}{\chi }_{{{\rm{C}}}}({{{\bf{k}}}}^{{\prime} }-{{\bf{k}}}){U}_{{{\rm{C}}}}\right]}_{st}^{pq}-({{\bf{k}}}p\leftrightarrow -{{\bf{k}}}t)\right\}.$$

(12)

Here we only take the zero-frequency component of χ. Note that in the SC pairing vertex calculations, only pq, st  ∈ nonzero U matrix indices contribute to the result. Thus we can restrict our calculations to the matrix block of these indices. Here we denote the matrix block by χ^dd. It is straightforward to see that we can simplify the calculations by replacing all χ₀, χ_S, and χ_C matrices with only dd block in (7–12) without any loss of the SC pairing vertex Information.

The weak-coupling SC gap equation is then constructed as⁴⁰:

$$\lambda \Delta ({{{\bf{k}}}}^{{\prime} })=-\frac{1}{{V}_{{{\rm{BZ}}}}}{\int}_{FS}\frac{{{{\rm{d}}}}^{2}{k}_{\parallel }}{| {v}_{{{\bf{k}}}}^{\perp }| }V({{{\bf{k}}}}^{{\prime} },{{\bf{k}}})\Delta ({{\bf{k}}}),$$

(13)

where the integration is done over the Fermi surface (FS), ${v}_{{{\bf{k}}}}^{\perp }$ corresponds to the Fermi velocity of the FS k points.