Introduction

Gas sensors, enhancing our olfactory capabilities, are prized for their reliability and sensitivity, with critical roles in air quality1,2,3,4, medical analysis5,6,7, and industrial monitoring8,9,10. Among gas sensors, the chemiresistive sensors are favored due to their small size, ease of manufacturing, simple operation, and their cost-effectiveness. Nonetheless, the principle that enables chemiresistive sensors to detect gases is based on alterations of resistance in different gaseous environments, which makes them vulnerable to temperature changes11,12,13,14. Such variations will cause a drift in the baseline resistance of R0, thereby compromising the precision of the sensor. Incorporating temperature compensation components into the sensor can mitigate issues arising from temperature variations15,16. However, this approach typically requires extra circuitry or complex algorithms, rasing cost of the overall device. Incorporating a self-tuning technique into a single material to achieve temperature compensated detection represents a formidable challenge.

Ratiometry measurement is an analytical technique that enhances measurement precision by comparing the ratio of signal intensities from two or more distinct signals17,18,19. This approach effectively reduces errors due to varying experimental conditions. Therefore, incorporating ratiometry measurement into gas-sensitive sensors presents a promising strategy to overcome the challenge of device accuracy loss due to baseline drift from temperature changes. Indeed, discovering a suitable reference factor that neutralizes baseline drift is essential for the ratiometric-gas sensor. In this regard, we present a ratiometric approach that cleverly employs the photoelectric response (Rph) of a material as an internal reference to its gas-sensitive response (Rgas). This innovative strategy relies on the synthesis of a material that exhibits high activity to both light of particular wavelength and target gaseous molecules, traditionally a challenging task given the contrasting design principles of gas and light sensing materials. Gas sensors typically depend on defects for sensing activity20,21,22,23, whereas light sensors are designed to minimize defects to improve photoelectric performance24,25,26,27. A thorough comprehension to harmonize the competing demands of gas sensing and photoelectric functionality in one material is still out of reach.

Emerging as a promising class of gas sensing materials, organic-inorganic hybrid covalent superlattice materials28,29 are poised to redefine the balance between gas sensitivity and photoelectric performance. This is due to: (1) The distinctive multi-quantum well structure of the superlattice, which gives rise to quantum confinement effects, and amplifies the photoelectric response30,31,32,33,34,35. (2) The surface of the organic-inorganic hybrid covalent superlattice is covered with long-range ordered functional groups, which can replace the defects of traditional materials, provide abundant active sites for gas detection, and significantly improve the sensitivity of the gas sensor36. Thus, organic-inorganic hybrid covalent superlattices are anticipated to deliver both robust photoelectric and gas sensing responses. Consequently, the application of this material for ratiometric-gas sensing could mitigate temperature-dependent interference.

Here, we introduce an organic-inorganic hybrid covalent superlattice material AgBDT (BDT = 1,4-benzenedithiol), which functions as a high-efficiency ratiometric gas sensing material. The two-dimensional continuous inorganic [AgS]n layers are interspersed by organic benzene rings, creating a distinctive multi-quantum well structure that lays the platform for an enhanced photoelectric response. The surface of AgBDT covered with long range ordered sulfhydryl functional groups endows it with exceptional sensitivity to nitrogen dioxide (NO2). Specifically, NO2 can be stably adsorbed on AgBDT nanosheets through Lewis acid-base interaction and hydrogen bonding with thiol groups. For the strong electron-withdrawing ability of NO2, electrons can be extracted from AgBDT and transferred to NO2, leading to a resistivity change of AgBDT. Leveraging its superior photoelectric and gas sensitivity properties, a ratiometric approach was formulated to gas sensing analysis (Fig. 1). This method shows that the ratio values are highly responsive to changes in gas concentration indicating the potential of NO2 gas detecting capability of AgBDT. The detection limit of ratiometric gas sensor is 3.06 ppb. Notably, this ratiometric gas sensing is impervious to operational temperature fluctuations, achieving a substantial reduction in the coefficient of variation (CV) value from 21.81% to 7.81%, greatly refining the precision of gas detection (limit of detection, LOD).

Fig. 1: Schematic design of superlattice materials for ratiometric-gas sensing detection.
figure 1

a The gas sensing response process. The concentration of hole carriers is influenced by gas concentration, which is depended on temperature changes. b The photo-response process. The concentration of hole carriers is affected by optical excitation, which is affected by temperature. c The ratiometric-gas sensing detection. The ratiometric-gas sensing response is the ratio of the gas-sensitive response to the photoelectric response, which is virtually unaffected by temperature changes. Ag: red; S: blue; C: gray; H: green.

Full size image

Results and discussion

The characterization of AgBDT obtained from the hydrothermal method

The nanosheets suitable for 3D electron rotation diffraction (3D ED) were synthesized by hydrothermal approach. Scanning electron microscopy (SEM) measurements revealed the rhombic morphology of the as-prepared AgBDT nanosheet with a length of several micrometers and a thickness of approximately ~120 nm (Fig. S1). Diffraction data revealed that AgBDT crystallized in the monoclinic space group P21/c (Fig. S2 and Table S1, supporting information). As depicted in Fig. 2a, each Ag+ ion coordinates with four S atoms to form a distorted AgS4 tetrahedron, which is further connected by sharing edges with adjacent tetrahedra to form a two-dimensional (2D) {AgS}n layer within the bc plane. In {AgS}n layer, silver atoms construct graphene-like configurations via Ag···Ag interactions, which is advantageous for optoelectronic applications37. The thickness of a single {AgS}n monolayer is approximately ~0.9 nm. The {AgS}n layers are further integrated through benzene by S–C covalent bonds, creating a 3D covalent superlattice with periodically stacked inorganic and organic sublattices (Fig. 2a). The high-resolution TEM (HRTEM) image (Fig. S3) shows the clear superlattice fringes with a spacing of 0.86 nm, corresponding to the lattice distance of the (100) plane of 0.88 nm. The surface of AgBDT nanosheets is adorned with uncoordinated sulfhydryl groups, as confirmed by X-ray photoelectron spectroscopy (XPS) spectrum (Fig. 2b, c). Powder X-ray diffraction (PXRD) patterns confirmed the crystallinity of AgBDT nanosheets, aligning well with simulated patterns from 3D electron diffraction (Fig. 2d), which suggested high phase purity of the AgBDT nanosheets. Additionally, elemental mapping via energy-dispersive X-ray spectroscopy (EDS) validated the uniform distribution of Ag, S, and C elements (Fig. S4).

Fig. 2: Basic characterizations of AgBDT (BDT = 1,4-benzenedithiol) nanosheets.
figure 2

a The packing structure of AgBDT covalently connected by the organic layer (left) and 2D {AgS}n inorganic layer (right) (hydrogen atoms are omitted for clarity). b X-ray photoelectron spectroscopy (XPS) spectra of Ag 3d and c S 2p for AgBDT. d Powder X-ray diffraction (PXRD) pattern. e Ultraviolet-Visible Spectroscopy (UV-vis) absorbance spectrum. Inset is the corresponding Tauc plot of UV–vis absorbance spectrum. f Ultraviolet photoelectron spectroscopy (UPS). Inset are the secondary electron cut off edge measured with He I (hν = 21.22 eV) and valence band of AgBDT with respect to the Fermi level (EF = 0). g Calculated band structure and projected density of states (PDOS). h Temperature-dependent I–V curves. Inset is the relationship between conductivity and temperature. i Arrhenius plots of conductivity. Source data are provided as a Source Data file.

Full size image

The optical bandgap of AgBDT, determined to be 2.56 eV (Fig. 2e) using ultraviolet-visible diffuse reflectance spectroscopy (UV–Vis), and the valence band position, ascertained through ultraviolet photoelectron spectroscopy (UPS), confirmed the p-type semiconductor nature of AgBDT (Figs. 2e, f and S5). Density functional theory (DFT) calculations (Details in ESI and Fig. S6) revealed that AgBDT exhibited an indirect bandgap structure (Fig. 2g). The valence band maximum (VBM) and conduction band minimum (CBM) are primarily constituted by the {AgS}n layer, with contributions from the d orbital of Ag and p orbital of S (Fig. S7). These findings suggest that the {AgS}n layers were separated by the benzene ring to form a multi-quantum well structure, which significantly affects the photoelectric properties.

The semiconductor properties of AgBDT were characterized by the standard two-probe method. The conductivity of AgBDT increased from 1.32 × 10−10 up to 3.81 × 10−9 S cm−1 across the temperature range of 303–383 K, indicating its typical semiconductive characteristic (Fig. 2h). Furthermore, the excellent linearity of ln(σ) versus 1000/T implies that AgBDT exhibits thermally activated band-like transport properties (Fig. 2i).

The gas sensing, photoresponse and ratiometric-gas sensing performances of AgBDT

The robust electron transfer facilitated by the sulfhydryl groups and NO2 endows the covalent superlattice material with an ultra-sensitive gas-sensing response to NO236. AgBDT stands out as an ideal candidate for the construction of chemiresistive gas sensors. The sensors were fabricated by depositing AgBDT nanosheets onto interdigitated electrodes using a drop-casting technique (Fig. 3a, b), with current signals recorded in response to various gas analytes. All measurements were performed at ambient temperature, utilizing air as the carrier gas, and NO2 detection was facilitated through the gas sensing system38,39. The current–time (I–t) curve of AgBDT (Fig. 3c) demonstrates its excellent response and recovery characteristics to a wide range of NO2 concentrations (1–100 ppm) at room temperature. The current through the AgBDT nanosheets surged significantly upon exposure to NO2 and swiftly reverted to the baseline upon air purging. Remarkably, AgBDT nanosheets with a thickness of 100–120 nm displayed a response value of approximately 15000.06% to 100 ppm NO2, surpassing that of 2D Ag(SPh-NH2)40 connected by weak Van der Waals forces. After four consecutive cycles of detecting 10 ppm NO2 at room temperature, the CV was found to be 6.00%, indicating good reproducibility (Fig. S8). The water contact angle of AgBDT nanosheets is 106.6°, suggesting its hydrophobic property of AgBDT (Fig. S9). The response value of AgBDT toward 5 ppm NO2 is 1041.64%, and the response value varies from 1238.52% to 967.57% with the CV of 8.52% across 0–90% humidity environments, indicating effective resistance to humidity interference (Figure S10). The dynamic response and recovery curves for 10 ppm NO2 showed that the response and recovery time of AgBDT nanosheets were 9.6 s and 38.2 s, respectively (Fig. 3d), outpacing the majority of room temperature sensing materials36,40,41,42,43,44,45,46,47,48,49,50, which typically exhibit response times exceeding 50 s. Further analysis confirmed the exceptional selectivity of AgBDT nanosheets, which effectively discriminated NO2 from 15 other interfering gases with cross-sensitivities, including acetone, toluene, carbon dioxide, sulfur dioxide, and hydrogen sulfide (Fig. 3e). Moreover, the concentration and response of AgBDT also showed a good linear relationship on the logarithmic plot. With a response threshold set at 10.00%, the LOD of AgBDT nanosheets was calculated to be 0.22 ppb (Fig. 3f). To the best of our knowledge, this represents the lowest value among all reported room temperature, non-light-assisted NO2 chemiresistive sensing materials, placing it at the forefront of the field (Fig. 3g and Table S2). Moreover, the response value of the AgBDT nanosheets showed no significant decay over a period of 20 days, indicating its excellent long-term stability (Fig. S11). To elucidate sensing mechanism in greater detail, comparative studies were conducted with PbBDT36, revealing similar sensing behaviors between AgBDT and PbBDT. As the oxidation process proceeds (Supporting information), the number of sulfhydryl groups decreases (Fig. S12). Time-resolved in-situ Fourier transform spectroscopy (DRIFTS) revealed the oxidation of -SH to the oxidation products (Fig. S13 and Table S3). After the oxidation of sulfhydryl groups, the gas sensitivity response value decreased (Fig. S14), this result confirmed that the sulfhydryl groups serve as the active site for gas sensing. However, the gas sensing tests were performed at ambient temperature, the concentration of NO2 was comparatively low (≤100 ppm), and the exposure for AgBDT to NO2 was short (≤30 s). Thus, under this condition the SH groups were not oxidized. We performed XPS analyses of the AgBDT before and after gas sensing test, and observed that the sulfhydryl groups remained consistent before and after the test (Fig. S15). From the results presented above, the potential sensing mechanism can be described as follows: NO2 can be stably adsorbed on the surface of AgBDT through Lewis acid-base interactions and hydrogen bond with the surface sulfhydryl groups, with an adsorption energy of −0.24 eV, suggesting a strong interaction between NO2 and AgBDT. When NO2 molecule adsorbs onto the surface of AgBDT, approximately 0.27 electrons are estimated to be transferred from AgBDT (Fig. S16), leading to an increase in the electrical conductivity of AgBDT.

Fig. 3: Gas sensing performances of the sensor at RT.
figure 3

a Fabrication processes of the prepared sensor. b Scanning Electron Microscopy (SEM) of AgBDT nanosheets. c Response and recovery curve to different NO2 concentrations at room temperature. d Response and recovery time curve under 10 ppm NO2. e Cross-sensitivities of AgBDT nanosheets towards 15 types of gases, inset is the enlarged view of an interfering gas with a response value of less than 0.25. f Linear log-log fitting of the response-NO2 concentration plot. g Comparison with other reported NO2 sensing materials at RT: Te Nanofibers41, LaFeO3 nanocubes42, SnO-SnO243, BP-In2O344, MnPS345, WS2/ZnS46, MoS2 film47, Vc-reduced GO48, Cu2O-rGO49, In(OH)3-rGO50, Ag(SPh-NH2)40, PbBDT36 (data are obtained or estimated from the corresponding reports). Source data are provided as a Source Data file.

Full size image

The quantum confinement effect within superlattices significantly amplifies light-matter interaction34, thereby bestowing optoelectronic devices with a high degree of tunability. Leveraging this effect, AgBDT, characterized by its multi-quantum well structure, has been adeptly employed for photodetection. AgBDT is a p-type semiconductor, where holes predominantly contribute to electrical conduction. Upon the absorption of photon energy, electrons in the p orbital of S and the d orbital of Ag are excited to the s orbital of Ag, the s orbital of S, and the p orbital of C (Fig. S17). This process increases the hole concentration in AgBDT, thereby enhancing the conductivity of AgBDT and generating photo-response. As shown in Fig. 4a and Fig. S18, the I–V curves of AgBDT demonstrate robust ohmic contact with metal electrodes under both dark conditions and illuminated by a xenon lamp. The optoelectrical switching ratio achieves a remarkable value of 190.10, indicating its potential for photodetection applications. The photoelectric characterization of AgBDT unveiled a marked sensitivity across the 380 to 650 nm wavelength range (Fig. 4b), with a pronounced peak in photoelectric activity at 475 nm, aligning with the absorption spectrum of AgBDT. The photocurrent exhibited a positive correlation with increasing light intensity, from 22 to 55 mW cm-2 (Fig. 4c) under 475 nm radiation. It is worth noting that, the on–off ratio of AgBDT reached to 1769.87 at light radiation of 55 mW cm-2 and wavelength of 475 nm, which is the highest on-off ratio compared to other reported conductive coordination polymers (CCPs) (Fig. 4d, Table S4). When subjected to periodic light pulses, AgBDT maintained consistent maximum photocurrent levels over multiple cycles, demonstrating excellent cyclic stability and repeatability (Fig. 4e). The relationship between photocurrent and optical power density follows a nonlinear power-law, expressed as Iph ∝ Pθ, with an experimental exponent value of 0.95, approaching the ideal exponent value of 1 (Fig. 4f). Moreover, AgBDT exhibited a rapid response time, with a short rise time of 1.5 s and a fall time of 17.3 s (Fig. 4g).

Fig. 4: Optoelectronic performance of AgBDT nanosheets.
figure 4

a Logarithmic I–V characteristics under dark and light conditions. b Wavelength-dependent normalized optoelectric switching ratio. The curve represents the intensity of the photoelectric response at different wavelengths. Inset are the Wavelength-dependent photoresponse curves. c Photoelectric response of AgBDT nanosheets under illumination with different light intensities with the wavelength of 475 nm. d Comparison of the optoelectronic on/off ratio of other 12 coordination polymers. NiHITP53, CdATP54, [Cd(adc)2(rctt-4-pncb)]n55, CuHITP53, CuTCNQ53, CuCAT53, Cu[Cu(pdt)2]53, CuBHT56, [Cu(muco)(3,5-dcp)]n57, Im@CuBTC58, {Ag(C5H4NS)}n53, PhSeAg53. e Time-dependent photoresponse under 475 nm periodic illumination. f Photocurrent as a function of optical power Intensity fitted by the power-law formula. g Response and recovery time curve under 475 nm light. Source data are provided as a Source Data file.

Full size image

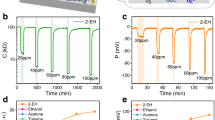
The chemiresistive sensor is based on resistance change caused by the contact of gas molecules with the surface of semiconductor materials to achieve detection. Due to the semiconductor properties of the material, changes in the operating environment (such as temperature) will change the base resistance of the material. Therefore, any alteration in the base resistance can influence the response value, which impacts the precision of the sensor. Inspired by ratiometric detection, we introduce a photoelectric response (Rph = ΔIp/I0) as a reference to the gas-sensitive response (Rgas = ΔIg/I0). By dividing these two responses (Rgas/Rph), we effectively eliminate the baseline current I0. In cases where the material shows a pronounced sensitivity to both gas and light, with ΔIg and ΔIp substantially exceeding I0 (ΔIg and ΔIp >> I0), ΔIg can be approximated to Ig, while ΔIp can be approximated to Ip. A meticulous analysis of the functional relationship between chemiresistive and photoelectric responses reveals that the ratio Ig/Ip (Please refer to Ratiometric-gas sensing measurement for detailed analysis) efficiently cancels out temperature-related factors and correlates directly with the concentration of the analyte gas. Figure 5a illustrates the schematic representation of the current fluctuation characteristic of ratiometric-gas sensing. As depicted in the figure, the current remains relatively at a low value in air atmosphere. Upon the introduction of NO2 gas, there is a noticeable increase in the current, which is typical behavior of conventional chemiresistive gas sensing. We integrated a photoelectric response component into the foundation of the above chemiresistive gas sensing, enabling the implementation of a ratiometric gas sensing methodology. As a result, the current increases to a higher level. Ratiometric-gas sensing is defined as the numerical ratio (Ig/Ip) of the current of the chemiresistive gas sensing to the current of the photoelectric response. From the practical tests conducted at various concentrations of NO2 (Fig. 5b), it is observed that both the ratiometric-gas sensing and the chemiresistive gas sensing exhibited a similar concentration-dependent trend in their responses. A double logarithmic plot (Fig. 5c) of concentration versus the value of ratiometric-gas sensitivity value revealed an excellent linear relationship with a coefficient of determination (COD) of 0.994. This result illustrated that the ratiometric-gas sensing detection could accurately measure the concentration of the target gas. The detection limit of the ratiometric-gas sensing, obtained using the triple the signal-to-noise ratio method48,51, was 3.06 ppb, which was comparable to the conventional chemiresistive methods. In order to validate the temperature resilience of the ratiometric-gas sensing, we measured the ratiometric-gas sensor responses to 10 ppm NO2 gas at various temperatures (Fig. 5d). Figure 5e illustrated that while the chemiresistive gas sensitivity response exhibited significant fluctuations from 25 °C to 65 °C, while the variation in the ratio gas sensitivity values was relatively minimal. Computational analysis of the CV at different temperatures revealed that the CV dropped from 21.81% for the chemiresistive gas sensor to 7.81% for ratiometric-gas sensor, effectively meeting the practical application requirement of being less than 10.00% (Fig. 5f). Thus, by adding the factor of photoelectric response to the chemiresistive gas sensing, the temperature-compensated detection of gas sensing is effectively realized in a single material.

Fig. 5: Ratiometric-gas sensing performance of AgBDT nanosheets.
figure 5

a Schematic diagram of current fluctuation characteristics of ratiometric-gas sensing. b Column chart of concentration-dependent response (left) and ratiometric-gas sensing characteristics (right). c Linear log-log fitting of the ratio NO2 concentration plot. d The actual bimodal response and recovery curve to different temperatures under 10 ppm NO2. e Column chart of temperature-dependent gas sensing response and ratio of gas sensing response to photoconductivity. f Box plots of CV values comparing between gas sensing response and ratio under the temperature range of 25−65 °C. Source data are provided as a Source Data file.

Full size image

In summary, an organic-inorganic hybrid covalent superlattice material AgBDT was successfully designed and prepared through coordination chemical self-assembly. Its unique multi-quantum well structure endows it with an exceptional photoelectric response, achieving an on/off ratio of 1769.87, which is the highest recorded among the coordinated polymers. The extensive coverage of long-range ordered sulfhydryl functional groups on the surface of AgBDT creates a multitude of active sites for gas detection, resulting in an extraordinarily sensitive response to NO2, with a response value reaching up to 15000.06% for 100 ppm NO2 and an impressively low detection of 0.22 ppb, which is the lowest reported values in fast-response chemiresistive NO2 sensing materials without light assistance. Due to its excellent photoelectric and gas response sensitivities, we have applied it to a ratiometric-gas sensor. The ratiometric-gas sensor test is capable of detecting NO2 molecules with an impressive detection limit of 3.06 ppb. Significantly, this method has successfully reduced the CV from 21.81% to 7.81% across a temperature range of 25 to 65 °C, demonstrating a strong resilience against temperature fluctuations. This research introduces an approach for gas sensing detection that successfully overcomes the challenges of temperature interference, addressing a key issue for practical use.

Methods

Starting materials

Unless otherwise noted, materials obtained from commercial suppliers were used without further purification. Silver nitrate (AgNO3, 99.8%) was purchased from Sinopharm Chemical Reagent Co., Ltd., China. 1,4-benzenedithiol (1,4-BDT, 97%+) was purchased from Adamas-beta, China. DMF was purchased from Sinopharm Chemical Reagent Co., Ltd., China. Deionized water was produced by Lab ultra-pure water system. Ag-Pd interdigital electrode plates with a channel of 200 μm were obtained from Hangzhou Jinbo Tech. Co., Ltd., China. The electrode plates were rinsed with ethanol and dried with nitrogen (N2) before use.

Synthesis of AgBDT

AgBDT nanosheets: AgBDT nanosheets were synthesized by hydrothermal reaction. Firstly, AgNO3 (17.0 mg, 0.10 mmol) was dissolved in deionized water (1 mL) and 1,4-benzenedithiol (42.6 mg, 0.30 mmol) was dissolved in DMF (1 mL). The solution of silver salt and ligand were then mixed and ultrasonicated for 30 min. Subsequently, the mixture was retained at 85 °C for 24 h. After cooling to room temperature, the precipitate was rinsed with ethanol by five times to remove any unreacted raw materials. Finally, the resulting powder was dried in a vacuum oven at 60 °C for 12 h for further characterization and investigation.

Preparation of gas sensor and photoresponse devices

The gas sensors were fabricated by a traditional drop-coating method. The prepared sample of AgBDT nanosheets was dispersed in isopropanol. 100 μL dispersion containing the sample was then drop-coated on the Ag-Pd interdigital electrode.

Characterization

Powder X-ray diffraction (PXRD) was performed on a Rigaku Smartlab X-ray diffractometer with Cu Kα1 radiation (λ = 1.5406 Å) at a scanning speed of 5° min−1 and a scan step of 0.02°. The 2θ scan range was 5–50°. UV-Vis-NIR diffuse reflectance spectra were collected on a Perkin Elmer Lambda 950 spectrophotometer. Barium sulfate powder was used as a non-adsorbing background. The data of X-ray photoelectron spectroscopy (XPS) was collected from a Thermo Scientific ESCALAB 250 Xi XPS system (monochromatic Al Kα X-rays (1486.6 eV) operating at 15 kV; the base pressure: 5.0 × 10−8 Pa). The FT-IR spectra were recorded from KBr pellets in the range 4000–400 cm−1 on Nicolet 170 SXFT-IR spectrometer. Scanning electron microscopy (SEM) images were recorded on a Zeiss Sigma 300 field emission scanning electron microscope. The used accelerating voltage was 3 kV. Transmission electron microscopy (TEM) images were collected on a FEI Talos-F200X G2 field emission transmission electron microscope at an acceleration voltage of 200 kV. Thermogravimetric analysis (TGA) was performed on a NETZSCH STA 449F3 analyzer under a stream of synthetic air of 20 mL min−1. The samples were heated from 30 to 1000 °C at a heating rate of 10 °C min-1. The electrical conductivity of AgBDT at different temperatures was determined by I–V measurements to the compressed cylinder pellet of AgBDT powder with a diameter of 2.5 mm. The electrical conductivity was calculated by the equation σ = L/(R·S), where L is the pellet thickness, R is the pellet resistance and S is the contact area of the cylinder pellet. The temperature was controlled by a sophisticated STIK BAO-35A drying oven (temperature control accuracy ± 1 °C). The I–V curves were measured by a Keithley 4200 semiconductor characterization system. The applied voltage range was −5 to 5 V at a scan step of 0.1 V.

3D-ED data collection

3D-ED data were collected using a 200 kV JEM-F200 Transmission Electron Microscope (JEOL Ltd., China), equipped with a hybrid-pixel electron detector (Cheetah 1800, 512 × 512 pixels, pixel size 55 μm, Amsterdam Scientific Instruments) and the software Instamatic. Cryogenic sample preparation of AgBDT followed the plunge-freezing protocol. The data collection strategy combines goniometer rotation with electron-beam tilt to obtain a precise tilt step of 0.1°–0.2°. Selected area electron diffraction (SAED) mode was used for data recording. The ABDT datasets were collected using a cryogenic sample holder (Gatan, Model 914), with data collection parameters optimized as follows: spot size = 4, exposure time = 0.5 s, tilt step = 0.1°. In total, 283 ED frames were recorded from AgBDT. During each data collection, the crystal was totally bathed in the incident beam.

Gas sensing measurement

The gas sensing performances of the sensor including the response value, selectivity, response time, and recovery time were evaluated by the dynamic gas mixing system that was developed in-house when it was exposed to the target gas. A constant bias voltage of 5 V was applied to the device, which was connected to a Keithley source meter model 2602B to monitor the changes in the sensing-current signal in real time. The carrier gas (dry compressed air) was mixed with the target gas (NO2) to obtain NO2 of various concentrations, and the flow ratios were adjusted using the corresponding mass flow controllers (CS-200C, Beijing Sevenstars Qualiflow Electronic Equipment Manufacturing Co., Ltd., China), after which the gas mixture was introduced into the gas testing chamber. A constant gas flow rate of 600 sccm (standard cubic centimeters per minute) was maintained.

The sensing response is defined as R (%) = Ig/I0, where Ig and I0 are the device currents when the gas sensor is exposed to the gas analytes and air conditions, respectively. The response time is defined as the time required for the current to reach 90% of its equilibrium value after the test gas is injected, and the recovery time is the time necessary for the sensor to attain a current of 10% below its original value in air. The LOD for the AgBDT sensor is defined as the concentration of the analyte that produces a response of 0.1.

Photoresponse measurement

The photonic conductance characteristics of the AgBDT devices were characterized using a semiconductor parameter analyzer (Keithley 2602B) within the visible light range. A Perfect Light xenon lamp light source (PLS-SXE300D, Shanghai Maomo Scientific Instrument Co., Ltd., China) was utilized as the irradiation source. The wavelength of the incident light was altered by changing filters, which were available at different wavelengths of 380, 400, 420, 450, 475, 550, 600, and 650 nm. The intensity of the light was modulated to a range of 22–55 mW cm-2. The light spot size through the quartz glass vacuum shield of the probe stage was sufficient to fully cover the active area of the AgBDT device. The transient photocurrent response of the device under on-off conditions was measured under a constant bias of 5 V. All measurements were conducted under an ambient air atmosphere.

The nonlinear relationship for the change of photocurrent against light intensity follows the power law Ip = APθ, where A is a constant for a certain wavelength, P is the optical power, and the exponent θ is the corresponding power index between 0 and 1 which determines the response of the photocurrent to light intensity. The photoelectric response on/off ratio is defined as Ip/Id, where Ip represents the photocurrent (the current generated in the presence of light) and Id represents the dark current (the current that flows in the absence of light).

Ratiometric-gas sensing measurement

For semiconductor gas sensors, the current value Ig typically depends on temperature and gas concentration, and this relationship can be described by the equation (Eq. (1)):

$${I}_{{{{\rm{g}}}}}({{{\rm{T}}}},{{{\rm{C}}}})={{{{\rm{A}}}}{{\cdot }}}{e}^{-\frac{{E}_{a}}{{kT}}}{{{\rm{\cdot }}}}(1+{{\alpha }}{{\cdot }}{{{{\rm{C}}}}}^{{{{\rm{m}}}}})$$
(1)

where A is a constant related to the sensor’s material and structure, Ea is the activation energy of the material, k is the Boltzmann constant, α and m are constants related to the sensor characteristics and the type of gas, T is the kelvin temperature, and C is the gas concentration.

In the case of a photoconductor, according to Physics of Semiconductor Devices52, the photocurrent Ip flowing between the electrodes can be described by the equation (Eq. (2)):

$$\,{I}_{{{{\rm{p}}}}}({{{\rm{T}}}})={{{{\rm{\eta }}}}}_{0}{\,{P}}_{{{{\rm{opt}}}}}{{{{\rm{R}}}}}_{{0}}{e}^{-\frac{{E}_{a}}{{kT}}}$$
(2)

where η0 is the quantum efficiency, R0 is the response constant, Popt is the incident light power, Ea is the activation energy determined by experimental fitting, k is the Boltzmann constant, and T is the temperature.

For ratiometric method, we introduce a photoelectric response (Rph = ΔIp/I0) as a reference to the gas-sensitive response (Rgas = ΔIg/I0). By dividing these two responses (Rgas/Rph), we effectively eliminate the baseline current I0. In cases where the material shows a pronounced sensitivity to both gas and light, with ΔIg and ΔIp substantially exceeding I0 (ΔIg and ΔIp >> I0), ΔIg can be approximated to Ig, while ΔIp can be approximated to Ip. A meticulous analysis of the functional relationship between chemiresistive and photoelectric responses reveals that the ratio Ig/Ip (Eq. (3)):

$$\frac{{I}_{{{{\rm{g}}}}}}{{I}_{{{{\rm{p}}}}}}=\frac{{{{\rm{A}}}}(1\,+{{{\rm{\alpha }}}}{{{\cdot }}C}^{{{{\rm{m}}}}})}{{{{{\rm{\eta }}}}}_{0}{P}_{{{{\rm{opt}}}}}{{{{\rm{R}}}}}_{0}}$$
(3)

efficiently diminishes temperature-related factors and correlates directly with the concentration of the analyte gas.

The calculation of LOD was performed using signal/noise ratio2. The sensor noise was calculated using the variation in relative sensor response with the baseline established by root mean square deviation (RMSD). We replotted 100 data points at the baseline concerning time before the NO2 exposure. Then a fifth-order polynomial fit (Eq. (4)):

$$y={{{{\rm{B}}}}}_{6}+{{{{\rm{B}}}}}_{1}x+{{{{\rm{B}}}}}_{2}{x}^{2}+{{{{\rm{B}}}}}_{3}{x}^{3}+{{{{\rm{B}}}}}_{4}{x}^{4}+{{{{\rm{B}}}}}_{5}{x}^{5}$$
(4)

where B1-B6 are the constants was performed over the range of data points. The curve fitting equation and statistical parameters of polynomial fitting were obtained. The stadeviation (S) was calculated by the equation (Eq. (5)):

$${V}_{\chi 2}=\varSigma {\left(y_{i}-y\right)}^{2}$$
(5)

where Vχ2 is the root mean square deviation, yi is the measured data point, and y is the corresponding value calculated from curve-fitting equation. Subsequently, we can calculate the sensor noise that is defined as

$${{{{\rm{RMS}}}}}_{{{{\rm{noise}}}}}=\sqrt{\frac{{S}^{2}}{N}}$$
(6)

where N is the number of data points (Eq. (6)). According to the IUPAC definition, LOD is 3 times the ratio of signal to noise

$${{{\rm{LOD}}}}=3\frac{{{{{\rm{RMS}}}}}_{{{{\rm{noise}}}}}}{{{{\rm{Slope}}}}}$$
(7)

where slope was obtained from NO2 concentration fitting plot (Eq. (7)).

CV, which represents the variation in response across different cycles, is defined as

$${{{\rm{CV}}}}={{{{\rm{R}}}}}_{{{{\rm{SD}}}}}/{{{{\rm{R}}}}}_{{{{\rm{average}}}}}\times 100\%$$
(8)

where RSD and Raverage are the standard deviation (SD) and the average value of responses with five successive cycles, respectively (Eq. (8)).