Introduction

Spinons are well-established quasiparticles in one-dimensional (1D) systems1,2, but their presence in dimensions higher than one remains a contentious topic3,4. In particular, spin-1/2 Heisenberg AFs on quasi-2D square lattices have been the subject of tremendous research effort in connection with high-temperature superconductivity (HTSC) in cuprates5. Despite the presence of Néel AF orders and the absence of apparent frustrations in these systems, earlier theoretical and experimental works have indicated that they can accommodate gapped spinon modes6,7,8. Indeed, the broad continua observed across many copper-based square-lattice AFs7,9,10, known as the ‘(π, 0) anomaly’, have been attributed to spinon excitations. Theoretically, their weights should increase in systems with enhanced long-range, multi-spin interactions competing with nearest-neighbor (NN) Heisenberg exchange (J)11,12, such as four-spin exchanges (Q)8,13,14, which can destabilize the Néel AF order in favor of more exotic phases. However, these parameters are difficult to control experimentally and the existence of spinons in square lattices remains unsettled.

The realization of spin-orbit-entangled pseudospin-1/2 square-lattice AFs in iridates offers novel material platforms for exploring the problem in an uncharted parameter regime. The strong spin-orbit coupling in iridates imparts unique properties to their exchange interactions, ranging from a nearly isotropic Heisenberg to a bond-directional Ising-like exchange interaction15. This leads to a variety of theoretical predictions for novel quantum magnets, including Kitaev spin liquid in honeycomb compounds15,16,17,18,19, U(1) or Z2 quantum spin liquid in hyperkagome compounds20,21. Similarly, in square-lattice iridates, enhanced higher-order spin interactions from spatially extended 5d orbitals and increased virtual charge fluctuations due to a small charge gap22 underlie the strong deviation of the single-layer (SL) Sr2IrO4 from the NN Heisenberg model23 and the exceptionally large spin gap in the double-layer (DL) Sr3Ir2O724,25.

Thus, the nature of exchange interactions in iridates varies widely even within the Ruddlesden-Popper (R-P) series Srn+1IrnO3n+1. This allows for the possibility of heterointerfacing different types of magnetism in a superlattice, which may induce magnetic frustration through proximity coupling of symmetry-distinct orders26. In this article, we demonstrate a heterostructure-based strategy to frustrate the Néel AF order in square-lattice iridates. We use time-resolved resonant x-ray diffraction (RXD) to measure the degree of quantum fluctuations through the recovery dynamics of the AF order after its transient suppression by an optical pump, which significantly slows down with enhanced frustration. We use polarization-resolved resonant inelastic x-ray scattering (RIXS) and high-energy-resolution RIXS to reveal the absence of single magnons in most part of the Brillouin zone away from the immediate vicinity of the ordering wavevector. Instead, the spectra are dominated by isotropic continua, which provide compelling evidence for spinons in a square-lattice Heisenberg AF.

Results

Scanning transmission electron microsocpy

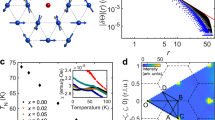
The recently discovered n = 1.5 member of the R-P series27 is a “natural” superlattice, which can be grown in a single-crystalline form using the flux method. Figure 1a displays the crystal and magnetic structures of Sr2IrO4, Sr3Ir2O7, and Sr5Ir3O11, corresponding to n = 1, 2 and 1.5 in the R-P series, respectively. Sr2IrO4 exhibits an in-plane canted AF order in the SL square lattice28, whereas the DL square lattice Sr3Ir2O7 is characterized by a c-axis collinear AF order29. Sr5Ir3O11 features an alternating stacking of SL and DL, preserving the magnetic structures as well as the gross features in the excitation spectra of the parent compounds27. The lattice structures of these three compounds are investigated by scanning transmission electron microscopy (STEM), as shown in Fig. 1b. The images taken along the [100] direction clearly reveal the alternating pattern of SL and DL stackings in Sr5Ir3O11 as well as the stacking patterns of SL and DL in Sr2IrO4 and Sr3Ir2O7, respectively.

Fig. 1: Crystal and magnetic structures of square-lattice iridates.
figure 1

a Crystal and magnetic structures of R-P series iridates. Unit cells are indicated by gray lines. Iridium ions and IrO6 octahedra in SL (DL) are colored blue (green). b Stacking patterns of R-P series iridates revealed in STEM images taken along the [100] projection, with corresponding structural models superimposed in the upper right corner of each panel. c The ratio of the ordered moment size of Sr2IrO4 to that of Sr3Ir2O7 (μ214/μ327), based on estimations from theoretical30,31,32,33,34 and experimental35,36,37 studies. This is compared to the ratio of the ordered moment size of SL to that of DL in Sr5Ir3O11 (μSL/μDL), which is measured directly in our RXD experiment shown in (d). d (1 0 L) scan of magnetic Bragg reflections of Sr5Ir3O11. The simulation for μSL/μDL = 0.6 (red line) is in good agreement with the experimental data (black circles). Numerical simulations are convoluted with a Gaussian function to account for the experimental momentum resolution and the finite correlation length of the AF order along the L direction. e Magnetization measurements of Sr2IrO4 and Sr5Ir3O11 adapted from Ref. 27. The induced moment size of Sr5Ir3O11 at 0.5 T is smaller than that of Sr2IrO4 by a factor of ≈ 0.9.

Full size image

Resonant x-ray diffraction

For these three compounds, Fig. 1c–e compare the sizes of the ordered magnetic moments, which depend on many factors such as Ir 5d–O 2p hybridization, IrO6 octahedra distortions, thermal and quantum fluctuations. Although the estimated values from both theory30,31,31,32,33,34 and experiment35,36,37 are widely scattered, an overall trend is that the moment size is smaller in Sr2IrO4 as compared to Sr3Ir2O7 (Fig. 1c). While this is expected because of stronger quantum fluctuations in the Heisenberg Sr2IrO4, we note that this effect is not captured in density functional theory based calculations. Our RXD result on Sr5Ir3O11 allows for a direct comparison of the moment sizes in SL and DL in Sr5Ir3O11. Figure 1d shows the intensity measured along (1 0 L) at the base temperature of 10 K. Both SL and DL contribute to magnetic Bragg reflections at every integer L, but their contributions can be separated by exploiting the fact that the DL contribution to the intensity oscillates due to its structure factor as \({\cos }^{2}(2\pi d/c)\)27,29, where d is the distance between the two layers comprising DL and c is the c-axis lattice parameter, whereas SL contributes a nearly constant intensity. The L dependence of the intensity can be reproduced by a simple model (see Supplementary Note 1), from which we estimate the SL moment size to be ≈ 60% of that of DL. Thus, our data reveal much stronger quantum fluctuations in SL relative to DL, assuming that other aforementioned factors do not differ significantly between SL and DL. Next, we compare the ordered moment size of SL in Sr5Ir3O11 to that in Sr2IrO4 (Fig. 1e). Because DL does not contribute to the net magnetization and the octahedra rotation angles are almost the same for the two compounds (see Supplementary Note 2), the moment sizes can be estimated through the net magnetization from the canting of the moments. We estimate the SL moment size in Sr5Ir3O11 to be around 90% of that in Sr2IrO4, indicating further reduction of the ordered moment by heterointerfacing. Although this may appear to be a small effect, we shall see below that it has a dramatic effect in the spin dynamics.

Time-resolved resonant x-ray diffraction

To provide further evidence for the magnetic frustration, we employ time-resolved RXD to follow the recovery of the AF order after its transient suppression induced by an optical pump pulse. Figure 2a–c compare the decay and recovery dynamics of Sr3Ir2O7, Sr2IrO4 and Sr5Ir3O11, respectively. Sr5Ir3O11 is measured at q = (−1 0 8) to minimize the contribution of DL27. For a quantitative analysis, the delay curves are fitted by a double exponential relaxation function f(t) expressed as38

$$f(t)= -\left[\frac{1}{2}\left(1+{{\rm{Erf}}}\left(\frac{2\sqrt{2}(t-{t}_{0})}{{\tau }_{{{\rm{decay}}}}}\right)\right)\right.\\ \left.\times \left(A{e}^{-(t-{t}_{0})/{\tau }_{{{\rm{fast}}}}}+B{e}^{-(t-{t}_{0})/{\tau }_{{{\rm{slow}}}}}\right)\right],$$
(1)

where t0 denotes the arrival time of an optical pump pulse and τdecay refers to the decay time of magnetic Bragg reflections. A and B represent the intensities recovered on two different timescales: τfast, representing the build-up of 2D correlations in a few ps, and τslow, representing a slower recovery of 10-100 ps timescale associated with restoration of three-dimensional (3D) correlations38. The decay process is fitted by the error(Erf) function. We fit the delay curves of Sr3Ir2O7 only below 5 ps with a single exponential relaxation function (Fig. 2a) as in the previous work39, which corresponds to B = 0 in Eq. (1), because extrinsic effects such as strain waves come into play beyond 10 ps, leading to an overshoot in the intensity of the Sr3Ir2O7 curve39. The extracted time constants for Sr2IrO4 and Sr3Ir2O7 align with those from previous studies38,39 (see Supplementary Note 3). We shall concern ourselves with τfast only as it is relevant to intraplane processes, and its fitted values are shown in Fig. 2d for various fluences from 1 to 4 mJ/cm2.

Fig. 2: Recovery dynamics of AF orders after optical stimulation.
figure 2

Delay curves (circles) for Sr3Ir2O7 (a), Sr2IrO4 (b), and Sr5Ir3O11 (c), with corresponding fitted curves (solid lines) spanning from −1 to 1000 ps, separated into fast (-1 to 3 ps) and slow (3 to 1000 ps) timescales. The latter is plotted on a logarithmic scale. The data for pump fluence of 2.30, 2.35 and 1.85 mJ/cm2 are shown for Sr3Ir2O7, Sr2IrO4 and Sr5Ir3O11, respectively. Error bars indicate the standard deviations from multiple measurements. The magnetic reflection of Sr5Ir3O11 is measured at (−1 0 8) to minimize the DL contribution27. The intensities of delay curves are normalized to −1 at their minima. d Pump fluence dependence of the fast recovery time constants. Error bars are the standard errors of the estimated parameters obtained from the fitting. e–h Transient equilibrium Landau free energies (solid curves) after an optical pump pulse at t = 0 (left panel) and time profiles simulated for order parameters (right panel) for ψ0 = 1.0 (e), 0.7 (f), 0.6 (g), and 0.1 (h). The schematic in e visualizes the recovery process. The potential well shown by the dashed line represents the Landau free energy immediately after the arrival of an optical pump pulse, leading to the decay of the order parameter. Over several picoseconds, the Landau free energy evolves to a transient equilibrium state (solid curves) with partial recovery of the AF order (solid green arrow).

Full size image

Sr3Ir2O7 exhibits a significantly faster 2D recovery (τfast) compared to Sr2IrO4 and Sr5Ir3O11, with Sr5Ir3O11 showing a slightly but clearly slower recovery than Sr2IrO4 for all fluences measured. The rapid 2D recovery observed in Sr3Ir2O7 is attributed to its Ising-type order, which has negligible quantum fluctuations. On the other hand, the longer τfast signifies an enhanced frustration in the SL of Sr5Ir3O11. We demonstrate this in Figs. 2e–h, using a phenomenological time-dependent Ginzburg-Landau theory (see Supplementary Note 4). In our simulation, the order parameter ψ0 are chosen to approximately match the relative moment sizes estimated in Fig. 1c–e: ψ0 = 1.0 for Sr3Ir2O7 (Fig. 2e), 0.7 for Sr2IrO4 (Fig. 2f), and 0.6 for Sr5Ir3O11 (Fig. 2g). ψ0 becomes zero as the electron temperature is instantaneously raised by the optical pump pulse, and subsequently recovers transient equilibrium value as heat is transferred to the lattice over a few ps timescale. The recovery process slows down when ψ0 is reduced and the potential well becomes shallow, semiquantitatively reproducing the experimental results in Fig. 2a–c. These results imply that enhanced magnetic frustration can manifest as slower recovery dynamics of magnetic Bragg reflections. In an extreme case where ψ0 approaches zero near the critical point, the recovery time diverges (Fig. 2h).

Resonant inelastic x-ray scattering

Armed with this information, we now address the long-standing issue of the origin of (π, 0) anomaly in square-lattice AFs. Figure 3 shows polarization-resolved RIXS measurements on Sr2IrO4 and Sr5Ir3O11. Although resolving the polarization of scattered x-ray is not currently feasible for hard x-ray RIXS, the polarizations of spin waves can be resolved by measuring the same q points in several different geometries (Ref. 40 and Supplementary Note 5). For Sr2IrO4 (Fig. 3a), the (π, 0) spectrum exhibits identical transverse (T) and longitudinal (L) responses, as revealed in our previous study40; i.e. the spectra are isotropic with no visible trace of single magnons, which should appear exclusively in the T channel. In contrast, the T spectrum at (π/2, π/2) displays a well-defined single magnon, superimposed on a broad feature that appears in both channels. In between these two points, polarization analyses show a gradual decay of single magnon into isotropic continua.

Fig. 3: Absence of magnons in polarization-resolved RIXS spectra.
figure 3

a Polarization-resolved spectra of Sr2IrO4 along the magnetic zone boundary from (π/2, π/2) to (π, 0), adapted from Ref. 40. Transverse (T) and longitudinal (L) components to the ordered magnetic moments are resolved. The inset shows a quadrant of the Brillouin zone, with the measured wave vectors highlighted by a red line. b Polarization-resolved spectra of Sr5Ir3O11 along the magnetic zone boundary. TSL and LSL denote the transverse and longitudinal components of SL, respectively, while UDL represents the polarization-unresolved background from DL. For the spectrum at (π/2, π/2), the contribution from the transverse component of Sr3Ir2O7 (Supplementary Fig. 6a) is indicated by a gray dashed line. c Polarization-resolved spectra of Sr2IrO4 at (π, π). The inset shows a quadrant of the Brillouin zone, with the measured wave vector highlighted by a red dot. d Polarization-resolved spectra of Sr5Ir3O11 at 0.95(π, π). The gray dashed line indicates the single magnon of DL in UDL extracted from fitting. The error bars are calculated through error propagation from the standard deviations of the raw spectra.

Full size image

More striking are the spectra of Sr5Ir3O11 (Fig. 3b), in which the anomaly is not limited to (π, 0) but spans the entire zone boundary. Although it is difficult to isolate the spin components of SL at the zone boundary, where the energies of the SL and DL magnons are close to each other27, there is no ambiguity in resolving the T and L components of SL, because DL contributes a common background for both channels (See Supplementary Note 5). The sharp peak observed at (π/2, π/2) is identified as the DL magnon mode by comparison with the spectra of Sr3Ir2O7 (Supplementary Fig. 6). Within our error bars, we observe no hint of single magnons from SL; the spectra are isotropic along the entire zone boundary. These isotropic continua carry significant spectral weight even very close to the zone center (Fig. 3d), where SL and DL modes are clearly separated in energy. This is in stark contrast with the (π, π) spectrum of Sr2IrO4, which is dominated by T single magnons (Fig. 3c).

As the SL mode in Sr5Ir3O11 is well separated from the DL mode in energy near the zone center (π, π), we use a high-energy-resolution setup (ΔE ≈ 10 meV) to measure RIXS spectra near (π, π). Figure 4a compares the low-energy excitations of Sr2IrO4 and Sr5Ir3O11 near the zone center at (xπ, xπ) (x = 0.99 to 0.92), where both samples are measured under the same experimental conditions. At x = 0.99, the peak in Sr5Ir3O11 is already not quite resolution-limited, whereas Sr2IrO4 exhibits a resolution limited single peak. At momenta further away from (π, π), the spectra of Sr5Ir3O11 exhibit a two-peak-like structure, which is clearly resolved at x = 0.94 and 0.92. Because we are not able to perform polarization analysis in the high-energy-resolution setup, and for the lack of an accurate theoretical model to fit the spectra, we provide a phenomenological description by fitting the spectra to two pseudo-Voigt functions, labeling them as ‘Peak 1’ and ‘Peak 2’. Figure 4b presents the 2D color plot of the high-energy-resolution RIXS of Sr5Ir3O11 from Fig. 4a, overlaid with the dispersions extracted from the fittings. The separation of Peaks 1 and 2 increases linearly with the distance from (π, π), representing the expanding energy range over which the spectral intensity is distributed. Clearly, the spectra of Sr5Ir3O11 has an extra component that cannot be accounted for by a single magnon excitation.

Fig. 4: Additional mode in high-energy-resolution RIXS spectra.
figure 4

a Comparison of spectra for Sr5Ir3O11 and Sr2IrO4 near the zone center (π, π). Low energy data for Sr5Ir3O11 (Sr2IrO4) are fitted using two (one) pseudo-Voigt peaks, shown as solid red and blue (black) lines. DL single magnons are fitted by the peaks in gray dashed lines. Error bars denote square roots of the absolute intensities. b 2D color plot of the high-energy-resolution RIXS spectra of Sr5Ir3O11 near the zone center, overlaid with peak positions extracted from the fits in a. `Peak 1' (red circles) and `Peak 2' (blue circles) are used to follow the excitations of Sr5Ir3O11. The single magnon dispersion of Sr2IrO4 is marked by black circles. A magnetic mode around 90 meV corresponds to DL single magnon in Sr5Ir3O11, which mirrors the single magnon mode of Sr3Ir2O724,27. Solid lines are linear fits to the peak positions. Error bars represent the standard error of the estimated parameters obtained from the fitting. c Ratio of coherent single-magnons to the total magnetic spectral weight throughout the Brillouin zone for Sr2IrO4 (left panel) and Sr5Ir3O11 (right panel), as estimated from the RIXS measurements in Fig. 3. Data points are marked as blue dots on the surfaces generated by interpolating them. d Schematic of magnon dispersion and low energy edge of spinon continua for Sr2IrO4 (left panel) and Sr5Ir3O11 (right panel). Two-spinon continuum is marked by the pink shaded area and the red line represents the lower bound of the continuum, as given by Eq. (2). The blue line represents the single-magnon dispersion extracted by fitting the data shown in Supplementary Fig. 7 using the J-Q model. The dashed part of blue lines indicates the decay of single magnons due to strong magnon-spinon couplings.

Full size image

Discussion

Although the broad high-energy continua observed in S = 1/2 sqaure-lattice AFs have often been attributed to spinon excitations7,8,9,10, there are other interpretations in terms of multi-magnons41,42. Strong magnon-magnon interactions have been shown to give rise to the formation of two-magnon “Higgs resonances” corresponding to a longitudinal magnon with finite lifetime. In addition, vertex corrections of effective observables lead to three-magnon continuum excitations in transverse channels42. In fact, the spectra of Sr3Ir2O7 reveal high-energy features in both transverse and longitudinal channels (Supplementary Fig. 6).

However, the spectra of Sr5Ir3O11 are inconsistent with the multi-magnon scenario in the following two aspects. First, the continua in transverse and longitudinal channels have different structures in Sr3Ir2O7, whereas they are identical in Sr5Ir3O11. In the multi-magnon scenario, transverse (longitudinal) continuum involves odd(even) number of magnons, and thus their spectra in general have different structures. Second, even after taking into account magnon-magnon interactions and vertex corrections, deviation from the linear spin-wave theory is marginal for low-energy magnons near the zone center, and different theoretical approaches (quantum Monte Carlo43, series expansion44, continuous similarity transformation41,42) agree with one another, consistent with the result for Sr2IrO4 (Fig. 3c).

Therefore, we conclude that the low-energy continua observed in Sr5Ir3O11 cannot be multi-magnons. Thus, we provide below an interpretation based on the spinon scenario. The 3D plots in Fig. 4c summarize the results of RIXS experiments displayed in Fig. 3. They show the momentum distribution of the coherent single-magnon weights in Sr2IrO4 and Sr5Ir3O11, interpolating the q-points between the zone center and boundary. For Sr2IrO4, a coherent single magnon completely vanishes only at (π, 0), while for Sr5Ir3O11 it completely breaks down not only at (π, 0) but across the entire zone boundary, with reduced weights even very close to (π,  π). We attribute these results to a smaller spinon gap in Sr5Ir3O11 compared to Sr2IrO4, as illustrated in Fig. 4d, induced by increased frustration in SL of Sr5Ir3O11.

In the J-Q model with a four-spin exchange Q, a spinon branch or a lower edge of the two-spinon continuum has a dispersion given by8

$${\omega }^{{{\rm{s}}}}({{\bf{q}}})={{{\Delta }}}^{{{\rm{s}}}}+{c}^{{{\rm{s}}}}\sqrt{1-{\cos }^{2}{q}_{x}{\cos }^{2}{q}_{y}},$$
(2)

where cs is the spinon velocity. The dispersion has its energy minimum at (π,  0) as shown in Fig. 4d. The spinon gap Δs is expected to decrease as Q/J increases, which corresponds to greater frustration of the AF order45,46,47, and ultimately vanishes at a critical value of Q/J8. In Sr5Ir3O11, interfacial magnetic couplings between AF orders with distinct symmetries in SL and DL (Fig. 1a) possibly enhance the frustration of the AF order in SL (Fig. 1d, e), increasing the effective Q/J ratio in the 2D spin model. When the spinon continuum falls below the magnon energy with a smaller spinon gap Δs, the coherent magnon peak is washed out due to strong magnon-spinon couplings8. Therefore, the complete breakdown of the coherent single-magnon peak at (π,  0) in Sr2IrO4 is due to an overlapping of magnon and spinon branches occurring only at this wave vector, as illustrated in the left panel of Fig. 4d. In contrast, for Sr5Ir3O11, a small spinon gap Δs leads to the breakdown of the coherent single-magnon across the zone boundary, as illustrated in the right panel of Fig. 4d.

Our work demonstrates an effective materials strategy for inducing magnetic frustration in square lattices by exploiting the diverse array of anisotropic interactions displayed by iridates and combining them in one material, providing compelling evidence for unconventional spin excitations in square-lattice AFs. The strong decay of single magnons even at very low energies is unprecedented in earlier works on cuprate square-lattices7,9,10, where the anomalous continua are confined to high energies. The fully isotropic spectra discovered in square-lattice iridate AFs are thus consistent with quantum-spin-liquid-like spin entanglement in the Néel AF ordered phase7. Thus, our findings represent a significant advance toward understanding the quantum spin dynamics in a quasi-2D square-lattice S = 1/2 Heisenberg AF. We expect that our work will stimulate further investigations into heterostructure-based approaches to frustrated magnetism in square-lattice iridates using layer-by-layer growth techniques48,49,50,51,52.

Methods

Sample synthesis

High-quality single crystals of Sr2IrO4, Sr3Ir2O7, and Sr5Ir3O11 were grown by the standard flux growth method as described in refs. 27,53 and characterized by Raman spectroscopy and x-ray diffraction.

STEM

STEM measurements were conducted using JEM-ARM200F, JEOL at 200 kV with fifth-order probe-corrector (ASCOR, CEOS GmbH, Germany) at the Materials Imaging & Analysis Center of POSTECH in South Korea. The specimens were prepared by a dual-beam focused ion beam with Ga ion beams of 30 kV (Nanolab G3 CX, FEI) and further milled by Ar ion beams of 100 meV (PIPS II, Gatan) to minimize the surface damage using Precision Ion Polishing System (PIPS II Pro 695, Gatan) at the Materials Imaging & Analysis Center of POSTECH in South Korea.

Time-resolved RXD measurements

Time-resolved RXD was performed at the XSS beamline of the PAL-XFEL with a 60 Hz pulse repetition rate. The incident x-ray beam was tuned to the Ir L3-edge at 11.215 keV. The time delay curves of Sr2IrO4 and Sr3Ir2O7 were measured at (-1 0 16) and at (-1 0 13), respectively, in a vertical scattering geometry with grazing incidences. A Jungfrau area detector was used for collecting magnetic Bragg reflection signals. The laser pump pulses of 2.0 μm was injected at an angle of 12∘ with respect to the x-ray pulses. The x-rays were focused by compound refractive lenses down to 20 × 20 μm2 FHWM and the laser spot size was 250 μm FWHM. The temporal resolution of the experiment was measured to be about 300 fs obtained from the delay curve of the (1 1 1) charge-density-wave reflection of a Bi(1 1 1) thin film. All time-resolved RXD measurements were conducted at T ≈ 100 K using a cryostream with liquid nitrogen.

Polarization-resolved RIXS

Polarization-resolved RIXS experiments were performed at the 27-ID-B beamline of the Advanced Photon Source. Combining a diamond(1 1 1) high-heat-load monochromator and a two-bounce Si(8 4 4) channel-cut monochromator, the incident x-ray beam was tuned to the Ir L3-edge (11.215 keV) with the energy bandpass of 14.8 meV. The beam was then focused by a set of Kirkpatrick-Baez mirrors, producing a spot size of 40 × 10 (H × V) μm2 FWHM at the sample position. Scattered photons were analyzed by a Si(8 4 4) diced spherical analyzer with a curvature of 2 m radius and with a mask of 2 cm diameter. The total instrumental energy resolution was about 30 meV. A horizontal scattering geometry was used with the incident π-polarization and the outgoing polarization was not resolved. The scattering angle (2θ) was kept around 90∘ to suppress elastic Thomson scatterings. For Sr2IrO4 and Sr5Ir3O11, an external magnetic field were applied to align the pseudospins along specific directions. More detailed information is provided in Supplementary Note 5.

High-energy-resolution RIXS

High-energy-resolution RIXS were performed at the 27-ID-B beamline of the Advanced Photon Source, employing similar setups as in the polarization-resolving setup, but using different second-monochromator and analyzer. A four-bounce Si (8 4 4) channel-cut monochromator was utilized to narrow the energy bandpass of the incident x-rays to 9 meV. Scattered photons were analyzed by a quartz (3 0 9) diced spherical analyzer with a curvature of 2 m radius and with a mask of 1 cm diameter. This setup achieved an overall energy resolution of 10 meV.

RXD and preliminary RIXS

RXD and preliminary RIXS measurements were performed at the 1C beamline of the Pohang Light Source-II54. Using Si (1 1 1) double-crystal monochromator, the incident x-ray beam was tuned to the Ir L3-edge (11.215 keV) with the energy bandpass about 1 eV. For RIXS experiments, additional two-bounce Si (8 4 4) channel-cut monochromator was installed to reduce the energy bandpass down to 15.8 meV. The beam was then focused by a set of Kirkpatrick-Baez mirrors, yielding a spot size of 25 × 5 (H × V) μm2 FWHM at the sample position. In RXD experiments, scattered photons were filtered by a Si (8 4 4) bent analyzer with a curvature of 1 m radius and collected using a DECTRIS EIGER2 2D area x-ray detector to suppress background signals. In RIXS experiments, scattered photons were analyzed by a Si (8 4 4) diced spherical analyzer with a curvature of 1 m radius and collected using a DECTRIS MYTHEN2 1D x-ray detector. The total instrumental energy resolution of preliminary RIXS was about 40 meV.