Introduction

Solid-state ionic materials serve as the foundation for various technologies, including solid-state batteries, solid-state sensors, fuel cells, and supercapacitors1. In the context of solid-state batteries, leveraging solid-state ionics with solid electrolytes (SEs) instead of traditional liquid electrolytes enhances safety and efficiency in energy storage systems2,3,4. Over the past decade, substantial endeavors have been directed to achieving SEs with fast room temperature ionic conductivities (σRT) exceeding 1 mS cm−1 and outperforming conventional flammable liquid electrolytes based on organic solvents5,6,7,8,9. Impressive examples of the proposed classes of Li-conducting SEs are: NASICON-type \({{{{\rm{Li}}}}}_{1.3}{{{{\rm{Al}}}}}_{0.3}{{{{\rm{Ti}}}}}_{1.7}{({{{{\rm{PO}}}}}_{4})}_{3}\)10, Li-Garnet Li7La3Zr2O1211, Sulfur based Li7P3S1112, and Li10GeP2S123 etc.

Lithium-argyrodites with chemical formula Li6MS5X (LMSX; M = P, Ge, Si, Sn; X = Cl, Br, I)13, represent a highly promising category of solid electrolytes (SE) that has undergone extensive experimental scrutiny14,15,16. These materials exhibit potential for the realization of operational lithium solid-state batteries (LSSB), demonstrating favorable cell performance17,18. Especially, LMSX SE demonstrates the ability to function as a separator in reservoir-free cells, allowing for in situ plating of lithium metal. Thus, LMSX class holds the potential for highly promising solid-state batteries (SSBs) with minimized interfacial resistance, as indicated in recent research19. Additionally, Argyrodite SEs showcase sustainable electrochemical performance and compatibility with silicon-based anodes20.

Consequently, gaining a comprehensive understanding of LMSX and SE materials design in general, is not only essential for advancing Li-ion battery technology but is also crucial for shaping the future of next-generation battery solutions21. It is noteworthy that an interplay between polarizable anionic and mobile cationic sublattices is a hallmark of solid state ionic materials beyond batteries22. The ion hopping hypothesis, proposed to elucidate charge transport in SEs, entails the coordinated motion of cations through sequential shifts among diverse coordination environments23,24. This concept is often supported by molecular dynamics (MD) simulations25,26,27. Quasi elastic neutron scattering (QENS) based experiment has been employed to examine short-length ionic motion in lithium-ion conductors28. Additionally, pulsed-field gradient (PFG) NMR experiments provide evidence for the diffusion of the mobile sublattice, particularly when compared to other framework components of the solid electrolyte29,30. Notably, the diffusivity obtained by PFG-NMR was observed to be smaller than that obtained by QENS measurements for SE, indicating that factors hindering diffusivity become apparent during longer-scale ionic migration28. This observation highlights the ongoing pursuit to clarify the role of different electronic and ionic interactions in influencing the ion migration process31,32.

It is noteworthy that both QENS and PFG-NMR experiments generally evaluate the average diffusion across all species of a specific nucleus/element within the framework31,32. Thus, there is a lack of direct experimental validation for the movement of cations through sequential shifts among diverse coordination environments. An electronic-structure methodology proven to be predictive for ion transport within battery materials may have broader implications in the field of solid-state ionics33. Unfortunately, consensus is lacking thus far as to what ingredients such a predictive electronic-structure method should contain34. While density-functional approximations (DFA) have been very helpful in interrogating the structure and properties of argyrodites35,36 and other ionic materials37,38, the structure, energetics, and diffusion properties often vary widely between DFAs39,40. This is not surprising because a multitude of factors influence ion-diffusion in the crystal, including crystal structure41, free volume42, lattice dynamics43, nature of the ion-diffusion pathways37, correlated motion26,44, and frustrated energy landscapes45, as demonstrated in previous studies. Consequently, a reliable description of various interactions, including Pauli repulsion, electrostatics, polarization, and dispersion, becomes essential to achieve predictive power in the development of SE as well as many other classes of functional materials. Furthermore, most studies that focus on the assessment of DFAs concentrate on the global unit cell structure and not on the key local structure within the unit cell that ultimately determines dynamical properties, such as electronic and ionic transport. In this work, we analyze the global and local structure, relative energetics, and transition barriers for argyrodite family (LMSX), as all these properties conspire to determine the ultimate functionality of modern SEs.

LMSX (Li6±xM1±yS5±zXn) framework can support the incorporation of various halogens (X: Cl, Br, I) and cations (M = P, Ge). Consequently, these frameworks display diverse levels of ionicity and covalence, contingent on the specific halogen component, cation blending, and chalcogen-halogen (S/X) site disorder. This diversity allows tuning of the functionalities, such as, stability and diffusivity. There have been four prime strategies adopted recently to achieve high Li-diffusivity within LMSX SEs: halogen(X)-effect46, cation-mixing47, anion-mixing48, and Li off-stoichiometry (Li excess or deficiency)47,49. For instance, depending on the X component in Li6PS5X Li-ion conductivity can vary from 10−3 to 2 mS cm−1, for X = I to X = Cl/Br, respectively46. In an earlier work48, one of the current authors has proposed a mixed-anionic Li-P-S-Cl-Br compositional space Li5.25PS4.25ClBr0.75 that surpasses the parent compound Li6PS5Cl in terms of ionic conductivity. The halogen-rich LMSX framework Li5.5PS4.5Cl1.5 was demonstrated by Zuo et al.18, showcasing an enhancement in Li-conductivity but also manifesting pronounced electrochemical decomposition at lower potentials. Ample examples provided by these studies indicate that the LMSX class is represented by a library of compositional variants with diverse structure-property relationships. As a result, insights derived from understanding the LMSX class can be extrapolated to other classes of SEs.

Despite numerous previous studies and ongoing research efforts in the field of argyrodite chemistry, the persistent puzzle concerning composition, local structure, stability and Li diffusivity, remains unresolved. For instance, despite the presence of polarizable iodine sublattice, Li6PS5I exhibits poor Li-conductivity compared to Li6PS5Cl. Zeier et al.46 have demonstrated that S/I site-disorder in Li6PS5I is almost zero while S/Cl site-disorder is 60% in Li6PS5Cl, leading to larger pre-factor and faster Li-conductivity in Li6PS5Cl. In contrast, the extent of S/I site-disorder in Li6.5P0.5Ge0.5S5I and S/Cl site-disorder in Li6PS5Cl are 3% and 60%, respectively, while the Li-ion conductivity in Li6.5P0.5Ge0.5S5I is almost one order of magnitude higher than the later47. Thus, the enduring puzzle lies in the local structure influenced by the varying degree of S/X site disorder and its effects on Li-conductivity within the LMSX SEs. Moreover, the role of X atoms extends beyond polarization, encompassing electrostatics, Pauli repulsion, and dispersion, with the latter three factors still not fully comprehended. Consequently, refining the compositional space of argyrodites remains an ongoing trial-and-error process.

LMSX-based and other SEs share common features, characterized by immobile anionic frameworks and mobile Li-ion sublattices, wherein covalent and ionic bonding coexists with polarization and van der Waals (vdW) interactions. Our study thoroughly investigates the influence of non-locality in both electronic exchange and correlation interactions. We demonstrate that HSE06+MBDNL, a functional incorporating nonlocality in both exchange and correlation energy, exhibits predictive accuracy in describing global and local structure as well as Li-diffusion properties. Our subsequent goal is to unravel a persistent puzzle: understanding the role of the X sub-lattice in adjusting the potential energy surface. The ultimate objective is to establish a comprehensive framework for understanding the interplay between structure and lithium conductivity across the LMSX compositional space. This comprehension holds potential value in providing insights into the chemistry of other classes of solid ionic materials.

Results and discussion

Global and local structure of the LMSX frameworks

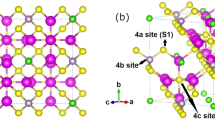
Figure 1 illustrates the conventional unit cell representation of Li6PS5X (X = Cl, I). In the ordered (O) configuration, X− anions form a face-centered cubic lattice (Wyckoff positions 4a), while P in \({{{{{\rm{PS}}}}}_{4}}^{3-}\) tetrahedra occupy Wyckoff positions 4b, and S2− anions fill half of the tetrahedral voids (Wyckoff positions 4c). In Li6PS5I, I− and S2− anions occupy separate crystallographic sites 4a and 4c, respectively, favoring an O-arrangement for X− and S2− (Fig. 1a)13,46. Conversely, Li6PS5Cl and Li6PS5Br exhibit notable S/X site disorder, likely due to their similar ionic radii, resulting in a disordered (D) local environment between the S and X sub-lattices13,50.

Fig. 1: Ordered and disordered configurations of the anionic sublattice in Li6PS5X (X = Cl, Br, I).
figure 1

a Ordered (O) configuration of the anionic sublattice in Li6PS5X, where X = Cl, Br, I, with X− and S2− anions located at distinct crystallographic sites 4a and 4c, respectively. b Disordered (D) configuration of the anionic sublattice caused by S2−/X− site-disorder.

Full size image

Figure 2a presents benchmarking results evaluating the performance of various DFAs in predicting cell volume. While TS and MBDNL yield consistent results when combined with PBE and HSE06, the D3 method produces significantly different volume estimates under the same conditions. Notably, the comparison between PBE+D3 and HSE06+D3 reveals large discrepancies, whereas the difference between PBE and HSE06 alone is minimal. This highlights that the inconsistency in our results stems primarily from the use of the D3 method, leading us to exclude these pairings from further consideration. The predicted volumes by PBEsol, optB88, and HSE06+MBDNL compare well with experimental measurements. The consideration of thermal effects at 300K on the unitcell volume further improves the performance of HSE06+MBDNL, but makes the agreement worse for optB88 and PBEsol. While at least three methods (optB88, PBEsol and HSE06+MBDNL) yield seemingly good volumes when compared to experiment, only HSE06+MBDNL yield qualitatively correct results for local structure within the unitcell (Fig. 2b).

Fig. 2: Comparison of computational and experimental structural properties of Li6PS5Cl and Li6PS5I.
figure 2

a Volume of the supercell (52 atoms) of Li6PS5Cl and Li6PS5I computed with various xc functionals. Room temperature experimental cell volumes have been shown in the extreme left column for the crystal structure of Li6PS5Cl (ICSD ID: 259205) and Li6PS5I (ICSD ID: 142471). Cell volume at 300K have been computed with quasi harmonic approximations at HSE06+MBDNL level of theory to compare with the room temperature experimental volume, as shown in extreme right column. b Cl-Li radial pair distribution functions, g(r), are calculated based on the Li6PS5Cl structures with S2−/X− disorder between 4c/4a sites (D) and S2−(4c)/X−(4a) site ordering (O). Experimental reference for g(r) has been obtained after averaging the characteristics of crystal structures of Li6PS5Cl from ICSD database, as shown by black solid line.

Full size image

Specifically, PBEsol and optB88 over-stabilize the distortion of ClLi6 polyhedra, resulting in a wide range of Li-Cl bond distances from 2.53 Å to 3.50 Å, contrasting with experimental data (ICSD-259205) which shows nearly isotropic Cl distribution around Li (Fig. 2b). The narrow range of Li-Cl distances (2.60–2.86 Å) predicted by HSE06+MBDNL agrees well with experimental observation. Hence, only the HSE06+MBDNL method with its non-local description of electronic interactions manages to correctly capture both the global unit cell structure and the local Li-Cl bonding within the Li6PS5Cl configuration, as illustrated in Fig. 2b. To investigate the origin of local structural distortion in ClLi6 polyhedra (using PBEsol and optb88 functionals), we attempt to disentangle the individual contributions of the ordered and disordered anionic (S2‒/X‒) sublattices. As shown in Fig. 2b, the Cl-Li radial distribution function aligns with the shape observed experimentally in the S/X disordered configuration. However, in the S/X ordered configuration, local structural distortion becomes apparent. These findings also suggest that Li atoms reorganize to establish the local environment of ClLi6 polyhedra based on the arrangement of the anionic sublattice. Additionally, the distribution of Li and vacancies is further affected by nonlocal exchange correlation terms that account for dispersion interactions.

As the next step, we evaluated the stability differences between ordered and disordered configurations (Eorder and Edisorder) to understand the role of S/X site disorder. The relative energy (ΔERE = Edisorder − Eorder) was used to quantify the propensity for S/X exchange, with negative or smaller ΔERE values indicating thermodynamically favorable disorder. Table 1 highlights the importance of selecting the appropriate dispersion scheme for predicting S/X site disorder. Our HSE06+MBDNL results align well with experimental findings, demonstrating significant anionic site disorder for X = Cl and Br, but negligible disorder for X = I (see Table 1). This trend is linked to weaker van der Waals stabilization for Cl and Br-approximately 15 meV/atom less than for I-which facilitates S/X disorder in materials like Li6PS5Cl and Li5.25PS4.25ClBr0.75, compared to Li6PS5I and Li6.5Ge0.5P0.5S5I.

Table 1 Thermodynamic stability, structural, and dispersion properties of ordered and disordered S/X site configurations in Li6PS5Cl, Li6PS5I, Li6.5Ge0.5P0.5S5I, and Li5.25PS4.25ClBr0.75
Full size table

In Li6PS5Cl, S2−/X− disorder induces more extensive geometric rearrangements and modifications of non-covalent interactions compared to the Cl-Br mixed framework Li5.25PS4.25ClBr0.75. We found that three key factors influence the extent of S2−/X− disorder: (1) the relative energy difference (ΔERE), (2) the change in volume (ΔV = Vdisorder − Vorder), and (3) the strength of van der Waals interactions (EDispersion). A reduction in any of these parameters lowers the likelihood of S/X site disorder. The optB88 results are broadly consistent with the HSE06+MBDNL predictions but tend to overestimate the cell volume and overly stabilize the ordered state in Li6PS5Cl due to incorrect distortion of the ClLi6 polyhedra. Similarly, the semi-local PBEsol DFA struggles to capture the thermodynamic stability of S/X disorder in Li6PS5Cl, as shown by the large ΔERE value in Table 1. Additionally, the pairwise van der Waals approximation (HSE06+TS) fails to correctly predict the volume, irrespective of the ordering within the S2−/X− sub-lattices.

These observations highlight the superior accuracy of the HSE06+MBDNL approach, which captures the interplay between electrostatics, polarization, and dispersion interactions essential for predicting the global and local structure of LMSX materials. In particular, a reliable treatment of dispersion interactions is critical for accurately modeling the degree of S/X disorder.

S/X site disorder and its impact on the Li-distribution

Building on the previous discussion of HSE+MBDNL’s capability to accurately predict both local structure (S/X disorder) and global volume, the impact of S/X disorder on Li connectivity is analyzed. The distribution of Li ions is evaluated within the LMSX framework both with and without S/X site disorder (Fig. 3). The count of Li-diffusion pathways across different Li-jump distances as depicted in Fig. 3, is determined by calculating potential geometric paths connecting Li atoms. However, it is important to note that Li-connectivity alone does not guarantee that these are energetically favorable paths. Shorter distances denote Li movements confined within the same cage, termed intra-cage hopping, while distances exceeding 3.1 Å correspond to movements between cages, known as inter-cage hopping. Diffusion lengths up to 5 Å indicate long-range Li-hopping, potentially involving consecutive shorter local hops.

Fig. 3: Effect of anionic site disorder on lithium diffusion.
figure 3

Influence of (a) ordered and (b) disordered S2−/X− sites on regulating the available lithium diffusion paths and corresponding Li-jump distances in Li6PS5Cl, Li6PS5I, Li5.25PS4.25ClBr0.75, and Li6.5Ge0.5P0.5S5I.

Full size image

Despite local structural variations caused by S/X site disorder (Table 1), the overall volume of the LMSX frameworks remains largely unchanged. Notably, these local structural changes influence the Li connectivity within the framework (Fig. 3). Although the activation energy (Ea) is only marginally affected by S/X site disorder48, distinct diffusion channel patterns indicate that Li distribution within the LMSX framework is modulated by the arrangement of S/X atoms, aligning with prior findings51. These results highlight the critical role of S/X disorder in shaping the local structure and governing Li-ion/vacancy ordering in the LMSX family. Further analysis employing HSE06, HSE06+TS, and HSE06+MBDNL (Supplementary Fig. S1 in the SI) reveals that the Li distribution varies depending on the dispersion scheme used, consistent with the differences in the predicted local Li structure across the different density functional approximations (DFAs).

In general, the disorder of the S/X site facilitates an increase in the number of Li diffusion channels compared to the ordered S/X framework (Fig. 3), resulting in elevated prefactor values and enhanced Li conduction, as evidenced in Li6PS5Cl (see Table 1). Conversely, in Li6PS5I, characterized by dominant S/X site ordering, fewer Li diffusion channels and lesser prefactor values are observed, as detailed in Table 1. In instances of Li-deficient (Li5.25PS4.25ClBr0.75) and Li-excess (Li6.5Ge0.5P0.5S5I) LMSX frameworks, crystal symmetry disruptions already exist, resulting in diverse Li diffusion channels irrespective of S/X site disorder. Notably, Li concentration also influences the prefactor in (Li5.25PS4.25ClBr0.75) and (Li6.5Ge0.5P0.5S5I). Consequently, despite available Li diffusion paths, Li5.25PS4.25ClBr0.75 exhibits a lower prefactor. Nevertheless, the impact of Li off-stoichiometry outweighs that of anion-site disorder. Hence, disorder at the S/X sites significantly modifies the Li distribution in stoichiometric LMSX frameworks, encompassing compositions like Li6PS5Cl, Li6PS5Br, and Li6PS5I.

Understanding the potential energy surface (PES) for Li-diffusion

Comprehending the potential energy surface (PES) that governs Li-diffusion is essential for optimizing Li-ion mobility in LMSX. Nevertheless, the longstanding question of the interplay between mobile cations and the anionic framework persists44,52,53. To gain a deeper understanding of the impact of these interconnected oscillations on Li migration, an analysis of the phonon modes using both pairwise and many-body dispersion methods (HSE06+TS and HSE06+MBDNL) was conducted (Fig. 4 and Supplementary Fig. S2). Analysis of phonon modes reveals that Li-X (X = Cl and I) dynamics implied weakly bound Li ions, characterized by low-frequency vibrations regardless of the specific X atom present. In both Li6PS5I and Li6PS5Cl, these vibrations manifest within distinct frequency ranges, reaching up to 5 THz and 7 THz, respectively. Importantly, these frequencies remain below the critical threshold of 8-10 THz, suggesting lower impact on hindering Li diffusion within the LMSX framework, as reported in previous studies54.

Fig. 4: Phonon spectra analysis and vibrational modes in Li6PS5Cl and Li6PS5I.
figure 4

Phonon frequencies computed with HSE06+MBDNL for: a Li6PS5Cl and b Li6PS5I. Vibrational modes associated with the highest frequency range of phonon spectra corresponding to P-S-Li stretching are highlighted in the insets. “Asymmetric vibration” is the degree of freedom by which net changes in the Li-displacement are facilitated. By “ordered vibration,” the absence of random forces is indicated, ensuring that no uncompensated forces result in any displacement of the mobile sublattice. In the inset of the structural and high frequency phonon modes, element sizes are arbitrary for clarity.

Full size image

In this low-frequency range of 1-7 THz, there is a coupled oscillation between the framework and Li-ions. For example, modes in the 2.2–2.6 THz range for Li6PS5I, which drive net Li-diffusion in a particular direction, are strongly linked to the motion of the framework X-atoms (Supplementary Fig. S3 in SI). These low-frequency vibrational modes can be thermally activated, implying that the thermal energy aiding Li-migration also supports the vibrations of the framework S and X-atoms. This finding holds true for both the pairwise and many body van der Waals interaction models (Supplementary Figs. S2 and S3 in SI). Notably, a distinction arises in the vibrational behavior specific to the X atoms. While the vibrational modes involving Iodine sublattice exhibit a sharp peak at a lower frequency 1.5 THz (ranging from 0.3 to 3.5 THz), those associated with Chlorine sublattice display a broader and blue-shifted peak at 3.5 THz spanning from 1.25 to 7 THz. Such lower frequency motion for X = I implies a competition with thermally activated Li dynamics in Li6PS5I. In contrast, the utilization of thermal energy for framework halogen vibration is comparatively reduced in Li6PS5Cl, thereby enabling a more effective utilization for Li activation and diffusion.

In the intermediate frequency range of 8–11 THz (33–45 meV), Li-diffusion is coupled with the sulfur sublattice, while phosphorus-sulfur (P-S) stretching is negligible (Fig. 4 and Supplementary Fig. S3). This finding aligns with previous research55 linking phonon energy to Li-diffusion behavior while the primary contributors to these phonon modes are the coupling between Li+ ions and rotational motion of \({{{{{\rm{PS}}}}}_{4}}^{3-}\) anions. At higher frequencies (>16 THz), Li-ions couple with P-S stretching modes (Supplementary Fig. S3), which potentially contributes to the immobilization of Li ions within the framework. The coupling between the framework and Li in these intermediate to high-frequency ranges is fine-tuned by the chosen van der Waals (vdW) scheme. For example, in the 9.1–9.3 THz range, multidimensional Li-diffusion in Li6PS5I is more feasible with a pairwise treatment of vdW interactions (Supplementary Fig. S3). The pairwise approximation derived phonon modes further indicate that the high-frequency P-S-Li vibrations are associated with facile Li migration, as shown by the net Li displacement vector at 16.7 THz (Supplementary Fig. S3). Consequently, using the pairwise vdW interaction scheme leads to the underestimation of the migration barrier (Fig. 5), while application of the many body dispersion scheme (MBDNL) avoids such discrepancy.

Fig. 5: Analysis of inter-cage Li-hopping pathways and vdW stabilization in Li6PS5Cl, Li5.25PS4.25ClBr0.75, Li6PS5I, and Li6.5Ge0.5P0.5S5I.
figure 5

Inter-cage Li-hopping with jump-distance of 3.3 Å are shown by the solid lines: a, e Li6PS5Cl, b, g Li5.25PS4.25ClBr0.75, c, f Li6PS5I, and d, h Li6.5Ge0.5P0.5S5I, computed with PBEsol, and HSE06 level of theories coupled with pair-wise (PW : TS) and or many body dispersion (MBDNL) schemes for vdW interaction. vdW contribution to the relative stability of the initial state and transition states is shown by the dashed lines connecting the spherical dots. The highest van der Waals stabilization exhibited by the particular reaction coordinate along the diffusion path, is scaled to zero.

Full size image

The high-frequency modes in the 16–18 THz range (computed using the HSE06+MBDNL method) are linked to the anisotropic stretching of the SLi6 octahedra in Li6PS5Cl (inset Fig. 4a), which facilitates the mobility of Li ions. In contrast, the isotropic nature of the Li-S coupling is dominant within the Li6PS5I framework (inset Fig. 4b). We emphasize that the nature of the P-S-Li frequency mode is passively modulated by the presence of the X atom in the framework, determining the extent of anisotropy. Anisotropic interactions facilitate Li diffusion because the Li migration process is inherently linked to anharmonic modes, a characteristic observed in diffusion across ionic solids. This is because the transition state does not experience additional destabilization from the anisotropic stretching, as seen in Li6PS5Cl. Conversely, symmetric stretching hinders the diffusion process due to the unfavorable mode associated with the transition state.

Li-diffusion paths with varying lengths and their corresponding barriers for Li6PS5Cl and Li6PS5I are detailed in Supplementary Figure S6. To understand the impact of dispersion interactions on the Li-migration process, an uniform hopping distance of  ≈3.3 Å is standardized for all four systems under consideration (Li6PS5Cl, Li6PS5I, Li5.25PS4.25ClBr0.75 and Li6.5Ge0.5P0.5S5I), which is reasonably close to these minimum energy paths as well (Fig. 5a–d). In Fig. 5a, the lattice is presented in its conventional crystallographic setting, while in Fig. 5b–d, it is shown in its primitive setting. These different representations are used to better visualize the selected Li-diffusion paths. To examine how different dispersion schemes influence the energetics, we performed self-consistent field calculations along the diffusion coordinates determined by HSE+MBDNL, using both PBEsol and HSE+TS methods (Fig. 5e–h). The energy differences observed between the initial and final states for certain diffusion paths (Supplementary Fig. S6) arise from the corrugated nature of the PES. This variation reflects the complex topology of the PES, where changes in atomic positions along a diffusion pathway result in different energy minima and transition points. The comparison also reveals distinct effects of the theoretical schemes. As shown in Fig. 5e, f, MBD interactions destabilize the transition state for Li6PS5I (contributing  ~10% of the total migration barrier) which is not the case for Li6PS5Cl. Thus, resistance to Li migration arises in frameworks with prevailing isotropy, causing the transition state to become relatively more destabilized, as seen in Li6PS5I. When considering Li off-stoichiometry in Li5.25PS4.25ClBr0.75 and Li6.5Ge0.5P0.5S5I, the intrinsic isotropic nature of the framework is perturbed. This leads to no additional destabilizing influence on the transition state. Therefore, it is imperative to understand the interplay between lattice-Li coupling and the consequent stabilization driven by MBD interaction in order to fully understand the Li ion dynamics within LMSX materials.

Further analysis has been conducted on additional diffusion paths with varying lengths and their corresponding barriers for Li6PS5Cl (Supplementary Fig. S7) and Li6PS5I (Supplementary Fig. S8). However, the conclusion remains unchanged-differences in the stability of the transition, initial, and final states are introduced by the pair-wise (PW: TS) approximation. The activation energy (Ea) is either underestimated or overestimated by the PW approximation, depending on the diffusion path, in comparison to the MBDNL approximation (Supplementary Figs. S7, S8). These findings further emphasize that the modulation of diffusion energetics depends on the chosen dispersion interaction scheme, regardless of the selected paths.

The impact of dispersion interaction is also reflected in the differing local coordination environments of diffusing Li ions when comparing results from the PW approximation and those incorporating MBDNL (Fig. 6). The most surprising observation is that many-body effects in vdW interactions can change the ionic Li-S and Li-X bond lengths in the transition state by as much as 0.24 and 0.66 Å, respectively. The enhanced role of MBD interactions on transition state geometries has been previously observed for point defects in covalently-bound semiconductors56, however LMSX materials exhibit much stronger MBD effects perhaps due to relatively weaker ionic bonds. Hence, the rigorous consideration of many-body dispersion interactions ensure the accurate prediction of stable Li-site structures as well as migrating Li ions at transition states. In agreement with previous literature on the role of MBD effects on the transition state of point defects in semiconductors56 and benzene interacting with different metal surfaces57, MBD yields different energy profiles along transition pathways in LMSX materials (Fig. 5), in contrast to more approximate PW approximations. This is due to nontrivial polarization screening captured by MBD and found in complex materials as shown in ref. 56, and confirmed by explicitly correlated electronic structure theory in ref. 58.

Fig. 6: Impact of pairwise vdW interactions and many-body dispersion on local coordination along diffusion pathways.
figure 6

The effect of pairwise (PW: TS) vdW interactions and non-local many-body dispersion (MBDNL) combined with the HSE06 method, on tuning the local coordination environment of the migrating Li-ion. Equilibrium states (stable sites, either initial or final as described in Fig. 5) are denoted as Li(S)PW/MBDNL, and transition states are denoted as Li(T)PW/MBDNL. Li-ion is tetrahedrally coordinated, with bond lengths for three Li-Sn bonds (n = 1, 2, 3) and one Li-X bond (X = Cl/Br/I) provided in Å. Lithium migration pathway for Li6PS5Cl, Li5.25PS4.25ClBr0.75, Li6PS5Cl and Li6.5Ge0.5P0.5S5I as described in Fig. 5, are considered.

Full size image

Discussion

In the literature, there have been extensive efforts to design and understand the chemistry of solid electrolytes. However, a universal design principle for solid electrolyte frameworks is yet to be developed, partly because of the lack of understanding of the factors that dictate local structure and diffusion behavior. Commonly utilized computational approaches for ionic solids often include PBE with empirical dispersion correction schemes or the recently developed PBEsol methods with a modified exchange and correlation term. Nevertheless, the non-locality of long-range exchange and correlation terms is frequently neglected in computational investigations of local structure. We have identified that the computational design of solid-state ionic materials is constrained by the loss of microscopic information because of inadequate description of the non-local many body dispersion (MBDNL) interactions. As a result, there is often a discrepancy between experimental findings and computational predictions, as demonstrated in this study using the argyrodite (Li6±xM1±yS5±zXn : LMSX) class as an example.

The applicability is far reaching to other solid electrolytes as well. For example, the importance of considering MBDNL for the dynamical stability is noted in the halide (Li3YCl6 : LYC), oxide (Li7La3Zr2O12 : LLZO), and sulfur-based (Li3PS4 : LPS) electrolyte systems (Supplementary Fig. S4). Supplementary Fig. S5 illustrates the prediction mismatch in species-resolved phonon contributions for LPS, LLZO, and LYC for two scenarios: with and without the MBDNL interaction. In the presence of the MBDNL effect, the highest frequency shifts from approximately 20 to 22 THz, primarily due to the modulation of the Li and O sublattice vibrations in LLZO. For LPS, the frequency range of 5 to 13 THz is modulated, mainly influenced by the Li and S sublattice. In the case of LYC, the motion of Li is modulated throughout the frequency range, with additional modulation in the 6–8 THz range attributed to the motion of Y and Cl. These results demonstrate that the dynamics of the solid electrolyte framework is significantly affected by MBDNL, leading to phonon frequency shifts that involve both the anionic sublattice and the mobile cation sublattice (Li). Notably, in the Garnet, a blue shift in the vibrational frequencies of the framework highlights the role of MBDNL interactions in predicting the stability of the oxide framework. For halide- and sulfur-based frameworks, MBDNL interactions modulate the intermediate frequency ranges associated with the S-Li coupling in LPS and the Cl-Li coupling in LYC. Thus, the broader implications of electronic structure methods and many-body dispersion interactions are identified for a diverse array of solid-state ionic materials.

Nonlocal many-body dispersion interactions play a crucial role in shaping Li-chemical environments, not only in equilibrium states but also across various geometries along the diffusion path, including transition states and intermediates. Energetics predicted by the commonly used pairwise dispersion approximation often result in inaccurately stabilized transition states and intermediates. In solid-state ionic frameworks, where metal ions encounter diverse local environments, accurately describing the energetics of these diffusion coordinates is essential for predicting migration barriers and overall conductivity. The lattice dynamics, particularly the translational motion of lithium ions associated with lattice-Li interactions, is significantly influenced by MBDNL effects. For instance, MBDNL interactions fine-tune the P-S-Li vibrational modes, thereby impacting ion mobility within the solid-state ionic framework. Consequently, the insights gained from the regulation of the PES for Li diffusion by MBDNL interactions are widely relevant to solid-state ionic diffusion in battery materials.

In summary, properties like global and local structure, lattice vibrational dynamics, and ion diffusion through solids have broad implications for various functional materials. In this study, our focus was on the argyrodite class of solid electrolytes, showcasing an intricate interplay among electrostatics, polarization, and dispersion interactions. Introduction of diverse halogens (X = Cl, Br, I) in Li6MS5X (M = P, Si, Ge, etc.) crystal results in distinct local structural ordering and Li-diffusion behaviors. Non-local many body dispersion (MBDNL) emerges as a crucial factor influencing local and global structures. Variations in M and X control aspects such as enhanced dispersion interactions, energy disparity between ordered and disordered S/X sublattices, and volume changes between ordered and disordered structures. These elements are linked to a reduced tendency for S/X site disorder, regulating the diffusion prefactor through the adjustment of available channels for Li diffusion.

Analyzing Li-X bonds highlights their role in accommodating loosely bound lithium ions that exhibit low-frequency vibrations (up to 7 THz), which are linked to the collective oscillations of the entire framework. These low-energy phonon modes allow thermal energy to influence the framework’s dynamics, rather than just overcoming the barrier to lithium migration. Interestingly, the Li6PS5I framework absorbs more thermal energy, competing with the activation of Li ions compared to the Li6PS5Cl framework. In addition, Li-S bonds confine Li ions within the framework, with the nature of P-S-Li vibrational modes passively modulated by X atoms. MBDNL interactions significantly influence asymmetric nature of these oscillations, impacting Li diffusion behavior. Commonly used semilocal xc functionals or those incorporating pairwise dispersion interactions are found to incorrectly stabilize transition-state structures relative to stable Li-sites, thereby affecting Li-migration barrier estimates. This emphasizes the imperative need to consider non-local exchange and dispersion interactions for a comprehensive understanding of the potential energy surface governing Li diffusion in solid ionic frameworks.

Methods

Material selection

The list of all LMSX materials studied in this work is presented in Table 2. Argyrodites covering four major cation/anion chemistries, including (a) Iodides, (b) Chlorides, (c) Li-deficient Cl-Br mixed anion, and (d) Li-excess Ge-P mixed cation compositions have been selected. The Table 2 showcases how the room temperature Li-ion conductivity (σRT) and Li-migration barrier (Ea) can be finely adjusted while tuning the LMSX compositions. Initial crystal structures were obtained from the Materials Project (MP)59 and the Inorganic Crystal Structure Database (ICSD)46,60. The conventional cell of Li6PS5Cl (ICSD ID: 259205) and Li6PS5I (ICSD ID: 142471), consisting of 52 atoms, were used for structural enumeration to identify the S/X site-disordered structures61. All enumerated structures were symmetrically distinct. The low-energy enumerated structures within relative energy limit of 30 meV/atom were averaged to find the radial pair distribution function. For disordered structures, structural enumeration was performed on supercells to obtain  ≈100 ordered candidates, and the lowest energy structure was used for further analysis.

Table 2 Argyrodite (Li6MS5X: LMSX) compositions investigated as solid electrolytes in this study
Full size table

First-principles calculations and the choice of exchange–correlation functional

Rigorous assessments were conducted on various computational methods to comprehensively explore the correlation between the structure and dynamics of LMSX SEs. The evaluation aimed to find a reliable semi-local exchange-correlation functional (xc-functional) along with an appropriate method for vdW dispersion interactions. Different DFAs, including Perdew-Burke-Ernzerhof (PBE)62, PBE for solids and surfaces (PBEsol)63, and the hybrid Heyd-Scuseria-Ernzerhof (HSE06) functional64, were assessed with various schemes for vdW interactions applied. Suitability of several vdW methods were scrutinized, encompassing commonly employed pairwise approximations like Grimme’s D-series65,66,67, the optB88 functional68,69 and the Tkatchenko-Scheffler (TS) approach70. Progressions in methodology extended to beyond atom-pairwise approaches, notably the range-separated self-consistently screened (rsSCS) variant of the Many-Body Dispersion (MBD) method71, represented as MBD@rsSCS72. The integration of the non-local variant of the MBD framework, denoted as MBDNL in this paper73, along with the non-local vdW density functional74, enabled an unbiased treatment of ionic, metallic, and non-covalent forces within LMSX frameworks.

All electronic structure calculations were carried out using the Fritz Haber Institute ab initio materials simulations (FHI-aims) code, employing the “tight” basis set75,76,77,78,79. Geometry relaxation was performed with energy and force convergence criteria of 10−6 eV and 0.02 eV/Å, respectively and the density of k-grid was set to 3.5 /Å−1. The computational cost of the applied methods is illustrated by reporting the time per SCF step for optimizing the initial geometry of Li6PS5I (CCSD ID 1731529, 52-atom supercell). The CPU times are as follows: PBE (20 s) and HSE06 (177 s). All benchmarks were performed on the Paramganga HPC cluster at IIT Roorkee, using 2 × Intel Xeon Cascadelake 8268 nodes with 48 cores per node. The inclusion of TS and MBDNL terms does not change these timings appreciably. As the number of atoms in larger cells increases, the time ratio between HSE and PBE calculations reduces to a factor of 2 to 3, as demonstrated by Kokott et al.80. The cell volume at 300 K was calculated using quasi-harmonic approximations at the HSE06+MBDNL level of theory, with volume expansion and compression constrained within a range of  − 10% to  + 10%. Phonon dispersion curves were computed by utilizing the finite displacement method as implemented in the PHONOPY code coupled with the HSE06-MBDNL functional81,82. To assess the tendency of LMSX structures to display S/X site disorder, the relative energy (ΔERE) was calculated by comparing the stability of two representative structural configurations: (1) Ordered (O), where S exclusively occupies 4c sites and X is positioned at 4a sites and (2) Disordered (D), characterized by fractional occupancy of S at 4a sites and X at 4c sites (Fig. 1). The Python Materials Genomics (pymatgen)61,83 and pymatgen-diffusion packages84 were used for the analysis of Li-diffusion paths. Activation barriers for a Li ion in LMSX lattices were calculated using the climbing-image nudged elastic band method with a force convergence criterion of 0.02 eV/Å85.