Introduction

As critical subsystems that straddle different topological phases, topological interfaces are host to exotic phenomena ranging from robust chiral anomalies to percolating edge states1,2. Particularly in higher dimensions, such interfaces become especially rich due to the directional interplay between different localization mechanisms, as epitomized by higher-order3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19 and hybrid skin-topological states20,21,22,23,24,25. Of late, the prospect of time-periodic (Floquet) driving has introduced yet another new level of complexity by opening up the temporal dimension26,27,28,29,30,31,32,33,34,35,36.

Drawing inspiration from topological phenomena and singularities arising from spatial lattice dislocation37,38,39,40,41,42,43,44,45,46,47, it naturally prompts the question of whether intriguing new physics may also emerge from dislocations in temporal space48,49. Time-varying materials have recently garnered significant attention due to their rich physics and potential for novel functionalities50,51,52,53,54,55. Existing phenomena induced by temporal variations or interfaces, such as temporal photonic crystals50, metasurfaces56, temporal reflection, and refraction52,53,54,55, have already found great promise in new signal processing applications, transcending the scope of space-varying materials in many aspects. However, interfaces between subsystems at different times have remained relatively elusive, partly due to their perceived experimental inaccessibility.

In this work, we, for the first time, theoretically and experimentally report observation of higher-order Floquet topological corner modes (TCMs) at the interface between subsystems effectively occurring at different times. This is achieved by representing our two-dimensional (2D) higher-order topological system in the frequency space, such that multiple copies of it are stacked along an additional frequency dimension. Notably, each 2D layer is translation invariant across the temporal boundary, even though the TCMs are spatially localized around it. Our resultant 3D lattice is physically realized in an electrical circuit metamaterial, whose freedom in node connectivity allows for the versatile implementation of its Floquet driving terms as inter-layer couplings. While electrical circuit arrays have been previously harnessed to realize static nodal and higher-order topological phenomena19,57,58,59,60,61,62,63,64,65,66, this is the first time it has been used to realize anomalous Floquet modes.

Results

Time-dislocation induced higher-order topological modes

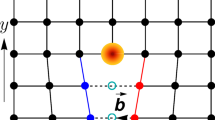
The concept of temporal dislocations extends our interpretation of time beyond its usual steady flow. In a periodically time-modulated system, different regions can effectively exist at different times if there exists a phase offset between them. This is analogous to having spatial dislocations (Fig. 1a), which occur when there is a disruption or misalignment in a spatial structure of the material. For instance, if one part of a system advances in time while another part lags behind, a time dislocation forms in the region where the system fails to be synced in time.

Fig. 1: Spatial and temporal dislocations.
figure 1

a A spatial lattice dislocation such as the screw dislocation breaks translation symmetry in the z-spatial direction. b A temporal dislocation can be generated by introducing time shifts or disruptions in a periodically driven system, and breaks time translation invariance. Temporal dislocations can give rise to Floquet topological c edge and d corner modes within the first- and second-order topological phases, respectively, even though the system remains spatially translation invariant. The red and blue balls (skinny arrows) represent the TCMs (TEMs) induced by the temporal dislocations and spatial boundaries, respectively.

Full size image

In this work, we consider temporal dislocations that exist in periodically driven Floquet topological lattices i.e., occur at the interfaces between different stages of the periodic driving (Fig. 1b), such as between H(t) and H(t + T/2) where T is the modulation period. As shown in Fig. 1c, d, distinct from topological spatial dislocations, temporal dislocations can lead to the emergence of Floquet topological edge modes (TEMs) and TCMs (see Supplementary Notes 2, 3 for more details). This work specifically delves into time-dislocation-induced TCMs in Floquet higher-order topological phases (HOTPs).

For definiteness, we consider the Benalcazar–Bernevig–Hughes (BBH) model3, a paradigmatic system for studying higher-order topological phases. As illustrated in Fig. 2a, this model can be interpreted as a two-dimensional Su–Schrieffer–Heeger model with alternating hopping amplitudes in both directions. The key distinction is the presence of a π-flux threading each plaquette, evidenced by the negative hopping terms denoted by the dashed lines. In the presence of periodic driving, it can be described by the following Bloch Hamiltonian

$$H(t)= (\gamma (t)+\lambda \cos {k}_{x}){\Gamma }_{1}-\lambda \sin {k}_{x}{\Gamma }_{4}\\ - (\gamma (t)+\lambda \cos {k}_{y}){\Gamma }_{3}-\lambda \sin {k}_{y}{\Gamma }_{2}$$
(1)

where the periodic driving is applied on the intra-cell couplings via \(\gamma (t)=\gamma -2V\cos (\Omega t)\), with V and Ω = 2π/T being the driving amplitude and frequency, respectively. Γ1 = τxσ0 and Γ2,3,4 = τyσx,y,z are the Dirac matrices defined in the sublattice space, γ and λ represents the intra- and inter-cell couplings. In the absence of periodic driving, the above Hamiltonian is reduced to the static BBH model, featuring nontrivial (trivial) static HOTPs for γ < λ (γ > λ), characterized by the mirror winding number ν = 1 (ν = 0)3.

Fig. 2: Time-dislocation induced Floquet higher-order topological modes.
figure 2

a Schematic illustration of Floquet BBH model H(t) and b its representation in the frequency space. Here the z-direction simulates the frequency dimension. c Circuit diagram for the inter- and intra-layer couplings. d Photograph of the printed circuit board for implementing Eq. (4). e Floquet mirror winding numbers (G0, Gπ) as a function of γ/λ and Ω/λ for V = γ, showing topologically nontrivial phases in much of parameter space except for (0, 0). f Simulated admittance spectrum at the resonant frequency ωr = 2π × 1.52 MHz (fr = ωr/2π) for the circuit with γ/λ = 0.5 and Ω/λ = 2.27, exhibiting in-gap Floquet topological modes (red and blue points) protected by (G0 = 1, Gπ = −1). g Zoomed-in Floquet spectrum of the real-space analog of the first quasienergy zone, revealing fourfold degeneracy in the topological modes. h, i Same as (a, b) except the right half representing H(t + T/2), effectively creating a temporal dislocation interface in the middle (dashed line). j Circuit diagram for the inter- and intra-layer couplings in the left and right sides of the temporal dislocation, and k the fabricated printed circuit board for implementing Eq. (S27) in Supplementary Note 7. l–n Same as (e–g) but for dislocation topological invariants (ΔG0, ΔGπ) and the admittance spectra in the (ΔG0 = 0, ΔGπ = 1) phase.

Full size image

Distinct from the static BBH model, the periodically driven BBH model features periodic quasienergy spectra and both 0- and π-mode gaps67,68,69. To identify its bulk topology, we introduce Floquet mirror winding numbers G0 and Gπ, which are defined in terms of the Floquet operators (see Supplementary Note 1 for the definition). The nontrivial (nonzero) values of G0 and Gπ, respectively, identify the 0- and π-mode gaps as topologically nontrivial. The corresponding topological phase diagram, depicted in Fig. 2e, is derived as a function of the ratio γ/λ and the driving frequency Ω. As shown, in sharp contrast to the static BBH model, which hosts two kinds of HOTPs, the periodically driven BBH model exhibits much richer nontrivial Floquet HOTPs, distinguished by the values of Floquet topological invariants (G0, Gπ). Notably, as γ > λ, the system even remains topologically nontrivial and hosts larger numbers of π-mode TCMs. Contrary to the static BBH model, this case is topologically trivial. The transitions between different Floquet HOTPs are determined by the closing of 0- or π-mode gaps, as indicated by the dashed or solid lines.

Although it is in-principle possible to realize the real-time modulated coupling in photonic26, acoustic70, electrical circuits71 or ultracold atomic72 platforms, for this work, we physically implement the temporal driving as physical couplings along an additional frequency dimension. This not only facilitates the implementation of temporal dislocations, but also allows for the direct observation of Floquet time-dislocation TCMs through steady-state impedance measurements.

The Floquet states for a periodically driven Hamiltonian is most clearly expressed in the frequency space73. As given in Eq. (1), the periodically driven BBH model contains a single-harmonic driving,

$$H(t)={H}_{{{{\rm{BBH}}}}}+{V}_{d}{e}^{i\Omega t}+{V}_{d}^{{{\dagger}} }{e}^{-i\Omega t}$$
(2)

where Vd = V(Γ3 − Γ1) and HBBH = H(V = 0). After transforming into frequency space, the above 2D lattice Hamiltonian takes a block-tridiagonal form (see the Method section) and acquires an additional frequency dimension n, described by a 3D Hamiltonian

$$H={\sum}_{{l}_{n}}({H}_{{{{\rm{BBH}}}}}+n\Omega )\otimes {c}_{{l}_{n}}^{{{\dagger}} }{c}_{{l}_{n}}+{V}_{d}\otimes {c}_{{l}_{n}}^{{{\dagger}} }{c}_{{l}_{n+1}}+\,{\mbox{H.c.}}\,,$$
(3)

where ln denotes the specific layer along the frequency space dimension n. As depicted in Fig. 2b–d, we utilize a circuit metamaterial array to implement the 3D lattice Hamiltonian, where the circuits aligned along the z-direction emulate the frequency space n74. Within each layer, the desired positive and negative intra- and inter-cell couplings are implemented by the inductors L1, L2, and capacitors C1, C2, together realizing the BBH model (see Supplementary Note 6). The layer-specific on-site energy shifts are engineered by carefully designing the grounding terms in each layer (see Supplementary Note 6). The couplings between nearest-neighbor layers are achieved by the inductor L0 and the capacitor C0. At the resonant frequency, \({\omega }_{r}=1/\sqrt{{L}_{1}{C}_{1}}=1/\sqrt{{L}_{2}{C}_{2}}=1/\sqrt{{L}_{0}{C}_{0}}\), the circuit Laplacian reads

$$J({\omega }_{r})=\, {\sum}_{{l}_{n}}({J}_{0}({\omega }_{r})+{\Omega }_{n}){c}_{{l}_{n}}^{{{\dagger}} }{c}_{{l}_{n}}\\ +V({\omega }_{r}){c}_{{l}_{n}}^{{{\dagger}} }{c}_{{l}_{n+1}}+V({\omega }_{r}){c}_{{l}_{n+1}}^{{{\dagger}} }{c}_{{l}_{n}}$$
(4)

where \({\Omega }_{n}=i\sqrt{{C}_{0}/{L}_{0}}n\Omega\), \(V({\omega }_{r})=i\sqrt{{C}_{0}/{L}_{0}}({\Gamma }_{3}-{\Gamma }_{1})\) and J0(ωr) = iHBBH, with C1 = γC0, C2 = λC0, L1 = L0/γ and L2 = L0/λ.

Due to topological bulk-boundary correspondence, the values of (G0, Gπ) respectively determine the numbers of 0- and π-mode (or  −π-mode) TCMs in the corners of this lattice. To confirm this, as exemplified in Fig. 2(f) for the phase (G0 = 1, Gπ = −1), we numerically simulate the admittance spectrum of the circuit Laplacian in Eq. (4) under open boundary conditions (OBCs). In the simulations, the truncation of the frequency lattice layers to  −2 ≤ n ≤ 2 negligibly affects the results. As illustrated, the corresponding admittance spectrum simulates the quasienergy spectrum of the periodically driven BBH model. Given the localized nature of the eigenstates, as shown in Fig. 2g, the spectrum of the truncated Hamiltonian remains a reliable approximation to the exact results within the real-space analog of the first quasienergy zone (even the second one)73. Outside of the first and second quasienergy zones, the translational invariance along the frequency dimension is broken due to finite-size truncation. It is clearly observed that, in addition to the four TCMs (blue points) emerged in the 0-mode (±2π-mode) gap, there are also four TCMs (red points) in the  ±π-mode (±3π-mode) gaps, which are unique to Floquet HOTPs.

Now, we describe how temporal dislocations are implemented in our physical 3D metamaterial setup. As illustrated in Fig. 2h, the left and right sections of the system are governed by H(t) and H(t + T/2), respectively. Upon mapping to frequency space, this temporal dislocation appears as an interface in the inter-layer couplings along the z (frequency) direction (Fig. 2i, k). Notably, the intra-layer couplings within the x-y plane remains untouched by the temporal interface, and are perfectly identical on either side of it, even though the interface TCMs would accumulate within the x-y plane. This interface is realized by appropriately designing z-direction circuit elements (Fig. 2j). In particular, we find that the frequency space of H(t + T/2) can be implemented by designing the right-side z-direction inter-layer couplings \(V({\omega }_{r})=-i\sqrt{{C}_{0}/{L}_{0}}({\Gamma }_{3}-{\Gamma }_{1})\) (see the Supplementary Note 7 for more details).

The topological characteristics of the temporal dislocation are characterized by the Floquet topological invariants on either side, i.e., \({G}_{0,\pi }^{L,R}\). A comparison between the topological phase diagrams for H(t) and H(t + T/2) is presented in Fig. S1a, c of Supplementary Note 1, in terms of \({G}_{0,\pi }^{L}\) and \({G}_{0,\pi }^{R}\), respectively. Based on their differences, we define the Floquet topological invariants for the temporal dislocation

$$\Delta {G}_{0,\pi }=\frac{{G}_{0,\pi }^{R}-{G}_{0,\pi }^{L}}{2},$$
(5)

which respectively determine the numbers of 0- and π-mode TCMs at the temporal dislocation interface. According to (ΔG0, ΔGπ), Fig. 2l illustrates that the system, situated within the same parameter space as Fig. 2e, exhibits nontrivial topological dislocations, characterized by (ΔG0 = 0, ΔGπ = 1), even for γ > λ.

As a concrete example, we showcase the TCMs for \(({G}_{0}^{L}=1,{G}_{\pi }^{L}=-1)\) and \(({G}_{0}^{R}=1,{G}_{\pi }^{R}=1)\), which yield (ΔG0 = 0, ΔGπ = 1). Notably, the time shift only affects the value of the topological invariant of the π-energy gap and do not affect the value of the topological invariant of the 0-energy gap. Therefore, when spatially connecting H(t) with H(t + T/2), the topological invariants associated with the 0-energy gap on both sides remain identical. Consequently, the four 0-energy modes at the corners of the right edge of H(t) and the left edge of H(t + T/2) would be annihilated. In the meantime, the four  ± π-energy modes at the corners of the right edge of H(t) and the left edge of H(t + T/2) persist at the time interfaces. Consequently, there would emerge time-dislocation induced four  ±π-energy corner modes at the temporal dislocation. The simulated admittance spectra in Fig. 2m, n show that, the spectra in the first and second quasienergy zones provide a good approximation to the exact quasienergy spectrum. Alongside the four TCMs (blue points) in the 0-mode (± 2π-mode) gaps, there are eight  ± π-mode TCMs (red points) in the  ±π-mode (± 3π-mode) gaps. As evident in their density distributions, four of the eight  ± π-mode TCMs are time-dislocation-induced TCMs.

Experimental observation of Floquet higher-order topological modes

Experimentally, as depicted in Fig. 2d, we implement the frequency space of the Floquet BBH model with a 3D electrical circuit metamaterial, comprising layers of 8 × 8 in the x-y plane and five layers extending along the z-direction. To spectrally demonstrate the in-gap modes in Fig. 2g in the (G0 = 1, Gπ = −1) phase as TCMs, we drive the corner or bulk circuit nodes at the position r and measure the corresponding impedances over the ground, denoted as Zr = ∑m∣ψm,r∣2/jm. The measured impedances in Fig. 3b, as a function of the driven frequency, exhibit excellent agreement with simulated results. Notably, a maximal impedance peak occurs at corner II precisely at the resonant frequency ωr, in stark contrast to the absence of such peaks at corner I, corner III, and the bulk nodes. This discrepancy serves as unequivocal evidence for the existence of 0-mode TCMs (jn = 0) situated at the corners of the layer l0. However, since the driving at the resonant frequency only excites the zero mode, the above method cannot directly detect the jn/(frCg1) = ±π modes.

Fig. 3: Observation of Floquet higher-order topological modes.
figure 3

a–c Measured and simulated impedances over the ground for (G0 = 1, Gπ = −1) versus the driving frequency at the bulk and corner I, II, and III circuit nodes (marked separately by the star, triangle, square, and circle in (e)), respectively corresponding to excite the π, 0, and  −π modes. d, e Theoretical density distributions for the emerged in-gap modes and measured impedance distributions in all circuit nodes at the resonant frequency ωr = 2π × 1.52 MHz. f–i Same as (d, e) but respectively for (G0 = 0, Gπ = −1) and (G0 = 1, Gπ = 0). The parameters are C0 = 1.1nF, L0 = 10 μH, a–e, h, i C1 = 1.1nF, C2 = 2.2nF, L1 = 10 μH, L2 = 5 μH, and f, g C1 = 2.2nF, C2 = 1.1nF, L1 = 5 μH, L2 = 10 μH. The circuit parameters for the grounding and on-site energy shifts are presented in Supplementary Note 6.

Full size image

To address this challenge, our strategy is to shift the entire admittance spectrum upwards (or downward) by π, while ensuring the resonant frequency remains unchanged. In Supplementary Note 8, we provide detailed procedures regarding the redesign of the grounding circuits for achieving this objective. This shift results in the  −π (π) mode in the admittance spectrum moving downwards (upwards) and transforming into jm = 0. Consequently, we can now excite the  ±π modes by driving the corner node at the same resonant frequency ωr. The corresponding measured impedances in Fig. 3a, c clearly indicate that, the maximal impedance peaks appear at the corner II and III (I) nodes for the case of the π (−π) modes excited, manifesting that the π (−π) modes predominantly occupy the corners of the layers l0 and l1 (l−1).

Figure 3d presents theoretical calculations of the density distributions of the 0- and  ±π-mode eigenmodes. As uncovered, the 0-mode TCMs predominantly occupy the four corners of the layer l0, while the π-mode (−π-mode) TCMs are predominantly found at the corners of the layers l0 and l1 (l−1). Likewise, the 2π-mode (−2π-mode) TCMs are primarily localized at the four corners of the layer l1 (l−1), and the 3π-mode (−3π-mode) TCMs are mainly located at the corners of the layers l1 and l2 (l−1 and l−2). This experiment aims to detect the 0- and  ± π-mode TCMs, including the next section addressing temporal dislocation. However, it’s important to note that the method can be directly utilized to detect the  ±2π-mode and  ±3π-mode TCMs as well.

In Fig. 3e, we measure the spatial distribution of the impedances in all circuit nodes at the resonant frequency. As shown, the impedances corresponding to the 0 and  ±π TCMs excited, maximally occupy the corners of the l0 layer and the l0,±1 layers, respectively, agreeing with the theoretical predictions in Fig. 3d. Figure 3f–i respectively investigate the case for the circuit in the (G0 = 0, Gπ = −1) and (G0 = 1, Gπ = 0) phases. As shown, the corresponding circuit only hosts 0- or  ±π-mode TCMs, demonstrated by the measured impedances maximally populating the corners of the l0 layer or the corners of the l0,±1 layers. By comparing the distinct features of measured TCMs, we comprehensively unveil the topological properties of three distinctive nontrivial Floquet HOTPs.

Experimental observation of time-dislocation induced Floquet higher-order topological modes

Having demonstrated the Floquet HOTPs, we now introduce a time-dislocation-induced interface into the circuit metamaterial. As illustrated in Fig. 2k, such a temporal dislocation in the frequency space can be directly implemented by a 3D circuit metamaterial array, containing 8 × 16 × 5 circuit nodes. The blue and red circuits, respectively, implement the frequency space of H(t) and H(t + T/2), with the interface representing the temporal dislocation.

To spectrally identify that the π-mode TCMs in Fig. 2n includes time-dislocation-induced TCMs at the corners of the interface, we drive the corner nodes of both the interface and the whole circuit, and measure the corresponding impedances relative to the ground. The measured impedances depicted in Fig. 4b demonstrate a notable agreement with the simulated outcomes. Specifically, at the resonant frequency, a distinct impedance peak is observed at the corner I node, while no such peak is evident at the corners II and III or at the bulk nodes. This disparity emphasizes the 0-mode modes as the TCMs of the layer l0. Similarly, we reconfigure the grounding circuits (see Supplementary Note 8) for exciting the  ±π modes at the same resonant frequency ωr. Figure 4a, c illustrates that the impedance peaks emerge at all three corners at the resonant frequency, indicating that the  ±π modes correspond to the TCMs of the whole circuit and the TCMs of the interface within the layer l0.

Fig. 4: Observation of time-dislocation induced Floquet higher-order topological modes.
figure 4

a–c Measured and simulated impedances over the ground for \(({G}_{0}^{L}=1,{G}_{\pi }^{L}=-1,{G}_{0}^{R}=1,{G}_{\pi }^{R}=1)\) versus the driving frequency at the bulk and corner I, II, and III circuit nodes (marked separately by the star, triangle, square, and circle in (e)), respectively corresponding to resonantly couple the π, 0, and  −π modes. d, e Theoretical density distributions for the emerged in-gap modes and measured impedance distributions in all circuit nodes at the resonant frequency ωr = 2π × 1.52 MHz. f–i Same as (d, e) but respectively for \(({G}_{0}^{L}=0,{G}_{\pi }^{L}=-1,{G}_{0}^{R}=0,{G}_{\pi }^{R}=1)\) and \(({G}_{0}^{L}=1,{G}_{\pi }^{L}=0,{G}_{0}^{R}=1,{G}_{\pi }^{R}=0)\). The parameters are C0 = 1.1nF, L0 = 10 μH, a–e, h, i C1 = 1.1nF, C2 = 2.2nF, L1 = 10 μH, L2 = 5 μH, and f, g C1 = 2.2nF, C2 =  1.1nF, L1 = 5 μH, L2 = 10 μH. The circuit parameters for the grounding and on-site energy shifts are presented in Supplementary Note 7.

Full size image

In Fig. 4d, the density distributions of the 0- and  ±π-mode eigenmodes are theoretically calculated for compression. It is found that the 0-mode TCMs primarily occupy the four corners of the layer l0, while the π-mode (−π-mode) TCMs mainly populate the corners of the layers l0 and l1 (l−1) as well as the corners of the interface within these layers. Similarly, the 2π-mode (−2π-mode) TCMs are predominantly localized at the four corners of the layer l1 (l−1), and the 3π-mode (− 3π-mode) TCMs are mainly located at the corners of the layers l1 and l2 (l−1 and l−2) as well as the corners of the interface within these layers.

We also measure the impedance distributions at all nodes at the resonant frequency (Fig. 4e). The experimental data reveals that when the 0 modes are excited, the impedances primarily concentrate at the corners of the layer l0. In contrast, for the  ±π modes, the impedances mainly populate the corners of the layers l0,±1 and the corners of the interface within these layers, aligning with the theoretical predictions in Fig. 4d. Figure 4f, g further explore the situation for the circuit with \(({G}_{0}^{L}=0,{G}_{\pi }^{L}=\!\!-1,{G}_{0}^{R}=0,{G}_{\pi }^{R}=1)\). It becomes evident that the circuit supports only eight  ±π-mode modes and does not host 0-mode modes. The measured impedance distribution (Fig. 4g) confirms this observation, as the  ±π-mode modes primarily occupy the corners of the layers l0,±1 and the corners of the interface within these layers, in according with Fig. 4f. The results in Fig. 4h, i for the circuit with \(({G}_{0}^{L}=1,{G}_{\pi }^{L}=0,{G}_{0}^{R}=1,{G}_{\pi }^{R}=0)\) show that this circuit hosts only four 0-mode modes. As expected, the measured impedances mainly concentrate at the corners of the layer l0. The experimental comparison of these distinctive topological scenarios unequivocally demonstrates the emergence of π-mode TCMs induced by temporal dislocation.

Discussion

In summary, we have theoretically constructed and experimentally observed Floquet higher-order topological corner modes induced by temporal dislocations, making use of an additional physical dimension to represent the frequency-space lattice. Interestingly, our time-dislocation topological modes are spatially localized in-plane across the temporal interface, despite all in-plane couplings being homogeneous across it.

Our demonstration would impact both experimental and theoretical studies of topological states. On the experimental side, our frequency-space engineering approach demonstrated in our experiment opens up a new pathway for implementing sophisticated Floquet topological models that are not achievable through direct implementation of periodic driving, particularly since high-frequency modulation leads to excessive component heating. This approach has a wide range of applications not limited to circuit platforms, being applicable also in topological photonic and acoustic platforms. On the theory side, our work has revealed that topological modes could also emerge in a temporal junction, alongside time reflection and refraction52,53,54,55, representing novel phenomena induced by temporal interfaces. In all, our study also presents an exciting prospect in demonstrating Floquet topological phenomena involving the intricate interplay between real-space, temporal-space and momentum-space topology.

Methods

Frequency-space Hamiltonian

The single-harmonic periodic driving Hamiltonian H(t) can be transferred into the enlarged frequency space (see Supplementary Note 4), taking the following block-tridiagonal structure

(6)

where the diagonal blocks are copies of the static BBH model Hamiltonian, with energies shifted up and down by integer multiples of the drive frequency Ω. Notably, this Hamiltonian can be interpreted and experimentally simulated as a three-dimensional tight-binding lattice, as shown in Eq. (3). In addition to having the BBH lattice model HBBH in the x-y plane, there are couplings along the third dimension, n, which physically corresponds to the frequency dimension ω. Specifically, the diagonal blocks represent n-dependent linear on-site potentials, which can be rewritten as \(n\Omega {c}_{{l}_{n}}^{{{\dagger}} }{c}_{{l}_{n}}\). The off-diagonal blocks arise from the frequency harmonics of the periodic driving in Eq. (2), where e±iΩt respectively describes transitions along the frequency dimension, which leads to the hoppings \({c}_{{l}_{n+1}}^{{{\dagger}} }{c}_{{l}_{n}}\) and \({c}_{{l}_{n}}^{{{\dagger}} }{c}_{{l}_{n+1}}\).

Sample fabrications and circuit measurements

The circuit metamaterials, including the PCB composition, stack-up layout, and grounding settings, are designed using the PAD software program. The PCB traces, and spacings between circuit elements are carefully designed to minimize parasitic inductances and spurious inductive couplings, respectively. To ensure the errors of circuit elements and series resistance of inductors are as low as possible, all components conform to a 5% error tolerance. Signal injection and detection are performed using BNC connectors soldered onto the PCB. For impedance distribution measurement, two-channel signal generators (Rigol-DG2102) serve as the AC excitation source, inputting a voltage with a peak-to-peak value of U = 5V, and scanning the driving frequency from a minimum of 0 MHz to a maximum of 3 MHz in a scanning time of 28 ms. Another two-channel signal generator (Rigol-DG1022U) is used to trigger and synchronize the process. An oscilloscope (Rigol-DS2202A) and a divider resistance (R =  430 ohm) are used to measure the impedance over ground for each circuit node.