Abstract
Semiconductor crystals driven by strong mid-infrared pulses offer advantages for studying many-body physics and ultrafast optoelectronics via high-harmonic generation. While the process has been used to study solids in the presence strong mid-infrared fields, its potential as an attosecond light source is largely underexplored. We demonstrate that high-harmonics emitted from zinc-oxide crystals produce attosecond pulses, measured through spectroscopy of alkali metals. Using a cross-correlation approach, we photoionize Cesium atoms with vacuum-ultraviolet high-harmonics in the presence of a mid-infrared laser field. We observe oscillations in the photoelectron yield, originating from the instantaneous polarization of atoms by the laser field. The phase of these oscillations encodes the attosecond synchronization of the high-harmonics and is used for attosecond pulse metrology. This source opens new spectral windows for attosecond spectroscopy, enabling studies of bound-state dynamics in natural systems with low ionization energies, while facilitating the generation of non-classical entangled light states in the visible-VUV.
Similar content being viewed by others
Introduction
In the last twelve years, the interaction between semiconductor crystals and intense laser fields has gained significant attention. This interest arises from the combination of advantages offered by many-body physics and ultrafast optoelectronics1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16. Extreme-ultraviolet (XUV) attosecond pulses produced in silicon dioxide (SiO2) crystals by visible single-cycle laser pulses have been used for investigating electronic dynamics in multi–petahertz range16. At the core of such investigations lies the process of high harmonic generation (HHG), where the low-frequency photons of a driving laser field are upconverted into photons of higher frequencies. In the majority of the aforementioned investigations, the high harmonics are produced by the interaction of intense mid-infrared (M–IR) (carrier wavelength λL ~ 3.2 μm) pulses with semiconductor crystals, such as zinc oxide (ZnO)8,14,17. While this process has been extensively employed to study the electron dynamics in solids in the presence of strong laser fields, its potential for generating attosecond pulses for applications in attosecond science18 has remained experimentally unexploited. Typically, the cut–off energy of the measured harmonics produced by the interaction of semiconductor crystals with intense M–IR laser pulses lies in the vacuum-ultraviolet (VUV) spectral range with photon energy in the range of a few eV1. These photon energies are relatively low compared to the tens of eV photon energies of the XUV harmonics produced by strongly laser-driven atoms19,20. Therefore, the photon energies of the generated VUV pulses are below the ionization threshold (IP) of the rare gases (which is IP > 12 eV) used in XUV attosecond pulse characterization techniques (e.g., ref. 21 and references therein), preventing their measurement and implementation in attosecond metrology. Here, we solve this issue by investigating the photoionization of Cesium (Cs) atoms (with IP(Cs) ≈ 3.89 eV) by a comb of VUV high-order harmonics and a delayed M–IR laser field. We find that the number of electrons ejected along the laser polarization direction oscillates at the frequency of the laser electric field. This modulation arises due to the strong polarization of the Cs atoms by the laser field. The photoelectrons originating from different high-harmonics oscillate almost in phase, indicating synchronization at the attosecond timescale, as predicted by our theoretical calculations conducted using Semiconductor Bloch Equations (SBE). These results establish a technique to characterize the attosecond pulses in the VUV range, which employs laser-dressing of the bound electrons rather than the continuum one, as in conventional attosecond metrology22.
Results
High harmonic generation in ZnO
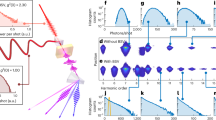
The experiment has been conducted at the ELI ALPS facility in the MIR laboratory, using the arrangement shown in Fig. 1a (see Methods, Supplementary Information (SI) and Supplementary Fig. S1). We used a p–polarized carrier-envelope-phase (CEP) stable few-cycle M–IR pulses of ≈ 58 fs duration and carrier wavelength of λL ≈ 3.2 μm23. The M-IR beam entered an interferometer by means of a beam splitter (BS). One arm contains the harmonics generated by the interaction of intense (≈ 5 × 1011 W/cm2) M–IR field with a 500 μm thick ZnO crystal, and the other, a time delayed (τ) M–IR dressing field. The ZnO optical axis was set perpendicular to the laser polarization in order to generate only the odd harmonic frequencies. The harmonics were recombined with the M–IR at a mirror with a hole at the center (holey mirror). Both were focused by an Aluminum coated spherical mirror into Cs atoms. The photoelectron spectrum produced by the superposition of VUV and M–IR pulses was recorded by a time-of-flight spectrometer to produce the spectrogram of Fig. 1b (see also Supplementary Fig. S2). The harmonics contributing to photoionization are those with photon energies ℏω > IP(Cs) ≈ 3.89 eV. Since this energy is above the band gap of ZnO crystal (Eg ≈ 3.3 eV) the detected harmonics are generated primarily by interband transitions8,14,17.
a Cross–correlation method used for the temporal characterization of the harmonics generated by the interaction of intense few-cycle CEP stable M–IR pulses with ZnO crystal. The harmonic and the M–IR fields are spatiotemporally overlapped in the Cs gas. The delay stage was used to control the time delay τ between the harmonics and the M–IR dressing field. BS and c–BSt, are an M-IR beam splitter and an M–IR central beam block, respectively. FM1,2 are focusing mirrors of 50 cm and 15 cm focal length, respectively. The generated photoelectrons are recorded by a μ–metal-shielded time–of–flight (TOF) spectrometer. b Spectrogram which shows the dependence of the photoelectron spectrum on the delay between the VUV and M-IR fields.
To estimate the degree of the synchronization of the emitted harmonics and temporal profile of the VUV pulses produced in the experiment, we performed theoretical calculations using the semiconductor Bloch equations24 (Methods, SI and Supplementary Figs. S3–S5). The calculated HHG spectrum in the region of interest (13 ≤ q ≤ 23, where q is the harmonic order) (black line in Fig. 2a) shows a reasonable correspondence with the experimental data (Fig. 1b). To investigate if the generated harmonics depict synchronization in the attosecond time scale, we have calculated the harmonic emission times \({t}_{e}^{(q)}\) (red yellow-filled circles in Fig. 2a) and the temporal structure of the harmonic superposition with 13 ≤ q ≤ 23 (Fig. 2b). Due to attosecond phase locking of the emitted harmonics, their superposition results in a VUV temporal profile which consists of a main pulse of ≈ 950 asec duration, surrounded by secondary pulses reaching 40% of the main pulse and showing a slightly longer duration. These theoretical results confirm the potential of this source for attosecond spectroscopy.
a Calculated HHG spectrum (black line) and the corresponding emission times \({t}_{e}^{(q)}\) (red yellow-filled circles) in the Cs interaction region. In the plot we have set \({t}_{e}^{(q=13)}=0\). The spectrum is shown in the spectral region used in the pump-probe experiment. b Calculated temporal structures of the harmonic superposition with 13 ≤ q ≤ 23, resulting in the formation of attosecond pulse trains with the duration of the main pulse in the train to be ≈ 950 asec.
Attosecond photoionization of Cs
One of the most important achievements of attosecond light sources relies on their ability to resolve the instantaneous response of atoms25, molecules26, or solids27 to the oscillations of the electric field of light. For instance, it has been found that when a small molecule, with polarizability around 20 atomic units (a.u.), is subjected to a strong IR laser field (≈ 1012 W per cm2), the oscillations of the electrons at the laser period induce a modulation of the XUV photoionization cross-section, which can be measured using an attosecond pulse train26. Similarly, it has been shown that when argon atoms (polarizability around 10 a.u.) are polarized by a strong IR field (≈ 5 × 1012 W per cm2) and probed by a single attosecond pulse, the photoelectrons are preferentially ejected in the IR laser field direction28. Here, we show that the VUV pulses synthesized by a superposition of high harmonics generated by semiconductors can be used to track the instantaneous polarization of Cs atoms. The photoelectron spectra shown in Figs. 1b and 3a consist of peaks corresponding to the absorption of different harmonics. Surprisingly, the spectra does not exhibit sidebands in between the harmonic peaks that would result from two-photon (1 VUV + 1 M–IR) transitions in the continuum, as is the case in RABBIT measurements22. The spectra does not show any sign of laser-induced streaking, typical of laser-dressed photoionization with single attosecond pulses29,30. This means that the laser intensity is too weak to induce non-linear transitions in the continuum. However, the overall photoelectron yield presents clear oscillations at the period of the laser field (T0 = 10.67 fs). In other words, more or less electrons are ejected towards the detector, depending on the delay between the VUV and M–IR field. The oscillations of the individual photoelectron peaks are shown in Fig. 3b (raw data as dots, bandpass-filtered data as lines). The electron yield oscillates with a typical modulation depth (“Methods”) in the range of 20% of the mean (Fig. 3b). These results show that the polarizability of Cs (around 400 a.u.31) is so high that the pump-probe signal is dominated by the response of the bound electrons to the laser field. This represents a paradigm shift compared to conventional XUV–IR attosecond spectroscopy experiments, where continuum-continuum transitions play a major role. Interestingly, this separation of bound- and continuum- responses to a laser field is a hot topic in surface science, where these two effects are respectively associated with Floquet and Volkov states32.
a Measured harmonic spectrum (black line gray-filled area) and the emission times \({t}_{e}^{(q)}\) (red triangles). In the plot we have set \({t}_{e}^{(q=13)}=0\). b Dependence of the photoelectron harmonic yield on the delay between the VUV and M-IR pulses (raw data as dots, bandpass-filtered data as lines) obtained from the spectrogram in Fig. 1b. The photoelectron peaks oscillate with the frequency of the M--IR field ω0. The shift between the maxima of the harmonic photoelectron yield corresponds to the harmonic emission times (shown in (a)) which have been used to obtain the harmonic phase distribution. c Average temporal profile of the attosecond pulses constituting the attosecond pulse train. The blue-dashed line depicts the attosecond pulse in the attosecond pulse train in the case of Fourier Transform Limited (FTL). The red line shows the average attosecond pulse in the attosecond pulse train obtained using the measured phases. The duration of the measured pulse in the train is \({\tau }_{q=13...23}^{{{\rm{meas}}}.}\approx 950\) asec.
The measurements presented in Figs. 1b and 3a, b also demonstrate that the harmonics produced by ZnO have a temporal structure, able to resolve the instantaneous variation of the atomic polarization. Indeed, we can use atomic polarization as an amplitude gate to resolve the attosecond synchronization of the different high-order harmonics33. If the harmonics were perfectly synchronized, then their photoelectron signals would maximize at the same delay. Our results show that this is not exactly the case. There is a positive shift of the harmonic photoelectron signal oscillations: the photoelectron yield from higher harmonics maximizes later, which means that the pulses produced in ZnO are positively chirped which is consistent with the results of ref. 5. The phase of the photoelectron oscillation provides the emission time \({t}_{e}^{(q)}\) of the contributing harmonics presented with red triangles in Fig. 3a. The results are in reasonable agreement with the theoretical predictions (red yellow-filled circles in Fig. 2a). The harmonic spectrum and emission times can be used (“Methods”) to retrieve the temporal profile of the average attosecond pulse in the attosecond pulse train. The results show that the attosecond pulses have a ≈ 950 asec pulse duration instead of ≈ 910 asec if there was no chirp (Fig. 3c). This is in good agreement with the theory.
In addition, we can infer some information on the duration of the attosecond pulse train from the measurements. In the HHG process, an attosecond pulse can be emitted at each laser half-cycle. Thus, in the VUV + M-IR photoionization process, two consecutive attosecond pulses, separated by half a laser period, experience opposite instantaneous polarization by the laser field, canceling the modulation observed at the laser frequency. This is illustrated in Fig. 4, in which we simulate the effect of an amplitude modulation δ(t − τ) = (1 + δ0EM−IR(t − τ)) induced by the laser field EM−IR in two-color time-resolved photoelectron spectra. When a single attosecond pulse, with a positive chirp similar to the one measured in our experiment, is used (Fig. 4a), the whole electron spectrum oscillates at the laser frequency ω0. The phase of the oscillations reflects the emission time of each frequency component of the spectrum. With a long train of attosecond pulses (Fig. 4b), this oscillation disappears, but side bands, oscillating at twice the laser frequency appear between the harmonic peaks. These side bands correspond to the appearance of quasi-stationary states of the periodically driven atoms, named Floquet states, and shifted by one photon energy with respect to the field-free states34,35. Lastly, we consider the intermediate situation of a short attosecond pulse train, consisting of a dominant central pulse surrounded by weaker satellites as predicted by the theory (Fig. 2). In that case, the photoelectron signal oscillates at frequency ω0 (Fig. 4c), as observed in our measurements. This simple model shows that the observation of the oscillations of the measured signal at the pump laser frequency is an indication that our HHG source produces a main attosecond pulse that can be used for pump-probe attosecond spectroscopy. We note that although the weak sidebands appearing between the main harmonic peaks (created by bound-bound transitions) in Fig. 4c were not visible in the present experiment due to limitations introduced by the signal-to-noise ratio, the phase of the oscillations of these photoelectron peaks shows the same variation with harmonic order as the phase of the main harmonic photoelectron peaks. Hence, they reflect the chirp of the attosecond pulses in the same way as the oscillations of the main harmonic photoelectron peaks. It is thus not necessary to detect the sidebands to obtain the temporal profile of the attosecond pulses.
a–c Spectrograms (contour plots), the corresponding frequencies obtained by the Fourier transform along the delay axis of the spectrogram (middle panels), for a single attosecond pulse (a), a long VUV attosecond pulse (b) and an 8 fs long VUV attosecond pulse train (c) (right panels). The latter corresponds to the case, which is closer to the experimental measurements. The insets show the spectrum of the corresponding VUV pulse.
Discussion
The findings introduce strongly laser-driven semiconductors as a new form of attosecond sources. VUV attosecond pulses are well-suited for investigating the ultrafast dynamics of neutral systems with low ionization energy thresholds. They can be utilized to study the attosecond electron dynamics of excited neutral atoms and the dynamics of coupled electronic and nuclear motion in molecules beyond the Born-Oppenheimer approximation36. In addition, the developed method is suitable for investigating the dynamics of high polarizability systems such as alkali metals31, as well as solids and surface science32,36.
Also, considering that the conversion efficiency of the HHG process is of the order of η ~ 10−6 37,38, we estimate that the photon number of the emitted harmonics is in the range of nVUV ~ 108 photons per pulse. Considering that the energy scaling laws that have been used in gas phase HHG media20 are applicable in solids, the VUV photon number can be significantly increased. Taking into account that the photon number of the generated harmonics is nVUV ∝ η ⋅ S ⋅ EL (S and EL is the interaction area and driving field energy, respectively), this can be achieved by means of high-power M-IR laser systems and loose M-IR focusing geometries. For example, by focusing into a ZnO crystal a ≈ 60 fs M-IR pulse of EL in a few-mJ per pulse range using a focusing mirror of ≈ 3 m focal length, it can be roughly estimated that the photon number of the emitted VUV pulses is in the range of nVUV ~ 1010 photons per pulse. Attosecond pulses of such photon numbers can support intensities sufficient to induce non-linear processes in matter.
Furthermore, the attosecond synchronization of the coherently emitted multimode harmonic frequency comb underscores the significance of strongly laser-driven semiconductors as a source for generating non-classical, massively entangled light states in the visible to VUV spectral region. Recently, it has been theoretically and experimentally demonstrated that HHG generated by intense laser-atom interactions can be used to produce optical “cat” states, squeezed states, and massively entangled light states39,40,41,42,43. These studies have been conducted in the strong field limit, where high harmonic generation is governed by electron motion in the continuum, with their recombination to the atomic core defining the harmonic emission times. In addition, using fully quantized approaches in strongly laser-driven ZnO crystals, it has been theoretically shown44,45 that such electron dynamics can also be used for the generation of non-classical and massively entangled states in semiconductors. Hence, the present findings represent a crucial experimental step in this direction, paving the way for numerous applications emerging from the symbiosis of attosecond science and quantum information science46.
In summary, we have theoretically and experimentally demonstrated that when semiconductor materials are subjected to strong mid-infrared laser fields, they emit attosecond pulses ranging from the visible to the VUV region. We have devised a technique for measuring the temporal synchronization of the generated high-harmonics and the duration of the VUV pulses created by their superposition. The scheme is capable of temporal characterization of the semiconductor HHG, and the produced pulses, once characterized, provide a new tool for applications in the VUV domain. The method relies on laser-dressed photoionization measurements of Cs atoms, particularly effective in the VUV portion of the harmonic spectrum. In addition, through this method we have conducted attosecond spectroscopy measurements in Cs atoms. This marks an advancement in the study of ultrafast processes and envisages the development of a robust table-top high-repetition rate attosecond light sources using solid state materials.
Methods
Experimental approach
The whole optical arrangement and detection units were operated under a pressure of ~ 10−6 mbar. A beamsplitter (BS) with 70% reflection and 30% transmission was used to separate the ≈ 1 cm diameter incoming M-IR beam in two arms of an interferometer. The reflected beam passed through a supper–Gaussian beam block, which creates an annular-shaped beam profile, and was focused by a 50 cm focal length mirror into a 500 μm thick ZnO crystal. To ensure optimal phase-matching conditions of the HHG process, the harmonic signal has been optimized by varying the energy of the driving M-IR. The highest harmonic signal and the highest harmonics were produced for a pulse energy of ≈ 25 μJ corresponding to an intensity IL ≈ 5 × 1011 W per cm2. This intensity value is in agreement with previously reported measurements (e.g., refs. 1,37). It is noted that when the mid-IR field interacts with a ZnO crystal, small self-compression proceeds may occur due to the group velocity dispersion (GVD) (-148.8 fs2 per mm47). This results in a ≈ 3% change in the M–IR pulse used in the present work and is therefore considered negligible. After the ZnO crystal, the harmonic beam, which is spatially confined at the center of the annular–shaped M-IR beam, was passing through a 4 mm diameter iris, which blocked the annular M-IR beam and let the harmonic beam pass through. No infrared light could be observed on thermal film past this aperture, indicating the efficiency of the M-IR filtering. In the second arm of the interferometer, the beam was delayed using a translation stage and recombined with the harmonic beam by a mirror with a hole at the center. The divergence of the M–IR beam was matched with that of the harmonics by means of the lens. The intensity of the M–IR field was controlled by means of an aperture (not shown) with an adjustable diameter placed before the mirror with a hole at the center (Fig. 1a). The intensity of the M–IR field in the Cs interaction region was roughly estimated to be in the range of ~ 1011 W per cm2. Both the harmonic and M–IR delayed fields were focused by a 15 cm focal length Aluminum mirror into Cs atoms introduced in the interaction region by means of a specially contracted effusion cell (SI and Supplementary Fig. S1) operating at a temperature of ≈ 40 °C. Any temperature fluctuation around ≈ 40 ∘C introduces small Cs pressure fluctuations in the M-IR/VUV interaction region. This results in instabilities in the recorded photoelectron signal shown in Fig. 1b and influences the error of the measurements. These instabilities have been included in the error analysis and error bar of the obtained harmonic emission times shown in Fig. 3a. An approach to minimize the shot-to-shot signal fluctuations caused by Cs pressure instabilities is to employ a skimmer-type approach alongside a high-accuracy temperature controller for the alkali oven. The generated photoelectrons were recorded by a TOF μ–metal shielded electron spectrometer with the TOF axis parallel to the laser polarization. The harmonic spectrum was recorded by measuring the photoelectrons produced by the interaction of the harmonics with Cs atoms in a single–photon ionization process. The signal was found to vanish when a fused silica window was inserted in the beam, confirming the lack of contribution of the M–IR beam to the ionization. Also, no Cs ions were observed when only the M–IR field was focused onto the Cs atoms. This has been measured by operating the TOF in the mass ion spectrometer mode using an ion repeller in the TOF interaction region (SI and Supplementary Fig. S1). The single photon ionization cross section of Cs for ℏω ≳ 5 eV, varies in the range of ~ 0.8 ± 0.2 Mbarn48,49, such that the photoelectron spectrum can be considered to faithfully reflect the shape of the spectrum of the ionizing radiation. For the pump-probe measurements shown in Fig. 3a, the Cs pressure was lowered to avoid polluting the chamber, such that only the lowest, most intense harmonics were detected. Photoelectron spectra were accumulated at each pump-probe delay. The delay step was 0.6 fs. When the Cs pressure was increased at the highest possible level, the photoelectron spectrum exhibited a plateau region extending up to the 31st harmonic (photon energy of ≈ 12 eV), followed by a cutoff region up to the 43th order (≈ 16.6 eV) (SI and Supplementary Fig. S2). In this case, and in order to avoid polluting the chamber with Cs, the measurement has been completed within a few seconds. For this reason, high Cs pressure conditions have not been used in a pump-probe configuration. The modulation depth discussed in harmonic signal oscillations shown in Fig. 3b is defined as M = 2(Smax − Smin)/(Smax + Smin), where Smax and Smin are the maximum and minimum values of the oscillating signal, respectively.
Theory of HHG in ZnO
Throughout this work, we employ a 1D two-band single-electron semiconductor Bloch equation-based model to tackle the electron dynamics inside the ZnO crystal. This approach has been extensively used for different materials and laser parameters (see e.g., ref. 24). Within this model, it is possible to include, phenomenologically, dephasing and correlation effects through a tunable dephasing time parameter. The valence and conduction bands of ZnO are obtained using a nonlocal pseudopotential approximation (for details, see e.g., ref. 3). The bandgap energy at the Γ-point is given by Eg = 0.1213 a.u. (≈ 3.3 eV), in very good agreement with reported experimental values. We use up to 500 k-grid points in the Γ-M direction of the Brillouin zone (BZ) in our simulations, but calculations have also been performed in the Γ-K direction. The former yields much better agreement with the experimental measurements. The intrinsic chirp of the HHG processes, similar to that observed in atoms, is considered through classical simulations (for more details see SI and Supplementray Figs. S3–S5). This enables us to take into account the effects of the attochirp in our theoretical calculations and extract the harmonic phase (see Fig. 2a) (see e.g., ref. 17). Our calculations allow for the isolation of the contribution of short electron trajectories by adequately tuning the dephasing time. Setting a dephasing time of 2 fs, we are able to clearly observe the harmonic peaks present in the experimental data. This value is compatible with well-established values3. Larger values of this parameter make the plateau region of the spectrum noisy and lacking clear harmonic peaks because both short and long electron trajectories contribute, and their coherent sum introduces interference (see SI). It can also be confirmed that, for the parameters used in the present work, the intraband contribution above the bandgap is negligible (see SI for more details). The harmonic phases have been obtained from the classical theoretical model using the relation \({\varphi }_{q}={\omega }_{q}({t}_{e}^{(q)}-{t}_{{E}_{0}})\), where \({t}_{{E}_{0}}\) is the time where the M–IR field E0 takes its maximum value and \({t}_{e}^{(q)}\) (shown in Fig. 2a) is the calculated harmonic emission time (see SI for details).
VUV pulse reconstruction
To reconstruct the temporal shape of the VUV pulses, we have used the measured harmonic spectral amplitudes and phase distributions (shown in Fig. 3a). The harmonic amplitude distribution has been obtained by integrating along the y-axis the recorded spectrogram shown in Fig. 1b. The oscillations of each harmonic at the laser frequency were analyzed by Fourier-transform. The phase of the oscillation of a given harmonic q provides the emission time \({t}_{e}^{(q)}\) of this harmonic within the laser cycle, up to an additive constant that is undetermined in our experiment. This means that we can reconstruct the emitted attosecond pulses, but not their synchronization with the driving laser field50. The phase of the different harmonics φq were obtained by integrating the emission times: \({t}_{e}^{(q)}=\frac{{\varphi }_{q+2}-{\varphi }_{q}}{{\omega }_{q+2}-{\omega }_{q}}\). The intensity profile of the average attosecond pulse in the train was finally obtained by using the harmonic amplitudes Aq and phases φq: \(I(t)=| \sum {A}_{q}{e}^{i{\varphi }_{q}}{| }^{2}\).
Dependence of the spectrogram on the VUV pulse duration
To investigate the effect of the VUV pulse and pulse train on the photoelectron spectrogram, we use the first-order perturbation theory under the single active electron approximation to calculate the transition amplitude Γv(τ). The transition amplitude Γv(τ) to the final continuum state \(\left\vert {{\bf{v}}}\right\rangle\) with the momenta v is given by29,
with
The recorded photoelectron spectrum does not show any side-bands which is due to low M-IR intensities. We thus approximate the action S to \(S={I}_{p}t+\frac{{v}^{2}}{2m}t\). Although the M-IR field strength is weak, it still induces an amplitude modulation in the photoelectron spectra due to the high polarizability of Cs. We model this by introducing an amplitude modulation of the dipole transition matrix element proportional to the M-IR field: \({{{\bf{d}}}}_{{{\bf{v}}}}(t-\tau )={{{\bf{d}}}}_{{{\bf{v}}}}^{0}(1+{\delta }_{0}{E}_{{{\rm{M}}}-{{\rm{IR}}}}(t-\tau ))\), where \({{{\bf{d}}}}_{{{\bf{v}}}}^{0}\) is the laser field free dipole transition matrix element and δ0 is the depth of amplitude modulation.
Data availability
The data that supports the findings are presented in the article and Supplementary Information. Source data are provided in this paper.
Code availability
The code and datasets generated and/or analyzed during this study are available from the corresponding authors upon request.
References
Ghimire, S. et al. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 7, 138–141 (2011).
Schultze, M. et al. Controlling dielectrics with the electric field of light. Nature 493, 75 (2013).
Vampa, G. et al. Theoretical analysis of high-harmonic generation in solids. Phys. Rev. Lett. 113, 073901 (2014).
Vampa, G. et al. All-optical reconstruction of crystal band structure. Phys. Rev. Lett. 115, 193603 (2015).
Vampa, G. et al. Linking high harmonics from gases and solids. Nature 522, 462–464 (2015).
Luu, T. T. et al. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature 521, 498–502 (2015).
Silva, R. E. F., Blinov, I. V., Rubtsov, A. N., Smirnova, O. & Ivanov, M. High-harmonic generation from bloch electrons in solids. Phys. Rev. A 91, 043839 (2015).
Vampa, G., McDonald, C. R., Orlando, G., Corkum, P. B. & Brabec, T. Semiclassical analysis of high harmonic generation in bulk crystals. Phys. Rev. B 91, 064302 (2015).
Chang, Z., Corkum, P. B. & Leone, S. R. Attosecond optics and technology: progress to date and future prospects. J. Opt. Soc. Am. B 33, 1081–1097 (2016).
Kruchinin, S. Y., Krausz, F. & Yakovlev, V. S. Colloquium: Strong-field phenomena in periodic systems. Rev. Mod. Phys. 90, 021002 (2018).
Vampa, G. et al. Strong-field optoelectronics in solids. Nat. Photon. 12, 465 (2018).
Silva, R. E. F., Blinov, I. V., Rubtsov, A. N., Smirnova, O. & Ivanov, M. High-harmonic spectroscopy of ultrafast many-body dynamics in strongly correlated systems. Nat. Photon. 12, 266–270 (2018).
Garg, M., Kim, H. Y. & Goulielmakis, E. Ultimate waveform reproducibility of extreme ultraviolet pulses by high harmonic generation in bulk dielectrics. Nat. Photon. 12, 291–296 (2018).
Ghimire, S. & Reis, D. A. High-harmonic generation from solids. Nat. Phys. 15, 10–16 (2019).
Juergens, P. et al. Linking high-harmonic generation and strong-field ionization in bulk crystals. ACS Photonics 11, 247–256 (2024).
Garg, M. et al. Multi-petahertz electronic metrology. Nature 538, 359–363 (2016).
Vampa, G., McDonald, C., Fraser, A. & Brabec, T. High-harmonic generation in solids: Bridging the gap between attosecond science and condensed matter physics. IEEE J. Sel. Top. Quantum Electron. 21, 8700110 (2015).
Agostini, P., Krausz, F. & L’Huillier, A. Nobel Lectures: For experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter. (2023).
Drake, G. W. F.Springer Handbook of Atomic, Molecular, and Optical Physics (Springer, 2023).
Weissenbilder, R. et al. How to optimize high-order harmonic generation in gases. Nat. Rev. Phys. 4, 713–722 (2022).
Orfanos, I. et al. Attosecond pulse metrology. APL Photon. 4, 080901 (2019).
Paul, P. M. et al. Observation of a train of attosecond pulses from high harmonic generation. Science 292, 1689–1692 (2001).
Kühn, S. et al. The ELI-ALPS facility: the next generation of attosecond sources. J. Phys. B 50, 132002 (2017).
Luu, T. T. & Wörner, H. J. High-order harmonic generation in solids: A unifying approach. Phys. Rev. B 94, 115164 (2016).
Uiberacker, M. et al. Attosecond real-time observation of electron tunnelling in atoms. Nature 446, 627–632 (2007).
Neidel, C. et al. Probing time-dependent molecular dipoles on the attosecond time scale. Phys. Rev. Lett. 111, 033001 (2013).
Schultze, M. et al. Attosecond band-gap dynamics in silicon. Science 346, 1348–1352 (2014).
Witting, T. et al. Generation and characterization of isolated attosecond pulses at 100 khz repetition rate. Optica 9, 145 (2022).
Quéré, F., Mairesse, Y. & Itatani, J. Temporal characterization of attosecond xuv fields. J. Mod. Opt.52, 339–360 (2005).
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163 (2009).
Schwerdtfeger, P. & Nagle, J. K. 2018 table of static dipole polarizabilities of the neutral elements in the periodic table. Mol. Phys. 117, 1200–1225 (2019).
Mahmood, F. et al. Selective scattering between floquet-bloch and volkov states in a topological insulator. Nat. Phys. 12, 306–310 (2016).
Mairesse, Y. et al. Attosecond synchronization of high-harmonic soft x-rays. Science 302, 1540–1543 (2001).
Shirley, J. H. Solution of the schrödinger equation with a hamiltonian periodic in time. Phys. Rev. 138, B979–B987 (1965).
Lucchini, M. et al. Controlling floquet states on ultrashort time scales. Nat. Commun. 13, 7103 (2022).
Borrego-Varillas, R., Lucchini, M. & Nisoli, M. Attosecond spectroscopy for the investigation of ultrafast dynamics in atomic, molecular and solid-state physics. Rep. Prog. Phys. 85, 066401 (2022).
Gholam-Mirzaei, S., Beetar, J. & Chini, M. High harmonic generation in zno with a high-power mid-ir opa. Appl. Phys. Lett. 110, 061101 (2017).
Tsatrafyllis, N. et al. Quantum optical signatures in a strong laser pulse after interaction with semiconductors. Phys. Rev. Lett. 122, 193602 (2019).
Lewenstein, M. et al. Generation of optical Schrödinger cat states in intense laser-matter interactions. Nat. Phys. 17, 1104–1108 (2021).
Rivera-Dean, J. et al. Strong laser fields and their power to generate controllable high-photon-number coherent-state superpositions. Phys. Rev. A 105, 033714 (2022).
Stammer, P. et al. High photon number entangled states and coherent state superposition from the extreme ultraviolet to the far infrared. Phys. Rev. Lett. 128, 123603 (2022).
Stammer, P. et al. Quantum electrodynamics of intense laser-matter interactions: A tool for quantum state engineering. PRX Quantum 4, 010201 (2023).
Stammer, P. et al. Entanglement and squeezing of the optical field modes in high harmonic generation. Phys. Rev. Lett. 132, 143603 (2024).
Rivera-Dean, J. et al. Nonclassical states of light after high-harmonic generation in semiconductors: A bloch-based perspective. Phys. Rev. B 109, 035203 (2024).
Gonoskov, I. et al. Nonclassical light generation and control from laser-driven semiconductor intraband excitations. Phys. Rev. B 109, 125110 (2024).
Bhattacharya, U. et al. Strong-laser-field physics, non-classical light states and quantum information science. Rep. Prog. Phys. 86, 094401 (2023).
Polyanskiy, M. N. Refractiveindex.info database of optical constants. Sci. Data 11, 94 (2024).
Singor, A., Fursa, D., Bray, I. & McEachran, R. A fully relativistic approach to photon scattering and photoionization of alkali atoms. Atoms 9, 42 (2021).
Suemitsu, H. & Samson, J. A. R. Relative photoionization cross sections of cs, cs2, rb, and rb2. Phys. Rev. A 28, 2752 (1983).
Dinu, L. C. et al. Measurement of the subcycle timing of attosecond xuv bursts in high-harmonic generation. Phys. Rev. Lett. 91, 063901 (2003).
Acknowledgements
We thank Bálint Kiss, Levente Ábrók, and Rajaram Shrestha for their technical support and their efforts in the operation of the mid-IR laser system. We also thank Arnold Péter Farkas, for the methods that he developed for introducing the Cs sample in the interaction chamber. The experiments were carried out at ELI ALPS, and ELI-ALPS is supported by the European Union and co-financed by the European Regional Development Fund (GINOP-2.3.6-15-2015-00001). P. Tzallas group at FORTH acknowledges support from: The Hellenic Foundation for Research and Innovation (HFRI) and the General Secretariat for Research and Technology (GSRT) under grant agreement CO2toO2 Nr.:015922, the European Union’s HORIZON-MSCA-2023-DN-01 project QU-ATTO under the Marie Skłodowska-Curie grant agreement No 101168628, the LASERLABEUROPE V (H2020-EU.1.4.1.2 grant no.871124), The H2020 Project IMPULSE (GA 871161), and ELI–ALPS. M. Lewenstein group at ICFO acknowledges support from: ERC AdG NOQIA; Ministerio de Ciencia y Innovation Agencia Estatal de Investigaciones (PGC2018–097027–B–I00 / 10.13039 / 501100011033, CEX2019–000910–S / 10.13039 / 501100011033, Plan National FIDEUA PID 2019–106901GB–I00, FPI, QUANTERA MAQS PCI 2019–111828–2, QUANTERA DYNAMITE PCI 2022–132919, Proyectos de I + D + I “Retos Colaboración” QUSPIN RTC 2019–007196–7); MICIIN with funding from European Union Next Generation EU (PRTR–C17.I1) and by Generalitat de Catalunya; Fundació Cellex; Fundació Mir-Puig; Generalitat de Catalunya (European Social Fund FEDER and CERCA program, AGAUR Grant No. 2021 SGR 01452, QuantumCAT U16–011424, co-funded by ERDF Operational Program of Catalonia 2014-2020); Barcelona Supercomputing Center MareNostrum (FI–2022–1–0042); EU Horizon 2020 FET–OPEN OPTOlogic (Grant No 899794); EU Horizon Europe Program (Grant Agreement 101080086 — NeQST), National Science Center, Poland (Symfonia Grant No. 2016/20/W/ST4/00314); ICFO Internal “QuantumGaudi” project; European Union’s Horizon 2020 research and innovation program under the Marie-Skłodowska-Curie grant agreement No 101029393 (STREDCH) and No 847648 ("La Caixa” Junior Leaders fellowships ID100010434 : LCF / BQ / PI19 / 11690013, LCF / BQ / PI20 / 11760031, LCF / BQ / PR20 / 11770012, LCF / BQ / PR21 / 11840013). Views and opinions expressed in this work are, however, those of the author(s) only and do not necessarily reflect those of the European Union, European Climate, Infrastructure and Environment Executive Agency (CINEA), nor any other granting authority. Neither the European Union nor any granting authority can be held responsible for them. P. Stammer acknowledges funding from: The European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 847517. J. Rivera-Dean acknowledges funding from: the Secretaria d’Universitats i Recerca del Departament d’Empresa i Coneixement de la Generalitat de Catalunya, the European Social Fund (L’FSE inverteix en el teu futur)–FEDER, the Government of Spain (Severo Ochoa CEX2019-000910-S and TRANQI), Fundació Cellex, Fundació Mir-Puig, Generalitat de Catalunya (CERCA program) and the ERC AdG CERQUTE. Y. Mairesse acknowledges funding from the Agence Nationale de la Recherche (ANR)–Shotime (ANR-21-CE30-038-01), and thanks Samuel Beaulieu for fruitful discussion. M. F. Ciappina and C. Granados acknowledge financial support from the National Key Research and Development Program of China (Grant No. 2023YFA1407100), Guangdong Province Science and Technology Major Project (Future functional materials under extreme conditions - 2021B0301030005) and Guangdong Natural Science Foundation (General Program project No. 2023A1515010871).
Author information
Authors and Affiliations
Contributions
A.N., D.R., B.F., and C.G.: Equally contributed authors. A.N.: Contributed to the development of the set-up, the experimental runs, and the data analysis. D.R.: Contributed to the data analysis. B.F.: Contributed to the preparation of the experiment and experimental runs. C.G.: Contributed to the development of the theoretical approach used for the description of the HHG process. P.S. and J. R–D.: Contributed to the theoretical part of the work. Th.L.: Contributed to the experimental part of the work. K.V.: Supported the experiment and contributed to the manuscript preparation. Y.M.: Supervised the spectrogram analysis and the relevant simulations. M.F.C. and M.L.: Supervised the theoretical part of the work. P.T.: conceived and supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Yangyang Liu, and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Nayak, A., Rajak, D., Farkas, B. et al. Attosecond metrology of vacuum-ultraviolet high-order harmonics generated in semiconductors via laser-dressed photoionization of alkali metals. Nat Commun 16, 1428 (2025). https://doi.org/10.1038/s41467-025-56759-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-56759-0
This article is cited by
-
High-harmonic generation meets quantum optics
Nature Photonics (2025)