Introduction

Superconductivity (SC) in two-dimensional (2D) electronic materials at low carrier densities has captivated the attention of physicists in recent years. The observation of SC in moiré1,2,3,4,5 as well as moiré-less graphene6,7,8,9 in the vicinity of correlation-induced insulators10 and spontaneously spin (or valley) polarized metallic states11 has raised the question of the extent to which pairing is due to the proximate electronic orders. The role of electron-electron vs. electron-phonon interactions in inducing SC in these platforms has also been scrutinized intensely, even as the experimental situation remains largely unclear12,13,14. The recent discovery of SC and an intertwined correlated insulator in twisted bilayers of WSe2 (tWSe2) near θ = 3.650 only at a commensurate filling15 present a number of fascinating puzzles that require a critical examination of strong-coupling effects, originating from electronic interactions. SC has also been reported at a larger twist-angle in twisted WSe216, where the bare electronic bandwidth is higher, and there are no proximate insulating phases in the phase diagram, suggesting weaker effective correlations.

While previous experimental work17 argued for possible signatures of SC in a doped insulator in tWSe2, the recent report15 highlights a number of unconventional features tied to its origin. We highlight below some of the important phenomenological observations at the smaller twist-angle, which need to be taken into serious consideration from the outset and will be the focus of our attention here, and which point towards a strong-coupling perspective, beyond a purely fermiology-driven paradigm. First and foremost, the superconducting region occurs only in the vicinity of the commensurate filling ν = 1, and away from the van-Hove filling. Second, the predominant phase at ν = 1 is a correlated interaction-induced insulator, which only gives way to SC over a narrow range of displacement fields near Ez = 0 below Tc. Notably, both the insulating and superconducting phases appear in the layer-hybridized regime, as opposed to the layer-polarized regime. Third, there appears to be a displacement field-induced continuous and direct superconductor-insulator transition at ν = 1. The insulator yields no topological response, as far as electrical transport is concerned, and reveals fluctuating local moments at high temperatures.

At first glance, the superconductor-insulator transition suggests the possibility of the insulator being a failed superconductor18—a localized crystal of phase-incoherent (electronic) Cooper pairs. However, the appearance of the local pairing only in the vicinity of ν = 1, rather than a wider range of dopings19 suggests that the origin of pairing must be tied to the proximate (commensurate) Mott insulator. The experimental data suggests that the origin of pairing, or the glue, is potentially present in the insulator itself. In other words, it is not the pairing of electrons, but of other particles (e.g., spinons) in the parent insulating phase, that might be responsible for the subsidiary electronic pairing in the superconducting phase, separated from the parent insulator via a quantum phase transition. Our proposed scenario is distinct from a weak-coupling electron fermiology-driven instability20,21,22,23,24,25,26,27 or a doping-induced instability28,29,30,31,32,33, which is generically not expected to yield a direct continuous superconductor-insulator transition at a fixed commensurate filling.

In this work, we analyze the above scenario for the interplay between the insulator and superconductor at the commensurate filling ν = 1. We start from a model Hamiltonian that is believed to capture many of the essential microscopic details of the electronic bandstructure, topological character, and interactions. Our basic proposal for the phenomenology at ν = 1 is of a fully gapped quantum spin-liquid insulator34,35, where the electron fractionalizes into neutral fermionic spinons which are paired, and a gapped holon which carries the electric charge. As noted above, the fermionic pairing arising within the insulator itself, and the transition into the electronic superconductor at a fixed filling arises once the holons condense as a function of the displacement field36. Clearly, the doped quantum spin liquid can, in principle, harbor SC, as will also be demonstrated within the same parton mean-field computations. However, we discuss at the end why this tendency can be suppressed in the present setting and why this remains one of the exciting directions for theory in future work.

Results

Model

To demonstrate the possibility of the above scenario in a concrete setting, we start from a three-orbital electronic model37 obtained from an underlying continuum model38,39. The general features of the model derive from taking the quadratic approximation for the topmost valence band of the monolayer valley, K, which is spin-split due to the strong spin-orbit coupling40. The opposite valley is related by time-reversal symmetry, and for AA stacking, the bands from both layers will feature spin ↑(↓) character for valley \(K\left(-K\right)\). The bands for the bottom and top layer are slightly displaced to the corners of the Brillouin zone κ±, whose location is determined by the twist-angle θ. For WSe2, the interlayer tunneling and the moiré potential has been determined from large-scale DFT calculations39. At large twist angles, the two topmost bands in the continuum model feature equal valley contrasting Chern numbers. Consequently, to capture the low-energy physics of these bands, a minimal model including at least three orbitals is needed to achieve a local real-space description37,41,42,43,44.

We focus on the following interacting model in what follows37: H = ∑σ=↑,↓Hσ + Hint, where

$${H}_{\uparrow }={\sum}_{{{{\bf{k}}}},\tau }{c}_{{{{\bf{k}}}},\tau }^{{{\dagger}} }\left[{h}_{1,\tau }\left({{{\bf{k}}}}\right)+{h}_{2,\tau }\left({{{\bf{k}}}}\right)\right]{c}_{{{{\bf{k}}}},\tau },$$
(1a)
$${H}_{{{{\rm{int}}}}}= {U}_{H} {\sum}_{{{{\bf{r}}}}\in H}{n}_{{{{\bf{r}}}}\uparrow }{n}_{{{{\bf{r}}}}\downarrow }+{U}_{T} {\sum}_{{{{\bf{r}}}}\in T}{n}_{{{{\bf{r}}}}\uparrow }{n}_{{{{\bf{r}}}}\downarrow }+V{\sum }_{{{{\bf{r}}}}\in T,{{{{\bf{r}}}}}^{{\prime} }\in H}^{{\prime} }{n}_{{{{\bf{r}}}}}{n}_{{{{{\bf{r}}}}}^{{\prime} }}\\ + J{\sum }_{{{{\bf{r}}}}\in T,{{{{\bf{r}}}}}^{{\prime} }\in H}^{{\prime} }\left[{e}^{i{\phi }_{{{{\bf{r}}}},{{{{\bf{r}}}}}^{{\prime} }}}{c}_{{{{\bf{r}}}}\uparrow }^{{{\dagger}} }{c}_{{{{\bf{r}}}}\downarrow }{c}_{{{{{\bf{r}}}}}^{{\prime} }\downarrow }^{{{\dagger}} }{c}_{{{{{\bf{r}}}}}^{{\prime} }\uparrow }+\,{\mbox{h.c.}}\,\right].$$
(1b)

Here, ck,τ represents a spinor in orbital space, and h1(k), h2(k) represent the nearest and further range hopping matrix elements, respectively. In the absence of the displacement field (Ez = 0), the MX/XM sites are degenerate in energy, and split by a constant energy ~δ relative to the energy of the MM sites; see Methods (Sec. IV) for details.

The choice of hoppings in the model is able to broadly capture the band topology of twisted TMD homobilayers by reproducing the C3 eigenvalues of orbitals obtained from the continuum model at γ, κ, and \({\kappa }^{{\prime} }\), which can be done by retaining nearest-neighbor hoppings in h1(k) and is consistent with DFT37,39. By additionally including further neighbor hoppings, the energetics of the topmost band can be reproduced to a high degree of accuracy at small twist angles. However, for θ = 3.65°, the top three bands of the continuum model for twisted WSe2 feature a combination of topological indices that disallows a local description45, which is reflected in the error incurred in the fit to the three-orbital model in Fig. 1. Nevertheless, the uncertainties in the parametrization of the continuum model leads us to focus on capturing only the topology of the two topmost bands. Unlike experimental evidence for the non-trivial topology associated with the two topmost bands46,47, there is no such available evidence for the non-trivial topology tied to the third band at present. While the insulator at ν = 1 does not show any clear experimental indications of topological edge-states or orbital ferromagnetism, a more detailed future study can help clarify the role of band-topology in the correlation-driven Mott insulator. Phenomenologically, this allows us to study the low-energy physics of the experiment within a local description, but setting up the problem directly in momentum space remains an interesting future direction. Even with this approximation, the Berry curvature distribution and quantum geometry of the topmost two bands can be reproduced faithfully from the continuum model. The integral of the Fubini-Study metric shows a particularly weak dependence on the displacement field, suggesting that localization of the Wannier orbitals at the level of the non-interacting bands is playing a subsidiary role, and the main effect of the displacement field may be to introduce a sublattice potential difference between XM and MX stacking regions.

Fig. 1: Three-orbital model for twisted WSe2.
figure 1

a Schematic of the interacting three-orbital model for tWSe2, where ●, ▼, ▲ symbols represent MM, XM, and MX sites, respectively; see Eq. 1a and b. b Non-interacting electronic dispersions of the continuum model (dashed lines) and the tight-binding fit to the three-orbital model (solid colored line), respectively, for the topmost, second, and third moiré valence bands. The color coding denotes honeycomb (H) for the MX/XM sites, and triangular (T) for the MM site.

Full size image

Turning now to the interactions (Eq. 1b), we have included an on-site repulsion UH, UT on the honeycomb and triangular sites, respectively, in addition to a nearest-neighbor (represented by \({\sum }^{{\prime} }\)) repulsion, V. Finally, the chiral-exchange interaction, J, arises between the T and H sites directly by projecting the Coulomb-interactions to the relevant bands, and the phase-factors \({\phi }_{{{{\bf{r}}}},{r}^{{\prime} }}=2\pi n/3\) with n an integer that increases counter-clockwise labeling the six nearest neighbors around a T site. This term preserves the time-reversal symmetry as it can be rewritten as the weighted sum of a Heisenberg and a two-spin Dzyaloshinskii-Moriya interaction. Note that we have not included a super-exchange interaction across the two valleys in the above description since it is expected to be small; nevertheless, such interaction will also drive the same pairing tendency of spinons32. In order to analyze the phases and phase-transitions associated with the above model, we employ the parton representation for the electronic operators (c = bf, with b and f being charged boson and neutral spinon, respectively); see Methods (Sec. IV) and Supplementary Materials Sec. I for details. We will begin by incorporating the mean-field decomposition of Hint, where the effect of the U, V − terms associated with the on-site and nearest-neighbor repulsions at the commensurate filling are included in the bosonic sector, and the effect of the chiral-exchange J − term is included in the fermionic sector, respectively. As a result, the Mottness associated with the repulsive interactions affects the holons and is expected to drive a superfluid-Mott transition at a fixed commensurate filling.

Field-induced superconductor-insulator transition

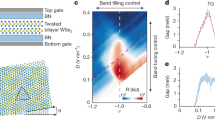
Let us begin by describing the patterns of the holon and spinon (de-)localization in real space on the different sublattice sites based on the solution of the parton mean-field equations (see Methods in Sec. IV), and summarizing the essential theoretical results. As shown in Fig. 2, the relative marker sizes are obtained from the solutions to the fully self-consistent parton mean-field computations, accounting for a superconducting and insulating spin-liquid solution in the vicinity of the Mott-transition. At Ez = 0, one of the key bandstructure inputs is the degeneracy tied to MX/XM sites, which is split by  ~δ from the energy of the MM site. At ν = 1, and for the typical values of tTH, tHH, UH, UT, V, we find the bosons delocalized across all three orbitals in a superfluid phase at small values of Ez, thereby quenching any tendency towards fractionalization. The evolution of 〈b〉 summed over all three sites is shown in Fig. 3a, along with the occupations nb on each of the three sublattice sites in Fig. 3b. The chiral-exchange term mediates attraction between the spinons, leading to an inter-valley and fully gapped extended s—wave singlet paired state. Note that the expectation value for the electron pairing operators (suppressing the spatial and orbital labels for simplicity) is given by, 〈cc〉 = 〈b2〉〈ff〉, within the mean-field approximation. When the bosons form a superfluid (〈b〉 ≠ 0) and the spinons are paired (〈ff〉 ≠ 0), the electron pair correlation function has a finite expectation value, and the resulting state is an electronic superconductor. On the other hand, across a Mott transition where 〈b〉 = 0, if the spinon pairing is not lost, the resulting state of gapped charge and paired spinons yields a fully gapped quantum spin liquid48,49. With increasing displacement field, the energies of the MX/XM sites are no longer degenerate, and split by the field, and we find that the holon and spinon localize only on the MX/MM sites, as shown in Fig. 2b. Note that the holon occupations are shared between the MX/MM sites as 1−ϵ, ϵ, respectively, with ϵ > 0; see, e.g., green  × -markers in Fig. 3a, b. We find that the  ±ϵ − fractions of the holons experience a net attraction due to the Coulomb interaction, V, which leads to a holon binding and an excitonic Mott insulator50,51. Note that the exciton here is formed between the positive and negatively charged holons, with compensated densities  ±ϵ. This phase is stabilized in the strong U and V limits. Importantly, the pattern of charge localization still implies an underlying layer-hybridized state. The spinon pairing also survives leading to an insulator with both spin and charge-gap; see green  × -marker in Fig. 4a, b. This is the promised fully gapped quantum spin liquid insulator. Further increasing the displacement-field, we find that the spinon occupations on the different sublattice sites change rapidly, with \({\langle {f}^{{{\dagger}} }f\rangle }_{{{{\rm{MM}}}}}\to 0\); see orange  × -marker in Fig. 4a, b. The nature of the chiral-exchange interaction (between the MM and MX/XM sites) is such that this automatically also leads to a loss of spinon pairing, without affecting the charge-localization in the Mott insulator. Thus, within this scenario, at large fields, there is a quantum phase transition between the LH spin-gapped Mott insulator to a layer-polarized Mott insulator with the charge and spinons localized on the triangular lattice sites consisting of the MX sites, as discussed in the Supplementary Material Sec. II. Within our mean-field ansatz, this can naturally yield a spin-liquid with spinon Fermi surface, but could also yield more conventional ordered states with a finite expectation value for 〈 f †σf 〉 ≠ 0 at specific ordering wavevectors. We leave a detailed study of competition between such states for future work. An unbiased determination of the energetics for the present model can only arise from numerically exact methods, which are beyond the scope of present work.

Fig. 2: Evolution of the local holon and spinon occupations with increasing displacement field.
figure 2

The upper and lower panels show the occupations for the holons (upper panel) and spinons (lower panel) obtained from the parton mean-field computation for the Hamiltonian in Eq. 1a and b. The empty (○, ▽, △) and filled (●, ▼, ▲) symbols represent holon and spinon occupations, respectively, on the MM, XM, and MX sites. The size of the markers is set so that the area of the bounding box surrounding them is proportional to the corresponding occupations determined from the parton mean-field computations. LH MI stands for layer-hybridized Mott insulator. a For small Ez, both the holons and spinons are LH; the spinons pair leading to an electronic superconductor when the holons are condensed (see text). b With increasing Ez, the holons are localized at MM and MX sites, forming an “excitonic" Mott insulator, and thus retain their LH character (see text). The spinons are also LH and remain paired, resulting in an electronic MI with charge and spin gaps, respectively. The plots in a, b are generated for values of the electric field corresponding to the red and green  × -markers in Figs. 3 and 4, respectively. With large Ez, the spinons and holons localize on the MX sites in a layer-polarized Mott insulator; see supplementary material Sec. II.

Full size image
Fig. 3: Evolution of the holon properties across the superfluid-Mott insulator transition.
figure 3

a The holon condensate 〈b〉, which is related to the holon superfluid density, summed over the three orbitals, and b boson occupation as a function of the displacement field. Red and green  × -markers correspond to the superconductor and gapped spin liquid illustrated in Fig. 2a, b, respectively. Orange  × -marker represents a layer-polarized Mott insulator with the spinons and holons localized on the MX sites, at much higher fields; see supplementary material Sec. II. The model parameters used for all of our simulations are: δ = −14.9 meV, \({t}_{TH}^{\left(1\right)}=10.78\,{\mbox{meV}}\,\), \({t}_{HH}^{\left(1\right)}=0.55\,{\mbox{meV}}\,\), \({t}_{TT}^{\left(1\right)}=-1.95\,{\mbox{meV}}\,\), \({t}_{TH}^{\left(2\right)}=-1.21\,{\mbox{meV}}\,\), \({t}_{HH}^{\left(3\right)}=5.4\,{\mbox{meV}}\,\), UH = 35 meV, UT = 20 meV, V = 40 meV, and J = 10 meV, respectively.

Full size image
Fig. 4: Evolution of the spinon properties with increasing displacement field.
figure 4

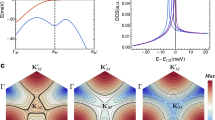
a Spinon pairing gap Δtot, obtained from parton mean-field computation as a function of displacement-field, Ez. The bosonic Mott critical field is denoted by Ec. Slightly beyond Ec, the spinon sector remains paired. b Evolution of spinon occupation with increasing displacement field. For Ez ≳ Ec (green  × -marker), the spinon remains paired and layer-hybridized; for Ez ≫ Ec (orange  × -marker), the spinon sector tends to layer polarize. c Spinon Bogoliubov spectral function Af(k, ω), evaluated at Ez/Ec = 0.1 and J = 10 meV. A spinon gap  ~2 meV is observed for the half-filled lowest band. d Spinon Bogoliubov spectral function Af(k, ω = 0) at Ez/Ec = 1.4 and J = 10 meV within moiré Brillouin zone. The spinon gap ∣Δtot∣ has been fully suppressed, and A(k, ω = 0) shows the spinon Fermi surface. Model parameters are the same as in Fig.3.

Full size image

In Fig. 3, we plot the evolution of the condensation expectation value, 〈b〉, summed over all the orbitals, which sets the superfluid density for the holons, and holon-densities with increasing displacement-field, obtained from the parton mean-field computation using Hb. As noted above, in small-displacement fields, the holons are clearly in a superfluid state (corresponding to Fig. 2a), with 〈b〉ℓ ≠ 0 &∀ℓ. On the other hand, beyond a critical Ez, numerically we find 〈b†b〉 ≠ 0 for nearest-neighbor MX/MM sites and 〈b〉→0. This is the Mott insulating phase (corresponding to Fig. 2b), which remains layer-hybridized. Eventually, with increasing Ez, the bosons favor layer-polarization (see Supplementary Material Sec. II), where the system effectively becomes a triangular lattice system constructed out of the MX sites. Simultaneously, it is useful to track the evolution of the spinon densities with increasing displacement fields; see Fig. 2 (bottom-row). At small-displacement fields, the spinon occupations \({\langle \, \, {f}^{{{\dagger}} } \, f\rangle }_{\ell }\,\ne \, 0\,\forall \ell\) (Fig. 2a) in a spinon-metallic-like regime, which is unstable to pairing due to the chiral-exchange interaction; see Fig. 4a. For J > 0, attraction is mediated in the inter-valley, spin-singlet channel as noted above. Note that we are technically not including the contributions from the gauge-field fluctuations beyond mean-field theory here, which can suppress the pairing tendency as a result of standard amperean effects52; we proceed with the assumption that the tendency towards spinon pairing remains prevalent.

Within the same self-consistent Parton mean-field theory computations (Supplementary Material Sec. I); the evolution of the angular-momentum (Lz)-resolved spinon pairing gap with increasing displacement-field is shown in Fig. 4a. The angular momentum Lz is defined as the phase winding of the spinon Cooper pairs which live on the three bonds connecting the T−H sites. For arbitrary Ez, only Lz = 0 (extended s-wave) and s = 0 (spin-singlet) channels develop a finite expectation value. At Ez = 0, the pairing between MM-MX and MM-XM is on an equal footing due to the presence of inversion symmetry. When 0 < Ez < Ec, a layer-imbalance develops, but the spinon pairing gap ∣Δtot∣ remains finite; for Ez ≳ Ec, the spinon pairing gap still remains finite whereas the boson is in Mott insulating phase (Fig. 3a), namely as Z2 spin liquid. When further increasing Ez, the pairing is fully suppressed by Ez, and the spinon sector tends to form a layer-polarized (LP) spinon-metal (Fig. 4b), which can become unstable to other forms of orders. These features are reflected in the spinon spectral function, Af(k, ω), in the LH paired (Fig. 4c) and LP unpaired (Fig. 4d) regimes, respectively. Note that we have intentionally refrained from quoting the absolute values of Ez in our analysis, as the values of the layer-polarization susceptibility for both of the matter fields are a priori unknown.

Clearly, the nature of the resulting many-body phase is determined by the combination of the bosonic and fermionic correlators, respectively. As was noted above, when 〈b〉 ≠ 0 in the superfluid phase, the resulting state is a superconductor as long as spinon pairing is present (Fig. 2a). As a function of increasing displacement-field, there can be a tendency towards spontaneously broken C3−symmetry20, as well as other broken symmetries that include long-range magnetic order. If the holons remain condensed, and in the absence of the magnetic order, the resulting state is a nematic superconductor, whereas if the critical field for C3—breaking is larger than the Mott transition for the holons, the nematicity onsets only in the gapped spin-liquid insulator. Within our present scenario, when 〈b〉 = 0 in the Mott-insulating phase, for small-displacement fields the ground state is an electrical insulator with both a charge and spin-gap, respectively. When the spinon pairing is lost, the system transitions into a Mott insulator with a charge gap but no spin gap, reminiscent of previous experiments in AA-stacked heterobilayers53.

Discussion

The intriguing phenomenology tied to the recently discovered continuous superconductor-to-insulator transition at a fixed commensurate filling in tWSe2 has naturally led us to a scenario where the origin of fermionic pairing (due to spinons) lies in the insulator, and the electrical response (due to holons) is determined purely by the interplay of Hubbard interactions and charge-transfer gap between the different orbitals. Our proposal already motivates the need for a number of future experiments, which will be crucial for developing deeper theoretical insights into this problem.

First and foremost, the temperature dependence of the magnetic susceptibility in the insulating phase using MCD (at low temperatures) will help reveal whether a spin gap exists along with the charge gap. This has revealed unparalleled insights in a previous experiment in a Mott-insulator53. The above scenario suggests that in the insulator across the transition from the superconductor, the asymptotic low-temperature susceptibility will be exponentially suppressed. It is also plausible, based in part on our computations, that there are two distinct insulators, separated by a spin-gap closing transition (without any closing of the charge-gap) that can be distinguished at the lowest temperatures based on the MCD data. The kink-like feature in the insulating region in the experiment15 might be indicative of such a transition.

It is worth addressing the possibility of other competing insulating states. For strongly interacting Hubbard-type models with geometrical frustrations, conventional antiferromagnetic orders are often more favored54. However, our focus here has been on the physics near the Mott transition, where the local-moment physics is not entirely developed. Such weak Mott insulators with a small charge gap are ideally suited for realizing candidate quantum spin-liquid states55. The state obtained here just across the transition, is an ideal parent state for the presumably unconventional superconductor. We note that a recent DMRG study for a much simpler, but classic, triangular lattice Hubbard model at fixed filling also found an exotic gapped spin liquid (in the bulk) across a metal-insulator transition56; the transition to the conventional magnetically ordered state only occurs deeper inside the insulating state. Establishing the full energy landscape for the present multi-orbital (topological) model in the intermediate to the strong-coupling regime is clearly beyond the realm of a (Parton) mean-field theory setup and remains an exciting frontier for both exact and approximate numerical methods. We also note in passing that given the continuous nature of the transition, and in the absence of any fine-tuning, any broken translation symmetries in the Mott-insulator proximate to the transition will be present in the superconductor; an alternative and more exotic scenario is that the critical point is deconfined, as has also been suggested in recent work57.

While our work serves as a useful starting point to study the relation between the experimental puzzles and our current understanding of the actual bandstructures in twisted homobilayers, the complexity associated with the three-orbital model and its associated topological character reveal a number of unique challenges. In future work and for complementary insights into the problem, it would be interesting to step away from the complicated microscopic details of the present setup and describe a simpler version of the model with the interactions projected to the relevant low-energy topological bands directly in momentum space. This can enable a better and universal understanding of the phase transition between a paramagnetic Mott insulator, including the fully gapped spin liquid considered here, and a superconductor in a model of C = ±1 Chern bands in a time-reversal symmetric setting at integer filling. A variational approach with the analog of a Gutzwiller-type wavefunction49, but implemented in momentum-space, would be an interesting first step.

We end by noting that one of the most exciting open questions is related to the nature of the metal-to-metal transition that occurs as a function of filling across the ν = 1 orders at a fixed displacement field. Approaching from ν → 1+, a renormalized Fermi liquid with an increasing effective mass transitions either into an insulator, or a superconductor in the near vicinity of ν = 1. For ν → 1−, the properties of the metallic state are not entirely clear at present, but there are marked phenomenological differences from a conventional Fermi liquid. Further studies of these metallic phases, incorporating also the effects of disorder, might lead to an improved understanding of the global low-temperature phenomenology in the vicinity of ν = 1 in tWSe2. In the present setup, we find that SC persists over a small range of fillings near ν = 1; see Supplementary Material Sec. III. Within the current scenario, it is worth noting that the superconducting Tc is controlled by the phase-stiffness and not the pairing gap, which can be small both at ν = 1 (e.g., due to disorder effects58 and suppressed tendency towards pairing52,59) and with doping. Moreover, given the spinonic origin of the pairing, doping away potentially leads to a dramatic suppression of this tendency, when the spinons are prone to confinement. Investigating these effects in more careful detail and utilizing more sophisticated methods remains an interesting open problem.

Note added

A related manuscript has also recently analyzed the pairing instabilities of spinons due to the chiral-exchange interaction60.

Methods

Three-orbital model

The non-interacting three-orbital model in the main text is given by

$${H}_{\uparrow }={\sum}_{{{{\bf{k}}}},\tau }{c}_{{{{\bf{k}}}},\tau }^{{{\dagger}} }\left[{h}_{1,\tau }\left({{{\bf{k}}}}\right)+{h}_{2,\tau }\left({{{\bf{k}}}}\right)\right]{c}_{{{{\bf{k}}}},\tau },\,\,{\mbox{where}}\,$$
(2a)
$${h}_{1}\left({{{\bf{k}}}}\right)=\left(\begin{array}{rcl}{E}_{z}-\mu &{t}_{TH}^{\left(1\right)}{g}_{{{{\bf{k}}}}}&{t}_{HH}^{\left(1\right)}{f}_{{{{\bf{k}}}}}^{*}\\ {t}_{TH}^{\left(1\right)}{g}_{{{{\bf{k}}}}}^{*}&-\delta -\mu &-{t}_{TH}^{\left(1\right)}{g}_{-{{{\bf{k}}}}}^{*}\\ {t}_{HH}^{\left(1\right)}{f}_{{{{\bf{k}}}}}&-{t}_{TH}^{\left(1\right)}{g}_{-{{{\bf{k}}}}}&-{E}_{z}-\mu \end{array}\right),$$
(2b)
$${h}_{2}\left({{{\bf{k}}}}\right)=\left(\begin{array}{rcl}0&-{t}_{TH}^{\left(2\right)}{g}_{-2{{{\bf{k}}}}}&{t}_{HH}^{\left(3\right)}{f}_{2{{{\bf{k}}}}}\\ -{t}_{TH}^{\left(2\right)}{g}_{-2{{{\bf{k}}}}}^{*}&{t}_{TT}^{\left(1\right)}{h}_{{{{\bf{k}}}}}&{t}_{TH}^{\left(2\right)}{g}_{2{{{\bf{k}}}}}^{*}\\ {t}_{HH}^{\left(3\right)}{f}_{{{2{\bf{k}}}}}^{*}&{t}_{TH}^{\left(2\right)}{g}_{2{{{\bf{k}}}}}&0\end{array}\right).$$
(2c)

The displacement field, Ez, modifies the on-site energies and μ is the chemical potential. The hopping matrix elements, tab (a, b ≡ T, H), for the triangular and honeycomb lattice sites are shown in Fig. 1a. The associated momentum-space form factors are defined as,

$${f}_{{{{\bf{k}}}}}={\sum}_{j=0,1,2}{e}^{i{{{\bf{k}}}}\cdot {{{{\bf{u}}}}}_{j}},\,\,{g}_{{{{\bf{k}}}}}={\sum}_{j=0,1,2}{e}^{i2\pi \left(j-1\right)/3}{e}^{i{{{\bf{k}}}}\cdot {{{{\bf{u}}}}}_{j}},$$
(3a)
$${h}_{{{{\bf{k}}}}}=2{\sum}_{j=1,2,3}\cos \left({{{\bf{k}}}}\cdot {{{{\bf{a}}}}}_{j}\right),$$
(3b)

where a1 = (aM, 0), \({{{{\bf{a}}}}}_{j}={C}_{3}^{j-1}{{{{\bf{a}}}}}_{1}\), u0 = (a1−a2)/3, \({{{{\bf{u}}}}}_{j}={C}_{3}^{j}{{{{\bf{u}}}}}_{0}\), and aM is the moire lattice constant. The specific orbital content is that of orbitals localized at the XM/MX (H) and MM (T) stacking regions of the bilayer with an s-wave character. The former (H) is layer-polarized as interlayer tuneling vanishes at these stacking regions, while the latter (T) is layer hybridized since MM stacking regions map to themselves under C2y symmetry, implying that they possess mixed character from both layers37.

Parton mean-field theory

The parton representation proceeds in the usual fashion61,62, where we express cr,ℓ,σ = br,ℓfr,ℓ,σ, with the br,ℓ representing spinless charged holon fields at site r with orbital ℓ, and the fr,ℓ,σ denoting spinful neutral spinons that also carry the orbital index ℓ. The holon annihilation operator can be written in terms of a quantum rotor representation, \({b}_{{{{\bf{r}}}},\ell }={e}^{i{\theta }_{{{{\bf{r}}}},\ell }}\), which raises the rotor charge \({n}_{{{{\bf{r}}}},\ell }^{\theta }\) by 1. The local constraint that helps project the problem back to the physical Hilbert space is given by \(\langle {\sum }_{\ell }{n}_{{{{\bf{r}}}},\ell }^{\theta }\rangle+\langle {\sum }_{\ell,\sigma }{n}_{{{{\bf{r}}}},\ell,\sigma }^{f}\rangle=\,{\mbox{const}}\,\). Note that the microscopic Hamiltonian does not forbid double occupancy, and we will implement the filling constraints for the parton fields on average in our numerical simulations.

The mean-field Hamiltonian takes the form, HMF = Hb({χ}) + Hf({χ, Δ, B}), where the variational parameters in the matter field sectors are tied to the correlators, \({B}_{{{{\bf{r}}}}{{{{\bf{r}}}}}^{{\prime} }}^{\ell {\ell }^{{\prime} }}\equiv \langle {b}_{{{{\bf{r}}}},\ell }^{{{\dagger}} }{b}_{{{{{\bf{r}}}}}^{{\prime} },{\ell }^{{\prime} }}\rangle\), \({\chi }_{{{{\bf{r}}}}{{{{\bf{r}}}}}^{{\prime} },\sigma }^{\ell {\ell }^{{\prime} }}\equiv \langle {f}_{{{{\bf{r}}}},\ell,\sigma }^{{{\dagger}} }{f}_{{{{{\bf{r}}}}}^{{\prime} },{\ell }^{{\prime} },\sigma }\rangle\), and \({\Delta }_{{{{\bf{r}}}}{{{{\bf{r}}}}}^{{\prime} },\sigma {\sigma }^{{\prime} }}^{\ell {\ell }^{{\prime} }}\equiv \langle {\varepsilon }_{\sigma {\sigma }^{{\prime} }}{f}_{{{{\bf{r}}}},\ell,\sigma }{f}_{{{{{\bf{r}}}}}^{{\prime} },{\ell }^{{\prime} },{\sigma }^{{\prime} }}\rangle\), respectively. Clearly, the B—correlator is evaluated with respect to Hb and renormalizes the spinon bandwidth in Hf. Similarly, χ is evaluated with respect to Hf, which arises both from the bare bandwidth and the chiral-exchange term, and renormalizes the boson hoppings in Hb, as well as the spinon hoppings in Hf. Finally, Δ is also evaluated with respect to Hf and drives the pairing of spinons. To deal with Hb, we utilize a 3-site cluster approximation comprising all three orbitals, within which we impose the global U(1) number conservation. Given that \({t}_{TH}^{(1)}\) is the dominant hopping, for the computations presented here, we consider the equilateral triangles comprising nearest-neighbor orbitals within the clusters; see Supplementary Material Sec. IV for additional details and a more elaborate choice of clusters.