Introduction

Origami sheets are two-dimensional surfaces with predefined creases that control their three-dimensional response to mechanical loads1,2,3,4. The fundamental principle behind the behavior of origami is the difference between the energy scales of elastic deformations that bend the panels (cubic in sheet thickness) and elastic deformations that stretch the panels (linear in sheet thickness). This scaling leads to a quasi-static, low-energy response dominated by the deformations that do not stretch the panels, which we refer to as linear isometries. Since this principle relies solely on the thickness of the sheet, the linear isometries corresponding to a particular crease pattern are largely material independent and therefore realizable in both metallic5,6,7,8,9 and polymeric10,11,12 materials over a range of length scales. Hence, an understanding of the origami kinematics tends to be more consequential than an understanding of the origami dynamics for the design of origami metamaterials. There are two specific applications of origami kinematics that motivate our work.

The first application of interest is the class of isometries referred to as rigid folding mechanisms that fold the origami sheet along its predefined creases while keeping the panels entirely rigid (no stretching or bending). These rigid folding mechanisms are useful for the deployment and transformation of structures found in various engineering applications including solar arrays13,14, heart stents15, and temporary shelters16. However, arbitrary quadrilateral-mesh crease patterns are not rigidly foldable and a significant body of work is devoted towards the development of design principles17,18,19,20,21,22. Moreover, arbitrary loads can lead to heterogeneous actuation of the mechanism23,24 as well as undesirable deformations due to the existence of isometries distinct from the rigid folding mechanism25 or the intersection of separate branches in the configuration space26. Therefore, efficient models for the response to external loads can inform the methods for deployment and transformation of origami structures along the programmed rigid mechanism without exciting undesirable responses via alternative low-energy instabilities.

The second application of interest is the continuum approximation (also referred to as homogenization or coarse-graining) of linear isometries in periodic origami tessellations. Such approximations are valuable for both surface fitting27 and effective elasticity models28,29,30, where deformations that do not stretch the individual panels generate apparently non-isometric deformations at the large scale. The main example in the existing literature is the class of parallelogram-based origami sheets, such as the Miura-ori crease pattern31,32. An origami tessellation in this class is quasi-planar, in that its two primitive lattice vectors always lie in the same two-dimensional plane, and exhibits one rigid folding mechanism that changes its lattice vectors. Simultaneously, such a tessellation also exhibits two nonrigid linear isometries that bend the panels in addition to folding the creases. Approximating the origami tessellation as a continuous sheet reveals that the rigid isometry generates in-plane strain, the first nonrigid isometry generates out-of-plane curvature, and the second nonrigid isometry generates out-of-plane twisting31,32,33,34,35,36. These three modes function as a basis for more general low-energy deformations in effect continuum models29,30. Moreover, analytical calculations show the crease geometry necessarily pairs a hydrostatic (dilation) strain mode with an anticlastic (saddle) curvature mode and a deviatoric (pure shear) strain mode with a synclastic (dome) curvature mode31,32,33,34,35,36.

Our work seeks to expand the investigation of parallelogram-based origami sheets to more generic tessellations which possess two crucial differences from those composed of parallelograms37,38. The first difference is that a generic tessellation is quasi-cylindrical, rather than quasi-planar, in that its two primitive lattice vectors rotate about a common axis from cell to cell. The second difference is that such a quasi-cylindrical tessellation exhibits two linear isometries (rather than the one rigid and two non-rigid isometries discussed in the previous paragraph) that retain the quasi-cylindrical geometry while changing its radius, height, and symmetry axis. We investigate these two linear isometries in rigidly-foldable trapezoid-based origami (TBO) tessellations, for which the constituent trapezoid faces have one less symmetry than the previously investigated parallelogram faces, to exemplify continuum approximations for the linear isometries in quasi-cylindrical origami tessellations. We show exemplar TBO folded from cardstock in their ground state configurations in Fig. 1A–D(i) and in rigidly folded configurations in Fig. 1A–D(ii). While such rigid folding mechanisms of TBO are identified for select geometries, such as the arc pattern, in previous works39,40, our work also identifies and models the nonrigid isometries shown in Fig. 1A–D(iii). Our theoretical model has two components. The first component determines and solves the compatibility conditions for the linear isometries within a single cell, which we show can be represented using the compatibility diagrams shown in Fig. 1A–D(iv) where the meaning of the line styles and colors is explained in Supplementary Note 4. The second component maps these linear isometries to their continuum approximation, which decomposes into one rigid breathing mode and one nonrigid shearing mode. We showcase our analytical results for a class of origami crease patterns derived from the geometry presented in ref. 34 that we refer to as the Arc-Morph and perform laboratory scale experiments on a specimen manufactured from polypropylene.

Fig. 1: Examples of trapezoid-based origami folded from cardstock.
figure 1

(i) quasi-cylindrical ground states, (ii) rigid folding cylindrical isometry, (iii) non-rigid shear isometry, and (iv) diagramatic representation of compatibility conditions with line styles signifying the coupling between amplitudes on the adjoined vertices and triangles indicating periodic directions (see Supplementary Note 4 for more details). A Cylindrical geometry from Arc-Miura. B Extension of the pattern in panel A exhibiting a locked configuration. C Archimedean spiral from a graded Arc-Miura pattern. D Lemniscate of Bernoulli from a graded Arc-Miura with a parallelogram interface.

Full size image

Results

As shown in refs. 37,38, periodic origami tessellations with generic faces adopt quasi-cylindrical ground states generated by the two primitive lattice vectors (ℓ1,2) and the two primitive lattice rotation matrices (S1,2) (see Fig. 2A). Importantly, the lattice rotations share a common axis (\(\hat{S}\)) about which local frames are rotated by the respective lattice rotation angle (η1,2) and the lattice vector components orthogonal to \(\hat{S}\) define a unique radius of curvature (R). Thus, we coarse-grain the lattice-scale geometry by taking the discrete cell indices (n1, n2) to the continuous surface coordinates (φ, z) (see Methods, Coarse-Graining). The coarse-grained geometry retains the cylindrical embedding (see Supplementary Note 1) so we approximate the ground state \({{\bf{X}}}(\varphi,z)=R\cos \varphi \hat{x}+R\sin \varphi \hat{y}+z\hat{z}\). From the embedding, we compute the tangent vectors tμ ≡ ∂μX (using subscripts μ, ν to denote the surface coordinates) and the normal vector \(\hat{n}\equiv {{{\bf{t}}}}_{\varphi }\times {{{\bf{t}}}}_{z}/| {{{\bf{t}}}}_{\varphi }\times {{{\bf{t}}}}_{z}|\) to construct the first fundamental form Iμν ≡ tμ ⋅ tν, the second fundamental form \(I{I}_{\mu \nu }\equiv \hat{n}\cdot {\partial }_{\mu }{{{\bf{t}}}}_{\nu }\), and the shape operator \({{\boldsymbol{{{\mathcal{S}}}}}}\equiv {{\bf{II}}}{{{\bf{I}}}}^{-1}\):

$${{\boldsymbol{I}}}=\left(\begin{array}{rc}{R}^{2}&0\\ 0&1\end{array}\right),$$
(1)
$${{\boldsymbol{II}}}=\left(\begin{array}{rc}-R&0\\ 0&0\end{array}\right),$$
(2)
$${\boldsymbol{{\mathcal{S}}}}=\left(\begin{array}{rc}-\frac{1}{R}&0\\ 0&0\end{array}\right).$$
(3)

The shape operator has eigenvalues equal to the principal curvatures (κ1 = − 1/R, κ2 = 0), eigenvectors equal to the principal directions (\({\hat{v}}_{1}=(1,0),\hat{{v}_{2}}=(0,1)\)), determinant equal to the Gaussian curvature (K = 0), and trace equal to twice the mean curvature (2H = − 1/R).

Fig. 2: Coarse-grained geometry.
figure 2

A Angled view of a quasi-cylindrical trapezoid-based origami tessellation with lattice vectors ℓ1,2, lattice rotation axis \(\hat{S}\), and characteristic height h. B Top-down view of the tessellation shown in (A) with lattice rotation angle η1, radius R, and azimuthal surface coordinate φ. Continuum illustration of the (C) breathing mode and (D) shearing mode induced by the linear isometries of the tessellation shown in (A).

Full size image

As shown in refs. 37,38, at the lattice-scale, these origami sheets generically exhibit two linear isometries under periodic boundary conditions which change the lattice vectors (ℓ1,2 → ℓ1,2 + Δ1,2) and the lattice rotation matrices (S1,2 → (1 + L1,2)S1,2), thereby inducing changes in the radius (R → R + δR) and the rotation axis (\(\hat{S}\to \hat{S}+\delta \hat{S}\)) while preserving the cylindrical character to first order (see Supplementary Note 1). We write the generic deformation X → X + δX in terms of the vector field \(\delta {{\bf{X}}}=\delta {X}_{n}(\cos \varphi \hat{x}+\sin \varphi \hat{y})+\delta {X}_{\varphi }(-\sin \varphi \hat{x}+\cos \varphi \hat{y})+\delta {X}_{z}\hat{z}\) and determine the changes in the radial direction (δXn), the azimuthal direction (δXφ), and the axial direction (δXz) that are mutually consistent with cylindrical deformations below (see Supplementary Note 2).

Since cylinders have zero Gaussian curvature, the deformation must satisfy δK = 0. The in-plane strain along the azimuthal and axial directions take arbitrary, but spatially constant, values (δIφφ = εφφ and δIzz = εzz) because they are unconstrained by the cylindrical character of the deformation. Lastly, we consider a generic deformation as a linear combination of a breathing mode that changes the first principal curvature (δκ1 = − δR/R2) without changing the principal directions (\(\delta {\hat{v}}_{1}=(0,0),\delta \hat{{v}_{2}}=(0,0)\)) and a shearing mode that changes the principal directions (\(\delta {\hat{v}}_{1}=(0,{\sigma }_{1}),\delta \hat{{v}_{2}}=({\sigma }_{2},0)\)) without changing the first principal curvature (δκ1 = 0). Such modes are the only two homogeneous deformations that maintain the cylindrical character (see Supplementary Note 2). Here, εφφ, εzz, δR, σ1, and σ2 all depend implicitly on the geometry of the underlying crease pattern, and this relationship constitutes the basis of the origami sheets as mechanical metamaterials. We find that the breathing mode (illustrated in Fig. 2C) is quantified by \(\delta {X}_{n}=\delta R,\delta {X}_{\varphi }=\left({\varepsilon }_{\varphi \varphi }/(2R)-\delta R\right)\varphi\), and δXz = εzzz/2. The corresponding changes to the fundamental forms are written:

$$\delta {{\boldsymbol{I}}}=\left(\begin{array}{rc}{\varepsilon }_{\varphi \varphi }&0\\ 0&{\varepsilon }_{zz}\end{array}\right),$$
(4)
$$\delta {{\boldsymbol{II}}}=\left(\begin{array}{rc}\delta R-\frac{{\varepsilon }_{\varphi \varphi }}{R}&0\\ 0&0\end{array}\right),$$
(5)
$$\delta {{\boldsymbol{{\mathcal{S}}}}}=\left(\begin{array}{rc}\frac{\delta R}{{R}^{2}}&0\\ 0&0\end{array}\right).$$
(6)

We find that the shearing mode (illustrated in Fig. 2D) is quantified by δXn = 0, δXφ = εφφφ/(2R) + σ1Rz, and δXz = εzzz/2 + σ2φ. The corresponding changes to the fundamental forms are written:

$$\delta {{\boldsymbol{I}}}=\left(\begin{array}{rc}{\varepsilon }_{\varphi \varphi }&{R}^{2}{\sigma }_{1}+{\sigma }_{2}\\ {R}^{2}{\sigma }_{1}+{\sigma }_{2}&{\varepsilon }_{zz}\end{array}\right),$$
(7)
$$\delta {{\boldsymbol{II}}}=-\left(\begin{array}{rc}\frac{{\varepsilon }_{\varphi \varphi }}{R}&R{\sigma }_{1}\\ R{\sigma }_{1}&0\end{array}\right),$$
(8)
$$\delta {{\boldsymbol{{\mathcal{S}}}}}=\frac{1}{R}\left(\begin{array}{rc}0&{\sigma }_{2}\\ -{\sigma }_{1}&0\end{array}\right),$$
(9)

Our work focuses on applying the above analysis to the particular case of rigidly foldable TBO, including all of the crease patterns shown in Fig. 1A–D(i) and, more generically, crease patterns for which the parallel edges of the trapezoidal faces ensure ℓ1 \(\perp \hat{S}\) and ℓ2 \(\parallel \hat{S}\) along the rigid folding configuration manifold. For the crease pattern in Fig. 1A(i), the orientation of the lattice vectors is because the subsequent parallel edges rotate the faces by complementary dihedral angles so that there is no net rotation, similar to the reason a parallelogram-based origami sheet stays planar. However, for the crease pattern in Fig. 1B, the dihedral angles are not complementary but still sum to 2π. The consequence is that the rigid folding mechanism (demonstrated in Fig. 1A–D(ii)) is characterized by the breathing mode of Eqns. ((4), (5), (6)), and, by process of elimination, the remaining isometry (demonstrated in Fig. 1A–D(iii)) is characterized by the shearing mode of Eqn. ((7), (8), (9)). Interestingly, the crease patterns shown in Fig. 1C, D exhibit similar behavior despite having spatially varying crease patterns, and hence spatially varying radii, that only repeat along the rotation axis.

We provide more clarity on these modes by developing unit cell compatibility conditions for the class of TBO with parallel edges that alternate in length. Rather than triangulating the crease pattern as frequently done in previous works31,32,33,34,35, we separately consider folding degrees of freedom on the vertices, denoted by the vertex amplitudes \({{\mathcal{V}}}\), and bending degrees of freedom on the faces, denoted by the face amplitudes \({{\mathcal{F}}}\) (see Methods, Linear Isometry Model) as introduced in ref. 36 for the special case of parallelogram-based origami. The amplitude on a vertex maps to changes in the dihedral angles, which are not required to be uniform along the edge unless the isometry is rigid. Instead, a gradient in the folding along a crease generates bending of the adjacent faces, as quantified by the respective face amplitudes. For this reason, constraints on the face amplitudes can be integrated out, thereby yielding compatibility conditions that map from vertex amplitudes to vertex constraints which we illustrate via the compatibility diagrams shown in Fig. 1A–D(iv). Here, each node is assigned a vertex amplitude and the line style of the edges indicate coupling coefficients that depend on the crease geometry (see Supplementary Note 4). When the coupling coefficients are uniform along the edges, such as in Fig. 1A(iv), the rigid mode (\({{\mathcal{F}}}=0\) for all faces) is represented by uniform assignment of vertex amplitudes (\({{\mathcal{V}}}=1\) for all vertices). In contrast, when the coupling coefficients are nonuniform along the edges, such as in Fig. 1B(iv), the vertex amplitudes of the rigid mode are proportional to one another to ensure the folding is uniform along the creases. In either case, we find that this family of TBO always exhibits a nonrigid mode represented by uniform face amplitudes (\({{\mathcal{F}}}=1\) for all faces) and zero vertex amplitudes (\({{\mathcal{V}}}=0\) for all vertices). Since the breathing (shearing) mode is generated by the rigid (nonrigid) isometry, its modal stiffness depends entirely on the stiffness of the creases (faces). This representation of the isometries effectively integrates the three-dimensional geometry out of the analysis to enable a succinct analytical classification of the modes.

Analysis of Arc-Morph origami

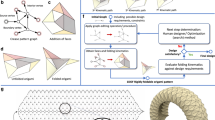
We introduce the family of Arc-Morph origami, such as the example shown in Fig. 3A. This family generalizes the Arc-Miura crease patterns presented in refs. 39,40 to include the non-developable vertex geometry from the family of Morph parallelogram-based origami introduced in ref. 34. The unit cell of these periodic crease patterns is constructed from copies of a base vertex that is parameterized by the two independently chosen sector angles α and β. The three remaining vertices of the cell have identical or supplementary (\({\alpha }^{{\prime} }\equiv \pi -\alpha,{\beta }^{{\prime} }\equiv \pi -\beta\)) sector angles and the distinction in the present work is that the vertices are arranged to form trapezoid faces rather than parallelograms. We exclusively consider isosceles trapezoids to simplify analytic expressions, but our model applies to tessellations composed of more general trapezoids and with larger unit cells such as those shown in Fig. 1B–D which contain increased numbers of faces. Thus, each of the trapezoids has two legs of length q, one base of length p, and one base of either \({s}_{\alpha }\equiv p-2q\cos \alpha\) or \({s}_{\beta }\equiv p+2q\cos \beta\) (see Fig. 3B). This yields the three-dimensional design space (α, β, q/p) for Arc-Morph, where the magnitude of p dictates the scale of the system which has no role in our kinematic analysis.

Fig. 3: Arc-Morph origami.
figure 3

A Perspective view of an example configuration with N1 = 4 cells in the azimuthal direction and N2 = 4 cells in the axial direction. B Primitive cell with vertices labeled a, b, c, and d, faces labeled \({{\mathcal{A}}},{{\mathcal{B}}},{{\mathcal{C}}}\), and \({{\mathcal{D}}}\), and edge lengths labeled p = 1, q = 0.7, sα, and sβ. C Sector angles labeled \(\alpha=1.1,{\alpha }^{{\prime} }\equiv \pi -\alpha,\beta=2.1,{\beta }^{{\prime} }\equiv \pi -\beta\) and dihedral angles labeled γ, ψ, ψ″ ≡ 2π − ψ, and θ, θ″ ≡ 2π − θ. D Compatibility diagram for vertex amplitudes with edges representing the coupling coefficients based on the folding coefficients ζ, ξ, and χ. E Nonlinear evolution of the height and radius of the crease pattern shown in panel A along the rigid folding mode, with the flat folded state shown in (F), maximal height state shown in (G), and closed state shown in (H). F–H Front and top-down views of states labeled in (E, I). I Linear response along the configuration manifold as a function of the dihedral angle, γ, quantified by the pitch p induced by the non-rigid mode and the ratio dh/dR of the rigid mode. The curve is shaded towards σ2 = 0 for illustration purposes.

Full size image

Such a crease pattern has a a rigid folding mechanism that we parameterize via the dihedral angle γ from which the remaining dihedral angles shown in Fig. 3C. (θ, θ″ ≡ 2π − θ, ψ, and ψ″ ≡ 2π − ψ) are determined. We compute the coarse-grained fundamental forms for a generic ground state then we use the mean curvature to determine the radius and the Jacobian to determine the characteristic height:

$$R=\frac{1}{4}\left(p+{s}_{\beta }+(p+{s}_{\alpha })\cos \frac{\eta }{2}\right)\csc \frac{\eta }{2},$$
(10)
$$h=2q\sin \alpha \sin \beta \sin \gamma \csc \frac{\eta }{2}.$$
(11)

We find the components of the fundamental forms exactly match those shown in Eqn. ((1), (2), (3)).We denote the number of cells in the azimuthal direction as N1 and the number of cells in the axial direction as N2, then identify the instantaneous bounds of the coordinates in our continuum approximation as 0 ≤ φ ≤ N1η(γ) and 0 ≤ z ≤ N2h(γ). Consequently, the configuration manifold is bounded by the closure condition of the faces γ = π shown in Fig. 3F and the closure condition of the cylinder N1η = 2π shown in Fig. 3H. We find these conditions restrict the space of viable configurations and system sizes, but we do not provide a thorough exploration of the design space in this work. We write the explicit expressions for the geometry along the rigid folding mechanism in Methods, Arc-Morph Geometry. We show the radius as a function of the height along the configuration manifold in Fig. 3E, and use the inset to highlight a change in slope after the cylinder reaches its maximum height as shown in Fig. 3G. Since we have explicit formulae for the radius and the height, it is straightforward to expand the fundamental forms about infinitesimal changes to the dihedral angle γ along the rigid mechanism (see Supplementary Note 5). However, we utilize our framework for the rigid isometry to compare it with existing methods.

We first construct the compatibility diagram shown in Fig. 3D to determine the amplitude representation for the rigid isometry. Since there are three unique dihedral angles, we define the three folding coefficients \(\zeta \equiv \sin \alpha \sin \beta \sin \gamma,\xi \equiv \sin {\alpha }^{2}\sin \theta\), and \(\chi \equiv \sin {\beta }^{2}\sin \psi\) to quantify the respective changes in the dihedral angles δγ, − δψ, and  − δθ. We see each edge of the diagram has a single color, and therefore conclude the rigid isometry of the mode is represented by the vertex amplitudes \({{{\mathcal{V}}}}^{a}={{{\mathcal{V}}}}^{b}={{{\mathcal{V}}}}^{c}={{{\mathcal{V}}}}^{d}=1\) and the face amplitudes \({{{\mathcal{F}}}}^{{{\mathcal{A}}}}={{{\mathcal{F}}}}^{{{\mathcal{B}}}}={{{\mathcal{F}}}}^{{{\mathcal{C}}}}={{{\mathcal{F}}}}^{{{\mathcal{D}}}}=0\). We integrate the changes in the lattice vectors and the lattice rotation matrices, then average according to our coarse-graining procedure to find:

$$\delta R=\frac{{\zeta }^{2}}{4}\left(p+{s}_{\alpha }+(p+{s}_{\beta })\cos \frac{\eta }{2}\right){\csc }^{3}\frac{\eta }{2},$$
(12)
$${\varepsilon }_{\varphi \varphi }={\zeta }^{2}\csc \eta R\left(4R\sin \frac{\eta }{4}+(p+{s}_{\alpha })\cos \frac{\eta }{2}\right),$$
(13)
$${\varepsilon }_{zz}=2\sin \alpha \sin \beta \cos \frac{\theta }{2}\cos \frac{\psi }{2},$$
(14)

where we determine εφφ and εzz directly from δIφφ and δIzz, respectively. These results are self-consistent with the continuum model which equates δIIφφ = δR − εφφ/R and \(\delta {{{\mathcal{S}}}}_{\varphi \varphi }=\delta R/{R}^{2}\), and we obtain them using a slight adjustment to the averaging step of our coarse-graining procedure (see Supplementary Note 5). However, the Jacobian relating the discrete lattice coordinates to the continuous surface coordinates plays an important role here: the terms entering the fundamental forms in Eqns. ((4), (5)) are not given by the partial derivative of those in Eqns. ((1), (2)) with respect to the dihedral angle that functions as the configuration parameter. Instead, the strains arise from the derivatives of the Jacobian which highlights the way the lattice geometry gives rise to the effective behavior of the material. The axial strain εzz maps to changes in the height δh = hεzz/2 of the cylinder whereas the azimuthal strain εφφ opens or closes the cylinder without changing its curvature, which instead are characterized by δR. We consider the ratio δh/δR analogously to the Poisson’s ratio but instead characterizing the relative amount of axial stretching and radial dilation. We see from our expressions in Eqns. ((12), (14)) that when one of the dihedral angles (ψ or θ) changes its mountain/valley assignment this ratio changes signs, which is the same observation made for the Poisson’s ratio in parallelogram-based origami. This further illustrates the functionality of Arc-Morph as a transformable mechanical metamaterial.

We repeat this analysis for the nonrigid isometry which we cannot describe in terms of changes to the dihedral angles exclusively. Since this crease pattern falls within the broader set of TBO that our theory applies to, the nonrigid isometry is represented by the vertex amplitudes \({{{\mathcal{V}}}}^{a}={{{\mathcal{V}}}}^{b}={{{\mathcal{V}}}}^{c}={{{\mathcal{V}}}}^{d}=0\) and the face amplitudes \({{{\mathcal{F}}}}^{{{\mathcal{A}}}}={{{\mathcal{F}}}}^{{{\mathcal{B}}}}={{{\mathcal{F}}}}^{{{\mathcal{C}}}}={{{\mathcal{F}}}}^{{{\mathcal{D}}}}=1\). We again integrate the changes in the lattice vectors and the lattice rotation matrices, then average according to our coarse-graining procedure to find:

$${\sigma }_{1}=1,$$
(15)
$${\sigma }_{2}=-{R}^{2}-\frac{1}{4}({p}^{2}+{s}_{\alpha }{s}_{\beta })\tan \frac{\eta }{2}\csc \frac{\eta }{2},$$
(16)

where we determine σ1 and σ2 directly from \({{{\mathcal{S}}}}_{z\varphi }={\sigma }_{1}/R\) and \({{{\mathcal{S}}}}_{\varphi z}={\sigma }_{2}/R\) and find that the diagonal components of the strain vanish: εφφ = εzz = 0. We confirm these quantities are self consistent with δIφz = δIzφ = R2σ1 + σ2, δIIφz = δIIzφ = Rσ1 without any adjustment to the averaging step of our coarse-graining procedure. Here, there is an apparent discrepancy regarding the units of σ1 and σ2: from dimensional analysis of Eqn. (7), σ1 must have units of inverse area and σ2 must be dimensionless. However, our calculations leading to Eqns. ((15), (16)) use a dimensionless face amplitude to simplify our calculations while the integration framework assumes the face amplitude has units of inverse length. This is in contrast to the vertex amplitudes which are always dimensionless. Introducing such a length scale, for example from the square root of the cell area, resolves the apparent discrepancy. The self consistency of our results relies on both the averaging process in our coarse-graining method and the inclusion of the Jacobian to transform from the discrete lattice coordinates to the continuous surface coordinates. While for the nonrigid isometries of parallelogram-based origami the averaging is also important, the Jacobian may be neglected because the ground states are quasi-planar.

Experiments of Arc-Miura origami

We fabricate and test an example Arc-Morph crease pattern (see Methods, Fabrication and Testing). We select a developable pattern (β = π − α) so that we can construct the crease pattern from a monolithic sheet (see Fig. 4A) rather than the assembly of individual panels, such as done in ref. 41. This is the Arc-Miura, or arc pattern, family of tessellations for which previous works investigated the rigid mode39,40. Since the sector angles are not independently chosen, these crease patterns have a two-dimensional design space parameterized by (α, q/p) with the geometry indicated in Fig. 4B, C, E and the compatibility diagram illustrated on the cell geometry in Fig. 4D. After fabrication, the creases undergo plastic deformation and adopt the quasi-cylindrical ground state shown in Fig. 4F; the tessellation tends to return to this particular configuration after any deformation.

Fig. 4: Fabricated Arc-Miura origami.
figure 4

A Fabricated tessellation with primitive lattice vectors ℓ1,2. B Primitive cell vertices labeled a, b, c, and d and faces labeled \({{\mathcal{A}}},{{\mathcal{B}}},{{\mathcal{C}}}\), and \({{\mathcal{D}}}\). C Sector angles labeled α and \({\alpha }^{{\prime} }\equiv \pi -\alpha\) and dihedral angles labeled γ, ψ, and ψ″ ≡ 2π − ψ. D Compatibility diagram with amplitudes \({{{\mathcal{V}}}}^{a},{{{\mathcal{V}}}}^{b},{{{\mathcal{V}}}}^{c}\), and \({{{\mathcal{V}}}}^{d}\) on the corresponding vertices and colors indicating the coupling coefficients ζ/q, − ξ/s, and  + ξ/p. E Edge lengths labeled p, q, and s. F View of folded specimen with height h, exterior radius Re, and interior radius Ri with the mountain valley assignment of the folded creases indicated. G Radius as a function of height comparing one set of experimental measurements on one sample with theoretical predictions. Black dashed line indicates flattened state. H Excitation of the non-rigid isometry. Scale bar is 30 mm in both panels (F, H).

Full size image

We perform a quantitative test of the nonlinear rigid isometry and a qualitative test of the linear nonrigid isometry. For the rigid isometry, we focus on the relationship between the height and radius then compare with our analytical theory. Rather than averaging over the vertices, which could lead to the accumulation of systematic error, we measure the radii of the innermost (Ri) and outermost (Re) components of the cross section. We show the experimentally measured values and the analytical predictions in Fig. 4G, along with images of the exact configurations measured in Fig. 5. We see good agreement between the measurements and predictions until the tessellation becomes fairly flattened at configuration 8. We attribute this discrepancy, which becomes more pronounced as the tessellation flattens further, to systematic error arising from the large angle subtended by the radial measurement. For the nonrigid isometry, we focus on the general shape induced under loading conditions incompatible with the rigid mode. We show the response of the sample loaded and supported from opposite corners in Fig. 4H. We see the type of shearing mode that is consistent with the mode shape shown in Fig. 2D based on our analytical calculations.

Fig. 5: Rigid folding experiments of Arc-Miura origami.
figure 5

Panels (A–H) show the configurations for the corresponding measurements shown in Fig. 4G with height h, inner radius Ri, and exterior radius Re.

Full size image

Discussion

Our work develops analytical expressions for the large-scale low-energy deformations of rigidly foldable TBO and demonstrates the validity of our theory through experiment. We identify TBO as an architecture for control of shearing and breathing modes of surfaces through the geometry of the underlying crease pattern. Hence, our results distinguish tessellations with trapezoid faces from those with parallelogram faces and help to establish the classification of crease geometries according to their large-scale response. This classification can be utilized for more efficient inverse design by constraining the design space according to which types of modes are compatible with the target behavior. Interestingly, we find the mountain/valley assignment controls the sign of the slope of the height-radius profile in the same way that the assignment controls the Poisson’s ratio of parallelogram-based origami34. This helps narrow the design space to β = π − α (Arc-Miura) for applications that require a radius increasing with height, β = α (Arc-eggbox) for a radius decreasing with height, and somewhere in between (Arc-Morph) for a non-monotonic profile. These results showcase new functionality for origami as mechanical metamaterials, either as thin-walled structures with target stiffnesses or tubular coverings for snake-like robots, cables, and other long one-dimensional assemblies. Further development is required for the experimental demonstration of isometries in non-developable TBO, as well as the quantitative validation of the rigid isometry near the flattened state and the nonrigid isometry along the configuration manifold. We note that the nonrigid isometries of parallelogram-based origami still require the development of an experimental apparatus for their quantitative validation. For both trapezoid- and parallelogram-based tessellations, such an experiment requires careful attention to the loading mechanism so that the mode of interest is isolated and to the measurement system so that displacements are accurately tracked through three-dimensional space.

The theory developed in the present work connects the discrete representation to the continuum representation of locally uniform isometric deformations in TBO, thereby characterizing their low-energy kinematics at the large scale. It remains to test this theory with more general trapezoid crease patterns via analytical or numerical calculations. However, the underlying principles extend to quadrilateral-mesh origami sheets without parallel edges, where the breathing mode and the shearing mode are coupled along the configuration manifold, as well as axisymmetric origami such as those in refs. 42,43,44, where the size of the faces changes between cells so that the continuum theory may adopt a conformally flat metric. Furthermore, our methods extend to spatially varying isometries, such as those explored linearly for parallelogram-based origami45,46 (see Supplementary Note 6) and nonlinearly for the cylindrical waterbomb origami47, where the fundamental forms and their derivatives are intimately related via the Gauss-Codazzi equations in the continuum regime48. Extending our work in this way provides a rich avenue for future investigations that seek to incorporate the large-scale response of origami tessellations into models based on elastic plate theory, where we anticipate sinusoidal variations of mean curvature in the bulk and finite amounts of Gaussian curvature localized towards the boundary of the system. We expect our approximation to improve as the number of cells increases, and the consistency between the response shown in Fig. 1A–D with crease patterns that have increased numbers of faces in the unit cells, non-isosceles trapezoid faces, and domain walls with parallelogram faces showcases the robustness of our predictions. Furthermore, our focus on geometric mechanics suggests our theory scales with the system size and the isometries should be observable at the sub-millimeter scale on crease patterns fabricated using, e.g., two-photon lithography as used in ref. 12.

In addition to characterizing the kinematics, quantifying the stiffness of the breathing and shearing modes is important for the application of our theory towards origami engineering. Such modal stiffness is frequently modeled via a truss model with Hookean potentials for the folding, bending, and stretching of the panels46,49,50. In contrast to our theory, such truss models utilize virtual creases across the diagonals of the panels to quantify panel bending. Since our theory attempts to directly model the deflection field of the panels instead, it may be possible to equate the stiffness associated with the vertex amplitudes and the face amplitudes with scaling relations based on the dimensions of the panels and the elastic moduli of the constituent material. This could be especially valuable for the design of impact mitigating origami crash-boxes that utilize trapezoidal faces51. Our vision is to extend the utility of the computational design enabled by, e.g., ref. 20 to include the target effective elastic behavior in addition to the target shapes.

Methods

Coarse-graining

We coarse-grain the ground states of a periodic origami tessellation by averaging its primitive lattice vectors over all admissible primitive unit cells to determine the coarse-grained tangent vectors of the tessellation. We do this in two steps. First, we average the lattice vectors over the copies of a standard unit cell that change which vertex is located at the origin and denote the result \({\bar{{{\boldsymbol{\ell }}}}}_{\mu }\). For example, one copy has vertex a at the origin with lattice vectors pointing between vertex a in adjacent cells and another copy has vertex b at the origin with lattice vectors pointing between vertex b in adjacent cells. Second, we average these copies between adjacent cells so that the forwards and backwards tangent vectors are equal and opposite. This yields our definition for the coarse-grained tangent vectors:

$${{{\bf{t}}}}_{\mu }\equiv \frac{1}{2}({{\bf{1}}}+{{{\bf{S}}}}^{-1}) \, {\bar{{{\boldsymbol{\ell }}}}}_{\mu }.$$
(17)

Additionally, we average the cell-to-cell change in the primitive lattice vectors over all admissible primitive unit cells to determine the change in the coarse-grained tangent vectors. We do this by averaging over the change in the tangent vector defined in Eqn. (17) from an initial cell to the subsequent cell and from the previous cell to the initial cell so that the forwards and backwards derivatives of the tangent vectors are equal and opposite. Since the change in the tangent vectors is given by the action of the lattice rotation matrix or its inverse, this yields our definition for the derivative of the coarse-grained tangent vectors:

$${\partial }_{\mu }{{{\bf{t}}}}_{\nu }\equiv \frac{1}{2}({{{\bf{S}}}}_{\nu }-{{{\bf{S}}}}_{\nu }^{-1}){{{\bf{t}}}}_{\mu }.$$
(18)

These partial derivatives satisfy ∂μtν = ∂νtμ. The indices of Eqns. ((17), (18)) remain the cell indices (n1, n2). We transform to the continuous surface coordinates \(({\hat{e}}_{1}=\varphi,{\hat{e}}_{2}=z)\) via the Jacobian \({J}_{\mu \nu }=\partial {\hat{e}}_{\mu }/\partial {n}_{\nu }\). For the trapezoid-based origami crease patterns we consider, we have \({J}_{\varphi 1}=1/\sin \eta,{J}_{z2}=1/h\), and Jφ2 = Jz1 = 0, where η is the lattice rotation angle and h is the magnitude of the second lattice vector.

We similarly coarse-grain the infinitesimal deformation of the periodic origami tessellation generated from a homogeneous isometry by averaging the corresponding lattice displacement (Δμ) and lattice angular velocity (Lμ) over all primitive unit cells. We again do this in two steps. First, we average the lattice displacement and lattice angular velocity over the same set of standard unit cells used to compute \({\bar{{{\boldsymbol{\ell }}}}}_{\mu }\) above. Here, there are an additional four copies of each standard cell distinguished by the orientation of the frame for each of the four corners that meet at the vertex set at the origin. We denote the results \({\bar{{{\mathbf{\Delta }}}}}_{\mu }\) and \({\bar{{{\boldsymbol{L}}}}}_{\mu }\). Second, we expand Eqns. ((17), (18)) in terms of these quantities:

$$\delta {{{\bf{t}}}}_{\mu }=\frac{1}{2}\left(\right.({{\bf{1}}}+{{{\bf{S}}}}_{\mu }^{-1}){\bar{{{\mathbf{\Delta }}}}}_{\mu }-{{{\bf{S}}}}_{\mu }^{-1}{\bar{{{\boldsymbol{L}}}}}_{\mu }{\bar{{{\boldsymbol{\ell }}}}}_{\mu },$$
(19)
$$\delta {\partial }_{\mu }{{{\bf{t}}}}_{\nu }=\frac{1}{2}\left(\left({{{\bf{S}}}}_{\nu }-{{{\bf{S}}}}_{\nu }^{-1}\right)\delta {{{\bf{t}}}}_{\mu }+\left({\bar{{{\boldsymbol{L}}}}}_{\nu }{{{\bf{S}}}}_{\nu }+{{{\bf{S}}}}_{\nu }^{-1}{\bar{{{\boldsymbol{L}}}}}_{\nu }\right){{{\boldsymbol{t}}}}_{\mu }\right).$$
(20)

Again, the partial derivatives satisfy δ∂μtν = δ∂νtμ and we transform from the discrete cell indices to the continuous surface coordinates via the Jacobian. While we do not compute an embedding directly, this procedure is sufficient to compute the fundamental forms and characterize the geometry of the origami tessellations. These methods extend to the crease patterns shown in Fig. 1C, D that are not periodic in the azimuthal direction but are still composed of cellular building blocks by performing the first step of our averaging between analogous, but nonequivalent, vertices in both the forward and backwards directions.

Linear isometry model

We model the linear isometries via the angular velocity field, denoted ω, which generates the infinitesimal rotation of elements of the sheet. We parameterize this angular velocity field via amplitudes on the vertices, denoted \({{{\mathcal{V}}}}^{a}\), and amplitudes on the faces, denoted \({{{\mathcal{F}}}}^{A}\), where we use lowercase (uppercase) Latin superscripts to label the vertex (face) within the primitive unit cell that the amplitude is assigned to. The meaning of the amplitudes is as follows. The difference in the angular velocity between the corners of two faces that meet at vertex a and share the ith edge of the vertex is:

$$\Delta {{\boldsymbol{\omega }}}={(-1)}^{i}{{{\mathcal{V}}}}^{a}{\zeta }_{i}^{a},$$
(21)
$${\zeta }_{i}^{a}\equiv {\hat{r}}_{i+1}^{a}\times {\hat{r}}_{i+2}^{a}\cdot {\hat{r}}_{i+3}^{a},$$
(22)

with i defined cyclically on the four edges emanating from vertex a and \({\hat{r}}_{i}^{a}\) the corresponding edge direction. We refer to the triple products \({\zeta }_{i}^{a}\) as the folding coefficients, which we can write explicitly as functions of the sector and dihedral angles. This local solution ensures that the net rotation around the vertex vanishes to first order in the angular velocity. Similarly, the difference in the angular velocity between the corners of face A that share the ith edge of the face is:

$$\Delta {{\boldsymbol{\omega }}}={(-1)}^{i}{{{\mathcal{F}}}}^{A}{\lambda }_{i}^{A},$$
(23)
$${\lambda }_{i}^{A}\equiv \left\{\begin{array}{l}| {{{\bf{r}}}}_{i+2}^{A}|,\,{{\mbox{parallel}}} \, {{\mbox{edges}}}\,,\hfill \\ | {{{\bf{r}}}}_{i}^{A}|,\,{{\mbox{non-parallel}}} \, {{\mbox{edges}}}\,\quad \end{array}\right.,$$
(24)

with i defined cyclically on the four edges bounding face A and \(| {{{\bf{r}}}}_{i}^{A}|\) the corresponding edge length. This local solution ensures that the net rotation and displacement around the face vanishes to first order in the angular velocity.

We compute the net change in the orientation between any two corners of the origami tessellation by choosing a path composed of corner-to-corner segments and summing over the amplitude-dependent contributions to the angular velocity from Eqns. ((21), (23)). Similarly, we compute the net change in the position between any two corners by computing the change in the orientation between the starting corner and each corner along the path, then summing each of their cross products with the subsequent corner-to-corner segment along the path. The amplitudes are constrained such that the total change in the angular velocity on a loop around any edge vanishes. These conditions ensure that both the net rotation and net displacement over any closed loop of the tessellation vanishes, and consequently that none of the elements of the sheet stretch to first order in the angular velocity. We provide a detailed derivation in Supplementary Note 2.

Arc-morph trapezoid-based origami geometry

We write the vertex basis vectors and the primitive lattice vectors for the family of Arc-Morph with vertex a at the origin of the primitive unit cell as:

$${{{\bf{r}}}}_{a}=\left(\begin{array}{rcl}0,&0,&0\end{array}\right),$$
(25)
$${{{\bf{r}}}}_{b}=\left(\begin{array}{rcl}p,&0,&0\end{array}\right),$$
(26)
$${{{\bf{r}}}}_{c}=\left(\begin{array}{rcl}{s}_{\alpha }+q\cos \alpha,&q\sin \alpha \cos \frac{\theta }{2},&q\sin \alpha \sin \frac{\theta }{2}\end{array}\right),$$
(27)
$${{{\bf{r}}}}_{d}=\left(\begin{array}{rcl}q\cos \alpha,&q\sin \alpha \cos \frac{\theta }{2},&q\sin \alpha \sin \frac{\theta }{2}\end{array}\right),$$
(28)
$${{{\boldsymbol{\ell }}}}_{1}=\left(\begin{array}{rcl}p+{s}_{\beta }\cos \frac{\eta }{2},&{s}_{\beta }\sin \frac{\eta }{2},&0\end{array}\right),$$
(29)
$${{{\boldsymbol{\ell }}}}_{2}=\left(\begin{array}{rcl}0,&0,&\frac{2q\sin \alpha \sin \beta \sin \gamma }{\sin \frac{\eta }{2}}\end{array}\right).$$
(30)

For all unit cells that appear in the averaging process, the lattice rotation angle is:

$$\eta=2(\pi -\delta ),$$
(31)

where we parameterize the dihedral angles entering Eqns. (27–31) through standard application of spherical geometry52:

$$\theta=2\arctan \left(\frac{\cos \beta -\cos \alpha \cos \delta }{\sin \alpha \sin \delta },\frac{\sin \beta \sin \gamma }{\sin \delta }\right),$$
(32)
$$\psi=2\arctan \left(\frac{\cos \alpha -\cos \beta \cos \delta }{\sin \beta \sin \delta },\frac{\sin \alpha \sin \gamma }{\sin \delta }\right),$$
(33)
$$\delta \equiv \arccos (\cos \alpha \cos \beta+\sin \alpha \sin \beta \cos \gamma ).$$
(34)

Fabrication and testing

We fabricate the Arc-Miura by milling a 1 mm thick black polypropylene sheet using a 3-axis CNC milling machine (Roland EGX-600, accuracy 10 μm), as illustrated in Fig. 6A and previously achieved in refs. 41,53. We form the mountain/valley creases by engraving 0.9 mm into the polypropylene sheet using a ball-end tool with a radius of 1 mm. To facilitate unconstrained folding, we add 2 mm diameter holes to each vertex of the tessellation. This measure is crucial for preventing stress concentration where multiple creases converge, taking into account the non-zero thickness of the actual sample. Finally, since the Arc-Miura is developable, we manually fold the milled/engraved polypropylene sheet. The resulting 428.78 mm by 383.63 mm specimen is chosen based on the size of the available tooling.

Fig. 6: Fabrication and experimental testing setup.
figure 6

A Manufacturing of trapezoid-based origami by a CNC milling machine. B Setup designed to perform the nonlinear rigid isometry experiments on the trapezoid-based origami. C Details of the setup showing the linear slide system used to change the configuration of the specimen during the experiments. The sample is constrained through multiple sliders inserted into a rail.

Full size image

We measure the height-radius profile along the nonlinear rigid isometry of the fabricated Arc-Miura using the experimental setup illustrated in Fig. 6B, C. The setup consists of a linear slide system equipped with several sliders connected to an optical table and is arranged horizontally to mitigate gravitational effects. We connect the sample to a linear slide system via three sliders: one in the middle and the other two at its ends. Each slider is equipped with a locking system to maintain the sample at a fixed height. We affix PMMA spacers to the sliders using 2 mm diameter bolts, as illustrated in Fig. 6B  to ensure secure connection between the sample and the sliders. Additionally, we connect two L-shaped plates to extra sliders to induce the rigid folding of the tessellation and establish the desired height for the sample. We design these plates to apply compression and tension to the sample, thereby facilitating both folding and unfolding.

We integrate two rulers into the setup: one to verify the imposed height of the sample and the other as a reference scale bar for post-processing analysis of captured photos. We position two cameras, oriented orthogonal to one another, to capture images of the sample as we induce the rigid folding motion. We position the first camera (Sony Alpha 9) in front of the sample to capture the frontal view, thereby facilitating the estimation of the radius. This camera is equipped with a telephoto G Master FE 100–400 mm lens to minimize distortion and enhance contrast between the foreground and the background. We position the second camera (Sony Alpha 6300) to the side of the sample to capture the lateral view, thereby facilitating the estimation of the height. This camera is equipped with a Vario-Tessar T* FE 24–70 mm lens.

The experiments proceeded as follows. A specific height is imposed on the sample using the L-shaped plates and the sample is secured in this configuration by locking the sliders with the locking system. We use a tape measure at various positions along the circular edge of the tessellation to manually verify the uniformity of the sample height. We then capture a photo with each of the two cameras in the locked configuration. We repeat this process for eight different configurations, specifically imposing heights of 31.5 cm, 32 cm, 33 cm, 34 cm, 35 cm, 36 cm, 37 cm, and 37.5 cm. Finally, we estimate the relationship between the height and radius via post-processing of these photos.