Introduction

Low-dimensional topological insulators (TIs) have emerged as prime candidates for next-generation quantum technologies, particularly in low-energy electronics and quantum computing. This is because of their unique electronic properties: an insulating bulk paired with symmetry-protected boundary states1,2,3,4,5,6,7,8. Significant progress has been made in discovering and characterizing various two-dimensional (2D) TIs hosting one-dimensional (1D) dissipationless edge states, such as band-inverted semiconductors, bismuthene, WTe2, and germanene9,10,11,12,13,14,15,16,17,18,19,20,21,22,23. To harness the potential of these 1D edge states in devices, it is essential to maximize their density per unit area24,25, which can be achieved by fabricating arrays of narrow nanoribbons. However, there may be a critical width below which the system transitions from a 2D to a 1D topological insulator, leading to the disappearance of the 1D edge states. This behavior is analogous to the dimensional crossovers observed when reducing three-dimensional (3D) TIs and semimetals to two dimensions19,26,27,28.

While 2D and 3D TIs exhibit conductive channels at their edges or surfaces, 1D TIs are characterized by 0D states at their ends. Realizing a 1D TI is both a major challenge and a promising avenue for advancing topological quantum computing, where protected 0D end states could enable fault-tolerant qubit designs25,29,30,31. Although theoretical models32,33,34,35,36,37 and quasi-1D structures, including graphene nanoribbons29,38,39,40, hint at feasibility, there are currently no experimentally verified 1D TIs with large spin-orbit coupling. Therefore, investigating the transition from 2D to 1D topology is a critical step, essential not only for forming dense networks of 1D topological states but also for realizing the 1D TI with symmetry-protected 0D end states.

In this study, we fabricated and characterized arrays of narrow, straight, and long germanene nanoribbons, a platform for achieving lateral arrangements of multiple 1D edge states in a system with large spin-orbit coupling. Using scanning tunneling microscopy (STM) and theoretical analysis, we explore how the topology of germanene nanoribbons varies with width, and reveal how it may be classified by considering the additional crystalline symmetry of the nanoribbons41,42. We identified the lower-dimensional limit of 2D topology, promoting further developments for scalable topological quantum systems, and realized a 1D topological insulator with robust, symmetry-protected end states.

Results and Discussion

Structure of Germanene nanoribbons

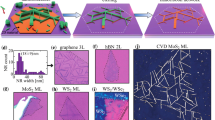
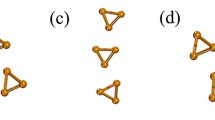
Germanene, a monolayer of germanium atoms in a low-buckled honeycomb lattice (Fig. 1a)22,43,44,45,46, has a spin-orbit coupling (SOC)-induced band gap at the K and K’ points, Fig. 1b, and is classified as a Kane-Mele-type TI (class AII) with topologically protected helical edge states1,2. The topological properties of 2D germanene were recently experimentally confirmed20,47. To explore these properties in one-dimensional confinement, we fabricated germanene nanoribbons by depositing ∼1 monolayer of Pt on a Ge(110) substrate, then annealing at 1100 K. Upon cooling, Ge segregates on the Pt layer forming elongated nanoribbons, a growth process similar to the growth of germanene nanoribbons on Ag films on Ge(110)48. For details, see the sample preparation section in Supplementary Information (SI). Two distinct structures emerge based on Pt coverage: short (10–50 nm), disordered Ge nanowires (small Pt coverages), and long (up to 1 μm), ordered nanoribbons (larger Pt coverages), oriented along the [\(\bar{1}\)10] direction. The nanoribbons have unique electronic properties and structural order, contrary to the disordered and electronically featureless nanowires (see SI). Fig. 1c shows a region with arrays of nanoribbons and nanowires, caused by local inhomogeneities in Pt coverage. An array of nanoribbons appears on the right, whereas a few isolated nanoribbons, surrounded by nanowires, are visible on the left in the STM image.

Fig. 1: Germanene nanoribbon structure.
figure 1

a Top- and side-view of germanene’s buckled honeycomb structure. Light and dark blue spheres represent the two vertically displaced sublattices. b The bandstructure of germanene with spin orbit coupling (SOC) (blue shaded area) and without SOC (dashed lines), depicting the topological gap and the two edge states with red and blue crossing the Fermi level. c Large-scale scanning tunneling microscope (STM) image of parallel germanene nanoribbons. Left side of the area has isolated nanoribbons, while the right side has an array of nanoribbons. The in-between regions are filled by nanowires and disorder domains (setpoints: 300 mV, 200 pA). The height scale of the image is 2.3 nm. d High-resolution image of several germanene nanoribbons recorded on a dense area (setpoints: −300 mV, 200 pA). The height scale of the image is 1.3 nm. e An atomic resolution STM image revealing the honeycomb lattice of the nanoribbon marked with a red square in panel c (setpoints: 50 mV, 200 pA). f Atomic resolution image of a germanene nanoribbon showing the honeycomb lattice and the zigzag termination (setpoints: −300 mV, 200 pA). g line profile recorded across the honeycomb lattice of the nanoribbon shown with the black dashed line in the inset, revealing a buckling of 0.35 Å. h Tentative structural model of germanene (red lattice) on Pt/Ge(110) substrate.

Full size image

Consistent with 2D germanene, atomic resolution STM images on the nanoribbons (Fig. 1d–f) reveal the honeycomb germanene lattice with a lattice constant of ∼4.2 Å43,44. Micro-spot low-energy electron diffraction (μLEED) confirms this structure (see SI). A monolayer of germanium forms a low-buckled honeycomb structure (germanene) due to the instability of high-buckled Ge(111), which exhibits imaginary phonon modes in a large part of the Brillouin zone43. The honeycomb lattice, contrasting the rectangular Pt/Ge(110) substrate (similarly to silicene nanoribbons on Ag(110)49,50 and germanene nanoribbons on Ag/Ge(110)48), indicates weak germanene-substrate interactions. The germanene nanoribbons align perfectly along the [\(\bar{1}\)10] direction (long axis) but experience a lattice mismatch with the substrate along [001], resulting in very narrow widths (1–6 nm) and very long lengths (Fig. 1d)51. Projection of the observed honeycomb lattice along the [\(\bar{1}\)10] direction reveals a zigzag termination along this direction. Additionally, atomically resolved images at the edge of the nanoribbons, shown in Fig. 1e, f and Supplementary Fig. 2, further confirm the zigzag termination along the long-axis direction. This is consistent with the lower formation energy of zigzag over armchair edges. Moreover, we observe a buckling with an upper bound of ∼0.35 Å (Fig. 1g). The germanene/Pt/Ge(110) structure exhibits also a larger centered rectangular lattice arising from the registry of germanene on the Pt layer. This larger symmetry is visible both in STM (either at large sample biases or specific tip conditions) and μLEED, see Fig. S2, and is similar to ref. 48. Because of these similarities, we have adapted the structural model proposed by Yuhara et al.48. Figure 1h shows a schematic representation of this structural model for a monolayer of germanene on Pt/Ge(110).

Topological Edge States

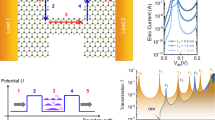
The formation of germanene nanoribbons opens up new avenues for investigating electronic behaviors distinct from those in extended 2D layers. To this end, we examined the spatial variation in the local density of states (LDOS) of a wide germanene nanoribbon (∼6 nm) using scanning tunneling spectroscopy (STS). Figure 2a shows the local differential conductance (dI(V)/dV) spectra recorded at the edge (red curve) and the middle (black curve) of the nanoribbon shown in the inset. A distinct difference between edge and bulk is evident, with a pronounced edge state at ∼30 meV, centered within the bulk gap. Due to proximity effects, the underlying Pt containing layer increases the topological bandgap of germanene to 100–150 meV (width of the dI/dV dip) at a germanene-Pt separation of 3.2 Å20, which exceeds that of free-standing germanene52. Note that the gap does not always reach zero, probably due to the tip convolution effects from the edge states or the influence of the Pt layer lifting the dI/dV baseline.

Fig. 2: Topologically protected edge states.
figure 2

a Differential conductance (dI(V)/dV) spectra at the edge (red) and interior (black) of the germanene nanoribbon, as shown in the inset (edges marked by black dashed lines). Measurement locations are indicated by red and black circles. Setpoints: −500 mV and 200 pA. b dI(V)/dV line spectroscopy across the nanoribbon, recorded at the position of the green arrow in a, showing clear edge states at both sides of the nanoribbon, highlighted by the red arrows. c dI/dV map recorded at the energy location of the edge state (150 mV for this case) showing the edge state running continuously along the nanoribbon edge. The fuzzy bright signal observed outside the nanoribbons is due to the roughness of the surface at this location. This roughness is also visible in the corresponding topography in the inset (which has spikes). d dI(V)/dV spectra recorded at the edge of a wide nanoribbon for different current setpoints in chronological order: 0.4 nA (red), 3 nA (black), and 0.5 nA (magenta), showing the electric field-induced destruction of the topological state (the arrows indicate the center of the gap). e dI(V)/dV spectra recorded at the edges (red) and interior (black) of nanoribbons of different widths (setpoints: −300 mV and 200 pA). Edge states vanish in ribbons narrower than 2.6 nm. Spectra are vertically offset for clarity, with blue horizontal lines indicating the zero levels. The red arrows indicate the edge state or the middle of the gap for narrow nanoribbons. f Calculated band structure for a 14-hexagon ribbon with crossing edge states. g Calculated band structure of a 2-hexagon ribbon, with gapped edge states and 0D end states marked by red/black squares in the inset.

Full size image

Figure 2b shows a dI(V)/dV line spectroscopy along the green arrow in the inset of Fig. 2a, highlighting edge states on both sides of the nanoribbon (marked by red arrows). The metallic edge states are shifted relative to each other by about 20–30 meV, indicating a different local electrostatic environment. The intensity of these states also varies, possibly due to the buckling. dI/dV mapping of the edge state, shown in Fig. 2c for a wide ribbon, reveals that the state runs continuously along the edge of the nanoribbon. The topological nature of these edge states is further confirmed by tip-induced electric field measurements20,53,54. By applying a perpendicular STM tip-induced electric field, we break band inversion symmetry, converting germanene into a trivial insulator devoid of edge states, as shown in Fig. 2d and also Supplementary Fig. 3. Here, increasing the current set-point (thus reducing the tip-sample distance) increases the tip-induced electric field, which opens a gap in the energy of the edge states under strong fields. This gap closes and the edge states reappear when the electric field is reduced to its original value, confirming that the transition is reversible. The estimated critical field based on the work function difference between tip and sample is about 2.3 V/nm. However, an accurate determination of the tip-induced electric field remains challenging due to uncertainties in estimating the tip-sample distance, buckling, work functions of the germanene and STM tip, and image charge effects lowering the barrier19,20. Miscalculating these contributions results in an offset in the electric field, but does not alter the qualitative picture of switching off the topological state and closing the bulk gap. The absence of such behavior in trivial surface states strongly reinforces the topological origin of these edge states, as does the reversible electric-field-induced transition, consistent with previous studies19,20.

Topological phase transition

The reversible tuning of edge states with an applied electric field highlights the unique topological characteristics of germanene nanoribbons. This behavior invites a closer examination of how the edge states depend on the width of the nanoribbon. The natural width variations of the nanoribbons observed in STM images provide an ideal opportunity to explore their width-dependent electronic properties. Fig. 2e depicts dI(V)/dV point spectra recorded at the interior (black) and edges (red) of nanoribbons with varying widths, namely ∼1 nm, ∼1.4 nm, ∼2.6 nm, ∼3.6 nm, and ∼6.0 nm. Strikingly, the presence of edge states strongly depends on the nanoribbon width. Nanoribbons wider than approximately 2.6 nm consistently display pronounced edge states, while narrower ribbons (below this threshold) exhibit nearly identical dI(V)/dV spectra at both the interior and edges, with a marked absence of edge states. Note that local doping variations on the sample (or between different samples) shift the energy position of the edge states and bulk gaps.

To understand this, we performed tight-binding calculations on zigzag germanene nanoribbons using the Kane-Mele model1,2 for spin-orbit coupling strength λSO = 0.3t, staggered mass Ms = 0.02t, long-range hopping t3 = 0.3t, and nearest-neighbor hopping t = −0.92 eV54,55. The geometry used for theoretical calculations is based on the experimental topographical maps, which show zigzag termination along their long axis and ‘pointy’ end terminations, i.e. they are aligned under 60-degree angles. Nevertheless, in the SI we present additional calculations for different ribbon terminations. For details on the theoretical calculations, see SI. The band structure is shown in Fig. 2f and g. A wide nanoribbon (14 hexagonal cells wide), showcases pronounced edge states and a bulk gap, see Fig. 2f. However, our band structure calculations of a 2-hexagon-wide nanoribbon reveal that the topological 1D edge modes fail to completely close the bulk gap, leading to gapped edge states, see Fig. 2g. This striking observation indicates a width-driven topological phase transition. Moreover, our theoretical results show the presence of 0D end states within this edge gap (or minigap), see Fig. 2g.

To examine this phase transition and the emergence of distinct end states in ultrathin nanoribbons, we conducted a detailed examination of the width-dependent electronic structure across various nanoribbon widths: wide (∼5 nm, or about 14 hexagons), intermediate (∼2.6 nm, or 6 hexagons), 3-hexagon-wide (∼1.4 nm), and 2-hexagon-wide (∼1 nm) nanoribbons. Our study encompasses both theoretical (Fig. 3a–d) and experimental (Fig. 3e–h) analyses. Spectra were recorded along various regions of the nanoribbons, where solid red lines indicate spectra from the top and bottom edges, black lines from the bulk, and blue lines from the ends (see inset of Fig. 3e–h for the corresponding topography). The theoretical LDOS curves are calculated for all energies in the bulk gap. As a result, bulk bands start to contribute around E ≈ ± t, yielding an increased LDOS. As we will discuss next, the theoretical description captures the main experimental features. For completeness, we also provide the corresponding dI(V)/dV line spectroscopy along the nanoribbon end for all four nanoribbon widths in Fig. 3i–l.

Fig. 3: Transition from a 2D topological insulator to a 1D topological insulator.
figure 3

a–d show tight-binding calculations of the Local Density of States (LDOS) at the edges (red), end (blue), and bulk (black) for wide (14 hexagon units), intermediate (6 hexagon units), 3-hexagon and 2-hexagon wide nanoribbons, respectively. Insets illustrate nanoribbon structures. e–h present dI(V)/dV spectra measured at the edges (red), end (blue), and bulk (black) for wide (∼5 nm), intermediate (∼2.6 nm, 6 hexagon units), a 3-hexagon (∼1.4 nm), and 2-hexagon (∼1 nm) wide nanoribbons, respectively. Insets show nanoribbon topographies and measurement locations. The data illustrate a reduction and disappearance of 1D topological edge states with decreasing width, and the emergence of 0D topological end states in agreement with theoretical calculations. i–l show the corresponding dI(V)/dV line spectroscopy from the bulk to the end of the nanoribbons recorded at the locations marked with red dashed lines in the insets of (e–h) (the maps are interpolated for clarity). The dI(V)/dV spectra were recorded with setpoints: −300 mV and 200 pA. m Topography and dI/dV maps for different energies of a 2-hexagon ultrathin nanoribbon showing the end states and its localization at the end of the nanoribbon.

Full size image

Experimental dI(V)/dV curves for the wide nanoribbon (∼5 nm) reveal similar intensities of in-gap states at both edges and ends (Fig. 3e, blue and red curves), consistent with Fig. 2a and with the properties of a 2D TI. Note that the peaked LDOS lacks physical meaning. For a 1D edge state, the LDOS should be constant, as shown in Fig. 3a. This discrepancy arises possibly due to the influence of k// (parallel momentum) in STS. The zigzag edge state connects the K and K’ points through the Γ point. In STS, the largest tunneling contributions come from states at the Γ point and decrease away from this point. As sample bias increases, we move away from the Γ point and the signal decreases, leading to a peaked LDOS (for details see SI and ref. 47). Spin-orbit interactions further modulate the dispersion, enhancing the effect56.

In contrast, the 6-hexagon-wide nanoribbon (Fig. 3f) has reduced LDOS for edge states (red) compared to the more prominent and sharper end state (blue). This behavior is seen both in the theoretical and the experimental spectra. Note, however, that the experiment is influenced by local doping, which shifts the peaks above the Fermi level. Strikingly, in the 3-hexagon-wide nanoribbon (Fig. 3g), both edge and end states vanish entirely. This observation is supported by our theoretical findings (Fig. 3c), which will be further elaborated upon later. Remarkably, the 2-hexagon wide nanoribbon (Fig. 3h), although also devoid of edge states, exhibits a very strong and pronounced end state (blue curve). This is unexpected, as class AII systems do not exhibit topological states in 1D. However, as demonstrated in the SI, these 0D end states are robust and topologically protected by the combined action of mirror and time-reversal symmetries. The emergence of the 0D end state in our experiments is fully supported by our theoretical calculations (Fig. 3d), where the blue curve (recorded at the end) displays a clear peak, signaling a 0D end mode, while the red and black curves show a dip. However, unlike the experimental curves, the calculated LDOS for 1D edge states does not completely vanish. The tight-binding calculations may underestimate the decay length of the 1D edge states, such that they fail to hybridize and disappear. The topography and dI/dV maps of an ultrathin (2-hexagon wide) nanoribbon at energies near and far from the end state energy (∼75 meV) are shown in Fig. 3m, highlighting the localization of the sharp energy state at the end of the nanoribbon. Finally, the difference between the 2- and 3-hexagon wide nanoribbons, i.e., an end mode for the former and no end-mode for the latter, is reminiscent of the different behavior predicted by Traverso et al.39 for graphene nanoribbons with even/odd number of hexagons. Their analysis was performed for a Haldane model, but since the Kane-Mele model consists of two time-reversal symmetric copies of the Haldane model, it can be applied also here.

The experimental observations and the theoretical LDOS curves suggest a critical width threshold below which end states emerge. In germanene nanoribbons, this corresponds to six hexagons. When sufficiently thin, nanoribbons transition to a 1D topological insulator, hosting 0D end modes residing in the gapped edge states. Indeed, the presence of 0D topological end states in the 2- and 6-hexagon wide nanoribbons is confirmed by a finite topological invariant obtained from the 1D Zak phase57, see SI. The 0D topological states are two exponentially localized modes at the ends of the nanoribbons. The minigap’s topological properties and size vary with nanoribbon width. The gap size scales inversely with width, and the end mode localization length scales inversely with gap size (see SI). Consequently, as we increase the ribbon width, the distinction between 0D end states and crossing 1D edge states becomes increasingly difficult. For wider nanoribbons, the 0D end states merge into the 1D edge states and are no longer visible. The 6-hexagon wide nanoribbon is an intermediate case, hosting both 1D edge states and 0D end states. In the SI, we show that nanoribbons of odd width (odd number of hexagons) always show a gap in the edge state spectrum, although this gap becomes exponentially small as we increase their width. This is in contrast with nanoribbons of even width, which have a gapless edge state spectrum. A staggered mass opens these gaps and reveals the 0D end states. Therefore, the topological behavior of the nanoribbons strongly depends on their width. This is exemplified in Supplementary Figs. 10d–e, which shows that the nanoribbons that are 2 hexagonal cells wide are topological for a larger parameter range than the nanoribbons that are 3 hexagonal cells wide. This is directly corroborated by the tight-binding and experimental results shown in Fig. 3c and g, where the nanoribbon is in its trivial state and has no end state. These findings emphasize the role of physical dimensions in the manifestation of topological properties.

Our theoretical and experimental investigation reveals the complex and rich topological behavior of germanene nanoribbons. We observe a transition from a class AII 2D quantum spin Hall phase to a 1D topological crystalline phase. We demonstrated that the 1D topological phase is influenced in a non-monotonic manner by many factors, i.e., ribbon width, spin-orbit coupling, next-nearest-neighbor hopping, and staggered mass. We classified this topological phase in terms of the invariant ν, based on the Zak phase, which is quantized by a combined mirror and time-reversal symmetry. These findings are crucial for understanding the transition from a 2D to a 1D topological insulator as a function of width, highlighting the significance of physical dimensions on topological properties and quantitatively defining the maximum number of 1D edge modes per sample area in germanene nanoribbon arrays. Furthermore, our results show that sufficiently narrow nanoribbons with mirror-symmetric termination can support end states of fractionalized electrons58,59,60,61, akin to Majorana zero modes, positioning them as a promising platform for exploring unique topological phases.

Methods

Scanning tunneling microscopy and low energy electron microscopy and diffraction

The experiments were done using a scanning tunneling microscope under ultra-high vacuum conditions and at 77 K. The samples were transferred from the preparation chamber to the STM chamber without breaking the vacuum. The conductivity and sharpness of the tips were tested on either an Au or a Pt-coated HOPG sample. STM imaging was done with typical current setpoints in the range of 0.2–0.5 nA and the voltage biases were typically limited between −0.5 V and 0.5 V. The STS (dI(V)/dV) data were obtained with the feedback loop open, using a lock-in amplifier with a modulation voltage of 10–20 mV AC at a frequency range of 1000–1200 Hz. The STM images and dI(V)/dV spectra were processed and analyzed using MATLAB, Gwyddion, and SPIP. A low-pass filter was applied to the topographic maps to suppress high-frequency noise. Low energy electron microscopy and diffraction (LEEM/LEED) experiments were performed using an ELMITEC LEEM-III instrument. The LEED patterns were recorded at room temperature, using 30 eV electrons.

Nanoribbon growth and structure

Ge(110) samples, cut from nominally flat 10 × 10 × 0.5 mm substrates with single-side polishing, were used. The samples were mounted on Mo holders, ensuring no contact with other metals during preparation or measurements. The Ge(110) samples were cleaned with 800 eV Ar+ ion sputtering, followed by annealing at 1100 (±25) K. The Pt was evaporated using resistive heating of a tungsten wire wrapped with high-purity Pt (99.995%). Germanene nanoribbons were synthesized using a two-step process: first, depositing approximately one monolayer of Pt on the clean Ge(110) substrate, and then annealing to about 1150 K. Upon cooling, Ge segregates on the Pt monolayer, similar to the approach by Yuhara et al.48 and refs. 62,63,64,65). The subsurface Pt layer conforms to the Ge(110) surface structure due to the good match between Pt(110) and Ge(110), with less than 2% strain in both directions. This results in a surface structure similar to Ag on Ge(110)48. After the annealing step, two types of structures emerge due to the segregation of Ge on top of the Pt-rich layer. These structures are contingent on the Pt coverage. An almost complete monolayer of Pt favors germanene nanoribbon growth, whereas lower local Pt coverages lead to Ge nanowire growth, with their density depending on the Pt coverage62, see Supplementary Fig. 1. Both nanoribbons and nanowires run in the same direction ([\(\bar{1}\)10]) due to crystal symmetry. Unlike the nanowires, the nanoribbons extend over hundreds of nanometers and have a more perfect and flat structure.