Gapped nodal planes and large topological Nernst effect in the chiral lattice antiferromagnet CoNb₃S₆

Abstract

The electronic structure of compensated antiferromagnets (CAF) creates large functional responses, reminiscent of ferromagnets and suitable for data storage and readout, despite (nearly) net-zero spontaneous magnetization. Many experimental signatures of CAF - such as giant thermoelectric Nernst effects - should be enhanced when two or more electronic bands are nearly degenerate in vicinity of the Fermi energy. Here, we report a zero-field, thermoelectric Nernst effect  >1 μV/K in the CAF CoNb₃S₆ despite its tiny net magnetization  ~2 milli − μ_B. As drivers of the functional Nernst and Hall effects, we identify near-degeneracies of electron bands at the upper and lower boundaries of the first Brillouin zone, which are vestiges of nodal planes enforced by a screw axis symmetry in the paramagnetic state. Hot spots of emergent, or fictitious, magnetic fields are formed at the slightly gapped nodal planes. Taking into account more than six hundred Wannier orbitals, our theoretical model reproduces the observed spontaneous Nernst effect, emphasizes the role of proximate spin-space group symmetries and nodal planes for the electronic structure of CAF, and demonstrates the promise of ab-initio search for functional responses in a wide class of materials with reconstructed unit cells (supercells) due to spin or charge order.

Introduction

Compensated antiferromagnets (CAF) are a large class of complex materials which have advantages for (fast) information control^1,2,3. The impact of crystal and magnetic symmetries on the electronic band structure of CAF, specifically on their widely spin-split bands and nodal band touchings, is a matter of active current research with prospects to enhance their functional thermoelectric and magnetooptical responses^{1,2,4,5,6,7,8,9,10,11,12}. While it is known that breaking combined time-reversal and translation symmetry is a precondition for these responses, the importance of proximate symmetries¹³ is a more recent focus of interest: for example, spin-space group symmetries that are broken only when relativistic spin-orbit coupling is accounted for^{7,10,14,15,16,17}.

We study the transport properties and electronic structure of the CAF CoNb₃S₆, whose twisted magnetic ground state simultaneously breaks time-reversal and inversion symmetry^{18,19,20,21,22,23}, with a scalar spin chirality

$$\chi=\sum\limits_{\langle ijk\rangle }{{{{\bf{S}}}}}_{i}\cdot \left({{{{\bf{S}}}}}_{j}\times {{{{\bf{S}}}}}_{k}\right)$$

(1)

defined as a sum over triangles of neighboring lattice sites (i, j, k) in real space^22,23.

First, we observe a large thermoelectric Nernst effect (NE) in zero magnetic fields (>1 μV/K), where the magnetization is nearly zero, and attribute it to an emergent, or virtual, magnetic field in momentum space produced by the spin-winding χ of the magnetic texture in real space²⁴. Second, we carry out state-of-the-art numerics in a large magnetic supercell of more than eighty atoms and successfully reproduce the NE of the electron gas, including its temperature dependence. Third, we consider the interplay of symmetry, electronic structure, and transport response using an effective tight-binding model. Spin-space group symmetries enforce near-degeneracies of Fermi surfaces, despite strong exchange splitting of the band structure on the scale of several hundred milli-electron-volts. We discuss the large zero-field NE as a cooperative phenomenon of CAF order^{18,20,21,22,23}, with its proximate spin-space group symmetries, and symmetry-enforced nodal planes in the thermally disordered, paramagnetic state. Our combined experimental and theoretical approach is relevant to a wide number of materials with reconstructed unit cells due to periodic charge or spin orders^{25,26,27,28,29,30,31}.

Results

Structure, compensated antiferromagnetism, and symmetry

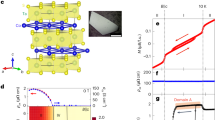
Figure 1 presents the hexagonal crystal structure of CoNb₃S₆, in which intercalated Co ions impose a $\sqrt{3}\times \sqrt{3}$ superlattice potential onto the NbS₂ sheets. The intercalation of Co ions breaks NbS₂’s mirror planes and inversion symmetry, resulting in a hexagonal chiral structure in space group P6₃22^19,32. In combination with time-reversal symmetry, the 6₃ screw axis in this space group enforces nodal plane degeneracies at the upper and lower boundaries of the Brillouin zone^33,34,35, see Fig. 1b. The Chern numbers and topological characteristics of these nodal planes are evaluated in Supplementary Note 6.

Fig. 1: Structure, magnetism, and symmetry in the compensated antiferromagnet CoNb₃S₆.

a Layered CoNb₃S₆ with chiral lattice, where blue shading indicates tetrahedra formed by Co atoms in adjacent layers. b Nodal plane enforced by screw symmetry in the paramagnetic (PM) state (illustration). Black lines, black dots, red surfaces, and red line indicate the boundary of the Brillouin zone, time-reversal invariant momenta at k_z = π/c, two Kramers-paired Fermi surfaces (FSs), and the intersection of these Fermi surfaces with the nodal plane. c Non-coplanar all-in-all-out (AIAO) magnetic order of cobalt ions (yellow spheres). Two magnetic domains are related by time reversal symmetry^22,23. d Magnetic field (B) - temperature (T) phase diagram of CoNb₃S₆ obtained from magnetization M(T) at various B. A single-domain AIAO or AOAI state (inset) can be selected by field-cooling (FC) the sample in positive or negative B, respectively. Dashed and solid arrows indicate the sample history during the cooling run and measurement run, respectively. T_N is the Néel temperature, and the magnetic field is parallel to the c-axis. e Proximate, non-symmorphic spin-space group symmetries in the AIAO state: For the three spin-only rotations by 180^∘ around the red and black axes, the spin direction rotates while its position (in real space) remains fixed. This is followed by a spin translation along a/2 − b/2, indicated by red dashed arrows paired with the red rotation axis.

Below T_N = 28 K, CoNb₃S₆ undergoes a magnetic phase transition to twisted, all-in-all-out (AIAO) antiferromagnetism of magnetic space group $P3{2}^{{\prime} }$¹⁰. The magnetic unit cell is four times larger than the paramagnetic cell and includes two tetrahedra formed by Co atoms in adjacent layers (Fig. 1a). The resulting eight magnetic sites, positioned at the corners of the tetrahedra, are illustrated in Fig. 1c^22,23. Magnetic moments point approximately inward or outward of a tetrahedron, giving nearly zero net magnetization. The magnetic phase diagram in the plane of external magnetic field B and temperature T is shown in Fig. 1d, with domains of all-in-all-out (AIAO) and all-out-all-in (AOAI) on the upper and lower sides of the plot, respectively.

The magnetic order in the AIAO state breaks the 6₃ screw symmetry and lifts the two-fold degeneracy at the (former) topological nodal planes (Fig. 1b). However, – if we ignore relativistic spin-orbit coupling and thus decouple spin and orbital spaces – there remain three non-symmorphic, spin-only rotations around axes piercing the tetrahedron, termed spin-space group symmetries of the AIAO state (Fig. 1e). In other words, a translation by a half magnetic unit cell along a/2 - b/2, combined with one of three 180° spin-only rotations in Fig. 1e, is a good symmetry of the spin sector in the compensated antiferromagnetic AIAO state. The generators of AIAO’s spin-space group are given in Supplementary Note 5.

Observation of the topological Nernst effect (TNE) in zero magnetic field

Figure 2a, b introduces the spontaneous topological Nernst effect in CoNb₃S₆ as a thermoelectric ON/OFF-type response originating from a CAF in the absence of sizable net magnetization M. The spin texture generates a voltage V_y along the direction mutually perpendicular to the temperature gradient (−∇_xT) and the small net magnetization ΔM ~ 2 × 10⁻³ μ_B/f.u. of the AIAO order. This ΔM is only about 0.1 % of the saturation magnetization expected for Co²⁺ ions, signaling compensated antiferromagnetism.

Fig. 2: Large, spontaneous topological Nernst effect (TNE) and topological Hall effect (THE) in the compensated antiferromagnet CoNb₃S₆.

a Experimental setup (schematic) for measurement of TNE. The magnetic field and temperature gradient are B∥c and − ∇ T∥a, respectively. b Isotherms of the total Nernst effect S_xy(B) before subtraction of the linear part related to the classical Lorentz force on moving charge carriers, and topological Nernst effect ${S}_{xy}^{{{{\rm{T}}}}}(B)$ after subtraction (left axis). The right axis shows the magnetization M at T = 26 K, just below the Néel temperature T_N. Dashed horizontal line: Expected saturation magnetization of Co²⁺ ions. Inset: expanded view of M in the low-B regime, with hysteresis. c, d Magnetic field dependence of thermoelectric and electric coefficients around T_N, with offset shifts. At T = 30 K and above, S_xy and ρ_yx are linear in B, reflecting the normal Hall and Nernst effects induced by B. e, f T-dependence of THE ${\rho }_{yx}^{{{{\rm{T}}}}}$ and TNE ${S}_{xy}^{{{{\rm{T}}}}}$ in B = 0, where red (blue) symbols correspond to field-cooling in positive (negative) B. Insets: experimental measurement geometries. g, h Temperature dependence of topological Nernst and Hall conductivities ${\alpha }_{xy}^{{{{\rm{T}}}}}$ and ${\sigma }_{xy}^{{{{\rm{T}}}}}$. The solid lines indicate ab-initio calculated values for Fermi energy E_F = 15 meV, while the symbols show experimental data obtained in B = 0 after field cooling (FC). See Supplementary Fig. 8 for detailed E_F dependence. i Magnetization dependence of zero-field (spontaneous) thermoelectric Nernst effects S_xy for CoNb₃S₆ and related magnetic materials.

The Nernst coefficient S_xy = V_y/(−∇_xT) at T = 26 K, just below the transition to the AIAO state, reaches 1 μV/K (Fig. 2c) – comparable in magnitude to the NE in ferromagnets^36,37,38,39. Consistent with prior work^18,40,41, we also find a large spontaneous Hall effect (HE) ρ_yx ≈ 3 μΩ cm (Fig. 2d). Both Hall and Nernst effects show clear hysteresis (±4 T) upon sweeping the magnetic field B, suggesting a common origin for HE and NE. This hysteresis relates to a first-order transition between AIAO and AOAI domains at zero magnetic field²². Above the hysteretic regime, S_xy and ρ_yx gently increase with magnetic field B, reflecting the cyclotron motion of electrons. Their linear slopes against B, S₀, and R₀, are shown in Supplementary Fig. 2. As compared to the spontaneous (zero-field) NE, especially the normal Nernst coefficient S₀ = dS_xy/dB is rather small, 6.6 nV/K per Tesla.

The coercive field so rapidly increases upon cooling that, even at 90 % of the Néel temperature T_N, we are unable to resolve a full hysteresis loop (Fig. 2c, d). To address this situation, we carefully prepare a single-domain AIAO (AOAI) state by field-cooling (FC) below T_N= 28 K in a positive (negative) c-axis field: the corresponding sample history is depicted in Fig. 1d by dashed and solid lines, respectively. At 5 K, the field is switched off, and transport coefficients are measured by slowly raising the temperature, yielding the spontaneous HE and NE shown in Fig. 2e, f. For later comparison to ab-initio calculations, we also introduce the thermoelectric Nernst and electric Hall conductivities α_xy and σ_xy as the off-diagonal elements of the tensors α and σ, which are defined by J = α(− ∇ T) and J = σE. Here, J and E are the electric current density and the applied electric field, respectively; α_xy and σ_xy can be directly calculated from S_xy and ρ_yx (“Methods”).

Finally, Fig. 2i illustrates the relationship between the spontaneous (zero-field) Nernst effect S_xy and the bulk magnetization M of CoNb₃S₆ and related magnetic materials, on a double-logarithmic scale⁴². In conventional ferromagnets subject to spin-orbit coupling (SOC), the spontaneous Nernst signal scales as $\sim \left\vert {Q}_{S}\right\vert {\mu }_{0}M$, where the coefficient $\left\vert {Q}_{s}\right\vert$ varies between 0.05 and 1 μV/KT (gray shaded area). CoNb₃S₆ exhibits a large Nernst signal of  >1 μV/K despite its tiny magnetization ΔM (μ₀ΔM ≈ 10⁻⁵ − 10⁻⁴ T). This large spontaneous Nernst effect in the CAF phase is orders of magnitude too large to be explained by the net magnetization of our AIAO order. Instead, the experiments indicate the existence of an internal (effective or emergent) magnetic field B_em generated by the geometric Berry phase of conduction electrons⁴³. This B_em is the physical quantity that bridges the realms of magnetic and electronic structures.

Momentum-space origin of the emergent magnetic field

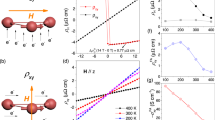
Assuming the conduction electron spin follows the texture of local moments adiabatically, the Hall effect in the magnetically ordered state is calculated as an integral  ~ ∫ d³k/(2π)³B_em(k)f_FD(ε_k) over occupied states in momentum space, where band crossings and near-degeneracies make large contributions to B_em(k) (Fig. 3a)^24,44,45; a similar expression holds for the Nernst effect (“Methods”). This is the k-space limit (momentum space limit). The calculation of B_em(k) for complex magnets requires full ab-initio modeling of the electronic structure in large magnetic supercells and has remained challenging^{25,26,27,28,46,47,48}. Approximations have been introduced to model the electronic properties of large-scale skyrmion lattices and other complex magnetic structures in terms of a spatially uniform emergent field B_em, which is opposite in sign for spin-up and spin-down conduction electrons^{49,50,51,52,53}. This is referred to as the real-space approximation (Fig. 3b).

Fig. 3: Emergent electromagnetism driven by spin chirality, and experimental evidence for the momentum-space limit in the compensated antiferromagnet CoNb₃S₆.

a, b Electronic band structure in the presence of spatially modulated (k-space limit, B_em(k)) and spatially uniform (real-space approximation, B_em) emergent magnetic fields derived from the Berry phase formalism (qualitative). B_em(k) arises from hybridized bands in the former, while B_em causes Zeeman-like band splitting in the latter (See text for details). c Parameter space of Matsui et al.⁵⁴, where J, v_F, τ, λ_s, and a are coupling strength between itinerant and local moments, Fermi velocity, carrier relaxation time, the size of the magnetic unit cell, and the size of the crystallographic unit cell. d Assuming the r-space approximation holds, spatially uniform emergent magnetic fields ${B}_{{{{\rm{em}}}}}^{{{{\rm{HE}}}}}$ and ${B}_{{{{\rm{em}}}}}^{{{{\rm{NE}}}}}$ are deduced from topological Hall effect (HE) and Nernst effect (NE) experiments, respectively, for various materials with twisted spin textures. MnSi (Eq.) indicates the transport response of the equilibrium skyrmion phase in MnSi. Circles (squares) mark data points where ${B}_{{{{\rm{em}}}}}^{{{{\rm{HE}}}}}$ and ${B}_{{{{\rm{em}}}}}^{{{{\rm{NE}}}}}$ have the same (opposite) sign. CoNb₃S₆ is an outlier, suggesting the failure of the real-space approximation.

First, Fig. 3c supports the k-space limit for the emergent magnetic field B_em(k) in CoNb₃S₆ by comparison to numerical calculations based on a Kondo Hamiltonian⁵⁴. Using reasonable materials parameters discussed in Methods, we place CoNb₃S₆ in the regime of small spin texture sizes λ_s and long relaxation times τ, toward the lower side of the figure panel.

Second, we introduce the relations ${\rho }_{yx}^{{{{\rm{T}}}}}={R}_{0}{B}_{{{{\rm{em}}}}}^{{{{\rm{HE}}}}}$ and ${S}_{xy}^{{{{\rm{T}}}}}={S}_{0}{B}_{{{{\rm{em}}}}}^{{{{\rm{NE}}}}}$ that have been established for the topological Hall resistivity and the topological Nernst effect in the real-space approximation^{47,50,52,55,56}. Here, R₀ and S₀ are normal Hall and Nernst coefficients, respectively. Figure 3d shows good agreement between ${B}_{{{{\rm{em}}}}}^{{{{\rm{HE}}}}}$ and ${B}_{{{{\rm{em}}}}}^{{{{\rm{NE}}}}}$ calculated from ${\rho }_{yx}^{{{{\rm{T}}}}}$ and ${S}_{xy}^{{{{\rm{T}}}}}$ in a number of materials with scalar spin chirality χ, including skyrmion phases. Hence, the real-space approximation is well suited to describe (thermo-)electric transport properties of such systems, despite their widely disparate materials chemistry (“Methods”).

We now assume the hypothesis of spatially uniform B_em in CoNb₃S₆ and demonstrate that the real-space approximation is inconsistent with the experimental evidence. Again using ${\rho }_{yx}^{{{{\rm{T}}}}}={R}_{0}{B}_{{{{\rm{em}}}}}^{{{{\rm{HE}}}}}$ and ${S}_{xy}^{{{{\rm{T}}}}}={S}_{0}{B}_{{{{\rm{em}}}}}^{{{{\rm{NE}}}}}$, we calculate ${B}_{{{{\rm{em}}}}}^{{{{\rm{HE}}}}}=+ 4\,$T and ${B}_{{{{\rm{em}}}}}^{{{{\rm{NE}}}}}=-100\,$T at T = 20 K. The details of this calculation and raw data for R₀ and S₀ are provided in Supplementary Fig. 2. In Fig. 3d, the CoNb₃S₆ data thus deviates from the diagonal dashed line, signifying the breakdown of the real-space approximation and the need for full ab-initio calculations in a large unit cell. Indeed, in k-space modeling, the Hall and Nernst effects exhibit a sharp dependence on the Fermi energy, which can explain the different values of ${B}_{{{{\rm{em}}}}}^{{{{\rm{HE}}}}}$ and ${B}_{{{{\rm{em}}}}}^{{{{\rm{NE}}}}}$ (Supplementary Note 3).

Ab-initio calculation and Nernst response

While previous work reported the electronic structure in the paramagnetic state of CoNb₃S₆^{18,40,41,57,58,59}, including the effect of electron correlations²¹, and considered magnetic states other than AIAO^20,29,41, there remains a need to perform ab-initio calculations of ${\sigma }_{xy}^{{{{\rm{T}}}}}$ and ${\alpha }_{xy}^{{{{\rm{T}}}}}$ in the AIAO CAF structure, to gain insight into the microscopic origin of topological Hall and Nernst effects. Figure 4a depicts the lower half of the magnetic unit cell, as viewed along the c-axis: four cobalt, twelve niobium, and twenty-four sulfur ions are crowded into this space, which corresponds to the size of four crystallographic unit cells (dashed box).

Fig. 4: Electronic structure and modeling of topological Hall and Nernst effects in CoNb₃S₆.

a Top view of the unit cell of CoNb₃S₆, where dashed and solid lines indicate the boundaries of paramagnetic (PM) and all-in-all-out (AIAO) antiferromagnetic unit cells, respectively. b Brillouin zone of PM CoNb₃S₆ (dashed line) and of the compensated antiferromagnetic AIAO phase (solid line); the magnetic structure in AIAO is described by three superimposed ordering vectors Q_ν (ν = 1, 2, 3). c, d Cut of the PM Brillouin zone at k_z= 0 plane and its full, three-dimensional view. e Fermi surface and first Brillouin zone in the AIAO compensated antiferromagnetic state. In (c–e), the Fermi energy is E_F = 0 meV and red shading indicates nodal planes at k_z = ± π/c, protected by chiral P6₃22 symmetry in PM, and slightly gapped in AIAO. Red lines are cross-sections of Fermi surface sheets with k_z = ± π/c. f, g Calculated Hall and thermoelectric Nernst conductivities ${\sigma }_{xy}^{{{{\rm{T}}}}}$ and ${\alpha }_{xy}^{{{{\rm{T}}}}}$ as a function of E_F. Red and blue lines show calculation results at high and low temperatures (“Methods”); changes of the ordered moment with T are discussed in Supplementary Fig. 8. Orange shading indicates the regime at E_F = + 10 − 15 meV with good agreement between theory and experiment. Insets: expanded view at low E_F values. h Sum of z-component of emergent magnetic field B_em(k) in slices of ${k}_{z}={{{\rm{const.}}}}$, symmetrized with respect to k_z (see text), for AIAO. Two values of the Fermi energy E_F = 0, 10 meV are labeled in yellow and green, respectively. Anomalies due to gapped nodal planes at k_z = ± π/c are highlighted in orange. All calculations take into account spin-orbit coupling (SOC); its quantitative effect on the transport response is discussed in Supplementary Fig. 14.

Figure 4 b–d shows the electronic bands of paramagnetic (PM) CoNb₃S₆, yielding a set of hole-type, tubular Fermi surfaces around the Brillouin zone center and more three-dimensional, electron-like Fermi surface sheets (blue surfaces, details in “Methods”). The red-shaded areas in Fig. 4d mark k_z = ± π/c, where nodal degeneracies of the Fermi surface (red lines) are enforced by a combination of time-reversal symmetry and a screw axis in the chiral PM state of CoNb₃S₆^33,34.

The AIAO state can be described as a superposition of three ordering vectors Q = a^*/2, b^*/2, and (− a^*+ b^*)/2, where a^* and b^* are reciprocal lattice vectors (Figs. 1b, 4b); this triple-Q texture realizes a lattice-commensurate and sub-nanometer analogon to larger-scale magnetic skyrmions^22,23,60,61. Figure 4b illustrates the shrinkage of the Brillouin zone in k-space corresponding to the enlarged magnetic unit cell. Taking the zone-folding effect into account, Fig. 4e shows the electronic structure of CoNb₃S₆ in the AIAO state below T_N, with large, concentrically arranged Fermi surface tubes. The compensated antiferromagnetic AIAO order breaks both time-reversal and screw symmetries, lifting the degeneracy of Kramers pairs even at k_z = ± π/c. Nevertheless, the splitting of Fermi surfaces is weak, especially around the (now broken) nodal plane at k_z = ± π/c.

We have further implemented the local Berry phase method^46,48 for calculating the k-dependent emergent magnetic field B_em(k) in the AIAO state (Methods). Figure 4f, g presents the band-filling dependence of ${\sigma }_{xy}^{{{{\rm{T}}}}}$ and ${\alpha }_{xy}^{{{{\rm{T}}}}}$ in AIAO obtained from our state-of-the-art numerical method that captures contributions of more than six hundred atomic orbitals. We also note that Fig. 2g, h demonstrates good agreement between the predicted and observed temperature dependences of ${\sigma }_{xy}^{{{{\rm{T}}}}}$ and ${\alpha }_{xy}^{{{{\rm{T}}}}}$, for a reasonable value of the Fermi energy E_F.

To understand the origin of the observed ${\sigma }_{xy}^{{{{\rm{T}}}}}$ and ${\alpha }_{xy}^{{{{\rm{T}}}}}$ in momentum space, we sum the k-space emergent magnetic field B_em(k) in slices of constant k_z to obtain B_em(k_z), depicted in Fig. 4h. We see enhanced contributions at k_z = ± π/c where the nodal plane degeneracy is lifted by AIAO order (Fig. 4h, orange highlights). In the following, we argue that these hot spots of enhanced B_em(k_z) appear due to a cooperative effect of (gapped) nodal planes in the electronic structure and spin chirality χ. This conclusion is supported by symmetry arguments and an effective tight-binding model. In Supplementary Fig. 14, we provide more details about spin-orbit coupling (SOC) and its effect on the calculated transport coefficients: Although SOC is required to quantitatively predict ${\sigma }_{xy}^{{{{\rm{T}}}}}$ and ${\alpha }_{xy}^{{{{\rm{T}}}}}$, the qualitative trends and magnitude of the signals are reproduced in the AIAO state even without SOC.

Discussion

A minimal tight-binding model with the symmetry of CoNb₃S₆ is constructed in Supplementary Note 7. We start from the paramagnetic state and perturbatively turn on a weak exchange interaction corresponding to the AIAO order. The minimal model yields sharp, k_z-even anomalies in B_em(k_z) at the k_z = ± π/c nodal planes even in the absence of SOC (Supplementary Fig. 15), generally consistent with the hot spots of B_em(k_z) in the ab-initio calculation of Fig. 4h. We may thus start from the limit of zero SOC for a qualitative discussion.

When SOC is negligible, contributions to B_em(k_z) away from k_z = ±π/c are relatively weak in the compensated antiferromagnetic AIAO state. To explain this, we note that – away from a nodal plane – bands are two-fold spin-degenerate in the paramagnetic state without SOC; they remain so at all momenta k even with the onset of AIAO order, due to non-symmorphic spin-space group symmetry (Methods, Fig. 1e). It is this spin-space group symmetry that prevents a uniform band hybridization across the Brillouin zone, and suppresses contributions to B_em(k_z) when k_z ≠ ±π/c. In contrast, the paramagnetic bands (no SOC) are four-fold degenerate at k_z = ±π/c, and in the AIAO phase the splitting between two band pairs is small compared to the magnitude of the exchange interaction. This means that sets of four bands can be hybridized at k_z = ±π/c to create the hot spots of B_em(k_z) seen in Fig 4h.

Even with SOC, the two-fold degeneracy of bands remains nearly intact throughout the Brillouin zone, as demonstrated by our ab-initio calculations (Fig. 4e). This implies proximate spin-space group symmetry and the applicability of the above, model-based argument to the electronic structure of CoNb₃S₆. Thus, it is the cooperative effect of scalar spin chirality χ from AIAO order and the nodal plane at k_z = ±π/c that gives rise to the emergent magnetic field localized in k-space and the large thermoelectric Nernst effect.

Previously, it was speculated that a large Hall effect appears when topological nodal planes are gapped by symmetry breaking, and toy model calculations for cubic B20 compounds suggested transport signatures dominated by electronic states close to the boundary of the Brillouin zone^33,34. Such work mostly focused on collinear ferromagnetic states, with a large exchange splitting. In contrast, our study targets compensated antiferromagnets and stresses the importance of proximate symmetries when considering the appearance of a large B_em(k) at a gapped nodal plane¹⁰.

For materials hosting charge or spin order with a large supercell, there have been only a limited number of theoretical attempts to model functional responses by density functional theory^{25,26,27,28,29,62}. The present success in describing the topological Hall and Nernst effects of CoNb₃S₆ by state-of-the-art ab-initio calculations is thus notable. It motivates further studies of cooperative phenomena between spin textures and k-space band topology in this vast material class, which includes not only the non-coplanar AIAO state of CoNb₃S₆ but also p-wave magnets and supercell altermagnets^30,31.

Methods

Crystal growth

Powders of elemental Co, Nb, and S are mixed together in a silica tube and annealed at 900 °C for 5 days. The process is repeated with re-grinding in between, to enhance the quality of the polycrystal¹⁸. Single crystals of CoNb₃S₆ are synthesized by chemical vapor transport (CVT) with iodine as a transport agent. CoNb₃S₆ crystallizes in a hexagonal thin-plate shape, with the largest surface orthogonal to the c-direction. The crystal structure is confirmed by powder X-ray diffraction and Rietveld refinement, and the crystal axes are determined by Laue X-ray back-scattering. The concentrations of Co, Nb, and S are confirmed by Scanning-electron microscopy (SEM) (Hitachi S-4300) and energy-dispersive X-ray spectroscopy (EDX) (Horiba EMAX x-act) measurements (Supplementary Fig. 17).

Magnetization and transport measurements

The DC magnetic response is measured using a superconducting quantum interference device magnetometer (MPSM 3, Quantum Design). For electric transport measurements, samples are cut into rectangular plate-like shapes and equipped with electrodes made from silver paste and thin gold wire (ø 40 μm). Measurements of longitudinal (ρ_xx) and Hall (ρ_yx) resistivities are performed using a Physical Property Measurement System (PPMS, Quantum Design).

Thermoelectric measurements

Thermoelectric experiments are carried out using a customized sample stage mounted in a commercial PPMS cryostat (Quantum Design, Inc.). Thermopower (Seebeck) and Nernst effect are recorded using a one-heater two-thermometer technique in steady-state mode⁴⁷. A temperature gradient − ∇ T is applied along the a-direction within the basal plane, while the magnetic field B is parallel to the c-axis. To correct the effect of contact misalignment, ρ_xx and S_xx (ρ_yx and S_xy) are (anti-)symmetrized against B, respectively. We take care to reduce spurious voltages from electromotive forces at metal junctions, and to detect voltages and temperatures for the calculation of S_xx at the exactly same position on the crystal. We acknowledge recent thermoelectric measurements, paired with wonderful imaging data, on thin-flake devices of CoNb₃S₆ using the AC technique, where the low-temperature data was reported without field-cooling procedure, and the observed S_xy is three times smaller than the presently observed values⁶³.

Density functional theory calculations

The electronic structure of paramagnetic and magnetically ordered CoNb₃S₆ is calculated using the OpenMX code⁶⁴ – in the paramagnetic case, by the same method as in the ARPES study of ref. ⁵⁹. We use the exchange-correlation functional within the generalized gradient approximation (GGA) and with norm-conserving pseudopotentials^65,66. The wave functions are expanded by a linear combination of multiple pseudoatomic orbitals^67,68. Spin-orbit coupling (SOC) is included through total angular momentum-dependent pseudopotentials⁶⁹. A set of pseudoatomic orbital bases was specified as Co6.0-s₃p₂d₂f₁, Nb7.0-s₂p₂d₂f₁, and S7.0-s₃p₃d₂, where the number after each element stands for the radial cutoff in Bohr radii; the integers after s, p, d, and f indicate the radial multiplicity of each angular momentum component. The lattice constants of paramagnetic CoNb₃S₆ are set to a = 11.498 Å and c = 11.886 Å and the spin-unpolarized condition is defined as equal spin-up and spin-down. For the all-in all-out (AIAO), non-coplanar magnetic structure (near-zero net magnetization), we use the same lattice constants with an additional 2 × 2 supercell. A charge density cutoff energy of 500 Ry and a k-point mesh of 6 × 6 × 5 are used. The DFT calculations in the main text include spin-orbit coupling (SOC), while Supplementary Fig. 14 discusses the effect of SOC on the transport response. The (small) net magnetization is along the crystallographic c-axis.

Calculation of topological charge of nodal plane

For evaluation of the topological charge of electronic nodal planes in the paramagnetic state, a separate ab-initio calculation based on the Vienna Ab-initio Simulation Package (VASP) code^70,71,72 is carried out, showing good consistency with the OpenMX calculations of the main text. The generalized gradient approximation (GGA) of Perdew-Burke-Ernzerhof is adopted for the exchange-correlation functional⁷³. In the self-consistent band structure calculations, a plane-wave cutoff of value 500 eV and a Γ-centered k mesh of 12 × 12 × 6 are used. The results are shown in Supplementary Note 6 and Supplementary Fig. 5. Furthermore, the rotation eigenvalues are calculated by the Irvsp package⁷⁴, and we obtain the Chern numbers C₁ = + 2 ± 6 and C₂ = + 2 ± 6 for the two nodal planes that intersect with the Fermi energy, respectively. The results are organized in Supplementary Tables 1 and 2.

Electric and thermoelectric conductivities

The electric conductivity and resistivity tensors are defined by the relations J = σE and E = ρJ, while the thermoelectric conductivity and Seebeck / Nernst tensors are defined via J = α(− ∇ T) and E = S(− ∇ T), respectively. Here J, E, and (− ∇ T) are the electric current density, the electric field, and a temperature gradient, respectively. In the formalism of Fig. 3b, the decompositions according to

$${\rho }_{yx}^{{{{\rm{T}}}}}={R}_{0}P{B}_{{{{\rm{em}}}}}^{{{{\rm{HE}}}}}$$

(2)

$${S}_{xy}^{{{{\rm{T}}}}}={S}_{0}P{B}_{{{{\rm{em}}}}}^{{{{\rm{NE}}}}}$$

(3)

with the normal Hall (Nernst) coefficient R₀ (S₀) and the spin polarization factor P hold under the condition of (a) moderately weak band splitting between ↑ and ↓ states and (b) a spatially uniform B_em^{52,53,55,56,75}. Fig. 3d shows that even the prototypical skyrmion host MnSi violates the proposed scaling at very low temperature, which is attributed to the increasing divergence of normal Hall coefficients ${R}_{0}^{\uparrow }$, ${R}_{0}^{\downarrow }$ for electrons of opposite spin polarization^53,75. In contrast, the CAF Mn₃Sn with breathing Kagome lattice – which has a weakly canted, non-coplanar state for B∥c – neatly obeys ${B}_{{{{\rm{em}}}}}^{{{{\rm{HE}}}}}={B}_{{{{\rm{em}}}}}^{{{{\rm{NE}}}}}$⁷⁶.

In our measurement geometry, where currents and temperature gradients are two-dimensional vectors confined to a high-symmetry plane of the crystal, σ and α are 2 × 2 matrices. For example, ρ = (ρ_xx, ρ_xy; ρ_yx, ρ_yy) so that the off-diagonal part of the conductivity tensor, i.e., the Hall conductivity, is ${\sigma }_{xy}={\rho }_{yx}/({\rho }_{yx}^{2}+{\rho }_{xx}^{2})$ when setting ρ_xx ≈ ρ_yy. Neglecting the off-diagonal thermal conductivity (thermal Hall effect), the thermoelectric conductivity can be related to Seebeck and Nernst effects as α_xy = σ_xxS_xy + σ_xyS_xx. Further discussion of α_xy, based on the Mott relation, can be found in Supplementary Note 3.

Calculation of intrinsic topological Hall and Nernst conductivities

The observed spontaneous Hall conductivity is on the order of 100 −1000 S/cm, and σ_xx is not too high,  ~10⁴ S/cm so that it is reasonable to focus on the intrinsic contribution to the Hall effect rather than extrinsic skew scattering⁴³. We use the local Berry phase technique to determine the intrinsic (anomalous or topological) Hall conductivity in the momentum-space limit, avoiding complexities associated with construction of a Wannier representation comprising more than six hundred atomic orbitals^46,48. The essential expression is⁴⁵

$${\sigma }_{xy}^{{{{\rm{int}}}}}(T)=-\frac{{e}^{2}}{\hslash }\int_{{{{\rm{BZ}}}}}\frac{{d}^{3}{{{\bf{k}}}}}{{(2\pi )}^{3}}\,{f}_{{{{\rm{FD}}}}}({{{\bf{k}}}},T)\,{B}_{{{{\rm{em}}}}}{({{{\bf{k}}}})}^{z}$$

(4)

where f_FD(k, T) and BZ denote the Fermi-Dirac distribution function and a volume integral over the Brillouin zone, and B_em(k)^z is the z-component of the emergent magnetic field (Berry curvature) in momentum (k-) space. From this, the thermoelectric Nernst conductivity follows as

$${\alpha }_{xy}^{{{{\rm{int}}}}}=(e{k}_{{{{\rm{B}}}}}/\hslash )\int_{BZ}\left[{d}^{3}{{{\bf{k}}}}/{(2\pi )}^{3}\right]s({{{\bf{k}}}},T){B}_{{{{\rm{em}}}}}{({{{\bf{k}}}})}^{z}$$

(5)

with s(k, T) the von Neumann entropy density of the electron gas. Here k_B, T, e and ε denote the Boltzmann constant, temperature, the fundamental charge, and the band filling (Fermi energy), respectively.

In the PM state with a chiral space group, combined time-reversal and C_2z symmetries ensure the opposite sign of B_em(k_z) for k_z and  − k_z. Remnants of this (anti-symmetric) behavior are visible even in the AIAO calculation (Supplementary Fig. 10). To emphasize the main contributors to the nonzero net Hall and Nernst conductivities in Fig. 4f, g, we symmetrize B_em(k_z) in Fig. 4h.

Temperature dependence of calculated Hall and Nernst conductivities

The intrinsic contribution to the topological Hall conductivity of CoNb₃S₆ in the low-T limit is calculated by the OpenMX code based on the local Berry phase⁴⁸ as in Eq. (4). The intrinsic Hall conductivity ${\sigma }_{xy}^{{{{\rm{T}}}},{{{\rm{int}}}}}$ and Nernst conductivity ${\alpha }_{xy}^{{{{\rm{T}}}},{{{\rm{int}}}}}$ at finite temperature are obtained, based on the Boltzmann transport equation and linear response theory, as follows:

$${\sigma }_{xy}^{{{{\rm{int}}}}}(T)=\int\,d\varepsilon \left(-\frac{\partial {f}_{{{{\rm{FD}}}}}(T)}{\partial \varepsilon }\right){\sigma }_{xy}^{{{{\rm{int}}}}}(\varepsilon,T=0)$$

(6)

$${\alpha }_{xy}^{{{{\rm{int}}}}}(T)=e\int\,d\varepsilon \frac{(\varepsilon -\mu )}{T}\left(-\frac{\partial {f}_{{{{\rm{FD}}}}}(T)}{\partial \varepsilon }\right){\sigma }_{xy}^{{{{\rm{int}}}}}(\varepsilon,T=0)$$

(7)

where f_FD is again the Fermi-Dirac distribution function. The numerical integral is performed on a 40 × 40 × 36 k-point grid. In Fig. 4, we use T = 10, 100  K for the low- and high-temperature limits, respectively.

Estimation of coupling strength and mean free path

In Fig. 3c, CoNb₃S₆ is placed in the momentum space limit based on comparison of several material parameters: The coupling strength between itinerant and local moments J ≈ 1.0 eV is estimated from our DFT calculations as the separation energy between spin-up and down states in the partial density of states, consistent with prior work⁴⁰. The mean-free path l_mfp is calculated as the product of Fermi velocity v_F and relaxation time τ. The former is estimated from angle-resolved photoemission (ARPES), where the linear slope of the band dispersion defines v_F = (1/ℏ)ΔE/Δk with v_F = 2.2 ⋅ 10⁵ m/s for Co-derived bands at the Brillouin zone edge of CoNb₃S₆^57,58,59. The bound for the carrier relaxation time, τ > 33 fs, is obtained from optical conductivity experiments in Supplementary Fig. 6.

Band degeneracies and spin-space group

The three non-symmorphic spin-space rotation symmetries in Fig. 1e have mutually perpendicular rotation axes and hence can be represented at all momenta k in the first Brillouin zone by the anti-commuting Pauli matrices iσ_n with n = x, y, z. After choosing one of the rotation axes in Fig. 1e as the spin quantization axis, each band is labeled by one of the symmetry eigenvalues λ_± = ± i of iσ_z. It follows that an eigenstate $| E,{\lambda }_{\pm }\left.\right\rangle$ with energy E of the Hamiltonian is related to an orthogonal state $| E,{\lambda }_{\mp }\left.\right\rangle \propto i{\sigma }_{x}| E,{\lambda }_{\pm }\left.\right\rangle$. Thus, such a set of spin-space group symmetries, in absence of spin-orbit coupling (SOC), enforces two-fold band degeneracies for all k^{10,14,15,16,17}, and – even if we re-introduce coupling of spin and lattice and lift these symmetries – proximate two-fold band degeneracies remain over large sectors of the Brillouin zone, as demonstrated also by our DFT calculations. In principle, the translation and rotation symmetries characterizing the spin-space group of AIAO are already present in the paramagnetic state, considering an expanded 2 × 2 unit cell.