Introduction

O3-type sodium-ion layered oxide cathodes hold great potential for utilization in large-scale energy storage devices and low-speed electric vehicles1,2. However, the cycling stability of such materials remains insufficient to meet practical requirements. The extraction of Na+ typically involves a complex phase transition (e.g., O3-NaMn0.5Ni0.5O2 → O'3 → P3 → P'3 → O3’) accompanied by a substantial volume change (23%)3. Furthermore, the intense interfacial reaction between Ni4+, Fe4+ and electrolyte during high voltage charging4,5, irreversible Li/transition metal (TM) cation migration6,7, and anion oxidation will further aggravate chemo-electrochemo-mechanical degradation, threatening the structural integrity in cathode material8. Therefore, it is imperative to conduct an in-depth investigation into the relationship between structural characteristics and cycling stability.

Researchers have endeavored to suppress the irreversible phase transition and cation migration by utilizing various cation doping strategies, including Li+, Mg2+, Cu2+, Zn2+, and Ti4+9,10,11,12. Previous studies have repeatedly demonstrated the modulating effect of doping elements on the coordination chemistry and local strain of transition-metal oxide slabs (TMO2) and sodium oxide slabs (NaO2), as depicted in Supplementary Fig. 113,14. However, a precise physical structural parameter that serves as a measure of stability estimation remains lacking.

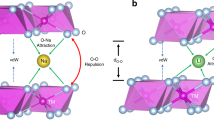
A delicate coordination structure between the TMO2 and NaO2 slabs in the O3-type layered cathode may contribute to the reversibility of the O3-P3 phase transition and inhibit the cation migration behavior15,16. Specifically, the transition from O3 to P3 is achieved through TM layer slip as shown in Supplementary Fig. 217. However, in the actual phase transition process, besides slipping in the plane ab direction, the expansion and contraction of the c-axis cannot be ignored (dynamic behavior of NaO2 and TMO2 slabs). These factors determine both the easiness of O3-P3 phase transition as well as the instantaneous rate of lattice parameter change18,19. Meanwhile, cation migration contributes to the cumulative formation of spinel phases and severe voltage decay during cycling, and attempts have been made to suppress this behavior by modulating the coordination structure of TM in the Na layer. This has inspired efforts to optimize the overall coordination structure of the TMO2 and NaO2 slabs to address the phase change and cation migration14,20.

Here, the NaO2 slabs to TMO2 slabs spacing ratio (R = dO-Na-O/dO-TM-O) was leveraged as a criterion for assessing the cycling stability of O3-type materials. To achieve this, a family of cathode materials with a wide range of R values is desired, yet conventional O3-type cathode materials turn into P2-type structure when R is above 1.62. Based on this, NaxMn0.4Ni0.3Fe0.15Li0.1Ti0.05O2 is deliberately chosen as the main composition, with a range of 0.55 ≤ x ≤ 1. These components exhibit extraordinary O3 phase behavior, characterized by R-values ranging from 1.969 to 1.543, far exceeding the boundary condition of R = 1.62. To our knowledge, 0.55 is the lowest reported Na ratio among O3-structured layered transition metal oxides21,22. The relationship between the structural parameter R and the cathode cycling stability was fully investigated using Na0.55 and Na1 as representative cases. High-rate in situ X-ray diffraction (XRD) characterization and in situ distribution of relaxation times (DRT) experiments of three-electrode pouch cell system were conducted, revealing that high R-value facilitates the rapid yet smooth phase transition process, resulting in a highly reversible O3-P3 phase transition. Furthermore, the high R-value characteristic induces tensile stretching of the interstitial tetrahedral site of the Na layer, effectively inhibiting cation migration behavior as demonstrated by bond valence site energy simulations. Lastly, it is noteworthy that after screening fourteen P2/O3 mixed-phase structures, we have observed that the high R-values feature in their O3 phase also plays pivotal roles in promoting their cycling stability besides the conventional wisdom of interlocking effect.

Results

Structural characterization of Na0.55 ~ Na1

The cathode materials were synthesized via solid-state reactions with details described in supporting information. The elements are uniformly distributed in the cathode without localized segregation as depicted in Supplementary Figs. 3 and 4. The crystal structures of the Na0.55, Na0.65, Na0.83, and Na1 samples were analyzed using XRD with Rietveld refinement, as shown in Supplementary Fig. 5, and the corresponding refined lattice parameters are listed in Supplementary Tables 1–4. The proportion of superlattice formed by local Li/TM ordering and minor nickel oxide phases occupy less than 5% and should not affect the current study. In addition, the crystal structures of Na0.55 ~ Na1 were further confirmed by neutron powder diffraction (NPD) measurements and were also refined using the Rietveld method (Fig. 1a, b and Supplementary Fig. 6). All the samples have high-quality long-range ordered structures well indexed to the R-3m space group. The refined lattice parameters for Na0.55 and Na1 were a = b = 2.928 Å, c = 16.414 Å, and a = b = 2.969 Å, c = 15.962 Å, respectively, which match with the XRD refinement results. The local structures were investigated based on the neutron pair distribution function (nPDF) as shown in Fig. 1c. As the Na content descends, the TM-O/interlayer O–O bonds contract and the Na-O/Na-TM bonds stretch, leading to changes in the coordination structure between neighboring layers. The structural details of the atomic layers in Na0.55 and Na1 were visualized by scanning transmission electron microscopy (STEM) equipped with high-angle annular dark-field (HAADF) and annular bright-field (ABF) detectors, as shown in Fig. 1d, e. The bright dots in the HAADF-STEM images represent the TM layer, and the columns of lighter darker dots correspond to the Na layer, which is the opposite of the ABF images23. In Na0.55, the distance between adjacent TMO2 slabs was measured to be 5.38 Å, comprising of TMO2 slabs with a thickness of 1.84 Å and NaO2 slabs with a thickness of 3.62 Å. For Na1, the distance between neighboring TMO2 plates was found to be 5.32 Å, consisting of 2.08 Å for TMO2 slabs and 3.24 Å for NaO2 slabs. These observations are consistent with the XRD/NPD refinement results and nPDF trend.

Fig. 1: Physicochemical characterizations and DFT calculations of the cathodes.
figure 1

Rietveld refinement of the NPD patterns of (a) Na0.55 and (b) Na1. HAADF-STEM and ABF-STEM images of (c) nPDF of Na0.55, Na0.65, Na0.83, and Na1. The variation of TM-O, Na-O, interlayer O–O, Na-TM bond lengths with Na content has been labeled. d, e HAADF-STEM and ABF-STEM images of the Na0.55 and Na1 samples. f Crystal structure of O3-type oxides. The interlayer distance dO-Na-O is the vertical distance of the NaO2 slabs and dO-TM/Li-O is the vertical distance of the TMO2 slabs. g Ratio between the interlayer distances of dO−Na−O and dO‑TM/Li‑O for Na0.55 ~ Na1. h, i DOS of Na0.55 and Na1. The major hybridization regions of TM 3 d and O 2p are marked with boxes.

Full size image

Based on XRD and NPD refinement results, the vertical distances between NaO2 slabs and TMO2 slabs in the Na0.55 ~ Na1 series were calculated, and the corresponding ratios were derived to be 1.969, 1.841, 1.622, and 1.543, respectively (Fig. 1f, g, and Supplementary Table 5). The ratios represent the structural bonding characteristics of the Na0.55 ~ Na1 due to the consistency of elements in the TMO2 layers. The density of states (DOS) of Na0.55 and Na1 were obtained by density-functional theory (DFT) calculations to investigate the role of high R-values on the electronic structural features (Fig. 1h, i). The Ni 3d eg* and Fe 3d eg* orbitals are located closer below the Fermi energy (Ef) level, suggesting that they are susceptible to electron transfer and are electrochemically active, with Ni 3d eg* being located higher up and tending to be the first to engage in charge compensation14. The positional distribution of the Mn 3d t2g (−1.63 eV) orbitals and Ti 3d orbitals implies electrochemical inertness (Supplementary Fig. 7), contributing mainly to the stability and structural integrity of the system. The O 2p orbital in Na0.55 rises closer to the Ef level and is deeply hybridized with Ni 3d eg* and Fe 3d eg*, this greatly boosts the covalent bonding strength of TM-O and contributes to the contraction of the TM-O bond, which is the reason for the tighter TM-O slabs. The effective hybridization of TM 3d and O 2p may facilitate the involvement of partial anion O2− in charge compensation in the deep desodiation state. The Na1 structure has less overlap of Ni 3d eg* and Fe 3d eg* with O 2p orbitals, and the orbital hybridization is weaker, which corresponds to its wider TM-O slab mentioned above.

Electrochemical performances

The relationship between structural features and electrochemical behavior was evaluated using Na metal as anode in half cells. Since Li, Fe, and Ti doping in the TM layer suppresses Na+/vacancy ordering22,24, Na0.55 and Na1 present smooth charge/discharge curve with capacity of 117.3 mAh g−1 and 132.6 mAh g−1 in the voltage range of 2.0–4.2 V at 0.1 C (12 mA g−1), respectively (Fig. 2a). The higher initial charge/discharge capacity of Na1 comes from the long O3-P3 phase transition near 2.8 V, and the slope portion of the capacity is almost identical. Long‐term cycling tests were performed at 1 C (120 mA g−1) to evaluate the Na+ storage durability in Na0.55 ~ Na1. As shown in Fig. 2b and Supplementary Fig. 8, Na0.55 has a capacity retention of 83.4% after 300 cycles, while Na0.65, Na0.83, and Na1 retain 80.7%, 68.9%, and 64.1%, respectively, which is proportional to the values of R. Meanwhile, the stability stems from the well-documented physical structural characteristics of the cathode phase (Supplementary Figs. 9–13). To compare the electrochemical reaction behaviors, the dQ/dV profiles for the initial 100 cycles at 1 C (120 mA g−1) are presented (Fig. 2c). Na0.55 exhibits highly reversible TM redox and anionic O redox (as will be discussed later) at 3.4 V–4.1 V and 4.1 V–4.2 V regions, respectively, whereas Na1 exhibits a gradual contraction and disappearance of the TM and O activity, which can be attributed to the enhanced hybridization of the TM3d eg*-O2p orbitals by the contracted TMO2 slab in Na0.55.

Fig. 2: Electrochemical performance of Na0.55 and Na1.
figure 2

a Galvanostatic charge and discharge profiles of Na0.55 and Na1 at 0.1 C (12 mA g−1) between 2 V and 4.2 V. b Long-term cycling performance at 1 C, all the error bars indicate the variation from three measurements. c dQ/dV profiles for the initial 100 cycles at 1 C (120 mA g−1). TM/O redox reversibility is labeled in different shaded areas. d Rate capability at different current rates from 0.1 C (12 mA g−1) to 10 C (1200 mA g−1), and all the error bars indicate the variation from three measurements. e Long-term cycling performance at 5 C rate and the shaded area represents the error of three different batteries. f, g Arrhenius plots and calculated activation energy of Na0.55 and Na1, respectively. h, i Na+ migration energy curves in Na0.55 and Na1. s and i stand for saddle and position, respectively.

Full size image

Another feature of the high R-value is the expanded NaO2 slabs, which significantly improves the Na+ migration kinetics. Figure 2d shows the rate performance of Na0.55 and Na1 from 0.1 C (12 mA g−1) to 10 C (1200 mA g−1). The Na0.55 can exert high specific capacities of 80.6 mAh/g and 60.2 mAh/g at 5 C (600 mA g−1) and 10 C (1200 mA g−1), while the Na1 only has 60 mAh/g and 46 mAh/g, respectively. The capacity retention at 5 C (600 mA g−1) is 90.8% for 1000 cycles and 74.3% for 2000 cycles, significantly higher than that in Na1 (61.8% for 900 cycles) (Fig. 2e). Electrochemical kinetics tests were performed for Na0.55 and Na1 (Supplementary Fig. 14 and Fig. 2f). The corresponding charge transfer activation energy is calculated to be 17.33 kJ mol−1, 39.66 kJ mol−1 for Na0.55 and Na1, respectively (Fig. 2g). As expected, the energy potential barrier required to activate Na+ transport in Na0.55 is much lower than that of Na1. This is consistent with the galvanostatic intermittent titration technique (GITT) test results (Supplementary Fig. 15). The migration paths of Na+ in the Na0.55 and Na1 were further simulated and visualized using bond valence pathway analyzer (BVPA) (Supplementary Figs. 16–23)25. Na+ diffusion in the Na0.55 shows much smaller octahedron-gap tetrahedron-octahedron amplitudes due to the extremely extended NaO2 slabs, which appears to be similar with the fast P-phase prismatic channel (Supplementary Figs. 18 and 19). The corresponding Na+ migration energy barriers of Na0.55 and Na1 are calculated to be 0.54 eV and 0.673 eV, respectively (Fig. 2h, i).

The Na+ (de)intercalation behavior and potential charge compensation mechanism of Na0.55 during 1 C (120 mA g−1) cycling were further investigated. After 3 formation cycles, the initial Na content of Na0.55 was revised to Na0.513 (Supplementary Fig. 24), corresponding to the extraction of 0.339 mol Na+ when a specific capacity of 100 mAh/g was achieved. At this stage, only 0.174 mol Na+ was left in the structure for the maintenance of the P3’ layered structure (see in situ XRD demonstration below), while in comparison, the layered structure consistently retained more than 0.34 mol Na+ for Na1 during cycling at a rate of 1 C (120 mA g−1) (Supplementary Fig. 25). Previous studies on the evolution of layered structures have shown that depletion of Na+ at high state of charge leads to interlayer slip, and the more Na retained in the layered host upon desodiation, the higher structural stability maintained during the charge−discharge process26,27. However, this is contrary to the results of the cyclic stability results. Further studies using XPS and Raman spectra tests revealed that not only Ni3+, Fe3+ undergo redox reactions during the charging process of Na0.55. When charged to 4.2 V, the typical Raman region for peroxo-like species can be observed at around 825 cm−1. Additionally, the oxidation of O2− to peroxo dimers (O2n−) is also observed in the O2p fine spectrum around 530.5 eV, which corresponds to the O2p orbit in DOS (Supplementary Figs. 26–28)28,29. The above results including excessive Na removal behavior of the host structure and the participation of anionic O2− in redox at high voltages are both supposed to be detrimental to the cycling stability of Na0.55, yet its capacity is well preserved after extensive cycling, which is indispensable from its unique structural properties, as will be discussed in later sections.

Phase transition reversibility

In order to examine the relationship between the high R-value features and the phase evolution, in situ XRD was utilized to monitor the structural evolution of Na0.55 and Na1 upon Na+ de-intercalation/intercalation between 2.0 and 4.2 V. Figure 3a, b present the 2D contour maps, initial charge-discharge curve and their refined lattice parameters of Na0.55 and Na1. The corresponding XRD patterns are shown in Supplementary Figs. 29 and 30, respectively. During the initial charging period, the O3 (003) and (104) peaks of Na0.55 and Na1 were shifted to lower and higher angles, respectively, which was caused by O–O electrostatic repulsion and TM oxidation, leading to the expansion of c and contraction of a lattice. With the extraction of only 0.04 mol Na+ in Na0.55, the characteristic peak position of O3 disappears and rapidly transforms into the P3 phase until charging to 4.1 V, when P3 undergoes only a slight symmetry reduction and distorts into the P3’ phase, which implies that 90.9% of the capacity contribution is extracted by the P-phase solid-solution reaction. This may also be the reason for its excellent rate performance. As a comparison, Na1 transiently transforms into a monoclinic O1 phase after the removal of 0.11 mol Na+, followed by a subsequent transition to the P3 phase as 0.13 mol Na+ is removed, the trend of the following phase transition is consistent with Na0.55. The O3-O1-P3 phase transition involves anisotropy and symmetry changes, and disorder during the phase transition not only reduces the Na+ transport kinetics, it also causes large interfacial energies and the accumulation of microcracks in the electrode material14,17. The high R-value feature puts Na0.55 itself in a preparatory state for the phase transition as its interlayer spacing is intrinsically high, with a rapid yet gentle O3-P3 phase transition (Supplementary Fig. 31), which was also observed in the in situ charge-discharge XRD of O3-Na0.65 (R = 1.841) (Supplementary Figs. 32 and 33).

Fig. 3: Dynamic phase structure and cell parameter evolution.
figure 3

Initial contour maps, charge-discharge curves of in situ XRD and corresponding lattice parameter changes of (a) Na0.55 and (b) Na1. c, d In situ XRD of Na.55 and Na1 at 1 C (120 mA g−1) rate. e, f In situ XRD of Na.55 and Na1 for two cycles at 5 C rate. After the first cycle, the O3 phase of Na1 disappears. g, h XRD refinement of Na0.55 and Na1 after 3 cycles at 5 C (600 mA g−1).

Full size image

The variations of the cell parameters during charging and discharging were obtained by XRD refinement. Na0.55 coexisted in the bi-phasic O3-P3 with a mismatch of Δa = 0.752%, Δc = 1.8%, and ΔV = 0.298%, whereas Na1 coexisted in the bi-phasic O1-P3 with a mismatch of Δa = 0.854%, Δc = 2.1%, and ΔV = 0.517%, indicating that the high R-value of Na0.55 reduces the degree of abrupt changes in lattice parameters during the phase transition, resulting in smaller internal stresses and interfacial energies within the electrode material. However, it should be noted that Na0.55 shows a similar rate of volume variation to Na1 throughout the whole Na+ extraction/insertion process (Na0.55, ΔV = −1.2% vs. Na1, ΔV = −1.28%). Charging-induced large overall variations in lattice parameters in the initial and final states have been considered as the main cause of disintegration of the electrode materials and decrease in electrochemical activity30,31. However, it was found that the transient changes in lattice parameters during the phase transition have a more important influence on the structural stability (Supplementary Fig. 34). Long cyclic stability tests were carried out for Na0.55, Na0.65, and Na1 at different potential intervals. As indicated by the in situ XRD results, the cutoff voltages up to 3.8 V, 4 V, and 4.2 V correspond to an overall increase in the rate of change of the lattice parameters. Na0.55, Na0.65, and Na1 showed similar capacity decay rates at different cutoff voltages, but at the same cutoff voltage, the capacity retention was proportional to the value of R (Supplementary Fig. 35). Supplementary Figs. 36 and 37 showed focused ion beam-scanning electron microscopy (SEM-FIB) images and XRD patterns of Na1 (2–3.8 V, 200 cycles) and Na0.55 (2–4.2 V, 200 cycles) after cycling under different conditions. Na0.55 exhibits a flat interface as well as a complete O3 phase structure over a wide voltage range. This confirms that the structural features of a high R-value promote the reversibility of the O3-P3 phase transition and moderate the instantaneous rate of change of the lattice parameter, which would inhibit the cathode cracking faults as well as the structural degradation to the Na-deficient phase.

High-rate charging and discharging introduce a larger electrode polarization and amplify the difficulty of the O3-P3 phase transition. In situ XRD was further utilized to monitor the structural evolution of Na0.55 and Na1 at high charge and discharge rates of 1 C (120 mA g−1) and 5 C (600 mA g−1) (Supplementary Fig. 38). Signals collected in the narrow 2 theta range around (003) diffraction indicate that Na0.55 can still undergo a reversible O3-P3 phase transition at 1 C (120 mA g−1) and 5 C (600 mA g−1) rates (Fig. 3c and e), and maintains 82.2% O3 phase and 17.8% P3 phase after 3 cycles under 5 C (600 mA g−1) (Fig. 3g). In contrast, in situ XRD showed that Na1 already showed a small fraction of irreversible P3 phase after the first cycle of discharge at 1 C (120 mA g−1) rate (Fig. 3d), and the O3 phase disappears after the first cycle at 5 C (600 mA g−1) rate (Fig. 3f). Specifically, XRD refinements showed only 5.2% of the pristine O3 phase was retained, and 94.8% was transformed into the P3 phase after 3 cycles at 5 C (600 mA g−1) rate (Fig. 3h).

The O3-P3 phase transition reversibility versus R-value relationship is further examined from the perspective of electrochemical responses. In situ charge/discharge EIS is an ideal tool to combine electrochemical performance with chemical composition and structure evolution analysis with high precision, while DRT can be used to isolate and resolve highly overlapping physicochemical processes in EIS32,33. We have obtained independent electrochemical and structural information of the cathode side by introducing reference electrodes into a single layer pouch cell to form a “three-electrode” test system (Supplementary Fig. 39). The in situ EIS of Na0.55 and Na1 in the second cycle were performed (Fig. 4a, b) and analyzed by the DRT technique (Fig. 4c, d). Based on the time constants, frequency ranges and the actual Na+ reaction processes33, the DRT peaks were assigned to five physical models, including contact ohmic resistance (τ1); Na+ transport through the solid electrolyte interface (CEI) layer on the cathode surface (τ2/τ3); charge transfer interfacial resistance (τ4, Rct), and solid-state diffusion of Na+ in bulk (τ5) (Fig. 4e)34,35,36. The appearance of τ2/τ3 suggests that Na0.55 and Na1 have generated CEI in the first cycle, and the gradual decrease in the impedance of the CEI layer to Na+ transport in the middle and at the end of the charging process suggests that partial decomposition of the CEI occurs at high potentials and recovers during the discharge process32. The τ4 peak of Na0.55 shifts to higher frequencies during charging with a rapidly decreasing peak, which is related to the rapid O3-P3 phase transition exhibited by Na0.55. Initially Rct acts as a major contributor to the total impedance, while the occurrence of the phase transition effectively improves the transport of Na+ at the P3 phase interface, leading to a weakening of the peak. The τ4 peak in Na1 exhibits a similar trend, but is accompanied by the appearance of τ4’ at the end of discharge. The appearance of the new Rct implies an irreversible O/P bi-phasic interface residue (Supplementary Fig. 40), which is difficult to be determined by XRD during a short period of time. The τ5 peak in Na0.55 also shows altered bulk phase transport due to phase structure changes, it has little effect on the overall peak, due to its high R-value feature that imparts fast bulk Na+ transport to the pristine O-phase structure. Compared with Na1, the high symmetry of τ4 and τ5 in the charging and discharging processes of Na0.55 implies the high reversibility of the structural phase transition process, which is consistent with the in situ XRD results.

Fig. 4: DRT and phase structure evolution.
figure 4

Kinetic and phase transition reversibility studies of Na0.55 and Na1 have been carried out using a pouch cell three-electrode system. In situ EIS of (a) Na0.55 and (b) Na1 during the second cycle. DRT curves for (c) Na0.55 and (d) Na1. e Physical meanings and schematic diagrams of the different peaks in the DRT curve.

Full size image

Cation migration behavior

The cation migration behavior under high R-value structural features is been further investigated. The migration behavior of Ni in the Na0.55 and Na1 structures was simulated using BVPA in initial model. The possibility of all migration paths of Ni in Na0.55 and Na1 and the top views are demonstrated in Fig. 5a–d. Overall, there are two main modes of Ni migration, one is vibrational migration from the equilibrium position within the TM layer, and the other is migration from the position of the TM layer 3a to the position of the Na layer interstitial tetrahedron 8a or the vicinity of the 3b position of the Na+. The denser shaded portion in Na1 compared to Na0.55 implies that Ni has more intralayer and interlayer migration tendencies. Figure 5e calculates that the migration energy barriers for Ni in the Na0.55 structure is 4.145 eV within the TM layer and 4.704 eV toward the interstitial tetrahedral 3b positions in the Na layer, which are significantly higher than those of 3.675 eV and 4.297 eV in Na1 (Fig. 5f).

Fig. 5: Cation migration pathways and energy barriers.
figure 5

Possible migration pathways for Ni in (a, c) Na0.55 and (b, d) Na1 structures (the yellow shaded area represent the migration pathways). e, f Migration energy barriers for Ni migration intralayer in Na0.55 and Na1 TM and to the interstitial tetrahedra of the Na layer. g, h Diagrams of cation migration in the Na0.55 and Na1 crystal structures. i Migration energy barrier distribution of cations in characteristic structures with different R-values. j Long-term discharge medium voltage retention of Na0.55, Na0.65, Na0.83, and Na1 in the voltage range of 2.0–4.2 V at 1 C (120 mA g−1) rate.

Full size image

The high R-value structure effectively inhibits cation migration behavior from three aspects, namely pre-migration, migration, and post-migration. A typical case for study is the migration of interstitial tetrahedral positions. Specifically, in Fig. 1g, the TM-O plate of Na0.55 contracts significantly, resulting in a substantial increase in the overlapped region and energy position of Ni/Fe 3 d eg*-O 2p orbitals. This implies an elevated bonding energy between Ni-O and Fe-O, boosting the migration energies of Fe and Ni, which reduces the likelihood of pre-migration. Secondly, the cation migration paths to the interstitial tetrahedra of the Na layer are the permeability network consisting of coplanar O in the Na-O-TM structure (labeled in red and green in Fig. 5g, h). The top-contracted O–O distance in Na0.55 (2.931 vs. 2.967 in Na1) and the reduced bottom tensor angle due to extreme stretching along the C-axis direction further narrow down the cation migration path from 3a-8a and increase its difficulty. Thirdly, the TM-O cannot achieve thermodynamically stable coordination by itself in such an extremely spiky tetrahedron, resulting in large bond angle tensions between chemical bonds and higher internal energies37. The above three aspects confirm that the high R-value structure is unfavorable for the whole cation migration process. Furthermore, Fig. 5i presents calculations indicating that the migration energy barrier distributions of Mn, Fe, Ni, and Li in Na0.55, Na0.65, Na0.83, and Na1 are all positively correlated with the R values (Supplementary Table 6), which is in agreement with our aforementioned analysis. Voltage decay has been identified as an important electrochemical signal for cation migration38,39, and Fig. 5j illustrates the voltage retentions of Na0.55, Na0.65, Na0.83, and Na1 over 200 cycles at 1 C (120 mA/g) rate are 96.5%,94.6%, 92.2%, and 91.8%, respectively. Additionally, the post-cycling Raman spectra of Na1 exhibit an attenuation in surface layered phase signals while those of Na0.55 remain almost unchanged (Supplementary Fig. 41). All these findings collectively demonstrate that a high R-value can inhibit the cation migration behavior.

Inference in mixed-phase structures

Based on the recognition of the favorable influence of high R-values on improving cyclic stability, a reevaluation has been conducted on the R-values within specific structures such as P2/O3 mixed-phase materials. As shown in Fig. 6a, an R-value above ~1.62 usually ensures a P2-type structure, while lower R-values promote the formation of O3 types21. Notably, the charge-discharge curves of P2/O3 mixed-phase materials exhibit a brief plateau during O3-P3 phase transition and confirm rapid yet smooth evolution of the O3 phase through in situ XRD results from other studies, aligning with features observed in O3-Na0.55, Na0.65 (Fig. 3a and Supplementary Fig. 32)40,41,42. A series of P2/O3 mixed-phase cathodes were prepared by adjusting the TM species and Na contents in the range of Na0.67 to Na0.83 (Fig. 6b), meanwhile we also extrapolated XRD patterns from previously published reports40,43,44,45. The lattice parameters of the P2 and O3 sub-structures in the mixed-phases were obtained using XRD refinement, and R-values were calculated accordingly. Interestingly, we observed that their O3 sub-phases already exhibited an R-value exceeding that of the conventional O3 phase. This finding suggests that the higher cycling stability observed in the P2/O3 hybrid phase is most likely attributed to these elevated R-values of O3 sub-phase rather than solely relying on the conventional “interlocking effect mechanism” between the P2 and O3 phases46.

Fig. 6: R values in typical P2, O3, and P2/O3 hybrid structures.
figure 6

a R-values of typical P2- and O3- type single-phase compounds. b R-values of P2 and O3 sub-structure among the numerous P2/O3 mixed-phase structures.

Full size image

Discussion

In summary, we have successfully designed O3-type cathodes across a broad range from Na0.55 to Na1 with R values far exceeding regular O3-type boundary conditions, and the impact of R-value (R = dO-Na-O/dO-TM-O) on their electrochemical properties, phase evolution, and cation migration behaviors were thoroughly investigated. The electrochemical performance of O3-Na0.55 with exceptionally high R-value demonstrates that the instantaneous rate for lattice parameter variation during the phase transition is a crucial determinant for cycling stability in O3-type materials. In situ XRD and in situ pouch cell three-electrode DRT tests verified that a high R-value facilitates an efficient preparatory stage for the subsequent O3-P3 phase transition, resulting in a rapid yet smooth phase transition process while reducing transient variations in lattice parameters as well as inhibiting cracking, faulting, and structural evolution towards Na-deficient phases. In addition, this high R-value feature strengthens the TM3d eg*-O2p orbital hybridization and deteriorates the cation migration path to the interstitial tetrahedra of the Na layer. Moreover, the R-value as a stability criterion parameter can be extended to P2/O3 mixed-phase structures, namely the higher R-value of O3 phase in the mixed-phase, the higher cycling stability. This work expands our understanding of how physical structure influences the stability of layered materials and provides new perspectives for modulating highly stable layered cathodes.

Methods

Materials synthesis

The Na0.55~1Mn0.4Ni0.3Fe0.15Li0.1Ti0.05O2 materials were synthesized by mixing desired amount of sodium carbonate anhydrous (99.5%, Macklin), Li2CO3 (99.99%, Macklin), Mn2O3 (98%, Macklin), nano-NiO (99.5%, Macklin), Fe2O3 (99%, Macklin), and TiO2 (99%, Macklin) thoroughly using planetary ball milling for 10 h at 500 rpm. Afterwards, the mixture was pressed into pellets and annealed in a tube furnace under air. The solid-state synthesis follows a two-step process, first, the furnace was heated to 500 °C with a ramping rate of 3 °C/min and kept isothermal for 2 h. Then, the furnace temperature was increased to 950 °C at the same ramping rate of 3 °C/min and kept for 10 h. Afterwards, the furnace was cooled down to room temperature with a rate of 5 °C/min. Before testing, they were ground thoroughly to crush the large chunks of particles. All samples were transferred to Ar atmosphere (glove box) immediately after sintering.

Characterizations

X-ray diffraction (XRD)

The powder XRD patterns were collected using a Rigaku Miniflex II XRD with Cu Kα radiation (λ = 1.5418 Å). Regular tests were conducted at a scan rate of 5°/min from 10° to 90°, the samples for Rietveld Refinements were measured at a scan rate of 1°/min from 10° to 90°.

In-situ XRD

The charge/discharge crystal structure information was collected using a designed in situ mold cell. The mold battery with holes for beam pass were used to make the in situ cell. The hole at the top cases of the mold battery were sealed with Kapton tape (Hefei Kejing, China) after cell assembly. The electrode had a mass loading of 13 mg/cm2, the in situ cell was rested for 3 h before doing in situ XRD. During the in situ experiment, LANHE Battery Tester was used to discharge/charge the cell using a constant rate of 24 mA/g between 2.0 and 4.2 V.

Scanning electron microscope (SEM)

SEM images were taken using ZEISS SUPRA55 scanning electron microscopy operating at 10 kV. Focused ion beam-scanning electron microscopy (FIB-SEM, Zeiss Crossbeam340) was applied to investigate cracks of the cycled electrodes.

X-ray photoelectron spectroscopy (XPS)

PHI 5000 Versa Probe X-ray photoelectron spectroscopy was used to analyze the chemical states of the chemical compositions.

Neutron powder diffraction and neutron pair distribution function (NPD and nPDF)

The NPD and nPDF were performed at the Multi-Physics Instrument with Q range of 1–50 Å−1, at the China Spallation Neutron Source. The detectors, which were divided into five banks (bank3 ~ bank7), were calibrated using a NIST-silicon powder standard prior to the measurements. The NPD and nPDF experiments were performed at 25 °C, where around 2.5 g of the sample were loaded in vanadium can separately and sealed under a Helium atmosphere, followed by placing the can into an automatic sample-changing device. Local structure analysis was performed using the PDFgui (v2.0.3) software. The nPDF data of samples were refined based on the least squares refinement method with a fitting range from 1.08 to 30 Å using the R-3m model. The instrumental parameters such as Qdamp and Qbroad were initially fixed (0.0039 and 0.035 Å−1) as obtained from the beamline calibration.

STEM

The samples were processed with focused ion beam (FIB) machining to achieve a thickness below 80 nm. The STEM images were captured using an aberration-corrected scanning transmission electron microscope (JEOL ARM 300) operated at 300 kV.

Laser particle size analyzer

The cathode powder was tested using a HORIBA-LA-960S2 instrument by taking 0.1 g of the test powder, wet aqueous dispersion, and sonication for 15 min.

Electrochemical measurements

The electrode was made by mixing the active material, Acetylene black (Hefei Kejing, China) and polyvinylidene fluoride (PVDF, 99%, Arkema) with a ratio of 85:7:8 dispersed in N-methyl-2-pyrrolidone (99%, Alfa Aesar) using a Thinky ARE350 mixer. The slurry was pasted onto Al foil and dried under 80 °C in a vacuum for 12 h. The active material loading was controlled to be around 8 mg/cm2. The electrode is rolled using a roller press (Hefei Kejing, China), the pressure value was set at 5 × 104N. The electrodes were assembled in a CR2032 coin cell in a glovebox filled with Argon gas (H2O < 0.1 ppm; O2 < 0.1 ppm), which consisted of a positive and negative stainless steel case, a single-coated cathode electrode, sodium foil, a separator (670 μm in thickness, Whatman), electrolyte, and two round stainless steel pieces. Na metal (Hefei Kejing, 99.7%) was used as the counter electrode. The Na metal is a commercial Na sheet with a thickness of 1 mm and a diameter of 15 mm. One hundred eighty microliter of electrolyte was added to ensure complete wetting of both electrodes. The electrolyte consisted of 1 M NaClO4 in Propylene carbonate (PC) with the addition of 5 vol.% fluoroethylene carbonate (FEC) (Dodochem, China). The charge/discharge data were collected between 2.0 and 4.2 V. The coin cells were tested using an LANHE Battery Tester (Wuhan, China). For the GITT measurements, the cells were charged at a current density of 0.1 C (0.1 C = 12 mA/g) for 15 min, followed by open circuit relaxation for 120 min. The in situ electrochemical impedance spectroscopy (EIS) experiments were executed using a EC-Lab electrochemical workstation (BioLogic, France) in a frequency range from 0.1 Hz to 100 KHz with an AC amplitude of 5 mV. EIS tests were performed after each potentiostatic intermittent titration technique program completed. The step potential difference was 0.1 V, and the step elapsed time was 3600 s. Each EIS test contains 30 data points. All the electrochemical tests were performed in a room with a controllable temperature of 25 °C.

Pouch cell three-electrode system

The electrode was made by mixing the Na0.55, Acetylene black and PVDF with a ratio of 92:6:2. For the anode side: Hard carbon (Kuraray, Japan), Acetylene black and PVDF with a ratio of 93:3:4, N/P ratio is controlled at ~1.1. Na3V2(PO4)3 as a reference electrode. Both Na0.55 electrode (5.7 × 7.7 cm, 9.11 mg/cm2 of active material) and hard carbon electrode (59 × 79 cm, 4.32 mg/cm2 of active material) were coated on one side, and a double-layer polypropylene (PP, 62 × 81 mm, Hefei Kejing, China) separator was selected between them, with the reference electrode located directly in the middle of the two layers. 1.0 M NaPF6 in PC:EC (1:1, v:v) containing 5% of FEC were used as the electrolyte. Tests were performed in the 1–4.1 V (vs. hard carbon) potential interval using the GITT program, and EIS was performed at the end of the resting period. Hard carbon negative electrode without pre sodiation treatment. Na1/hard carbon pouch cell three-electrode system was also prepared as described above. The reference electrode was made by mixing the Na3V2(PO4)3, Acetylene black and PVDF with a ratio of 85:7:8, coated on one side of aluminum foil with a loading of about 1.1 mg/cm2, vacuum dried in an oven at 80 °C for 8 h, and then cut into long strips of 0.8 × 5.5 cm, and preserved in a glove box.

DFT Calculation

The Vienna ab initio simulation package (VASP) was employed for all first-principle calculations, utilizing the projector augmented wave (PAW) method within the framework of Density Functional Theory (DFT)47. To account for the strong correlation effects of Mn, Ni, and Ti, the DFT calculations included the Hubbard U correction, with the U-J parameters set to 3.9, 6.2, 1.5, and 5.3 for Mn, Ni, Ti, and Fe ions, respectively. The calculations used a spin-polarized generalized gradient approximation (GGA) with the Perdew−Burke–Ernzerho (PBE) exchange−correlation functional48,49. A cutoff energy of 520 eV was chosen, and the convergence criteria for the total energy and the forces on each atom were set to 10−5 eV and 0.05 eV/Å, respectively. The Monkhorst–Pack scheme was used for k-point sampling in the Brillouin zone.