Introduction

Surface acoustic wave (SAW) devices underpin radio frequency electronics applications such as signal filtering because these devices can be simultaneously compact and inexpensive1. There is also significant interest in the use of SAW devices as highly sensitive gas sensors2 or biosensors3, with the possibility of direct integration into lab-on-a-chip platforms4. SAW devices also promise a large variety of intriguing nanoscale applications5 ranging from straintronics6 to quantum communication7,8,9. High-spatiotemporal-resolution characterization is critical for both application-driven and fundamental research in all of these applications. The transduction from electric energy to mechanical energy and vice versa in SAW devices is typically achieved with interdigital transducers (IDTs)10,11, which are two interlocking comb-shaped arrays of metallic electrodes on a crystalline piezoelectric substrate. One of the transducer electrodes is grounded while an oscillating voltage is applied to the other, resulting in a spatially and temporally periodic strain field near the surface of the piezoelectric crystal. The strain field propagates at speed in the range of a few km/s, forming an acoustic wave at the surface. The oscillation frequency of the SAW is in the hundreds of MHz to a few GHz range, and is typically too fast for direct imaging with state-of-the-art high speed scientific cameras12.

The mechanisms and magnitude of acoustic loss are critical in determining the performance of SAW devices13. Loss mechanisms are studied with electrical measurements by using the frequency response of the electrical parameters, most commonly the scattering S, impedance Z and admittance Y-parameters14,15. While highly sensitive to loss, those electrical parameters provide information only at the scale of the entire device and lack the spatial or temporal resolution necessary to understand the origins of the loss. Spatially resolved information can be acquired using scanning probe techniques with optical16,17, mechanical18 or x-ray19 probes. The spatial resolution of optical measurements is ultimately limited to hundreds of nanometers by the optical diffraction limit. Significant progress has been made recently on the quantitative extraction of the SAW amplitude through modeling and iterative fitting in mechanical measurements of SAWs using cantilevers20. Crucially however, the low resonance frequency of the cantilevers does not provide sufficient time resolution to create time-resolved images of SAWs operating at much higher frequencies. Response in the time domain can be further obtained by pump-probe imaging. In the special case of stroboscopic imaging, the excitation or pump signal is frequency-locked to the probe pulses. The stroboscopic scheme significantly improves the signal-to-noise ratio (SNR) in pump-probe imaging as it allows integration of millions of pulses on the detector, but requires a dynamic process that is reversible over the entire integration period. Stroboscopic optical21 and x-ray22,23 methods have been able to demonstrate a time resolution on the order of 100 ps, sufficient for studying SAW devices of as fast as 5 GHz at their Nyquist frequency. Direct observation of Rayleigh wave with micrometer spatial resolution using stroboscopic x-ray topography was first demonstrated four decades ago24. Stroboscopic scanning diffraction x-ray microscopy improved the spatial resolution to 25 nm, with a relatively small field of view (FoV) due to time spent on raster scans25. Other imaging approaches have included x-ray photoemission electron microscopy (PEEM). In one particular study, the strain in a 50 × 50 μm2 area was imaged using stroboscopic PEEM26. However, PEEM typically requires a conductive surface under ultra-high vacuum condition which limits its direct application on many commonly used piezoelectric substrates27. These state-of-the-art methods have shown a sensitivity to the surface displacement on the order of 100 pm16,18,19,21,22,23,25,26,27. X-ray diffraction methods have the potential for significantly higher sensitivity because they measure directly the acoustically induced strain waves. However, such higher sensitivity has not been realized due to the absence of necessary analytical techniques or data reduction methods.

We report the development of stroboscopic full field diffraction x-ray microscopy (s-FFDXM) and an associated wave decomposition analysis method that, together, achieve high-resolution high-throughput spatiotemporal imaging of the acoustically induced strain waves. The method has a strain sensitivity of  ~ 10−7, corresponding to a surface displacement of 1 pm, that is a factor of 100 times better than most existing methods. The high strain sensitivity was enabled by the high SNR of the stroboscopic scheme, and demonstrated thanks to the highly deterministic strain states in the SAW device. Measurements on a prototypical one-port SAW resonator reveal multiple mechanisms of acoustic loss with distinct spatial and time dependencies. Specifically, the strongest SAW amplitude was not observed at the anti-resonance frequency, despite electrical measurements confirming maximum impedance at this frequency. The imaging study reveals that this discrepancy arises from a non-uniform SAW excitation at the anti-resonance frequency, resulting in large and unanticipated side and end leakages. Parasitic excitation generated by the electric field between the tip of the IDT fingers and the opposite bus bar was also observed. The SAW amplitude associated with these loss mechanisms as well as several key device parameters were determined with quantitative analysis, allowing for their optimization in future designs.

Results

Stroboscopic strain imaging of surface acoustic waves

Figure 1 a shows a schematic of the s-FFDXM experiment. A single-port synchronous SAW resonator device28 was fabricated on a Y-cut LiNbO3 substrate with a design wavelength of λSAW = 10 μm and a design resonance frequency of 339 MHz. Applying an oscillating electric field between adjacent IDT fingers generated a series of SAWs propagating along the +Z and –Z crystalline direction. These SAWs were subsequently reflected by the gratings at the ends of the IDT array, leading to the formation of a standing wave in the resonator area.

Fig. 1: Stroboscopic full-field diffraction x-ray microscopy.
figure 1

a The surface acoustic wave excitation was electronically synchronized to the x-ray pulses with a tunable delay. A dark-field image was formed on a two-dimensional x-ray detector by projecting a magnified image of the diffracted beam using an x-ray objective lens. The white square outlines the area investigated in this work. Analysis of the dark field images acquired during a θ–2θ scan allowed visualization of the strain wave, as shown in (b) and (c). The reflector gratings and the two interdigital transducer electrodes appear in orange, red, and blue, respectively. b Instantaneous strain map for an excitation at 333 MHz showing the moment when the standing wave amplitude was at its minimum, one frame from Supplementary Movie 1. c Instantaneous strain map for an excitation at 342 MHz showing the moment when the standing wave amplitude was at its minimum, one frame from Supplementary Movie 2. Strong leakage into the bus bar area (X > 0) were observed.

Full size image

The excitation for the stroboscopic imaging experiments was synchronized to the x-ray pulses. A burst consisting of 64 periods of a sine waveform were generated with a repetition rate of 1.42 MHz (704 ns) and a peak-to-peak voltage of 3 V. The time-dependent response of the SAW device was studied by shifting the start time of the electrical burst with regard to the x-ray pulses using an electronic delay. At a fixed delay t, x-ray photons from different pulses probed the same time dependent event at time t after the start of the electrical signal. The temporal resolution of the technique is estimated to be 135 ps FWHM.

The SAW device was illuminated with a quasi-parallel x-ray beam with an incident convergence angle of 10−5 rad. The pseudo-cubic 300 reflection of the LiNbO3 substrate was chosen for the diffraction experiments. The intensity and wavevector of this reflection carry information about ϵyy, the strain tensor along the surface normal (Y) direction. The diffracted beam was collected by an objective lens to form a dark field image on the detector. The effective pixel size was 114 nm. An area of 250 × 250 μm2 was imaged with each detector acquisition, which allowed high-throughput strain imaging of multiple device areas simultaneously at various excitation frequencies as shown in Fig. 1b and c as well as in Supplementary Movies 1 and 2.

Stroboscopic x-ray diffraction microscopy observation of the resonance

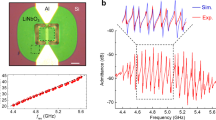
The device performance was first evaluated using the integrated s-FFDXM intensity. As explained in the Methods, the integrated intensity is proportional to the magnitude of the local curvature of the piezoelectric substrate, which is in turn proportional to the SAW amplitude29. Figure 2a shows the integrated s-FFDXM intensity from the resonator region as a function of SAW excitation frequency. A dip in the intensity at 339 MHz indicates on average a weaker SAW amplitude, which is expected as 339 MHz corresponds to the resonance frequency at which the device exhibits minimum impedance (maximum admittance in Supplementary Fig. 1). A peak in the intensity at 342 MHz indicates a higher SAW amplitude, which is also expected because 342 MHz is the anti-resonance frequency at which the device exhibits maximum impedance (minimum admittance in Supplementary Fig. 1). However, Fig. 2a indicates that the maximum SAW amplitude was instead observed at an off-resonance frequency of 333 MHz. A spatiotemporal analysis of the acoustic response of the device, below, reveals the origin of the s-FFDXM intensity maxima.

Fig. 2: s-FFDXM observation of SAW resonance.
figure 2

a Integrated stroboscopic full-field diffraction x-ray microscopy intensity from the resonator as a function of surface acoustic wave excitation frequency. The baseline with excitation was 1.7 × 108 photons measured at an excitation frequency of 350 MHz. The baseline without excitation was 1.1 × 108 photons. b Integrated stroboscopic full-field diffraction x-ray microscopy intensity as a function of the electronic delay t. The surface acoustic wave was excited with a burst of 64 periods of a sine waveform at 333 MHz. The start of the burst is at t = 0.

Full size image

Two-dimensional wave pattern in the resonator

The acoustic response of the SAW device was studied in detail at 333 MHz. As shown in Fig. 2b, the s-FFDXM intensity increased at the start of the burst at t = 0 ns and reached a maximum after 25 periods. The intensities then remained constant before decreasing after the end of the burst at t = 192 ns. Figure 3a shows the instantaneous strain map of the device at t = 144 ns, corresponding to the beginning of the 48th burst period. The color scale is centered at zero strain, such that brighter and darker shading indicate compressive and tensile strain, respectively. The maximum amplitude was 3 × 10−5. The strain values were determined using the center-of-mass analysis for 31 s-FFDXM images acquired during a θ-2θ x-ray scan. Details of the analysis are further described in the “Methods” section.

Fig. 3: Strain imaging of acoustic response at 333 MHz and 342 MHz.
figure 3

a Strain map of the surface acoustic wave device at t = 144 ns and an excitation frequency of 333 MHz. The resonator is at the lower left corner of the imaged area, in the region of positive Z and negative X. The top reflector occupies the region of negative Z and negative X. The bus bar is in the region with X  > 0. The scale bar is 50 μm. b Primary excitation from t = 141.6 to 144.6 ns. The X position at which the time-resolved data was extracted is indicated by the red arrow. The spatiotemporal strain map in (b) spans the same range in Z as the map in (a). c Parasitic excitation from t = 141.6 to 144.6 ns. The Z position at which the time-resolved data was extracted is indicated by the blue arrow. The spatiotemporal strain map in (c) shares the same X coordinates as (a). d Strain map of the surface acoustic wave device at t = 140 ns and an excitation frequency of 342 MHz. e Primary excitation from t = 140 to 143 ns. The X position at which the time-resolved data was extracted is indicated by the red arrow. The spatiotemporal strain map in (e) spans the same range in Z as the map in (d). f Parasitic excitation from t = 140 to 143 ns. The Z position at which the time-resolved data was extracted is indicated by the blue arrow. The spatiotemporal strain map in (f) spans the same range in X as the map in (d).

Full size image

The strain map in Fig. 3a reveals a two-dimensional wave pattern in the resonator area. Supplementary Fig. 2 shows the Fourier transform of the two-dimensional wave pattern. The strain amplitude had a spatial period of 10.0 ± 0.06 μm along the Z direction. We refer to this modulation as the primary excitation because both the direction of the modulation and its spatial period match the designed acoustic response of the device. A modulation of the strain amplitude along the X direction was not intended in the design and is referred to as the parasitic excitation. At 11.06 ± 0.11 μm, the spatial period of the parasitic excitation was 10.6% larger than what was observed for the primary excitation, the cause of which is further explored below.

End leakage of the primary excitation

Figure 3 b shows the spatiotemporal strain evolution of the primary excitation wave. Information in the time domain was acquired by combining strain maps (given in Supplementary Movie 3) that were measured at 11 evenly spaced delay values spanning the 3 ns period of the 48th acoustic burst excitation. The contribution of the parasitic excitation was suppressed in Fig. 3b by averaging the strain over one spatial period along the X direction. A propagating wave was observed in the reflector area at Z < 0. With increasing t, the peaks and valleys of the strain wave were shifted to smaller Z values, indicating that the observed propagating wave was in fact end leakage into the reflector area traveling in the –Z direction.

Away from the reflector, at Z > 50 μm, a standing wave pattern was observed in the resonator area. The positions of the IDT electrodes and reflector gratings were determined using methods described in Supplementary Fig. 3, and are schematically shown in Fig. 4a. The nodes (i.e., with minimum strain amplitude) of the standing wave were centered on the IDT electrodes, while the anti-nodes (i.e., with maximum strain amplitude) were located equidistant from two adjacent IDT electrodes. The position of the nodes and anti-nodes confirms that the primary excitation was the designed acoustic response of the device, which operated at the entrance of the stop-band for the Rayleigh wave in the electrodes grating.

Fig. 4: Results of the wave decomposition analysis at 333 MHz.
figure 4

a Spatiotemporal strain map of the primary excitation in the region near X = − 100 μm from t = 141.6 to 144.6 ns. The positions of the reflector gratings are marked in orange. The positions of the interdigital transducer electrodes are marked in blue and red. The spatiotemporal strain map for individual wave components ψz+, ψz− and ψt are shown. The sum of these contributions is shown in the sub-panel labeled FIT. The sub-panel labeled EXP is the experimental spatiotemporal strain map previously shown in Fig. 3b, for comparison. b Spatiotemporal strain maps for individual wave components ψx+ and ψx− of the parasitic excitation in the region near Z = 30 μm from t = 141.6 to 144.6 ns. The sum of these contributions is shown in the sub-panel labeled FIT. The sub-panel labeled EXP is the experimental spatiotemporal strain map previously shown in Fig. 3c, for comparison. The colormap is rescaled from Fig. 3c to improve the visibility of the weak wave amplitudes.

Full size image

Wave decomposition analysis was performed on the primary excitation by fitting the strain amplitude of a wave model to the experimentally observed spatiotemporal strain evolution. Procedures for the fitting as well as descriptions of the wave model are listed in the “Methods” section. Figure 4a shows the best fit result of the wave model, in excellent agreement with the experimental data shown in Fig. 3b. At Z <  100 μm, the spatiotemporal strain evolution matches, as expected, the superposition of two waves, ψz+, the wave traveling in the +Z direction and ψz−, the wave traveling in the –Z direction. In the resonator area (Z > 0), the maximum amplitude of ψz− was 40% stronger than for ψz+. In the top reflector area (Z < 0), the amplitude of the reflected wave ψz+ was negligible, which indicated a low reflectivity of the grating at 333 MHz. Similarly, the amplitude of the transmitted wave ψz− was high into the reflector area, signifying a substantial end leakage.

The model consisting of only two traveling waves did not explain the spatiotemporal strain evolution in the lower part of the resonator at Z > 100 μm. Matching the superposition of ψz− and ψz+ with the spatiotemporal strain evolution in Fig. 3b revealed the presence of a third wave component ψt. As shown in Fig. 4a, ψt oscillated in time at twice the frequency of the electrical burst excitation. The maximum amplitude of ψt was observed when the amplitude of the applied electric field was maximized, regardless of the voltage polarity. Additionally, the amplitude of ψt did not exhibit a periodic oscillation in space, indicating that it was not caused by higher harmonics generation. Further evidence supporting the existence of ψt can be found in Supplementary Fig. 4.

Origin of the parasitic excitation

Figure 3 c shows the spatiotemporal strain evolution of the parasitic excitation wave. The contribution of the primary excitation to the map in Fig. 3c was suppressed by averaging the strain over one spatial period along the Z direction. The strain amplitude of the parasitic wave was a factor of ten weaker than the primary wave, which explained the lower strain amplitude observed in Fig. 3c. The spatiotemporal strain evolution of the parasitic excitation wave can be described by the superposition of two waves, ψx+ traveling in the +X direction and ψx− traveling in the –X direction. Their summed amplitude, shown in Fig. 4b, is an excellent match for the experimental data in Fig. 3c. A standing wave pattern was observed in the resonator area for X < 0, while a pure propagating wave was observed in the bus bar area for X > 0. With increasing t, the peaks and valleys of the propagating wave were shifted to larger X values. This indicates that the observed propagating wave was in fact side leakage into the bus bar area traveling in the +X direction.

The wave decomposition in Fig. 4b shows that at any given time t, ψx+ and ψx− were in phase at X = 0, leading to the conclusion that the source of the parasitic excitation was at the boundary separating the resonator and the bus bar. The maximum strain amplitude of both ψx− and ψx+ were found at X = 0, which further supports this explanation. At X > 0, the strain amplitude of ψx+ decreased as the wave propagated further away from its source of origin. The part of ψx+ at X < 0 was generated at the other boundary located on the other side of the resonator at X = −300 μm, its strain amplitude also decreasing as the wave propagated further away from its source of origin. We hypothesize that the parasitic excitation was generated by the electric field between the tip of one IDT finger and the opposite bus bar, as illustrated in Supplementary Fig. 5a. The generation of the parasitic wave via this mechanism explains the much weaker amplitude of the parasitic excitation compared to the primary excitation because there were much fewer electrodes for generating ψx± than for generating ψz±.

Having established the direction in which the parasitic excitation wave propagates, we can now explain the 10.6% larger modulation period compared to the primary excitation. The period of the modulation is proportional to the velocity of the SAW, which varies along different crystallographic directions due to anisotropic elasticity30. The ratio of observed modulation period is consistent with previous pulse inference measurements which indicated that the SAW velocity along the X direction is 12% faster than along the Z direction31.

Acoustic response at the anti-resonance frequency

The acoustic response of the SAW device was also studied at the anti-resonance frequency of 342 MHz, as shown in Supplementary Movie 4. Figure 3d shows an instantaneous strain map of the device at t = 140 ns, corresponding to the beginning of the 48th burst period at 342 MHz. The strain map at the anti-resonance differs from the previous map at 333 MHz in several ways. First, a less uniform distribution of the SAW amplitude was observed in the resonator area at 342 MHz compared to 333 MHz. The SAW amplitude was much stronger in the narrow area within 40 μm from the bus bar than in the rest of the resonator. Second, standing waves were observed in the reflector area, as evident from the spatiotemporal strain evolution shown in Fig. 3e at Z < 0. The presence of standing waves indicates more propagating waves were reflected back by the grating, which is indicative of a high reflectivity of the reflector grating at 342 MHz. Third, and most importantly, Fig. 3d shows a much stronger wave propagating into the bus bar area. The leakage into the bus bar area consists of mainly the primary excitation, which are waves with a spatial periodicity along the Z direction. The amplitude of the parasitic excitation (i.e., waves with a spatial periodicity along the X direction) was actually weaker than at 333 MHz, as is evident from the spatiotemporal strain map shown in Fig. 3f.

Quantitative comparison of the wave excitation

The results of the wave decomposition analysis for excitation frequencies of 333 and 342 MHz are shown in Fig. 5. The spatially resolved strain amplitudes, extracted individually for each wave component, allowed a quantitative comparison of the relative strength of the side and end leakages, as well as the determination of key device parameters such as the standing wave ratio (SWR) and the grating reflectivity.

Fig. 5: Amplitude map of the wave components at 333 and 342 MHz.
figure 5

Strain amplitude map at 333 MHz for (a) ψz−, (b) ψz+, (c) ψt, (d) ψx− and (e) ψx+. Strain amplitude map at 342 MHz for (f) ψz−, (g) ψz+, (h) ψt, (i) ψx− and (j) ψx+. The color scale presented in each column applies to both 333 MHz and 342 MHz. The imaged areas are the same as in Fig. 3a and d. The boundaries separating the resonator, reflector and bus bar are marked with dashed lines. The scale bar is 50 μm.

Full size image

At 333 MHz, a standing wave with uniformly distributed amplitude was formed by the two primary wave components ψz− (Fig. 5a) and ψz+ (Fig. 5b) in the resonator area. An amplitude mismatch was observed between ψz− and ψz+. The device level SWR was 6:1, calculated using averaged values of the wave amplitude over the observable resonator area. The reflectivity of the top grating was 12 ± 2%, calculated using the amplitude ratio in the reflector area between the transmitted wave ψz− and reflected wave ψz+. A low reflectivity was expected at 333 MHz due to the synchronous design of the resonators, where the same periodicity was used for both the reflector and transducer electrodes. The experimentally determined reflectivity was in good agreement with our finite element modeling which predicted a reflectivity of 10% at 333 MHz. We further note that the grating reflectivity cannot be directly measured with electrical methods. The maximum amplitude of ψt was a factor of 3 times weaker than ψz±. From Fig. 5c, we confirm that ψt was only found at the bottom part of the resonator. Although the maximum wave amplitude of ψx− (Fig. 5d) and ψx+ (Fig. 5e) were a factor of 2 smaller than ψt, the parasitic excitations ψx± were apparently responsible for higher loss compared to ψt due to their presence in a larger area of the device.

At 342 MHz, the maximum wave amplitude of the primary excitations was 11% higher than at 333 MHz. However, a SAW with strong wave amplitude was only observed in a narrowly confined area within 40 μm from the boundary separating the resonator and the bus bar. As a result, the area averaged SAW amplitude in the resonator was actually 20% weaker at 342 MHz than at 333 MHz, consistent with the observed s-FFDXM intensity difference in Fig. 2a. The calculated device level SWR of 6:1 at 342 MHz was the same as at 333 MHz. The persistently low SWR value at the device level indicates that a true standing wave was not achievable in the resonator area under continuous excitations. A higher SAW amplitude was observed in the reflector at 342 MHz. The maximum strain amplitude of the end leakage ψz− (Fig. 5f, reflector area) was a factor of 3 higher at 342 MHz than at 333 MHz. The substantial end leakage observed at 342 MHz was despite a high reflectivity of the grating, measured at 38 ± 11% using the amplitude of the transmitted save ψz− and reflected wave ψz+ (Fig. 5g, reflector area). The experimentally determined reflectivity was in reasonable agreement with our finite element modeling which predicted a reflectivity of 50% at 342 MHz. A substantial amount of side leakage was also observed. The leaked primary excitation ψz− propagated in the +X direction into the bus bar, to a distance more than 5 times further at 342 MHz than at 333 MHz. The wave amplitude for ψt (Fig. 5h) and for the parasitic excitations ψx− (Fig. 5i) and ψx+ (Fig. 5j) were actually weaker at 342 MHz than at 333 MHz, which is understandable as the device was designed to operate close to 342 MHz.

Discussion

In this work, we have studied, in operando, the loss mechanisms in a single-port surface acoustic wave resonator device using stroboscopic full field diffraction x-ray microscopy. The integrated s-FFDXM intensities were proportional to the SAW amplitude, which indicated the presence of a stronger SAW in the resonator at an off-resonance frequency of 333 MHz instead of at the expected frequency of 342 MHz. Detailed spatiotemporal analysis showed that much of the SAW excited at 342 MHz was narrowly confined within 40 μm from the edge of the resonator. The non-uniformity of the excited SAW led to substantial side and end leakage. For comparison, a standing wave with uniformly distributed amplitude was excited at 333 MHz. The result is the observation of a more efficient electrical-to-mechanical energy conversion at 333 MHz in spite that the IDTs (higher maximum strain amplitude) and the gratings (higher reflectivity) were optimized for 342 MHz. The discrepancy between the electrical and s-FFDXM measurement highlights the importance of temporally and spatially resolved technique for SAW device characterization. Additionally, we have discovered acoustic loss in modes described above by ψt, ψx− and ψx+ using wave decomposition analysis. The origin of ψt is unknown. Although the doubled oscillation frequency in time and the absence of oscillation in space indicate that ψt could be related to Joule heating, the temperature oscillation at the surface of LiNbO3 would not keep up with the high frequency input, due to its finite heat capacity and low thermal conductivity. To reach a thermal time constant of 1.6 ns (666 MHz) would require an ultra thin slab of LiNbO3 of 70 nm thick (assuming a thermal diffusivity of 3 × 10−7 m2 s−132), which is two orders of magnitude smaller than the penetration depth of the SAW or the x-ray. Both ψx− and ψx+ were generated by the electric field between the tip of one IDT finger and the opposite bus bar. We note that the parasitic excitation is different from the transverse modes reported in SAW resonators33. The transverse modes arise from the diffraction of the surface wave propagating underneath the electrodes, with a characteristic wavelength that is typically one order of magnitude larger than what was observed with s-FFDXM. The discovery and quantitative understanding of this parasitic excitation is crucial to its mitigation through design optimization34. We have illustrated in Supplementary Fig. 5b an example that uses dummy electrodes and a tilted transducer design to suppress the propagation of the parasitic waves by preventing their coherent excitation.

s-FFDXM in this work has demonstrated a high strain sensitivity. In the “Methods” section we have estimated the strain sensitivity of our technique to be on the order of 10−7. The high sensitivity was attributed to a combination of many factors. Matching the penetration depths of the x-ray probe and the excited SAW led to a suppression of the diffraction signal from the unstrained bulk LiNbO3. As is shown in Supplementary Fig. 6, the instrument broadening of the Bragg reflection and low uncertainty due to high photon count rate further allowed precise determination of the peak shifts at far below the angular step size of the measurement. The high strain sensitivity is essential for the observation of weak acoustic losses. As shown in Supplementary Fig. 7, for a device with a period of λSAW = 10 μm, the penetration depths of both the SAW and the x-ray are about 10 μm. A SAW induced strain of 10−7 in this case corresponds to a surface displacement of 1 pm (see Supplementary Fig. 8), which is about 100 times smaller than the detection limit of most x-ray and optical methods16,18,21,22,23,25. More importantly, s-FFDXM measures the depth-averaged strain which is complementary to the surface strain determined by stroboscopic-PEEM26,27. As shown in Supplementary Fig. 7b, it is possible to further tune the depth-sensitivity of s-FFDXM by changing the photon energy and the choice of reflection thanks to the exponential depth-dependence of the x-ray attenuation. The wave decomposition analysis developed in this work is critical to the identification of unknown loss mechanisms. Residual analysis of the fitted model was essential to revealing the acoustic loss ψt in the resonator area. Conventional loss analysis considered the wave amplitude, and are mostly sensitive to leakage out of the resonator area35,36. The detection of loss within the resonator area is difficult because the observed wave amplitude is typically dominated by the much stronger primary excitation. Fourier analysis can reveal weak loss overlapping with the strong primary excitation, but only works if the loss oscillates in space at a multiple of the fundamental frequency37. In comparison, the residual analysis used in this work detects loss with any spatial and temporal dependence.

s-FFDXM complements electrical characterization by offering a high-resolution spatiotemporal strain imaging method for the quantitative discovery of loss mechanisms. Beyond the system investigated in this work, s-FFDXM is generally applicable to the imaging of dynamic strain modulation in other nanoscale acoustic5, electronic6, optical38 and quantum7 solid-state devices. With a wide FoV of 250 × 250 μm2 and a typical exposure time of a second, s-FFDXM allows high-throughput and concurrent characterizations of multiple device regions exhibiting diverse spatiotemporal behavior. The time resolution of 135 ps is sufficient for studying devices of up to 3 GHz at their Nyquist frequency. The ultimate time resolution is below 100 fs if performed at a free electron laser facility39. The spatial resolution is 200 nm for the compound refractive lenses used in this work and can be potentially improved to below 50 nm with the use of high numerical aperture diffractive lenses40. The high spatiotemporal resolution and high strain sensitivity would, for instance, allow operando imaging of Bragg-type phononic crystals with a lattice parameter of 50 nm, corresponding to the manipulation of high-frequency phonons in the 100 GHz regime41.

Methods

Surface acoustic wave device fabrication

Black Y-cut LiNbO3 wafers were immersed in Caro’s acid (H2SO4:H2O2 9:1) for 10 min and then rinsed in deionized (DI) water at 80 °C. The wafers were then immersed in an RCA surface clean 1 solution, H2O2:NH4OH:H2O, for 10 min at 70 °C before a second rinsing in DI water at 80 °C, followed by a quick dump rinse and drying. A uniform aluminum-silicon (Al0.98Si0.02) alloy layer with a thickness of 100 nm was deposited using sputter deposition. Bis-trimethylsilyl-amine was used to promote the adhesion of photoresist (UV4, 450 nm) on the Al0.98Si0.02. After spin coating, the photoresist was baked at 130 °C for 120 s. A deep-ultraviolet (UV) mask aligner was used in hard contact mode for pattern exposure. A post-exposure bake was then performed at 130 °C for 60 s, before development for 15 s in AZ-326MIF and rinsing in DI water and drying. The Al0.98Si0.02 was wet-etched in a commercial aluminum etch solution for 195 s, before stripping the photoresist in acetone. The wafers were rinsed in alcohol, then in DI water, and dried.

A single-port SAW resonator design was realized, with one IDT placed between two reflective gratings. The IDT consists in an array of 51 interdigital electrodes aligned perpendicular to the main flat of the Y-cut LiNbO3 wafer to allow propagation along the Z axis. On each side of the resonator area, there are two bus bars. These bus bars are metal strips that connect the interdigital electrodes to a common electric potential. The labeling of the directions follows the IEEE convention, with X, Y, Z corresponding to respectively the [110], [100] and [001] crystallographic direction42. The crystallographic orientation of the sample was also verified with pole figure measurements. The two gratings, or reflectors, are each made of 50 shorted Al0.98Si0.02 fingers. All the fingers are exactly 100 nm thick and 2.6 μm wide, with a pitch size of 5 μm. Assuming a SAW velocity of ~3.4 km/s43, the central resonance frequency is expected at about 340 MHz.

The functionality of the resonators was first checked with on-wafer measurements using Ground-Signal-Ground Probes connected to an Agilent N5230A vector network analyzer (VNA). The impedance of the device was 25 Ω. The LiNbO3 wafer was then diced into small chips containing individual SAW devices, which were subsequently glued on a Printed Circuit Board (PCB) and wire-bonded. The functionality of the SAW devices was checked again with the VNA to ensure that the wire-bonds and the PCB did not significantly affect the electrical response.

Stroboscopic full-field diffraction x-ray microscopy

Stroboscopic full-field diffraction x-ray microscopy experiment was performed at the ID01 beamline of the European synchrotron (ESRF)44. The photon energy was 8 keV. The SAW device was illuminated with a quasi-parallel x-ray beam with a convergent angle of about 10−5 rad. The pseudo-cubic 300 reflection of LiNbO3 was chosen with an incident angle of 31.4º and a 2θ angle of 62.8°. The specular reflection allows unambiguous access to the atomic displacements in the direction of the surface normal (Y direction in Fig. 1). The diffracted beam was imaged with an objective lens consisting of 50 Be compound refractive lenses (CRLs) with 50 μm apex radius of curvature45. The sample-to-lens distance was 114 mm. An Andor Zyla 4.2 sCMOS camera with 6.5 μm pixel size, mounted behind 15 μm of Gadox scintillator, was placed at 6.4 m downstream the objective lens46. The effective pixel size was 114 nm in the (v)ertical direction and 202 nm in the (h)orizontal direction. The elongation in the horizontal direction was caused by image projection along the exit wave direction. As shown in Supplementary Fig. 9, the spatial resolution using the Be CRLs is around 200 nm and can be improved to below 50 nm using high numerical aperture diffractive lenses40. With each acquisition, a dark-field image of the sample is obtained, corresponding to a field of view of 250(h) × 250(v) μm2. We note that the FFDXM setup at the ID01 beamline47 is conceptually similar to the Dark Field X-ray Microscope (DFXM) setup at the ID06 (now ID03) beamline of the ESRF48.

In the 4-bunch operation mode, four evenly spaced electron bunches circulate in the storage ring. A delay generator (BCDU8) converts the 352 MHz radial frequency signal from the storage ring to a synchronized 1.42 MHz signal used to trigger the acoustic devices. 1.42 MHz is known as the bunch clock frequency as it corresponds to the frequency of the electron bunches generating the x-ray pulses. Stroboscopic imaging is accomplished by adjusting the electronic delay added to the trigger signal, which can move in fine steps of 11 ps. The temporal resolution of the technique is estimated to be 135 ps FWHM, given by the convolution between the x-ray pulse width, at 100 ps FWHM49, the temporal jitter of the delay generator, at 30 ps FWHM, and of the waveform generator, at 85 ps FWHM. For an exposure time of 1 sec, for example, the detector accumulates diffraction signals from more than a million x-ray pulses. But because of the synchronization, all these x-ray pulses would probe the exact same snapshot of the device in time. The excitation signal applied to the SAW devices was generated using a Keysight 81160A signal generator.

At a given delay, θ-2θ scan was performed by simultaneously moving the sample incident angle by Δθ, and both the objective lens and detector by 2Δθ. For all the θ-2θ scans described in this work, the step size was Δθ = 0.001°. A dark field image of the sample was acquired for each acquisition with a typical exposure time of 2.5 s.

The SAW device is designed to generate Rayleigh waves, which are evanescent waves propagating primarily near the surface50. The amplitude of the SAW decreases exponentially as a function of depth, confining the elastic energy approximately within a depth of one SAW wavelength51. The atomic displacement in the Y direction at a depth of 10 μm is about 1/5 of the atomic displacement at the surface level52. The depth sensitivity of s-FFDXM probe also follows an exponential decay, owing to the absorption of x-rays entering and exiting the crystal. The conditions in our setup were tuned such that the absorption corrected x-ray intensity per unit volume decreased to 1/5 for a depth of 10 μm leading to a coincidence of the probed depth and the active depth of the SAW.

Integrated intensity as an indicator for the SAW amplitude

The presence of SAW induces local bending at the surface. For a crystal with a narrow x-ray rocking curve such as LiNbO3, bending leads to an increase in the diffracted intensity due to the broadening of the angular acceptance of the reflection53. For weak bending, the integrated intensity I is inversely proportional to the radius of curvature R54,55. The equation is simplified in the current case of co-planar Bragg diffraction,

$$I\propto \frac{1}{R}\exp \left(\frac{-2\mu t}{\sin \theta }\right),$$
(1)

where μ is the linear attenuation coefficient, t is the thickness of the bent crystal, and θ is the incident angle. For a SAW with a period of λSAW, traveling in the Z direction (see Supplementary Fig. 10), the local radius of curvature is inversely proportional to the maximum out-of-plane displacement Δy, following

$$\frac{1}{R}\approx \frac{32\Delta y}{{\lambda }_{{{{\rm{SAW}}}}}^{2}}.$$
(2)

Because Δy itself is proportional to the maximum strain amplitude Δa/a, we have thus

$$I\propto \frac{\Delta a}{a}.$$
(3)

We shall also evaluate the validity of the weak bending assumption in our case. For a maximum out-of-plane displacement Δy of 10 pm, every 5 μm length of surface is bent at a radius of curvature of R = 3 mm. This results in a deformation parameter β of about 0.5 μm−1 with

$$\beta=\frac{2}{R\delta }.$$
(4)

Here, the Darwin width δ equals 14 μrad. The extinction length Λ is 4 μm. The assumption of weak bending is thus valid in our case with βΛ ~ 1. We note that even in the strong bending case (βΛ > > 1), the diffraction intensity still remains as a good indicator for the SAW amplitude albeit at an non-linear dependence56.

Wave model for the SAW device

The SAW device is designed to generate a standing wave in the resonator area, achieving by reflecting and adding together two waves propagating respectively in the –Z and +Z direction.

$${\psi }_{z-}(z,t)={A}_{z-}\sin ({k}_{z}(z-{z}_{0})+\omega (t-{t}_{0})),$$
(5)
$${\psi }_{z+}(z,t)={A}_{z+}\sin ({k}_{z}(z-{z}_{0})-\omega (t-{t}_{0})).$$
(6)

Here, Az− and Az+ are the amplitudes of the two waves. kz is the spatial frequency and z0 is the spatial phase. The expected value for kz is 2π/λSAW, where λSAW is the acoustic wavelength. ω is the temporal (angular) frequency and t0 is the temporal phase. The expected value for ω is 2πfSAW where fSAW is the frequency of the burst excitation.

Fitting ψz− + ψz+ to some parts of the experimental data results in a residual term that is best described as

$${\psi }_{t}(t)={A}_{t}\cos (2\omega (t-{t}_{0})).$$
(7)

At is the amplitude. The residual term does not oscillate along the Z direction, which explains the absence of the spatial frequency parameter in the equation. It is also in phase temporally with the two propagating wave, as it can be fitted with the same parameters ω and t0.

The parasitic wave is also a standing wave, formed by adding together two waves propagating in opposite directions (–X and +X)

$${\psi }_{x-}(x,t)={A}_{x-}\sin ({k}_{x}(x-{x}_{0})+\omega (t-{t}_{1})),$$
(8)
$${\psi }_{x+}(x,t)={A}_{x+}\sin ({k}_{x}(x-{x}_{0})-\omega (t-{t}_{1})).$$
(9)

Here, Ax− and Ax+ are the amplitudes of the two waves. kx is the spatial frequency specific for the parasitic waves and x0 is the spatial phase. The expected value for kx is 2π/λPar, where λPar is the period of the parasitic wave at about 11 μm. ω is the time (angular) frequency and t1 is the temporal phase. ω is the same as for ψx−, ψx+, ψz−, ψz+ and ψt, which confirms the source generator being the one single origin for all the waves described in this model.

The standing wave ratio was calculated as the sum of the averaged amplitude of the two traveling wave \(\overline{{A}_{z-}}+\overline{{A}_{z+}}\) divided by their difference \(\overline{{A}_{z-}}-\overline{{A}_{z+}}\). The average was performed over the observable resonator area. This value was intended as an indicator of the amplitude mismatch on the device level between ψz− and ψz+, which takes into account both propagation loss as the wave travels in opposite directions and the reflectivity of the two gratings.

Procedures for the wave decomposition analysis

A 4D dataset was acquired at each frequency. The four dimensions are respectively the Z, X positions on the sample, the angular setting of the θ–2θ scan, and the delay time. For a given delay, the 31 dark field images of the same θ–2θ scan were first aligned using a shift correction algorithm. This corrects for the shift of the sample in the FoV, primarily in the X direction, due to an imperfect alignment of the center of rotation axis. Next, a single strain value was calculated for each aligned sample position, and for each delay value, based on the center of mass 2θ position using the weighted sum technique. This step reduces the 4D data into three dimensions.

The spatially resolved and time dependent strain variation was analyzed using the wave model described in the previous section. For the analysis of the primary wave with a modulation along the Z direction, the data was first convoluted in the X direction over one period of the parasitic wave. Least square fitting of the parameters was performed simultaneously on a series of sample points within a sliding window in the Z direction. The size of the sliding window was arbitrary, but was never smaller than 88 pixels which is the size of one acoustic wavelength (10 μm). The fitting was performed in an iterative manner. The z0 and t0 parameters were first fitted, then again together with k and ω. The parameters A0, A1 and A2 were the last to be fitted. And the fitting starts again with z0 and t0 until a good agreement was reached. The fitting window then slides by 1 pixel in the Z direction to initiate fitting on the next sample location. For the analysis of the parasitic wave with a modulation along the X direction, the data was first convoluted in the Z direction over one period of the primary wave. The fitting procedure is otherwise very similar to what was described for the primary excitation.

Strain sensitivity of s-FFDXM

X-ray diffraction typically has a strain resolution of 10−5, as limited by many factors including the energy bandwidth, beam convergence, motor resolution, detector pixel size and detector distance. The strain resolution is generally thought to be worse when combining an objective lens with a pre-focused incident beam, because x-rays originated from the same sample position but corresponding to slightly different diffracted angles are collected by the lens to form a single pixel on the dark field images. The result is a broadening of the diffraction peak which can be observed on the θ–2θ scan profile shown in Supplementary Fig. 6. This seems to be in contradiction with the strain resolution reported in this work. For instance, a strain amplitude on the order of 10−6 was reported in Fig. 4b. Below we discuss some of the main factors that have contributed to the high strain sensitivity of this work and attempt to evaluate the uncertainty of the determined strain value.

As stated before, the penetration depth of the s-FFDXM probe matches the penetration depth of the evanescent SAW. Consequently, only diffraction from the acoustically strained portion of the LiNbO3 substrate was measured. In the absence of the diffraction peak from the unstrained portion of the substrate, each θ-2θ scan profile in Supplementary Fig. 6 contains one single peak, which can then be fitted to a Gaussian line shape (Supplementary Fig. 11a). Performing Gaussian fitting independently for 4 million detector pixels and at 11 different time delays can be computationally expensive. Instead, the 2θ positions in this work were determined using the center of mass calculations. Supplementary Fig. 11b shows the 2θ positions determined with least square Gaussian fitting and with center of mass calculations, for 880 pixels spanning 100 μm in the Z direction at a fixed time delay. The calculated values are in good agreement with each other. Because of the good agreement, we can substitute the uncertainty from the least square fits for the uncertainty from the center of mass calculation, as the latter is not straightforward to evaluate.

To evaluate the uncertainty from the least square fits, we adopt the boot strap method57. For each θ-2θ scan profile, 100 sets of synthetic data were generated by adding residuals randomly picked from the least square fits, and then optimized using the same algorithm as used on the actual data. Supplementary Fig. 11c shows a histogram of the uncertainty for the fit 2θ value, obtained after performing the bootstrap methods on the θ–2θ scan profiles of the 880 pixels mentioned above. The uncertainty for the fit 2θ value, σ2θ, is about 10−7 rad for a confidence level of 95.44% at 2σ. We note that the uncertainty for the determined 2θ shift, σΔ2θ has the same value, as σ2θ = σΔ2θ.

The measured strain is directly related to the 2θ shift Δ2θ by

$${{{\rm{strain}}}}=\frac{\Delta a}{a}=-\frac{\Delta q}{q}=-\frac{\Delta 2\theta }{2\tan \frac{2\theta }{2}}\approx -0.82\times \Delta 2\theta$$
(10)

Here, a is lattice parameter of LiNbO3 along the Y direction. q is the momentum transfer of the 300 reflection. The uncertainty of the determined strain σstrain is thus related to the uncertainty of the 2θ shift σΔ2θ by the same relationship

$${\sigma }_{{{{\rm{strain}}}}}\approx -0.82\times {\sigma }_{\Delta 2\theta }\approx 1{0}^{-7}$$
(11)

An uncertainty on the order of 10−7 could explain why leaked SAW with a strain amplitude on the order of 10−6 could be accurately imaged with s-FFDXM. Interestingly, had the Bragg peak measured with the θ-2θ scans not been broadened and has, for instance, a FWHM of less than one angular step or 0.002°, the Gaussian fitting or the center of mass calculation would have been much less accurate. In a way, the pre-focusing and the use of objective lens make it easier to detect peak shift of sub angular step size, which in turn increased the accuracy of the determined strain amplitude.

Finite element modeling

Finite element modeling of the acoustic mode properties was performed using the COMSOL Multiphysics package. The structure considered is a thin slab corresponding to a portion of one aluminum electrode. The thickness of the slab is 0.05λSAW, where λSAW is the periodicity of the electrodes. The slab is located atop a portion of LiNbO3 substrate, the thickness of which is 5λSAW. To prevent reflections of waves at the bottom of the modeled volume, a perfectly matched layer is added below the finite LiNbO3 substrate. A vacuum enclosure is also added over the substrate and around the electrode to provide a realistic electrostatic environment. The crystal orientation of the LiNbO3 substrate is considered through a rotation of its material frame using Euler angles (0°, 90°, 0°). The periodicity of the electrodes is considered through the application of periodic boundary conditions with a Floquet wave-vector of (0, 0, 2π/λSAW) along the edges of the structure perpendicular to the propagation direction (Z direction in Fig. 1). The electrodes are considered infinitely long by application of periodic boundary conditions with a Floquet wavevector of (0, 0, 0) along the edges of the structure intersecting the electrode. For Supplementary Figs. 7 and 8, a harmonic calculation was performed, by applying a harmonic voltage of 1 V to the electrode and varying the frequency. The corresponding displacements or strains were extracted at the frequencies of interest after interpolation of the calculated fields on a regular rectangular grid. Otherwise, the electrode was set to 0 V, and an eigenvalue analysis provided the frequencies of the first modes of interest and their modal displacements.