Stability of optical knots in atmospheric turbulence

Abstract

Topology advances the understanding of many branches of science and technology, from elementary particle physics to condensed matter physics. While the topological stability of mathematical knots implies robustness to perturbations and suggests their potential as information carriers, the behavior of optical knots in perturbative environments is largely unexplored. Here, we experimentally and theoretically investigate the effects of atmospheric turbulence on optical knot stability and demonstrate that their topological invariant can be preserved in the weak turbulence regime but may not be conserved in the stronger turbulence conditions, despite their topological nature. Such topology transitions occur through reconnection events, where the additional optical modes resulting from the interactions with the turbulent medium change the vortex lines in space. Additionally, we propose an optimization algorithm to maximize the distance between the phase singularities at each longitudinal plane, facilitating measurements of optical knots and improving their performance in the presence of turbulence.

Introduction

Topological concepts such as singularities of the phase, polarization, or energy flow, topological textures, super-oscillations, and spin-orbit interactions, once considered primarily in abstract mathematics or theoretical physics, are now entering the field of classical and quantum optics. Knots are ubiquitous, being present in various fields ranging from fishing, maritime culture, and tying shoelaces to biopolymers, surgery, elementary particle physics, fluid dynamics, and optics. A knot can be formally defined as an embedding of a circle in the three-dimensional Euclidean space. In optics, knotted solutions in optics were predicted in the non-paraxial regime by superposing Bessel beams and tracking the phase singularities trajectories along the longitudinal direction¹. Later, isolated knotted fields were obtained by expanding the Milnor polynomial of a particular mathematical knot unto the Laguerre-Gaussian (LG) basis in both phase and polarization domains^2,3,4, as shown in Fig. 1a for the particular case of a trefoil knot.

Fig. 1: Turbulence effect on optical knots.

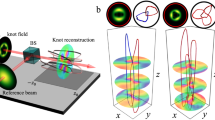
a Superposition of LG beams in a trefoil knot, where $(p,l)$ are the respective radial and azimuthal indices of the modes. b Schematic of the system investigated in this work. In the presence of turbulence, the probability of an originally knotted field (trefoil knot) getting untied increases. In this case, the trefoil knot transforms into a Hopf link or an unknot as it loses crossings due to the refractive index perturbations inside the turbulent medium.

While the mathematical theory of knots and links has developed over many decades, optical knot behavior in realistic perturbative physical media remains largely unexplored. Understanding the topological stability of knotted solutions is important for their potential applications in the fields of classical and quantum communications^5,6,7, microfabrication^8,9, and quantum computing^10,11. In topology, objects (e.g., knots) are equivalent if one can be transformed into the other through continuous deformation without cutting the lines or allowing the lines to pass through themselves, i.e., ambient isotopy^12,13. In other words, the singularity lines of the trefoil knot can deform in size and shape yet maintain the same number of crossings, i.e., topologically invariant. Notably, the number of crossings is just one of many topological invariants widely used in the field of optical or acoustical knots.

Leveraging the topological properties of optical knots for their robustness in turbid and turbulent media is of interest not only from a fundamental science viewpoint but may also yield novel insights in such applications as biomedical imaging, optical manipulation, and probing atmospheric turbulence. While the topological stability of optical knots for optical communications in realistic environments has been mentioned in many publications, only recently the first study addressing the robustness of optical knots under specific types of phase aberrations and setup misalignments modeled by the Zernike polynomials has been reported¹⁴. However, understanding the stability of optical knots in turbulent media remains challenging.

Here, we theoretically and experimentally investigate the behavior of optical knots in atmospheric turbulence and discuss their topological stability in the context of the conventionally used topological invariant and beyond. The overall effect of rapid fluctuations in the refractive index of the medium on the three-dimensional structure of the optical knots is summarized in Fig. 1b. Due to the interaction with turbulence, the topology of an initially unperturbed beam—specifically, a trefoil knot—can pass through a series of dis- and re-connection events taking place due to the multiple crosstalk between the additional modes appearing in the complex medium. As a result of these processes, the original trefoil knot can lose one of the singularity-line crossings, transitioning into a Hopf link, or if another crossing is lost, it can further be transformed into an unknotted structure. Interestingly, similar reconnection events of vortex knots were previously studied in the context of superfluid vortices, whose dynamics are governed by the Gross-Pitaevskii equation, and the topological evolution of such structures in time is observed until the initial knotted solution gets completely untied¹⁵.

Results

Turbulence is a universal phenomenon that occurs in the atmosphere, the oceans, the wake of a boat, and even in galaxies^16,17,18,19. Atmospheric turbulence leads to beam wandering, scintillation, and, most importantly, phase front distortion, primarily caused by random temperature variations and convective processes. Although some of these effects can be compensated by using aperture averaging²⁰, phase distortions are more difficult to counteract. While the exact theoretical modeling of turbulent flows is one of the most challenging problems of modern physics, the Kolmogorov model for turbulent flow accurately describes turbulence by relating random temperature variations and convective processes that perturb the wavefront of the optical beam to refractive index fluctuations. There are two characteristic parameters used to describe the turbulence: an inner scale, ${l}_{0},$ which is typically on the order of millimeters and results in distortions of the wavefront of the beam, and an outer scale, ${L}_{0}$, which is on the order of meters and is associated with beam wandering²¹. In particular, the Kolmogorov model assumes ${l}_{0}=0$ and ${L}_{0}\to \infty$. As for many random processes, theoretical descriptions of turbulence rely on statistical averages for the random variations of the refractive index of the atmosphere. However, experimental results confirm that such statistical descriptions are accurate in most practical cases^22,23.

A few approaches are commonly used to simulate turbulence in a laboratory environment. Heaters and fans have been used to emulate randomly changing refractive index distribution in a turbulent chamber by controlling the temperature gradient and air convection²⁴. Another technique relies on the random diffusive glass plate fabricated with a random-phase screen, where dynamic turbulence can be realized by rotating the plates^25,26. Another versatile technique is the holographic approach implemented using spatial light modulators (SLM) and digital micro-mirror devices with phase screens altered on demand with a refresh rate of up to 32 kHz, mimicking the dynamics of real-world turbulence^27,28,29. Therefore, in this study, we used an SLM to encode the knotted field and a controlled turbulent chamber to create a turbid environment, followed by a single-shot measurement of the complex electric field approach to recover the knots from the phase singularities³⁰. Figure 2a shows the experimentally realized Mach-Zehnder interferometer with the SLM in the signal arm to generate the knotted structure at a wavelength of 532 nm, where an example of the hologram utilized to create the trefoil knot is shown in Fig. 2b. The hot-air turbulence chamber is placed at the image plane of the SLM, where the structured beam starts to propagate inside the chamber after the 1st diffraction order is filtered using an iris. The CMOS camera captures the knotted beam at the waist plane, meaning that the hologram encodes the corresponding superposition of LG modes at $z=-L$, where $L$ corresponds to the total propagation distance starting at the image plane of the SLM until the CMOS camera. This distance, together with the beam waist of the optical modes, is cautiously calculated based on outdoor, realistic turbulent links previously reported in ref. ³¹. We rely on the Fresnel scaling number $F={w}_{0}^{2}/\lambda L$ to construct an experimental setup that mimics the propagation of a 6 mm beam size ($1/{e}^{2}$) propagating over a 270 m turbulent channel. Here, ${w}_{0}$ stands for the beam waist radius (or the beam’s radius at $z=0$, where its size is the smallest throughout the propagation), $\lambda$ is the wavelength, and $L$ is the turbulence link length. The Fresnel scaling number assures that the optical beam in the scaled-down experiment experiences the same (scaled to a shorter length) propagation conditions as in the outdoor, long-distance turbulent link. Using mirrors to reflect the beam multiple times within the turbulence chamber, the total propagation distance is L_lab=1.5 m. Figure 2c shows an example of an experimentally retrieved unperturbed trefoil knot, and more details on the hologram generation and the three-frame step technique to measure the complex field can be found in the “Methods” section.

Fig. 2: Experimental setup.

a In the experiments, a Mach-Zehnder interferometer is used to measure the complex field (amplitude and phase) using a three-frame step technique. Here, L lens, BS beam splitter, SLM spatial light modulator, M mirror, I iris, TC turbulence chamber, CMOS complementary metal oxide semiconductor camera. b Hologram to generate the optical trefoil knot. c Experimentally recovered trefoil knot without turbulence. Each black dot refers to a phase singularity, which, after connecting all dots in 3D, forms the closed singularity line of a trefoil knot.

In numerical simulations, we propagate the w₀= 6 mm beam over the L = 270 m turbulent channel, which is represented by three equally spaced random phase screens. These phase screens are calculated using the Kolmogorov power spectrum, and the minimum number of screens required to accurately recreate a given turbulent medium can be estimated as ${N}_{{{\rm{sc}}}}={\left(10{\sigma }_{R}^{2}\right)}^{-6/11}$, where ${\sigma }_{R}^{2}=1.23{C}_{n}^{2}{k}^{7/6}{L}^{11/6}$ represents the Rytov variance, ${C}_{n}^{2}$ the refractive index structure parameter, and $k=2\pi /\lambda$ the wavenumber³². In practice, using ${N}_{{{\rm{sc}}}}$ phase screens ensures that each individual phase screen represents weak turbulence, allowing the total turbulence effect to be correctly accumulated over the entire propagation path. This way of propagation path segmentation ensures the validity of our simulation approach by accurately capturing the cumulative effects of weak turbulence over long distances. For more details on the phase screen generation using the Kolmogorov power spectrum, see “Methods”. To ensure that numerical simulations using multiple phase screens and experimental setup using a heated airflow chamber create the same turbulence levels, we calibrate the chamber by adjusting the temperature and measuring the scintillation index ${\sigma }_{I}^{2}=\langle {I}^{2}\left({{\boldsymbol{0}}}\right)\rangle /{\langle I\left({{\boldsymbol{0}}}\right)\rangle }^{2}-1$ that characterizes the rapid intensity fluctuations due to the refractive index variations at the on-axis position. The calibration curve is included in section S1 of Supplementary Materials, alongside the estimated values of the refractive index structure ${C}_{n}^{2}$ and the Fried parameter ${r}_{0}$.

Optical knots’ coefficient adjustments

Using the analytical expression for the isolated knotted fields², we developed a numerical optimization procedure to minimize the perturbations, including both experimental setup misalignments and aberrations and actual turbulence-induced distortions. In the absence of turbulence, Dennis et al.² showed that by minimizing the cost function ${\sum }_{{{\rm{voxels}}}\; {{\rm{in}}}\; {{\rm{volume}}}}{\left[\min \left(\right.{I}_{{sat}},I({{\bf{r}}})\right]}^{-1}$, where I_sat represents the saturated intensity, the accuracy of optical knot measurements can be significantly improved. Throughout this manuscript, we will refer to this process as intensity optimization. Following several hundred iterations, this method results in properly spaced inner singularities and straightened singularity lines along the propagation direction. This process enhances the precision of optical knot measurements and characterization under laboratory conditions. Inspired by this method, we developed an algorithm to maximize the distance between phase singularity points in the 3D space for optical knots in turbulence where the random refractive index perturbations may lead to reshaping and, potentially, disconnections and reconnections of the singularity lines. This developed process will be referred to as singularity position optimization. While our discussion will focus on a particular case of the trefoil knot, the same procedure can be applied to any other knot.

Let us start with a superposition of the ${{\rm{L}}}{{{\rm{G}}}}_{p,l}$ beams, where $(p,l)$ respectively denote the radial and azimuthal orders, carrying individual ${c}_{p,l}$ amplitude weights for each mode written as

$${E}_{{trefoil}}= {c}_{0,0}\left(w\right){{\rm{LG}}}_{0,0}+{c}_{1,0}\left(w\right){{\rm{LG}}}_{1,0}+{c}_{2,0}{\left(w\right){\rm{LG}}}_{2,0}+{c}_{3,0}{(w){\rm{LG}}}_{3,0} \\ +{c}_{0,3}{(w){\rm{LG}}}_{0,3},$$

(1)

directly obtained from the projection of the Milnor polynomial with a fixed Gaussian beam width parameter $w=1.15$, which is the envelope for the Milnor polynomial at $z=0$. For further details, see sections S2 and S3 of the Supplementary Materials for the complete derivation of LG modes required for a trefoil knot and details on their coefficients, respectively. Subsequently, the amplitudes of each LG mode in decomposition were swept until the geometry of the knot satisfied the following criteria. First, the topology of the optical knot must stay unchanged, i.e., in our case, the knot must remain a trefoil. Second, extra singularities that may appear due to the Gaussian envelopes of LG beams, as discussed below, must be located at a distance no less than the preset minimum distance from the isolated knot along the propagation direction. We found that setting this minimum distance to be 25% of the total knot length along the direction of propagation was enough to prevent the merging of the knot and these extra singularities appearing due to turbulence. Third, the values of amplitudes of the LG modes at a particular iteration step are kept if the value of the cost function ${[\min (|{{{\bf{r}}}}_{i}^{k}-{{{\bf{r}}}}_{j}^{k}|)]}^{-1}$ decreased compared to the previous step. Otherwise, the procedure of varying these amplitudes continues. In the expression of the cost function $k$ corresponds to different transverse $\left(x,y\right)$ cross-sections along the knot, while $i$ and $j$ are integers corresponding to all singularities in a particular $k$-plane assuming $i\ne j,$ ${{{\bf{r}}}}_{i}^{k}$ and ${{{\bf{r}}}}_{j}^{k}$ are the vectors corresponding to the points where the singularity lines constituting the knot cross a particular $k$-plane (see Fig. 3). Note that in some planes, extra singularity crossing points may appear due to the bending of the singularity line (e.g., on either end of the knot where a single line crosses the transverse plane twice as shown in plane ${k}_{2}$ in Fig. 3d, f)). In this case, not all pairs of points should be considered when calculating the cost function. If these points do not change the topology, we skip the distance calculation between them. Here, by a particular topology, we understand the number of crossings possessed by a certain recovered structure, which can be translated to the associated Alexander polynomial. The sweeping of the LG modes amplitudes required to build the optimized trefoil knot was performed within the range of 3% of the current maximum coefficient value and took a few hundred iterations to be completed. Figure 3d presents the structure of the optimized trefoil knot, compared with the structure obtained using the standard mathematical expression, as shown in Fig. 3a.

Fig. 3: Optimization of knotted fields.

Un-optimized (a–c) and optimized (d–f) trefoil knots sliced in two different cross-sections ${k}_{1}$ and ${k}_{2}$. Phase distribution at k₁ (b, e) and ${k}_{2}$ (c, f) planes, where an example of the distance between two singularities $\left|{{{\bf{r}}}}_{1}^{k}-{{{\bf{r}}}}_{2}^{k}\right|$ is illustrated in panel (e) and their respective amplitude distribution is shown in the inset. Red dots indicate the points where the singularity lines cross a particular $k$-plane at each plane. f This shows that, even though the singularities 3–5 are close to each other, their connection does not change the topology of the knot. In this plane, the algorithm focuses on optimizing the distance between singularities 7 and 3−6. The coefficients for the un-optimized [optimized] optical trefoil knot for each LG mode $(p,l)$ are (0,0) 1.71 [1.29]; (1,0) −5.66 [−3.95]; (2,0) 6.38 [7.49]; (3,0) −2.3 [−3.28]; (0,3) −4.36 [−3.98].

Stability of optical knots

The refractive index perturbations in turbulence modify the coefficients in the LG superposition, thus altering the topology of the singularity lines. As turbulence becomes stronger, the probability of the original knot losing crossings increases. For instance, a trefoil knot tends to change the topology to either a Hopf link or unknot, as shown in Fig. 4. To grasp the nature of the topological robustness, a statistical analysis was performed after propagating 300 knotted fields through the turbulence of multiple strength level. After measuring the complex field at a single plane (waist plane), the three-dimensional field is recovered by using the angular spectrum method to numerically propagate it in both forward and backward propagation directions³⁰. Subsequently, the phase singularities are identified in each propagation plane, and their connections are established. This method improves precision in determining the positions of singularities, coupled with rapid, automated phase measurements. The topological structure of these singularity lines is then classified, as detailed in section S4 of Supplementary Materials.

Fig. 4: Stability of recovered knots.

a The percentage of numerically (black dots) and experimentally (green diamonds) recovered trefoil knots obtained using the singularity position optimization for different scintillation values. b Same as in (a), but using the intensity optimization process². The shaded area denotes the 95% confidence level. c Histograms showing the recovered trefoil knots, Hopf links, and unknots for various turbulence strengths using the singularity position optimization.

Figure 4a shows the percentage of numerically and experimentally recovered trefoil knots as a function of the strength of the turbulence obtained using our proposed coefficients’ optimization procedure, marked using black dots and green diamonds, respectively. In panel (b), the same markers depict the numerical and experimental performance of the intensity optimization technique², respectively. In both panels and throughout Supplementary Materials, the shaded area corresponds to the statistical confidence interval, fixing the confidence level at 95% for 300 realizations. This implies a 95% certainty that the true percentage of preserved trefoil knots falls within the shaded area for each corresponding case. In section S5 of  Supplementary Materials, we numerically compare the percentage of recovered trefoils using both optimization methods discussed in the previous section, together with the case where no optimization is performed. It is worth noticing that performing experiments using a convective, hot airflow chamber implies a temporally moving media, which might lead to inaccuracies while performing the three-phase steps technique to measure the complex field. Our turbulence system has a Greenwood frequency of about f_G ≈ 35 Hz, while the SLM has a maximum framerate of 60 Hz. This means that, in contrast to the numerical simulations, the knotted beam experiences non-static turbulence during the complex field measurements. To address this, we numerically mimic fast-changing turbulence levels by using random uncorrelated phase screens for each interferogram required for the phase recovery (Supplementary Materials, section S1). This clarifies the decrease in the percentage of recovered trefoils, where fast-moving turbulence with respect to the data acquisition time can be seen as uncorrelated phase screens throughout the experimental phase recovery, while the numerical simulations correspond to the ideal case with instantaneous data acquisition and no temporal change in the turbulence dynamics. Figure 4c shows the percentage of recovered trefoil knots, Hopf links, and unknots for each turbulence strength using the singularity optimization. The reconnection events reshape the initial trefoil knot and progressively change its topology to Hopf links and unknots as the turbulence strength increases. Turbulence adds more orthogonal modes in the field superposition, leading to collective crosstalk among the interacting modes.

The knot transformation from a higher-order topology to a lower-order one is similar to the higher-order charge splitting in OAM-carrying beams. In the case of the OAM beams, any perturbations in complex media lead to higher-order topological charges splitting into multiple ±1 topological charges. In the case of optical knots, we observe a similar behavior, but instead of reducing the topological charge, higher-order optical knots tend to transform into lower-order knots through reconnection events. Additionally, it is important to highlight a major difference in the topological properties between 2D and 3D structured fields while interacting with turbulence. Typically, OAM-carrying beams lead to a spectrum of states upon perturbation by a turbid media, possessing an associated crosstalk between them²⁰. Here, the spectrum might or might not be centered around the initial topological mode, depending on the turbulence strength. In the optical knots case, the topology is determined by the knot type (trefoil, Hopf link, or an unknot) recovered at the receiver, which depends on both relative amplitudes and phases of the constituent LG components.

In section S6 of Supplementary Material, we show the LG spectrum for the cases where the trefoil maintained its shape, transformed into a Hopf link, and changed into an unknot. Here, we observe that the complex field experiences more crosstalk as it transitions into a Hopf link and unknot structures. In the same section, we also locate the position where the reconnection events occurred for cases where the trefoil knot changed its topology. Additional examples of recovered topologies are included in section S7 of Supplementary Materials.

Discussion

As discussed in the introduction, despite the significant interest in utilizing the topological properties of knotted solutions for their transmission in turbid and turbulent environments, an understanding of the stability of optical knots in such media remained largely unexplored. In this work, we experimentally and numerically demonstrated that optical knots stability, characterized by the number of singularity line crossings (one of the commonly used topological invariants), can be preserved in the weak turbulence regime but may not be conserved in the stronger turbulence conditions, suggesting that mathematical topological stability of knots may not guarantee the stability of their optical counterparts. However, we note that several avenues exist to improve their stability. For instance, constructing the knot with more constituent LG modes may be used for further stability improvement. Furthermore, we show that the stability of optical knots can be improved by optimizing their constitutive modes’ parameters, such as amplitudes and beam waists. This conclusion is of significant importance for their potential applications in the fields of classical and quantum communications^5,6, microfabrication^8,9, and quantum computing^10,11.

Another important finding of this work is that the singularities surrounded by higher field contrast wander less than those surrounded by lower field amplitudes. Both optimization methods (that of ref. ² and the one developed in this work) lead to higher amplitude contrast around the multiple singularities disposed throughout the optical field compared to the Milnor polynomial-based knots. Note that the intensity-based optimization² aimed to facilitate the laboratory measurements of unperturbed knots. Here, we found that in the presence of atmospheric turbulence, increasing the amplitude contrast leads to less singularity wandering and, thus, to higher stability for three-dimensional singularity lines. We stress that several additional degrees of freedom to improve the stability of optical knots remain unexplored. In particular, other optimization approaches aiming at achieving higher amplitude contrast surrounding the optical singularities will likely improve knots’ stability further.

In conclusion, our results indicate that the topological structure of optical knots is relatively stable in the weak-turbulence regime. However, knot optimization and post- or pre-correction algorithms may need to be added to maintain the shape of the knot in strongly perturbed environments, such as a strong-turbulence regime³³. Therefore, our study indicates the topological stability of mathematical knots does not inherently imply the stability of optical knots, at least in terms of the commonly used topological invariant—the number of singularity crossings. Note that the knots considered in this study are formed after the constituent LG beams are transmitted in turbulence. Therefore, depending on the strength of the turbulence, the LG beams interfere in 3D space to form a deformed 3D interference pattern that we then classify as a trefoil knot, Hopf link, or an unknot based on the number of crossings. Remarkably, even in the case when the number of crossings changes, overall 3D patterns closely resemble the targeted optical knot, suggesting that the classification of the knots formed in turbulence based on the number of crossings may not be an ideal approach in such a complex medium and, perhaps, a different invariant/criterion needs to be defined to classify the knots in turbulent media. Using such a 3D shape-based criterion is expected to result in a larger percentage of original knots or links being recovered after turbulence. The limitations of the proposed optimization and classification methods are further discussed in section S8 of Supplementary Materials. Once the new and more efficient criterion is established, knotted fields can be further considered as potential information carriers in future communication systems, metrology, and sensing applications. The results study might also be important to other physical systems, such as Bose-Einstein condensates, fluids, and quantum optics, to cite a few.

Methods

Encoding holograms and phase recovery

Optical knots that are the null solutions of the Helmholtz equation in three-dimensional free space have only recently been demonstrated in optical experiments through overlapping multiple LG beams with carefully chosen relative amplitudes in 3D space such that their 3D interference pattern consists of closed loops of complete darkness that can be described as

$${E}_{{knot}}\left(r\right)={\sum}_{p,l}{c}_{p,l}{{\rm{LG}}}_{p,l}\left(r,{w}_{0}\right),$$

(2)

where the sum is taken over all modes where ${c}_{p,l} \, \ne \, 0$, and each term satisfies the linear paraxial Helmholtz equation. Here, ${c}_{p,l}$ are the coefficients of the respective ${{\rm{LG}}}_{p,l},$ where $p$ and l are the radial and azimuthal indices, respectively, ${w}_{0}$ is the LG beam width parameter that is assumed to be the same for all ${{\rm{LG}}}_{p,l}$ modes (see the Supplementary Materials (S2)). After encoding the holograms into the SLM using an approximated inverse sinc-function method³⁴, the phase distribution $\phi$ and amplitude $A$ are measured by numerically inverting the expression $\tan \left(\phi \right)=\left({I}_{3}-{I}_{2}\right)/\left({I}_{1}-{I}_{2}\right)$ and $A=\sqrt{{\left({I}_{3}-{I}_{2}\right)}^{2}+{\left({I}_{1}-{I}_{2}\right)}^{2}}$. Here, I_i(i = 1,2,3) is phase-shifted interferograms by $\left(2i-1\right)\pi /4$³⁵.

Generating turbulent phase screens

The approach described below translates the changes in the refractive index of the atmosphere, which is caused by fluctuations in the temperature, into phase-only perturbations. After propagation, these phase-only perturbations result in both amplitude and phase distortions of the optical field. The thin-phase screen approximation is particularly interesting for condensing the properties of turbulent media into a single-phase screen³⁶.

To model the random phase screen $\varPhi$ associated with atmospheric turbulence, we define the following phase structure function

$$\varPsi \left({{\boldsymbol{r}}}\right)=\left\langle {\left|\varPhi \left({{{\boldsymbol{r}}}}^{{\prime} }{{\boldsymbol{+}}}{{\boldsymbol{r}}}\right)-\varPhi \left({{{\boldsymbol{r}}}}^{{\prime} }\right)\right|}^{2}\right\rangle,$$

(3)

where $\left\langle \cdot \right\rangle$ refers to the ensemble average, and we relate the Weiner spectrum $\Theta$ to the phase structure function as

$$\varPsi \left({{\boldsymbol{r}}}\right)=2\int \varTheta \left({{\boldsymbol{k}}}\right)\left[1-\cos \left(2\pi {{\boldsymbol{k}}}\cdot {{\boldsymbol{r}}}\right)\right]{d}^{2}{{\boldsymbol{k}}}.$$

(4)

One can write the above expressions for the Kolmogorov spectrum as³⁷

$$\varPsi \left({{\boldsymbol{r}}}\right)=6.88{\left(\frac{\left|{{\boldsymbol{r}}}\right|}{{r}_{0}}\right)}^{5/3},$$

(5)

and,

$$\varTheta \left({{\boldsymbol{k}}}\right)=\frac{0.023}{{r}_{0}^{5/3}}{\left|{{\boldsymbol{k}}}\right|}^{-11/3},$$

(6)

where ${r}_{0}$ is the Fried parameter. In other words, the Wiener spectrum $\Theta$ is the covariance function of the random power spectrum $P\left({{\bf{k}}}\right)$, which is defined as

$$P\left({{\boldsymbol{k}}}\right)={{\mathcal{F}}}\left\{\varTheta \right\}=\int \varTheta \exp \left[-i2\pi {{\boldsymbol{k}}}\cdot {{\boldsymbol{r}}}\right]{d}^{2}{{\boldsymbol{r}}},$$

(7)

with ${{\mathcal{F}}}$ denoting the Fourier transform operator. Now, we calculate the random power spectrum $P({{\bf{k}}})$ by sampling a random distribution with zero mean and variance equal to $\Theta ({{\bf{k}}})$³⁸. This leads to a Kolmogorov Wiener spectrum with $N\times N$ entries denoted by

$$\varTheta \left(i,j\right)=0.023{\left(\frac{2D}{{r}_{0}}\right)}^{5/3}{\left({i}^{2}+{j}^{2}\right)}^{-11/3},$$

(8)

where $D$ is the aperture size in which $\varPhi$ is calculated, and $i,j$ are the indices of each entry of the Kolmogorov spectrum in a square grid. Multiplying $\sqrt{\Theta }$ by a random matrix ${{\bf{M}}}$, composed of complex values with zero mean and variance $1$, leads to the power spectrum $P({{\bf{k}}}),$ which, after taking the inverse Fourier transform, results in the desired phase screen $\varPhi$.

As the smallest generated frequency is $1/D$, this does not accurately describe the phase screen dependency on ${|{{\bf{k}}}|}^{-11/3}$. These subharmonic contributions are considered by evaluating the power spectrum at those frequencies with periods greater than $D$ (or frequencies smaller than $1/D$). Finally, the phase screen is obtained by taking the real part as

$$\varPhi {\mathfrak{=}}{\mathfrak{R}}\left\{{{{\mathcal{F}}}}^{-1}\left\{{{\boldsymbol{M}}}\sqrt{\varTheta }\right\}\right\},$$

(9)

now including the subharmonic contributions.