Leveraging pleiotropic clustering to address high proportion correlated horizontal pleiotropy in Mendelian randomization studies

Abstract

Mendelian randomization harnesses genetic variants as instrumental variables to infer causal relationships between exposures and outcomes. However, certain genetic variants can affect both the exposure and the outcome through a shared factor. This phenomenon, called correlated horizontal pleiotropy, may result in false-positive causal findings. Here, we propose a Pleiotropic Clustering framework for Mendelian randomization, PCMR. PCMR detects correlated horizontal pleiotropy and extends the zero modal pleiotropy assumption to enhance causal inference in trait pairs with correlated horizontal pleiotropic variants. Simulations show that PCMR can effectively detect correlated horizontal pleiotropy and avoid false positives in the presence of correlated horizontal pleiotropic variants, even when they constitute a high proportion of the variants connecting both traits (e.g., 30–40%). In datasets consisting of 48 exposure-common disease pairs, PCMR detects horizontal correlated pleiotropy in 7 out of the exposure-common disease pairs, and avoids detecting false positive causal links. Additionally, PCMR can facilitate the integration of biological information to exclude correlated horizontal pleiotropic variants, enhancing causal inference. We apply PCMR to study causal relationships between three common psychiatric disorders as examples.

Introduction

Examining the causal relationships between complex traits and pinpointing the causal risk factors for diseases are pivotal in unraveling the etiology of various conditions. Mendelian randomization (MR) is a powerful method that harnesses genetic variants to probe these causal relationships¹. MR offers several advantages over observational studies, notably in its ability to alleviate the influence of non-genetic confounding factors and circumvent the need to measure outcomes within the exposure factors. Furthermore, its broad applicability is underscored by its requirement for only two sets of GWAS summary statistics – one for the exposure and another for the outcome². This streamlined approach enhances the versatility and accessibility of MR in unraveling the complex relationship between various traits and diseases.

The fundamental principles of MR are visually depicted in Fig. 1a³, serving as the cornerstone of the MR methodology. The widely employed inverse variance weighted (IVW) method⁴ operates under the assumption that all significant genetic variants adhere to these core principles, thereby qualifying as valid instrumental variables (IVs)⁴. However, the practical reality often involves violating these assumptions, introducing complexities that compromise the integrity of MR testing and result in inaccurate causal inferences^5,6. A common challenge arises in horizontal pleiotropy, where genetic variants fail to influence the outcome variable (Y) solely through the exposure variable (X). Horizontal pleiotropy manifests in two distinct categories. Correlated horizontal pleiotropic variants exhibit associations with confounding factors impacting both X and Y concurrently, with effects on Y correlated to those on X. In contrast, uncorrelated horizontal pleiotropic variants directly impact Y, with effects on Y independent of those on X⁷. Both types of horizontal pleiotropy pose the risk of generating false-positive causal relationships, underscoring the significance of addressing pleiotropy in current methodological developments within the field.

Fig. 1: Assumptions of instrument variables and the PCMR model.

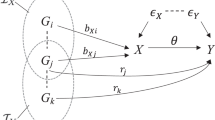
a Causal diagram by valid instrument variables. The valid IV lacks correlated and uncorrelated horizontal pleiotropy, and affects the outcome $Y$ solely through exposure $X$. b The unified IV framework for valid or invalid IVs. We designated a link factor representing the entire associated pathways between ${Z}_{i}$ and $X$ as ${L}_{i}$, where the effect of the ${L}_{i}$ on X is normalized to 1. ${L}_{i}$ serves as a normal confounder $U$ being scaled the effect on $X$ to 1 when ${\eta }^{i}\ne 0$. ${Z}_{i}$ affects $X$ only through the link factor being a valid IV if ${\eta }^{i}=0$ and ${\theta }^{i}=0$; ${Z}_{i}$ is an uncorrelated horizontal pleiotropic variant if ${\eta }^{i}=0$ and ${\theta }^{i}\ne 0;$ ${Z}_{i}$ is in the presence of uncorrelated and correlated pleiotropy simultaneously if ${\eta }^{i}\ne 0$ and ${\theta }^{i}\ne 0.$ c Simulated classification by PCMR when the causal effect is zero without correlated horizontal pleiotropy. PCMR classified IVs into two similar IV categories with similar correlated HVP effects. d Simulated classification by PCMR when the causal effect is zero with 50% correlated horizontal pleiotropic variants. PCMR classified IVs into distinct IV categories, with the largest IV category (in blue), according to the clustering proportion, exhibiting correlated horizontal pleiotropy. It is challenging to differentiate which IV category is used to estimate the causal effect. In both plots, (c) and (d), effect-size estimates for exposure and outcome are indicated by points. The error bars displayed around the points have a length equal to 1.96 times the simulated standard error (s.e.) of the estimate on each side. The slopes indicate estimated correlated HVP effects by each IV category, where the blue IV category is at a higher proportion than the gray IV category. The range of shaded areas represents the variance of correlated HVP effects.

Addressing uncorrelated horizontal pleiotropy is relatively more straightforward, and several methodologies have been proposed to tackle this issue. For instance, Egger regression, a well-established method⁸, operates on the assumption that all IVs exhibit a consistent uncorrelated horizontal pleiotropic effect. Alternatively, methods like PMR-VC⁹ and BWMR¹⁰ posit that uncorrelated horizontal pleiotropic effects across all IVs conform to a Gaussian distribution. A recent advancement, MRAID¹¹, introduces a nuanced approach by incorporating the modeling of uncorrelated horizontal pleiotropy, assuming that a subset of IVs with such effects follows a normal distribution. In contrast, GSMR¹² and MR-PRESSO⁶ rely on outlier removal techniques to eliminate IVs displaying uncorrelated horizontal pleiotropy.

Addressing correlated horizontal pleiotropy presents formidable challenges, with existing methodologies grappling to disentangle causality from this intricate phenomenon. Approaches such as Weighted median¹³, Weighted mode¹⁴, MRMix¹⁵, CAUSE⁷, MR-CUE¹⁶, and MRAID¹¹ either presume a limited proportion of correlated horizontal pleiotropic variants or hinge on the zero modal pleiotropy assumption (ZEMPA). Across all instruments, ZEMPA designates the most frequent IV estimates to causal effect¹⁴. However, in reality, shared biological mechanisms among traits and diseases contribute to genetic correlation, potentially resulting in a prevalent occurrence of a substantial proportion of correlated horizontal pleiotropic variants^17,18,19. Examples include psychiatric disorders and the interplay between high-density lipoprotein (HDL) and coronary artery disease (CAD)^7,20. In these traits with correlated horizontal pleiotropic variants, especially a notable proportion, the assumptions may become problematic, introducing the potential for biased estimates and false positives. The intricate interplay of genetic factors in complex traits underscores the ongoing challenges in accurately disentangling causal relationships amidst correlated horizontal pleiotropy.

In this paper, we introduce Pleiotropic Clustering of Mendelian Randomization (PCMR), an approach for classifying IVs using GWAS summary statistics. The aim of PCMR is to detect correlated horizontal pleiotropy and enable comprehensive causal inference in trait pairs with correlated horizontal pleiotropic variants. PCMR acknowledges the mathematical indistinguishability between correlated horizontal pleiotropic effect and causal effect by merging them into a unified correlated horizontal and vertical pleiotropic (HVP) effect. Effectively categorizing IVs, including those determined to exhibit causal effects, PCMR leverages clustering to develop a pleiotropy test capable of detecting correlated horizontal pleiotropy. Moreover, PCMR’s causality evaluation makes an assumption of Discernable ZEMPA to causal inference in the presence of correlated horizontal pleiotropic variants. In extensive simulations, we compare PCMR’s pleiotropy test with MR-PRESSO for detecting horizontal pleiotropy. Furthermore, we assess the performance of PCMR’s causality evaluation and compare it with six alternative MR methods. To illustrate the applicability of these methods, we apply them to 48 pairs of common diseases and three types of common psychiatric disorders. This comprehensive evaluation aims to demonstrate the efficacy and versatility of PCMR in detecting and revealing causal relationships in correlated horizontal pleiotropy.

Results

Overview of the pleiotropic clustering framework of Mendelian randomization

PCMR is built upon the Gaussian mixture model that clusters IVs according to various horizontal and vertical pleiotropic (HVP) effects. In MR analysis, variants strongly associated with exposure are usually selected as IVs, and we propose to put all IVs into a single framework (Fig. 1b) where both valid and invalid IVs can be denoted with different parameters. Mathematically, we express the relationship between the associated coefficients for the outcome and exposure at an IV, denoted as ${\beta }_{Y,i}$ and ${\beta }_{X,i}$, respectively, through a unified formula:

$${\beta }_{Y,i}=\left(\gamma+{\eta }^{i}\right){\beta }_{X,i}+{\theta\, }^{i}$$

(1)

Here, $\gamma$ and ${\eta }^{i}$ represent vertical pleiotropic (also known as causal) effect and correlated horizontal pleiotropic effect, respectively, while ${\theta }^{i}$ denotes the uncorrelated horizontal pleiotropic effect. In a specific scenario, when ${\eta }^{i}=0$ and ${\theta }^{i}=0$, it indicates $i$-th IV that does not exhibit any horizontal pleiotropic effect. A notable feature of PCMR is the integration of correlated horizontal pleiotropic effect ${\eta }^{i}$ and vertical (causal) effect $\gamma$ as a sum effect ${\phi }^{i}\,=\gamma+{\eta }^{i}$ (defined as correlated HVP effect throughout this paper), as both effects are part of the slope and are mathematically indistinguishable. The correlated HVP effects are assumed to belong to distinct normal distributions. To facilitate classification, we propose a Gaussian mixture model:

$${\phi }^{i}\sim {q}_{1}N\left({\phi }_{1},{\sigma }_{{\phi }_{1}}^{2}\right)+{q}_{2}N\left({\phi }_{2},{\sigma }_{{\phi }_{2}}^{2}\right)+\cdots+{q}_{{n}_{\eta }}N\left({\phi }_{{n}_{\phi }},{\sigma }_{{\phi }_{{n}_{\phi }}}^{2}\right)$$

(2)

where ${q}_{j},j=1,\cdots,{n}_{\phi }$ represent the proportion of each normal distribution and$\,{\sum }_{j}{q}_{j}=1$. The corresponding parameters are estimated using the expectation-maximization (EM) algorithm (see “Methods”). It is important to note that while the proposed PCMR framework can theoretically model multiple pleiotropic effect categories, a simplified two-class model may also be suitable for causality inference when the number of available IVs in existing studies is usually not large, usually $\le$200 (Supplementary Table 4). Hence, in this paper, we focus on considering, at most, two groups of different correlated HVP effect (${n}_{\phi }\le 2$).

Following classification, PCMR also provides a valid heterogeneity test for assessing correlated horizontal pleiotropy—PCMR’s pleiotropy test (Table 1). Correlated horizontal pleiotropic and valid IVs would lead to distinct correlated HVP effects. PCMR can effectively classify IVs with similar estimated correlated HVP effects in the absence of correlated horizontal pleiotropy, or with various estimated effects in the presence of correlated horizontal pleiotropy, as illustrated in (Fig. 1c, d). PCMR’s pleiotropy test relies on bootstrapping to test for statistical differences between the estimated effects (see “Methods”). In our analysis of common diseases, approximately $15\%\,(7/48,\,{P}_{{plei}-{test}}\,\le 0.05)$ of trait pairs significantly in correlated horizontal pleiotropy (Table 2).

Table 1 False positive rate and Power to detect correlated horizontal pleiotropy in MR for different methods

Table 2 Summary of results for trait pairs categorized by prior information about causality

Considering the difficulty in differentiating the true causal effect from correlated horizontal pleiotropy, as shown in Fig. 1d, we extend the zero modal pleiotropy assumption (ZEMPA) to the Discernable ZEMPA (DZEMPA) (see “Methods”). Based on this assumption, we employ a likelihood ratio test (LRT) to evaluate whether the largest IV category in a sample is discernible for the dominant population IV group and supports a non-zero causal effect—called PCMR’s causality evaluation. The LRT integrates all IVs to evaluate the existence of the dominant IV category supporting a non-zero causal effect rather than making causal inferences based on a specific IV category (see “Methods”). In other words, if either of two similarly sized IV categories shows a zero effect, it would be hard to determine the dominant IV category supporting a non-zero causal effect, and the causality evaluation may be insignificant. PCMR’s causality evaluation effectively controls false positive rates in correlated horizontal pleiotropy, especially in scenarios with a high ratio $(\ge30\%)$ of correlated horizontal pleiotropic variants (Fig. 2d, e).

Fig. 2: Performance of PCMR and other MR methods in simulated data.

a–c Box plot of estimated causal effect by methods. a, b Comparison of estimated effect in correlated horizontal pleiotropy. The proportion of correlated horizontal pleiotropic variants from $0\%$ to $50\%$, and the heritability of outcome mediated by exposure and confounding, ${\tau }^{2}+{\omega }^{2}$, is 5%. a $\gamma=-0.1$ is in the opposite direction with correlated horizontal pleiotropic effect ($\eta=\sqrt{{\omega }^{2}}$); b $\gamma=0.1$ is the same direction with correlated horizontal pleiotropic effect. c Comparison of estimated effect in the absence of correlated pleiotropy. The heritability of outcome mediated by exposure, ${\tau }^{2},$ from 1% to 5% ($\gamma=\sqrt{{\tau }^{2}}$). ZEMPA-PCMR indicates the correlated HVP effects supported by the largest IV category of PCMR. PCMR (smaller/larger category) contains the smaller/larger correlated HVP effects, being $\min ({\phi }_{1},{\phi }_{2})$/$\max ({\phi }_{1},{\phi }_{2})$ of PCMR. Box plots display the median (central line), interquartile range (25th–75th percentiles), whiskers extending to non-outlier extremes within 1.5×IQR, and outliers as individual points. d, e False positive rate of two-sided test in the null hypothesis ($\gamma=0$). Testing true causality indicates that when the IV category determining true causal effect is identified, causal inference for this IV category relies on bootstrapping. d Q–Q plot of original p-values by MR methods in the presence of 40% correlated pleiotropic variants ($q=40\%$). e False-positive rates in the presence of correlated pleiotropic variants range from $0\%$ to $50\%,$ and correlated horizontal pleiotropic effects from $\sqrt{0.01}$ to $\sqrt{0.05}$. There are 100 simulations in each scenario using a p-value threshold of 0.05, labeled by the gray horizontal line.

PCMR provides an effective classification for IVs supporting causal or pleiotropic effects

We first evaluated the clustering performance of PCMR in the presence of correlated horizontal pleiotropy through extensive simulation studies. PCMR can effectively classify IVs, where IVs were classified into two distinct categories, and one of the estimated correlated HVP effects closely matched the true causal effect, as depicted in Fig. 2a, b and Supplementary Fig. 2. For example, when the true causal effect was $0.1$ and $40\%$ of variants exhibited correlated horizontal pleiotropy, the median of smaller estimated correlated HVP effects by PCMR was 0.087 (Fig. 2b$q=40\%$). That is also true even when the proportion of correlated horizontal pleiotropic variants is as high as 50% (Fig. 2a, b$q=50\%$). In such a high proportion of correlated horizontal pleiotropic variants, six other alternative methods (Egger, IVW, CAUSE, MRAID, Weighted median, and Weighted mode) produced biased median estimated causal effects. In addition, if the largest IV category by PCMR was also assumed to support the causal effect (ZEMPA), we also saw the biased estimated causal effects, though it was the smallest among the methods. For example, when the true causal effect is $-0.1$ with $40\%$ correlated horizontal pleiotropic variants, the median estimated causal effect (standard error) of Weighted mode, MRAID, CAUSE, and ZEMPA-PCMR were −0.031(0.071), 0.043(0.075) and 0.014(0.017) and −0.077(0.098), while the median of smaller estimated correlated HVP effects by PCMR was $-0.091(0.036)$. When the proportion of correlated horizontal pleiotropic variants decreases to below 30%, ZEMPA demonstrates enhanced accuracy in estimating the true causal effect, and ZEMPA-PCMR and Weighted mode outperform the other five Mendelian randomization (MR) methods that continue to yield biased estimates (Fig. 2a, b). For instance, considering a true causal effect of −0.1 with 20% correlated horizontal pleiotropic variants, the median estimated causal effect (standard error) for ZEMPA-PCMR, Weighted mode, MRAID, and CAUSE were −0.110 (0.050), −0.085 (0.034), 0.096 (0.138), and −0.029 (0.018), respectively. Methods like Egger and IVW, lacking consideration for correlated horizontal pleiotropy, are expected to produce biased estimates in their presence. CAUSE and MRAID exhibit effectiveness primarily for a small proportion of correlated horizontal pleiotropic variants, achieving relatively accurate estimates only when the proportion is 10% or less. These findings underscore the challenge of differentiating causal effect from correlated horizontal pleiotropic effect, while PCMR can accurately isolate a specific IV category that determines the causal effect.

In the absence of correlated horizontal pleiotropy, PCMR classified IVs into two similar categories, and both estimated correlated HVP effects were close to the true causal effect (Fig. 2c). For instance, when the true causal effect was $0.1$, the estimates of Egger, IVW, CAUSE, MRAID, Weighted median, and Weighted mode were 0.104, 0.090, 0.080, 0.091, 0.091 and 0.090, while the median of ZEMPA-PCMR and two estimated correlated HVP effects by PCMR were 0.094, $0.079$ and $0.101$. The classification distinction between the presence or absence of correlated horizontal pleiotropy suggests that PCMR can effectively assess the existence of correlated horizontal pleiotropy.

PCMR’s pleiotropy test detects the presence of correlated horizontal pleiotropy

Through extensive simulations, we thoroughly assessed PCMR’s pleiotropy test for detecting correlated horizontal pleiotropy. Initially, these simulations demonstrated that PCMR’s pleiotropy test maintains a reasonable type 1 error rate. In scenarios lacking horizontal pleiotropies, PCMR’s pleiotropy test exhibited average false positive rates of 4.67% at ${P}_{{plei}-{test}}\le 0.05$ across various causal effects, similar to an alternative test, MR-PRESSO, 4.33% (Table 1, Supplementary Table 1). Notably, PCMR’s pleiotropy test displayed a notable advantage over MR-PRESSO by uniquely examining the presence of correlated horizontal pleiotropy even in uncorrelated horizontal pleiotropy. In contrast, MR-PRESSO failed to discriminate between correlated and uncorrelated horizontal pleiotropies. In the scenarios solely with uncorrelated horizontal pleiotropy, PCMR’s pleiotropy test showed an average false positive rate of 4.67%, while MR-PRESSO reported significant findings of 48.00%. This disparity arises from MR-PRESSO’s consideration of horizontal pleiotropies without distinguishing their specific type, while PCMR’s pleiotropy test exclusively characterizes and detects correlated horizontal pleiotropy. Consequently, MR-PRESSO is expected to yield slightly higher power than PCMR’s pleiotropy test in indiscriminatingly both types of detecting horizontal pleiotropies, and the statistical power of PCMR’s pleiotropy test can also be reduced by uncorrelated horizontal pleiotropy (Table 1, Supplementary Table 2). Nevertheless, these findings underscore the critical capabilities of PCMR’s pleiotropy test in only detecting one type of horizontal pleiotropy, correlated horizontal pleiotropy.

PCMR’s causality evaluation enhances causal inference in the presence of correlated horizontal pleiotropy

We assess the performance of PCMR’s causality evaluation in controlling Type-I error rates for the null hypothesis in the presence of correlated horizontal pleiotropy by simulation studies. PCMR’s causality evaluation demonstrates effective control of false positives. It produced expected p-values even when a high proportion (e.g., $40\%$) of correlated horizontal pleiotropic variants were present (Fig. 2d, e). In contrast, IVW, Weighted median, and MRAID always yielded inflated false positives in correlated horizontal pleiotropy. Egger, CAUSE and Weighted mode could control the false positive rates only when the proportion of correlated horizontal pleiotropic variants is small (e.g., $\le 20\%$). However, as the proportion (q) increased, these three methods also exhibited inflated false positive rates. For instance, when the correlated horizontal pleiotropic effect ($\eta$) is $\sqrt{0.05}$ and $q=40\%$, the false positive rate of Egger, CAUSE, Weighted mode and PCMR’s causality evaluation at p-value threshold $0.05$ were $28\%$, $46\%$, $12\%$ and $3\%$. Note when q is as high as 50%, the correlated horizontal pleiotropic and causal effects are almost indiscernible based on the proportional discrepancy. PCMR’s causality evaluation only had a slight inflation in the Type-I error rate, for example, at 13% even when $\eta=\sqrt{0.05}$ and q = 50%, while Median mode and CAUSE are as high as 30% and 64%, respectively.

Furthermore, we compare the power of PCMR’s causality evaluation with other methods in correlated horizontal pleiotropy under the alternative hypothesis. PCMR’s causality evaluation exhibits substantially higher power than the three methods with relatively controllable type I error rates (Egger, CAUSE, and Weighted mode) when correlated horizontal pleiotropic and causal effects are in opposite directions (Supplementary Fig. 1a). For example, in the scenario of opposite direction when ${{\rm{\gamma }}}=-0.1$ and $q=30\%$, the power of PCMR’s causality evaluation, Egger, CAUSE and Weighted mode, were $51\%$, $8\%$, $4\%$, and $11\%$ respectively. That is because the offset of the causal effect and the opposite correlated horizontal pleiotropic effect leads to an underestimated causal effect for these alternative methods. When ${{\rm{\gamma }}}=-0.1$ and $q=30\%$, the median estimates by PCMR(smaller category), Egger, CAUSE and Weighted mode were $-0.109$, $0.016$, $-0.005$ and$\,-0.067$. In scenarios where correlated horizontal pleiotropic and causal effects are in the same direction, resulting in an overestimated causal effect, PCMR’s causality evaluation still has higher power than Egger and Weighted mode. For instance, when ${{\rm{\gamma }}}=0.1$ and $q=30\%$, the power of PCMR’s causality evaluation, Egger and Weighted mode were 80%, 59% and 50%, while CAUSE obtained 100% power due to inflated median of estimated causal effect, $0.152$.

Evaluating the performance of PCMR in a dataset of common diseases

We further conducted a performance evaluation of the PCMR and six other MR methods using a real dataset previously used in the CAUSE study⁷. The dataset consisted of twelve potential risk factors and four common diseases (Supplementary Table 3), with the causality credibility categorized into five groups: Considered causal, Supported by the literature, Unknown or conflicting evidence, Implausible or unsupported, and Considered non-causal. Focusing on these well-studied risk factors and diseases allows for comparing results across different approaches.

Table 2 offers a comprehensive summary of estimates, p-values, and the evaluation of correlated horizontal pleiotropy presence, with detailed results provided in Supplementary Data 1. The IVs utilized by each MR method are outlined in Supplementary Data 2. MR-PRESSO detected horizontal pleiotropy for most trait pairs at a threshold of 0.05, while PCMR’s pleiotropy detected only $15\%$ (7/48 at a threshold of ${P}_{{plei}-{test}}\le 0.05$) of pairs associated with correlated horizontal pleiotropy, around $50\%$ (26/48 at a threshold of ${P}_{{plei}-{test}}\le 0.20$) of trait pairs potentially influenced by correlated horizontal pleiotropy. A lenient p-value threshold is used here due to the prevalence of correlated horizontal pleiotropy²¹, a major contributor to false-positive causal inference. Within the trait pairs classified as Implausible or unsupported or Considered non-causal, a total of eight trait pairs were falsely identified by at least one of the alternative methods, seven of which were potentially influenced by correlated horizontal pleiotropy (${P}_{{plei}-{test}}\le 0.20$), with three exhibiting statistical significance (${P}_{{plei}-{test}}\le 0.05$). Notably, the relationship between high-density lipoprotein (HDL) and coronary artery disease (CAD) was yielding the highest statistical significance (${P}_{{plei}-{test}}=2.38\times {10}^{-4}$). These findings underscore the importance of using MR methods immune to correlated horizontal pleiotropy for accurate trait causation inference.

We then applied PCMR’s causality evaluation to those trait pairs that potentially presented correlated horizontal pleiotropy (${P}_{{plei}-{test}}\le 0.20$). PCMR’s causality evaluation obtained a P-value over 0.05 for all pairs in the Implausible or unsupported and Considered non-causal categories. HDL and CAD (Fig. 3d), identified by all alternative methods except Egger, can be considered a typical false positive example. This false positive of these alternative methods may be attributed to biased estimates. IVW, Weighted median, Median mode, MRAID, and CAUSE estimated the causal effect as $-0.184$, $-0.151$, $-0.131$, $-0.156$ and $-0.181$, respectively. In contrast, PCMR classified all IVs into two distinct IV categories with correlated HVP effects of ${\phi }_{1}=-0.07$ (${\sigma }_{{\phi }_{1}}^{2}=0.027$) and ${\phi }_{2}=-0.469\,({\sigma }_{{\phi }_{2}}^{2}=0.308)$, respectively. The effect of $-0.07$, supported by the largest IV category with a discernable probability of 97.1%, was close to Egger’s estimate of −0.068. Both PCMR’s causality evaluation and Egger revealed an insignificant relationship between HDL and CAD (${P}_{{PCMR}}=0.126,\,{P}_{{Egger}}=0.186$), which is consistent with the findings of Voight et al.²². Among the trait pairs classified as Considered causal and Supported by the literature, ten potentially present correlated horizontal pleiotropy, of which PCMR’s causality evaluation identified nine, with seven identified by all alternative methods. The remaining pair undiscovered by PCMR’s causality evaluation, fasting glucose and type 2 diabetes, as shown in Fig. 3c, was discussed in the Supplementary Discussion, Section SN 4.1. In addition to false positives, the opposite direction between correlated horizontal pleiotropic effect and causal effect results in conservative power. IVW and CAUSE did not identify the two causal relationships in body fat (BF) on CAD and BF on type 2 diabetes (T2D), possibly due to the estimated causal effect offset by opposite correlated horizontal pleiotropy (Fig. 3a, b). For instance, in the case of BF and CAD, the estimated causal effects of IVW and CAUSE were $-0.036$ and $0.13$, respectively, while PCMR estimated two opposite correlated HVP effects, being ${\phi }_{1}=0.448$ and ${\phi }_{2}=-0.665$. Moreover, the lack of an identified causal relationship between smoking and T2D by any method may also be attributed to the opposite correlated horizontal pleiotropy (Supplementary Discussion, Section SN 4.2). These analyses showed that PCMR’s causality evaluation avoided the false positives in the presence of correlated horizontal pleiotropy and identified causal relationships, even when there was an opposite correlated horizontal pleiotropic effect.

Fig. 3: Clustering results by PCMR for four trait pairs in the presence of correlated horizontal pleiotropy.

a, b BF and CAD, and BF and T2D. Both pair traits in the presence of significant correlated horizontal pleiotropy (PCMR’s pleiotropy test performing a two-sided hypothesis test of $\eta \,=\,0$: ${P}_{{BF}\to {CAD}}=1.16\times 1{0}^{-2},{P}_{{BF}\to T2D}=9.74\times {10}^{-3}$). IVW and CAUSE overlooked these two causal relationships, while PCMR’s causality evaluation, MRAID, Weighted median and Weighted mode found significant causal relationships. c FG and T2D. PCMR’s pleiotropy test detected significant correlated horizontal pleiotropy, ${P}_{{FG}\to T2D}=3.61\times {10}^{-2}$. Egger, Weighted mode and PCMR’s causality evaluation yielded insignificant relationship. d HDL and CAD. PCMR’s pleiotropy test found significantly correlated horizontal pleiotropy between HDL and CAD. (PCMR’s pleiotropy test: ${P}_{{HDL}\to {CAD}}=2.38\times {10}^{-4}$). Only PCMR’s causality evaluation and Egger avoided the potential false positive relationship. The error bars displayed around the points have a length equal to 1.96 times the standard error (s.e.) of the estimate on each side. The slopes indicate estimated correlated HVP effects by each IV category, where the blue IV category is at a higher proportion than the gray IV category. The range of shaded areas represents the variance of correlated HVP effects.

Besides, the classified IV categories by PCMR facilitate the integration of biological information for mechanism interpretation, offering an avenue to exclude correlated horizontal pleiotropic variants for enhancing causal inference (Supplementary Data 3). For instance, we conducted an enrichment analysis of biological processes among genes mapped by variants in different IV categories, aiding in identifying the IV category for causality. Notably, we observed enrichment differences among many trait pairs, such as triglycerides (TG) and coronary artery disease (CAD), FG and T2D, and other pairs (Supplementary Data 8). For example, in the case of high-density lipoprotein (HDL) and CAD, PCMR classified IVs into BLUE IV category and GRAY IV category, as shown in Fig. 3d. Enrichment analysis revealed that the BLUE category exhibited significant enrichment in 23 biological processes primarily related to lipids, with phospholipid homeostasis being the most significant ($1.58\times {10}^{-4}$). On the other hand, the GRAY category showed significant enrichment in 71 biological processes, primarily related to plasma lipoproteins, with plasma lipoprotein particle organization being the most significant ($6.32\times {10}^{-8}$). In particular, the enriched biological processes were consistent with studies linking plasma lipoproteins to CAD^23,24,25, indicating the GRAY category might exhibit correlated horizontal pleiotropy. So, we employed a bootstrap test to make a causal inference based on the IVs excluding the GRAY category, being the BLUE category, which inferred the relationship between HDL and CAD was insignificant (${\phi }_{{blue}}=-0.071$, ${P}_{{blue}}=0.184$, $95\%{CL}:\left(-{\mathrm{0.154,0.034}}\right)$). The result aligns with Voight et al.²², which avoided the false positive by discarding variants associated with other lipid and metabolic traits. This integrated analysis demonstrates the potential of PCMR in enhancing causal inference by excluding correlated horizontal pleiotropic variants through exploring biological processes.

PCMR facilitates causal inference for common psychiatric disorders

We applied PCMR to explore the intricate interrelationships among three common psychiatric disorders: schizophrenia (SCZ), major depressive disorder (MDD), and bipolar disorder I (BIP1). Given their substantial clinical and genetic overlaps²⁶, the potential causation relationships between these disorders remain controversial, bearing significance in understanding their pathogenic mechanisms. The inherent correlated horizontal pleiotropy within these disorder pairs further complicates the investigation into potential causal effects among these psychiatric disorders. As anticipated, PCMR’s pleiotropy test successfully identified three disorder pairs with significantly correlated horizontal pleiotropy at a threshold of ${P}_{{plei}-{test}}\le 0.05,$ and all pairs at a threshold of ${P}_{{plei}-{test}}\le 0.20$, with the most significant correlation at the SCZ and MDD pair (${P}_{{plei}-{test}}=1.83\times {10}^{-7}$) (Supplementary Data 4). Furthermore, the enriched biological processes demonstrated clear distinctions among classified IV categories in enrichment analyses across disorder pairs (Supplementary Data 8). To delve deeper into these relationships, we applied PCMR’s causality evaluation and six alternative methods to these disorder pairs. All alternative methods reported significant causal relationships (Supplementary Data 4), except for Egger, which found an insignificant relationship of causation from BIP1 on MDD ($P=0.099$), and MRAID, which identified two insignificant causal relationships: SCZ on MDD ($P=0.405$) and MDD on BIP1 ($P=0.228$). In contrast, PCMR’s causality evaluation identified three pairs with insignificant causation (consistent with those detected by Egger or MRAID): BIP1 on MDD ($P=0.968$), SCZ on MDD ($P=0.329$), and MDD on BIP1 ($P=0.159$), as illustrated in Fig. 4a.

Fig. 4: Causal relationships between three psychiatry disorders.

a The inferred causal relationships based on PCMR’s causality evaluation. b The inferred causal relationships based on the IV category with smaller correlated HVP effect by bootstrapping tests. Solid lines represent statistically significant relationships after Bonferroni correction (original p-value $\le 0.05/6$). c Enrichment analysis based on classified IV categories by PCMR in SCZ and MDD. The error bars displayed around the points have a length equal to 1.96 times the standard error (s.e.) of the estimate on each side. The slopes indicate estimated correlated HVP effects by each IV category, where the blue IV category is at a higher proportion than the gray IV category. The range of shaded areas represents the variance of correlated HVP effects. The table represents the enrichment analysis of biological processes among genes mapped by variants in the BLUE/GRAY IV category.

In addition, we explored the enrichment analysis of biological processes to exclude correlated horizontal pleiotropic variants for enhancing causal inference. Apart from MDD on SCZ, the enrichment analyses suggest that disorder pairs exhibit positively correlated horizontal pleiotropy (Supplementary Figs. 5–7). For instance, in the case of SCZ on MDD, PCMR classified IVs into BLUE IV category (${\phi }_{1}=0.187,\,{\sigma }_{{\phi }_{1}}^{2}=0.002$) and GRAY IV category (${\phi }_{2}=0.017,{\sigma }_{{\phi }_{2}}^{2}=0.004$) as shown in Fig. 4c. The BLUE category showed significant enrichment in 16 biological processes primarily related to signaling transmission, with chemical synaptic transmission being the most significant ($P=5.87\times {10}^{-4}$), while the GRAY category exhibited did not demonstrate enrichment in any biological process. As psychiatric disorders are associated with signal transmission²⁷, the BLUE category with a larger correlated HVP effect might exhibit correlated horizontal pleiotropy (${\phi }_{1}=\gamma+\eta$). Besides, meta-analysis has reported that variants associated with one psychiatric disorder increase the risk of the other two disorders²⁸, indicating positively correlated horizontal pleiotropy. Therefore, the IV category with a larger correlated HVP effect in these disorder pairs is likely to exist in correlated horizontal pleiotropy. We employed a bootstrap test to make causal inference based on the IV category with smaller correlated HVP effects, as shown in Fig. 4b, and discovered three disorder-pairs exhibiting insignificant causations, BIP1 on MDD ($\gamma=0.000,P=0.866$), SCZ on MDD ($\gamma=0.017,{P}=0.391$), and MDD on BIP1 ($\gamma=0.338,{P}=0.164$).

Discussion

This study introduces PCMR, a Pleiotropic Clustering model for MR analysis adept at clustering IVs with horizontal or vertical pleiotropic effects, to detect the trait pairs with correlated horizontal pleiotropy and enable a comprehensive causal inference for these trait pairs using GWAS summary statistics. Our extensive simulation studies illustrate PCMR’s performance in accurately isolating causal effects (Fig. 2a–c) and detecting correlated horizontal pleiotropy (Table 1). Furthermore, PCMR’s causality evaluation extends the ZEMPA and effectively controls false positive rates in the presence of correlated horizontal pleiotropy, even with a high proportion (Fig. 2d, e). PCMR is superior over alternative methods in scenarios where the causal effect and correlated horizontal pleiotropic effects exhibit opposing directions, leading to enhanced statistical power (Supplementary Fig. 1a). In real benchmark datasets, PCMR found about 15% (7 out of 48) trait pairs in common diseases and three out of six disorder pairs with significantly correlated horizontal pleiotropy (Table 2), including high-density lipoprotein (HDL) and coronary artery disease (CAD), and schizophrenia and major depressive disorder. In these pairs with correlated horizontal pleiotropy, PCMR identified the considered causal relationships and avoided the potential false positive between HDL and CAD. It also integrated biological processes to exclude correlated horizontal pleiotropic variants, enhancing causal inference and revealing the possible causal relationships between three common psychiatric disorders (Fig. 4a, b).

The resilience of PCMR to the influence of correlated horizontal pleiotropy stems from its methodological innovations. Firstly, diverging from previous approaches^7,11,16, PCMR amalgamates correlated pleiotropic and causal effects into a singular model component termed the unified correlated HVP effect. This integration is based on our observation that distinguishing between pleiotropic and causal effects at the level of individual IVs is mathematically impractical. Traditional methods that attempt to separate these effects into discrete model parameters may result in misestimations of either effect due to the indistinguishability, especially in the presence of many IVs with correlated pleiotropic effects. Secondly, this unified correlated HVP facilitates the creation of a flexible, classification-based framework capable of isolating potential causal effects without the need to presuppose the proportion of correlated horizontal pleiotropic effects. That represents a shift towards a hypothesis-free, data-driven approach, in stark contrast to many existing MR methods, which presuppose a minimal incidence of correlated horizontal pleiotropy relying on Bayesian priors to account for it^7,11—a technique that proves inadequate in our study when the prevalence of such effects is substantial (Fig. 2a, b and Supplementary Fig. 2). Lastly, this framework enables an evaluation method to accurately infer causality amidst a high prevalence of variants with correlated horizontal pleiotropic effects. Contrary to the widely held belief in the field that the largest groups of IVs are most indicative of causal effects (the ZEMPA assumption), our analysis suggests that IVs exhibiting correlated horizontal pleiotropy could erroneously form the largest group, especially exceeding 30% variants with correlated horizontal pleiotropy (Fig. 2a, b and Supplementary Fig. 2), potentially due to stochastic noise and sampling errors. This insight highlights why traditional MR methods may experience elevated false positive rates. In a departure from this, PCMR’s causality evaluation, which extends the ZEMPA scrutinizing the entire spectrum of IVs, directly tests for the presence of a non-zero causal effect by examining a differential dominance of IV categories. This approach equips PCMR to maintain controlled false positive rates, even when correlated horizontal pleiotropy is prevalent at levels as high as 40% (Fig. 2d, e).

The PCMR’s hypothesis-free classification paves the way for developing a pleiotropy test. This test uniquely identifies the presence of correlated horizontal pleiotropy, distinguishing it from uncorrelated pleiotropy. Unlike existing methods, such as MR-PRESSO, which failed to differentiate between the two, PCMR’s test can target correlated horizontal pleiotropy. This focus is crucial since correlated horizontal pleiotropy poses a greater challenge in avoiding false positives^7,29. In our analysis of real datasets, we found that about 15% (7 out of 48), with a ${P}_{{plei}-{test}}\le 0.05$ of trait pairs exhibited significantly correlated horizontal pleiotropy in the four common diseases (Stroke, T2D, Asthma and CAD), and this percentage increased to 50% at a more lenient threshold (${P}_{{plei}-{test}}\le 0.20$). Specifically, in the context of three common psychiatric disorders, three disorder pairs with significantly correlated horizontal pleiotropy at a threshold of ${P}_{{plei}-{test}}\le 0.05,$ and all pairs at a threshold of ${P}_{{plei}-{test}}\le 0.20$. These findings on the prevalence of correlated horizontal pleiotropy align with prior research⁷, which raises a challenge in differentiating true causal effects in practice.

Caution is warranted when interpreting the results of PCMR. Firstly, although PCMR can account for multiple correlated horizontal pleiotropies (Supplementary Fig. 10), determining the precise number of distinct types of correlated horizontal pleiotropy remains challenging in practice. Identifying the optimal number of categories in clustering algorithms is an open question. While we attempted to use traditional information criteria, such as AIC and BIC, to estimate the number of categories, the AIC tended to show more categories as the number of IVs increased, and the BIC tended to show fewer ones in real examples (Supplementary Table 4). However, if the primary goal is to investigate causal effects and perform causal analysis, the two-category model of PCMR may be sufficient in practice. In our analysis of 48 trait pairs, although the AIC criterion suggested that nine pairs (e.g., body mass index and type 2 diabetes) might benefit from a three-category model (Supplementary Fig. 8a, b), the estimates for the largest group—likely representing the causal effect—were highly correlated ($r=0.972$) between the two- and three-category PCMR models (Supplementary Fig. 8d). This strong correlation indicates that the two-category model may be sufficient for clustering the causal effect in practice. Furthermore, PCMR models correlated horizontal pleiotropies using a random effects model and demonstrated robustness in multiple correlated horizontal pleiotropies. Our extensive simulations confirmed that the two-category model provided reliable causality evaluations without inflating the type I error rate across scenarios involving two distinct correlated horizontal pleiotropies (Supplementary Fig. 11). Secondly, there is no universally optimal MR method for all scenarios. The two-category model of PCMR demonstrates superior performance in scenarios featuring correlated horizontal pleiotropy, showing lower false positive rates. However, in cases where correlated horizontal pleiotropy is absent, the two-category model tends to produce conservative results due to the introduction of redundant parameters. This conservatism can be mitigated by using a one-category model for the evaluation instead (Supplementary Fig. 12b). In practical application, PCMR’s pleiotropy test can be used to identify the presence of correlated horizontal pleiotropy, which in turn informs whether to apply a two-category causality evaluation. While some trait pairs may be falsely identified as pleiotropic, leading to conservative results, PCMR still retains statistical power comparable to methods such as Egger and Weighted Mode when correlated pleiotropy is absent (Supplementary Fig. 12c).

PCMR extends MR to accommodate scenarios with a high degree of correlated pleiotropy, allowing for isolating a specific IV category that determines the causal effect (Fig. 2a, b). However, it does not directly tell which group represents the true dominant group, showing the causal effect. Despite this, PCMR can estimate the likelihood that the largest IV group represents the dominant group, which helps gauge confidence in the inferred causal effect (see “Methods”). For example, across 26 common disease pairs (${P}_{{plei}-{test}}\le 0.20$), the estimates derived from the largest IV groups showed a strong correlation with the Weighted-mode method (r = 0.957, Supplementary Fig. 8c). However, the probability of these effects being truly causal varied widely, ranging from 50.5% to 97.1%. Only four trait pairs demonstrated a probability above 90%: High-density Lipoprotein and Coronary Artery Disease (largest IV effect: −0.07, probability: 97.1%), Triglycerides and Asthma (−0.011, 95.7%), Height and Asthma (0.036, 94.5%), and Birth Weight and Stroke (−0.246, 91.8%) (Supplementary Data 1).

Further analyses of the exact causal effects should incorporate more information to exclude correlated horizontal pleiotropic variants. Our study also shows how PCMR’s classification framework integrates biological insights to interpret the results on correlated horizontal pleiotropy. We grouped genes linked by these IVs by categorizing IVs based on their pleiotropic profiles, enabling subsequent bioinformatics analyses. Real data analyses reveal notable patterns: genes linked to potentially correlated horizontal pleiotropy tend to enrich Gene Ontology (GO) categories relevant to both exposure and outcome traits. For instance, in our examination of HDL to CAD causation, genes from smaller group IVs significantly enrich in processes related to plasma lipoproteins GO categories, which are relevant to both phenotypes^23,24,25 and indicate correlated horizontal pleiotropy. The inference based on the other IV group shows no causal link from HDL to CAD, consistent with previous studies^22,30. Similarly, in investigating SCZ to MDD causation, genes from the larger group of IVs enrich signaling transmission processes (Fig. 4c). These are biological characteristics highly relevant to both disorders^31,32,33, suggesting significant correlated horizontal pleiotropy within this group for both psychiatric diseases. Then, the absence of a significant correlated HVP effect (P = 0.38) within the other (the smaller) IV group supports no causal link from SCZ to MDD.

In summary, the proposed PCMR provides complements to the existing methodology: (1) its pleiotropy test detects the trait pairs with correlated pleiotropy, which is an important cause of false positives with existing methods; (2) its causality evaluation ensures valid causal analysis in the presence of correlated pleiotropy; and (3) its classification aids in integrating biological information to rule out pleiotropic variants for enhancing causal inference. PCMR offers efficient solutions for MR in detecting and addressing correlated horizontal pleiotropy.

Methods

PCMR for GWAS summary statistics

We use independent variants strongly associated with exposure as instrument variables (IVs), ${Z}_{i}\left(i=1,\cdots,p\right)$, at a threshold of $5\times {10}^{-8}$. Let $\left({\hat{\beta }}_{X,i},{\hat{s}}_{X,i}\right)$ and $\left({\hat{\beta }}_{Y,i},{\hat{s}}_{Y,i}\right)$ be effect estimates and standard errors at the IV ${Z}_{i}$ for traits exposure ($X$) and outcome ($Y$) in GWAS summary statistics. Assuming ${\beta }_{X,i}\,{{\rm{and}}}\,{\beta}_{Y,i}$ be the true marginal associations of ${Z}_{i}$ with $X$ and $Y$. We assume the effect estimates as normally distributed with global correlation⁷:

$$\left({{\hat{\beta }}_{X,i}}\atop{{\hat{\beta }}_{Y,i}}\right)\sim N\left(\left({{\beta }_{X,i}}\atop{{\beta }_{Y,i}}\right),{S}_{i}\left(\rho \right)\right)$$

(3)

where ${S}_{i}\left(\rho \right)=\left(\begin{array}{cc}{\hat{s}}_{X,i}^{2} & \rho {\hat{s}}_{X,i}{\hat{s}}_{Y,i}\\ \rho {\hat{s}}_{X,i}{\hat{s}}_{Y,i} & {\hat{s}}_{Y,i}^{2}\end{array}\right)$ and $\rho$ accounting for sample overlap is estimated empirically.

In the model of PCMR, we first put all IVs, including both horizontal pleiotropic IVs, into a unified framework as Fig. 1b. And we can express the relationship between the true marginal coefficients for the outcome ${\beta }_{Y,i}$ and exposure ${\beta }_{X,i}$ at $i$-th IV through this unified formula:

$${\beta }_{Y,i}=\left(\gamma+{\eta }^{i}\right){\beta }_{X,i}+{\theta\, }^{i},$$

(4)

where $\gamma$ is the causal effect of $X$ on $Y$, ${\eta }^{i}(\ne 0)$ is the correlated horizontal pleiotropic effect of ${Z}_{i}$ affecting $Y$ through confounder ${L}_{i}$ (scaling the effect of ${L}_{i}$ on $X$ to 1), and ${\theta }^{i}$ is an uncorrelated horizontal pleiotropic effect of ${Z}_{i}$ affecting $Y$ directly. Different parameters correspond to various types of IVs. It is important to note that $\gamma$ and ${\eta }^{i}$ are partial of the slope in the formula, and both effects are mathematically indistinguishable. Therefore, we integrate both effects as the sum of correlated horizontal and vertical pleiotropic effects, ${\phi }^{i}=\gamma+{\eta }^{i}$, labeled as correlated HVP effect. Besides, we simplify the two-dimensional normal distribution of ${\left({\hat{\beta }}_{X,i},{\hat{\beta }}_{Y,i}\right)}^{{{\rm{T}}}}$ to a one-dimensional normal distribution. We substitute Eq. (4) into Eq. (3) and obtain:

$${\hat{\beta }}_{Y,i}-{\phi }^{i}{\hat{\beta }}_{X,i}-{\theta }^{i}|{\phi }^{i},{\theta }^{i}\sim N\left(0,{\hat{s}}_{Y,i}^{2}-2{\phi }^{i}\cdot {cov}\left({\hat{\beta }}_{X,i},{\hat{\beta }}_{Y,i}\right)+{\left({\phi }^{i}\right)}^{2}\,{\hat{s}}_{X,i}^{2}\right)$$

(5)

where ${Cov}\left({\hat{\beta }}_{X,i},{\hat{\beta }}_{Y,i}\right)={Corr}\left(\frac{{\hat{\beta }}_{X,i}}{{\hat{s}}_{X,i}},\frac{{\hat{\beta }}_{Y,i}}{{\hat{s}}_{Y,i}}\right)\,{\hat{s}}_{X,i}\,{\hat{s}}_{Y,i}\approx \rho {\hat{s}}_{X,i}\,{\hat{s}}_{Y,i}$. This one-dimensional formulation is easier to solve for the parameters than the two-dimensional one.

In practice, the $n$ IVs selected from GWAS might affect the outcome through distinct pathways. For example, there may be a subset of these IVs that affect the outcome solely through exposure being valid (e.g., set ${C}_{1}$), being ${\eta }^{i}={\eta }_{1}=0$, and thus ${\phi }^{i}=\gamma,\,i\in {C}_{1}$; Another subset of IVs (e.g., set ${C}_{2}$) may influence both exposure and outcome through a shared heritable factor, such as a shared gene or pathway, leading to correlated pleiotropic effect ${\eta }_{2}({\eta }_{2}\ne 0),$ being ${\eta }^{i}={\eta }_{2}$, and thus ${\phi }^{i}=\gamma+{\eta }_{2}$ for$\,i\in {C}_{2}$; When additional IV categories (e.g., sets ${C}_{3},{C}_{4},\cdots$) are associated with distinct shared genes or pathways, multiple correlated pleiotropic effects ${\eta }_{j}({\eta }_{j}\ne 0)$ arise, leading to$\,{\phi }^{i}=\gamma+{\eta }_{j}$ for$\,i\in {C}_{j},j > 2$. It should be noted that even if multiple IVs (e.g., sets ${C}_{1},{C}_{2},\cdots$) may generate correlated pleiotropy through the same pathway; variations can occur due to differences in their specific locations within that pathway. It is more reasonable to assume that correlated horizontal pleiotropic effect follows a distribution like ${\eta }^{i}\sim N\left({\eta }_{j},{\sigma }_{{\eta }_{j}}^{2}\right),\,i\in {C}_{j}$. Consider that different IVs may have unique confounders affecting exposure X with outcome $Y$, as well as distinct direct effects on Y, leading to various correlated and uncorrelated pleiotropic effects. We apply mix-normal distribution to account for correlated HVP effects and uncorrelated horizontal pleiotropic effects, assuming

$$\left\{\begin{array}{c}{\phi }^{i}\sim {q}_{1}N\left({\phi }_{1},{\sigma }_{{\phi }_{1}}^{2}\right)+{q}_{2}N\left({\phi }_{2},{\sigma }_{{\phi }_{2}}^{2}\right)+\cdots+{q}_{{n}_{\eta }}N\left({\phi }_{{n}_{\phi }},{\sigma }_{{\phi }_{{n}_{\phi }}}^{2}\right)\\ {\theta\, }^{i}\sim {\pi }_{1}N\left({\theta }_{1},{\sigma }_{{\theta }_{1}}^{2}\right)+{\pi }_{2}N\left({\theta }_{2},{\sigma }_{{\theta }_{2}}^{2}\right)+\cdots+{\pi }_{{n}_{\theta }}N\left({\theta }_{{n}_{\theta }},{\sigma }_{{\theta }_{{n}_{\theta }}}^{2}\right)\end{array}\right.,$$

(6)

where ${n}_{\phi }$ and ${n}_{\theta }$ represent the types of correlated HVP effects (${\phi }_{1},{\phi }_{2},\cdots,{\phi }_{{n}_{\phi }}$) and uncorrelated horizontal pleiotropy (${\theta }_{1},{\theta }_{2},\cdots,{\theta }_{{n}_{\theta }}$), ${q}_{j},j=1,\cdots,{n}_{\phi }$ represent the proportion of IVs with correlated horizontal pleiotropic effect of ${\eta }_{j}$ and ${\sum }_{j}{q}_{j}=1$, and ${\pi }_{k},k=1,\cdots,{n}_{\eta }$ represent the proportion of IVs with uncorrelated horizontal pleiotropic effect of ${\theta }_{k}$, and ${\sum }_{k}{\pi }_{k}=1$. Two intuitive examples of conforming to a mixed-normal distribution were shown in Supplementary Discussion, SN 6.

We construct an equivalent form since constructing a joint density function of parameters is difficult. To simplify the derivation process of the model, we derive formulation (5) in a specific category of correlated and uncorrelated horizontal pleiotropic effects. i.e., ${q}_{1}\cdot {\pi }_{1}$ proportion of IVs with correlated HVP effect ${\phi }^{i}\sim N({\phi }_{j},{\sigma }_{{\phi }_{j}}^{2})$ and uncorrelated pleiotropic effect ${\theta }^{i}\sim N\left({\theta }_{k},{\sigma }_{{\theta }_{k}}^{2}\right)$. Substituting the parameters of this IV category into formulation (5), we can obtain:

$${\hat{\beta }}_{Y,i}-{\phi }_{j}{\hat{\beta }}_{X,i}-{\theta }_{k}\sim N\left(0,{\sigma }^{2}\right)$$

(7)

where ${\sigma }^{2}={\hat{s}}_{Y,i}^{2}-2{\phi }_{j}\cdot \rho {\hat{s}}_{X,i}\,{\hat{s}}_{Y,i}+{\left({\phi }_{j}\right)}^{2}\,{\hat{s}}_{X,i}^{2}+{\beta }_{X,i}^{2}{\sigma }_{{\phi }_{j}}^{2}+{\sigma }_{{\theta }_{k}}^{2}$. The density function of this normal distribution, $f\left({\hat{\beta }}_{Y,i}-{\phi }_{j}{\hat{\beta }}_{X,i}-{\theta }_{k}|{\phi }_{j},{\theta }_{k}\right)$, can be seen as an equivalence of the joint density function $f\left({\hat{\beta }}_{X,i},{\hat{s}}_{X,i},{\hat{\beta }}_{Y,i},{\hat{s}}_{Y,i}|{\phi }_{j},{\theta }_{k}\right)$.

Subsequently, we utilize the expectation-maximization (EM) algorithm to estimate parameters of interest in PCMR. Similar to the Gaussian mixed clustering model, we construct a log-likelihood function for the observed GWAS summary statistics based on the equivalent density function:

$${{\rm{ln}}}L\left(\Theta \right)\propto{\sum }_{i}{\sum }_{j}{\sum }_{k}\left[Q\left({Z}^{{\,}\left(i\right)}=\left(j,k\right)\right){{\rm{ln}}}\frac{f\left({\hat{\beta }}_{Y,i}-{\phi }_{{\,}j}{\hat{\beta }}_{X,i}-{\theta }_{k},\big | {\phi }_{j},{\theta }_{k}\right)\cdot {q}_{{\phi }_{j}}{\pi }_{{\theta }_{k}}}{Q\left({Z}^{\left(i\right)}=\left(j,k\right)\right)}\right]$$

(8)

where $\Theta$ represents unknown parameters in the model, including the parameters of interest (${q}_{j},{\phi }_{j},{\sigma }_{{\phi }_{j}}^{2},{\pi }_{k},\,{\theta }_{k},{\sigma }_{{\theta }_{k}}^{2}$), and $Q\left({Z}^{\left(i\right)}=\left(j,k\right)\right)$ is the probability of ${\phi }^{i}$ belongs to $N({\phi }_{j},{\sigma }_{{\phi }_{j}}^{2})$ and ${\theta }^{i}$ belongs to $N\left({\theta }_{k},{\sigma }_{{\theta }_{k}}^{2}\right)$. The unknown parameters can be estimated through maximum likelihood estimation, $\hat{\Theta }={{{\rm{arg}}}\,{\max}}_{\Theta}{\mathrm{ln}}L(\Theta)$. It should be noted that in addition to the parameters of interest, true marginal effects ${\beta }_{X,i}$ are unknown in the variance ${\sigma }^{2}$ of distribution (7). Although ${\beta }_{X,i}$ also can be estimated in EM algorithm, the excessive parameters lead to a complex and non-robust model. To address this issue, we propose two submodules of PCMR. The fixed effect model, which is similar to existing methods (like CAUSE), assumes that the $j$ th IV category shares the same confounder, resulting in ${\sigma }_{{\phi }_{j}}^{2}=0$ and ${\beta }_{X,i}{\sigma }_{{\phi }_{j}}^{2}=0$; In contrast, the random effect model considers the sharing of various confounders, resulting in ${\sigma }_{{\phi }_{j}}^{2}\ne 0$, and approximates ${\beta }_{X,i}$ by ${\hat{\beta }}_{X,i}$ to ensure the parameter estimation. We estimate the parameters of interest under these submodules in detail in Supplementary Methods, Section SN 1. Both submodules of PCMR are implemented in an open R package and applied in our simulations (The random effect model: Fig. 2, Supplementary Fig. 2; The fixed effect model: Supplementary Figs. 3 and 4). The random effect model is more reasonable in actual analysis and more sensitive in detecting correlated horizontal pleiotropy than a fixed effect model. Although the substitution of ${\beta }_{X,i}$ with ${\hat{\beta }}_{X,i}$ introduces estimation bias, the bias is small (More detail seeing Supplementary Discussion, SN 5). In this paper, the random effect model of PCMR is used by default.

Parameters setting and initialization

The EM algorithm requires initial parameter values before the start of the iteration. For correlated horizontal pleiotropy, we utilize quartiles of the effects estimated from all IVs as the initial values for correlated HVP effects:

$${\phi }_{j}={quantile}\left(\left\{\frac{{\hat{\beta }}_{Y,i}}{{\hat{\beta }}_{X,i}}{;\; i}={1,2},\cdots,p\right\}\,,\frac{j}{{n}_{\phi }+1}\right),{j}=1,\cdots,{n}_{\phi }.$$

(9)

Moreover, we maintain identical mixed proportion (${q}_{i}={q}_{j},i\,\ne\, j$) and set the variance of the correlated HVP effect to zero (${\sigma }_{{\phi }_{j}}^{2}=0,{j}=1,\cdots,{n}_{\phi }$) as the initial values. It should be noted that although PCMR can model multiple pleiotropic effect categories, the limited GWAS sample size and the number of available IVs can result in insufficient information for estimation. In this study, we focus on considering, at most, two groups of different correlated HVP effects (${n}_{\phi }\le 2$). When ${n}_{\phi }=1$, PCMR accounts for only one correlated HVP effect, namely the causal effect, similar to IVW. (Supplementary Data 1 and 4 PCMR(${n}_{\phi }=1$)) When ${n}_{\phi }=2$, PCMR models two types of correlated HVP effects: correlated horizontal pleiotropy and the causal effect. The PCMR with ${n}_{\phi }=2$ is the one we analyzed and compared in this paper.

For uncorrelated horizontal pleiotropy, we also consider only two types of uncorrelated horizontal pleiotropic effect, and we further simplify the mixed distribution into:

$${\theta \, }^{i}\sim {\pi }_{1}N\left({\theta }_{1},{\sigma }_{{\theta }_{1}}^{2}\right)+{\pi }_{2}{\theta }_{1}.$$

(10)

This assumption for uncorrelated horizontal pleiotropy is similar to MRAID¹¹. In addition, we introduce a parameter ${\theta }_{1}$ to assess overall uncorrelated horizontal pleiotropy. Under the distribution, the uncorrelated horizontal pleiotropic effect of the $i$-th IV follows a normal distribution with mean ${\theta }_{1}$ and variance ${\sigma }_{{\theta }_{1}}^{2}$ with probability ${\pi }_{1}$, while with probability ${\pi }_{2}$, it takes the value of ${\theta }_{1}$. We apply PCMR, setting ${\phi }_{j}=0,j=1,\cdots,{n}_{\phi },$ to estimate initial values for uncorrelated horizontal pleiotropy based on randomly selected variants.

PCMR’s pleiotropy test

The estimated correlated HVP effects by PCMR are identical or close in the absence of correlated horizontal pleiotropy but distinct when present. This difference between the two correlated HVP effects serves as an indicator to assess the presence of correlated horizontal pleiotropy. We utilize bootstrapping to measure whether the difference is significant. We perform $1000$ bootstraps to estimate the mean and variance of the correlated HVP effects. In each bootstrap iteration, we assign the smaller estimated correlated HVP effect to set S and the larger one to set L. L (or S) is a bootstrapping set of the larger (or smaller) correlated HVP effect. Then, we construct a statistic ${D}_{{HVP}}$ to measure the difference in estimated HVP effects:

$${\hat{D}}_{{HVP}}=\frac{{\left({\bar{\phi }}_{L}-{\bar{\phi }}_{S}\right)}^{2}}{{Var}\left({\phi }_{L}\right)+{Var}\left({\phi }_{S}\right)}.$$

(11)

This statistic considers the difference between estimated HVP effects and the stability of estimations using variances. In the absence of correlated horizontal pleiotropy (The null hypothesis), PCMR may also be influenced by the number of IVs, the dispersion of exposure effect estimates (${\hat{\beta }}_{X,i}$), the actual causal effect and the uncorrelated horizontal pleiotropy. To evaluate these four confounders, obtaining the distribution of ${D}_{{HVP}}$ in the null hypothesis, we conducted a sampling procedure to estimate c:

• 1. Keep the effect estimates and standard errors, $\left({\hat{\beta }}_{X,i},{\hat{s}}_{X,i}\right),i=1,\cdots,p$, retaining the same number of IVs and the dispersion of exposure effect estimates.

• 2. Estimate the causal effect $\hat{\gamma }$ by PCMR(${n}_{\phi }=1$), that is a consistent estimate of causal effect in the null hypothesis.

• 3. We then randomly sample $p$ variants and obtain effect estimates ${\hat{\beta }}_{Y,i}^{r}$ and standard errors ${\hat{s}}_{Y,i}^{r}$ of these variants for outcome ($Y$). And we simulate the marginal effects of instruments to outcome ($Y$) by:

  $$\left\{\begin{array}{c}{\widetilde{\beta }}_{Y,i}={\hat{\beta }}_{Y,i}^{r}+\hat{\gamma }\cdot {\beta }_{X,i}^{*}\\ {\widetilde{s}}_{Y,i}={\hat{s}}_{Y,i}^{r}\end{array}\right.,$$

  (12)

  where ${\beta }_{X,i}^{*}\sim N\left({\hat{\beta }}_{X,i},{\hat{s}}_{X,i}^{2}\right)$.

• 4. The simulated IVs contain all influences for PCMR except correlated horizontal pleiotropy. And we apply PCMR to calculate ${\hat{D}}_{{HVP}}^{r}$ in the null hypothesis by bootstrapping for ${K}_{1}$ times based on these simulated IVs.

• 5. Replicate the Steps 2–4 ${K}_{2}$ times, obtaining empirical distribution in the null hypothesis, ${\hat{D}}_{{HVP}}^{r},\,r=1,\cdots,{K}_{2}$.

Theoretically, PCMR’s pleiotropy test can assess the presence of correlated horizontal pleiotropy based on the empirical distribution. However, bootstrapping for the empirical is time-consuming and difficult to implement. To reduce the replication of bootstrapping, we propose to fit the empirical distribution by an approximate chi-square distribution, ${\chi }^{2}\left(c\right)$. We set ${K}_{1}=30$ and ${K}_{2}=100$ in our simulations, and estimate the factor $\hat{c}$ by fitting the ${\hat{D}}_{{HVP}}^{r},\,r=1,\cdots,{K}_{1}$ to the chi-square distribution ${\chi }^{2}\left(c\right)$. This approximation greatly reduces the times of bootstrapping and has a superior approximation (Supplementary Fig. 9). Considering the influence of ${K}_{1}$ and ${K}_{2}$ for the heterogeneity test, we also estimate the standard error of the factor $\hat{c}$ through simulation and evaluate the statistic range of PCMR’s pleiotropy test implemented in our open R package.

DEZMPA and causal estimation

PCMR extends the zero modal pleiotropy assumption (ZEMPA) to the discernible zero modal pleiotropy assumption (DZEMPA). Specifically, the assumption has two key components:

• 1. All variants associated with exposure are the statistical population of IVs in the whole genome. We assume the most frequent (or the dominant) estimates at the population IVs can be used to estimate the causal effect, being $\gamma={\phi }_{{{\rm{argmax}}}{q}_{j}}$. That is consistent with the ZEMPA;

• 2. However, only partial variants strongly associated with exposure are selected as the sample IVs, which might not correspond to the dominant population IVs due to the randomness inherent in GWAS sampling. Here, we assume the largest sample IV group should be discernible for the dominant population IVs (representing ${{\rm{argmax}}}{\hat{q}}_{j}={{\rm{argmax}}}{q}_{j}$) if they can be used to estimate the causal effect.

In the two-category model of PCMR, the dominant IV group is the majority group, making the DZEMPA equivalent to the discernible majority assumption. Compared to existing assumptions like ZEMPA and majority assumption, the proposed assumption considers potential inconsistency between the population IV group and the sample IV group due to randomness inherent in GWAS sampling.

The causal effect is driven by the dominant population IV group; however, estimating the causal effect based solely on the sample IVs is challenging. Estimating exact causal effects under specific assumptions can lead to bias in the presence of correlated horizontal pleiotropy. Our simulations showed that the exact causal effect estimation by alternative MR methods, including ZEMPA-PCMR, would become biased as the proportion of correlated horizontal pleiotropic variants increases (Fig. 2a, b). In contrast, PCMR estimates the causal effect by the discernible largest sample IV group, which is robust against the randomness inherent in GWAS sampling and tends to be the dominant population IV group. It is probabilistic that the largest sample IV group will be discernable as the dominant IV group. We use bootstrapping to calculate the probability of the largest sample IV group being discernible. Specifically, we perform 1000 bootstrap iterations to determine how often the correlated HVP effect supported by the largest sample IV group remains dominant across bootstraps. This frequency is interpreted as the probability that the largest sample group can be used to estimate the causal effect.

PCMR’s causality evaluation

We employ a likelihood ratio test (LRT) to evaluate whether there is a discernible dominant IV group supporting a non-zero causal effect:

$$\varLambda=2\left\{\mathop{sup }_{\varTheta }L\left(\varTheta |{q}_{j}={q}_{j}^{*},j=1,\cdots,{n}_{\phi }\right)-{sup }_{{\varTheta }_{0}}L\left({\varTheta }_{0}|{q}_{j}={q}_{j}^{*},j=1,\cdots,{n}_{\phi }\right)\right\}$$

(13)

Here, ${q}_{j}^{*}$ is the proportion of population IVs with correlated HVP pleiotropic effect of ${\phi }_{j}$. Under DEZMPA, the estimated effects of the dominant IV group (${{\arg}}\max \left({q}_{j}^{*}\right)$) are assumed to be free from correlated horizontal pleiotropy, i.e., ${\eta }^{i}=0$ and ${\phi }_{{{\arg}}\max \left({q}_{i}^{*}\right)}=\gamma$. $\varTheta$ represents the parameter space spanned by all parameters $\left(q,\phi,\cdots \right)$, and ${\varTheta }_{0}$ is the subset of $\varTheta$ where ${\phi }_{{{\arg}}\max \left({q}_{i}^{*}\right)}=\gamma=0$. The test statistic Λ follows a chi-squared distribution with 1 degree of freedom, and the LRT is a causal evaluation with ${n}_{\phi }-1$ types of correlated horizontal pleiotropy. When ${n}_{\phi }=1$, indicating a single correlated HVP effect as the casual effect, the LRT is akin to IVW method (Supplementary Data 1, 4). In this study, we primarily focus on demonstrating correlated horizontal pleiotropy (${n}_{\phi }=2$). The actual proportion ${q}_{j}^{*}$ of correlated horizontal pleiotropic variants is unknown, and we approximate it using the clustering proportion estimation ${\hat{q}}_{j}$ by PCMR.

Generating GWAS summary statistics

We simulate summary statistics using the R package causeSim, a CAUSE method simulation procedure⁷. In this package, the LD structure dataset is estimated by 19,490 HapMap variants on chromosome 19 in the CEU 1000 Genomes population, and this LD pattern is replicated 30 times, generating a genome-sized dataset of 584,700 variants. The effects of SNPs are generated by:

$${\beta }_{Y,i}\big|{Z}_{i}=\gamma {\beta }_{X,i}+{Z}_{i}{\eta }^{i}{\beta }_{X,i}+{\theta \, }^{i}$$

(14)

where $\gamma$ is the causal effect of $X$ on $Y$, and ${\eta }^{i}$ is the correlated pleiotropic effect of $U$ on $Y$ (scaling the effect of $U$ on $X$ to 1). ${Z}_{i}$ is an indicator that the $i$-th variant affects $U$ and is a 0-1 variable with probability $q$. ${\theta }^{i}$ represents the uncorrelated pleiotropy effect of variant $i$ on $Y$. Note that ${\tau }^{2}={\gamma }^{2}{h}_{X}^{2}/{h}_{Y}^{2}$ is proportion heritability of outcome $Y$ mediated by $X$ and ${\omega }^{2}=q{({\eta }^{i})}^{2}{h}_{X}^{2}/{h}_{Y}^{2}$ is the proportion heritability of outcome $Y$ mediated by $U$. In simulations, we apply the same parameters of the CAUSE method⁷, setting the heritability of exposure $X$(${h}_{X}^{2}$) and outcome $Y({h}_{X}^{2})$ to 0.25, the number of susceptible variants of exposure $X({m}_{X})$ and outcome $Y({m}_{Y})$ to $1000$ and the GWAS sample size of exposure and outcome to 40,000. A median of 107 genome-wide significant loci (defined as ${P} < \,5\,\times \,{10}^{-8}$) are identified as IVs after LD-pruning with an ${r}^{2}$ threshold of 0.1.

To test the effectiveness of PCMR, we simulate scenarios in the null and alternative hypotheses.

• In the null hypothesis ($\gamma=0$), we simulate scenarios with a proportion of correlated horizontal pleiotropic variants $\left(q=0\%,10\%,20\%,30\%,40\%,50\%\right)$ with different correlated horizontal pleiotropic effects from $\sqrt{0.01}$ to $\sqrt{0.05}$ (${\eta }^{i}=\sqrt{0.01},\sqrt{0.02},\sqrt{0.03},\sqrt{0.04},\sqrt{0.05}$).

• In the alternative hypothesis ($\gamma \ne 0$), we simulated three types of scenarios:

  • a. In the absence of correlated horizontal pleiotropy, we set the proportion heritability of outcome $Y$ mediated by $X$ (${\tau }^{2}=\frac{{\gamma }^{2}{h}_{X}^{2}}{{h}_{Y}^{2}},\,{\tau }^{2}=1\%,2\%,3\%,4\%,5\%$) to simulate with causal effects;

  • b. The correlated horizontal pleiotropic effect is in the same direction as the causal effect, setting the causal effect as $0.1$. We simulate scenarios with a proportion of correlated horizontal pleiotropic variants $\left(q=0\%,10\%,20\%,30\%,40\%,50\%\right)$, and set the proportion heritability of outcome $Y$ mediated by $X$ and $U$ at 0.05 (${\omega }^{2}+{\tau }^{2}=5\%$) to simulate positive correlated horizontal pleiotropic effects (${\eta }^{i} > 0$).

  • c. The correlated horizontal pleiotropic effect is in the opposite direction of the causal effect, setting the causal effect as $-0.1$. We simulate scenarios with a proportion of correlated horizontal pleiotropic variants $\left(q=0\%,10\%,20\%,30\%,40\%,50\%\right)$, and set the proportion heritability of outcome $Y$ mediated by $X$ and $U$ at 0.05 (${\omega }^{2}+{\tau }^{2}=5\%$) to simulate positive correlated horizontal pleiotropic effects (${\eta }^{i} > 0$).

In these simulations with correlated horizontal pleiotropy, the correlated HVP effects were denoted as ${\phi }^{i}=\gamma+0$ or ${\phi }^{i}=\gamma+{\eta }^{i}$. It should be noted that the simulated correlated horizontal pleiotropic effects are all positive ($\gamma+{\eta }^{i} > \gamma$), and the smaller correlated HVP effect would serve as the causal effect, being $\gamma=\min (\gamma,\gamma+{\eta }^{i})$. For the scenarios with negatively correlated HVP effects (${\eta }^{i} < 0$), they were mirror scenarios of the positive scenarios and did not affect the performance of PCMR (More detail seeing Supplementary Discussion, SN 7).

Summary level data

In the analysis of the dataset for common diseases, we referred to Morrison et al.⁷ to select a dataset comprising 12 common risk factors and four common diseases. The 12 common risk factors include: Triglycerides³⁴, low-density lipoprotein cholesterol³⁴, high-density lipoprotein cholesterol³⁴, height³⁵, body mass index³⁶, body fat percentage³⁷, birth weight³⁸, diastolic blood pressure³⁹, systolic blood pressure³⁹, fasting blood glucose⁴⁰, ever regular smoker⁴¹, and drinks per week⁴¹. The four common diseases are: coronary artery disease⁴², any stroke⁴³, type 2 diabetes⁴⁴, and asthma⁴⁵. In addition, another dataset we utilized pertains to three mental disorders: Schizophrenia³³, Major depressive disorder⁴⁶, and Type 1 bipolar disorder⁴⁷.

We followed steps similar to those implemented by Morrison et al.⁷ to preprocess the public GWAS summary data. To conduct MR analyses, we utilized the ‘gwas_merge‘ function from the CAUSE package. This function merged the GWAS summary statistics of trait pairs, and we retained only SNPs that reached genome-wide significance (z-test p-value $\le \,5\,\times \,{10}^{-8}$) in the exposure trait as potential IVs for their respective studies. In addition, we performed LD pruning with an ${r}^{2}$ threshold of $0.1$ to select a set of independent IVs for each analysis by PLINK1.9. The comprehensive list of all IVs used in the analysis is in Supplementary Data 2 for common diseases and Supplementary Data 5 for psychiatric disorders.

Enrichment analysis

PCMR excels in effectively clustering instruments, facilitating biological information integration for further analysis. Our additional simulations demonstrated that the proportion of correlated horizontal pleiotropic variants varies across the classified IV categories (Supplementary Table 5), offering the opportunity to combine biological insights to exclude pleiotropic categories. In real datasets, PCMR categorizes instrumental variables (IVs) into distinct groups based on the probability of belonging to distinct IV categories, as outlined in Supplementary Data 3 for common diseases and Supplementary Data 6 for psychiatric disorders. The mapped genes by these classified IV categories can be obtained at https://biit.cs.ut.ee/gprofiler/snpense, and biological process enrichment analysis can be conducted at https://biit.cs.ut.ee/gprofiler/gost⁴⁸.

Alternative MR methods

We compare the performance of PCMR with six alternative methods, including IVW, Egger, Weighted median, Weighted mode, CAUSE and MRAID. These comparison methods are based on different assumptions. IVW assumes that all variants used are valid IVs. Egger is based on the INSIDE assumption⁸. Weighted median and weighted mode utilize robust statistics, specifically the median and ZEMPA (Zero-Mode Pleiotropy Assumption), respectively. These three methods are implemented in the MendelianRandomization R package. CAUSE and MRAID assume that only a small proportion of correlated horizontal pleiotropy exists. We also compare PCMR’s pleiotropy test with MR-PRESSO outlier test in detecting two types of horizontal pleiotropy. The detailed parameterization of each method is provided in the Supplementary Methods, Section SN 2.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.