Introduction

Ever since Einstein and Schrödinger discussed “the characteristic trait of quantum mechanics” back in 19351,2, scientists have been studying its mysterious properties, with Feynman proposing to harness it for quantum computing3,4. Relatively recently, in 2022, the Nobel Prize in Physics was awarded jointly to Alain Aspect, John F. Clauser, and Anton Zeilinger “for experiments with entangled photons, establishing the violation of Bell inequalities and pioneering quantum information science”5. This is an appreciation of experimental implementations demonstrating non-locality of quantum mechanics with photons6,7,8,9,10 dating back to John Stewart Bell’s suggested experiment in 196411.

These early demonstrations did not consider all potential “loopholes” during experimental tests, which means that a local hidden variable theory could theoretically reproduce the gathered data12. So-called “loophole-free” Bell tests—experiments closing all major loopholes simultaneously—were demonstrated in 2015 and following years13,14,15,16,17 with NV centres in diamond and photons. In 2023 a loophole-free violation of Bell’s inequality was demonstrated with superconducting qubits, where a 30 m long cryogenic link was used in a remarkable effort to achieve spatial separation of the entangled qubits18,19.

Spin qubits in silicon are strong contenders for building a full-scale quantum computer due to their compatibility with semiconductor foundry processes20. The first violation of Bell’s inequality in silicon was demonstrated in an electron-nuclear donor spin system21. Although many demonstrations of Bell state tomography in gate-defined quantum dots have followed22,23,24,25,26,27, an experimental violation of Bell’s inequality in gate-defined quantum dots is still missing as of yet.

In this work, we violate Bell’s inequality in gate-defined quantum dots close to the theoretical quantum correlation limit28 and with 86σ confidence. We achieve this by operating electron spin qubits in silicon with state preparation and measurement (SPAM) and universal logic fidelities approaching the requirements for surface code error correction29,30,31,32. Even at elevated temperatures of 1.1 K, we measure Bell signals above the classical limit S = 2, with over 16σ confidence. Finally, we apply a dynamical decoupling sequence to store the generated entanglement for over 100 μs.

Full-scale fault-tolerant quantum computing processors require quantum logic operations across the entire chip with errors below the quantum error correction threshold to harness their full capabilities. However, operating large-scale qubit chips in densely packed cryogenic platforms generates excessive thermal loads, surpassing available cooling power at millikelvin temperatures33,34,35,36,37. Quantum entanglement is the fundamental requirement for the exponential computational advantage of quantum computers over classical computers. Despite possible loopholes, violating Bell’s inequality experimentally marks a key milestone for silicon quantum dot qubits, serving as a meaningful performance benchmark for simultaneous high-fidelity state preparation, manipulation, and measurement in a single quantum information processor.

Results

Device and two-qubit operation

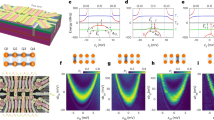
We operate the silicon-metal-oxide-semiconductor (SiMOS) device (Fig. 1a, b) in a double quantum dot with three electrons in each dot isolated from the reservoir (Fig. 1c). Two electrons in each dot form a spin-zero closed shell in the lower conduction band valley state and the remaining unpaired electron in the upper valley states of each silicon quantum dot forms an effective two-level system under influence of an external d.c. magnetic field operated as a qubit38,39. The quantum dots are electrostatically confined by a multi-layer aluminium gate-stack40 fabricated on top of an isotopically enriched  28Si substrate with 800 ppm residual  29Si41. The device is biased such that the quantum dots are separated by ~60 nm occupying around 80 nm2 underneath the plunger gates (P1, P2) at the Si/SiO2 interface. The exchange gate (J) in between gives control over the inter-dot separation and two-qubit exchange42,43,44 at an exponential rate of 24 dec V−1 (Fig. 1d). For single-shot charge readout, we integrate for tRO = 100 μs the radiofrequency single-electron transistor (RF-SET)45 signal at 165 MHz. An on-chip antenna delivers the a.c. magnetic field B1 to drive the electron spin state transitions.

Fig. 1: Device and basic operation.
figure 1

a Scanning electron micrograph of a device nominally identical to that used in this work. Active gate electrodes and the microwave antenna are highlighted with colours. An external d.c. magnetic field B0 and the antenna-generated a.c. magnetic field B1 are indicated with arrows. The system operates at T = 0.1 K, unless otherwise specified. b Transmission electron micrograph of the “active” region with schematics indicating the quantum dot and electron spin qubit formation at the Si/SiOx interface including exchange control. c Charge stability diagram in isolated mode as a function of P1, P2 voltage detuning ΔVG = −ΔVP1 = ΔVP2 and the J gate voltage VJ, showing six loaded electrons across the double-dot system. The d.c. plunger gate voltages are VP1 = 1.22 V and VP2 = 1.404 V. The operation points for readout (RO), single-qubit operation (Joff) and two-qubit operation (Jon) are labelled as star (⋆), square (■), and triangle (▴), respectively. d, e Probability of detecting a blockaded state, Pblockade, after a microwave burst of fixed power and duration at different J gate voltages VJ when preparing a mixed odd state \(\frac{1}{\sqrt{2}}(\left\vert \! \downarrow \uparrow \right\rangle+\left\vert \! \uparrow \downarrow \right\rangle )\) (d) and a pure state \(\left\vert \! \downarrow \downarrow \right\rangle\) (e). The power and duration of the microwave burst are roughly calibrated to a single-qubit π-rotation. The following experiments are conducted with \(\left\vert \! \downarrow \downarrow \right\rangle\) initialization, unless otherwise specified. f, g Q1 and Q2 single-qubit Rabi oscillations at VJ = 0.71 V as a function of pulse time tESR, respectively. h Decoupled controlled phase (DCZ) oscillations as a function of exchange time texchange and VJ at fixed ΔVG = −40 mV. i DCZ exchange oscillation fingerprint for fixed exchange time texchange = 5 μs as a function of ΔVG and VJ. The two-qubit operation point (Jon) labelled as a triangle (▴) is picked due to largest resilience against detuning noise. Readout probability is unscaled in all data. Error bars represent the 95% confidence level.

Full size image

A mixed odd state \(\frac{1}{\sqrt{2}}(\left\vert \! \downarrow \uparrow \right\rangle+\left\vert \! \uparrow \downarrow \right\rangle )\) can be initialized with a tinit = 2 μs ramp at VJ = 0.86 V across the (2,4) to (3,3) inter-dot charge transition (Fig. 1c, d). A pure odd state \(\left\vert \! \downarrow \uparrow \right\rangle\) is initialized by ramping across the anti-crossing at an increased VJ = 0.96 V (Supplementary Fig. 1). The pure even state \(\left\vert \! \downarrow \downarrow \right\rangle\) is then obtained by a π rotation on qubit 2 and confirming the state’s even parity46 (Fig. 1e). A detailed explanation of heralded initialization is under the “Methods” subsection “Heralded initialization protocol”.

We read out (RO) the spin state parity based on Pauli spin blockade (PSB)47. Charge movement near the inter-dot charge transition from (3,3) to (2,4) is blockaded when both unpaired spins are parallel.

Single-qubit gates are performed at VJ = 0.71 V (Joff) to minimize residual exchange interaction,  <10 kHz, between the two electron spins. Figure 1f, g show coherent Rabi oscillations of both qubits. Our two-qubit gates are implemented as decoupled controlled phase gates (DCZ)22,25 that are performed at VJ = 0.98 V (Jon). Figure 1h, i show exchange oscillations and the exchange fingerprint map at texchange = 5 μs.

Two-qubit benchmarking

In Fig. 2a we plot the full 2-qubit gate set’s average gate fidelity benchmarked by gate set tomography (GST)48,49 as a function of the Larmor frequency feedback rate ffeedback (see the “Methods” subsection “Larmor feedback protocol”). Faster feedback rates allow us to achieve significant improvements in the two-qubit XI and IX gates from FXI,avg = 94.42 ± 0.31% and FIX,avg = 97.54 ± 0.23% up to FXI,avg = 98.96 ± 0.12% and FIX,avg = 99.64 ± 0.10% by reducing the stochastic IZ and ZI error components attributed to phase loss50. Furthermore, the entangling DCZ gate is improved from FDCZ,avg = 97.82 ± 0.24% to FDCZ,avg = 98.98 ± 0.10%. The error components with the most significant reduction in infidelity contribution are the stochastic XI, YI, XZ, ZX, and YZ (see Supplementary Fig. 2). Additionally, we use the GST results to apply an informed phase correction calibrating for residual Larmor frequency mismatch (data point ⋆ in Fig. 2a).

Fig. 2: Two-qubit benchmarking using GST.
figure 2

a Gate infidelity as a function of the Larmor frequency feedback rate and number of GST sequences per feedback cycle. Other routinely performed feedback protocols65, like on the SET top gate voltage and spin resonance driving amplitude, remain unchanged throughout the manuscript. The star (⋆) indicates additional phase corrections based on the previous GST results. The green dashed line indicates the commonly considered 99% threshold. The inset is a zoom-in of the black-dashed box. b, c State preparation and measurement (SPAM) matrix, respectively. The insets show the respective theory matrix. d–f Error magnitude of error components for the XI, IX, and DCZ gates from GST with (coloured bars) and without (uncoloured bars) additional phase correction. The average gate fidelity is given above each plot for the phase corrected GST measurement. The on-target X gate fidelity FX,Qi can be calculated from the relevant error components. Hamiltonian errors contribute to the fidelity in second order, while stochastic errors contribute in first order. Error bars represent the 95% confidence level.

Full size image

Using these corrections, we can push all average gate fidelities above the commonly targeted threshold of 99%, including the state preparation and measurement (SPAM) fidelity (Fig. 2b, c): FXI,avg = 99.20 ± 0.11%, FIX,avg = 99.74 ± 0.10%, FZI,avg = 99.96 ± 0.11%, FIZ,avg = 99.87 ± 0.11%, FDCZ,avg = 99.09 ± 0.10%, and FSPAM = 99.23 ± 0.23%. Figure 2d–f compare the error magnitude of the XI, IX, and DCZ gates with and without the additional phase correction informed by GST. We calibrated the correction to minimize the Hamiltonian IZ and ZI phase error components, without affecting other error components. To emphasize the distinction from the average gate fidelities in the two-qubit context, we also calculate the single-qubit gate fidelities, which are FX,Q1 = 99.98 ± 0.22% and FX,Q2 = 99.93 ± 0.20%.

Bell test

Figure 3a shows the Bell experiment protocol; starting from a \(\left\vert \! \downarrow \downarrow \right\rangle\) state, we prepare one of the four Bell states (i) Φ+, (ii) Φ−, (iii) Ψ +, and (iv) Ψ −, followed by measurement via either a (I) rotated basis parity readout or (II) quantum state tomography. We use the latter to confirm the generation of the four maximally entangled Bell states with fidelities of \({F}_{{\Phi }^{+}}=97.17\pm 0.31\%\), \({F}_{{\Phi }^{-}}=96.94\pm 0.26\%\), \({F}_{{\Psi }^{+}}=96.50\pm 0.38\%\), and \({F}_{{\Psi }^{-}}=96.47\pm 0.31\%\), uncorrected for SPAM errors and at base temperature T = 0.1 K (Fig. 3d).

Fig. 3: Bell test.
figure 3

a Protocol for conducting the Bell test in a gate-defined double-dot electron spin system. After preparation of a maximally entangled Bell state (i–iv), the quantum correlation is measured via (I) a direct parity measurement after rotation of each qubit to obtain the desired combination of projection axes in two bases, rotated by π/4, or (II) quantum state tomography. b Schematic of the two projection basis \((\alpha,{\alpha }^{{\prime} })\) and \((\beta,{\beta }^{{\prime} })\) of the electron spin qubit in quantum dot 1 and 2, respectively. c Histograms of RF-SET readout signal for all four Bell states in all possible combinations of axis projections at T = 0.1 K. The data is fitted with a bimodal Gaussian distribution. The intersect of the two Gaussian curves is indicated by a dashed line defining the threshold for distinguishing odd (unblockaded) and even (blockaded) parity. d Quantum state tomography results for all four Bell states at T = 0.1 K. No corrections have been applied to compensate for initialization and readout errors. Insets indicate the theoretical density matrix of each Bell state. Error bars represent the 95% confidence level.

Full size image

Bell’s theorem11 provides a means to experimentally verify that local hidden variables do not play a role in quantum mechanics. This is done through the violation of the Clauser–Horne–Shimony–Holt (CHSH) inequality6 and requires measurement of the quantum correlations of the two-qubit spin pair along all combinations of measurement bases α = 0, \({\alpha }^{{\prime} }=-\pi /2\), β = π/4, and \({\beta }^{{\prime} }=-\pi /4\) (Fig. 3b). With parity readout, the quantum correlation in each of the four bases (α, β), \(({\alpha }^{{\prime} },\beta )\), \((\alpha,{\beta }^{{\prime} })\), and \(({\alpha }^{{\prime} },{\beta }^{{\prime} })\) becomes

$$E =\, \frac{{N}_{\uparrow \uparrow }-{N}_{\uparrow \downarrow }-{N}_{\downarrow \uparrow }+{N}_{\downarrow \downarrow }}{{N}_{\uparrow \uparrow }+{N}_{\uparrow \downarrow }+{N}_{\downarrow \uparrow }+{N}_{\downarrow \downarrow }}=\frac{{N}_{{{{\rm{even}}}}}-{N}_{{{{\rm{odd}}}}}}{{N}_{{{{\rm{total}}}}}}\\ =\,{P}_{{{{\rm{even}}}}}-{P}_{{{{\rm{odd}}}}}=2{P}_{{{{\rm{even}}}}}-1,$$
(1)

with the number of even, odd, and total number of readout events Neven = N↑↑ + N↓↓, Nodd = N↑↓ + N↓↑, and Ntotal = Neven + Nodd, respectively. Additionally, we use that the readout signal is either even or odd (Podd = 1 − Peven). With that, the CHSH inequality becomes

$$S =E(\alpha,\beta )-E(\alpha,{\beta }^{{\prime} })+E({\alpha }^{{\prime} },\beta )+E({\alpha }^{{\prime} },{\beta }^{{\prime} })\\ =2({P}_{{{{\rm{even}}}}}^{\alpha,\beta }-{P}_{{{{\rm{even}}}}}^{\alpha,{\beta }^{{\prime} }}+{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },\beta }+{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },{\beta }^{{\prime} }}-1)\ge 2,$$
(2)

and proves Bell’s theorem, if a Bell signal S > 2 is measured.

Hence, we can utilize parity measurements in these bases to obtain a direct insight into the correlation of quantum entanglement of the spin system. Figure 3c shows histograms of the RF-SET readout signal for all measurement basis combinations (α, β), \(({\alpha }^{{\prime} },\beta )\), \((\alpha,{\beta }^{{\prime} })\), and \(({\alpha }^{{\prime} },{\beta }^{{\prime} })\) for the four maximally entangled Bell states. Bimodal Gaussian fits allow us to extract the charge readout fidelity51 and the threshold used to best distinguish between even and odd parity. The measured Bell signals \({S}_{{\Phi }^{+}}=2.731(88)\), \({S}_{{\Phi }^{-}}=2.703(114)\), \({S}_{{\Psi }^{+}}=2.659(113)\), and \({S}_{{\Psi }^{-}}=2.675(115)\) are up to more than 16σ above the classical limit S = 2 from Bell’s theorem.

An alternative way to calculate the even parity probability Peven is by analytically transforming the density matrices measured via quantum state tomography (Fig. 3d) into the rotated bases

$${P}_{{{{\rm{even}}}}}^{\alpha \beta } ={P}_{\downarrow \downarrow }^{\alpha \beta }+{P}_{\uparrow \uparrow }^{\alpha \beta }\\ ={\left[R(\alpha )\otimes R(\beta )\times \rho \times \overline{R(\alpha )\otimes R(\beta )}\right]}_{00}\\ \,\,\,\,\,\,+{\left[R(\alpha )\otimes R(\beta )\times \rho \times \overline{R(\alpha )\otimes R(\beta )}\right]}_{33},$$
(3)

with the X gate rotation matrix

$${R}_{{{{\rm{X}}}}}(\varphi )=\left[\begin{array}{cc}\cos \varphi /2&-{\rm {i}}\sin \varphi /2\\ -{\rm {i}}\sin \varphi /2&\cos \varphi /2\end{array}\right].$$
(4)

By respective combinations of α  = 0, \({\alpha }^{{\prime} }=-\pi /2\), β = π/4, and \({\beta }^{{\prime} }=-\pi /4\) we can calculate the Bell signal S according to Eq. (2). At base temperature T = 0.1 K we achieve \({S}_{{\Phi }^{+}}=2.721(30)\), \({S}_{{\Phi }^{-}}=2.711(28)\), \({S}_{{\Psi }^{+}}=2.703(32)\), and \({S}_{{\Psi }^{-}}=2.693(16)\) with up to more than 86σ above the classical limit S = 2 from Bell’s theorem. Comparing both methods we get matching and consistently high Bell signals.

Bell test—temperature dependence

We extend the violation of Bell’s inequality to operation temperatures of up to 1.1 K in Fig. 4a. We maintain Bell signals of \({S}_{{\Phi }^{+}}=2.101(64)\), \({S}_{{\Phi }^{-}}=2.100(71)\), \({S}_{{\Psi }^{+}}=2.088(53)\), and \({S}_{{\Psi }^{-}}=2.061(39)\) measured via state tomography (filled symbols), and \({S}_{{\Phi }^{+}}=2.068(154)\), \({S}_{{\Phi }^{-}}=2.036(181)\), \({S}_{{\Psi }^{+}}=2.127(176)\), and \({S}_{{\Psi }^{-}}=2.142(109)\) measured via basis rotation, i.e., direct parity measurement (open symbols), respectively. Values consistently above the classical limit demonstrate that the quantum correlation is maintained up to this temperature. Density matrices and RF-SET signal histograms of all Bell states and temperatures up to 1.1 K are shown in Supplementary Figs. 3 and  4, respectively.

Fig. 4: Bell test—temperature dependence.
figure 4

a Bell signal S as a function of temperature T for all four maximally entangled Bell states measured by the direct parity measurement (open symbols) and quantum state tomography (filled symbols). b Bell state (FBell) and charge readout (FCRO) fidelities as a function of temperature T for all four maximally entangled Bell states obtained from quantum state tomography and RF-SET signal histograms, respectively. Error bars represent the 95% confidence level.

Full size image

Figure 4b shows the Bell state and charge readout fidelities as a function of operation temperature. The charge readout fidelity is almost unity up to T = 0.7 K and then only drops to FCRO = 99.02 ± 0.13% when the histogram peaks start to overlap significantly at T = 1.1 K. Naturally, this could be improved by increasing the integration time if it were considered a limiting factor for the quantum correlation measurement. However, the decrease of the uncorrected Bell state fidelity originating from a combination of deteriorated initialization, coherence and spin-to-charge conversion is evidently the reason for approaching the classical limit.

Bell state lifetime

After having discussed how the Bell state fidelity and level of entanglement are affected by temperature, in this section, we focus on the effect of idling time. This is particularly relevant for quantum information purposes when considering running an actual quantum circuit. Figure 5a shows the protocol for Ramsey and Hahn Echo experiments on Bell states measured using quantum state tomography. Figure 5b shows the Bell signal as a function of the wait time after the state preparation at base temperature. We observe that the Bell states undergo decoherence and stay above the classical limit (S > 2) for about 15 μs. The frequency detuning of Q1 and Q2 from their respective Larmor frequency leads to an oscillation in the Ramsey signal of the Φ and Ψ Bell states following (fMW,Q1 − fL,Q1) ± (fMW,Q2 − fL,Q2), respectively. The Φ and Ψ states are naturally grouped due to their respective symmetric and antisymmetric character, resulting in the accumulation of the same phase. We find a small correlation coefficient of ρ = 0.15(14) for low-frequency noise assuming a Gaussian quasi-static noise model52. This most likely originates from charge noise that affects both qubits slightly since nuclear spin noise is expected to be uncorrelated.

Fig. 5: Bell state lifetime.
figure 5

a Protocol for conducting (I) Ramsey and (II) Hahn echo experiments on maximally entangled Bell states. The density matrix is measured by quantum state tomography. b Bell signal S as a function of wait time τwait after preparation of the four maximally entangled Bell states at T = 0.1 K. c Bell signal S of the four maximally entangled Bell states as a function of a total wait time τwait being equally separated by a single, consecutive refocusing π pulse on Q1 and Q2 at 0.1 K. The Q1 and Q2 single qubit coherence times are indicated by the blue and red dashed lines, respectively. Error bars represent the 95% confidence level.

Full size image

The lifetime of maximally entangled Bell states can be prolonged by an order of magnitude to above 100 μs when applying a Hahn echo refocusing pulse (Fig. 5c), and we expect the lifetime can be prolonged even further by higher-order dynamical decoupling sequences. The oscillations in the Bell signal originate from the time-correlated nature of the IZ and ZI noise in the spin system. The decay times of the envelopes are extracted from exponential fits to the square sum of the state’s Pauli projections (Supplementary Fig. 5). We do not observe significant spatial correlation during Hahn echo experiments, since the product of the single-qubit decays \({T}_{{{{\rm{2,Q1*Q2}}}}}^{{{{\rm{Hahn}}}}}=235\pm 21\,\mu {{{\rm{s}}}}\) matches the Bell state lifetimes. At higher temperatures the Bell state Ramsey and Hahn lifetimes decrease from around 20 and 250 μs to 5 and 50 μs, respectively (Supplementary Figs. 6–8). The temporal and spatial noise correlations are unchanged (Supplementary Figs. 9 and 10).

Discussion

The deterministic preparation, storage and measurement of the maximally entangled quantum states that violate Bell’s inequality with S = 2.731(88) at 0.1 K and 2.142(109) at 1.1 K provides a milestone for quantum information processing with gate-defined quantum dots in silicon. Systematically reducing the error sources, carefully identified during this study, will allow us to improve operation fidelities further and bring the fundamental quantum limit28 even closer. We also expect those improvements and longer dynamical decoupling sequences to further enhance the capabilities to prolong the lifetime of entanglement stored in a quantum circuit required for computation.

Evidently, incoherent dephasing errors are the dominating source of gate infidelities. In the future, we expect to increase qubit operation fidelities by improving the quality of the Si/SiO2 interface and the SiO2 layer as well as implementing more sophisticated, real-time phase tracking methods in the experimental setup. Additionally, the fabrication of SiMOS devices in industrial foundries20,53 will bring a reduction in defects, charge impurities54,55, and residual  29Si, which will increase qubit coherence times and decrease required feedback schemes.

GST enables us to develop error-dependent, tailored control pulse shapes to mitigate coherent errors arising from miscalibration and parameter drifts, as demonstrated by successfully implementing Hamiltonian phase corrections. Furthermore, we identified dephasing during free precession of the idling qubit as the major infidelity contribution in this study. To realize a full-scale fault-tolerant quantum computer based on silicon spin qubits, we need scalable control techniques, such as the multi-qubit SMART protocol56,57,58,59. In the SMART protocol, qubits are continuously driven by a modulated microwave field, which decouples the qubits from noise and eliminates free precession, and hence the major infidelity source. Scaling up the number of high-fidelity silicon spin qubits with successful CMOS chip manufacturing methods60, will enable us to extend this work to quantum correlation measurements on a tripartite61 or multipartite62 system to violate Mermin’s inequality63 and conduct quantum teleportation64 experiments in ever larger gate-defined quantum dot processors. Furthermore, these larger systems can be utilized to close possible loopholes, which remained unaddressed in this study.

Methods

Experimental device

The device studied in this work was fabricated using multi-layer aluminium (Al) gate-stack silicon MOS technology on isotopically enriched silicon-28 substrates of 800 ppm residual 29Si. An 8 nm high-quality SiO2 was thermally grown on the silicon substrate. Al gates were fabricated using electron-beam lithography, thermal deposition of Al and lift-off process. Each Al electrode is electrically isolated by a layer of aluminium oxide of 4 nm formed via thermal oxidation on a hotplate at 150 °C. The devices are designed with a plunger gate width of 35 nm and a gate pitch as small as 55 nm. This allows a 20 nm gap between the plunger gates for the J gate.

Measurement setup

The device is measured in a K100 Kelvinox dilution refrigerator and mounted on the cold finger. Up to T = 1.1 K, elevation from the base temperature is achieved by switching on and tuning the heater near the sample. Stable temperatures above 1.1 K can only be achieved by reducing the amount of He mixture in the circulation and consequently the cooling power.

An external DC magnetic field is supplied by an IPS120-10 Oxford superconducting magnet. The magnetic field points along the [110] direction of the Si lattice. DC voltages are supplied with a QDevil QDAC, through DC lines with a bandwidth from 0 to 100 Hz–10 kHz. Dynamic voltage pulses are generated with Quantum Machines OPX+ and combined with DC voltages via custom voltage combiners on top of the refrigerator at room temperature. The OPX+ has a sampling time of 4 ns. The dynamic pulse lines in the fridge have a bandwidth of 0–50 MHz, which translates into a minimum rise time of 20 ns. Microwave pulses are synthesized using a Keysight PSG8267D Vector Signal Generator, with the baseband I/Q and pulse modulation signals supplied by the OPX+. The modulated signal spans from 250 kHz to 44 GHz, but is band-limited by the fridge line and a DC block.

The charge sensor comprises a single-island SET connected to a tank circuit for reflectometry measurement. The return signal is amplified by a Cosmic Microwave Technology CITFL1 LNA at the 4 K stage followed by two Mini-circuits ZFL-1000LN+ LNAs at room temperature. The Quantum Machines OPX+ generates the tones for the RF-SET and digitizes and demodulates the signals after the amplification.

Heralded initialization protocol

The heralded initialization protocol follows:

  1. 1.

    Initialize a pure odd state \(\left\vert \! \downarrow \uparrow \right\rangle\) with a detuning ΔVG ramp at VJ = 0.96 V in tinit = 2 μs over the anti-crossing. The J-level and ramp time can be easily calibrated in PESOS-like map by fixing the control point and sweeping the J-level and ramp time.

  2. 2.

    Convert the pure odd state \(\left\vert \! \downarrow \uparrow \right\rangle\) to a pure even state \(\left\vert \! \downarrow \downarrow \right\rangle\) with a well-calibrated π rotation on qubit 2.

  3. 3.

    The state's parity is checked via readout. (a) If the state is unblockaded (\(\left\vert \! \downarrow \uparrow \right\rangle\) or \(\left\vert \! \uparrow \downarrow \right\rangle\)), the initialization restarts. (b) If the state is blockaded (\(\left\vert \! \uparrow \uparrow \right\rangle\) or \(\left\vert \! \downarrow \downarrow \right\rangle\)), the initialization is complete.

This initialization protocol heralds into an even parity state (\(\left\vert \! \uparrow \uparrow \right\rangle\) or \(\left\vert \! \downarrow \downarrow \right\rangle\)) by single-qubit control and measurement. Two-qubit control allows you to implement a more advanced algorithmic initialization protocol to further differentiate between the even parity states46. This has not been used during this study as the pure odd state \(\left\vert \! \downarrow \uparrow \right\rangle\) initialization is high-fidelity (Supplementary Fig. 1).

Larmor feedback protocol

The Larmor frequency feedback protocol—based on a modified Ramsey sequence—follows:

  1. 1.

    Apply a π/2 rotation around the x-axis on the target qubit to bring it into a superposition \(\frac{1}{\sqrt{2}}(\left\vert \! \! \downarrow \right\rangle+\left\vert \! \! \uparrow \right\rangle )\).

  2. 2.

    Let the qubit idle for a time twait = 20 ns.

  3. 3.

    Apply a π/2 rotation around the  ±y-axis to obtain  ±Z projection on the readout basis.

  4. 4.

    Apply a proportional correction of αL,corr to the Larmor frequency stored in the FPGA based on the difference in return spin–flip probabilities of the two projections.

In the ideal case of no frequency detuning, the two projections both return spin–flip probabilities of 0.5. This and other feedback protocols are commonly used in silicon spin qubits65.

Bell’s theorem and quantum correlation

The quantum correlations of the spin pairs are

$$E =\frac{{N}_{\uparrow \uparrow }-{\,N}_{\uparrow \downarrow }-{\,N}_{\downarrow \uparrow }+{\,N}_{\downarrow \downarrow }}{{N}_{\uparrow \uparrow }+{N}_{\uparrow \downarrow }+{N}_{\downarrow \uparrow }+{\,N}_{\downarrow \downarrow }}\\ =\frac{{N}_{\uparrow \uparrow }-{\,N}_{\uparrow \downarrow }-{\,N}_{\downarrow \uparrow }+{N}_{\downarrow \downarrow }}{{N}_{{{{\rm{total}}}}}}\\ =\frac{{N}_{{{{\rm{even}}}}\,}-{\,N}_{{{{\rm{odd}}}}}}{{N}_{{{{\rm{total}}}}}}\\ ={P}_{{{{\rm{even}}}}}-{P}_{{{{\rm{odd}}}}}\\ =2{P}_{{{{\rm{even}}}}}-1,$$
(5)

while assuming parity readout. The Clauser–Horne–Shimony–Holt (CHSH) inequality6 then becomes

$$S =\langle \alpha,\beta \rangle -\langle \alpha,{\beta }^{{\prime} }\rangle+\langle {\alpha }^{{\prime} },\beta \rangle+\langle {\alpha }^{{\prime} },{\beta }^{{\prime} }\rangle \\ =E(\alpha,\beta )-E(\alpha,{\beta }^{{\prime} })+E({\alpha }^{{\prime} },\beta )+E({\alpha }^{{\prime} },{\beta }^{{\prime} })\\ =2({P}_{{{{\rm{even}}}}}^{\alpha,\beta }-{P}_{{{{\rm{even}}}}}^{\alpha,{\beta }^{{\prime} }}+{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },\beta }+{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },{\beta }^{{\prime} }}-1)\\ \ge 2,$$
(6)

with combinations of measurement basis α = 0, β = π/4, \({\alpha }^{{\prime} }=-\pi /2\), and \({\beta }^{{\prime} }=-\pi /4\). For the four different Bell states we have to adjust the signs/measurement axis to

$${S}^{\Phi+} =E(\alpha,\beta )+E(\alpha,{\beta }^{{\prime} })+E({\alpha }^{{\prime} },\beta )-E({\alpha }^{{\prime} },{\beta }^{{\prime} })\\ =2({P}_{{{{\rm{even}}}}}^{\alpha,\beta }+{P}_{{{{\rm{even}}}}}^{\alpha,{\beta }^{{\prime} }}+{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },\beta }-{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },{\beta }^{{\prime} }}-1),$$
(7)
$${S}^{\Phi -} =E(\alpha,\beta )-E(\alpha,{\beta }^{{\prime} })+E({\alpha }^{{\prime} },\beta )+E({\alpha }^{{\prime} },{\beta }^{{\prime} })\\ =2({P}_{{{{\rm{even}}}}}^{\alpha,\beta }-{P}_{{{{\rm{even}}}}}^{\alpha,{\beta }^{{\prime} }}+{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },\beta }+{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },{\beta }^{{\prime} }}-1),$$
(8)
$${S}^{\Psi+} =-E(\alpha,\beta )-E(\alpha,{\beta }^{{\prime} })-E({\alpha }^{{\prime} },\beta )+E({\alpha }^{{\prime} },{\beta }^{{\prime} })\\ =2(-{P}_{{{{\rm{even}}}}}^{\alpha,\beta }-{P}_{{{{\rm{even}}}}}^{\alpha,{\beta }^{{\prime} }}-{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },\beta }+{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },{\beta }^{{\prime} }}+1),$$
(9)

and

$${S}^{\Psi -} =-E(\alpha,\beta )+E(\alpha,{\beta }^{{\prime} })-E({\alpha }^{{\prime} },\beta )-E({\alpha }^{{\prime} },{\beta }^{{\prime} })\\ =2(-{P}_{{{{\rm{even}}}}}^{\alpha,\beta }+{P}_{{{{\rm{even}}}}}^{\alpha,{\beta }^{{\prime} }}-{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },\beta }-{P}_{{{{\rm{even}}}}}^{{\alpha }^{{\prime} },{\beta }^{{\prime} }}+1).$$
(10)

We measure the even parity of the spin states after the physical rotation to the (α, β), \((\alpha,{\beta }^{{\prime} })\), \(({\alpha }^{{\prime} },\beta )\), and \(({\alpha }^{{\prime} },{\beta }^{{\prime} })\) bases.

An alternative approach is to measure the Bell states’ density matrix ρ with quantum state tomography and apply the respective rotation analytically. For that, we apply the rotation matrix

$${R}(\varphi )=\left[\begin{array}{cc}\cos \varphi /2&-{ {i}}\sin \varphi /2\\ -{{i}}\sin \varphi /2&\cos \varphi /2\end{array}\right]$$
(11)

with α = 0, β = π/4, \({\alpha }^{{\prime} }=-\pi /2\), and \({\beta }^{{\prime} }=-\pi /4\) to calculate the even parity

$${P}_{{{{\rm{even}}}}}^{\alpha \beta } ={P}_{\downarrow \downarrow }^{\alpha \beta }+{P}_{\uparrow \uparrow }^{\alpha \beta }\\ ={\left[R(\alpha )\otimes R(\beta )\times \rho \times \overline{R(\alpha )\otimes R(\beta )}\right]}_{00}\\ \,\,\,\,\,\,+{\left[R(\alpha )\otimes R(\beta )\times \rho \times \overline{R(\alpha )\otimes R(\beta )}\right]}_{33}.$$
(12)

Error taxonomy with pyGSTi

When examining the fidelity results, we are also interested in understanding the dominant error sources behind the XI, IX, and DCZ gate infidelity. To categorize the gate errors, we use gate set tomography for decomposing errors implemented in the pyGSTi package66,67.