Observation of Berry curvature in non-Hermitian system from far-field radiation

Abstract

Berry curvature that describes local geometrical properties of energy bands can elucidate many fascinating phenomena in solid-state, photonic, and phononic systems, given its connection to global topological invariants such as the Chern number. Despite its significance, the observation of Berry curvature poses a substantial challenge since wavefunctions are deeply embedded within the system. Here, we theoretically propose a correspondence between the geometry of far-field polarization and the underneath band topology in non-Hermitian systems, thus providing a general method to fully capture the Berry curvature without strongly disturbing the eigenstates. We further experimentally observe the Berry curvature in a honeycomb photonic crystal slab from polarimetry measurements and quantitatively obtain the nontrivial valley Chern number. Our work reveals the feasibility of retrieving the bulk band topology from escaping photons and paves the way to exploring intriguing topological landscapes in non-Hermitian systems.

Introduction

Topology, namely the mathematics of conserved properties under continuous deformations, is creating a range of new opportunities throughout matters, photonics, phononics, and other wave systems^1,2,3,4,5,6. To characterize the topology in physics, the Berry curvature^7,8 is an essential concept that describes the local, gauge-invariant, geometric manifestation of the wavefunctions in the parameter space, which is closely related to the global topological invariants such as a variety of Chern numbers^{9,10,11,12,13}. However, since Berry curvature belongs to the intrinsic topological property of wavefunctions, it is usually deeply bound inside the system and difficult to observe. Although using tomography can reconstruct the wavefunctions in some particular scenarios^14,15, much effort has been devoted to retrieving the Berry curvature from its external consequence in physics. Examples include Hall drift in driving optical lattice^16,17,18 or synthetic gauge field^19,20, Aharonov–Bohm interference of magnetic-controlled ultracold atom^21,22,23,24, and pseudospin^{25,26,27,28,29,30} or dichroism^31,32 in exciton-polariton-correlated material. Even though the specific physics varies, the mentioned observations of Berry curvature generally rely on the strong light-matter interaction to imprint the topological features of bulk wavefunction to external observables, and thus they should be categorized into the class of “strong measurement”³³, namely the observation strongly interfering with the system. In comparison, the method of measuring the Berry curvature without much disturbing the eigenstates³⁴ remains absent.

It is well-recognized that open photonic systems necessarily lose photons to their surroundings. As a major route of energy exchange, the far-field radiation naturally carries information about wavefunctions and thus allows direct access to the intrinsic bulk topology, which would be conventionally thought impossible. Here, the escaping photons simply act as the “messengers” that weakly interact with the system, and could bridge the bulk band and radiation. For example, some advances in probing Chern numbers from the far field are reported, in which either phases and intensity³⁵, or frequency and quality factor³⁶ are chosen as observables. However, due to the difficulty in experiments and the lack of degree-of-freedom (DOF), they are probably not ideal observables to enable the direct observation of Berry curvature in general non-Hermitian multi-level photonic systems^{6,37,38,39,40}. Hereby we propose that, the far-field polarization is a more applicable candidate because it provides sufficient DOFs, and more importantly, the orientation and ellipticity of polarization can be readily and robustly measured in a time-averaging manner. In fact, the nontrivial geometric features of far-field polarization^{41,42,43,44,45,46,47} has attracted much attention in recent years because they give rise to interesting physical consequences such as polarization half-charge around paired exceptional point^48,49, vortex beam⁵⁰, chiral devices with circular dichroism^51,52, bound states in the continuum (BICs)^{53,54,55,56,57,58,59,60,61} and unidirectional guided resonances (UGRs)^62,63,64. However, the intrinsic connection between the polarization and the bulk wavefunction is still unrevealed, and how to retrieve the Berry curvature from the far-field polarization features still remains an elusive question.

Here we theoretically establish a correspondence between the band topology and radiation geometry to experimentally observe the Berry curvature by characterizing the polarization of escaping photons from a non-Hermitian photonic crystal (PhC) slab system. We prove that, Berry curvatures of bulk bands can be captured by using observable bi-orthogonal polarization vectors in a non-Hermitian system⁴⁰. As long as the radiation fields are smooth and well-defined, a full tomography of the Berry curvature can be realized by simply measuring the polarization of a number of radiation channels. Specifically, for a two-level system, only one radiation channel is sufficient. Accordingly, we experimentally observe the nontrivial Berry curvatures originating from the diabolic point (DP) in a honeycomb-latticed PhC slab by using a standard polarimetry measurement⁶⁵. The Berry phases^2,7,66 of γ ~ ±π are obtained in an individual valley by employing integrals of the observed Berry curvature, showing nontrivial valley-Chern numbers^11,13 of ${C}_{v}^{{{{\mathcal{K}}}}} \sim \pm 1/2$ as expected, and thus quantitatively validate our method.

Results

The bulk-radiation correspondence of the Berry curvature

We start from an infinite two-dimensional (2D) PhC slab operating in the radiation continuum as schematically illustrated in Fig. 1A, which has translational symmetry in both x and y directions. According to the Bloch theorem, the system is ruled by a bulk momentum-space Hamiltonian $\hat{H}({{{{\bf{k}}}}}_{\parallel })$, supporting multiple bulk Bloch modes whose cell-periodic Bloch function is denoted as $| {u}_{n}({{{{\bf{k}}}}}_{\parallel })\left.\right\rangle$. The subscript n labels the energy bands, and k_∥ is the in-plane Bloch wavevector. Due to the truncation in the z-direction, photons can partially escape from the PhC slab, radiating towards some specific out-of-plane directions owing to the diffraction of periodically modulated permittivity. The far-field radiation in each radiation channel C_q can be formulated by a vector of $| {\Psi }_{n,q}\left.\right\rangle={[{c}_{x;n,q},{c}_{y;n,q}]}^{T}$, where c_x,y;n,q are complex-valued electric field components of radiative wave in the x and y directions, respectively, and subscript q labels the radiation channel. The field components in s and p directions are discussed in Supplementary Materials section 1.

Fig. 1: Correspondence between bulk band topology and far-field radiation.

A The schematic of radiation process from the PhC slab to the far field in real space. The wavefunction of the Bloch mode $| {u}_{n}\left.\right\rangle$ in the PhC slab is diffracted by the periodic lattice into several diffraction directions, acting as the radiation channels C₁₋₃. Each channel (i.e. C₃) depends on a 3D wavevector (i.e., k₃), and can be described by the polarization vector (i.e., $| {\Psi }_{n,3}\left.\right\rangle$) marked as the spiral arrows. The 3D wavevector for each channel (i.e., k₁ for channel C₁) can be decomposed to the vertical component (i.e., k_z,1) and in-plane component (i.e., β₁), both determined by the Bloch wavevector k_∥. B The “bulk-radiation correspondence" of Berry curvature in momentum space. The radiation polarization field (middle panel) can bridge the bulk Berry curvature B_n defined in wavefunction $| {u}_{n}\left.\right\rangle$ (bottom panel) with the radiation Berry curvature ${B}_{n}^{r}$ defined in far-field radiation vector $| {\Psi }_{n}\left.\right\rangle$ (top panel). c_x,y are complex amplitudes of the radiative waves in the x−y plane.

Generally, as illustrated in Fig. 1A, the radiation vector is characterized by a three-dimensional (3D) wavevector k_q, which can be decomposed into the in-plane component β_q and the vertical component ${k}_{z,q}=\sqrt{{\omega }_{n}^{2}/{c}^{2}-| {{{\beta }}}_{q}{| }^{2}}$. Since the radiative waves are diffracted from the Bloch mode, β_q, as well as k_q, is directly determined from the Bloch wavevector k_∥. To investigate the connection between bulk Bloch modes and its radiation, we focus on the dependence of radiative waves on the Bloch wavevector k_∥ rather than the 3D wavevector k_q. Consequently, at each k_∥, the radiation process in a given channel C_q can be understood as a linear mapping of ${{{{\mathcal{P}}}}}_{q}:| {u}_{n}({{{{\bf{k}}}}}_{\parallel })\left.\right\rangle \mapsto | {\Psi }_{n,q}({{{{\bf{k}}}}}_{\parallel })\left.\right\rangle={\hat{P}}_{q}({{{{\bf{k}}}}}_{\parallel })| {u}_{n}({{{{\bf{k}}}}}_{\parallel })\left.\right\rangle$, governed by a projection matrix denoted as ${\hat{P}}_{q}$. The detailed expressions of β_q with respect to k_∥ for each channel can be found in Supplementary Materials section 1. In the following discussions, we focus on a single channel, thus omitting the subscript q for simplicity.

The PhC slab we considered here is intrinsically non-Hermitian, due to the existence of radiation losses. Thus, the Berry curvature of the bulk Bloch bands in the 2D Brillouin zone (BZ) can be calculated from the wavefunctions as ${B}_{n}({{{{\bf{k}}}}}_{\parallel })=i{\nabla }_{{{{{\bf{k}}}}}_{\parallel }}\times \langle {v}_{n}({{{{\bf{k}}}}}_{\parallel })| {\nabla }_{{{{{\bf{k}}}}}_{\parallel }}{u}_{n}({{{{\bf{k}}}}}_{\parallel })\rangle$, denoted as bulk Berry curvature (bottom panel, Fig. 1B). Here $\left\langle \right.{v}_{n}({{{{\bf{k}}}}}_{\parallel })|$ represents the left vector accompanied by the right vector $| {u}_{n}({{{{\bf{k}}}}}_{\parallel })\left.\right\rangle$, ruled by the bi-orthogonal normalization relation of 〈v_m(k_∥)∣u_n(k_∥)〉  =  δ_mn. Accordingly, the right vector $| {u}_{n}({{{{\bf{k}}}}}_{\parallel })\left.\right\rangle$ can be projected to the radiation vector $| {\Psi }_{n}({{{{\bf{k}}}}}_{\parallel })\left.\right\rangle$ through the projection matrix $\hat{P}$. If $\hat{P}$ is an invertible matrix, the left vector $\left\langle \right.{v}_{n}({{{{\bf{k}}}}}_{\parallel })|$ also corresponds to a radiation vector in the term of $\left\langle \right.{\Phi }_{n}({{{{\bf{k}}}}}_{\parallel })|=\left\langle \right.{v}_{n}({{{{\bf{k}}}}}_{\parallel })| {\hat{P}^{-1}}({{{{\bf{k}}}}}_{\parallel })$. It is ready to derive that $| {\Psi }_{n}\left.\right\rangle$ and $\left\langle \right.{\Phi }_{n}|$ form another bi-orthogonal basis for the Hamiltonian of ${\hat{H}^{r}}=\hat{P}\hat{H}{\hat{P}^{-1}}$, leading to another Berry curvature ${B}_{n}^{r}({{{{\bf{k}}}}}_{\parallel })=i{\nabla }_{{{{{\bf{k}}}}}_{\parallel }}\times \langle {\Phi }_{n}({{{{\bf{k}}}}}_{\parallel })| {\nabla }_{{{{{\bf{k}}}}}_{\parallel }}{\Psi }_{n}({{{{\bf{k}}}}}_{\parallel })\rangle$ denoted as the “radiation Berry curvature” (top panel, Fig. 1B). We find that ${B}_{n}^{r}$ and B_n are related as ${B}_{n}^{r}({{{{\bf{k}}}}}_{\parallel })={B}_{n}({{{{\bf{k}}}}}_{\parallel })+i{\nabla }_{{{{{\bf{k}}}}}_{\parallel }}\times \left\langle \right.{v}_{n}({{{{\bf{k}}}}}_{\parallel })| {\hat{P}^{-1}}{\nabla }_{{{{{\bf{k}}}}}_{\parallel }}\hat{P}| {u}_{n}({{{{\bf{k}}}}}_{\parallel })\left.\right\rangle$. We further prove that (see Supplementary Materials section 1 for details), in the case that the matrix $\hat{P}$ is smooth and doesn’t give rise to extra amplitude vortexes such as BICs that carry zero radiation (〈Ψ_n(k_∥)∣Ψ_n(k_∥)〉 = 0), the second term of ${B}_{n}^{r}$ vanishes, and the system follows a simple correspondence between the band topology and radiation topology, given by:

$${B}_{n}^{r}\approx {B}_{n}$$

(1)

The above equation reveals that the escaping photons project the bulk Berry curvature onto the far-field radiation through the matrix $\hat{P}$ (mid panel, Fig. 1B). Although the wavefunctions $| {u}_{n}\left.\right\rangle$ and $\left\langle \right.{v}_{n}|$ are difficult to access because they belong to the near-field features of bulk Bloch modes, the radiation vectors $| {\Psi }_{n}\left.\right\rangle$ and $\left\langle \right.{\Phi }_{n}|$ are directly observable. Therefore, Eq. (1) offers a possibility to extract the bulk band topology directly from the far-field radiation. The detailed derivation of such a bulk-radiation correspondence can be found in Supplementary Materials section 1. An example that poor-defined $\hat{P}$ collapses the bulk-radiation correspondence is discussed in Supplementary Materials section 2. The physical origin and measurement methods of the left radiation vector $\left\langle \right.{\Phi }_{n}|$ is discussed in the Supplementary Materials section 3.

In theory, the radiation in a particular radiation channel gives a perspective projection of the wavefunctions, and thus it is noteworthy to discuss whether the projection is complete. For a general vector system where N eigen modes exist, the number of internal DOFs of the system is N and both $| {u}_{n}\left.\right\rangle$ and $\left\langle \right.{v}_{n}|$ are N-dimensional vectors. Here we consider the case of N ≥ 2 since N  = 1 refers to a scalar single-valuable system and thus only one scalar observable can fully characterize the system. As we stated above, for each bulk Bloch mode, one radiation channel can only characterize two DOFs (${[{c}_{x;n},{c}_{y;n}]}^{T}$), so $\hat{P}$ should be a 2  ×  N matrix. For the case with N  >  2, $\hat{P}$ can’t be directly inverted, indicating that a single radiation channel can’t provide enough information to depict the bulk wavefunctions, and it’s necessary to measure multiple radiation channels simultaneously—observe the same object from different views. As a specific case, if the system is a simple two-level one with N  =  2, the measurement of only one radiation channel is sufficient to make the projection of wavefunctions complete. Namely, we can reverse the projection process to directly determine the bulk wavefunctions from far-field radiations if $\hat{P}$ is a non-singular invertible 2  ×  2 matrix. In this work, we focus on the simplest N  =  2 case to present and validate our theory.

Non trivial Berry curvature in honeycomb lattice

To elaborate the correspondence, we consider a 2D PhC slab of Si₃N₄ material with circular air hole patterns on a honeycomb lattice (Fig. 2A). The radii of two air holes in rhombus unit-cell are denoted as r₁ and r₂, and the lattice constant and slab thickness are denoted as a and h, respectively. The reciprocal lattice is shown in Fig. 2B, where the gray shading area denotes the reduced BZ. According to the Bloch theorem, the wavefunction $| {u}_{n}\left.\right\rangle$ can be expanded as a superposition of a series of quasi-plane waves with discrete momentum, represented by the dots in the reciprocal lattice, and we refer to them as “diffraction orders”⁶⁷. Around the second ${{{\mathcal{K}}}}$ point that resides in the continuum, several diffraction orders fall into the light cone and thus open radiation channels. We take ${{{{\mathcal{K}}}}}_{1}$ point as a specific example, around which exist three radiation channels C₁₋₃ (red arrows, Fig. 2B) whose in-plane wavevectors are ${{{{\boldsymbol{\beta }}}}}_{1}=({k}_{x}+\sqrt{3}/3){\beta }_{0}{{{\bf{x}}}}$ and ${{{{\boldsymbol{\beta }}}}}_{2,3}=({k}_{x}-\sqrt{3}/6){\beta }_{0}{{{\bf{x}}}}+({k}_{y}\;\mp \; 1/2){\beta }_{0}{{{\bf{y}}}}$, respectively. Here, k_x and k_y are dimensionless numbers describing the Bloch wavevector k_∥ deviating from the ${{{{\mathcal{K}}}}}_{1}$ point, and ${\beta }_{0}=4\pi /\sqrt{3}a$ is the reciprocal lattice constant. Three quasi-transverse-electric (TE) polarized modes marked as TE_A,B,C with dominated components of (E_x, E_y, H_z) can be found around the ${{{{\mathcal{K}}}}}_{1}$ point due to C_6/3 symmetry, forming a three-level system with well-separated frequency from the other Bloch modes. For the case that δ_r  =  r₂  −  r₁  =  0 preserving the C₆ symmetry (left panel, Fig. 2C), a twofold degeneracy of TE_A and TE_B right at the ${{{{\mathcal{K}}}}}_{1}$ point emerges. As a contrary, r₁ ≠ r₂ lifts the degeneracy (right panel, Fig. 2D). In the case that the in-plane symmetry breaking is sufficiently weak that allows the coupling from the TE_C mode being neglectable, TE_A,B modes form a two-level subsystem near the ${{{{\mathcal{K}}}}}_{1}$ point, described by an effective Hamiltonian of:

$${\hat{H}}_{t}=\omega+\delta {\sigma }_{z}+\eta {k}_{x}{\sigma }_{x}+\eta {k}_{y}{\sigma }_{y}$$

(2)

in which ω is the degenerate frequency at ${{{{\mathcal{K}}}}}_{1}$ point; δ ∝ δ_r characterizes the in-plane asymmetry and η is the group velocity. Due to the radiation loss, ω  =  ω_r  +  iγ₀ is a complex one, and γ₀ denotes the radiation decay rate. When C₆ symmetry is preserved (δ  =  0), the eigenvectors of Eq. (2) can be derived as $| {u}_{n}\left.\right\rangle={[1,\pm | \eta | {e}^{i\theta }/\eta ]}^{T}$ where ${e}^{i\theta }=({k}_{x}+i{k}_{y})/\sqrt{{k}_{x}^{2}+{k}_{y}^{2}}$, creating a diabolic point at the ${{{{\mathcal{K}}}}}_{1}$ point which is exactly a non-Hermitian counterpart of the Dirac point in Hermitian case, and we still denote it as the DP for short without any confusion.

Fig. 2: Demonstration of Berry curvature observation on a honeycomb-latticed PhC slab.

A SEM image of the fabricated PhC sample, showing a honeycomb-latticed structure of SiN slab on SiO₂ substrate with different hole radii. Inset: the side view of the air hole. The structural parameters are given as a  = 440 nm, r₁  =  50 nm, r₂  =  54 nm, h  =  180 nm, respectively. δ_r is defined as r₂ − r₁. B The reciprocal lattice of the PhC sample. Gray shading area: the reduced BZ; purple dot: the Γ point; blue dot: the ${{{{\mathcal{K}}}}}_{1}$ point; red vectors: three diffraction orders acting as radiation channels C₁₋₃; green vectors: non-radiative diffraction orders. C, D The band structures of PhCs around ${{{{\mathcal{K}}}}}_{1}$ point with (δ_r  = 0) and without (δ_r  = 4 nm) the inversion symmetry. Owing to the C₆ symmetry with δ_r  =  0, TE_A mode (purple sheet) and TE_B mode (blue sheet) are degenerate at ${{{{\mathcal{K}}}}}_{1}$ point, giving rise to a DP. When δ_r  ≠  0, the DP splits to open a nontrivial bandgap. E, F The polarization fields in momentum space of TE_A (purple, the top panels) and TE_B (blue, the bottom panels) modes around ${{{{\mathcal{K}}}}}_{1}$ point with (δ_r  =  0) and without (δ_r  =  4 nm) the inversion symmetry, respectively. For δ_r  =  0 with the C₆ symmetry, half charges emerge at ${{{{\mathcal{K}}}}}_{1}$ point due to the DP for both TE_A,B modes. When δ_r  ≠  0, two CPs with opposite handness emerge around the ${{{{\mathcal{K}}}}}_{1}$ point instead. Black dot: DP; red marks: the quasi-CPs. All data are calculated by numerical simulations (COMSOL Multiphysics).

Degeneracy at DP creates nontrivial bulk band topology. According to Eq. (2), the close form of the theoretical bulk Berry curvature in such a two-level subsystem follows:

$${B}_{n;t}=\pm \frac{4\delta {\eta }^{2}}{{[4{\delta }^{2}+4{\eta }^{2}({k}_{x}^{2}+{k}_{y}^{2})]}^{3/2}}$$

(3)

where the subscript “t” distinguishes B_n;t from the B_n while the latter one takes TE_C into account; the signs “±” denote the two bands n  =  A, B, respectively. Since TE_C mode can be neglected in our case, we have B_n  ≈  B_n;t. For a C₆ symmetric system (δ  = 0), the bulk Berry curvature shows as a δ-function peaked at the ${{{{\mathcal{K}}}}}_{1}$ point (k_x  =  k_y = 0). While for δ  ≠  0, the DP splits and opens a topologically nontrivial bandgap, leading to a nontrivial bulk Berry curvature in the vicinity of ${{{{\mathcal{K}}}}}_{1}$ point that gives rise to nonzero valley-Chern number.

As we stated above, if the projection matrix $\hat{P}$ doesn’t cause extra amplitude vortexes, B_n;t can be determined by directly observing the radiation Berry curvature ${B}_{n;t}^{r}$ according to bulk-radiation correspondence in Eq. (1). To achieve this, both right and left radiation vectors should be measured. Specifically, the right radiation vector $| {\Psi }_{n}\left.\right\rangle$ corresponds to the far-field polarization: ${\overrightarrow{S}}_{n}={[{s}_{1},{s}_{2},{s}_{3}]}^{T}/{s}_{0}=\langle {\Psi }_{n}| \hat{{{{\mathbf{\sigma }}}}}| {\Psi }_{n}\rangle /\langle {\Psi }_{n}| {\Psi }_{n}\rangle$, where $\hat{{{{\mathbf{\sigma }}}}}={[{\hat{\sigma }}_{z},{\hat{\sigma }}_{x},{\hat{\sigma }}_{y}]}^{T}$ are the Pauli’s matrices, and ${\overrightarrow{S}}_{n}$ refers to the Stokes’ vector which can be directly measured by using standard polarimetry method⁶⁵. Here we present the simulated polarization vector fields in Fig. 2E, F, showing the footprints of DP in the far-field radiation with the C₆ symmetry. Polarization vortexes can be found in momentum space, each carrying a half-integer topological charge right at the ${{{{\mathcal{K}}}}}_{1}$ point (Fig. 2E). Once the symmetry-breaking lifts the degeneracy, the polarization vortexes degrade to a meron-like and anti-meron-like configurations⁶⁸ with circular-polarization (CPs) in opposite helicities around the ${{{{\mathcal{K}}}}}_{1}$ point for TE_A,B modes, respectively (Fig. 2F). These far-field geometric features can be employed as observable signatures to validate the theory. As for the left radiation vector $\left\langle \right.{\Phi }_{n}|$, it can be readily determined according to the bi-orthogonal normalization relation of 〈Φ_m∣Ψ_n〉  = δ_mn.

Experimental observation of Berry curvature

To experimentally observe the Berry curvature, we first fabricate the PhC sample by using e-beam lithography (EBL) and inductively coupled plasma etching (ICP) processes on a Si₃N₄ slab of thickness h = 180 nm on silica substrate (see Methods section for details). The air holes are arranged as a honeycomb lattice of a  =  440 nm with two slightly different hole radii of r₁  = 50 and r₂  =  54 nm, respectively, as the scanning electron microscope (SEM) images shown in Fig. 2A. The angle-resolved measurement system is schematically illustrated in Fig. 3A, in which a supercontinuum white light source is first sent through an acoustic-optic tunable filter (AOTF) and then linearly polarized by POL1 to generate incoherent light in a wavelength range from 550 to 580 nm. After passing through a quarter-wave plate (QWP1), the light is focused by a lens (L1) onto the rear focal plane (RFP) of an infinity-corrected objective lens (NA  =  0.95), and then illuminates the sample to excite the optical modes. The radiations from the PhC sample are collected by the same objective lens and imaged by a charge-coupled device (CCD) camera which is co-focused with the RFP of the objective lens. By inserting another polarizer (POL2) and another quarter-wave plate (QWP2) before the CCD, we can fully characterize the Stokes’ vector of radiation through a polarimetry method (see Methods section for details).

Fig. 3: Polarimetry measurement of far-field polarization fields.

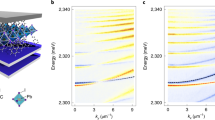
A Schematic of the measurements setup. AOTF acoustic-optic tunable filter; POL1 and POL2 polarizers, QWP1 and QWP2 quarter-wave plates, L1 convex lens with 20-cm focal length, BS beam splitter, RFP rear focal plane, Obj objective lens with NA of 0.95 and working distance of 150 μm, 4f lens system with magnification rate of × 6. B The observed image of three scattered beams from radiation channels C₁₋₃ within the NA range. In the experiment, we excite the optical modes from channel C₁ by moving lens L1 to a proper position and then collect the radiative waves in channel C₃ after it is magnified by the 4f system. C Schematic of isofrequency contours of the two-level system near the ${{{{\mathcal{K}}}}}_{1}$ point. The yellow plane denotes the wavelength of λ_i =  570.328 nm. Purple sheet: TE_A mode; blue sheet: TE_B mode. D The measured isofrequency contour S₀ and Stokes' parameters S₁₋₃ at a wavelength of λ_i  =  570.328 nm. The Stokes' parameters are determined through different configurations of POL2 and QWP2. Dashed line: the simulated isofrequency contour at λ_i. E The measured polarization distributions in momentum space around the ${{{{\mathcal{K}}}}}_{1}$ point, by overlapping several isofrequency contours and evaluating the overall Stokes' parameters. Red marks: the quasi-CPs.

As shown in Fig. 3B, three scattered beams inside the aperture of the objective lens can be found, corresponding to the radiation channels C₁₋₃ plotted in Fig. 2B. As we discussed above, only one radiation channel is sufficient to capture the bulk band topology of the two-level subsystem consisting of TE_A,B. Therefore, we excite the modes from the C₁ channel and observe them from the C₃ channel to avoid the direct reflected light for a better signal-noise ratio. The C₂ channel is unused. To achieve the best excitation, we fine-tune the incident angle by moving the L1 lens in the x– y plane. Moreover, POL1 and QWP1 are employed to adjust the polarization of incident light: left-handed circular polarization (LCP) for TE_A mode and right-handed circular polarization (RCP) for TE_B mode, respectively. When the AOTF selects a specific wavelength, the scatterings originating from fabrication disorders would make the isofrequency contour at such a wavelength visible due to the on-resonance pumping mechanism^48,62,69 (Fig. 3C). Then, a cascaded 4f system is applied to zoom-in the contour at a magnification rate of  × 6. Further, by recording the CCD images at particular arrangements of POL2 and QWP2 as polarimetry measurements, we can obtain the Stokes’ coefficients for each contour. The result at the wavelength of λ_i = 570.328 nm is presented in Fig. 3D, in which the dashed line is the isofrequency contour calculated from numerical simulation for visual guidance. By overlapping all the isofrequency contours in the wavelength range of 559.383 – 564.861 nm for the TE_A band and 565.203 –571.352 nm for the TE_B band, we obtain the polarization vector fields for both TE_A,B bands (Fig. 3E). In the vicinity of the ${{{{\mathcal{K}}}}}_{1}$ point, an LCP and an RCP can be found on the TE_A and TE_B bands, respectively (red circles, Fig. 3E), which agree well with our prediction in simulation as shown in Fig. 2F.

The radiation Berry curvature ${B}_{n;t}^{r}$ can be directly obtained from the polarization vector fields measured from channel C₃. Here we consider four samples with radius differences of δ_r  =  0, 4, 7, 10 nm, and measure the ${B}_{A,B;t}^{r}$ of each sample (top panels, Fig. 4). As a comparison, we numerically calculate the bulk Berry curvature B_A,B by employing the semi-analytical coupled-wave theory framework^56,70,71 (bottom panels, Fig. 4). To better show the evolution of Berry curvatures, we plot the unit-cell geometry of each sample and the corresponding band structures of TE_A,B as the insets in the top and bottom panels of Fig. 4. Specifically, we start from a realistic sample with δ_r  =  0 (Fig. 4A), where the fabrication imperfections would inevitably break the DP degeneracy at ${{{{\mathcal{K}}}}}_{1}$ point and give rise to a very small bandgap. We estimate that the bandgap is equivalent to the case of δ_r  =  2 nm. In this case, we found that the ${B}_{A,B;t}^{r}$ show as bright spots centered at ${{{{\mathcal{K}}}}}_{1}$ point—quite like δ-functions (top panels, Fig. 4A), agreeing well with the numerical bulk Berry curvatures B_A,B (bottom panels, Fig. 4A). Note that the signs of ${B}_{A;t}^{r}$ and ${B}_{B;t}^{r}$ are exactly opposite, agreeing well with the theoretical prediction in Eq. (3). Further, we gradually open the bandgap by increasing δ_r from 4 to 10 nm (Fig. 4B). During this process, the Berry curvatures ${B}_{B;t}^{r}$ and B_B both gradually diffuse to a larger region in momentum space while their peak absolute values decrease. At δ_r  =  10 nm, the bandgap becomes quite large, and thus both ${B}_{n;t}^{r}$ and B_n become fully dispersed and no longer congregate around ${{{{\mathcal{K}}}}}_{1}$ point. ${B}_{A;t}^{r}$ and B_A also match well with each other and have similar behaviors (see Methods section). The great agreement between the experimentally observed radiation Berry curvatures ${B}_{A,B;t}^{r}$ and the numerically calculated bulk Berry curvature B_A,B confirms the bulk-radiation correspondence we propose in Eq. (2). It’s noteworthy that Berry curvatures are generally complex values in a non-Hermitian system. For our PhC slab in which only radiation contributes to the non-Hermiticity, the imaginary parts of Berry curvature are quite small compared to their real parts (see Supplementary Materials section 1 for details).

Fig. 4: Experimental observation of Berry curvatures.

A The measured radiation Berry curvatures ${B}_{n;t}^{r}$ for the PhC sample with δ_r ≈ 0 (top panels) and the numerically calculated bulk Berry curvatures B_n with δ_r  =  2 nm (bottom panels) for a comparison. For a realistic sample with δ_r  =  0, the fabrication errors would slightly lift the DP at ${{{{\mathcal{K}}}}}_{1}$ point to create a small bandgap. We estimate that the bandgap is equivalent to the case of δ_r  = 2 nm. In this case, the Berry curvatures congregate around the ${{{{\mathcal{K}}}}}_{1}$ point since the bandgap is very small, showing opposite signs for TE_A and TE_B modes. B The measured radiation Berry curvatures ${B}_{B;t}^{r}$ (top panels) and the numerically calculated bulk Berry curvatures B_B (bottom panels) for TE_B mode when δ_r  = 4 nm (left), 7 nm (middle), and 10 nm (right). Along with the increasing δ_r, the bandgap gradually opens, and the Berry curvature gradually diffuses to a larger region in momentum space. Insets in top panels: SEM images of the unit cell of each PhC sample; insets in bottom panels: band structures of the two-level system accordingly.

To further quantitatively validate the bulk-radiation correspondence, we calculate the geometric phases (Berry phases) ${\gamma }_{n;t}^{r}$ and γ_n by applying 2D integrals over the radiation (measured) and bulk (numerical) Berry curvatures of ${B}_{n;t}^{r}$ and B_n in Fig. 4, respectively. As a reference, we also derive the analytic expression of geometric phase γ_n;t according to Eq. (3), in which the contribution of TE_C band is neglected:

$${\gamma }_{n;t}=\pm \left(\pi -\frac{2\delta }{\sqrt{4{\delta }^{2}+4{\eta }^{2}{k}_{s}^{2}}}\pi \right)$$

(4)

According to valleytronics¹¹, the integral of Berry curvature upon the individual valley region determines the valley-Chern number (blue shading, Fig. 5A). Considering that the nontrivial Berry curvatures congregate around the ${{{{\mathcal{K}}}}}_{1}$ point, here we choose a circular integral region with radius of k_s  =  0.03 for simplicity and thus calculate ${\gamma }_{n;t}^{r}$ (triangle), γ_n (circle), and γ_n;t (solid line) shown in Fig. 5B, C. According to Eq.(4), the analytic geometric phases γ_n;t exactly equals to  ±π at δ_r  =  0 for TE_A,B bands⁷², corresponding to the nontrivial quantized valley-Chern number of ${C}_{v}^{{{{\mathcal{K}}}}}=\pm 1/2$ in an individual valley¹¹. When δ_r  ≠  0, the open bandgap (nonzero δ) would make the geometric phases deviate from  ±π, unless the integral region k_s tends to be infinite². Our experimental observation verifies such a behavior. For instance, at δ_r  =  10 nm, we obtain ${\gamma }_{A,B;t}^{r} \approx \pm 0.7\pi$ deviated from  ±π due to the impact of nonzero bandgap. On the other hand, we find the three geometric phases ${\gamma }_{n;t}^{r}$, γ_n and γ_n;t agree well with each other when δ_r is relatively small, quantitatively proving the validity of bulk-radiation correspondence. For a large δ_r, both analytic geometric phase γ_n;t solved from the two-level model and the measured ${\gamma }_{n;t}^{r}$ from radiation slightly deviate from the bulk Berry phase γ_n, due to the exclusion of the third TE_C band. Because the TE_C mode also contributes to far-field radiation, the deviation upon ${\gamma }_{n;t}^{r}$ is more notable than that upon γ_n;t. Actually, we found ${\gamma }_{B;t}^{r} \, < \,{\gamma }_{B;t}\, \lesssim \,{\gamma }_{B}$ for TE_B mode. To improve the measurement accuracy for large δ_r, TE_C mode can’t be neglected, and we need to measure the polarization distributions from two independent radiation channels (i.e., C₃ and C₂) to completely capture the information of the three-level system with higher DOFs (N  =  3). The exemplary example and more discussions are presented in Supplementary Materials section 4 and  5.

Fig. 5: Geometric phases obtained from measured Berry curvatures.

A Schematic of an individual valley (blue shading) around the ${{{{\mathcal{K}}}}}_{1}$ point (blue dot) in the reciprocal lattice. The integral on Berry curvature over the individual valley gives the geometric (Berry) phases. Considering that the Berry curvatures congregate around the ${{{{\mathcal{K}}}}}_{1}$ point when δ_r is relatively small, we perform the integral on a circular region (black circle) to simplify the calculation. Gray shading: the first BZ; purple dot: the Γ point; blue dot: the ${{{{\mathcal{K}}}}}_{1}$ point. B, C The geometric phases for TE_A,B modes. Blue solid line: theoretical bulk Berry phase γ_n;t of the two-level model according to Eq. (4); red circles: numerical bulk Berry phase γ_n obtained from the integral of bulk Berry curvatures B_n calculated in Fig. 4; yellow triangles: geometric phase ${\gamma }_{n;t}^{r}$ obtained from measured radiation Berry curvature ${B}_{n;t}^{r}$ shown in Fig. 4. When δ_r = 0, the theoretical Berry phases are exactly  ±π for TE_A,B modes owing to the existence of DP, corresponding to quantized valley-Chern numbers of  ±1/2. When δ_r gradually increases, all the geometric phases gradually deviate from the quantized  ±π. Moreover, when δ_r becomes relatively large, the theoretical γ_n;t and measured ${\gamma }_{n;t}^{r}$ slightly deviate from the numerical γ_n, due to the impact of TE_C mode.

Discussion

We emphasize that although the non-Hermiticiy in our exemplary system doesn’t give rise to nontrivial topological effects, the system is still intrinsically non-Hermitian due to the radiation loss, and hence, its mathematical structure must follow a bi-orthogonal relation of left and right vectors together. This indicates that the far-field observables must provide sufficient DOFs to solve the Berry curvatures. Compared to the observables such as wavelength and Q-factor, which are only associated with the complex frequencies of Bloch modes, the far-field polarization is a direct projection of the wavefunction itself that naturally presents the information about it (see Supplementary Materials section 4 for details). Therefore, we conclude that the polarizations should be a better candidate to measure the Berry curvature. Our theory and method are valid for general non-Hermitian photonic systems, even with multi-internal DOFs, as long as the measurable radiation exists.

In the experiment stated above, we directly measure the two right vectors $| {\Psi }_{A,B}\left.\right\rangle$ at the k_∥ point and obtain the left vectors $\left\langle \right.{\Phi }_{A,B}|$ by using the bi-orthogonal normalization relation. However, the left vector can also be directly measured. According to the law of reciprocity, the left radiation vector at the k_∥ point would correspond to the right radiation vector at the  − k_∥ point (see Supplementary Materials section 3 for details). Therefore, one can also observe one band at both k_∥ and  − k_∥ points to retrieve the system’s topology, instead of measuring two bands simultaneously.

Our findings reveal that the radiation polarization does contain the fingerprint of bulk topology described by the Berry curvature upon a bi-orthogonal basis, but it remains elusive whether all the topological features in the far-field originate from the band topology. Our short-cut answer is negative. Specifically, different from the Berry curvature depending on bi-orthogonal basis, we can also define a “right-right" curvature of ${B}_{n;rr}^{r}=i{\nabla }_{{{{{\bf{k}}}}}_{\parallel }}\times \langle {\Psi }_{n}({{{{\bf{k}}}}}_{\parallel })| {\nabla }_{{{{{\bf{k}}}}}_{\parallel }}{\Psi }_{n}({{{{\bf{k}}}}}_{\parallel })\rangle$ upon the right radiation vector $| {\Psi }_{n}\left.\right\rangle$ only⁴⁰, capturing the geometric features of the polarization field itself. In fact, the integral over “right-right" curvature presents the Pancharatnam-Berry (PB) phase^73,74,75,76 of far-field polarization, showing the swirling structure of Stokes’ vector ${\overrightarrow{S}}_{n}$ in momentum space. We note that, nontrivial polarization features of meron and anti-meron in Fig. 3E don’t correspond to the valley-Chern number of bulk topology but are related to the Skyrmion numbers^77,78,79 given by the PB phases (see Supplementary Materials section 6 for details).

In summary, our findings of “bulk-radiation correspondence” of Berry curvature reveal the feasibility of retrieving the band topology from characterizing far-field radiation. We prove in theory and demonstrate in experiments that employing the polarizations of one radiation channel can accomplish a complete map of wavefunctions in a two-level non-Hermitian system, to directly access the Berry curvature and Chern number without strongly disturbing the system. The proposed method can also be extended to multi-level systems by measuring more radiation channels simultaneously, and utilized to extract other topological features such as quantum geometric tensor^{25,26,27,28,80,81}. Our work demonstrates a simple and effective way of directly observing the Berry curvature in non-Hermitian systems and thus could shed light on the exploration of the intriguing phases in topological systems.

Methods

Sample fabrication

A LPCVD deposited Si₃N₄-SiO₂-Si wafer with 1-μm-thick lower cladding of SiO₂ was used. The pattern was defined by electron-beam lithography (EBL). The sample was firstly spin-coated with ZEP520A photo-resist, followed by exposure to EBL (Elionix ELS-F125G8) at the current of 1 nA and field size of 500 μm. After the exposure, the sample was etched with inductively coupled plasma (ICP, Oxford) by a mixture of CHF₃ and O₂. The ICP etching time and chamber pressure are carefully controlled for etching depth and smooth side walls.

Measurements

As shown in Fig. 6, the supercontinuum light source (SuperK Compact; NKT Photonics) is broadband in the range of 450–2400 nm. The incident light is followed by an acoustic-optic tunable filter (AOTF; Gooch & Housego) to scan and pick up the resonance wavelength. After passing through a polarizer (POL1) and a quarter-wave plate (QWP1), the incident light is focused by a lens (L1) onto the rear focal plane (RFP) of the objective lens for exciting the sample. We control the incident light to be left-handed and right-handed circular polarized by arranging POL1 and QWP1 to excite TE_A and TE_B bands, respectively. The radiation field of the sample, collected by the objective lens, is magnified by a two-stage 4f system (L2– L5) and passes through a quarter-wave plate (QWP2) and a polarizer (POL2) before observed by a CCD camera (CCD1). Another 4f system (L6 – L7) and camera (CCD2) are used to monitor the near field of the sample surface. We perform polarimetry measurement of the diffraction from the C₃ radiation channel by six configurations of QWP2 and POL2: (1) no QWP2, POL2 oriented along the x-axis; (2) no QWP2, POL2 oriented along the y-axis; (3) no QWP2, POL2 oriented at 45° with respect to the x-axis; (4) QWP2 fast axis fixed along y-axis, POL2 oriented at 45° with respect to the x-axis; (5) no QWP2, POL2 oriented at 135° with respect to the x-axis; (6) QWP2 fast axis fixed along y-axis, POL2 oriented at 135° with respect to the x-axis. The far-field images are recorded by a CCD camera for further processing.

Fig. 6: The experiment setup.

The focal lengths of lenses L1, L2, L3, L4, L5, L6, and L7 are 300, 200, 300, 75, 300, 200, and 125 mm, respectively. AOTF acoustic-optic tunable filter, POL polarizer, QWP quarter-wave plate, BS beam splitter, RFP rear focal plane, Obj objective lens (50X and NA = 0.95), CCD charge-coupled device.

Measurement results of the Stokes’ parameters

We present the measurement results of the Stokes’ parameters of both TE_A and TE_B bands for the PhC slab of δ_r  =  4 nm, shown in Fig. 7. The experiment and the simulation results match well with each other.

Fig. 7: Measured and simulated Stokes’ parameters for PhC slab of δ_r  =  4 nm.

Left panels: Measured (top panels) and simulated (bottom panels) Stokes' parameters (S₁₋₃) for TE_A mode when δ_r  = 4; Right panels: Measured (top panels) and simulated (bottom panels) Stokes' parameters (S₁₋₃) for TE_B mode when δ_r =  4. For both two modes, the experiment results agree well with the simulated ones.

Berry curvature for TE_A band

We present the evolution of measured radiation Berry curvature for TE_A band when δ_r varies in Fig. 8. Also, the experiment results agree well with the simulation results (bulk Berry curvature).

Fig. 8: Experimental observation of Berry curvatures for TE_A mode.

Top panels: Measured radiation Berry curvature ${B}_{A;t}^{r}$ when δ_r  ≈ 0 (the first from left), δ_r  =  4 nm (the second from left), 7 nm (the third from left), and 10 nm (right). Bottom panels: simulated bulk Berry curvature B_A when δ_r  =  2 nm (the first from left), δ_r  =  4 nm (the second from left), 7 nm (the third from left), and 10 nm (right). The experimental results agree well with the simulated ones. Along with the increasing δ_r, the bandgap between TE_A mode and TE_B mode increases, and the Berry curvatures gradually diffuse to a larger region in momentum space.