Introduction

Hyperbolic phonon polaritons (HPhPs) arise from the strong coupling between infrared light and directional lattice vibrations in anisotropic Van der Waals materials1,2,3 and polar crystals4, and feature hyperbolic iso-frequency contours (IFCs) in momentum space which confer them strong directionality and confinement5,6,7. In recent years, they have attracted significant attention because of their low-loss propagation8,9,10, sub-wavelength optical confinement11,12 and sub-diffractional focusing13,14,15 at the nanoscale.

In some classes of low-symmetry polar dielectrics where the crystal structure is monoclinic, HPhPs emerge as hyperbolic shear polaritons (HShPs) characterized by strongly asymmetric and frequency-tunable direction of propagation16,17. Compared to conventional HPhPs, the asymmetric loss distribution of shear polaritons allows one of the branches to access larger momenta, leading to shear hyperbolic waves with stronger light localization and directionality.18 This makes them appealing for applications in nanophotonics and wave engineering in the mid-infrared (mid-IR). However, direct observation of HShPs in natural materials has been so far limited to only few polar dielectrics such as beta-phase gallium oxide (β-Ga2O3)19 and cadmium tungstate (CdWO4)17. The manipulation of HShPs in these natural phononic materials is hindered by the available crystal symmetries and by the charge neutrality of phonons, which makes them not subject to electrostatic control. To modulate HShPs, research efforts have been exploring different excitation conditions and the launcher geometry, which can control to some extent the resulting propagation features of HShPs19. However, this control is rather limited, and real-time reconfigurability has not been fully explored yet.

Two-dimensional (2D) materials, characterized by their low-dimensional geometry20,21,22, exceptional external field coupling capabilities23,24,25,26, and strong interaction with light27,28, have become an excellent platform for engineering polaritons29. Among them, alpha-phase molybdenum trioxide (α-MoO3), a layered 2D Van der Waals material, has garnered significant attention due to its capability to support in-plane HPhPs within the Reststrahlen band ranging from 818 cm−1 to 974 cm−1 2,30. Its versatility and intrinsic characteristics enable the engineering of HPhPs through various approaches, including multi-layer stacking31,32,33, modulation via coupling with graphene34,35,36,37,38,39,40, lattice engineering41, etc. These endeavors have yielded the observation of intriguing polariton phenomena, such as canalized propagation31,33,35, topological transitions31,35,36, and negative refraction34,42,43. However, within this versatile system, a systematic exploration of HShPs and their related tuning strategy has yet to be undertaken. This investigation would integrate the distinct features of HShPs and the extensive tunability of 2D materials, enabling multi-dimensional engineering of extremely confined and low-loss phonon polaritons.

To generate HShPs in 2D materials, in the following we explore twist engineering of stacked α-MoO3 flakes, varying the relative angle to lower the symmetry of the system. Twist engineering, as evidenced in the case of bilayer graphene44,45 and bilayer transition-metal dichalcogenides46, offers the opportunity to rationally control emergent phenomena. Here, twisted α-MoO3 bilayers are expected to reduce the symmetry of the system, introducing effective shear phenomena that may be tuned through the twist angle, even though each flake retains its intrinsic lattice symmetry.

In this work, we theoretically and experimentally demonstrate tunable HShPs within a 2D material framework by engineering twisted bilayer α-MoO3 structures, and combine twist-induced dispersion engineering with dynamic gating to achieve reconfigurable HShP engineering based on twisted 2D materials. To understand the mechanisms of the variation in HShP behavior in twisted bilayers, we systematically change the twist angle and thickness of an α-MoO3 layered structure to tune the HShP features and maximize shear effect through optimizing the angle/thickness configuration. Furthermore, we integrate the twisted bilayer α-MoO3 with graphene and investigate the effect of varying the Fermi energy of graphene on the propagation of HShPs, achieving the in-situ dynamic control of HShPs without varying laser source polarization or frequency. Finally, by extracting data from both near-field measurements and comprehensive full-wave simulations, we quantify both the shear effect of HShPs and the loss redistribution to provide a thorough description of HShP behavior, offering an in-depth characterization of HShPs. Our realization of versatile and diverse control over HShPs enables the optimization of loss redistribution, along with the maximization of asymmetric propagation and field confinement.

Results

The realization of HShPs in twisted bilayer α-MoO3

Monoclinic polar crystals, like β-Ga2O3 and CdWO4, exhibit multiple non-orthogonal phonon resonances within given lattice planes, leading to strongly anisotropic optical responses. These responses are characterized by a non-diagonal permittivity tensor47,48, and a frequency-dependent optical axis orientation (axial dispersion). This, in turn, leads to the emergence of HShPs on their surface16,17, characterized by pronounced asymmetric propagation and loss resilience. By contrast, the anisotropic response of orthorhombic 2D materials like α-MoO3 results from orthogonal phonon resonances with opposite signs of permittivity tensors along the crystal orientations, supporting the propagation of conventional HPhPs within their volume2,10. However, stacking two flakes of α-MoO3 at a finite twist angle can induce an effective shear in the system, due to the broken mirror symmetry in the bilayer configuration (Fig. 1a). Such a twist arrangement may therefore potentially support HShPs in 2D materials.

Fig. 1: The realization and loss redistribution of hyperbolic shear polaritons (HShPs) in twisted bilayer α-MoO3.
figure 1

a Schematic of a measurement performed with infrared scattering-type scanning near-field optical microscopy (s-SNOM) on engineered HShPs (red and blue fringes) in twisted bilayer α-MoO3. The structure comprises two layers with thicknesses d1 and d2, respectively, and a twist angle θ between them. The x and y axes are along the [100] and [001] crystallographic orientations of the bottom α-MoO3, respectively. The inset (white arrows) illustrates the non-orthogonal twist-induced phonon resonances. b Increasing values of θ change the iso-frequency contours (IFCs) of HShPs transition from hyperbolic (yellow) to canalized (blue). Here, d1 = 130 nm and d2 = 200 nm. c Similarly, for fixed θ = 60° and d2 = 170 nm, the top-layer thickness is used to manipulate the shape of the IFCs. d, e Reflection coefficient (Im(rpp)) from the transmission matrix method (TMM; see Supplementary Note 3 for details) and real-space field distribution (Re(EZ)) obtained by the Finite-Difference Time-Domain (FDTD) simulations (see Supplementary Note 5 for details). Two twisted bilayer structures with identical layer thicknesses (d1 = 130 nm and d2 = 200 nm), but different twist angles of 0° (d) and 30° (e), are compared. The curved arrow indicates twist-induced loss redistribution, creating asymmetric loss between the branches of the hyperbolic IFCs. k0 is the free-space light wave vector at 931 cm−1.

Full size image

To better understand how the shear properties of HShPs are influenced in this asymmetric bilayer structure, we apply Maxwell’s equations to analyze their dispersion in this layered structure. We examine two in-plane semi-infinite layers of α-MoO3 stacked on a SiO2 substrate, applying continuous boundary conditions for the tangential electric and magnetic field across each interface. Distinct from the method proposed in ref. 31, this analysis considers both the thicknesses of the layers (denoted as d1 for the top layer and d2 for the bottom one, respectively) rather than approximating the plane with sheet conductivities. The analytic expression for the IFCs of HShPs (see Supplementary Note 1 for a detailed derivation), which gives the relation between the in-plane momentum k and its angle φ with respect to the kx axis, is given by the following non-linear dispersion equation:

$$k\rho \,\left(\varphi \right)\,{d}_{2}-\arctan \frac{{\varepsilon }_{{{{\rm{sub}}}}}}{{\varepsilon }_{z}\rho \left(\varphi \right)}-\arctan \frac{\rho \,\left(\varphi \right)}{\rho \,\left(\varphi -\theta \right)}\tan \left(\arctan \frac{{\varepsilon }_{{{{\rm{air}}}}}}{\rho \,\left(\varphi -\theta \right)\,{\varepsilon }_{z}}-k\rho \,\left(\varphi -\theta \right)\,{d}_{1}\right)+m\pi=0,$$
(1)

where θ is the twist-angle that quantifies the absolute angular displacement of the top layer’s crystal orientation relative to that of the bottom layer, εsub is the permittivity of substrate SiO2, εair is the permittivity of air, ω is the excitation frequency, m is an integer, and \(\rho \left(\varphi \right)=i\sqrt{\frac{{\varepsilon }_{x}{\cos }^{2}\left(\varphi \right)+{\varepsilon }_{y}{\sin }^{2}\left(\varphi \right)}{{\varepsilon }_{z}}}\). Here, εx,y,z are the permittivities of α-MoO3 along the [100], [001] and [010] crystallographic directions, respectively. The IFCs resulting from the solution of equation (1) are depicted in Fig. 1b, c. The former demonstrates that the twist angle can be utilized to break symmetry and control axial dispersion due to the induced effective monoclinicity in the bilayer, whereas the latter illustrates that the thickness of the layers is also a useful parameter for tuning the dispersion contours and effective optical axis. Due to the computational intensity of equation (1), the mode expansion method is employed throughout the article for efficiency, yielding results consistent with equation (1), as elaborated in Supplementary Note 2.

To better illustrate the shear effect introduced by the twist angle, we calculate the generalized reflection from the multi-layer using TMM and conduct Finite-Difference Time-Domain (FDTD) simulations. The resulting reciprocal space map closely approximates the Fourier transform of the real-space electric field profile generated by a point source placed close to the structure. Figure 1d, e showcase the reciprocal space maps along with corresponding real-space field distributions, with parameters of d1 = 130 nm, d2 = 200 nm. At θ = 0°, the system exhibits mirror-symmetric features in both reciprocal and real space (Fig. 1d). In contrast, at θ = 30°, the symmetry is broken, resulting in hyperbolic branches with asymmetric loss and a more directional hyperbolic wave (Fig. 1e). Introducing a twist angle in the α-MoO3 bilayer leads to a loss redistribution between the branches of the hyperbolic IFCs. Specifically, the loss increases in one branch while decreasing in the other, resulting in an asymmetric loss distribution. This redistribution significantly influences polariton behavior, where the branch with reduced loss demonstrates enhanced field confinement by accessing larger momenta. To quantify the shear effect of HShPs in our structure against twist angle and layer thickness, we adopt an analytical strategy similar to the one described in ref. 19. An illustrating example displaying a distinct hyperbolic shear dispersion is given in Fig. 2a. Then we use the IFCs derived using the mode expansion method, i.e., the red and blue curves in Fig. 2a, as paths for calculating the line integrals of the reflection coefficient, denoted as Ired and Iblue, respectively. These curves are overlapped on the reciprocal space map according to specific rules (see Supplementary Note 4 for details). Finally, to evaluate the asymmetric distribution of the IFCs of HShPs, we introduce a global shear factor defined as \(\left| \frac{{I}_{{{{\rm{blue}}}}}-{I}_{{{{\rm{red}}}}}}{{I}_{{{{\rm{blue}}}}}+{I}_{{{{\rm{red}}}}}}\right|\) (see Supplementary Note 4 for more details).

Fig. 2: Maximizing the propagation asymmetry of HShPs in twisted bilayer α-MoO3.
figure 2

a TMM-calculated reflection coefficient for the bilayer. The reciprocal space map corresponds to d1 = 130 nm, d2 = 200 nm, and θ = 30°. White lines partition momentum space into four regions, originating from the global minimum momentum. The overlaid calculated red and blue curves are used as paths to calculate the line integral of Im(rpp) and obtain the shear factor, which quantifies the propagation asymmetry of HShPs. The resulting shear factor (blue to red colormap) as a function of θ: when both d1 and d2 vary equally (b); when only d1 varies while keeping d2 constant at 200 nm (c). Maximal asymmetry is found with different thicknesses over a narrow range of twist angles (red peak). The star indicates the shear factor calculated from IFCs in (a).

Full size image

To elucidate the shear properties in relation to structural symmetries, we examine the shear factors in simulations as functions of twist angle and thickness under two distinct tuning schemes. In the first scheme (Fig. 2b), we change the twist angle and set d1 = d2 = d, varying d while preserving the mirror symmetry in the z direction. When the twist angle is neither 0° nor 90°, the in-plane mirror symmetry is broken and thus causes the desired shear effect, which peaks at twist angles close to 45°. Interestingly, the second scheme (Fig. 2c), which involves varying d1 while keeping d2 fixed at 200 nm, yields the highest asymmetry. As illustrated in Fig. 2c, both thickness and twist angle significantly influence the shear factors of PhPs, enabling tunability from HPhPs (value of zero) to HShPs (close to value of one) with an enhanced shear effect. Because of the broken mirror symmetry along the z axis, the point of maximal shear is non-trivially moved to θ ≃ 75° and for a range of thicknesses 80 nm ≤ d1 ≤ 120 nm. As the layer thickness increases approaching the one of a bulk material, the system exhibits diminished sensitivity to the twist angle. This happens because each layer behaves like a low-symmetry bulk material, where shear is less affected by near-field coupling between the interfaces and by the twist angle. Conversely, as the thickness decreases, the two-dimensional material properties become more pronounced, the dispersions of two hyperbolic polaritons get closer in momentum space, thus interlayer couplings are enhanced because phase-matching condition of the interactions is more inclined to meet. However, beyond a certain threshold in Fig. 2c, ultraconfined polaritonic modes in the thinned top layer suppress interlayer coupling, driving the system toward single-layer α-MoO3 behavior and correspondingly diminishing the shear factor. This aspect highlights the unique advantage of engineering HShPs in a thin twisted bilayer of α-MoO3 where small adjustments of the twist angle can be used to fine-tune and enhance shear properties, a feature not as pronounced in bulk materials. In addition to the influence of twist angle and layer thickness, we analyze the frequency dependence of the shear factor as detailed in the Supplementary Note 9.

Twist and thickness modulations on shear engineering

To experimentally characterize engineered HShPs in twisted bilayer α-MoO3, we fabricate two distinct sets of samples (see “Methods” for details). In each one, we either vary the twist angle or the thickness, enabling a precise analysis of the individual contribution of each parameter to the shear effect. We then employ infrared near-field nanoimaging (s-SNOM) to investigate the samples, where HShPs are excited by a metallic atomic force microscopy (AFM) tip and the corresponding real-space imaging is facilitated by nano-holes of 200 nm diameter through the layered structure. All experiments are performed at a frequency of 931 cm−1.

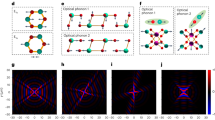
For the first set, we transfer α-MoO3 flakes onto a uniform α-MoO3 bottom flake with d2 = 202 nm, all closely matched in thickness but varying in twist angles, as shown by optical microscopy in Fig. 3a. For almost null twists, i.e., θ = 2°, we observe the expected nearly symmetric hyperbolic dispersion of conventional HPhPs, as shown by both the near-field image (Fig. 3b) and its Fourier spectrum (Fig. 3f). As we gradually increase θ from 17° to 46°, the shear effect is significantly enhanced, as evidenced by the growing asymmetry of the wavefronts (Fig. 3c–e) and their related Fourier spectra (Fig. 3g–i). For increasing twists, we assist with the redistribution of HShPs’ propagation loss along different branches in momentum space and their enhancing of directional propagation49,50, as highlighted by the increasingly growing spectral intensity associated with more confined momenta components. In addition, the validity of the experimental observation (Fig. 3b–e) and Fourier spectra (Fig. 3f–i) is corroborated by FDTD simulations (Fig. 3j–m) (see also Supplementary Note 5, Supplementary Fig. 9).

Fig. 3: Shear engineering and measurements of HShPs with varying twist angles.
figure 3

a Optical image of α-MoO3 flakes with similar thicknesses at varying twist angles on a single α-MoO3 flake. Near-field images of HShPs for different twist angles: θ = 2° (d1 = 133 nm) (b); θ = 17° (d1 = 128 nm) (c); θ = 30° (d1 = 130 nm) (d); θ = 46° (d1 = 134 nm) (e), all with d2 = 202 nm. I2: second harmonic near-field signal. The x axis is along the [100] direction of the bottom α-MoO3 layer. Red dashed lines indicate the fitting direction of line intensity profiles used to extract the momentum-specific Q factor. f–i Experimental, and j–m simulated Fourier spectra, corresponding to (b–e). n The shear factor (red data) and the Q factor (blue data) grow for increasing twist angles θ from 0° to 90° due to increasing asymmetry in the system, as shown by both experimental (hollow dots) and simulated (solid dots) results. The error bars represent the 95% confidence intervals.

Full size image

In Fig. 3n we quantitatively evaluate the impact of twist angle on the shear effect, calculating both the shear factor (red y axis) and Q factor (blue y axis) of induced HShPs as functions of the twist angle. Here, we define the quality factor as Q = Re(k)/Im(k), where Re(k) and Im(k) represent the in-plane real and imaginary momentum components of the HShPs, respectively (see Supplementary Note 6 for details). The shear factor, a global quantity, is calculated using the same approach discussed above (e.g., Fig. 2b, c), but this time using Fourier spectra of experimental data, rather than the calculated reflection coefficient. In contrast, the Q factor is defined for a specific momentum component, and is obtained by fitting the line intensity profiles along the direction of the longest propagation path, indicated by the red dashed lines in Fig. 3b–e.

Notably, Fig. 3n clearly shows a direct dependency between increasing shear factor and increasing Q factor. This connection originates from loss redistribution, which induces an asymmetric loss distribution between the branches of the hyperbolic IFCs, thereby enhancing the shear factor. Simultaneously, the branch with reduced losses accesses higher momentum regions, resulting in stronger field confinement and an increased Q factor. This effectively represents the shear effect’s ability to improve the directionality of energy flow within the wavefronts and extend the propagation length of high-momentum components. In fact, as the twist angle increases from near-zero to 60°, the shear factor increases from 0.11 to 0.47 and the Q factor from 7.0 to 19.9, both showing significant enhancement. These experimental data behaviors are confirmed by simulations, although the latter show consistently larger values than the former. We ascribe this discrepancy to defect-induced scattering in our sample, which increases the global material loss and hence reduces the propagation length of polaritons.

Apart from the in-plane asymmetry introduced by the twist angle, twisted bilayer α-MoO3 consequently enables adjustment of vertical symmetry through thickness modulation, allowing thickness to be another key parameter in engineering HShPs. To explore how the top-layer thickness influences the shear effect, we lay α-MoO3 flakes with different thicknesses on top of a single α-MoO3 bottom flake, which has fixed thickness d2 = 170 nm (Fig. 4a). This configuration is specifically designed to preserve a uniform twist angle of θ = 60°. A single layer of α-MoO3 (i.e., d1 = 0 nm) supports conventional symmetric hyperbolic shape in both real-space image (Fig. 4b) and its corresponding Fourier spectrum (Fig. 4f). However, by increasing the thickness of the top layer, the hyperbolic wavefronts (Fig. 4c–e) become increasingly slanted in real space, while showing mode enhancement along two of the hyperbolic arms in momentum space (Fig. 4g–i). Note that as d1 increases, we also observe a transition of the polariton dispersion from almost flat/canalized to a hyperbolic sheared, accompanied also by a slight reduction in the shear effect at larger thicknesses (Fig. 4e). Our simulations including real-space images (Supplementary Fig. 10) and the corresponding Fourier spectra (Fig. 4j–m), show good agreement with experimental findings. Moreover, further computational analysis revealed that adjusting the bottom layer thickness while keeping the top layer constant has similar consequences on the shear effect (Supplementary Fig. 11).

Fig. 4: Shear engineering and measurements of HShPs with varying α-MoO3 thicknesses.
figure 4

a Optical image of α-MoO3 flakes with varying thicknesses at a fixed twist angle on a single α-MoO3 flake. Near-field images of HShPs for different d1 values: 0 nm (b); 80 nm (c); 113 nm (d); 255 nm (e), with d2 = 170 nm and θ = 60°. The x axis is along the [100] direction of the bottom α-MoO3 layer. Red dashed lines show the fitting direction of line intensity profiles used to extract the momentum-specific Q factor. f–i Experimental, and j–m simulated Fourier spectra, corresponding to (b–e). n The shear factor (red data) extracted from Fourier spectra and Q factor (blue data) vary with increasing d1 due to broken vertical symmetry between the layers, as shown by both experimental (hollow dots) and simulated (solid dots) results. The error bars represent the 95% confidence intervals.

Full size image

Similar to Fig. 3n, Fig. 4n shows the impact of changing the top-layer thickness d1 on both the shear factor (red y axis) and Q factor (blue y axis). The plot shows that with an increase in the top-layer thickness, d1, both the shear and Q factors initially rise, reflecting enhanced vertical asymmetry. However, as d1 increases to a certain thickness, the shear factor begins to decrease, a trend that corroborates the theoretical analysis presented in Fig. 2c. Such behavior indicates a shift towards bulk-like properties that diminish the distinct advantages of layer asymmetry introduced by both the twisting angle and the thickness. Simultaneously, the Q factor experiences a significant reduction, due to both a diminished shear effect from lessened asymmetry and the increased layer thickness, which independently lowers the Q factor further. This suggests that there exists an optimal thickness range where the balance between enhancing asymmetry and avoiding bulk-like behavior maximizes both shear and Q factors. Although the shear factors and Q factors extracted from simulations qualitatively agree with those from experiments, the magnitude of the former is larger due to increased loss in fabricated samples.

Dynamic engineering and reconfiguration of HShPs

Engineering HShPs through fine-tuning of the twist angle and thickness of materials unlocks a comprehensive spectrum of control over their loss redistribution, asymmetric propagation, and confinement. However, this method is inherently static, rendering the structure unmodifiable post-fabrication. To overcome this limitation and achieve a reconfigurable device, we employ gate-tuned graphene joined with the α-MoO3 bilayer (Fig. 5a). Such an approach to dynamically manipulate polaritons has been well-demonstrated in previous studies23,24,34,37 and is anticipated to enable real-time adjustments and control of HShPs, thereby offering new possibilities for responsive and adaptive functionalities.

Fig. 5: Gate tuning and reconfiguration of HShPs in twisted bilayer α-MoO3/graphene device.
figure 5

a Schematic of a twisted bilayer α-MoO3/graphene heterostructure. Ein and Eout denote the incident and scattered electric fields, respectively. VDS, drain-source voltage. VBG, back-gate voltage. b Calculated IFCs of HShPs for different Fermi energy EF show that gate tuning can be used to change the topology and direction of HShPs, transitioning from hyperbolic (yellow) to elliptic (blue). The top and bottom α-MoO3 layer thicknesses are d1 = 96 nm and d2 = 78 nm, respectively. The twist angle θ is 62°. The x axis is along the [100] direction of the top α-MoO3 layer. Experimental near-field images for HShPs at EF of 0 eV (c), −0.18 eV (d), −0.33 eV (e), −0.43 eV (f), and −0.51 eV (g), respectively. As the Fermi energy becomes more negative, the direction of maximal propagation of shear waves changes, along with their topology. h–l Experimental, and m–q simulated Fourier spectra, corresponding to (c–g). r The growing shear factor obtained for increasingly negative EF shows the gate-tuning induced enhanced asymmetry of HShPs, as demonstrated by both experiments (red dots) and simulations (blue dots).

Full size image

In our device, the gate tuning is achieved by applying a voltage across the device, modulating the Fermi energy (EF) of graphene via a 285 nm-thick silica dielectric layer, as shown in the schematic view in Fig. 5a (the method for determining EF is detailed in Supplementary Note 7). The top and bottom α-MoO3 layers with thicknesses of d1 = 96 nm and d2 = 78 nm, respectively, are sequentially stacked with a relative twist angle of θ = 62° on the monolayer graphene. These designed parameters were chosen to optimize the observation of shear waves using the mode expansion method.

As illustrated by the calculated IFCs in Fig. 5b, increasing EF induces a change in the optical axis direction, accompanied by a topological transition35,36 of the HShPs from open (yellow) to almost canalized (orange) to close (blue). This transition impacts the symmetry of the IFCs, thereby influencing the loss redistribution mechanism that governs the shear factor and Q factor. This complex behavior is captured by our experimental and simulation results shown in Fig. 5 and Supplementary Fig. 13. At the charge neutral point (EF = 0 eV, Fig. 5c), HShPs show asymmetric hyperbolic wavefront in real space, consistent with the corresponding Fourier spectra from measurements and simulations (Fig. 5h, m). As EF increases, we observe the wavefront rotating, indicating that the change in the Fermi energy can be used to steer the polariton direction of propagation. This distinctive feature is maintained up to EF = −0.33 eV, as seen in Fig. 5d, e, i, j, with increasing asymmetry and loss redistribution, indicating an enhanced shear effect with increasing EF. Moreover, at EF = −0.51 eV, the HShPs’ dispersion contour flattens, indicating a topological transition35,36 from a hyperbolic to an elliptical shape (Fig. 5k, l), maintaining shear features throughout the transition. In this state, we observe sheared diffraction-less (canalized) propagation for momenta closer to the light cone and mostly flat IFCs with slight curvatures. Sample imperfections slightly reduce the clarity of this transition; however this result is also confirmed by simulations (Fig. 5q).

In Fig. 5r, we quantify the shear factor, demonstrating that a more negative Fermi energy enhances the propagation asymmetry and effective shear response of the bilayer. In fact, as EF becomes more negative, the asymmetry of the polaritons increases. Specifically, as the Fermi energy increases, the carrier density in graphene rises, modifying its dielectric response. This results in a stronger contrast between the dielectric environments at the bottom (graphene-Si/SiO2) and top (air) interfaces. According to Fig. 2b, c, the asymmetry along the z-direction enhances the shear effect. Therefore, the incorporation of graphene with increasing Fermi energy at the interface amplifies this asymmetry, leading to an increased shear effect and, consequently, an enhanced shear factor, as shown in Supplementary Fig. 16a. The experimental trend aligns with the simulation but increases more rapidly at high Fermi energy. This discrepancy primarily arises from fluctuations due to the signal-to-noise ratio in experimental imaging, material coupling, and nanofabrication-induced defects. As evidenced by the FFT analysis, the weaker branch of the hyperbolic IFCs in the experimental data exhibits a significantly lower signal compared to the simulation, leading to a larger shear factor.

Additionally, we observe that shear polaritons travel a longer distance due to the increased Q factor of modes in low-loss branch, as a result of loss redistribution. We calculated the maximum Q factor from both experimental and simulation results and plotted its variation with Fermi energy, as shown in Supplementary Fig. 19. The Q factor initially increases with Fermi energy, exhibiting a trend consistent with that of the shear factor. This alignment highlights graphene’s ability to modulate asymmetry, control energy flow, and enhance the Q factor. At higher Fermi energy, however, the Q factor decreases, which may be attributed to the reduction in the real part of the polariton wave vector. This behavior suggests that tuning the Fermi energy not only allows reconfiguring the shear properties and the direction of propagation but it also improves the overall propagation efficiency of the polaritonic waves. Similar observations of this phenomenon were replicated in another device, with detailed data and results documented in Supplementary Fig. 14.

Discussion

In this work we demonstrated that twisted bilayers of orthorhombic material α-MoO3 can host emerging shear phenomena for the supported polaritons, serving as an optimal platform to introduce and control HShPs in 2D materials, overcoming the intrinsic constraints typical of natural bulk materials that limit the accessibility and tunability of these confined states. We showed with theory and experiments that both the thickness of the two layers and their relative twist angle are crucial in controlling the asymmetry of phonon polariton propagation and controlling their shear phenomena. Specifically, we showed that this platform allows to shear conventional HPhPs, boosting their Q factor–up to four times. Additionally, by coupling gate-tuned graphene with the α-MoO3 bilayer, we realized a device capable of real-time reconfiguration of shear polaritons, enabling their in-situ manipulation. This approach allows for the tunability of their propagation direction, controls their lifetime and maximizes the shear effect without the need for altering the geometry or excitation conditions.

Our results confirm the significant influence of symmetry-breaking of phonon polaritons in twisted bilayer systems, and outline a strategy for effectively manipulating light-matter interactions in 2D materials at the nanoscale through both static and dynamic approaches. The precise control over the dispersion and loss redistribution of HShPs, coupled with a real-time response, unlocks substantial opportunities in cutting-edge applications. The enhanced Q factor and directionality make this platform ideal for on-chip polaritonic circuits, enabling efficient, high-speed optical signal processing with real-time tunable wavefront steering and multiplexing capabilities, alongside sub-diffractional imaging and spectroscopy. Additionally, the dynamic tunability of polariton behavior provides a flexible foundation for reconfigurable polaritonic devices, including adaptive optical switches and modulators.

Methods

Sample and device fabrication

All α-MoO3 flakes used were mechanically exfoliated from commercially available bulk materials (SixCarbon technology, Shenzhen). Prior to use, the desired thicknesses of α-MoO3 flakes were selected and verified under optical microscopy and AFM. The SiO2 (285 nm)/Si substrates employed in experiments underwent plasma treatment (SUNJUNE PLASMA VP-R3).

For the fabrication of twisted bilayer α-MoO3 samples, the bottom α-MoO3 flake was first exfoliated from bulk materials onto SiO2 (285 nm)/Si substrate, the top α-MoO3 flake was dry transferred onto the bottom α-MoO3 flake at a precisely controlled twist angle using a micromanipulator. After assembly, point defects were introduced through etching of samples using a standard electron beam lithography system and a reactive ion etcher (RIE). We avoid using gold disks as launchers to prevent uneven excitation of HShPs in different directions stemming from their fabrication imperfection. To fabricate the twisted bilayer α-MoO3/graphene device, monolayer graphene was obtained via mechanical exfoliation of graphite crystals (Shanghai Onway Technology Co., Ltd.) onto a SiO2 (285 nm)/Si substrate. The bottom α-MoO3 flake was exfoliated and then dry transferred onto monolayer graphene. Another α-MoO3 flake was then stacked above the bottom α-MoO3 flake with a specific twist angle. Source and drain electrodes, composed of 50 nm Au and 5 nm Cr, were patterned onto monolayer graphene using thermal deposition. To facilitate electrical gating, all electrodes were wire-bonded to a chip carrier.

Scattering scanning near-field optical microscopy

The infrared nanoimaging of polaritons was performed using a commercially available s-SNOM system (Bruker nanoIR3s), operating on a tapping mode AFM at an oscillating frequency Ω ≈ 250 kHz. The apex of a gold-coated AFM tip (160AC-GG, OPUS) was illuminated by an infrared beam from a CO2 laser (Access Laser, L4SL-13CO2) with a frequency of 931 cm−1, functioning concurrently as an infrared antenna and a near-field probe. The waves excited by tip interfere with those reflected by the point defects, generating discernible fringes in near-field images that represent half of the polariton wavelength. The tip-scattered field was collected with an off-axis parabolic mirror and directed towards a HgCdTe (MCT) photodetector. Detected signals were demodulated at the second harmonic of the tip resonant frequency to effectively extract the near-field signal from the sample and suppress the background.

Electrical transport measurements

The electrical transport characteristics were assessed using a setup comprising a SourceMeter (Keithley, 2450) for applying the back-gate voltage and a lock-in amplifier (Sine Scientific Instruments, OE1022) for recording the graphene resistance. Throughout the entire measurement process, the device was maintained in a dry air environment at room temperature.