INTRODUCTION

Many physical systems driven out-of-equilibrium by an external force are characterized in terms of a velocity-frequency or velocity-force relation1,2,3,4, which is an analog of the current-voltage characteristic measured in superconducting junctions5,6, carbon nanotubes7,8,9, graphene10,11 and other electronic circuits12. When subjected to a time-periodic force, the internal dynamics of these systems may synchronize with the external driving. The synchronization effect manifests itself in the form of constant plateaus of voltage or velocity versus mean current or force. Such plateaus, known as Shapiro steps, were first reported for a superconducting Josephson junction driven by a microwave signal13,14, where discrete steps in the voltage arise from the synchronization between the applied signal and oscillations of the Josephson phase15,16.

Since their discovery, understanding the nature of Shapiro steps has been important not only for elucidating basic mechanisms underlying superconductivity but also for new technological developments, including, for example, the realization of metrological voltage controllers17,18.

In classical driven systems, the presence of discrete steps in the velocity-force curves can be the signature of different physical effects, from speed reduction due to friction19,20,21, to the onset of a pinning-depinning transition22,23, synchronization24,25 or locking26,27,28 with an underlying energetic landscape. In many-particle systems, collective particle motions through periodic29,30,31,32 or random33,34 landscapes are often mediated by defects, which move like a single particle and display a complex sequence of plateaus with integer or fractional values of their speed. Due to the subtle interplay of interparticle and particle-substrate interaction, defect propagation takes place in complex periodic energy landscapes.

Modern advancements in optical manipulation of microscale matter have made it possible to engineer such potentials with tunable energetic wells and inter-well distances35,36,37. With this capability, one can manipulate and drag microscopic particles38,39, biological systems40,41, measure tiny forces42,43, or even assemble matter in two44,45 or three dimensions46,47,48. In this context, integer Shapiro steps have been recently reported for a single colloidal particle driven through an optical sinusoidal potential by an underlying oscillating substrate49. The plateaus emerged due to dynamic mode locking24, where synchronization with the oscillating substrate leads to a sequence of transport modes characterized by a constant speed.

By engineering non-sinusoidal periodic potentials with several maxima per wavelength, we show here that a single particle can display integer and fractional steps in the average speed under time-dependent driving. Employing individual particle tracking, we unveil the microscopic mechanisms leading to the emergence of these steps and show how it is possible to control them by constructing diagrams of phase-locked modes. Our driving strategy implements the time modulation directly within the periodic potential without the need to translate or oscillate the substrate, which could induce a delay in the particle response and hydrodynamic back-flow. The non-sinusoidal shape allows the particle to synchronize with the driving potential in a variety of modes, generating both pronounced integer and fractional Shapiro steps. Using our ability to tune the optical landscape and the driving protocol, we can even increase the prominence of some fractional Shapiro steps over others.

Results

Designing time-modulated periodic optical potentials

We drive a single polystyrene colloidal particle of diameter σ = 4 μm across a time-dependent periodic potential generated by passing an infrared continuous-wave laser through a pair of acousto-optic deflectors, as sketched in Fig. 1a. The particles sediment close to the bottom surface where they float due to balance between gravity and electrostatic repulsive interactions. Since the particles are illuminated by the laser from the top, they are trapped in two dimensions, i.e., close to the bottom plane. Technical details are given in the Methods Section.

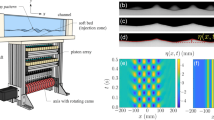
Fig. 1: Time-modulated sinusoidal and non-sinusoidal optical potentials.
figure 1

a Colloidal particle driven along a rotating ring of optical traps created by fast-scanning tweezers. The ring rotates with a time-dependent angular frequency ω(t) modulated according to a square wave. The inset at the top displays the modulation with period τ and amplitude Δω around a mean frequency ω0. b, c Density plots of \({N}_{{{\rm{tr}}}}=30\) optical traps with positions on a circle of radius R = 29.6 μm. In (b), the optical traps are arranged equidistantly and create a sinusoidal potential with wavelength λs = 2πR/30 along the ring. In (c), the traps are arranged in 10 groups of triplets, yielding a periodic non-sinusoidal potential with wavelength λns = 2πR/10. In each triplet, spacing between neighboring traps are 5λns/12, λns/4, and λns/3. d, e Corresponding profiles of the optical potential U extracted from torque measurements. Supplementary Videos 1–6 in the Supporting Information show representative motions of the particle in these two potentials.

Full size image

The laser is rapidly steered through \({N}_{{{\rm{tr}}}}=30\) positions on a circle of radius R = 29.6 μm. Each trap position is visited every 20 μs50,51,52, a time scale much smaller than the self-diffusion time of the particles in the absence of driving, σ2/D ~ 280 s, where D ~ 0.057 μm2 s−1 is the self-diffusion coefficient. As the scanning is much faster than the particle motion, the particle feels an effective, quasistatic potential. When a laser passes through a position along the circle, its spot creates a Gaussian potential well with a depth proportional to the laser power. As described in the Methods section, the periodic potential felt by the colloidal particle results from the superposition of these Gaussian wells.

We engineer two types of periodic potentials, a sinusoidal one Us with wavelength λs = 2πR/30, Fig. 1b, d, and a non-sinusoidal one Uns with wavelength λns = 3λs, Fig. 1c, e. The Uns is generated by placing the traps in groups of three per wavelength λns, with trap centers located at positions 0, λns/3, and 7λns/12 in [0, λns). With this arrangement, we obtain three distinct potential wells per wavelength λns with inter-well spacings λns/3, λns/4, and 5λns/12. The profiles of the periodic potentials are calculated from measured particle trajectories, see Methods Section for details. These profiles, shown in Fig. 1d for the sinusoidal potential and in Fig. 1e for the non-sinusoidal one, exhibit energetic barriers of about 500 kBT. Thus, thermal fluctuations are rather weak in our system.

The selected distances between the optical traps were chosen such that the overlap of the Gaussian potential wells generated a simple periodic but non-sinusoidal potential able to induce integer and fractional Shapiro steps in the particle current. The distance between the potential wells were chosen such that each potential well was able to stably trap a colloidal particle. Indeed, for a distance smaller than the particle diameter, the wells could have been not distinguished as different by the particle, which would feel them as a single, larger well rather than two distinct ones. On the other hand, potential wells very far from each other could be unable to stably trap the particle along a ring, due to small but still present thermal fluctuations along the radial direction.

By rotating all traps with an angular speed ω, the particle is driven along the circle, as illustrated in Fig. 1a. For inducing Shapiro steps in the average particle velocity, ω is modulated periodically in time with period τ, yielding a time-modulated driving of the particle. Specifically, as shown in Fig. 1a, we apply a square-wave protocol with mean frequency ω0 and amplitude Δω: ω(t) = ω0 + Δω for t ∈ [nτ, (n + 1/2)τ) and ω(t) = ω0 − Δω for t ∈ [(n + 1/2)τ, (n + 1)τ), n = 0, 1, 2, …

Shapiro steps in mean particle velocity

For a constant angular velocity ω0, the particle trapped in one of the potential wells tends to follow the trap rotation in a clockwise direction but experiences resistance due to the Stokesian friction exerted by the surrounding water. This friction gives rise to a torque in the counter-clockwise direction. Since this torque is a constant proportional to ω0 in a frame corotating with the traps, we analyze the particle motion in this frame. The average velocity \(\bar{v}\) along the tangential direction in the corotating frame corresponds to an average velocity \({\bar{v}}_{{{\rm{lab}}}}=\bar{v}-{\omega }_{0}R\) in the laboratory frame.

Applying the square-wave modulation ω(t), we measure \(\bar{v}\) for both the sinusoidal [Fig. 1d] and the non-sinusoidal potential [Fig. 1e]. Figure 2a, b show the results of these measurements for varying ω0 at fixed period τ = 1.047 s and amplitude Δω = 0.6 rad s−1 of the driving (red circles with error bars). In both figures, intervals of ω0 occur, where \(\bar{v}\) remains constant, corresponding to a sequence of Shapiro steps. In these plateau regimes of constant \(\bar{v}\), the particle synchronizes its motion with the oscillatory driving, leading to phase-locked particle velocities in the corotating reference frame. The experimental results are in excellent agreement with Brownian dynamics simulations (blue lines) detailed in the Methods Section.

Fig. 2: Phase-locked mean particle velocities reflecting motion synchronized with the driving.
figure 2

a, b Average velocity \(\bar{v}\) in the corotating frame versus mean azimuthal velocity ω0R of trap rotation for the sinusoidal (a) and the periodic but non-sinusoidal optical potential (b). In both images, we vary ω0 at fixed R = 29.6 μm, τ = 1.047 s, and Δω = 0.6 rad s−1. c, d Average velocity \(\bar{v}\) as a function of the characteristic oscillatory driving velocities λs/τ = vs and λns/τ = vns for the sinusoidal potential (c) and the non-sinusoidal one (d). In both images, we vary τ at fixed ω0 = Δω0 = 0.6 rad s−1, and R = 29.6 μm. In all graphs scattered red dots are experimental data, the error bars denote the standard deviation of three experimental measurements, and blue lines are results from numerical simulations. Continuous black lines mark integer steps, and dashed lines mark fractional ones. Values on top of the graphs in (c, d) indicate slopes n and p/q of the lines according to equations (1) and (2). The colored arrows denote measurements, whose particle trajectories are shown in Fig. 3.

Full size image

For the sinusoidal potential [Fig. 2a], all steps are integer multiples of the characteristic speed vs = λs/τ = 5.92 μm s−1 of the driving, yielding phase-locked values

$${v}_{n}=n{v}_{{{\rm{s}}}},\quad n=1,2,\ldots$$
(1)

These steps are indicated by the horizontal black lines in Fig. 2a for n = 1,…,4. While not all steps are equally well pronounced, only integer plateaus were observed. These steps arise from a synchronized particle motion, where in one period τ of the driving, the particle is displaced by n wavelengths λs of the sinusoidal potential.

For the non-sinusoidal potential [Fig. 2b], we observe steps (dashed horizontal black line)

$${v}_{p,q}=\frac{p}{q}\,{v}_{{{\rm{ns}}}}\,,$$
(2)

which are fractions p/q of the characteristic velocity \(\bar{v}={v}_{{{\rm{ns}}}}={\lambda }_{{{\rm{ns}}}}/\tau=17.76\,\mu {{\rm{m}}}\,{{{\rm{s}}}}^{-1}\). Also, the integer step with \(\bar{v}={v}_{{{\rm{ns}}}}={\lambda }_{{{\rm{ns}}}}/\tau\) occurs (solid horizontal black line). The fractional plateaus arise from a synchronized particle motion, where in q periods τ of the driving, the particle is displaced by p wavelengths λns of the non-sinusoidal potential.

The fractional plateaus are smaller than integer ones and, thus, more challenging to resolve. In our experiments, we increased ω0R in steps of 1.5 μm s−1. For this resolution, none of the fractional steps in Fig. 2b covers an interval of ω0R consisting of more than two experimental points. However, the numerical simulations shown by the blue lines in Fig. 2b provide evidence of the presence of the fractional steps in the non-sinusoidal potential in Fig. 2b.

Nonetheless, to unambiguously demonstrate synchronized motion with phase-locked velocities according to equations (1) and (2) in our experiments, we can also keep ω0 and Δω fixed and vary the period τ of the driving. For a good choice of ω0 and Δω, the driving should be such that the particle can surmount the potential barriers at the square wave’s high-value ω0 + Δω, while it remains trapped in a potential well at the low-value ω0 − Δω. This can be ensured for the trapping by taking Δω = ω0. For surmounting barriers, we choose ω0 = 0.6 rad s−1, which is comparable to the critical frequency at which the particle starts slipping in the potential.

Figure 2c, d show the mean particle velocity as a function of the characteristic velocities λs/τ and λns/τ for ω0 = Δω = 0.6 rad s−1. Now, phase-locking according to Eqs. (1) and (2) manifests itself as \(\bar{v}\) varying linearly with vs = λs/τ and vns = λns/τ. Fractional phase locking in Fig. 2d is much more clearly visible than in Fig. 2b: a linear increase of \(\bar{v}\) with λns/τ occurs in broad intervals with fractional slopes p/q = 1/4, 1/3, 1/2, and 2/3. Again, simulations (blue lines) in both Fig. 2c, d are in excellent agreement with the experimental observations.

The error bars in Fig. 2a–d represent the spread between three different sets of measurements, each conducted with a different particle from the same stock solution. They are relatively small when the particle is phase-locked with the oscillating potential and become larger when it is not. This can be understood from the fact that for synchronized motion, fluctuations of the particle position due to thermal noise are suppressed. The effect is reflected in a lower diffusion coefficient of the particle in a phase-locked state53.

The ability to precisely track the colloidal particle allows us to analyze in detail its movement across the two types of periodic potentials. In Fig. 3, we show particle trajectories for various driving frequencies 1/τ at fixed ω0 = Δω for the sinusoidal [Fig. 3a] and non-sinusoidal potential [Fig. 3b].

Fig. 3: Synchronized and non-synchronized particle trajectories.
figure 3

a, b Scaled angular particle positions Rφ/λs,ns versus scaled time t/τ in the corotating reference frame at fixed ω0 = Δω = 0.60 rad s−1 as in Fig. 2c, d for (a) the sinusoidal and (b) the non-sinusoidal potential for various driving frequencies 1/τ. The chosen frequencies correspond to values of λs/τ and λns/τ indicated by the colored arrows in Fig. 2c, d. Optical potentials are shown at the bottom. Trajectories are displayed in a reduced zone scheme, i.e., when they exit at the right side of the graph they are continued at the left side. Synchronized trajectories corresponding to Shapiro steps overlap and are colored in orange, green, and blue. Non-synchronized trajectories are marked in gray. In (a), mean velocities \(\bar{v}\) obtained from the synchronized trajectories are integer multiples of vs. In (b), fractions p/q of vns appear, which correspond to particle displacements by p wavelengths λns in q periods of the driving. The small schematics on the side of the images illustrate the particle position within the periodic potential corresponding to an integer step (side of a) and to a fractional one (side of b). The videos 1–6 in the Supplementary Information show the synchronized particle motion across the periodic potentials.

Full size image

Colored synchronized trajectories collapse onto space-time periodic limit cycles apart from thermal fluctuations. Along the synchronized trajectories in Fig. 3a, the particle moves n = 1, 2, 3 wavelengths λs in one period τ of the driving, giving a mean particle velocity \(\bar{v}=n{v}_{{{\rm{s}}}}\). Along the synchronized trajectories in Fig. 3b, the particle moves p wavelengths λns in q periods τ, giving the mean particle velocity \(\bar{v}=(p/q){v}_{{{\rm{ns}}}}\) with fractions p/q = 1/2, 2/3, 1/1. Gray lines in both graphs correspond to particle trajectories that are not synchronized with the driving. In the schematics on the sides of Fig. 3, we illustrate the particle displacements in successive half periods τ/2 for the phase-locked modes with n = 2 in Fig. 3a and p/q = 2/3 in Fig. 3b.

For the sinusoidal potential, we see that integer Shapiro steps with \(\bar{v}={v}_{{{\rm{s}}}},2{v}_{{{\rm{s}}}},\ldots\) occur when the particle is trapped in a potential minimum for half a period of the driving and then moves a distance λs, 2λs, … in the other half. The trapping, at the minimum, aids the synchronization as a way of “resetting” the particle position during each period.

An analogous situation occurs for the non-sinusoidal potential, but now the particle displays an additional backward or forward movement to reach the closest potential minimum. These additional movements can be seen, for example, in the bunches of orange particle trajectories in Fig. 3b, which correspond to the step at \(\bar{v}=\frac{1}{2}{v}_{{{\rm{ns}}}}\) in Fig. 2b.

Next we show that it is possible to calculate the type of phase-locked modes characterized by p/q in Eq. (2) and thus to control the experimental parameters that give rise to a selected step.

We consider the particle motion in the absence of thermal fluctuations and determine the propagator G(x), which gives the position of the particle after one period of driving if it started at position x = Rφ. After \({q}^{{\prime} }\) periods of driving, the particle position is obtained by the \({q}^{{\prime} }\)-fold composition \({G}^{({q}^{{\prime} })}(x)=G\circ \ldots \circ G(x)\) of G(x). For a mode to occur with value \({q}^{{\prime} }\), the particle must be at an equivalent position in the potential after \({q}^{{\prime} }\) periods of the driving. This means that there must exist an x* ∈ [0, λns), where the difference \({G}^{({q}^{{\prime} })}({x}_{*})-{x}_{*}\) is an integer multiple of λns, i.e., such x* must satisfy the fixed point equation

$${G}^{({q}^{{\prime} })}({x}_{*})\,{{\mathrm{mod}}}\,\,{\lambda }_{{{\rm{ns}}}}={x}_{*}\,,$$
(3)

where \(a\,{\mathrm{mod}}\,\,b\in [0,b)\) is the remainder when a is divided by b. The smallest \({q}^{{\prime} }\), for which at least one stable fixed point x* exists, is the q of a phase-locked mode. The number p of wavelengths λns by which the particle is displaced after q periods is p = ∣G(q)(x*) − x*∣/λns. This fixed-point method allows us to calculate q and p for any given driving parameters ω0, Δω, and τ. Technical details are given in the Methods Section.

Figure 4a–c demonstrate the application of the fixed-point method for the non-sinusoidal potential and the same parameters as in Fig. 2d when λns/τ = 50 μm s−1. For q = 1 [Fig. 4a] and q = 2 [Fig. 4b], no fixed-point solutions of Eq. (3) exist, while a limit cycle of three stable fixed points x* (bullets) is obtained for q = 3 [Fig. 4c], giving p = ∣G(q)(x*) − x*∣/λns = 1. Accordingly, the theoretically predicted mode is 1/3, in agreement with the experimental observation.

Figure 4d shows the diagram of phase-locked modes when varying ω0R and λnsτ, and setting Δω = 0.6 rad s−1. The vertical and horizontal lines in this diagram represent the variation of parameters considered in Fig. 2b, d and show good agreement with the experimental observations: for example, the modes with p/q = 1/2, 2/3, and 1 at fixed τ = 1.047 s are predicted to occur for ω0R in the intervals 7−10 μm s−1, 10−14 μm s−1, and 15−23 μm s−1 according to Fig. 4d, which match the intervals where the modes occur in Fig. 2b. Likewise, the modes with p/q = 2/3, 1/2, and 1/3 at fixed ω0R = 17.76 μm s−1 are predicted to occur for λns/τ in the intervals 20−28 μm s−1, 29−36 μm s−1 and 42−57 μm s−1, matching the intervals in Fig. 2d.

Fig. 4: Diagram of phase-locked modes.
figure 4

a–c Propagators G(q)(x) giving the position of the particle after q periods of the driving if it started at x. Parameters are as in Fig. 2d when λns/τ = 50 μm s−1. Intersections of G(3)(x) with the diagonal line in (c) imply that a limit cycle of three stable fixed points (bullets) is present, giving p = ∣G(q)(x*) − x*∣/λns = 1. The theoretically predicted mode of phase locking thus is 1/3, in agreement with the experimental finding in Fig. 2d. d Diagram of phase-locked modes for the non-sinusoidal potential obtained by the fixed-point analysis when applying it to a wide range of values λns/τ and ω0R at fixed Δω = 0.6 rad s−1. Yellow regions indicate integer Shapiro steps, and blue regions mark fractional steps. Following the vertical and horizontal lines in the diagram correspond to the variations of ω0R and λns/τ in Fig. 2b, d, respectively.

Full size image

Discussion

We report the observation of integer and fractional Shapiro steps in the average speed of a single colloidal particle driven across a spatially and temporally modulated potential landscape. Fractional steps appear only when the potential is not sinusoidal. Through direct measurement of the particle and trap positions and using theoretical arguments, we unveil the phase-locking mechanisms at the origin of the fractional steps and demonstrate the possibility to tune them by engineering the optical driving.

In our periodic potentials, Shapiro steps emerge via the following mechanisms. During the part of the period when the driving is zero, the optical potential has a stabilizing role for both integer and fractional steps. For the sinusoidal potential, the particle relaxes once per driving period, giving rise to integer steps. For the non-sinusoidal potential, due to the complexity of the potential landscape, the particle can relax towards different potential minima in each driving period. This leads to richer particle dynamics, enabling the synchronization in fractional Shapiro steps in addition to integer ones.

From the application point of view, we have shown how to manipulate the lengths of the fractional plateaus via potential engineering, which is important for particle transport in materials and devices. The occurrence of fractional steps in periodic potentials with anharmonicities is generic. They can be used for versatile steering of particles with stable velocities that are robust against noise as well as small perturbations of driving parameters and spatial periodicity. This should allow, for example, for setting a prescribed mean velocity of a particle driven by an external signal within a microfluidic or a lab-on-a-chip device. Another potential application is to use fractional steps for probing characteristic features of periodic potentials, like its deviation from a sinusoidal form, symmetry, or number of wells per period. As diagrams of phase-locked modes are very sensitive to the shape of the potential, the corresponding measurements can be employed as a way to determine carefully the parameters in periodic force fields. Thus, these modes can be used in sensor applications to detect subtle shifts in the external force in a similar way to metrological voltage controllers developed for Josephson junctions17,18.

Unraveling microscopic synchronization mechanisms leading to Shapiro steps is important in the analysis of transport of particles across periodically structured landscapes, a generic situation encountered when studying non-equilibrium dynamics in condensed matter systems. Plateaus are not just a signature of non-linearity; they offer a window for exploring details of the coupling between the particle’s motion and that of the underlying landscape.

While our work has centered on a single driven particle, future directions may explore complex behavior in collective motions of many particles, or across disordered landscapes, which can be easily realized with optical engineering. This will further enrich the study of resonant transport and phase locking in periodically driven out-of-equilibrium systems.

Methods

Experimental setup

We use monodisperse spherical polystyrene particles with a diameter σ = 4 μm (CML, Molecular Probes). The particles are dispersed in highly deionized water (Milli-Q water) at room temperature T = 293 K, and the suspension is confined within a fluidic cell assembled with two coverslips separated by  ~ 100 μm. The cell is placed on the stage of a custom-built optical microscope and exposed to a set of fast-scanning optical tweezers. The tweezers are created by passing an infrared laser beam with wavelength 1064 μm and power P = 3 W (manlight ML5-CW-P/TKS-OTS) through a pair of acousto-optic deflectors (AODs, AA Optoelectronics DTSXY-400-1064). Combined with the AODs is a two-channel radio frequency wave generator (DDSPA2X-D431b-34), which is addressed by a digital output card (National Instruments cDAQ NI-9403) with a refresh frequency of 150 kHz. A Nikon 40 × microscope objective (plan Apo), illuminated by a light emitting diode, and a complementary metal oxide camera (Ximea MQ003MG-CM) are used to record the particle positions at 30 Hz.

Optical potential

We define by φi = ϕi(t) − θ(t), \(i=1,\ldots,{N}_{{{\rm{tr}}}}\), the fixed azimuthal positions of the \({N}_{{{\rm{tr}}}}\) trap centers in the co-moving frame, where ϕi(t) are the rotating positions in the laboratory frame and

$$\theta (t)=-\int_{0}^{t}{{\rm{d}}}{t}^{{\prime} }\omega ({t}^{{\prime} })\,\,\,.$$
(4)

Each laser spot creates a Gaussian potential well with a depth A proportional to the laser power, and a width w. The total potential felt by the particle at position φ in the corotating frame is given by the superposition of the \({N}_{{{\rm{tr}}}}\) Gaussian potential wells,

$${U}_{0}(\varphi )=-A{\sum }_{i=1}^{{N}_{{{\rm{tr}}}}}\exp \left(-\frac{{R}^{2}{(\varphi -{\varphi }_{i})}^{2}}{2{w}^{2}}\right)\,.$$
(5)

Due to a slight imperfection in the optical tweezer setup, the well depth is not perfectly uniform across the ring of traps. It is weakly modulated with two nearly equidistant local maxima along the ring, giving rise to an amplitude modulation \(\propto \cos (2\varphi )\) of the optical potential. Taking this weak modulation into account, the potential in the corotating frame becomes

$$U(\varphi,t)=\left(1+\xi \cos [2(\varphi+\theta (t)]){U}_{0}(\varphi )\right.,$$
(6)

where ξ is the strength of the amplitude modulation. With phase shifts α and β of the amplitude modulation and trap positions in the fixed laboratory frame, the functional form of the optical potential is

$$U(\varphi,t)=(1+\xi \cos [2(\varphi+\theta (t)+\alpha )]){U}_{0}(\varphi+\beta ).$$
(7)

To determine the parameters ξ, α, and β, and the parameters A and w entering U0(φ + β) via Eq. (5), we follow a similar procedure as in ref. 51. We rotate the potential landscape with a constant angular frequency ω0 = 0.6 rad s−1 large enough to allow for the particle to cross potential barriers (Δω = 0). The time series of particle’s positions ϕ(t) in the laboratory frame is recorded for 20 minutes at 30 frames per second, that is with a time step of δt = 1/30 s. With the positions φ(t) = ϕ(t) + ω0t in the corotating frame, the angular velocities [φ(t + δt) − φ(t)]/δt are calculated and we extract the torques

$$M(t)=\frac{{k}_{{{\rm{B}}}}T{R}^{2}}{D}\left[\frac{\varphi (t+\delta t)-\varphi (t)}{\delta t}+{\omega }_{0}\right]$$
(8)

acting on the particle in the cororating frame51.

Mean values of torque vary with the position along the ring and are periodic in time with period 2π/ω0. To determine the mean torques from the times series M(t), the intervals [0, 2π) and [0, 2π/ω0) of azimuthal positions and times are divided into Nφ = 210 and Nt = 10 equally sized bins. Averaging the M(t) in each bin, we obtain the mean torques \(\bar{M}(\varphi,t)\), which must agree with the derivative of U(φ, t) with respect to φ,

$$-\frac{\partial U(\varphi,t)}{\partial \varphi }=\bar{M}(\varphi,t)\,.$$
(9)

The parameters A, w, ξ, α, and β are obtained by fitting ∂U(φ, t)/∂φ to the measured \(\bar{M}(\varphi,t)\) with the least square method. For the sinusoidal potential, A = 559 kBT = 1.36 MJ/mol, w = 1.45 μm, ξ = 0.09, α = 1.81, and β = 0.23. For the non-sinusoidal potential, A = 548 kBT = 1.34 MJ/mol, w = 1.60 μm, ξ = 0.10, α = 0.80, and β = 0.18.

We checked that our simulation results for the average particle velocities in Fig. 2 are almost unaffected by small perturbations of the positions φi of the optical trap centers as well as small i-dependent random modulations of A in Eq. (5).

Brownian dynamics simulations

Equation (6) gives the potential U(φ, t) in the corotating frame. In the laboratory frame, it is Ulab(ϕ, t) = U(ϕ − θ(t), t), and the Langevin equation for the overdamped Brownian motion of the particle reads

$$\gamma R\frac{{{\rm{d}}}\phi }{{{\rm{d}}}t}=-\frac{1}{R}\,\frac{\partial {U}_{{{\rm{lab}}}}(\phi,t)}{\partial \phi }+\sqrt{2{k}_{{{\rm{B}}}}T\gamma }\,\eta (t)\,.$$
(10)

Here, Rϕ is the particle displacement along the ring, γ is the Stokesian friction coefficient, and η(t) is a thermal noise modeled by the Gaussian white noise process with zero mean and correlation function \(\langle \eta (t)\eta ({t}^{{\prime} })\rangle=\delta (t-{t}^{{\prime} })\).

In the corotating frame with angle variable φ = ϕ − θ(t), \(\dot{\varphi }(t)=\dot{\phi }(t)-\omega (t)\), and Eq. (10) becomes

$$\frac{{{\rm{d}}}\varphi }{{{\rm{d}}}t}=-\frac{D}{{k}_{{{\rm{B}}}}T{R}^{2}}\frac{\partial U(\varphi,t)}{\partial \varphi }+\omega (t)+\frac{\sqrt{2D}}{R}\eta (t),$$
(11)

where D = kBT/γ is the diffusion coefficient according to the fluctuation-dissipation theorem. Equation (11) is solved numerically using the Euler-Maruyama method.

Theoretical prediction of phase-locked modes

The fixed point method can be applied to both the sinusoidal and non-sinusoidal potential. It relies on the propagator G(x) = G(1)(x), which is determined by the numerical solution of the Langevin equation (11) in the limit of zero noise [η(t) = 0]. The fixed points of \([{G}^{(q)}(x)\,{\mathrm{mod}}\,\,\lambda ]\) given by equation (3), with λ = λs or λ = λns, are zeros of the function \({H}^{(q)}(x)=[{G}^{(q)}(x)\,{{\mathrm{mod}}}\,\,\lambda ]-x\).

To obtain the zeros of H(q)(x), we divide the interval [0, λ) into M = 50 equidistant points x1 < … < xM, and search for all pairs of successive points xi and xi+1, where H(q)(xi) and H(q)(xi+1) have different signs. Let m be the number of such pairs \({x}_{i}^{(\alpha )}\), \({x}_{i+1}^{(\alpha )}\), α = 1, …, m. In each interval \([{x}_{i}^{(\alpha )},{x}_{i+1}^{(\alpha )})\), we determine the point \({x}_{0}^{(\alpha )}\) of sign change with high accuracy by applying the Wijngaarden-Dekker-Brent method54. The sign change at \({x}_{0}^{(\alpha )}\) does not necessarily imply that \({x}_{0}^{(\alpha )}\) is a zero because H(q)(x) can jump at \({x}_{0}^{(\alpha )}\). A zero is considered to be present at \({x}_{0}^{(\alpha )}\), if \(| {H}^{(q)}({x}_{0}^{(\alpha )}-\delta )-{H}^{(q)}({x}_{0}^{(\alpha )}+\delta )| \le \epsilon\) for δ = 10−6λ and ϵ = 10−3λ.

For a zero x0 of H(q)(x) to be a stable fixed point x* of \([{G}^{(q)}(x)\,\,{\mathrm{mod}}\,\,\lambda ]\), it must hold ∣∂xG(q)(x*)∣ < 155. Such stable fixed point x* corresponds to a limit cycle of \([G(x)\,\,{\mathrm{mod}}\,\,\lambda ]\) running through q points, which forms an attractor of the stationary particle motion. Each of the q points of the limit cycle is a stable fixed point of \([{G}^{(q)}(x)\,\,{\mathrm{mod}}\,\,\lambda ]\). For the example shown in Fig. 4c, the three points marked by the bullets are stable fixed points of one limit cycle. The two other points, where \({G}^{(q)}(x)\,\,{\mathrm{mod}}\,\,{\lambda }_{{{\rm{ns}}}}\) intersects with the diagonal line, are unstable fixed points.

The q of the phase-locked mode is the smallest \({q}^{{\prime} }\), where \([{G}^{({q}^{{\prime} })}(x)\,\,{\mathrm{mod}}\,\,\lambda ]\) exhibits a stable fixed point. We thus obtain q by starting with \({q}^{{\prime} }=1\) and incrementing it by one until a stable fixed point occurs, i.e., a zero x* of H(q)(x) satisfying ∣∂xG(q)(x*)∣ < 1.

For the mode diagram shown in Fig. 4d, we have carried out the analysis for a wide range of parameters ω0R, λns/τ, and q values up to four. Parameter regions where either synchronized motion with q > 4 or non-synchronized motion occurs, are marked in white.