Introduction

The spin logic devices have been proposed as a promising candidate of next-generation logic devices1,2,3,4,5,6,7,8,9,10,11,12, based on spin field-effect transistor5,6,13, magnetization switching14,15,16,17,18,19,20,21, domain wall motion11,12,22,23, and spin wave24,25,26. Among those, only the logic operation based on magnetization switching and domain wall motion has been experimentally demonstrated. While the readout of the chirality of the domain wall relies on the polar MOKE imaging and the device is also very complicated, which makes it difficult to be integrated intoa silicon chip. Spin logic devices based on spin orbit torque (SOT) induced magnetization switching is considered to have a particular advantage due to their reconfigurable logic operation in a single device. The inputs are electric currents, and the output (magnetization state) depends only on if the amplitude sum of all the input currents (scalar adder) is larger than the critical switching current, where only the value of the currents plays the role in the logic operation. The implementation of complex logic functions still requires multiple devices.

Here, we introduce a new variable in a spin logic device that is both the input and output are in the form of vector where we add a degree of freedom-direction of the current. The sum of vectors is schematically shown in Fig. 1a, which follows the parallelogram principle. We take vector \(\vec{{{\bf{A}}}}\) and \(\vec{{{\bf{B}}}}\) as the inputs and the vector sum as the output. Figure 1b shows the result of the finite element simulation for the input current \(\vec{{{{\bf{I}}}}_{{{\bf{1}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{2}}}}}\) with the directions perpendicular to each other. We find that at the center of the cross-point of two currents, the resultant current direction is along 45° with respect to the current \(\vec{{{{\bf{I}}}}_{{{\bf{1}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{2}}}}}\), which follows the direction of vector sum. Contrary to the scalar adder, this is coined as the vector adder. By changing the directions of the input currents, different outputs can be obtained. However, it is challenging to read the output- the vector sum.

Fig. 1: Working principles of vector adder.
figure 1

a Vector sum of two vectors. b Simulation of a vector adder, the current vectors sum at the center of device. c Schematic illustration of three different vector adders proposed in L11 CuPt/CoPt.

Full size image

It has been reported that SOT manipulating magnetic states is dependent on the applied current direction in materials with special crystal structure27,28,29,30,31,32,33,34,35,36, e.g., current induced out of plane SOT and magnetization switching in CuPt/CoPt heterostructure shows 3-fold symmetry, in which only when the current is along broken mirror symmetry direction, the field-free switching of perpendicular magnetization can be observed34,35,36. Thus, current vector output, i.e., vector sum of two input current vectors, can be represented by different magnetization states in a single L11 CuPt/CoPt device. As shown in Fig. 1c, \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) are two input current vectors and \(\vec{{{{\bf{I}}}}_{{{\bf{t}}}}}\) represents the resultant vector direction of the vector sum. When \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) are along two mirror symmetry axis (\({{\mathscr{M}}}\)) directions, the resultant vector \(\vec{{{{\bf{I}}}}_{{{\bf{t}}}}}\) of vector sum of \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) can be along \({{\mathscr{M}}}\) axis direction or along broken mirror symmetry axis \(({{\mathscr{M}}}\times )\) directions, a positive, zero and negative OOP effective field can be generated and then magnetization switching from down to up, no switching and magnetization switching from up to down can be achieved, which can be used to design spin logic units. Similarly, other combinations of \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\), e.g. one along broken mirror symmetry axis direction and the other along mirror symmetry axis direction, or both along broken mirror symmetry axis directions, can also induce 3 distinct output results in the form of the direction of the vector sum \(\vec{{{{\bf{I}}}}_{{{\bf{t}}}}}\), and be used for designing the different spin logic devices, which enable implement more complex logical operation in a single device.

Results

Current vector adder enabled reconfigurable logic gates

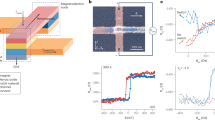
We firstly demonstrate the concept of current vector adder in L11 CoPt (111)/CuPt (111) bilayer with 3-fold crystal rotation symmetry. The CuPt (10 nm)/CoPt (4 nm) is epitaxially grown on single crystal SrTiO3 (111) substrate by magnetron sputtering at elevated temperature. The high-resolution scanning transmission electron microscopy (HR-STEM), as illustrated in Fig. 2a, shows the (1-10) lattice plane of the CuPt crystal. The atomic ABC rhombohedral stacking along [111] direction confirms the three-fold symmetry of CuPt crystal, which is verified again by the phi-scan of x-ray diffraction (XRD) (Supplementary Fig. 1). Then, the device with 4 current channels along different crystal axis is fabricated as shown in Fig. 2b. The dark gray channel is CuPt, while the light grey pillar surrounded by blue circle is in-memory logic bit, CoPt. Current vector inputs \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\), \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) are along three equivalent crystal axes [11-2], with ΦI = π/6, –π/6, and –π/2, respectively. The pre-set or configuration current \({\vec{{{\bf{I}}}}}_{{{\bf{con}}}}\) is along the [1-10] crystal direction – the \({{\mathscr{M}}}\) breaking direction, along which the electric current can induce the deterministic switching of the perpendicular magnetization. The anomalous Hall signal, RAHE is used to read the magnetization state of the logic bit. The RAHE with sweeping the magnetic field is shown in Fig. 2c, which indicates a good perpendicular magnetic anisotropy of the logic bit. The “↑” (“↓”) state of CoPt is defined as binary information “1” (“0”) corresponding to the high (low) RAHE value.

Fig. 2: Current vector adder.
figure 2

a Scanning transmission electron microscope (STEM) image of (1-10) lattice plane. The crystallographic direction is indicated. b Optical microscope image of the device for demonstration of vector adder. The CoPt pillar used for logic operation is circled by blue dash line. c Anomalous Hall signal of the CoPt pillar used for logic operation. Schematic of vector adder function. d–f electric manipulation of the magnetic state by sum of current vector. The inset is the schematic illustration of CuPt (111) plane in which the black arrow shows the input current. The sum of current vector is along \({\phi }_{I}=({{\rm{d}}})0\space({{\rm{e}}})-\frac{\pi }{6}\) \(({{\rm{f}}})-\frac{\pi }{3}\) indicated by red dash arrow. g Schematic of magnetization switching with current input \( \vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) under in-plane magnetic field. h switching loops with in-plane magnetic field along different directions. i In-plane magnetic field direction dependence of switching ratio of the perpendicular magnetization of CoPt pillar.

Full size image

Then we demonstrate that the output current vector direction follows the sum of the input vectors as plotted in Fig. 1c. Two of the current vectors can be summed under the CoPt pillar and the direction of the current vector sum can be examined by the magnetic state of CoPt pillar. To verify our propose, two input current vectors \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\), as shown in the Fig. 2d, are along \({{\mathscr{M}}}\left({\phi }_{I}={{\rm{\pi }}}/6,\, -\!\! {{\rm{\pi }}}/6\right)\). The field-free deterministic magnetization switching of CoPt can’t be achieved with each input current vector alone. While, as a comparison, when two current vectors are applied simultaneously, the magnetization is switched, indicating the direction of the sum of \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) is along [1-10] direction \(({{\phi }_{I}}=0)\) which is the \({{\mathscr{M}}}\)× direction. Two more examples for different current input combinations are provided. In the Fig. 2e, when \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) are simultaneously, the magnetic state does not change, indicating the sum of \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) is along the \({{\mathscr{M}}}\) of CuPt. As shown in Fig. 2f, when \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) are simultaneously applied, the magnetization switching with an opposite switching polarity to the situation in Fig. 2d, confirming the sum of \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) and \(\vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) is along \({{\mathscr{M}}}{\times}\left({\phi }_{I}=- \!\! {{\rm{\pi }}}/3\right) \) since it well corresponds to our previously constructed symmetry-dependent field-free switching model34,35,36. Note that, these three basic switching phenomena are unique features in the 3-fold rotational symmetry crystal which can be designed as the basis for designing the following reconfigurable logical devices, and switching performance according to the logic operations of our vector adder is highly reliable, and even changes in pulse width do not compromise the reliability of our device as shown in Supplementary Fig. 21.

To further confirm the vector adder in CoPt/CuPt bilayer structure, we measure the direction of the current vector under CoPt pillar by magnetic-field-dependent switching experiment. When applying a large enough in-plane magnetic field Hex (here is 200 Oe) to the device, the switching behavior of the CuPt/CoPt device is no longer dominated by the crystal symmetry, but by Hex. In the classic SOT-induced magnetization switching, only Hex perpendicular to the in-plane SOT direction (parallel to the current direction) can break the in-plane mirror symmetry and lead to deterministic switching of perpendicular magnetization37,38,39. As shown in Fig. 2g, the input current directions are \({\phi }_{I}={{\rm{\pi }}}/3 \, {{\rm{and}}} \, {\phi }_{I}=- \!\!{{\rm{\pi }}}/3\), and an external magnetic field of 200 Oe is applied with an angle ϕH with respect to [1-10] direction. The reversal of switching polarity is overserved when the magnetic field change from \({\phi }_{H}=0\) to \({\phi }_{H}={{\rm{\pi }}}\). Moreover, the switching is suppressed when the \({{\phi }_{H}}={{90}^{\circ }}\) (Fig. 2h) indicating the output current direction is \({\phi }_{I}=0\). Figure 2i summarizes the ϕH dependence of the switching ratio, which is defined by the ratio of magnetic-induced AHE change (RAHE) and current-induced AHE variation (∆R). A sin(ϕH) tendency can be clearly observed, and the phase at 0° proves the sum of inputs current is along \({\phi }_{I}=0\). These results unambiguously indicate the output current direction follows the sum of the input vector.

Different Boolean logic gates can be demonstrated in a single device with a proper and consistent definition of the current direction. We take the AND gate as an example to elaborate the logic operation by the current vector adder. The symbol of AND gate and its corresponding logic SOT device with input \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}},\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) and output \(\vec{{{{\bf{I}}}}_{{{\bf{t}}}}}\) are schematically illustrated in Fig. 3a. The detail of the circuit connection of the Boolean logic device shows three bipolar current sources to apply input \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}},\vec{{{{\bf{I}}}}_{{{\bf{b}}}}} \; {{\rm{and}}} \; \vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) on the device. Any two of them can be combined to realize a different logic operation. An external trigger is used to ensure pulsed current is generated simultaneously in different current channels. In each current channel, the relative direction of the applied current can be defined as binary. For instance, the current along the direction with ϕI = –π/6 (–7π/6) represents “1” (“0”) in \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\), and the current with ϕI = π/6 (7π/6) represents “1” (“0”) in \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\). A configuration current \(({\vec{{{\bf{I}}}}}_{{{\bf{con}}}})\) along [1-10] direction (\({{\mathscr{M}}}{\times}\) direction) is used to initial the magnetization state before every operation. It is worth emphasizing that different selections of the two input current directions together with different polarity of configuration current (“1” or “0”) can make a single device programmable.

Fig. 3: Reconfigurable Boolean logic device.
figure 3

a Schematic drawing and optical image of the device for demonstration of reconfigurable Boolean logic device. Logic input \( \vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \( \vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) are current direction produced from different current channel by bipolar current source. Logic output is the direction of the sum current indicating by the magnetic state of CoPt pillar. b Truth table of AND/OR by using \( \vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) and \( \vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\). The Boolean operation can be reconfigurable by both changing configuration current polarity and used current channel (current direction). c AND gate operations with a negative configuration current. Both MOKE signal and Hall voltage are used to read out in the device.

Full size image

As shown in Fig. 3b, with current inputs \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}{{\rm{and}}} \, \vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\), the device is able to implement AND or OR logic operation depending on the configuration current direction –Icon = –21 mA or Icon = 21 mA corresponding to “0” or “1”. The input current directions, output current direction, and their corresponding defined binary logic values of AND operation are illustrated in Fig. 3c. The logic operation of AND gate is described as follows. The magnetization initializes to 0 (“↓”) before each operation by Icon = –21 mA. When the logic input is (0,0), the direction of the current vector sum is ϕI = π, which favors for “↓” state in CoPt, resulting in an output “0”. The output is read out by the black domain in S-MOKE or low Hall voltage state in electrical transport measurement. For logic input (1,1), the direction of the current vector is ϕI = 0, and the magnetization of the CoPt pillar is switched to “↑” state corresponding to the output “1”. For logic input (1,0) and (0,1), since the directions of the current vectors sum are ϕI = π/2 or –π/2, which is along \({{\mathscr{M}}}\) direction, the magnetization switching does not occur. Therefore, the outputs remain magnetization state “0” (“↓”). When the configuration current Icon = +21 mA, with \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}/\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\) as the inputs, the same device works as a OR gate. As shown in Supplementary Fig. 4, the NAND/NOR gates can also be realized by changing the input current vectors to \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}} \, {{\rm{and}}} \, \vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) with different configurable currents. Furthermore, the more complicated IMPLY gate is realized by using input currents \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}} \, {{\rm{and}}} \, \vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) with a positive configuration current. The operations of all the logic gates are experimentally verified by the S-MOKE and Hall voltage (Supplementary Fig. 5).

Current vector adder enabled full adder

We now illustrate the superiority of vector adder by realizing the more complicated full adder. The conventional realization of full adder relies on cascading of a series of Boolean logic gates12,40,41, as shown in Supplementary Fig. 6. However, based on the proposed spin logic device, the full adder can be constructed by only using two devices, in which one device performs 3-input majority logic gate to achieve the carry operation (i.e., carry unit) and another device performs 3-input XOR gate to achieve the sum operation (i.e., sum unit), as shown in Fig. 4a.

Fig. 4: Demonstration of full adder.
figure 4

a Illustration of carry and sum device for the full adder. b input, output current vector, and corresponding Boolean logic value in sum operation. c Sum operation characterized by S-MOKE and Hall voltage. A configuration current same as the input \(\vec{{I}_{a}}\) is used to initialize the device before each operation.

Full size image

The carry function is the same as the truth table of Fig. 3b, where the configuration current \({\vec{{{\bf{I}}}}}_{{{\bf{con}}}}\) is replaced by the \(\vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\), which is the calculation result from the previous sum unit. If two or three of \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}},\vec{{{{\bf{I}}}}_{{{\bf{b}}}}} \, {{\rm{and}}} \, \vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) are “1”, the device output is “1”. If two or three of \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}},\vec{{{{\bf{I}}}}_{{{\bf{b}}}}} \, {{\rm{and}}} \, \vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) are “0”, the device output is “0”. That is 3-input majority logic.

The device implementing the sum function (S) as shown in Fig. 4a is different from the carry unit. Three current vector inputs \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}},\vec{{{{\bf{I}}}}_{{{\bf{b}}}}} \, {{\rm{and}}} \, \vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) are equivalent due to the 3-fold rotation symmetry and are applied along \({{\mathscr{M}}}{\times}\) axes by bipolar current source. Following this consideration, the sum can be implemented by the XOR operation for \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}},\vec{{{{\bf{I}}}}_{{{\bf{b}}}}} \, {{\rm{and}}} \, \vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\). If the number of “1” in \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}},\vec{{{{\bf{I}}}}_{{{\bf{b}}}}} \, {{\rm{and}}} \, \vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) is odd, the device output is “1”, such as (1,1,1), (1,0,0), (0,1,0) and (1,0,0). If the number of “1” in \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}},\vec{{{{\bf{I}}}}_{{{\bf{b}}}}} \, {{\rm{and}}} \, \vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\) is even, the device output is “0”, such as (1,1,0), (1,0,1), and (0,1,1). Moreover, one of the three inputs is used as the configuration current. The truth table of the sum function is illustrated in Fig. 4b. We experimentally demonstrate sum function of the device by S-MOKE image and Hall voltage as the read-out, as shown in Fig. 4c. Before every operation, one of the input is used as the configuration current, here \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}={\vec{{{\bf{I}}}}}_{{{\bf{con}}}}\), to set the initial magnetization state of CoPt pillar. For (\(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\), \(\vec{{{{\bf{I}}}}_{{{\bf{b}}}}}\), \(\vec{{{{\bf{I}}}}_{{{\bf{c}}}}}\)) is (1,0,0), \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) = “1” (here \({I}_{a}\) = +21 mA), the initial magnetization state is in “↑” state. The direction of the current vector sum is along a mirror symmetry-breaking direction (\({\phi }_{I}=0\)) and the magnetization of the CoPt pillar is aligned to “↑” state by the positive OOP effective field, corresponding to the \(\vec{S}\) = “1”. For \((\vec{{{{\bf{I}}}}_{{{\bf{a}}}}},\vec{{{{\bf{I}}}}_{{{\bf{b}}}}},\vec{{{{\bf{I}}}}_{{{\bf{c}}}}})\) is (1,1,0), \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) = “1”, the initial magnetization state is still in “↑” state. The direction of the current vector sum is also along a mirror symmetry-breaking direction (\({\phi }_{I}={{\rm{\pi }}}/3\)) but opposite to that for (1,0,0). The magnetization of the CoPt pillar is therefore switched to “↓” state by the negative OOP effective field, corresponding to the \(\vec{{{\bf{S}}}}\) = “0”. For all the inputs are “1” (“0”), \(\vec{{{{\bf{I}}}}_{{{\bf{a}}}}}\) = “1” (“0”), and the initial magnetization state is in “↑” (“↓”) state. The three input current vectors are canceled at the center of the cross-point under the CoPt pillar. The magnetization state of the CoPt pillar remains unchanged and is the same as the initial state, corresponding to the \(\vec{{{\bf{S}}}}\) = “1” (“0”). By combining the curry unit and sum unit, a full adder is realized. The circuit connection of all logic devices is summarized in Supplementary Fig. 2.

Discussions

To prove the superiority of our vector adder, the quantitative analysis of the device’s latency, power consumption, and area efficiency is implemented by simulation (Benchmarks comparing of the vector adder with other logic gates in Methods). We compared our device with the MTJ based full adders and SOT-based full adders which represent the advanced performance of logic devices in industry and research works. The power and time consumption of a full adder also goes beyond a single SOT device, incorporating the performance of the associated integrated circuits. This provides a more comprehensive and realistic benchmark for evaluating spin logic schemes in practical applications. Our device implements a full adder with only 0.92% of the area, 0.059% of the power consumption, and 0.99% of the time consumption of the SOT-based full adder which utilizes the domain wall motion12 (Supplementary Table 1). The spin logic with our devices shows low power consumption, high area efficiency, and low latency. The simulation shows the large performance advantages of our vector adder over previous logic devices.

Although the introduction of current vectors has significantly reduced both the area and energy consumption of a 1-bit full adder and its arithmetic operations, practical applications, such as AI and scientific computing, often demand cascading designs, which inevitably adds extra power consumption and area overhead. To estimate the effect of cascading of the full adder, here we take an example of a 4-bit cascade adder implementation based on 1-bit full adder as shown in Supplementary Fig. 19a. As detailed in Section S6 of the Supplementary Information, implementing 4-bit full adders necessitates cascading four 1-bit full adders. First, each full adder comprises two vector adders, each requiring four NMOS transistors in the current-driven circuit to determine current direction based on input signals, and multiple PMOS and NMOS transistors in the read circuit to sense the MTJ’s magnetization state. Consequently, for a 4-bit adder, four such full adders must be cascaded, increasing the overall transistor count and layout area in proportion to the number of bits. Second, the circuit introduces extra delay because of a standard MTJ read-out process: the read path must be pre-charged, discharged, and then compared with a reference voltage before the carry-out is passed on. Each of these steps incurs additional delay and power consumption, repeated at every level of cascading to ensure accurate data propagation. Despite these added transistors and operational time, the vector adder device’s inherent ability to handle both sums and carry in a single unit leads to more compact designs than traditional CMOS. Furthermore, as shown by a 4-bit multiplication circuit in Supplementary Fig. 19c, Section S6, the same cascading principal scales seamlessly to more complex operations. Although the design and optimization of such cascade circuits is not the primary focus of this work, a thorough exploration of these aspects will be essential in future research to further mitigate the overhead in large-scale applications. In subsequent studies, a balanced strategy that carefully weighs the impact of cascading against the inherent efficiency of the device’s computational core may further lower the overall power consumption in practical scenarios.

The spin logic with vector adder is not limited to this specified L11CuPt/CoPt heterostructure and may be applicable to various SOT materials and devices as long as the current vector can be encoded by the materials or devices’ anisotropy. The materials/devices could be divided into two categories: devices with the amorphous/polycrystalline materials and single crystals.

Firstly, we discuss the devices with amorphous/polycrystalline materials by which we can utilize the vector adder to construct the spin logic. The SOT devices should be able to realize the field-free switching of perpendicular magnetization, which has in-plane unidirectional anisotropy (one-fold anisotropy)42. Therefore, when the currents flow along the longitudinal and transverse directions the SOTs are different. For example, the unidirectional anisotropy of the device can be achieved by the device wedge43, lateral electric field44 and the exchange bias field45. This is the simplest case, which can be used to design basic logic gates such as AND, OR based on the current vector adder. The working principle is schematically shown in Supplementary Fig. 17. Assuming the initial state is magnetization up. When the current vector sum is along the mirror plane, the magnetization cannot be switched as shown in shown in Supplementary Fig. 17a and c. When the current vector sum is in the direction perpendicular to the mirror plane, the magnetization can be switched from up to down or from down to up as shown in Supplementary Fig. 17b and d. Moreover, the devices with amorphous/polycrystalline materials have the potential to achieve three-fold rotational symmetry. For example, based on the working principle of the aforementioned one-fold rotational symmetry achieved by a lateral electric field, three lateral electric fields can build a three-fold rotational symmetry system. It is possible to fabricate complex logic such as NAND, NOR, IMPLY, and full adder except for AND, OR, with this device by current vector adder similar to single crystals with three-fold rotational symmetry. Secondly, we introduce the SOT devices with the single crystal with one-fold and three-fold rotational symmetry. The most well-known crystal with one-fold rotational symmetry in SOT is 2-dimession van der Waals materials- WTe227. The out-of-plane spin polarization is different along the a axis and b axis in this material. For the three-fold rotational symmetry, except CuPt/CoPt, we also found the single layer fcc CoPt36 has an angle-dependent free field switching with a three-fold rotational symmetry. Furthermore, many other materials could induce similar three-fold and even 6-fold symmetrical field-free magnetization switching due to triangle or hexagonal warping of Fermi surfac35: for example, bilayer graphene46 whose Fermi surface has triangle warping, Bi-based topological insulators (Bi,Sb)2/(Se,Te)347,48,49 and Bi4Te350, which have the hexagonal warping with a six-fold spin-momentum locking. Finally, antiferromagnets with high crystal symmetry but lower magnetic symmetry could also be used for spin logic devices based on current vector adder, e.g. Mn3Sn32 and Mn3Pt31, RuO229, by which the magnetization switching or Néel vector switching depends on crystal directions.

Summary

In this work, we have proved that two current vectors can be added up to form a new current vector. We also demonstrated that this current vector adder can be used to realize complex spin logic functions including various Boolean logic gates and full adder. To date, scientists have proposed a few spin logic devices by which different reprogrammable Boolean logic operations can be realized. However, the spin logic device based on the vector adder is much simpler for implementation of some complicated logic functions such as full adder than other spin logic devices. The simple device configuration for complex logic function would significantly increase the effective computing capability and realize high area efficiency, low power consumption, and low latency in a realistic chip. Note that our proposed spin logic is compatible with standard SOT and magnetic tunnel junction (MTJ) based logic devices, which have the advantage of high speed and low energy consumption. The output - the magnetization state can be easily read out by the sizable tunneling magnetoresistance in the MTJ, instead of the AHE voltage or S-MOKE used in our work.

Methods

Device fabrication

L11 CuPt film with 10 nm was first deposited on a SrTiO3 (111) substrate at a temperature of 500 °C by d.c. magnetron sputtering with a base pressure of 1 × 10−8 torr and Ar pressure of 5 × 10−3 torr. Then 4 nm CoPt film was sputtered on the CuPt layer at a temperature of 300 °C. The film was patterned into the logic device with a CoPt pillar in 3 μm diameter using a combination of Ultraviolet Maskless Lithography machine (TuoTuo Technology) and ion beam etching. The electrode of Ti (5 nm)/Cu (200 nm) was then deposited by thermal evaporation.

Electrical measurement

The magnetization switching and logic operation are driven by the pulsed current generated with Keithley 6221. Different Keithley 6221 are triggered simultaneously by an external pulse generator (Model PM8672A). Three Keithley 6221 were used for the current flowing along three directions. Keithley 2182 was used to read out the anomalous Hall voltage of the CoPt pillar with a 100 μA d.c. current by Keithley 6221.

MOKE microscopy measurement

Magneto-Optical Kerr Microscope was used to examine the magnetization state of the CoPt pillar. A proper background image was subtracted to achieve differential images with magnetic contrast. For the up (down) state image, the background image is the down (up) state. To avoid the remanence magnetic field influence of the coil, the coil is removed during measurement. The current pulses were applied simultaneously as the same as the electrical measurement.