Introduction

Quantum entanglement is an essential and viable resource for future quantum technologies. It has proven its worth in applications as diverse as secure quantum communication1,2,3, even over large distances in satellite based networks4,5, quantum computing6,7,8, quantum imaging of complex objects9,10, quantum metrology11 and lithography12,13. However, it is well known that noise deteriorates entanglement, for instance, due to noisy detectors (shot and thermal noise), stray light (e.g., daylight), depolarizing channels, lost photons to name but a few, all examples of generic (isotropic) noise that results in the decay of quantum information in realistic quantum scenarios14,15,16. The consequence is a diminished ability to certify, identify and exploit the full benefits of quantum entanglement for information processing14,17,18,19. High dimensional (d > 2 dimensions) entangled states are able to increase the noise threshold to which the usual entanglement witnesses certify entanglement15,20,21,22,23,24 but comes with the cost of limited state purity16 and complex quantum state analysis25. Although some mitigation techniques exist such as real-time channel analysis26 and entanglement purification27, real-world noise correction remains challenging in general photonic systems28,29, prohibiting noise-free communication when information is distributed by entanglement.

An emerging trend is to exploit quantum topological photonics30, which has already realized stable quantum emitters31,32,33, robust transport of entanglement through quantum circuits34,35 and entanglement storage36 but here the topology is not in the quantum state but in topologically structured matter. Recently the notion of optical topology has emerged, specifically optical skyrmions37, with the potential to embed measurable topological properties into the non-separable spatial and polarization degrees of freedom of classical38,39,40,41,42 and quantum43 photonic states. A motivation for the interest in skyrmions is their potential to act as resilient information carriers in the presence of noise, a topic very much in its infancy. So far, resilience of classical optical skyrmions under known (non-random) perturbations has been demonstrated experimentally44, yet numerical studies of such classical skyrmions to realistic noise scenarios have returned mixed outcomes45. To the best of our knowledge, no evidence (theoretical or experimental) exists for the resilience of quantum skyrmionic topologies to noise.

Here we show both theoretically and experimentally that quantum skyrmions and their topological quantum observables remain resilient to noise even as typical entanglement witnesses and quantum observables of the state decay. To realize this we create a nonlocal skyrmionic topology as a shared property of two entangled photons and pass the quantum topology through noise, as illustrated in Fig. 1, which we simulate by a generic (isotropic) noise model, a standard approach to test quantum states in noise46,47,48. We provide an intuitive explanation, supported by a rigorous theoretical treatment, as to why such noise can be considered a smooth deformation of the state - an operation that does not modify its topology - independent of its topological class. We present experimental results across various topologies and for a wide range of noise levels, confirming the topological invariance despite the decay of typical entanglement witnesses. Our work opens a path to quantum information processing and communication in real-world noisy quantum systems and channels without the need for compensation or mitigation strategies.

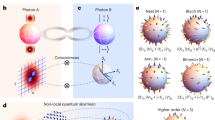
Fig. 1: Quantum skyrmions through noise.
figure 1

Photons A and B form an entangled state characterized by a non-local quantum skyrmion, shown as a stereographic projection of vectors on a sphere. Passing such a state through noise diminishes the quality of the entangled state, but leaves the topological observable unaltered so long as some entanglement persists.

Full size image

Results

Quantum skyrmions

As our aim is to study quantum skyrmionic topology in the presence of noise, we begin by constructing a bi-photon entangled state of the form \(\left\vert \Psi \right\rangle=\frac{1}{\sqrt{2}}\left({\left\vert {\ell }_{1}\right\rangle }_{A}{\left\vert {P}_{1}\right\rangle }_{B}+{e}^{i\delta }{\left\vert {\ell }_{2}\right\rangle }_{A}{\left\vert {P}_{2}\right\rangle }_{B}\right)\), as depicted graphically in Fig. 2a. Here ℓ1 and ℓ2 denote orbital angular momentum (OAM) of ℓ1ℏ and ℓ2ℏ per photon, respectively, \(\left\vert {P}_{1}\right\rangle,\left\vert {P}_{2}\right\rangle\) are orthogonal polarization states and δ allows for a relative phase between the two components of the state vector. When ∣ℓ1∣ ≠ ∣ℓ2∣ the bi-photon correlations form the desired skyrmionic mapping from \({{{{\mathcal{R}}}}}^{2}\to {{{{\mathcal{S}}}}}^{2}\), so that the entanglement defines a topology43. The topological invariant, the Skyrmion number (N), characterizes the number of times \({{{{\mathcal{R}}}}}^{2}\) (stereographically projected Hilbert space of photon A) wraps \({{{{\mathcal{S}}}}}^{2}\) (Hilbert space of photon B), i.e., the number of times photon B’s collapsed states wrap its own Hilbert space after completing a full set of spatial position measurements on photon A. This mapping is evident when expressing the OAM states of photon A in the position basis, using \(\left\vert \ell \right\rangle={\int}_{{{{{\mathcal{R}}}}}^{2}}| {{{\mathrm{LG}}}}_{\ell }\left({{{\bf{r}}}}\right)| {e}^{i\ell \phi }\left\vert {{{\bf{r}}}}\right\rangle \,{d}^{2}r\) where \({{{\mathrm{LG}}}}_{\ell }\left({{{\bf{r}}}}\right)\) are the Laguerre-Gaussian fields and \(\left\vert {{{\bf{r}}}}\right\rangle\) are position states corresponding to coordinates vectors \({{{{\bf{r}}}}}_{A}\in {{{{\mathcal{R}}}}}^{2}\). Ignoring global phase factors, this recasts our state to

$$\left\vert \Psi \right\rangle=\int_{{{{{\mathcal{R}}}}}^{2}}{\left\vert {{{\bf{r}}}}\right\rangle }_{A}\left(a({{{{\bf{r}}}}}_{A}){\left\vert {P}_{1}\right\rangle }_{B}+b({{{{\bf{r}}}}}_{A}){\left\vert {P}_{2}\right\rangle }_{B}\right)\,{d}^{2}{r}_{A},$$
(1)

where the coefficients \(a({{{{\bf{r}}}}}_{A})\equiv | {{{\mathrm{LG}}}}_{{\ell }_{1}}\left({{{{\bf{r}}}}}_{A}\right)|\) and \(b({{{{\bf{r}}}}}_{A})\equiv \exp (i(\Delta \ell {\phi }_{A}+ \delta ))| {{{\mathrm{LG}}}}_{{\ell }_{2}}\left({{{{\bf{r}}}}}_{A}\right)|\) are chosen to be normalized according to ∣a(rA)∣2 + ∣b(rA)∣2 = 1 for all \({{{{\bf{r}}}}}_{A}\in {{{{\mathcal{R}}}}}^{2}\) and Δℓ = ℓ2 − ℓ1. The Skyrmion number of such a state is then calculated from38

$$N=\frac{1}{4\pi }\int_{{{{{\mathcal{R}}}}}^{2}}{\epsilon }_{pqr}{S}_{p}\frac{\partial {S}_{q}}{\partial x}\frac{\partial {S}_{r}}{\partial y}dxdy\,,$$
(2)

where ϵpqr is the Levi-Civita symbol and it is assumed that the sphere has been normalized such that \({\Sigma }_{i=1}^{3}{S}_{i}^{2}=1\), i.e., a mapping to the unit sphere. To find the necessary quantum Stokes parameters, Si, one computes the expectation values of the Pauli matrices, calculated by taking the diagonal matrix element at position r for photon A and the partial trace over photon B, such that \({S}_{i}={{{\mathrm{Tr}}}}_{B}({\langle | {{{\bf{r}}}}\rangle }_{A}\langle {{{\bf{r}}}}{| }_{A}\otimes {\sigma }_{B,i}\rangle )={{{\mathrm{Tr}}}}_{B}\left({\sigma }_{B,iA}\langle {{{\bf{r}}}}| \Psi \rangle {\langle \Psi | {{{\bf{r}}}}\rangle }_{A}\right)\).

Fig. 2: Topological rejection of noise.
figure 2

a We create a bi-photon entangled state, with photon A in the spatial degree of freedom and photon B in the polarization degree of freedom, for a non-local skyrmionic topology as a shared emergent property of the two photons, shown as a stereographic projection. b The Skyrmion number is a digitized observable, shown here for integer values from N = −2 to N = 2, remaining intact along with the topology after the isotropic noise even while the entanglement decreases, except in the case when the entanglement reaches its minimum, indicating a non-entangled state. c In the geometric picture of photon B's Hilbert space as expressed by Stokes vectors (Sx, Sy, Sz), the change of state purity due to noise is a sphere of diminishing size, which for partially mixed states can always be renormalized while leaving the topology unaltered. Once the state is maximally-mixed, the Hilbert space of photon B has zero radius, no entanglement, and thus only a trivial topology (N = 0).

Full size image

Topological protection

A common way to simulate real-world noisy conditions is to use a generic (isotropic) noise model, by mixing the initially pure state with a maximally mixed state49, covering a wide range of random noise sources e.g., from the source (multi-photon events), the channel (background and lost photons), and the detector (dark counts). To keep the conclusions general we will use the purity of the state as our measure of the noise, and not knowledge of the noise source itself, i.e., an agnostic measure of the noise impact. Without loss of generality we restrict ourselves to the original two dimensional OAM subspace of the Hilbert space of photon A so that the density matrix can be written as

$$\rho=p\,\left\vert \Psi \right\rangle \left\langle \Psi \right\vert+\frac{1-p}{4}{{\mathbb{1}}}_{4},$$
(3)

and \({{\mathbb{1}}}_{4}\) is the 4 × 4 identity matrix on the tensor product of the Hilbert space of photon B and the subspace of photon A that we restrict to. See the supplementary information for an explicit account. The purity of this state is given by \(\gamma=\,{{\mathrm{Tr}}}\,({\rho }^{2})={p}^{2}+\frac{1-{p}^{2}}{4}\) with p ∈ [0, 1], e.g., a pure state (\(\left\vert \Psi \right\rangle \left\langle \Psi \right\vert\)) for p = 1 and a maximally mixed state (\(\frac{1}{4}{{\mathbb{1}}}_{4}\)) for p = 0. To calculate the Skyrmion number we must determine the effect of the noise on the quantum Stokes parameters, whose action is to produce new parameters, \({S}_{i}^{{\prime} }\).

The proposed noise rejection mechanism can be understood if we consider the spectral decomposition of the Pauli observables, given by \({\sigma }_{B,i}={\lambda }_{i}^{+}{P}_{i}^{+}+{\lambda }_{i}^{-}{P}_{i}^{-}\) where \({P}_{i}^{\pm }=\left\vert {\lambda }_{i}^{\pm }\right\rangle \left\langle {\lambda }_{i}^{\pm }\right\vert\) for positive and negative eigenvalues λ± = ±1, thus

$${S}_{i}^{{\prime} } = {{{\mathrm{Tr}}}}_{B}\left({P}_{i}^{+}\left[{p}_{A}\langle {{{\bf{r}}}}| \Psi \rangle {\langle \Psi | {{{\bf{r}}}}\rangle }_{A}+\frac{1-p}{2}{\mathbb{{1}_{2}}}\right]\right)\\ -{{{\mathrm{Tr}}}}_{B}\left({P}_{i}^{-}\left[{p}_{A}\langle {{{\bf{r}}}}| \Psi \rangle {\langle \Psi | {{{\bf{r}}}}\rangle }_{A}+\frac{1-p}{2}{\mathbb{{1}_{2}}}\right]\right) \\ =({I}_{i,{{{\rm{pure}}}}}^{+}+{I}_{i,{{{\rm{noise}}}}}^{+})-({I}_{i,{{{\rm{pure}}}}}^{-}+{I}_{i,{{{\rm{noise}}}}}^{-}),$$
(4)

where \({I}_{i,{{{\rm{pure}}}}}^{\pm }={{{\mathrm{Tr}}}}_{B}\left({P}_{i}^{\pm }{p}_{A}\langle {{{\bf{r}}}}| \Psi \rangle {\langle \Psi | {{{\bf{r}}}}\rangle }_{A}\right)\) and \({I}_{i,{{{\rm{noise}}}}}^{\pm }=\frac{1-p}{2}{{{\mathrm{Tr}}}}_{B}\left({P}_{i}^{\pm }{\mathbb{{1}_{2}}}\right)=\frac{1-p}{2}\). This exposes a subtle point: the noise rejection mechanism stems from subtracting measured values of the projections \({P}_{i}^{\pm }\), which each contain the same noise contribution, \({I}_{i,{{{\rm{noise}}}}}^{+}={I}_{i,{{{\rm{noise}}}}}^{-}\). This invariance is depicted in Fig. 2b where the Skyrmion number remains constant in the presence of noise despite the decay of the initial state, quantified by a decrease in typical entanglement witnesses. Normalizing each of the \({S}_{i}^{{\prime} }\) parameters by \({S}_{0}^{{\prime} 2}={{{\mathrm{Tr}}}}_{B}\) (A〈r∣ρ∣r〉A) reveals the smooth deformation that takes place under the addition of this noise to the system. Without this normalization it can be shown that \(\mathop{\sum }_{i}^{3}{S}_{i}^{{\prime} 2}=\frac{4{p}^{2}}{{(p+1)}^{2}}\le 1\) which reveals that photon B’s state is mapped to a state on a shell in the interior of its Hilbert space (a unit two sphere), with a radius dictated by the purity of the state, as depicted in Fig. 2c. This does not change the topology: \({{{{\mathcal{R}}}}}^{2}\) still maps to a sphere \({{{{\mathcal{S}}}}}^{2}\), albeit one of a smaller radius, with the same Skyrmion number. When the state is maximally mixed, \(\gamma=\frac{1}{4}\), the calculated Skyrmion number vanishes as the radius of the shell has reduced to zero. In this singular limit \({{{{\mathcal{R}}}}}^{2}\) maps to a single point, depicted in Fig. 2c, consistent with the fact that when there is no entanglement, there can be no non-trivial topology43. Importantly, this analysis does not assume anything about the initial pure state under investigation. Thus the texture, controlled via a change of polarization basis or relative phase, δ, and initial topology of the state does not play a role in ensuring that the topology of the state remains invariant. The topology remains robust to the noise so long as some entanglement persists.

In the interest of creating a useful topological alphabet within a practical setting, in what follows we focus on states with ∣N∣ > 0. The motivation is that all topological states are entangled, but not all entangled states are topological. Thus states with N = 0 with no topology may or may not be entangled, negating the benefit of entanglement distributed information, and further, a topological detection scheme would not be able to distinguish between pure states and completely mixed states when N = 0.

Experiment

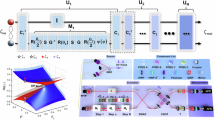
To verify the concept we use the experiment depicted in Fig. 3a, with full details given in the SI. Entangled OAM biphotons of wavelength 710 nm were generated through spontaneous parametric down-conversion (SPDC) in a 3 mm long Type-I Barium Borate (BBO) nonlinear crystal pumped by a 355 nm wavelength collimated Gaussian beam. A spiral bandwidth measurement (top left inset) was performed from which a Schmidt number of K = 11 was calculated25. This allows for hybrid state generation with OAM order as high as ℓ = ±5. To achieve our topologically non-trivial states we used the spatial-to-polarization coupling (SPC) state preparation stage, exchanging the OAM-OAM correlations between photons A and B for OAM-Polarization correlations. To do so, Photon A was left unaltered while photon B’s spatial information was coupled to its polarization using a double bounce off a spatial light modulator (SLM B). The incoming horizontally polarized photons were modulated in the first pass and the vertically polarized photons in the second (by splitting the SLM screen in two parts), with the quarter-wave plate (QWP) serving to accommodate the fact that the SLM can only modulate horizontally polarized light. For non-trivial topologies the holograms displayed on SLM B were set such that ∣ℓ1∣ − ∣ℓ2∣ ≠ 0. It should be noted that while this approach allowed for the dynamic selection of a desired hybrid state, it came at the cost of efficiency which limited the creation of hybrid states to OAM values ∣ℓ∣ ≤ 3. However, these losses may be mitigated by more compact and efficient methods of dynamic spin-orbit coupling techniques50,51. In the detection stage, photon A was directed to a spatial light modulator (SLM A) for spatial projective measurements while photon B was passed through a HWP orientated to 45∘ and a linear polarizer orientated at 90∘ for polarization projective measurements. Both photons were collected by single-mode fibres (SMFs) coupled to an avalanche photon detector (APD) and measured in coincidence. Six projective measurements on each photon allowed for an overcomplete quantum state tomography (QST) with 36 entries, which was used to reconstruct the quantum state (with and without noise), with full details given in the SI. Initially, the experiment was run without noise to certify the creation and detection of the example state \(\left\vert \Psi \right\rangle=\frac{1}{\sqrt{2}}\left({\left\vert 1\right\rangle }_{A}{\left\vert H\right\rangle }_{B}+{\left\vert 0\right\rangle }_{A}{\left\vert V\right\rangle }_{B}\right)\). Figure 3b shows the reconstructed density matrix and 3c non-local topology of the state with a Neél-type Skyrmion texture, adopting the convention Sz = S1 (See SI for full details on vector textures). The data is in agreement with the results expected from the desired pure state, with a purity of γ = 0.80 and Skyrmion number N = 0.96 ± 0.01 (theory: N = 1). To introduce noise we used an incoherent light source of variable intensity, which is known to be a good approximation to isotropic noise15. The contribution of the white light source to the final state was determined from the average quantum contrast, Qc, which estimated the signal-to-noise (SNR) ratio in our system (See SI for full details), reaching values as high as 32.3 and as low as 2.24 for low and high levels of noise, respectively. This impacts directly on the purity of the state following \(\gamma=\frac{1}{4}\left[3{\left(\frac{{Q}_{c}-1}{{Q}_{c}+1}\right)}^{2}+1\right]\), which we used as a measure of the impact of the noise, ranging from our target pure state (no noise, Qc ≫ 1) to a maximally mixed (separable) state (high noise, Qc ≈ 1). In Fig. 4 the experimentally obtained purity is plotted against average quantum contrast and is in excellent agreement with theory with a calculated mean-squared error of 0.02, with minor deviations occurring at higher noise levels likely occurring from random noisy detector contributions and small fluctuations between projective measurements which are averaged over to determine the quantum contrast for a single state. This demonstrates that precise control over the experimental purity was achieved through control over the quantum contrast of the system. Moreover, as the impact of the noise was characterized based on how it affected the state and quantified using a universal metric, Qc, we expect our model and experiment to remain agnostic to the origin of the noise whether that be the entanglement source, the detectors or the channel, thus emphasizing the applicability of our results to real world scenarios.

Fig. 3: Experimental generation of quantum skyrmions.
figure 3

a Experimental setup for the generation, preparation and detection of non-local skyrmionic quantum states, with details given in the main text and Supplementary Information. The desired hybrid states are prepared via a spatial-to-polarization coupling (SPC) technique. A spiral bandwidth measurement (shown as an inset) reveals the available OAM modes in the initial high-dimensional entangled state. To confirm the system performance we show b the reconstructed experimental density matrix and, c non-local topology for the ideal example state, \(\left\vert \Psi \right\rangle=\frac{1}{\sqrt{2}}\left({\left\vert 1\right\rangle }_{A}{\left\vert H\right\rangle }_{B}+{\left\vert 0\right\rangle }_{A}{\left\vert V\right\rangle }_{B}\right)\). Abbreviations: Barium Borate (BBO), band-pass filter (BPF), 50:50 beam splitter (BS), lens (L), spatial light modulator (SLM), avalanche photodiode (APD), single mode fibre (SMF), coincidence counter (CC), half-wave plate (HWP), quarter-wave plate (QWP), linear polarizer (LP).

Full size image
Fig. 4: Noise characterization.
figure 4

Purity as a function of quantum contrast, with theory (dashed lines) and experiment (points) in good agreement. The inset is used to show the error bars from the experiment derived from Poissonian statistics. We use quantum contrast as our measure of the noise impact as it is agnostic to the noise source.

Full size image

The experiment was run for six different initial states with varying topology, N ∈ { − 3, − 2, − 1, 1, 2, 3}, and textures: Neél-type (N = 1), anti-skyrmion (N = −1) and higher-order Skyrmions (N > 1) and anti-skyrmions (N < −1), each for a wide range of isotropic noise levels, and in each case the quantum Stokes parameters inferred from a quantum state tomography. Example data is shown in Fig. 5a–c for the states \(\rho=p\left\vert \Psi \right\rangle \left\langle \Psi \right\vert+\frac{1-p}{4}{{\mathbb{1}}}_{4}\) where \(\left\vert \Psi \right\rangle=\frac{1}{\sqrt{2}}\left({\left\vert 3\right\rangle }_{A}{\left\vert H\right\rangle }_{B}+{\left\vert 0\right\rangle }_{A}{\left\vert V\right\rangle }_{B}\right)\) in the presence of varying isotropic noise levels from pure (point 1, γ = 0.80) to partially-mixed (point 2, γ = 0.45) and then maximally mixed (point 3, γ = 0.25). As expected the QST data shown in Fig. 5a reveals a constant noise contribution across all projections within a single QST measurement, further indication of the isotropic nature of the noise as the contribution of noise is independent of the type of polarization and spatial projection performed. Furthermore, the QST reveals a characteristic saturation of each projection measurement with an increase in isotropic noise. This is accompanied by a clear transition of the density matrix describing a pure state (entangled) to that describing a maximally-mixed state (no entanglement) as shown in Fig. 5b. The quantum Stokes vector, \(\overrightarrow{S}(x,y)={({S}_{x},{S}_{y},{S}_{z})}^{T}\), derived from each density matrix is plotted in Fig. 5c. As expected, the magnitude of the quantum Stokes vector diminishes with decreasing purity (increasing noise), until it collapses to a point with zero magnitude. The Skyrmion number for these three states (1–3) was calculated to be N = 2.99 ± 0.01, N = 2.99 ± 0.01 and N = 0.01 ± 0.01, respectively, revealing that the skyrmion number remains intact until the entanglement vanishes altogether.

Fig. 5: Experimental verification of topological resilience.
figure 5

a QST results for the example state \(\left\vert \Psi \right\rangle=\frac{1}{\sqrt{2}}\left({\left\vert 3\right\rangle }_{A}{\left\vert H\right\rangle }_{B}+{\left\vert 0\right\rangle }_{A}{\left\vert V\right\rangle }_{B}\right)\) in the presence of varying noise levels from pure (point 1, γ = 0.80) to partially-mixed (point 2, γ = 0.45) and then maximally-mixed (point 3, γ = 0.25). b The experimental density matrices extracted from the QST of each state. c The quantum Stokes vector, \(\overrightarrow{S}(x,y)={({S}_{x},{S}_{y},{S}_{z})}^{T}\), derived from each density matrix corresponding to points 1 to 3 in part a. d Skyrmion number as a function of quantum contrast, with experiment (points) in excellent agreement with theory (dashed lines). The collapse of the topology when the maximally-mixed state limit (Qc = 1) is reached is shown in the zoomed-in inset. e While the Skyrmion number is stable to noise, typical entanglement witnesses such as concurrence, fidelity and purity are not, as shown experimentally (points) and theoretically (lines).

Full size image

Figure 5d shows data for the rest of the entangled states considered. The theoretical (dashed lines) and experimental (points) results for the Skyrmion number as a function of quantum contrast are in excellent agreement across all topologies, providing further evidence for topological robustness across all topological classes. The zoomed inset shows experimental data near the classical limit where it is clear that a topological transition from N ≠ 0 to N = 0 occurs because without entanglement there can be no topology. This robustness of the topological observable is in stark contrast to the decay of typical entanglement witnesses such as concurrence, fidelity and state purity (See SI for the definitions of these quantities), as shown in Fig. 5e using the same example state as that used in Fig. 5a–c. While each of the entanglement witnesses decay continuously until they each reach their expected minima for a 2D maximally mixed state (C = 0, F = 0.25, γ = 0.25), the Skyrmion number remains intact regardless of the degree of noise present, only decaying once the state is maximally mixed.

We can further visualize this in Fig. 6, where we show the ideal topology without noise along side that with noise, for three Skyrmion numbers. We see that the topology remains unchanged as noted by the position, length and orientation of the vectors, resulting in an almost unchanged Skyrmion number that is in excellent agreement with the ideal case (within experimental uncertainty). The insets show one zoomed in vector from each sphere to confirm the equivalence.

Fig. 6: Invariance of topology to noise.
figure 6

The topology of the ideal (Topology without noise) and experimentally retrieved state after passing through the noisy channel (Topology with noise), shown as stereographic projections of the state vectors (normalized to aid visualization) of photon B on a sphere. The experimental state vectors exhibit minimal deviation from the ideal case as the noise acts only to scale the vectors, not to change their orientation. The calculated Skyrmion number is given for each case, confirming the robustness and the conceptual picture of Fig. 2b.

Full size image

Discussion

Typical quantum information encoding schemes rely on the entanglement of non-separable quantum states, a resource that is highly vulnerable to noise, as we have shown. In contrast, we propose encoding quantum information into robust topological observables of entangled states. Despite being rooted in the state’s entanglement, these topological features remain entirely intact, even as the state itself degrades when transmitted through a noisy channel. Our approach to noise rejection can be understood in the context of information digitization, where continuous analogue signals are replaced by a discrete signal of bits through binning, e.g., by declaring signals below some threshold as 0 and those above it as 1. At the quantum level, employing discrete subsystems represented as qubits does not achieve the desired discretization. The basic quantum resource, entanglement, is encoded in correlations between the subsystems and simply using subsystems with a finite number of states does not render these correlations discrete. We moot that the topology of the wavefunction with its associated discrete observable naturally achieves this. Why is the discretization of entanglement interesting? Discrete signals are always more robust against the effects of noise. This follows because for discrete signals the noise can’t produce an arbitrarily small perturbation of the signal: the noise must be able to flip the signal between two discrete states before any effect is registered. In the same way that digital signals enabled successful classical computation and communication, digital quantum signals may allow successful quantum computation and communication. Given a discretization scheme, it then becomes urgent to establish that noise is not able to drive the jumps between discrete states that would corrupt the discrete signal. The importance of our work is that, for a physical and realistic source of noise, we have been able to demonstrate this.

Skyrmionic photonic topologies have been celebrated for their potential to act as resilient information carriers37, with some convincing experimental results shown for the resilience of classical optical skyrmions under known operations with optical elements44. This report offers, to the best of our knowledge, the first experimental results on the resilience of quantum skyrmions to noise, confirming that such quantum channels are map preserving: they can be viewed as a smooth deformation of the state (map) and thus preserves topology even when the entanglement itself is decaying. Moreover, the isotropic model employed in this work makes no assumptions about the photons’ degrees of freedom and can be extended to investigate its impact on higher-dimensional states. This enables the exploration of topological properties distributed across distances in diverse higher-dimensional entangled states in the presence of noise. We believe that this noise rejection by topology mechanism could be exploited in practical quantum information processing and communication protocols, e.g., quantum communication under ambient (daylight) conditions, or quantum computing on noisy photonic chips, and could be used in conjunction with the entanglement preserving strategies mentioned in the introduction for preservation of entanglement and information. The demonstrated resilience comes without the need for error mitigation or state purification techniques, thus offering an approach to quantum information resilience in realistic and non-ideal conditions.

In conclusion, we have shown both theoretically and experimentally that quantum skyrmions and their topological quantum observables remain resilient to isotropic noise, a generic form of quantum noise that captures realistic effects from the source, channel, and detector, e.g., multi-photon events, dark counts, shot and thermal noise, background light (e.g., daylight) and lost photons. We present experimental results across various topologies (up to orders N = ±3) and for a wide range of noise levels, confirming the topological invariance and only collapsing once there is no entanglement at all. We show that traditional quantum measures decrease continuously under the same conditions, highlighting the advantage of discrete rather than continuous observables. Our work opens a pathway to quantum information processing and communication in noisy quantum systems and channels without the need for compensation or mitigation strategies.